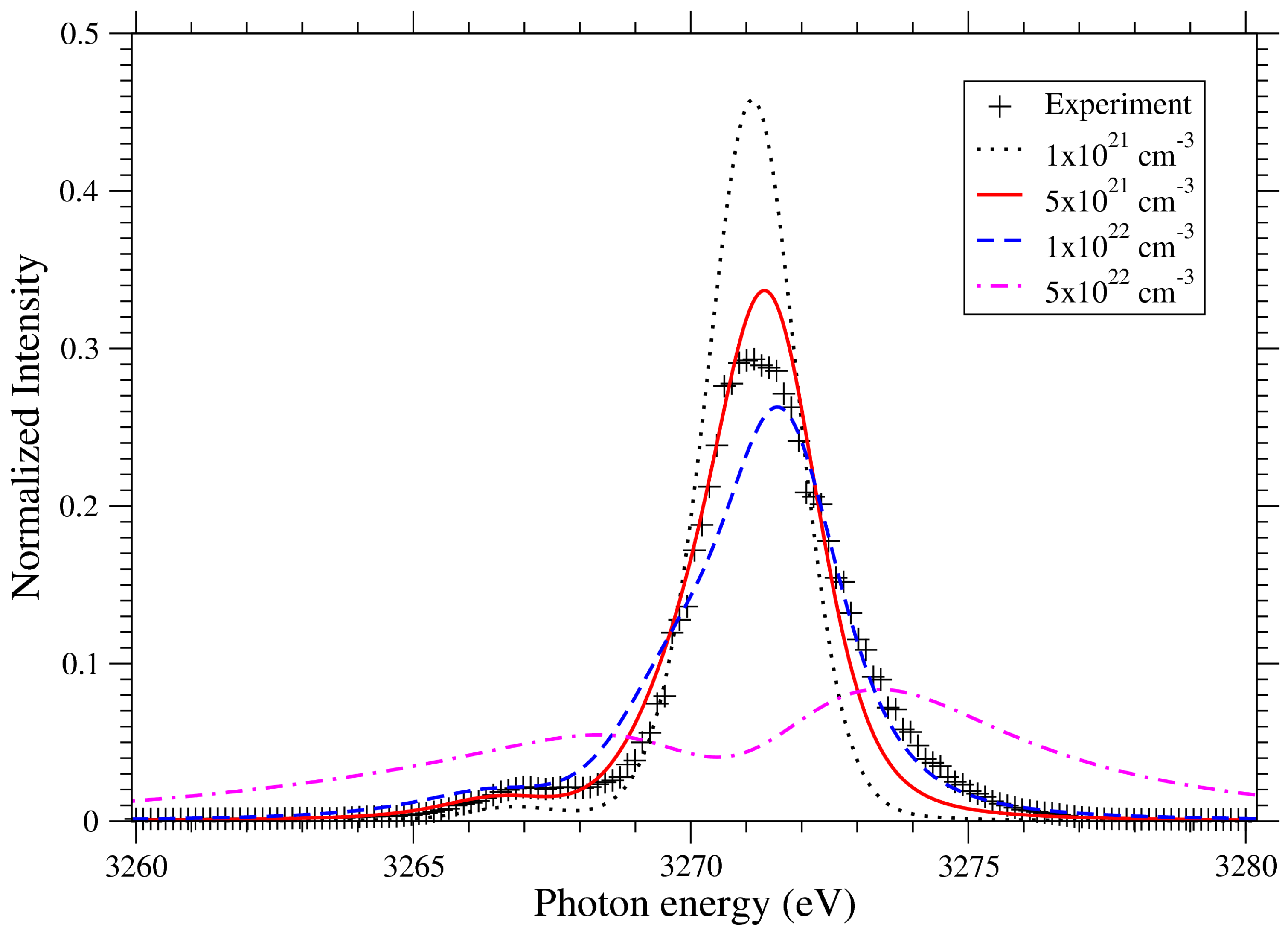
2.1. Quasi-Static and Binary Collision Approximations for Stark Effect
In general, microfields generated by ion and electron perturbers evolve on different time scales because of their relative mass. Since the typical fluctuation rate of the electron field is greater than for ions by at least two orders of magnitude, one can often separate the contribution of both species: ions are considered as quasi-static during the emission process, whereas electrons are dynamic and treated as fast binary interactions with ions. The
impact approximation for electrons assumes that the collisions are complete during the time of interest and is thus valid only near the center of the profile. This approximation may be softened by using a
binary collision relaxation theory which can account for incomplete collisions, resulting in a frequency-dependent electron broadening operator (see
Section 2.2) which preserves the static limit in the far wings. Moreover, the
quasi-static approximation being valid only in the wings of the profile (large frequency detuning or small time interval), corrections due to
ion-dynamics effects must be taken into account near the center of the line since this corresponds to radiation over time long enough for the ions to move (see
Section 2.4).
The quasi-static line shape profile is given by:
where
is the normalized probability that the emitter undergoes the static-ion field
F. The field-dependent profile reads:
where
is the Liouville operator associated to the electron-radiator Hamiltonian
,
is the normalized radiator density operator,
d is the radiator dipole operator,
is the electron broadening operator and
C is a constant factor ensuring the normalization of the spectral profile.
The trace in Equation (
2) represents the average of the inverse Fourier Transform of the system’s dipole-dipole autocorrelation function. It must be performed on the product of matrices
,
and
which involve tetradic operators, i.e., acting on four sets of internal states of the emitter corresponding to two initial and two final states. The inversion of matrix
A in the complex domain is one the most time-consuming task in a line-shape code. In order to speed up the calculations, we make the following assumptions. First, perturbers are not allowed to induce a transition between the lower and upper states involved in the radiator emission process (no-quenching approximation). We only consider linear Stark effect, so that the electron-radiator Hamiltonian reads
,
being the unperturbed (no field) Hamiltonian. We assume that only states belonging to the same Layzer complex (see
Section 3 for definition) may be mixed by Stark and/or Zeeman effects (
interaction channels). The broadening operator
is calculated to the second-order in the radiator-electron interaction (dipole approximation). The imaginary part of
, which corresponds to small plasma-generated static level shifts, is neglected. We also neglect the interference terms between upper and lower states in
. It is important to mention that we plan to relax some of these approximations in future versions of the code (see discussions in
Section 4).
Since the trace is invariant under any unitary transformations, it is more convenient to use the matrix
that diagonalizes the Liouville operator,
, where
is a diagonal matrix in the dual space, with matrix elements noted
corresponding to the energy of the Stark component
. Numerical computations can use the fact that the matrix associated to
L is real and symmetric, yielding a real transformation matrix
that can be easily computed and inverted (by taking its transpose
). The problem is that the broadening operator
is not diagonal with the eigenfunctions of
L in general, i.e., when applying the transformation:
. For the conditions where homogeneous broadening is small compared to the inhomogeneous broadening produced by the static ions [
12], it is, however, possible to neglect the off-diagonal matrix elements of
and to retain only the diagonal matrix elements denoted by
(this approximation will be relaxed in future versions of the code with the consideration of the interference terms). With all the above hypothesis, the trace can now be evaluated by the expression
which involves easy inversion of a diagonal matrix. If we denote by
the set of orthogonal wave-functions in the new basis, the line shape (
2) can be simplified to the expression:
The normalization factor, , is the total line strength of the transitions, which is invariant under any unitary transformation (it may be evaluated with the unperturbed wave-functions).
The calculation of matrix elements of Liouville, dipole and electron broadening operators in the new basis requires knowledge of matrix elements of these operators between unperturbed (no field) wave-functions, denoted by
. For an arbitrary operator
O, we have:
where
are the eigenvectors of the unitary transformation (each column of matrix
). In practice, we use an external atomic database generated with the multi-configuration Dirac-Fock code MCDF [
13] or the cFAC code [
14,
15]. The data stored are: the total angular momentum
J, energy, parity and configuration label for a collection of levels related to the unperturbed Dirac Hamiltonian
; and the signed reduced matrix element for electric-dipole (E1) and magnetic-dipole (M1) [See
Section 2.3] transitions between these levels. The use of Wigner-Eckart theorem allows one to compute the matrix elements
from the corresponding reduced-matrix elements in the database. For instance, the dipole matrix elements of the Stark Hamiltonian
between two unperturbed states read:
where
is the Bohr radius,
is the spherical harmonic tensor operator of rank 1, and using a level description based on the total angular momentum
J, its projection
M and some other quantum numbers
to account for Pauli exclusion principle. For hydrogenic emitters, the required atomic data (energies, reduced matrix elements) may be evaluated directly using analytical formulas [
16]. It is worth mentioning that perturbers (ions or electrons) are assumed to produce a randomly oriented microscopic field, so that the emission spectrum is not polarized in general. The quantization axis may be thus chosen arbitrarily.
As concerns the population of states, , we have different options:
Local Thermodynamics Equilibrium (LTE):
where
is the Boltzmann constant and
is the electron temperature.
Statistical Weight Approximation (SWAP):
where
g is a constant factor ensuring that
. This corresponds to the high-temperature limit of LTE plasmas.
Non-Local Thermodynamics Equilibrium (non-LTE):
where the populations of states
are derived from results of an external collisional- radiative model [
10] which do not account for the splitting of levels by Stark effect (the CR model is based on degenerate levels). Denoting by
the non-LTE probability of the parent level of state
j, we use a SWAP assumption within each level:
where
is the total angular momentum of the level.
We have the possibility to include other homogeneous broadening mechanisms: Doppler effect, natural width, autoionization or any other radiative or collisional processes in the plasma limiting the lifetime of states. Lifetime of states is estimated from collisional-radiative calculations by using the diagonal terms of the rate matrix. If we assume that the matrix elements of the electron broadening operator do not depend on the photon frequency
(it is evaluated at the line center, i.e., impact approximation: see
Section 2.2), then the convolution of expression (
2) with other Lorentzian or Gaussian functions leads to a sum of Voigt functions (see
Appendix A). The integration over the ion microfield distribution in (
1) may be readily estimated by a sum over a well-chosen set of field values. As a result, the quasi-static line shape can be written in compact form as a sum of Voigt profiles arising from different Stark components and different ion field values,
where the normalized weight factors
(such that
) include the probability of the ion microfield and the strength of the relevant Stark component of energy
. The width parameters of the Voigt functions are defined by:
where
is the ion temperature,
is the ion mass,
is the intrumental FWHM (possibly taking into account the spectral resolution of the spectrometer in an experiment),
is the electron impact width and
is an additional homogeneous broadening width (natural, autoionization, etc.).
2.2. Electron Broadening Operator
The main contribution in
comes from weak electron collisions of duration much shorter than the inverse HWHM of the profile, i.e., much shorter than the decay timescale of the dipole autocorrelation function. Using the perturbation theory up to the second-order in the radiator-electron interaction, we obtain for the Maxwell-averaged operator:
where
is the detuning frequency from line center,
m is the electron mass,
is the electron density. There are many ways to estimate the
G-function. It may be related to charge-density fluctuations in the plasma by using the dielectric constant
of an equilibrium plasma as follows [
17]:
where
is the wavenumber associated to the momentum transfer in the radiator-electron collision. The dielectric function may be estimated in the Random-Phase Approximation for a Maxwellian plasma [
18],
where
is the inverse of the Debye length
1,
and
is the Dawson function. A cutoff
is introduced in order to limit the momentum transfer due to close (and strong) collisions and to avoid the divergence of the integral. For hydrogenic ions of charge
Z, radiating from the upper shell of principal quantum number
n, we use:
The numerical evaluation of the integral (
9) is however rather painful. Following the model of Lee [
19], it is possible to approximate this cumbersome integral by an analytic expression using the asymptotic limits of the G-function at
and
:
where
and
is the exponential integral of first order and
is the plasma frequency.
The semiclassical GBK model [
20] yields a
G-function which is slightly different from Lee’s model, in particular near the center of the line:
where Ryd is the Rydberg energy. Using the same cutoff expression (
11), we may rewrite the above formula as:
which is equivalent to Lee’s formula
when
.
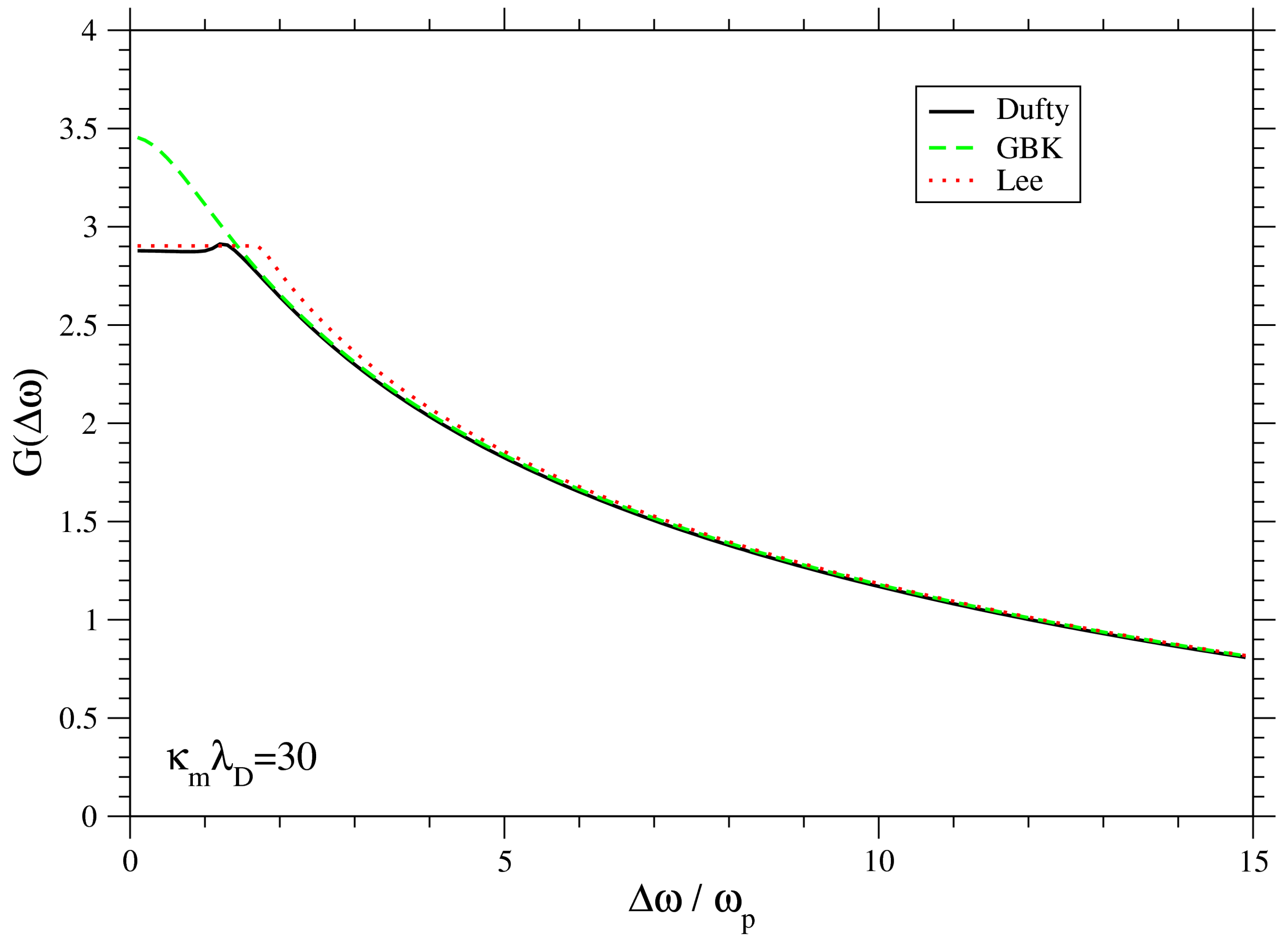
A comparison of the
G-functions computed for
with different methods and approximations is shown in
Figure 1. The
G-function is obtained: (i) numerically from Equations (
9)– (
11) for Dufty’s model; (ii) Equations (
12) and (
13) for Lee’s model; (iii) by Equation (
15) for GBK. In Dufty’s model, we observe a saturation of the
G-function at low detuning: this is due to the fact that the exchange of electromagnetic energy
between the electron subsystem and the radiator is inefficient below the plasma frequency for a classical plasma. We note that this behaviour is well reproduced by the approximate model of Lee, but not in GBK. The discrepancy with the GBK model amounts to roughly
near the center of the line, whereas all models have the same asymptotic behaviour for large detuning. We have plotted in
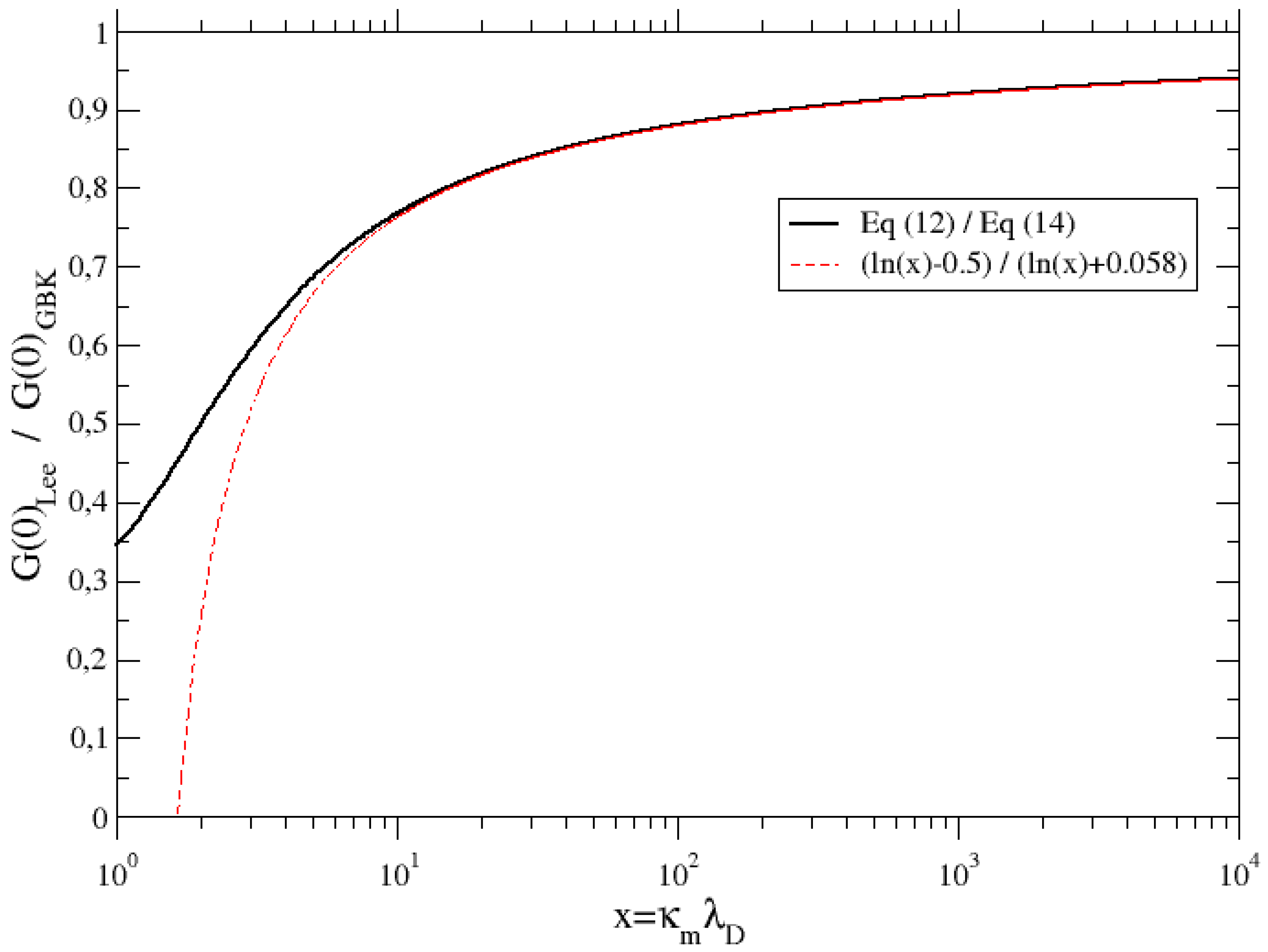
Figure 2 the ratio of the electron impact widths at the line center, obtained with the model of Lee and the model of GBK, as a function of the parameter
. The latter quantity represents the ratio of maximal over minimal impact parameters for the electron-radiator collision. As we can see, both models agree only when
(low-density and/or high-temperature limit). We observe a discrepancy of less than
for
. For smaller parameters, the differences can go up to a factor of 3; however, the validity of semiclassical approaches is questionable as
tends to one.
For classical plasmas (low-density and high-temperature limit), the parameter
is often very large so that one can further simplify the expression of the
G-function. In the limit
, it is easy to show that both models (GBK and Lee) yield an electron collision width depending on the Coulomb logarithm
2, as expected in the impact approximation:
for the GBK model (
is the Euler’s constant) and
for the model of Lee. The noticible difference is the factor
which explains why Lee’s model yields smaller impact widths than GBK in general (see dashed curve in
Figure 2).
The collisions whose impact parameter is lower than the cutoff
cannot be treated in the framework of the perturbation theory. To account for these so-called
strong (or close) collisions, which are missing in the above models, a constant term
is added to the
G-function as suggested in the reference [
20],
where
n is the principal quantum number of the active electron,
,
,
,
,
for
.
Neglecting the interference terms, the diagonal matrix elements of the broadening operator read:
This frequency-dependent expression is used only when the line shape is evaluated through Equations (
1) and (
3). When the Doppler effect is taken into account, we introduce the approximation
so that the line shape reduces to a simple sum of Voigt functions, as seen in Equation (
6). This approximation is also necessary in our implementation of the FFM ion-dynamics approach (see
Section 2.4).
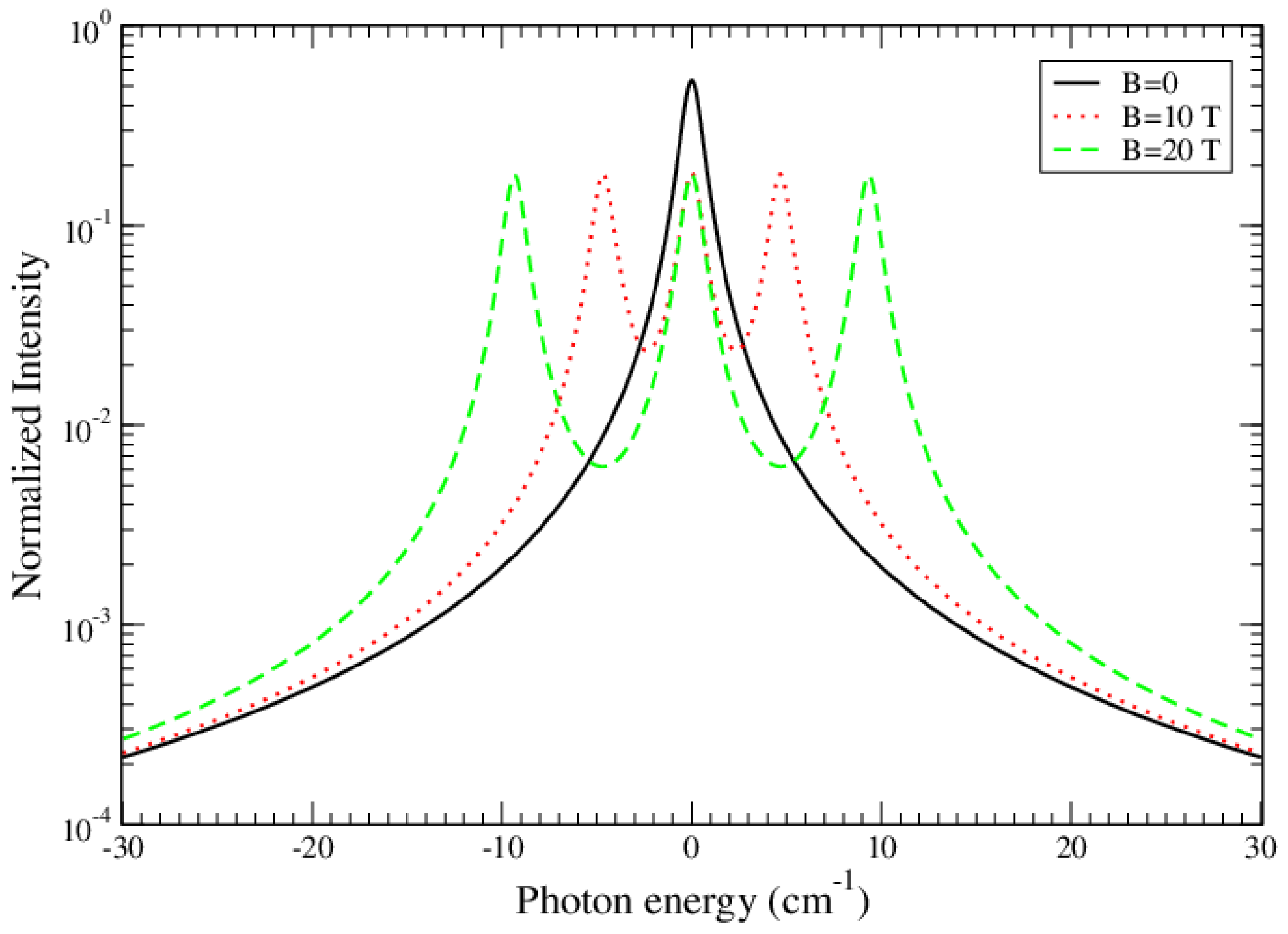
2.3. Zeeman Effect
The effect of a static magnetic field
on the emission spectrum may be taken into account in the code by adding the term
to the radiator Hamiltonian
, where
is the anomalous gyromagnetic ratio for electron spin,
is the Bohr magneton,
and
are spin and total angular momenta. In the case of a combined Stark-Zeeman calculation, the Hamiltonian to be diagonalized thus reads
, where
and
are respectively the unperturbed Hamiltonian and the Stark Hamiltonian, as introduced in
Section 2.1. This requires the calculation of additional matrix elements of the type:
The reduced matrix elements in the above expression are identical to those encountered in the calculation of magnetic-dipole transitions (M1). They are thus taken from the external atomic database, in a manner similar to the use of electric-dipole transitions (E1) for Stark effect. In principle, the code can take into account the Zeeman effect in the emission spectrum of any radiator ions (not limited to one-electron system) and for a magnetic field of arbitrary value (not limited to Paschen-Back nor weak-field limits), depending only on the ability to generate an appropriate atomic database.
A particularity of Zeeman effect is that the quantization axis is imposed by the direction of the static magnetic field, so that the emission is polarized in general. Therefore, the emission profile depends on the angle
between the direction of
and the line of sight of the observer:
where
and
. In this notation,
is the intensity calculated for a given polarization
which can take only 3 possible values:
(
polarization) and
(
polarizations). Moreover, the introduction of a preferential quantization axis breaks the spherical symmetry and the integration over the microfield becomes anisotropic and must be performed in the three directions of space [
21,
22]:
where
is the cosine of the angle
between the electric and magnetic fields.
2.4. Ion Dynamics Effects
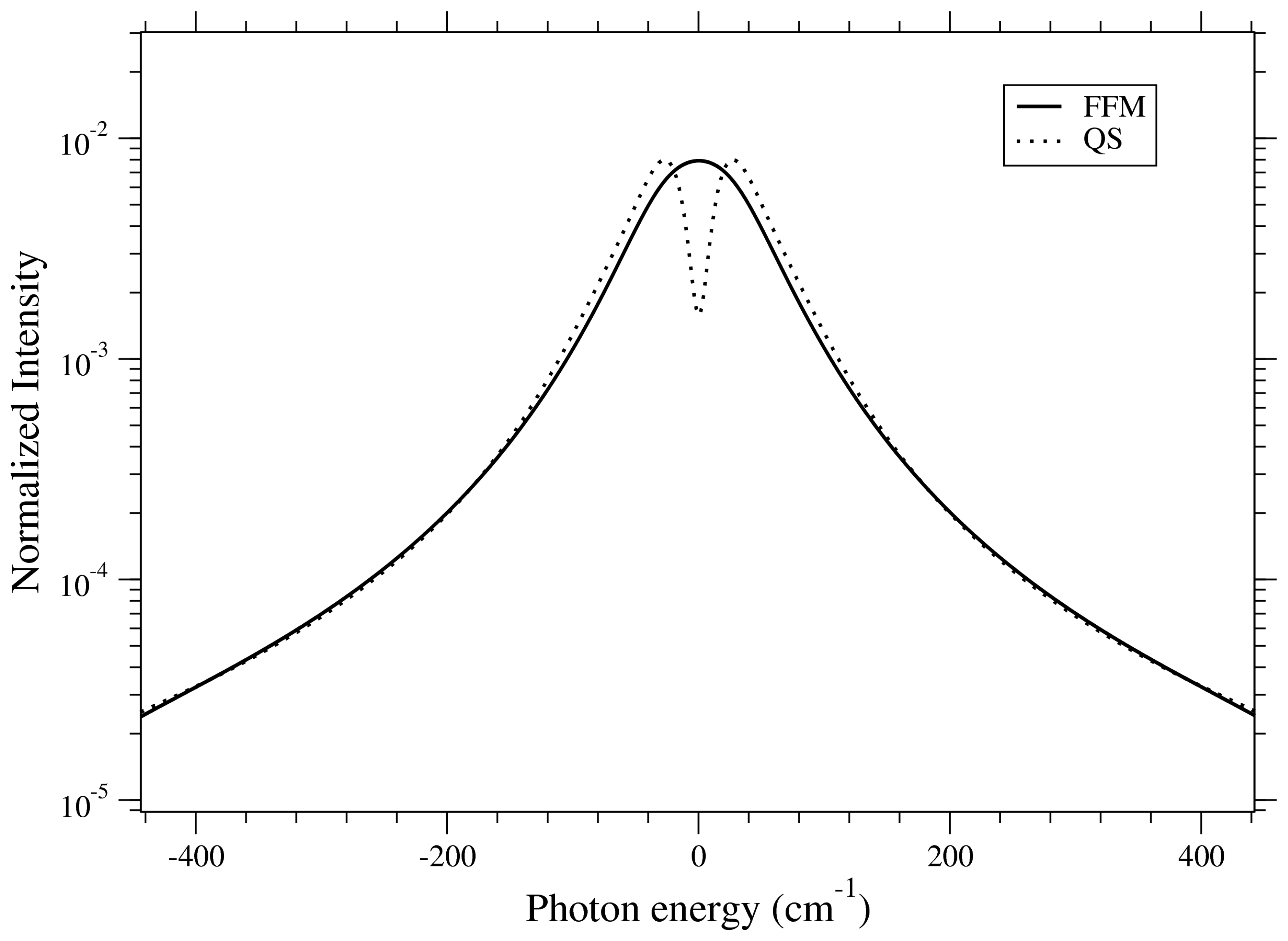
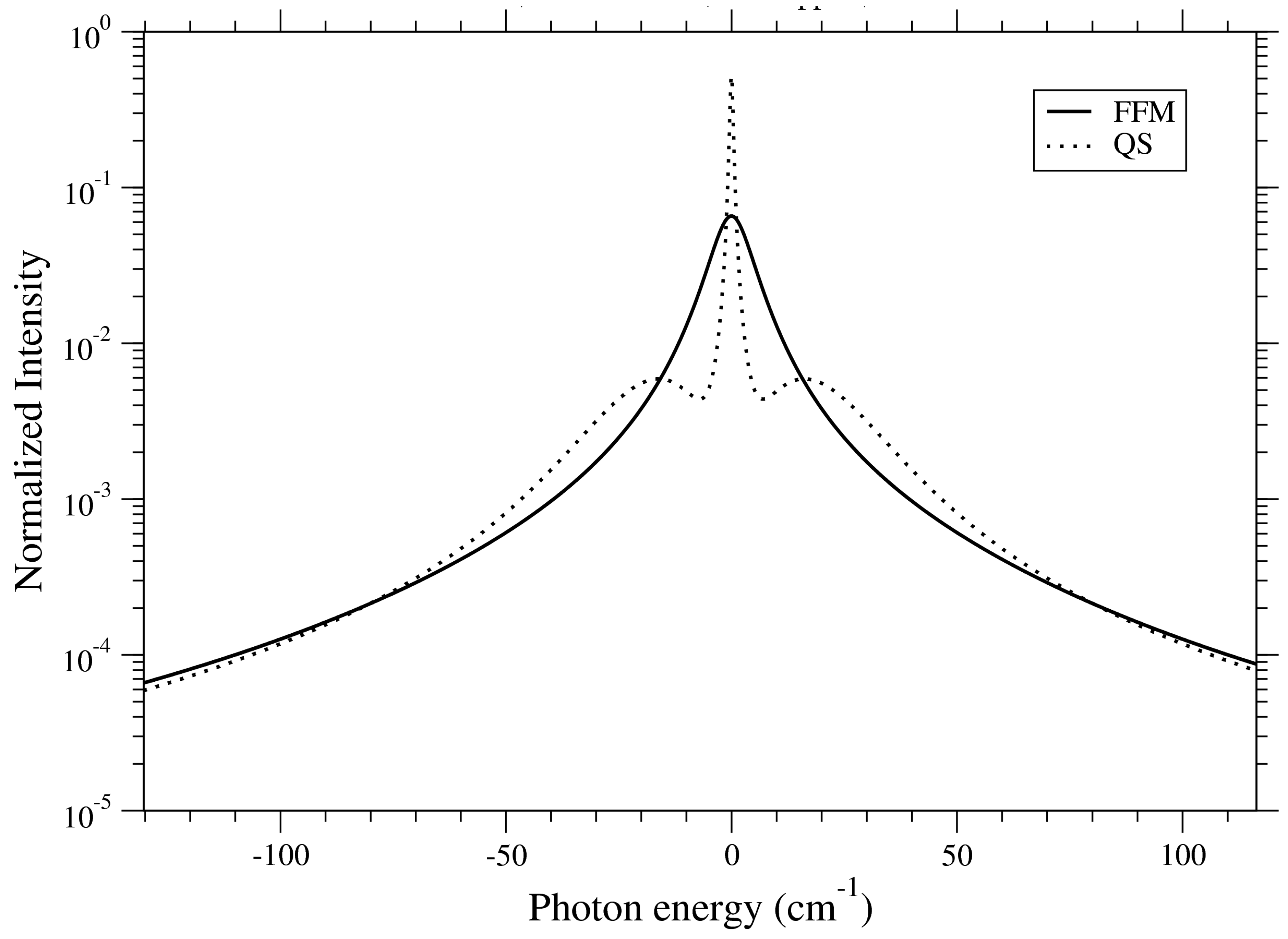
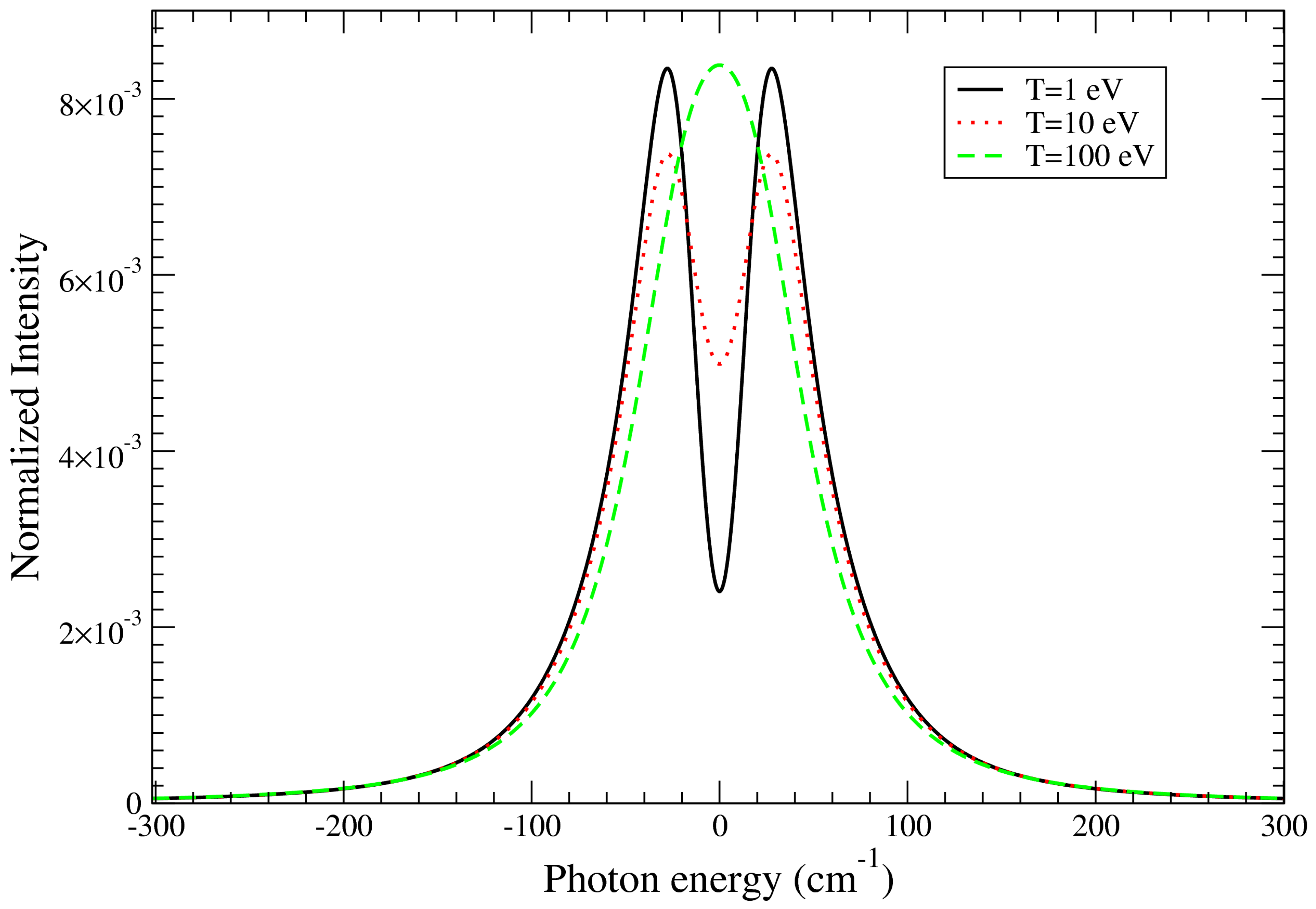
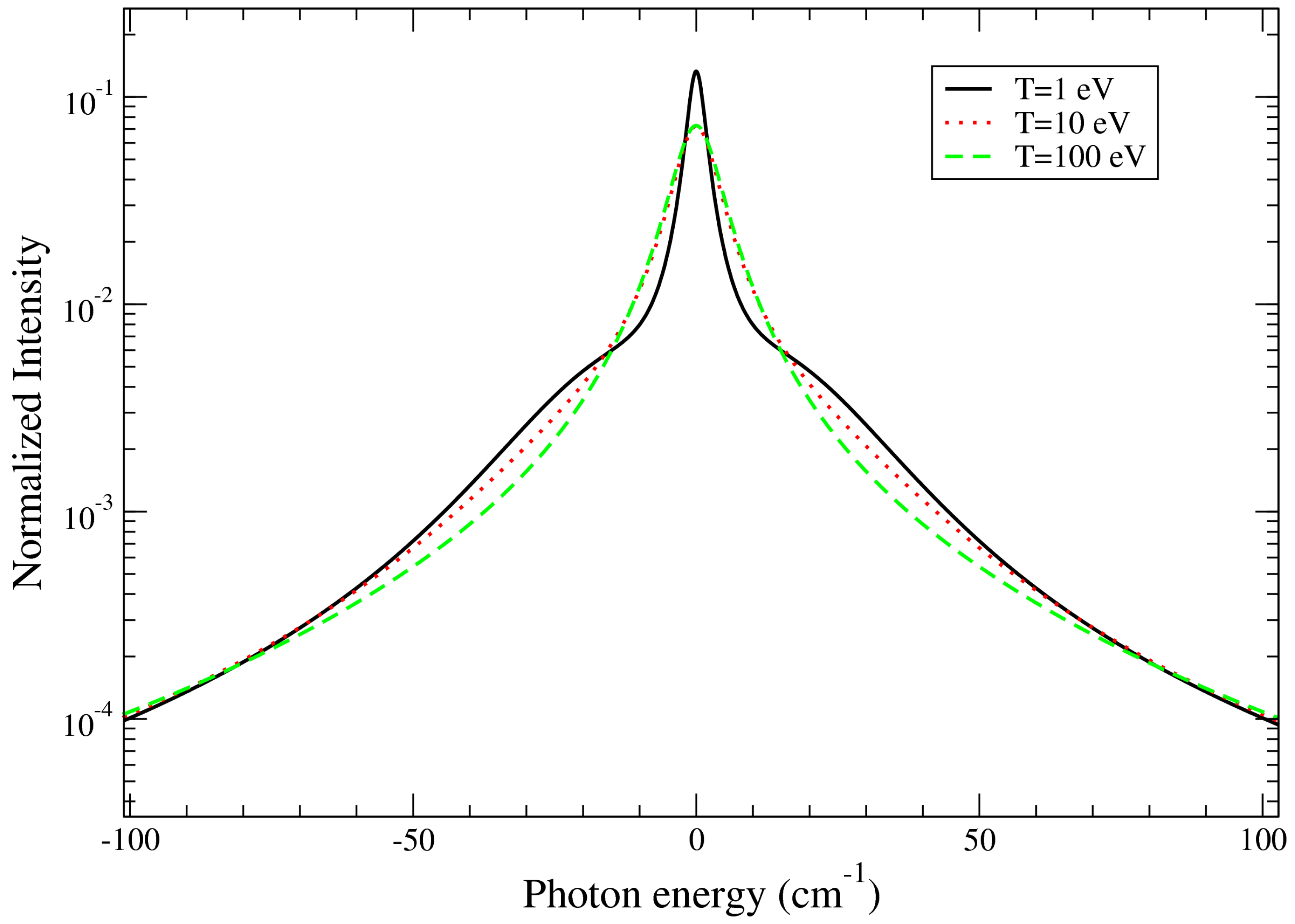
The quasi-static approximation usually breaks down near the center of the line since this region corresponds to radiation over times long enough for the ions to move. Ion dynamics effects are implemented in the ZEST code using the fast Frequency-Fluctuation Model (FFM) [
11]. The time-dependent ion field fluctuations are treated as a collision-type process causing an exchange between the quasi-static radiative channels. This mixing is modeled by a stationary Markovian process using a single relaxation rate
, characteristic of the ion field fluctuations. This rate is estimated by taking the ratio of the most probable ion velocity in the plasma (assuming a Maxwellian distribution) to the average ion-ion distance:
where
is the mean ionization of the plasma. The spectral profile accounting for the FFM ion dynamics method is given by the expression:
with:
In the above expression,
is the quasi-static line shape given by Equation (
6). If we assume that the electron broadening operator does not depend on the frequency detuning (
i.e., impact approximation), then, from Equations (
6) and (
22), we note that the function
involves the convolution of Voigt functions (i.e., the convolution of Lorentzian and Gaussian functions) with the complex function
. Taking the Fourier transform
3 of
,
and using the convolution theorem,
we obtain:
where
is the Heaviside function. Taking the inverse Fourier transform of the last expression, we obtain:
with
where
is the complex Faddeeva function [
23] which may be computed efficiently by different numerical methods. We note that the real part of
is related to the Voigt function (the latter is often evaluated this way; see
Appendix A). The Faddeeva function is frequently encountered in the theory of the Brownian motion when considering the narrowing of the Doppler broadening due to collisions (Dicke effects) [
24]. In order to avoid the manipulation of complex numbers, we use an efficient and fast routine [
25] which evaluates separately the real and imaginary parts of the Faddeeva function. Introducing the functions
and
, the dynamic line-shape profile finally reads:
In the case
, the last expression recovers the quasi-static limit as expected:
For a very high fluctuation rate, the radiator system is unable to follow the ultra-fast modulations of the ion field, and the line spectrum is expected to tend approximately to the
only electrons profile. However, it is known that the FFM approach does not reach this asymptotic form for
[
26]. In order to force the impact-approximation limit for both electrons and ions, it may be necessary to introduce a field-dependent fluctuation rate
or to use a semi-empirical amendment [
8,
27,
28] to expression (
20). One can also modify the FFM approach following the method described in reference [
29]. Another possibility is to use the Frequency Separation Technique (FST) [
30], which separates the phase space into fast and slow perturbers. In the FST method, the line shape is approximated as a convolution of two profiles: a fast component based on the impact broadening theory, and a slow component for which we can use the FFM approach.
2.5. Microfield Distribution
There are many approaches to estimate the static ion fields distribution in a plasma [
31], for instance: the expensive Molecular Dynamics simulations (MD) [
32]; more affordable numerical models like the Adjustable Parameter EXponential approximation (APEX) [
33] or the Monte-Carlo method (MC) [
34]; simple analytic formulas with a restricted domain of validity like Holtsmark (for uncorrelated plasmas), Mayer (strongly correlated plasma) or Nearest Neighbour distributions (strong fields). We need a fast and accurate description of the ion microfield distribution which covers a broad range of plasma conditions. To achieve this goal, we use analytic fits of numerous Monte-Carlo simulations (MC) which reproduce
with a great accuracy [
35]. The MC simulations were performed at a neutral or charged point using Debye quasi-particles interacting through screened Coulomb potentials. The screening length
accounts for the shielding of ion-ion interactions by a constant neutralizing electron background. In the MC simulations, a plasma configuration is represented by a collection of
interacting particles in a cubic box (one emitter and
N perturbers) whose dimension
L is related to the ion density
. All perturbers are assumed to have the same charge
. During the MC run, a sampling procedure is applied in the configuration space, by choosing randomly a particle in the box and its displacement. This displacement is limited to a maximum value which accounts for the plasma conditions (ion coupling parameter and screening length). The effects of distant particles are replicated by using periodic boundary conditions. The state of equilibrium is searched by the Metropolis algorithm, yielding a set of configurations of minimal energy from which it is possible to determine the electric fields distribution at the emitter. The microfield distributions obtained from numerous MC simulations covering a broad range of plasma conditions were then fitted with a reduced number of parameters including the ion coupling parameter
, the screening factor
and the reduced microfield variable
(where
is the normal field between two perturbers). These fits cover the domain:
and
.
Since the MC calculations use the same charge
for all the perturbers (and possibly for the charged emitter), we assume that this charge is equal to the mean ion charge of the plasma:
. In the average-atom model, the ion-coupling parameter reads:
where
is the mean ionization of the plasma,
is the ion temperature and
is the mean distance between two ions (Wigner-Seitz radius). The screening parameter is defined by:
The electron-ion screening length
is evaluated in the Thomas-Fermi-Debye-Hückel approach [
2], which makes a bridge between the classical description of Debye-Hückel and the Thomas-Fermi quantum theory:
where
is the complete Fermi-Dirac integral of order
n,
is the reduced chemical potential. This allows one to tackle situations from hot and diluted plasmas (relevant to laser-plasma conditions) to cold dense plasmas (encountered in astrophysics), for which we recover the Debye-Hückel length and the Thomas-Fermi screening length at zero temperature, respectively (see the derivation of these asymptotic limits in
Appendix B).
The microfield distribution
is determined in the following manner. The plasma conditions (atomic number
Z,
,
and
) are used to determine the mean ionization
of the plasma in LTE or non-LTE, and the electron density
(alternatively, it is possible to fix
and to determine
). The chemical potential
is then calculated in the Thomas-Fermi approximation by solving the equation:
We can now determine the parameters
,
and the normal field which read
. The microfield distribution is then obtained from the analytical fitting formula
:
There are two different formulas: one for a charged emitter (assuming the same charge as the perturbers, i.e., ) and another one for a neutral emitter.
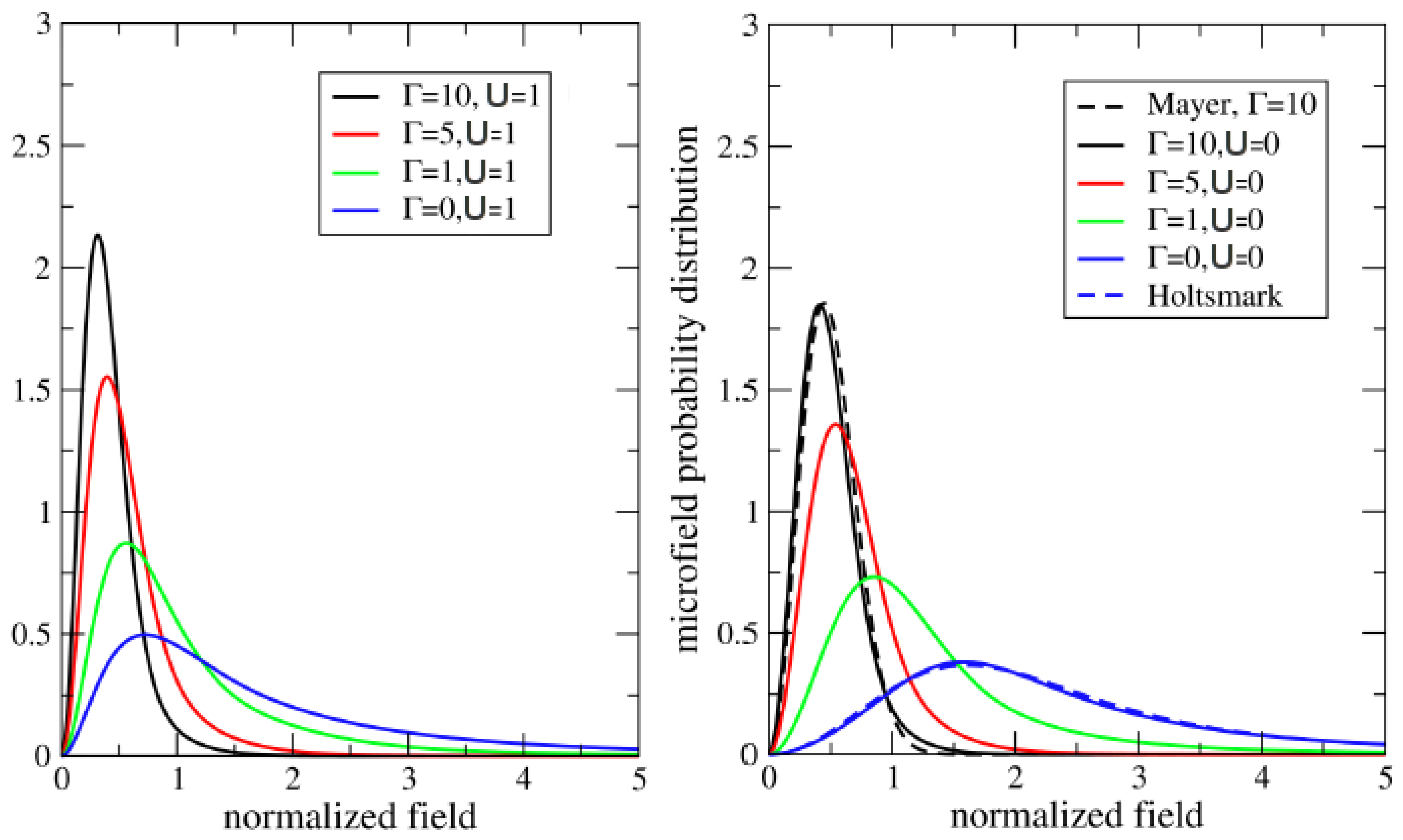
A comparison of the distributions obtained with different sets of parameters is shown in
Figure 3. The left part addresses screened plasma ions (with
), whereas the right part is for unscreened (
) one-component plasma (OCP). As expected, the effect of the screening is to narrow the distribution and to shift it toward smaller field values. In the case of OCP, two extreme cases are recovered: the Mayer distribution for strongly-coupled plasmas and the Holtsmark distribution for uncorrelated plasmas.