Abstract
As the object of investigation, astrophysical fully ionized electron-ion plasma is chosen with positively charged ions of two different kinds, including the plasmas of higher non-ideality. The direct aim of this work is to develop, within the problem of finding the mean potential energy of the charged particle for such plasma, a new model, self-consistent method of describing the electrostatic screening. Within the presented method, such extremely significant phenomena as the electron-ion and ion-ion correlations are included in the used model. We wish to draw attention to the fact that the developed method is suitable for astrophysical applications. Here we keep in mind that in outer shells of stars, the physical conditions change from those that correspond to the rare, practically ideal plasma, to those that correspond to extremely dense non-ideal plasma.
1. Introduction
Thematically, this work is the natural extension of the research on plasma’s inner electrostatic screening, the results of which are presented in the papers [1,2,3]. In these papers, the single- and two-component systems are discussed with their properties in the region of higher non-ideality degree. This topic itself, the discussion and the search for more consistent models of screening and more realistic potentials in plasmas are still continuing and are very real (see [4,5,6,7,8,9]). The screening in astroplasma surroundings is a collective effect of many correlated particle interactions. It strongly affects the electronic structure, that is, the spectral properties of atoms and properties of their collision processes with respect to those for isolated systems [10,11]. In the last decade, a large number of theoretical as well as experimental investigations of plasma screening has been performed. For an example, it has been experimentally noted that the atomic spectral lines are redshifted in a high-power laser, producing dense plasmas as the result of these effects [12].
Here we consider, for the first time, systems of the next level of complexity, that is, three-component systems that contain free electrons and positively charged ions of two different kinds. Because of this, we recall that the conducted research had the following task: to investigate, within the problem of finding the mean potential energy of the charged particle in the plasma, whether the physical model of plasma’s inner electrostatic screening, introduced in [13], is already exhausted by the Debye-Hückel (DH) method, as described in the same paper, or whether it still allows for the development of an alternative. As in the previous papers, here we keep in mind the electrostatic screening in fully ionized plasmas. Although the paper [13] was devoted to electrolytes, it had a profound trace in plasma physics and in adjacent disciplines [14,15,16,17,18]. Its influence is felt even today in various fields of physics, such as ionospheric plasma physics, astrophysics, and laboratory plasma research [19,20,21,22,23,24,25]. Thus, in numerous papers, direct DH or DH-like methods are used, as well as their products such as the DH potential and DH radius (see [26,27,28,29]). This has all induced the interest for the possibility of going beyond the sphere of influence of [13] and for the development of the mentioned alternative method. Additionally, another stimulus exists for the development of alternative methods, connected with finding a characteristics length greater than the Debye radius ([30,31,32,33,34,35]; see also [3]).
We recall that the essential properties of the mentioned model are the following:
- The presence of an immobile probe particle, which represents one kind of charged particle in the real system (plasma, or electrolyte).
- The treatment of the considered components, which contain free charged particles of different kinds as ideal gases in states of thermodynamical equilibrium, without the assumption that all temperatures are equal.
- The treatment of the existing total electrostatic field in the considered system as an external field with respect to the considered ideal gas.
- Finally, among the properties of this model is usage, as its relevant mathematical apparatus, of equations, which describe the mean local electrostatic field and the conditions of conservation of thermodynamical equilibrium for the considered components. As in the previous papers, this model is treated here as the basic model.
The task formulated above itself has enforced a special referent role of the mentioned DH method, the predictions of which shall be compared with a possible new method that would arise as the result of the undertaken investigation. In accordance with this, the main aim of our previous research became the creation of a “self-consistent” method of describing the mentioned electrostatic screening mechanism, which is completely free of the DH method’s disadvantages. We note that the definition of a self-consistent method implies that all the relevant characteristics are determined within this method itself and are expressed only through its basic parameters, that is, the particle densities, temperature, and so forth.
However, it has been shown that, except for the case of a single-component system (e.g., electron gas on a positively charged background), it was very difficult to finish the entire procedure of eliminating the disadvantages of the DH method in a self-consistent way. An analysis that was performed later convinced us that this result was not accidental, as the outer differences between the DH and the presented method were not practically significant, and the principal differences between these methods are of a conceptual nature.
Consequently, aside from finding the mean potential energy of the charged particles in the plasmas, the direct objective of this research became the development of a self-consistent method of describing the electrostatic screening in the considered three-component system, for which the relevant additional conditions (equivalent to the conditions of the conservation of particle numbers in finite systems) are included from the beginning.
In order to show the differences between the results of applying and neglecting the relevant additional conditions, we recall the behaviour of electron density in two cases of the electron-ion plasmas with the probe particle whose charge is equal to that of an ion, which was considered in [2] and is illustrated here in Figure 1a,b. The first of these illustrates the application of the method developed in [2], which makes sure that the area of higher electron density is followed by an area of its lowering. This is in accordance with the role of the probe-particle approximation: the situation in the vicinity of the probe particle could be considered as a reflection of the real situation in the vicinity of any ion in the considered plasma, and it should enable usage of the results illustrated by the figure to the case of the real plasma, as these do not influence the mean electron density. The systems with similar behaviour in the electron density are treated here as the “closed” systems. In Figure 1b, the behaviour of the DH electron density is shown in electron–proton plasma with the probe particle whose charge is equal to that of the proton. From this figure, a monotonous increasing of the electron density can be seen, with a decrease in the distance from the probe particle from infinity to zero. In the considered case, such behaviour causes the creation of an excess of 1/2 electron and 1/2 proton in the vicinity of the probe particle. This phenomenon, which is unacceptable from the point of view of a method that includes additional conditions, is discussed in detail in Section 6.

Figure 1.
(a) The behavior of the electron density in the case of the electron–ion plasma with the probe particle whose charge is equal to that of the ions; (b) the behavior of the Debye-Hückel (DH) electron in the case of the electron-proton plasma with the probe particle whose charge is equal to that of the protons.
This work is dedicated to plasmas that are treated as fully ionized, including the plasmas of higher non-ideality. The region of electron densities from to cm and temperatures from to K are studied. The developed theory is also applicable to a wider area of plasma parameters. The order of its exposing mostly follows that which is presented in our previous papers [1,2,3].
2. Theory Assumptions
2.1. The Initial System and Basic Characteristic
A stationary homogeneous and isotropic system is taken here as the initial model of some real physical objects, suitable for applications of the results of this research. It is assumed that is constituted by a mixture of a gas of free electrons and two gases of free ions of different kinds with positive charges and , where , and e is the modulus of the electron charge. The electron charge is denoted also by , where . We consider that these gases are in equilibrium states with mean densities of and and temperatures of for the ions, and a mean density of and temperature of for the electrons. All the particles are treated as point-like, non-relativistic objects and their spins are taken into account only as factors that influence the chemical potentials of the considered gases. Satisfying the condition
is assumed, which provides local quasi-neutrality of the system . We emphasize that the case is also considered here (see Section 6.1), as it reflects the existence of some real systems with two physically different kinds of ions with the same charge, for example, H and D, or H and He, and so forth.
In the subsequent considerations, several characteristic lengths are used that are connected with the parameters and , namely, the Wigner–Seit’s (WS) radii and the “ion self-spheres” radii (see [3]), denoted here by and , respectively. These are defined by the relations
From here, it follows that Equation (1) can be presented in the form
where the parameters and describe the primary distribution of the space between the self-spheres of all ions of the first kind and all ions of the second kind.
2.2. The System Properties and Conditions
In accordance with the basic model and the composition of the system , the electrostatic screening of the charged particles is modeled here in three corresponding auxiliary systems. It is assumed that each of these contains the following: the electron component, two ion components with the same charges and , and one immobile probe particle with the charge , which is fixed at the origin of the used reference frame (the point O).
As in [1,2], only such cases are studied here for which the probe particle can represent one of the charged particles of the system , for example, when , and . Two ion cases are denoted below with and , and the electron case-with , while the corresponding auxiliary systems are denoted with , and , respectively.
All systems are treated below as isotropic and are characterized by the corresponding mean local ion and electron densities: , and , which retain the properties of the corresponding components in the system and satisfy the boundary conditions:
where , and is the radius vector of the observed point. Their other necessary characteristics are the mean local charge density defined by the relation
and the mean local electrostatic potential , which is treated as the potential of the external electrostatic field. We take into account the fact that and have to satisfy Poisson’s equation:
where is the three-dimensional delta function [14], and . Satisfying the boundary conditions
is assumed, which guaranties a physical sense of the mentioned electrostatic potential and connection with the system and is compatible with the electro-neutrality condition of the auxiliary systems. Because is the mean electrostatic potential at the point O, the quantity
is the mean potential energy of the probe particle and is simply the searched mean potential energy of the probe particle. In the usual way, and are treated as approximations to the mean potential energies of the ion and electron in the initial system .
In accordance with the basic model the electron, all ion components of all auxiliary systems are treated as ideal gases. Therefore, we encompass the characteristics of the auxiliary systems by chemical potentials and of the corresponding ideal ion and electron gases, which can depend on the corresponding particle spins and on their boundary values, that is, = and .
2.3. The System Equations
It can be shown that on the basis of the procedure that was developed and described in detail in [1,2] for the case of a system that is electro-neutral as a whole, it is possible to switch from Poisson’s equation to the equation for the potential , which is more suitable for further consideration. This equation is given by
and is taken here in such a form.
In order to find other necessary equations, we consider the conditions of conservation of thermodynamical equilibrium (conservation of the electro-chemical potential) for those components that are represented by the corresponding probe particles, namely,
where, in accordance with the basic model, is treated as the potential of the external electrostatic field, and is the distance from the point O of the chosen fixed (starting) point: . From here, by means of the usual linearization procedure, the necessary equations for the particle densities are obtained in the form
which is applicable under the condition
Here we use the fact that such equations can be applied not only to the classical cases, but also to the quantum-mechanical cases, including the case of ultra-degenerated electron gas [15,17].
2.4. The Additional Conditions
In [1,2], the conditions were already introduced for the component that is represented by the probe particle and in which the charge of the probe particle appears. In the considered three-component case, these conditions are given by
where . This means that the ratio in the expression inside the square brackets is of the order of magnitude of 1. This equation is especially important, as it provides the continuity of the model. In order to show this fact, it is enough to consider the situation for which the charge density is negligible and the considered three systems for physical reasons can be treated as a two-component system. Then, as an approximation, we can replace the electron component by the negatively charged nonstructural background and return to a one-component system. It is important that the single-component case is now used for mathematical modeling of the plasma internal electrostatic screening (Iosilevskiy 2011, private communication). We note that in the single-component case (which was not considered in [13]), this first condition can be used instead of the electro-neutrality condition.
In [2], the additional conditions for the electron density were introduced. Here the corresponding conditions are given by the equations
The additional conditions for the ion components and are taken into consideration analogously to the electron components, as there are no principal differences between them. The corresponding relations are given by
We note that in this work, the considered physical systems, as well as other physical systems that are described by means of additional conditions, are treated as systems of the closed type (see also a detailed version [36]).
As it is known, in our investigation, we take care that our results are compared with the results of the DH method, which provides electro-neutrality of the considered system as a whole. In principle, this would justify introducing into consideration the corresponding electro-neutrality condition, namely,
3. Ion Cases: Complete Expressions
3.1. The Ion Densities
As a result of their importance, the ion densities are presented separately for the case in the form
and separately for the case in the similar form
where the functions and the coefficients , , , and are given by the relations
and the screening constants
3.2. The Electron Densities
The complete expressions for the electron densities are presented here in the form
where the ion densities and are given by Equations (17)–(19). The number , in accordance with the above, is given by the relations
We note that these parameters, as well as , , and , are determined as described in Section 5.
4. Complete Expressions for the Electron and Ion Densities: The Case (e)
Here we can repeat the procedures from [2] verbatim. We obtain the expression for the electron density:
which determines in the whole region . The obtained expressions are given here by the relations
where and are given by Equation (28). We note that the ratios and the characteristic length are determined as described in the next section.
5. Determination of the Parameters
The parameters and are determined separately for the cases and ; namely, within the used procedure, the first case, where , is equivalent (from the point of view of the determination of ) to the case of the two-component plasma with the same , and . Consequently, in the case for which , the following relations are valid:
where in accordance with [2], is defined by
In the case for which , the parameters are given by the relation
and are established by direct calculations where and are given by Equations (2) and (3).
It is important that the electron–ion correlation coefficient and the characteristic lengths are determined, as is described below, independently of all other parameters; namely, this is why the existing conditions are sufficient for the determination of the characteristic lengths , and , and the ion–ion correlation coefficient .
The very important parameters , that is, the distances from the point O at which the manner of describing the ion densities changes, are determined from
through a procedure for which it is taken that
where are new parameters, which are used in the calculations in such a way that they vary with the small steps where . As the results of this procedure, we obtain the values of the parameters , that is, the main considered characteristic length, which corresponds to the current value of the ion–ion correlation coefficient . The final value of this coefficient itself is determined through a procedure that implies scanning with a very small step in the interval from 0 to 1 and examining at each step whether the equation
is satisfied, which provides the physical meaning of the obtained solutions. The whole procedure ends when the equation is satisfied.
The parameter is determined from
as in [1,2], using and Equation (2). It can be presented in two equivalent forms:
where , , and the coefficients and are connected with the electron non-ideality parameters and as described in [3].
Finally, we note that the partial electron and ion densities and , because of the structure of the equation for the coefficients and (Equation (28)), can be determined by Equations (27), (29) and (33) in both the and cases. Therefore, it is necessary to take the corresponding values of and only in these expressions, for example, if .
The behaviour of the characteristic length , the electron–ion correlation coefficients , the parameters and the ion–ion correlation coefficients is shown in Table 1 and Table 2. These tables cover the regions of from to cm for K. These tables show that the values of all the parameters are within the expected boundaries. Additionally, one may note that particularly for , the electron–ion correlation coefficient , and the ion–ion correlation coefficient , a significant increase in the correlation coefficient values and is registered in the region of extremely high electron density ( cm).

Table 1.
The characteristic length (in cm), the non dimensional electron–ion correlation coefficients , the main characteristic length (in cm), the non-dimensional ion–ion correlation coefficients and the potential energies (in eV) and (in eV) for the cases of and at K in the region of electron densities cm cm. The densities are in cm.

Table 2.
The same as in Table 1 but for the case of .
6. Results and Discussions
6.1. The Properties of the Obtained Solutions
As a continuation of our previous research [1,2], in this work, fully ionized electron–ion plasmas are chosen with the positive ion charges of two different kinds. Such a choice is especially important, as increasing the number of ion components further would not cause the appearance of any new phenomena.
One can see that the procedures of obtaining Equations (17)–(33), as well as the values of the existing parameters, provide that these expressions are self-consistent; satisfy all the conditions from Section 2.1, including Equations (37) and (39); and can be applied not only to the classical but also to the quantum-mechanical systems (see [2]), including here the plasmas of higher non-ideality. Because the presented expressions do not contain the particle masses, they can also be used for describing some other systems (the corresponding electrolytes and dusty plasmas). The behaviour of the ion and electron densities is illustrated in Figure 2 and Figure 3 for the examples of the cases of and for and , respectively.
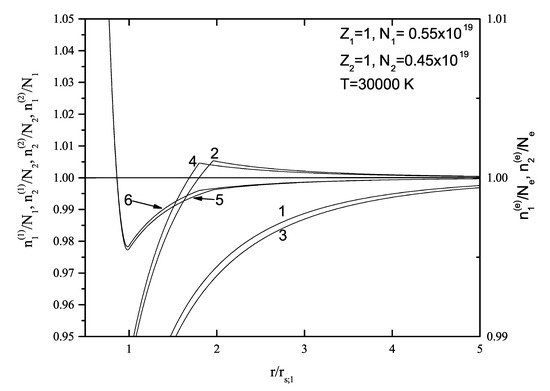
Figure 2.
The behavior of reduced densities (curve marked with 1), (curve marked with 2), (curve marked with 3), (curve marked with 4), and (curve marked with 5 and 6) in the case of , and , where T = 30,000 K.
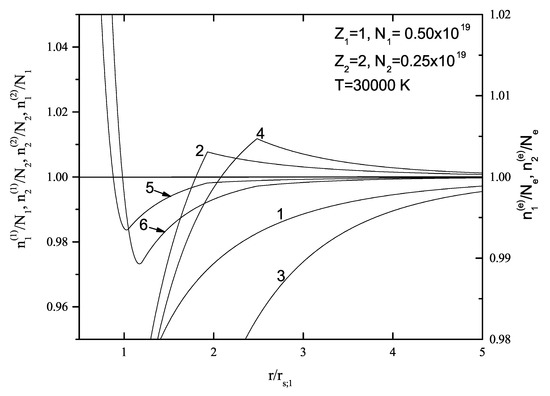
Figure 3.
The behavior of reduced densities (curve marked with 1), (curve marked with 2), (curve marked with 3), (curve marked with 4), and (curve marked with 5 and 6), in the case of , and , where T = 30,000 K.
Because Equations (27) and (32) show that the solutions and are singular at the point , it is useful to note that the existence of singularities in model solutions is fully acceptable, if it does not have other non-physical consequences. Such solutions are well known in physics; it is enough to mention, for example, the Thomas–Fermi models of electron shells of heavy atoms ([37,38]; see also [39]), which have been used in plasma research up to the present (see e.g., [40]). Except for the potential and , the systems are certainly characterized by radial charge densities According to [3], each of the functions has at least one strongly expressed maximum, whose position is an important characteristic of the distribution of charge in the neighborhood of the probe particle.
In order to demonstrate the very large differences between the alternative and DH-like characteristics, we compare the asymptotic behaviour of the potential and DH-like potential :
where the ion screening constants are given by Equation (24) and the DH screening constant , where and are determined by Equations (24) and (29). Here, we consider the case of classical plasma with , where and, consequently, the relations
are valid. These relations show that the ion asymptotic screening constants always have to be significantly smaller than , and at the same time, the corresponding screening radii always have to be significantly larger then . It is important that a similar result obtained in [2] was noted there as an evident shortcoming of the DH solution.
From Equation (43), it follows that has a completely different asymptotic behavior compared to . We note that we reach the same conclusion by comparing the behavior of the radial charge density to its DH-like analog.
As the main characteristics of the considered plasmas we take here, the probe particle mean potential energies are later identified with the mean potential energies of ions in the real plasmas. In order to determine these ion energies , it is necessary to know the values of the potential :
where denotes the charge density. We recall that the case can correspond to the case of plasma with the ion H or He(1s), and so forth. Within this work, the energies and are determined for two cases: and , and . In both cases, the calculations are performed for plasmas with the electron densities cm cm, for K. The obtained results are presented in Table 1 and Table 2 with fairly small ion-density steps. In order to investigate the dependance of the energies of the systems on the temperature, the calculations of and were performed and are presented in Table 3 and Table 4 for cm and for the temperatures , , and K. From these results, one can see that the potential energies and are sensitive to a considerable lowering of the temperature ( K).

Table 3.
The potential energies (in eV) and (in eV) for the case of and at cm and , , , and K. The densities are in cm.

Table 4.
The same as in Table 3 but for the case of .
6.2. Interpretation of the Obtained Results
Results such as those presented in the previous section (see Equation (43)) might leave an impression of having an absolute advantage over the DH-like methods (or other similar methods). Such an impression is incorrect, as an absolute advantage of the presented method is for the case of a system of the closed type. In the same context, it is necessary to interpret the phenomena that were described in the introduction concerning the results presented in the Figure 1a,b; these phenomena can be interpreted as physically unacceptable when the DH or DH-like methods are used on the system of the closed type. However, the system receives treatment as closed-type only in the case in which it is described by means of the above-mentioned additional conditions. Consequently, in the opposite case (when additional conditions are absent), the system can be successfully described by means of DH-like or similar methods. Concerning this, we refer to Figure 4a,b, which shows the results of the application of the DH method to the considered plasma ((a) and , and (b) ). It is useful to compare this figure with Figure 2 and Figure 3. In this context, we draw attention to the fact that such a treatment itself has to be determined on the basis of the properties of the considered system and the physical problem, which can be solved using that system.
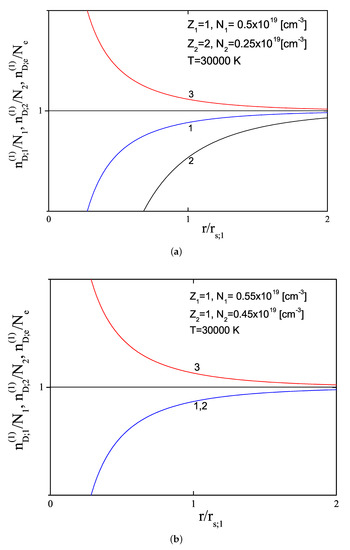
Figure 4.
(a) The reduced Debye-Hückel (DH) densities (curve marked with 1), (curve marked with 2) and (curve marked with 3) in the case of , and , where T = 30,000 K. (b) The reduced DH densities (curve marked with 1), (curve marked with 2), and (curve marked with 3) in the case of and , where T = 30,000 K.
At the end of this point, it would be useful to linger on such influence of the additional conditions on the properties of the obtained solutions, which could be treated as a manifestation of their deviation from thermodynamic equilibrium. Here, we refer to the necessity of substituting the equation obtained from the condition of thermodynamic equilibrium by the equations obtained in different ways—the electron charge density in the region of large r, and the ion charge density , also in the region of large r. However, we draw attention to the fact that all changes have purely phenomenological characteristics and do not influence the thermodynamic properties of the considered gases: gas with temperature T remains a gas with the temperature T. Additionally, we recall the fact that in all regions of r, where the considered components can be treated independently from one another, their state was described by means of equations obtained from the condition of thermodynamic equilibrium.
From the above-presented material, it follows that the basic model can generate only the DH or some DH-like methods. In this sense, this model has already exhausted its potential, but as one can see, it enables, with minimal deviation from the basic model (in the area of mathematical apparatus), us to leave the DH-like sphere and develop a new model method of describing the plasma’s inner electrostatic screening.
6.3. The Possible Ion–Ion Probe Systems
From the presented work, it follows that the main properties of the considered three-component system originate from the analogy with the properties of a positron–ion probe system. Concerning this, it is useful to note the fact that was established by means the molecular dynamic (MD) simulation of a dense electron-proton plasma in [41]. In this work, some characteristics of the considered plasma were determined as the results of averaging over all ion configurations possible under the considered conditions, for different values of the ratio , where and are the electron and proton masses. These values were changed from to , but the changes of the results of MD simulations could be neglected. This can be very interesting, even only for the similarity of the procedures that were used here and in [41]. However, it can be particularly important under the assumption that a similar conclusion is valid in the case of plasma that contains electrons and ions of some heavy atoms, particularly if the non-negligible probability is taken into account, meaning that the value of the mentioned ratio can be even greater than .
7. Conclusions
The object of the investigation of fully ionized electron-ion plasma was chosen with positively charged ions of two different kinds, including here the plasmas of higher non-ideality. Within the presented method, such extremely significant phenomena as the electron-ion and ion-ion correlations are included. The collective effect of many correlated particle interactions strongly affects the spectral properties of atoms and properties of their collision processes with respect to those for isolated systems. The screening characteristics of the considered plasmas in a wide region of the electron densities and temperatures have been calculated. Here, the case of the three-component system was considered, which is especially important as we expect that a further increase in the number of ion components in the more complicated systems would not cause the appearance of any new phenomena.
Acknowledgments
The authors are thankful to the Ministry of Education, Science and Technological Development of the Republic of Serbia for the support of this work within the projects 176002 and III44002.
Author Contributions
All authors contributed equally to the work presented here.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mihajlov, A.; Vitel, Y.; Ignjatović, L.M. The new screening characteristics of strongly non-ideal and dusty plasmas. Part 1: Single-component systems. High Temp. 2008, 46, 737–745. [Google Scholar] [CrossRef]
- Mihajlov, A.; Vitel, Y.; Ignjatović, L.M. The new screening characteristics of strongly non-ideal and dusty plasmas. Part 2: Two-component systems. High Temp. 2009, 47, 1–12. [Google Scholar] [CrossRef]
- Mihajlov, A.; Vitel, Y.; Ignjatović, L.M. The new screening characteristics of strongly non-ideal and dusty plasmas. Part 3: Properties and applications. High Temp. 2009, 47, 147–157. [Google Scholar] [CrossRef]
- Demura, A. Physical models of plasma microfield. Int. J. Spectrosc. 2009, 2010, 42. [Google Scholar] [CrossRef]
- Calisti, A.; Ferri, S.; Mossé, C.; Talin, B.; Lisitsa, V.; Bureyeva, L.; Gigosos, M.A.; González, M.A.; del Río Gaztelurrutia, T.; Dufty, J.W. Slow and fast micro-field components in warm and dense hydrogen plasmas. arXiv, 2007; arXiv:0710.2091. [Google Scholar]
- Mihajlov, A.A.; Sakan, N.M.; Srećković, V.A.; Vitel, Y. Modeling of continuous absorption of electromagnetic radiation in dense partially ionized plasmas. J. Phys. A Math. Gen. 2011, 44, 095502. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Sakan, N.M.; Srećković, V.A.; Vitel, Y. Modeling of the Continuous Absorption of Electromagnetic Radiation in Dense Hydrogen Plasma. Balt. Astron. 2011, 20, 604–608. [Google Scholar] [CrossRef]
- Mihajlov, A.; Srećković, V.; Sakan, N.; Ignjatović, L.M.; Simić, Z.; Dimitrijević, M.S. The inverse bremsstrahlung absorption coefficients and Gaunt factors in astrophysical plasmas. J. Phys. Conf. Ser. 2017, 810. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Srećković, V.A.; Sakan, N.M. Inverse Bremsstrahlung in Astrophysical Plasmas: The Absorption Coefficients and Gaunt Factors. J. Astrophys. Astron. 2015, 36, 635–642. [Google Scholar] [CrossRef]
- Mao, D.; Mussack, K.; Dappen, W. Dynamic Screening in Solar Plasma. Astrophys. J. 2009, 701, 1204. [Google Scholar] [CrossRef]
- Das, M.; Sahoo, B.K.; Pal, S. Plasma screening effects on the electronic structure of multiply charged Al ions using Debye and ion-sphere models. Phys. Rev. A 2016, 93, 052513. [Google Scholar] [CrossRef]
- Leng, Y.; Goldhar, J.; Griem, H.; Lee, R.W. C VI Lyman line profiles from 10-ps KrF-laser-produced plasmas. Phys. Rev. E 1995, 52, 4328–4337. [Google Scholar] [CrossRef]
- Debye, P.; Huckel, E. The theory of electrolytes. I. Lowering of freezing point and related phenomena. Phys. Z. 1923, 24, 185–206. [Google Scholar]
- Ichimaru, S. Basic Principles of Plasma Physics; Benjamin: Reading, MA, USA, 1973. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics, 4th ed.; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Drawin, H.; Felenbok, P. Data for Plasmas in Local Thermodynamic Equilibrium; Gauthier-Villars: Paris, France, 1965. [Google Scholar]
- Kraeft, W.; Kremp, D.; Ebeling, W.; Ropke, G. Quantum Statistics of Charged Particle System; Academie-Verlag: Berlin, Germany, 1986. [Google Scholar]
- Dimitrijević, M.S.; Mihajlov, A.A.; Djurić, Z.; Grabowski, B. On the influence of Debye shielding on the Stark broadening of ion lines within the classical model. J. Phys. B 1989, 22, 3845–3850. [Google Scholar] [CrossRef]
- Mussack, K.; Däppen, W. Dynamic screening in solar and stellar nuclear reactions. Astrophys. Space Sci. 2010, 328, 153–156. [Google Scholar] [CrossRef]
- Nina, A.; Čadež, V.; Srećković, V.; Šulić, D. Altitude distribution of electron concentration in ionospheric D-region in presence of time-varying solar radiation flux. Nucl. Instrum. Methods Phys. Res. B 2012, 279, 110–113. [Google Scholar] [CrossRef]
- Nina, A.; Čadež, V.; Šulić, D.; Srećković, V.; Žigman, V. Effective electron recombination coefficient in ionospheric D-region during the relaxation regime after solar flare from 18 February 2011. Nucl. Instrum. Methods Phys. Res. B 2012, 279, 106–109. [Google Scholar] [CrossRef]
- Potekhin, A.Y.; Chabrier, G. Thermonuclear fusion in dense stars—Electron screening, conductive cooling, and magnetic field effects. Astron. Astrophys. 2012, 538, A115. [Google Scholar] [CrossRef]
- Nina, A.; Čadež, V.M.; Popović, L.Č.; Srećković, V.A. Diagnostics of plasma in the ionospheric D-region: Detection and study of different ionospheric disturbance types. Eur. Phys. J. D 2017, 71, 189. [Google Scholar] [CrossRef]
- Gajo, T.; Ivković, M.; Konjević, N.; Savić, I.; Djurović, S.; Mijatović, Z.; Kobilarov, R. Stark shift of neutral helium lines in low temperature dense plasma and the influence of Debye shielding. Mon. Not. R. Astron. Soc. 2016, 455, 2969–2979. [Google Scholar] [CrossRef]
- Kobzev, G.; Jakubov, I.; Popovich, M. (Eds.) Transport and Optical Properties of Non-Ideal Plasmas; Plenum Press: New York, NY, USA; London, UK, 1995. [Google Scholar]
- Shukla, P.K.; Eliasson, B. Screening and wake potentials of a test charge in quantum plasmas. Phys. Lett. A 2008, 372, 2897–2899. [Google Scholar] [CrossRef]
- Zhao, L.B.; Ho, Y.K. Influence of plasma environments on photoionization of atoms. Phys. Plasmas 2004, 11, 1695–1700. [Google Scholar] [CrossRef]
- Lin, C.Y.; Ho, Y.K. Effects of screened Coulomb (Yukawa) and exponential-cosine-screened Coulomb potentials on photoionization of H and He+. Eur. Phys. J. D 2010, 57, 21–26. [Google Scholar] [CrossRef]
- Lin, C.Y.; Ho, Y.K. The photoionization of excited hydrogen atom in plasmas. Comput. Phys. Commun. 2011, 182, 125–129. [Google Scholar] [CrossRef]
- Gunther, K.; Radtke, R. Electric Properties of Weakly Nonideal Plasmas; Akademie: Berlin, Germany, 1984. [Google Scholar]
- Vitel, Y.; El Bezzari, M.; Mihajlov, A.; Djurić, Z. Experimental verification of semiclassical and RPA calculations of the static conductivity in moderately nonideal plasmas. Phys. Rev. E 2001, 63, 026408. [Google Scholar] [CrossRef] [PubMed]
- Günther, K.; Radtke, R. Elektrische Leitfähigkeit von Xenon-Impulsplasmen. Contrib. Plasma Phys. 1972, 12, 63–72. [Google Scholar] [CrossRef]
- Gunther, K.; Popović, M.; Popović, S.; Radtke, R. Electrical conductivity of highly ionized dense hydrogen plasma. II. Comparison of experiment and theory. J. Phys. D 1976, 9, 1139–1147. [Google Scholar] [CrossRef]
- Goldbach, C.; Nollez, G.; Popović, S.; Popović, M. Electrical conductivity of high pressure ionized argon. Z. Naturforsch. A 1978, 33, 11–17. [Google Scholar] [CrossRef]
- Gunther, K.; Lang, S.; Radtke, R. Electrical conductivity and charge carrier screening in weakly non-ideal argon plasmas. J. Phys. D 1983, 16, 1235–1243. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Ignjatović, L.M.; Srećković, V.A. The new model method of the electrostatic screening describing: three-component system of the ’closed’ type. arXiv, 2017; arXiv:1703.07613. [Google Scholar]
- Thomas, L.H. The calculation of atomic fields. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1927; Volume 23, pp. 542–548. [Google Scholar]
- Fermi, E. Eine statistische Methode zur Bestimmung einiger Eigenschaften des Atoms und ihre Anwendung auf die Theorie des periodischen Systems der Elemente. Z. Phys. 1928, 48, 73–79. [Google Scholar] [CrossRef]
- Gombas, P. Theorie und Losungsmethoden des Mehrteilchenproblems der Wellenmechanik; Springer: Basel, Switzerland, 1950. [Google Scholar]
- Mendonça, J.; Tsintsadze, N.; Guerreiro, A. Thomas-Fermi model for a dust particle in a plasma. Europhys. Lett. 2002, 57, 362–367. [Google Scholar] [CrossRef]
- Reinholz, H.; Morozov, I.; Röpke, G.; Millat, T. Internal versus external conductivity of a dense plasma: Many-particle theory and simulations. Phys. Rev. E 2004, 69, 066412. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).