Stark Broadening from Impact Theory to Simulations
Abstract
1. Introduction
2. Impact Broadening
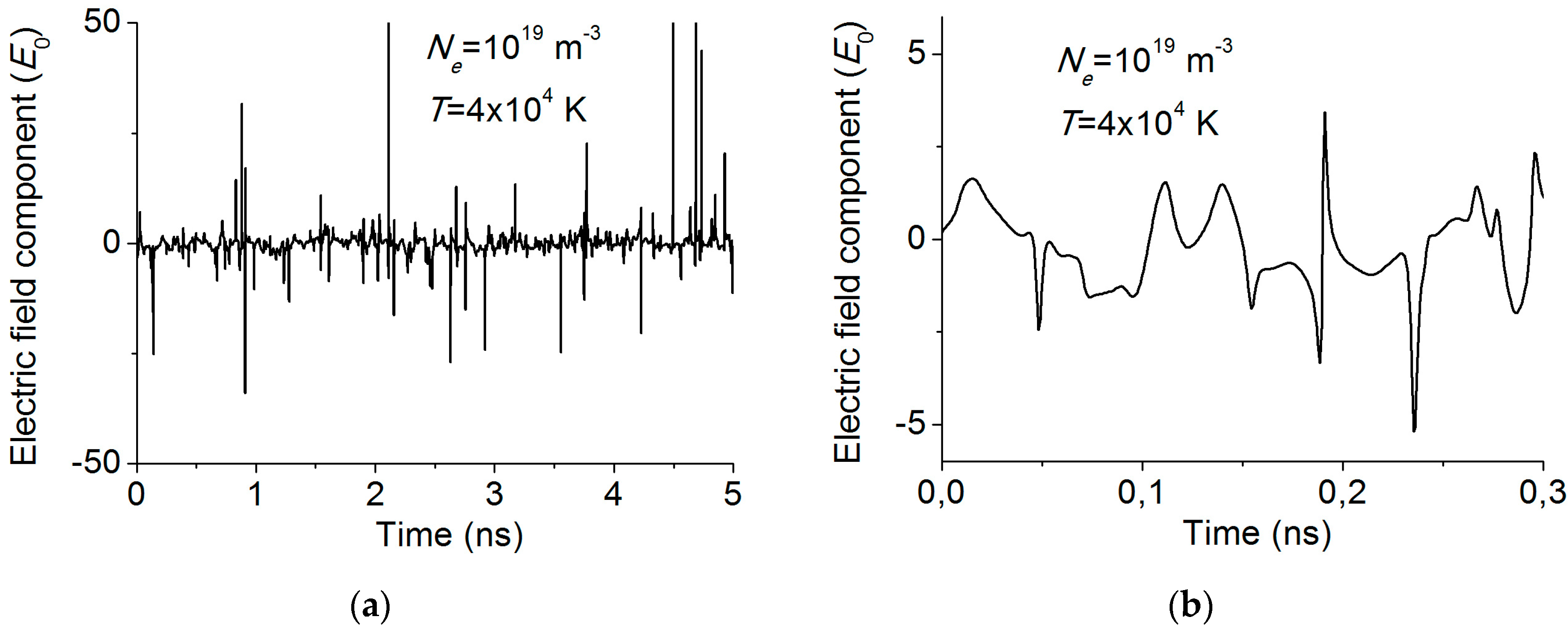
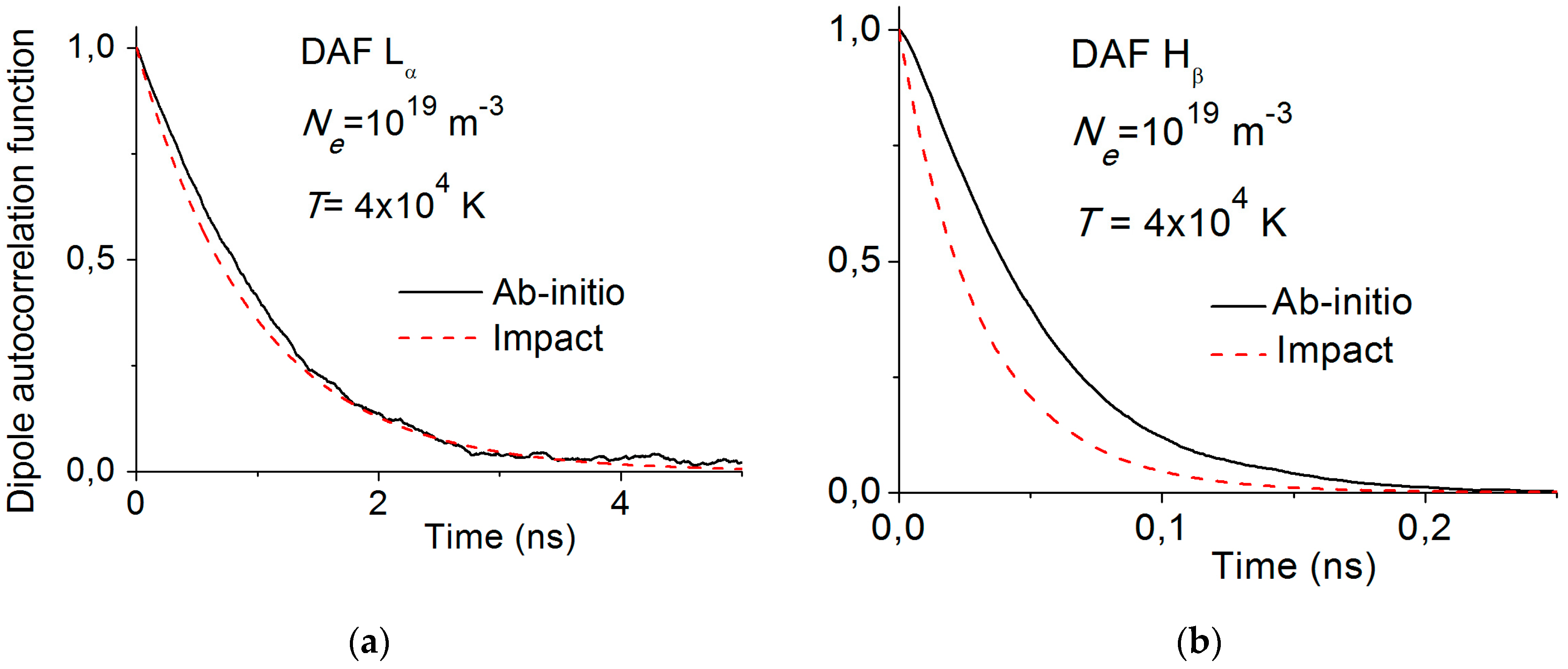
3. Simulations of Impact Theory and Ion Dynamics
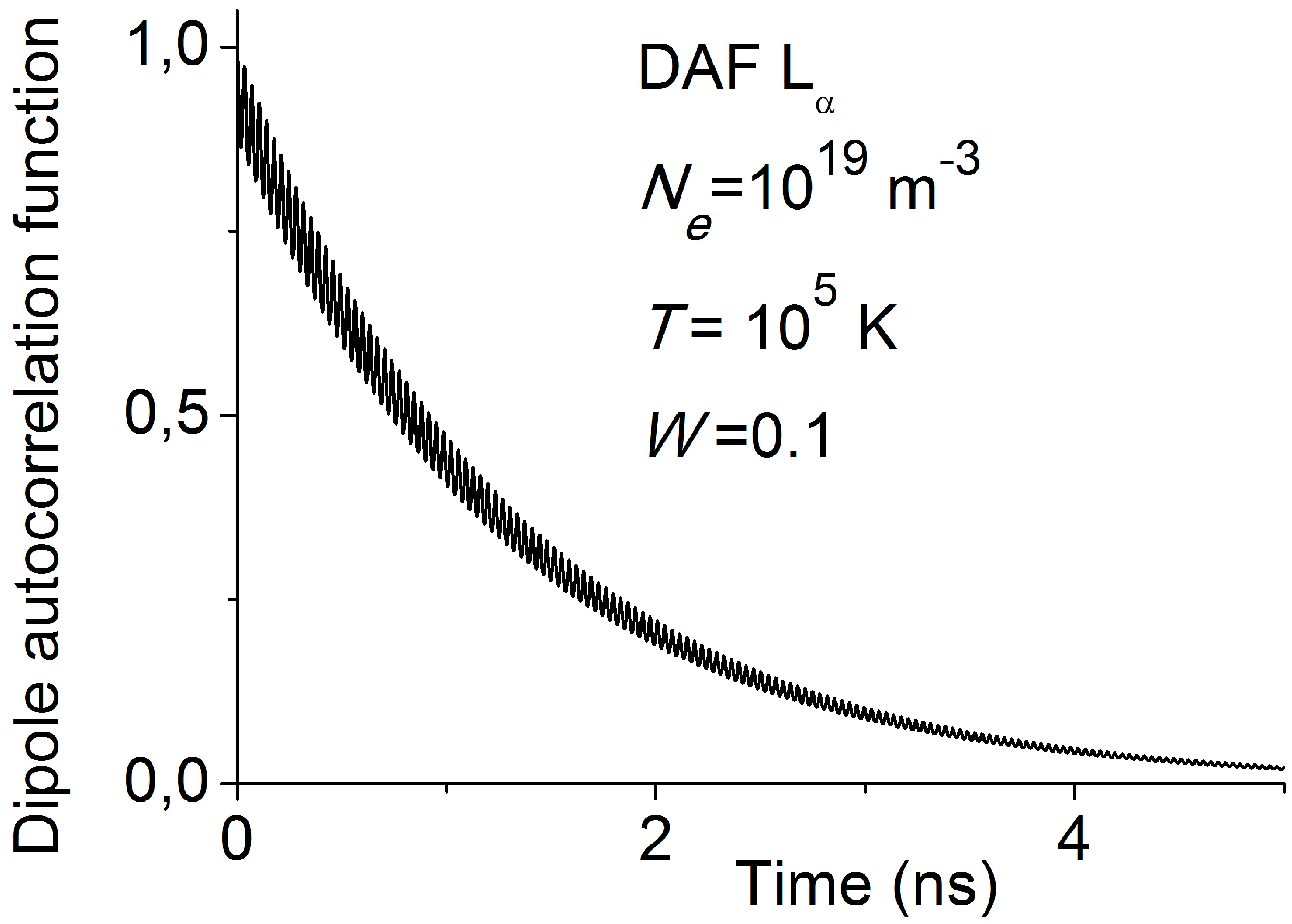
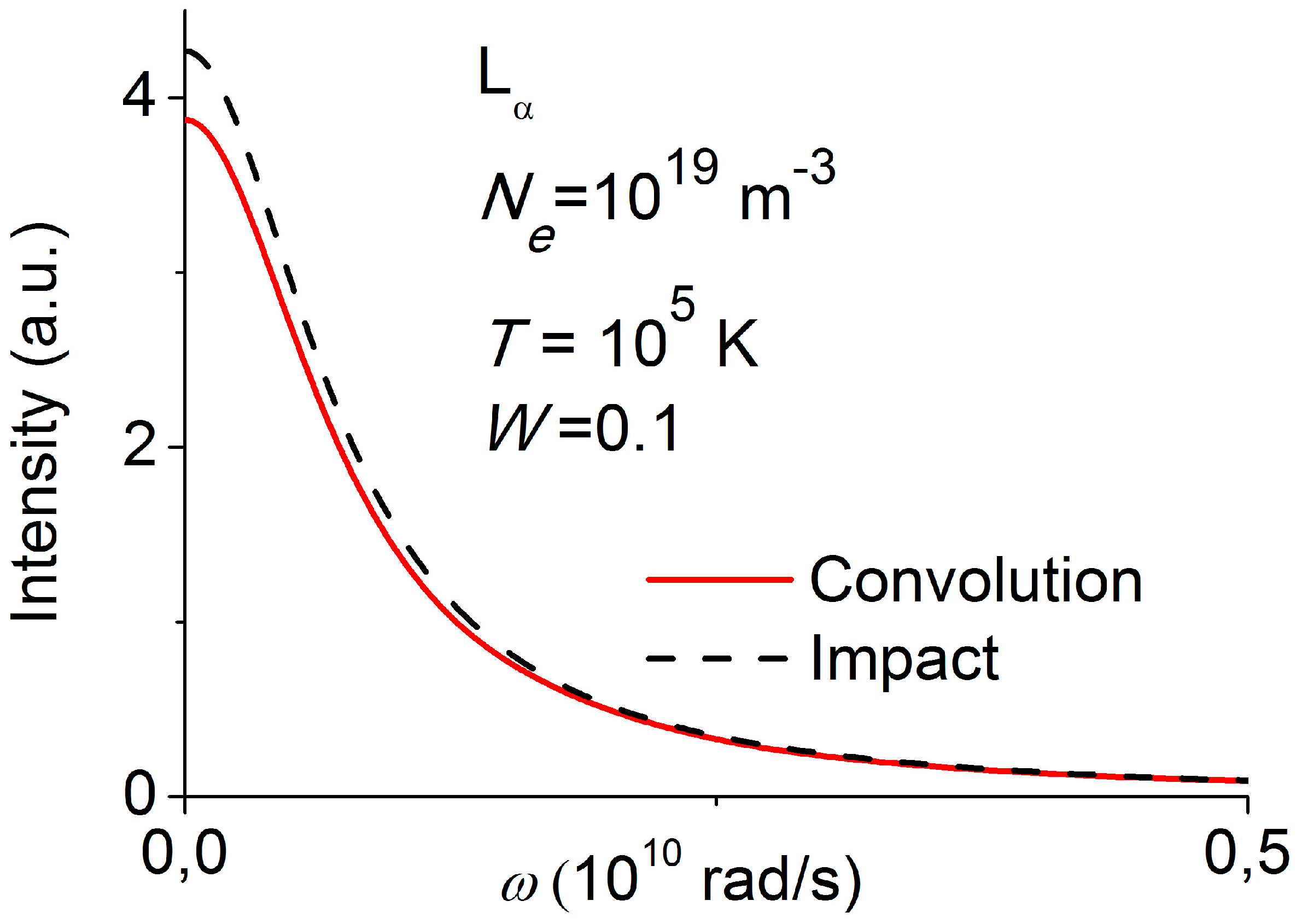
4. Effect of Plasma Waves
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dimitrijević, M.S.; Konjević, N. Stark widths of doubly- and triply-ionized atom lines. J. Quant. Spectrosc. Radiat. Transf. 1980, 24, 451–459. [Google Scholar] [CrossRef]
- Baranger, M. General Impact Theory of Pressure Broadening. Phys. Rev. 1958, 112, 855–865. [Google Scholar] [CrossRef]
- McMahon, J.M.; Morales, M.A.; Pierleoni, C.; Ceperley, D.M. The properties of hydrogen and helium under extreme conditions. Rev. Mod. Phys. 2012, 84, 1607–1653. [Google Scholar] [CrossRef]
- Barnes, K.S.; Peach, G. The shape and shift of the resonance line of Ca+ perturbed by electron collisions. J. Phys. B 1970, 3, 350–362. [Google Scholar] [CrossRef]
- Bely, O.; Griem, H.R. Quantum-mechanical calculation for the electron-impact broadening of the resonance line of singly ionized magnesium. Phys. Rev. A 1970, 1, 97–105. [Google Scholar] [CrossRef]
- Elabidi, H.; Ben Nessib, N.; Sahal-Bréchot, S. Quantum-mechanical calculations of the electron-impact broadening of spectral lines for intermediate coupling. J. Phys. B 2004, 37, 63–71. [Google Scholar] [CrossRef]
- Elabidi, H.; Sahal-Bréchot, S.; Dimitrijević, M.S. Quantum Stark broadening of Ar XV lines. Strong collision and quadrupolar potential contributions. Adv. Space Res. 2014, 54, 1184–1189. [Google Scholar] [CrossRef]
- Griem, H.R. Semi-empirical formulas for the electron-impact widths and shifts of isolated ion lines in plasmas. Phys. Rev. 1968, 165, 258–266. [Google Scholar] [CrossRef]
- Van Regemorter, H. Rate of collisionnal excitation in stellar atmospheres. Astrophys. J. 1962, 136, 906–915. [Google Scholar] [CrossRef]
- Griem, H.R.; Kolb, A.C.; Shen, K.Y. Stark broadening of hydrogen lines in a plasma. Phys. Rev. 1959, 116, 4–16. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S.; Dimitrijević, M.S.; Ben Nessib, N. Widths and shifts of isolated lines of neutral and ionized atoms perturbed by collisions with electrons and ions: An outline of the semiclassical perturbation (SCP) method and of the approximations used for the calculations. Atoms 2014, 2, 225–252. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S.; Dimitrijević, M.S.; Moreau, N. STARK-B Database; LERMA, Observatory of Paris, France and Astronomical Observatory: Belgrade, Serbia, 2014; Available online: http://stark-b.obspm.fr (accessed on 12 August 2017).
- Griem, H.R. Principles of Plasma Spectroscopy; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Alexiou, S.; Lee, R.W. Semiclassical calculations of line broadening in plasmas: Comparison with quantal results. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 10–20. [Google Scholar] [CrossRef]
- Elabidi, H.; Sahal-Bréchot, S.; Ben Nessib, N. Quantum Stark broadening of the 3s-3p spectral lines in Li-like ions; Z-scaling and comparison with semi-classical perturbation theory. Eur. Phys. J. D 2009, 54, 51–64. [Google Scholar] [CrossRef]
- Wiese, W.L.; Kelleher, D.E.; Paquette, D.R. Detailed study of the Stark broadening of Balmer lines in a high density plasma. Phys. Rev. A 1972, 6, 1132–1153. [Google Scholar] [CrossRef]
- Voslamber, D. Unified model for Stark broadening. Z. Naturforsch. 1969, 24, 1458–1472. [Google Scholar]
- Smith, E.W.; Cooper, J.; Vidal, C.R. Unified classical-path treatment of Stark broadening in plasmas. Phys. Rev. 1969, 185, 140–151. [Google Scholar] [CrossRef]
- Grützmacher, K.; Wende, B. Discrepancies between the Stark–broadening theories of hydrogen and measurements of Lyman-α Stark profiles in a dense equilibrium plasma. Phys. Rev. A 1977, 16, 243–246. [Google Scholar] [CrossRef]
- Stamm, R.; Voslamber, D. On the role of ion dynamics in the Stark broadening of hydrogen lines. J. Quant. Spectrosc. Radiat. Transf. 1979, 22, 599–609. [Google Scholar] [CrossRef]
- Stamm, R.; Smith, E.W.; Talin, B. Study of hydrogen Stark profiles by means of computer simulation. Phys. Rev. A 1984, 30, 2039–2046. [Google Scholar] [CrossRef]
- Stamm, R.; Talin, B.; Pollock, E.L.; Iglesias, C.A. Ion-dynamics effects on the line shapes of hydrogenic emitters in plasmas. Phys. Rev. A 1986, 34, 4144–4152. [Google Scholar] [CrossRef]
- Rosato, J.; Capes, H.; Stamm, R. Ideal Coulomb plasma approximation in line shapes models: Problematic issues. Atoms 2014, 2, 253–258. [Google Scholar] [CrossRef]
- Vesely, F. Computational Physics, an Introduction; Plenum Press: New York, NY, USA, 1994. [Google Scholar]
- Brissaud, A.; Frisch, U. Theory of Stark broadening-II exact line profile with model microfield. J. Quant. Spectrosc. Radiat. Transf. 1971, 11, 1767–1783. [Google Scholar] [CrossRef]
- Stehlé, C. Stark broadening of hydrogen Lyman and Balmer in the conditions of stellar envelopes. Astron. Astrophys. Suppl. Ser. 1994, 104, 509–527. [Google Scholar]
- Talin, B.; Calisti, A.; Godbert, L.; Stamm, R.; Lee, R.W.; Klein, L. Frequency-fluctuation model for line-shape calculations in plasma spectroscopy. Phys. Rev. A 1995, 51, 1918–1928. [Google Scholar] [CrossRef] [PubMed]
- Spectral Line Shapes in Plasmas (SLSP) Code Comparison Workshop. Available online: http://plasma-gate.weizmann.ac.il/slsp/ (accessed on 20 July 2017).
- Moslem, W.M.; Shukla, P.K.; Eliasson, B. Surface plasma rogue waves. EPL 2011, 96, 25002. [Google Scholar] [CrossRef]
- Ahmed, S.M.; Metwally, M.S.; El-Hafeez, S.A.; Moslem, W.M. On the generation of rogue waves in dusty plasmas due to modulation instability of nonlinear Schrödinger equation. Appl. Math Inf. Sci. 2016, 10, 317–323. [Google Scholar] [CrossRef]
- Mc Kerr, M.; Kourakis, I.; Haas, F. Freak waves and electrostatic wavepacket modulation in a quantum electron–positron–ion plasma. Plasma Phys. Control. Fusion 2014, 56, 035007. [Google Scholar] [CrossRef]
- Erkintalo, M.; Genty, G.; Dudley, J.M. Rogue-wave-like characteristics in femtosecond supercontinuum generation. Opt. Lett. 2009, 34, 2468–2470. [Google Scholar] [CrossRef] [PubMed]
- Bludov, Y.V.; Konotop, V.V.; Akhmediev, N. Matter rogue waves. Phys. Rev. A 2009, 80, 033610. [Google Scholar] [CrossRef]
- Zakharov, V.E. Collapse of Langmuir waves. Sov. Phys. JETP 1972, 35, 908–914. [Google Scholar]
- Robinson, P.A. Nonlinear wave collapse and strong turbulence. Rev. Mod. Phys. 1997, 69, 507–573. [Google Scholar] [CrossRef]
- Bailung, H.; Sharma, S.K.; Nakamura, Y. Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys. Rev. Lett. 2011, 107, 255005. [Google Scholar] [CrossRef] [PubMed]
- Hannachi, I.; Stamm, R.; Rosato, J.; Marandet, Y. Effect of nonlinear wave collapse on line shapes in a plasma. EPL 2016, 114, 23002. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stamm, R.; Hannachi, I.; Meireni, M.; Godbert-Mouret, L.; Koubiti, M.; Marandet, Y.; Rosato, J.; Dimitrijević, M.S.; Simić, Z. Stark Broadening from Impact Theory to Simulations. Atoms 2017, 5, 32. https://doi.org/10.3390/atoms5030032
Stamm R, Hannachi I, Meireni M, Godbert-Mouret L, Koubiti M, Marandet Y, Rosato J, Dimitrijević MS, Simić Z. Stark Broadening from Impact Theory to Simulations. Atoms. 2017; 5(3):32. https://doi.org/10.3390/atoms5030032
Chicago/Turabian StyleStamm, Roland, Ibtissem Hannachi, Mutia Meireni, Laurence Godbert-Mouret, Mohammed Koubiti, Yannick Marandet, Joël Rosato, Milan S. Dimitrijević, and Zoran Simić. 2017. "Stark Broadening from Impact Theory to Simulations" Atoms 5, no. 3: 32. https://doi.org/10.3390/atoms5030032
APA StyleStamm, R., Hannachi, I., Meireni, M., Godbert-Mouret, L., Koubiti, M., Marandet, Y., Rosato, J., Dimitrijević, M. S., & Simić, Z. (2017). Stark Broadening from Impact Theory to Simulations. Atoms, 5(3), 32. https://doi.org/10.3390/atoms5030032






