Configuration Interaction Effects in Unresolved 5p65dN+1−5p55dN+2+5p65dN5f1 Transition Arrays in Ions Z = 79–92
Abstract
:1. Introduction
2. Results
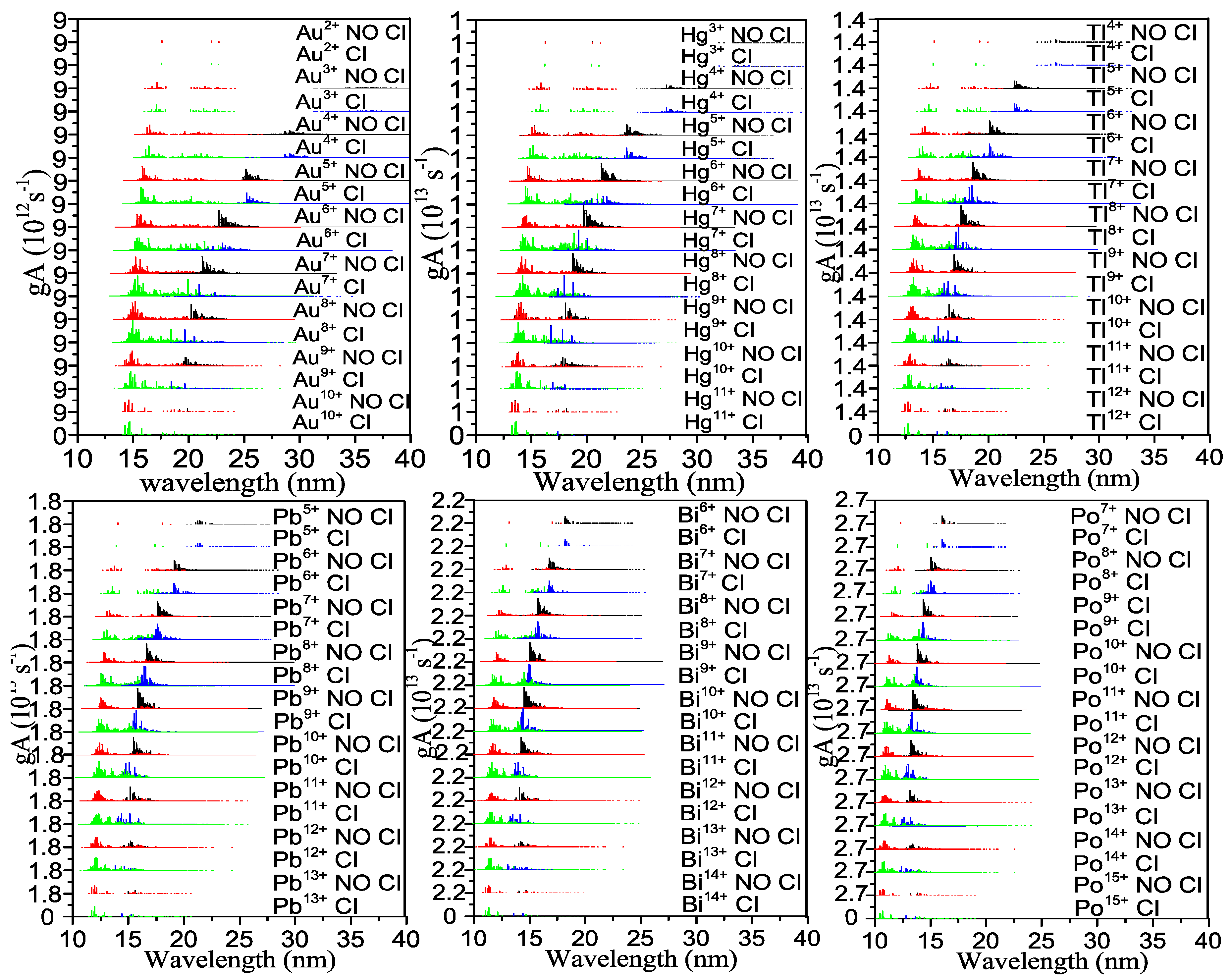
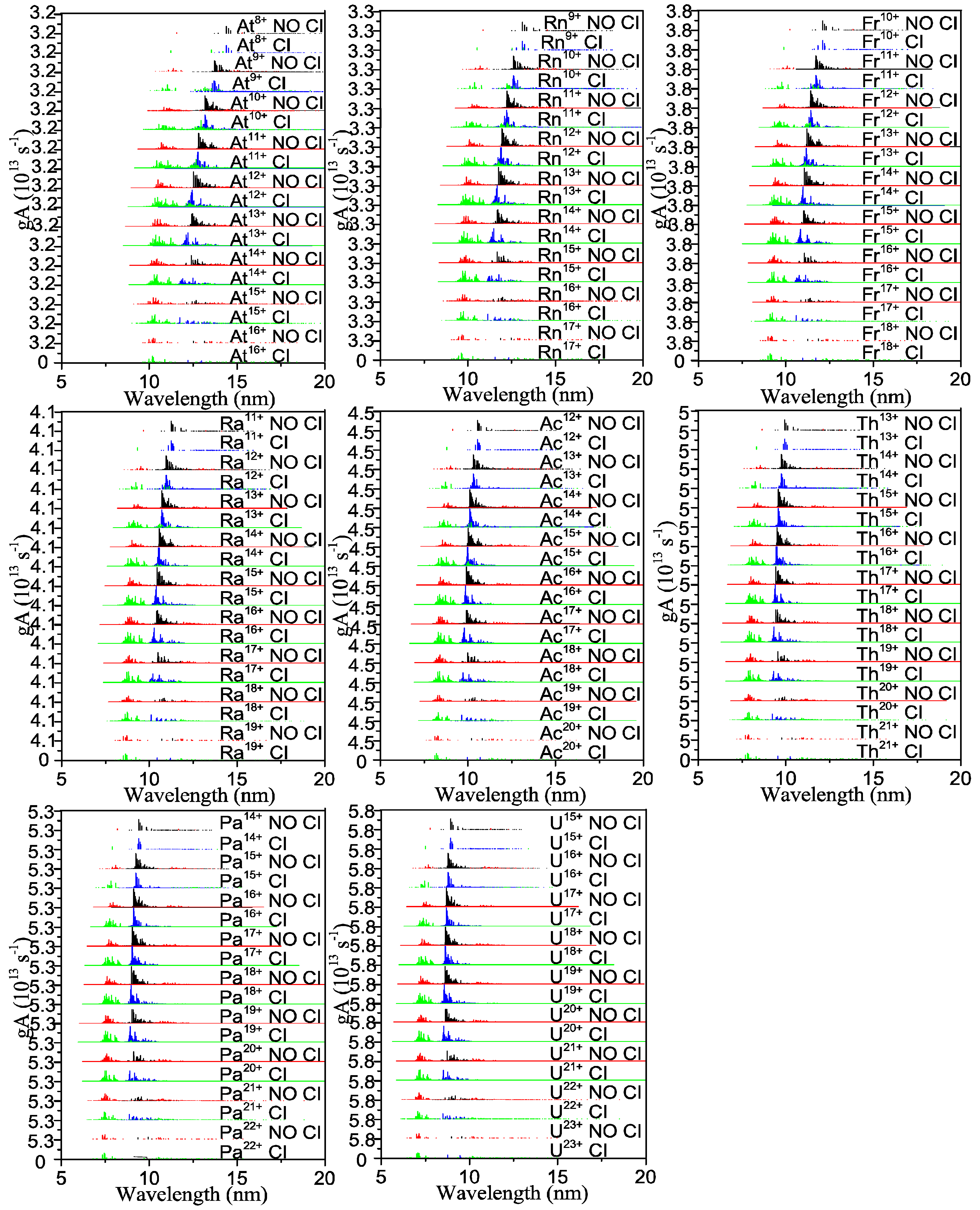
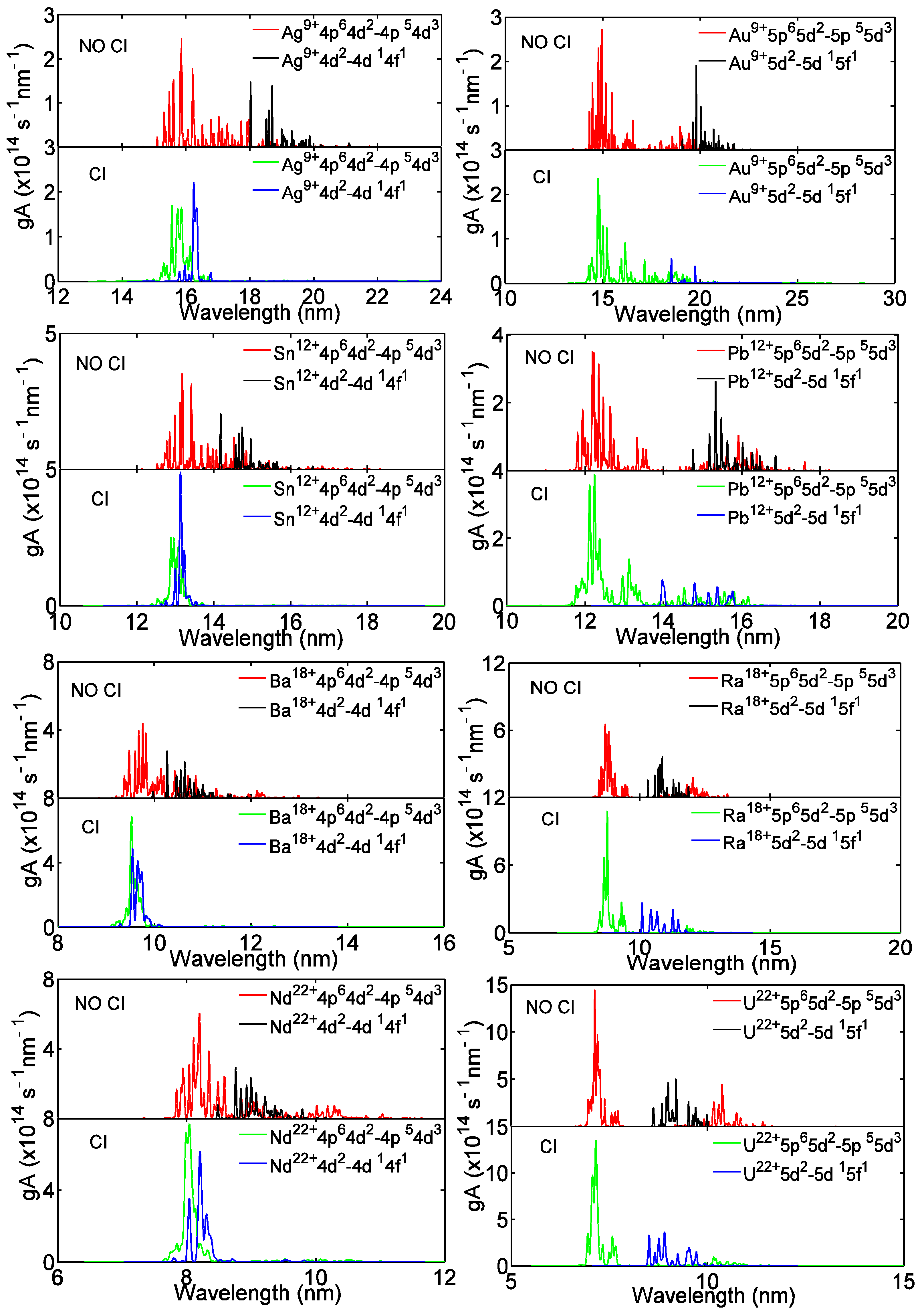
2.1. 5p−5d and 5d−5f Unresolved Transition Arrays of Ions with Z = 79-92
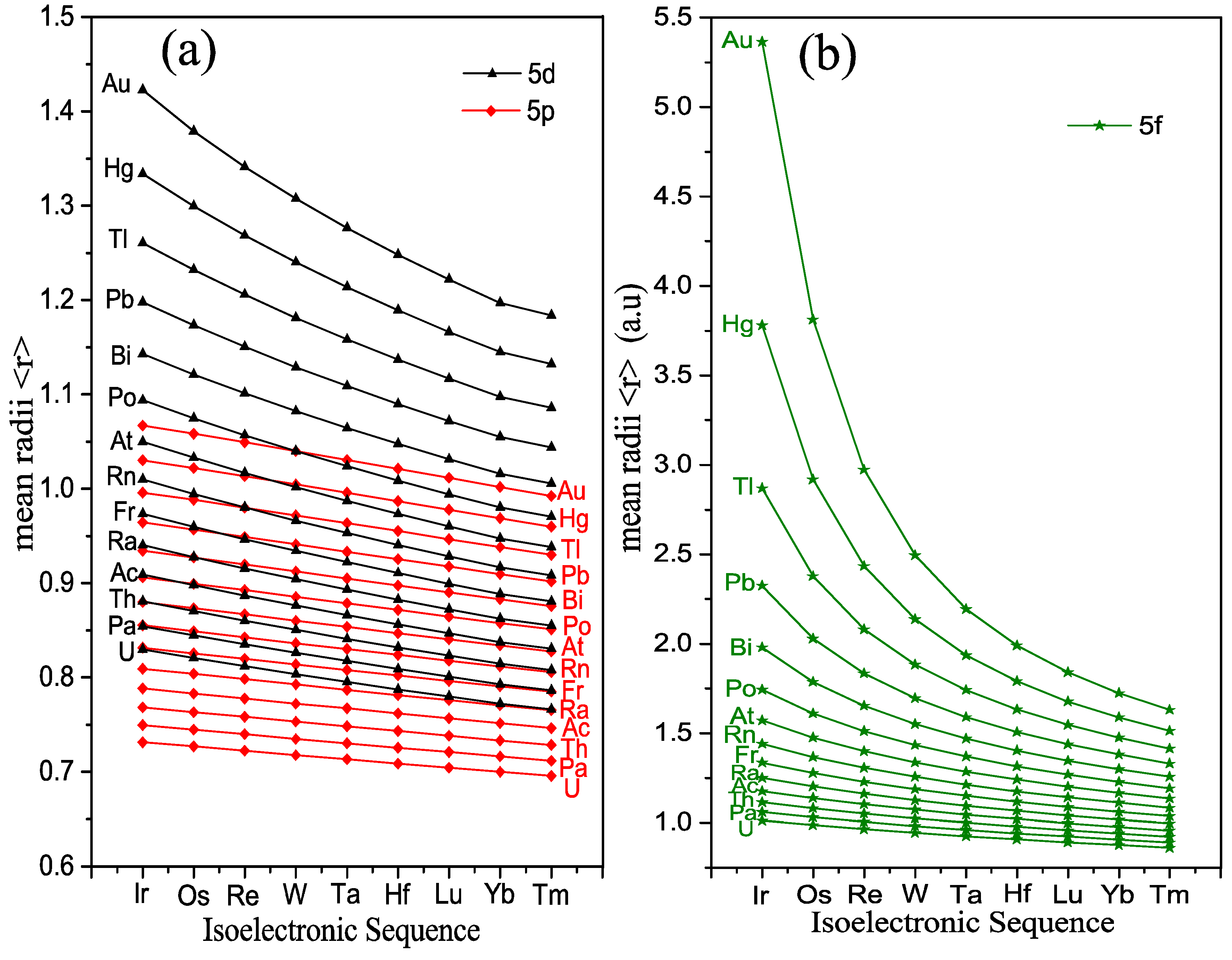
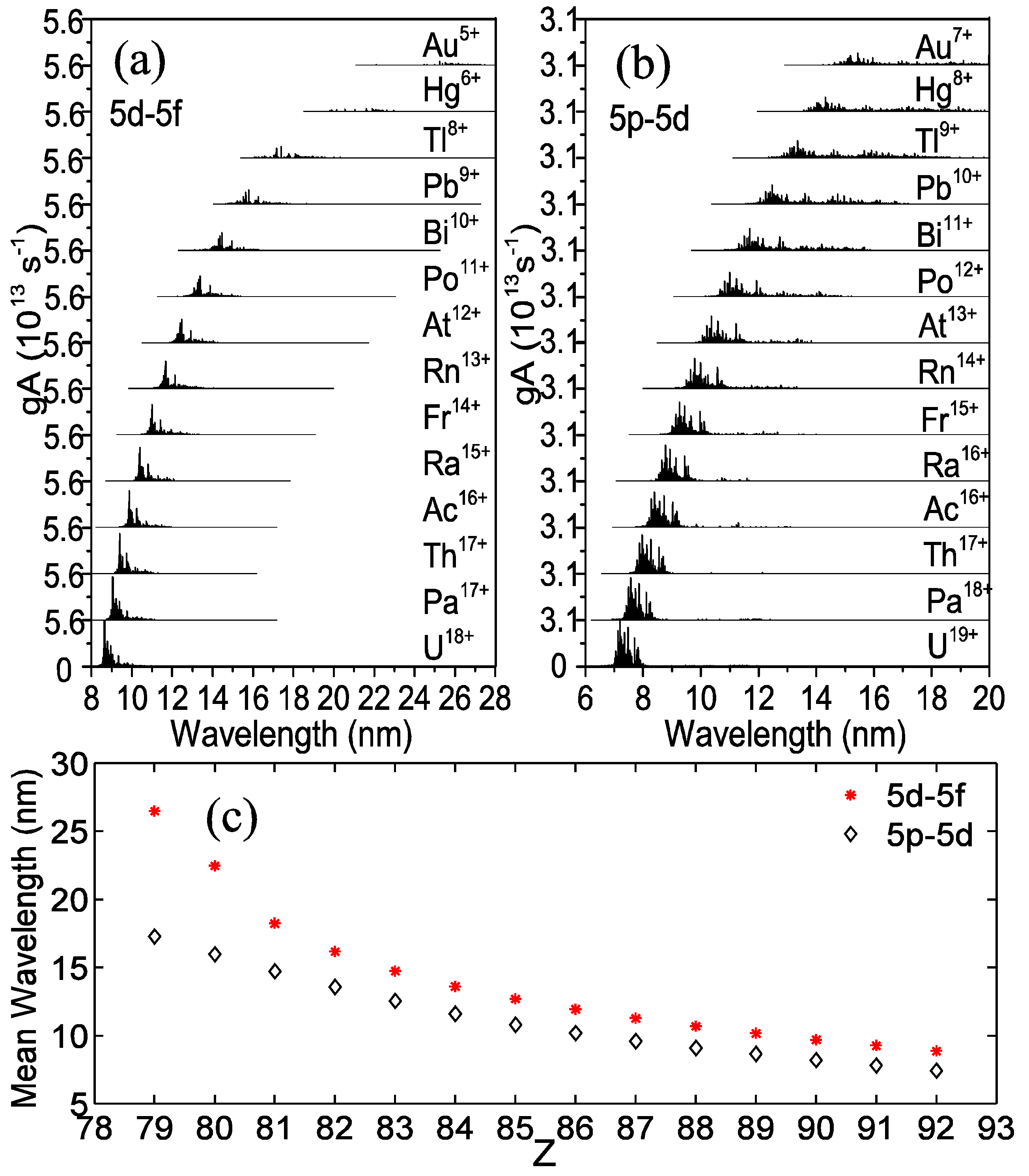
2.2. 5p−5d and 5d−5f UTA Statistics of Ions with Z = 79–92
3. Comparison of 5p65dN+−5p55dN+2+5p65dN5f1 with 4p64dN+1−4p54dN+2+4p64dN4f1 Arrays
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Van den Zande, W. EUVL exposure tools for HVM: It’s under (and about) control. In Proceedings of the EUV and Soft X-Ray Source Workshop, Amsterdam, The Netherlands, 7–9 November 2016. [Google Scholar]
- O’Sullivan, G.; Li, B.W.; D’Arcy, R.; Dunne, P.; Hayden, P.; Kilbane, D.; McCormack, T.; Ohashi, H.; O'Reilly, F.; Sheridan, P.; et al. Spectroscopy of highly charged ions and its relevance to EUV and soft X-ray source development. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 144025. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distributions of energy levels and of the transition arrays in atomic spectra. Phys. Rev. A 1979, 20, 2424–2439. [Google Scholar] [CrossRef]
- O’Sullivan, G.; Faulkner, R. Tunable narrowband soft X-ray source for projection lithography. Opt. Eng. 1994, 33, 3978–3983. [Google Scholar]
- Churilov, S.S.; Ryabtsev, A.N. Analysis of the Sn IX-Sn XII spectra in the EUV region. Phys. Scr. 2006, 73, 614. [Google Scholar] [CrossRef]
- Attwood, D.T. Soft X-rays and Extreme Ultraviolet Radiation: Principles and Applications; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Churilov, S.S.; Kildiyarova, R.R.; Ryabtsev, A.N.; Sadovsky, S.V. EUV spectra of Gd and Tb ions excited in laser-produced and vacuum spark plasmas. Phys. Scr. 2009, 80, 045303. [Google Scholar] [CrossRef]
- Cummins, T.; Otsuka, T.; Yugami, N.; Jiang, W.; Endo, A.; Li, B.; O’Gorman, C.; Dunne, P.; Sokell, E.; O’Sullivan, G.; et al. Optimizing conversion efficiency and reducing ion energy in a laser-produced Gd plasma. Appl. Phys. Lett. 2012, 100, 061118. [Google Scholar] [CrossRef]
- Yoshida, K.; Fujioka, S.; Higashiguchi, T.; Ugomori, T.; Tanaka, N.; Ohashi, H.; Kawasaki, M.; Suzuki, Y.; Suzuki, C.; Tomita, K.; et al. Efficient extreme ultraviolet emission from one-dimensional spherical plasmas produced by multiple lasers. Appl. Phys. Express 2014, 7, 086202. [Google Scholar] [CrossRef]
- Louis, E.; Mullender, S.; Bijkerk, F. Multilayer development for extreme ultraviolet and shorter wavelength lithography. In Proceedings of the International Workshop on EUV and Soft X-ray Sources, Dublin, Ireland, 7–9 November 2011. [Google Scholar]
- Skoglund, P.; Lundström, U.; Vogt, U.; Hertz, H.M. High-brightness water window electron-impact liquid-jet microfocus source. Appl. Phys. Lett. 2010, 96, 084103. [Google Scholar] [CrossRef]
- McDermott, G.; le Gros, M.A.; Larabell, C.A. Visualizing cell architecture and molecular location using soft x-ray tomography and correlated cryo-light microscopy. Annu. Rev. Phys. Chem. 2012, 63, 225–239. [Google Scholar] [CrossRef] [PubMed]
- Wachulak, P.W.; Bartnik, A.; Fiedorowicz, H.; Rudawski, P.; Jarocki, R.; Kostecki, K.; Szczurek, M. “Water window” compact, table-top laser plasma soft X-ray sources based on gas puff target. Nucl. Instrum. Methods B 2010, 268, 1692–1700. [Google Scholar] [CrossRef]
- Higashiguchi, T.; Otsuka, T.; Yugami, N.; Jiang, W.; Endo, A.; Li, B.; Dunne, P.; O’Sullivan, G. Feasibility study of broadband efficient “water window” source. Appl. Phys. Lett. 2012, 100, 014103. [Google Scholar] [CrossRef]
- Mandelbaum, P.; Finkenthal, M.; Schwob, J.L.; Klapisch, M. Interpretation of the quasicontinuum band emitted by highly ionized rare-earth elements in the 70–100-Å range. Phys. Rev. A 1987. [Google Scholar] [CrossRef]
- Koike, F.; Fritzsche, S.; Nishihara, K.; Sasaki, A.; Kagawa, T.; Nishikawa, T.; Fujima, K.; Kawamura, T.; Furukawa, H. Precise and Accurate Calculations of Electronic Transitions in Heavy Atomic Ions Relevant to Extreme Ultra-Violet Light Sources. J. Plasma Fusion Res. 2006, 7, 253. [Google Scholar]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Kilbane, D.; O’Sullivan, G. Ground-state configurations and unresolved transition arrays in extreme ultraviolet spectra of lanthanide ions. Phys. Rev. A 2010, 82, 062504. [Google Scholar] [CrossRef]
- Kilbane, D. Transition wavelengths and unresolved transition array statistics of ions with Z=72–89. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 165006. [Google Scholar] [CrossRef]
- Ohashi, H.; Higashiguchi, T.; Suzuki, Y.; Arai, G.; Li, B.; Dunne, P.; O’Sullivan, G.; Sakaue, H.A.; Kato, D.; Murakami, I.; et al. Characteristics of X-ray emission from optically thin high-Z plasmas in the soft X-ray region. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 144011. [Google Scholar] [CrossRef]
- Wu, T.; Higashiguchi, T.; Li, B.W.; Arai, G.; Harac, H.; Kondo, Y.; Miyazaki, T.; Dinh, T.-H.; O'Reilly, F.; Sokell, E.; et al. Analysis of unresolved transition arrays in XUV spectral region from highly charged lead ions produced by subnanosecond laser pulse. Opt. Commun. 2017, 385, 143–152. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J. Statistical approach to the spectra of plasmas. Phys Scr. 1992. [Google Scholar] [CrossRef]
- Condon, E.U.; Odabasi, H. Atomic Structure; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Bauche-Arnoult, C.; Bauche, J. Variance of the distributions of energy levels and of the transition arrays in atomic spectra. Phys Rev. A 1979, 20, 2424–2439. [Google Scholar] [CrossRef]
- Carroll, P.K.; O’Sullivan, G. Ground-state configuration of ionic species I through XVI for Z=57–74 and the interpretation of 4d-4f emission resonances in laser-produced plasma. Phys Rev. A 1982, 25, 275. [Google Scholar] [CrossRef]
- Connerade, J.P.; Mansfield, M.W.D. Term-dependent Hybridization of the 5f wave functions of Ba and Ba++. Phys. Rev. Lett. 1982. [Google Scholar] [CrossRef]
- O’Sullivan, G. The origin of line-free XUV continuum emission from laser-produced plasmas of the elements 62≤Z≤74. J. Phys. B 1983. [Google Scholar] [CrossRef]
- Connerade, J.P.; Esteva, J.M.; Karnatak, R.C. Giant Resonances in Atoms, Molecules and Solids; Springer: New York, NY, USA, 1987. [Google Scholar]
- Fano, U.; Cooper, J.W. Spectral distribution of atomic oscillator strengths. Rev. Mod. Phys. 1968. [Google Scholar] [CrossRef]
- Cheng, K.T.; Fischer, C.F. Collapse of the 4f orbital for Xe-like ions. Phys. Rev. A 1983. [Google Scholar] [CrossRef]
- Band, I.M.; Trzhaskovskaya, M.B. On the 5d photoabsorption spectra in the gaseous and metallic states of uranium and thorium. J. Phys. B At. Mol. Opt. Phys. 1992. [Google Scholar] [CrossRef]
- Carroll, P.K.; Costello, J.T. Giant-dipole-resonance absorption in atomic thorium by a novel two-laser technique. Phys Rev. Lett. 1986. [Google Scholar] [CrossRef] [PubMed]
- Carroll, P.K.; Costello, J.T. The XUV photoabsorption spectrum of uranium vapor. J. Phys. B At. Mol. Opt. Phys. 1987. [Google Scholar] [CrossRef]
- Carroll, P.K.; Costello, J.T.; Kennedy, E.T.; O’Sullivan, G. XUV emission from uranium plasmas: The identification of U XIII and U XV. J. Phys. B At. Mol. Opt. Phys. 1984. [Google Scholar] [CrossRef]
- Carroll, P.K.; Costello, J.T.; Kennedy, E.T.; O’Sullivan, G. XUV emission from thorium plasmas; the identification of Th XI and Th XIII. J. Phys. B At. Mol. Opt. Phys. 1986, 19, L651. [Google Scholar] [CrossRef]
- Carroll, P.K.; O’Sullivan, G. The observation of 5d-5f resonant emission in thorium in high ion stages (≈VIII to XVI). Phys. Lett. A. 1981. [Google Scholar] [CrossRef]
- Finkenthal, M.; Lippmann, S.; Moos, H.W.; Mandelbaum, P.; The TEXT Group. Highly ionized uranium emission in the soft-X-ray region 50–100 Å. Phys. Rev. A 1989. [Google Scholar] [CrossRef]
- Hayden, P.; Cummings, A.; Murphy, N.; O’Sullivan, G.; Sheridan, P.; White, J.; Dunne, P. 13.5 nm extreme ultraviolet emission from tin based laser produced plasma sources. J. Appl. Phys. 2006. [Google Scholar] [CrossRef]
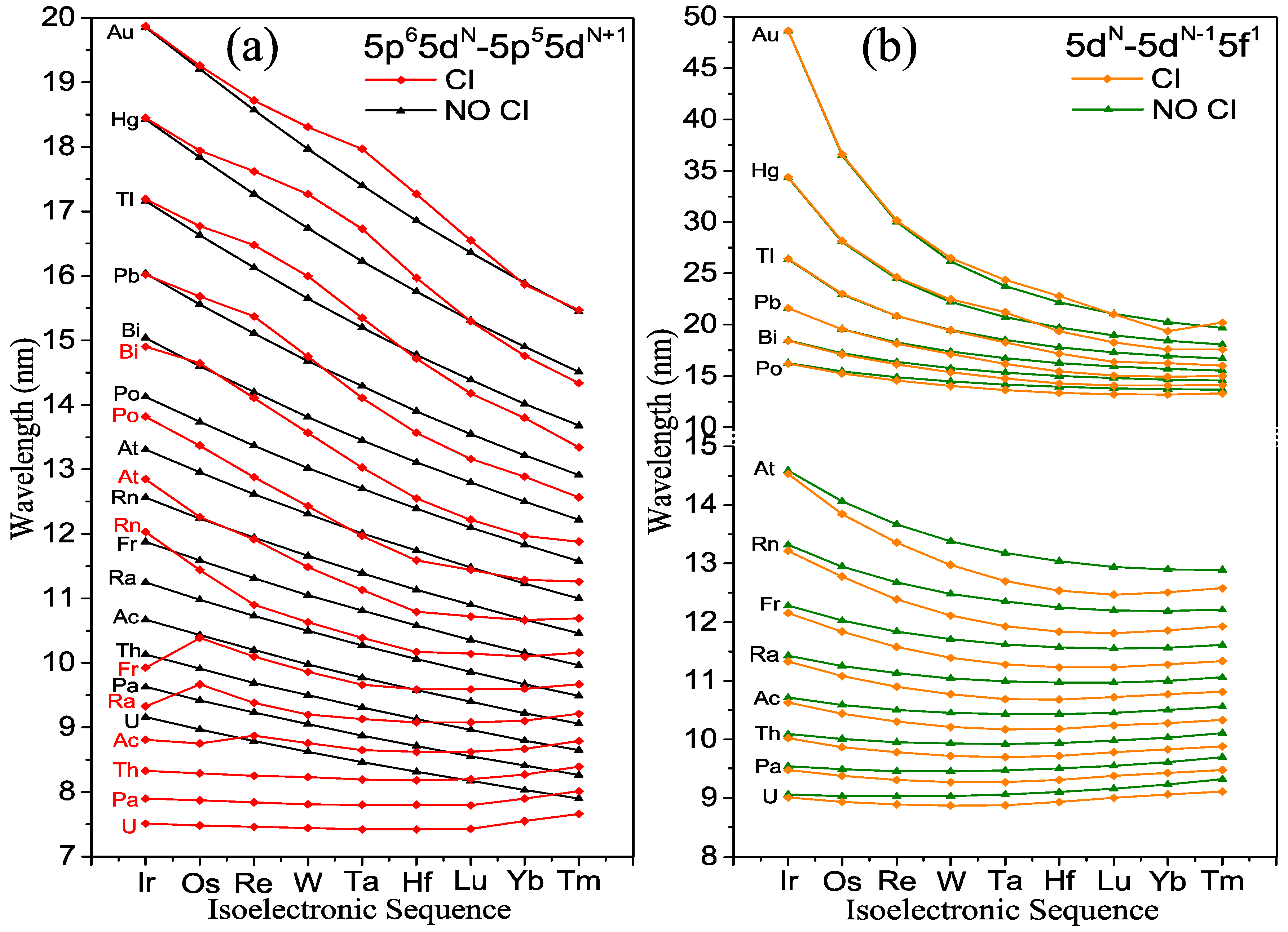
| 5d−5f (No CI) | Au | Hg | Tl | Pb | Bi | Po | At | |||||||
| Ion | ||||||||||||||
| Ir-like | 48.62 | 5.99 | 34.33 | 3.11 | 26.40 | 1.97 | 21.59 | 1.47 | 18.45 | 1.23 | 16.23 | 1.08 | 14.59 | 0.98 |
| Os-like | 36.54 | 3.83 | 28.09 | 2.39 | 22.96 | 1.80 | 19.58 | 1.51 | 17.21 | 1.34 | 15.44 | 1.22 | 14.06 | 1.13 |
| Re-like | 29.99 | 2.77 | 24.48 | 2.09 | 20.84 | 1.77 | 18.27 | 1.57 | 16.36 | 1.43 | 14.87 | 1.32 | 13.67 | 1.24 |
| W-like | 26.17 | 2.35 | 22.23 | 1.98 | 19.45 | 1.76 | 17.37 | 1.61 | 15.75 | 1.48 | 14.46 | 1.38 | 13.38 | 1.30 |
| Ta-like | 23.77 | 2.16 | 20.74 | 1.91 | 18.48 | 1.74 | 16.72 | 1.60 | 15.31 | 1.49 | 14.15 | 1.40 | 13.18 | 1.32 |
| Hf-like | 22.17 | 2.00 | 19.70 | 1.82 | 17.79 | 1.67 | 16.25 | 1.55 | 14.99 | 1.45 | 13.94 | 1.37 | 13.04 | 1.29 |
| Lu-like | 21.05 | 1.80 | 18.96 | 1.65 | 17.29 | 1.53 | 15.91 | 1.43 | 14.77 | 1.35 | 13.79 | 1.28 | 12.94 | 1.21 |
| Yb-like | 20.25 | 1.48 | 18.42 | 1.37 | 16.92 | 1.29 | 15.67 | 1.21 | 14.61 | 1.15 | 13.69 | 1.10 | 12.90 | 1.05 |
| Tm-like | 19.67 | 0.87 | 18.03 | 0.83 | 16.67 | 0.80 | 15.51 | 0.78 | 14.52 | 0.76 | 13.65 | 0.75 | 12.89 | 0.74 |
| 5d−5f (CI) | Au | Hg | Tl | Pb | Bi | Po | At | |||||||
| Ion | ||||||||||||||
| Ir-like | 48.64 | 6.00 | 34.36 | 3.16 | 26.43 | 2.10 | 21.60 | 1.69 | 18.43 | 1.45 | 16.19 | 1.25 | 14.53 | 1.10 |
| Os-like | 36.62 | 3.90 | 28.17 | 2.60 | 23.02 | 2.17 | 19.58 | 2.00 | 17.09 | 1.90 | 15.24 | 1.56 | 13.85 | 1.30 |
| Re-like | 30.15 | 2.99 | 24.63 | 2.69 | 20.86 | 2.66 | 18.16 | 2.51 | 16.13 | 2.07 | 14.55 | 1.61 | 13.36 | 1.36 |
| W-like | 26.48 | 2.89 | 22.47 | 3.18 | 19.43 | 3.05 | 17.12 | 2.58 | 15.33 | 2.03 | 14.00 | 1.59 | 12.98 | 1.37 |
| Ta-like | 24.34 | 3.15 | 21.21 | 3.46 | 18.24 | 3.00 | 16.18 | 2.35 | 14.75 | 1.85 | 13.62 | 1.55 | 12.70 | 1.39 |
| Hf-like | 22.79 | 3.29 | 19.36 | 3.60 | 17.19 | 2.64 | 15.46 | 2.03 | 14.26 | 1.68 | 13.33 | 1.50 | 12.54 | 1.43 |
| Lu-like | 21.01 | 3.24 | 18.25 | 2.88 | 16.35 | 2.08 | 15.02 | 1.73 | 14.06 | 1.61 | 13.20 | 1.51 | 12.47 | 1.43 |
| Yb-like | 19.37 | 2.34 | 17.60 | 1.79 | 16.25 | 1.42 | 14.92 | 1.70 | 14.06 | 1.53 | 13.18 | 1.37 | 12.51 | 1.37 |
| Tm-like | 20.19 | 0.16 | 17.56 | 0.12 | 15.99 | 1.05 | 14.98 | 1.00 | 14.09 | 0.97 | 13.29 | 0.94 | 12.58 | 0.92 |
| 5d−5f (No CI) | Rn | Fr | Ra | Ac | Th | Pa | U | |||||||
| Ion | ||||||||||||||
| Ir-like | 13.32 | 0.91 | 12.28 | 0.85 | 11.43 | 0.80 | 10.71 | 0.77 | 10.09 | 0.73 | 9.54 | 0.71 | 9.06 | 0.68 |
| Os-like | 12.95 | 1.06 | 12.03 | 1.00 | 11.25 | 0.95 | 10.59 | 0.90 | 10.01 | 0.86 | 9.49 | 0.83 | 9.03 | 0.80 |
| Re-like | 12.68 | 1.16 | 11.84 | 1.10 | 11.13 | 1.04 | 10.50 | 1.00 | 9.95 | 0.95 | 9.46 | 0.92 | 9.03 | 0.88 |
| W-like | 12.48 | 1.22 | 11.71 | 1.16 | 11.04 | 1.10 | 10.45 | 1.05 | 9.93 | 1.01 | 9.46 | 0.97 | 9.03 | 0.94 |
| Ta-like | 12.35 | 1.25 | 11.62 | 1.18 | 10.99 | 1.13 | 10.43 | 1.08 | 9.92 | 1.04 | 9.47 | 1.00 | 9.06 | 0.97 |
| Hf-like | 12.25 | 1.23 | 11.57 | 1.17 | 10.97 | 1.12 | 10.43 | 1.08 | 9.94 | 1.04 | 9.50 | 1.00 | 9.10 | 0.97 |
| Lu-like | 12.20 | 1.16 | 11.55 | 1.11 | 10.97 | 1.07 | 10.45 | 1.03 | 9.98 | 1.00 | 9.55 | 0.97 | 9.16 | 0.94 |
| Yb-like | 12.19 | 1.01 | 11.56 | 0.98 | 11.00 | 0.95 | 10.50 | 0.92 | 10.03 | 0.90 | 9.61 | 0.88 | 9.23 | 0.86 |
| Tm-like | 12.21 | 0.73 | 11.61 | 0.72 | 11.06 | 0.72 | 10.56 | 0.71 | 10.11 | 0.71 | 9.70 | 0.71 | 9.32 | 0.71 |
| 5d−5f (CI) | Rn | Fr | Ra | Ac | Th | Pa | U | |||||||
| Ion | ||||||||||||||
| Ir-like | 13.22 | 0.99 | 12.16 | 0.84 | 11.33 | 0.77 | 10.63 | 0.71 | 10.02 | 0.68 | 9.48 | 0.65 | 9.01 | 0.63 |
| Os-like | 12.78 | 1.11 | 11.84 | 0.98 | 11.08 | 0.90 | 10.44 | 0.83 | 9.87 | 0.79 | 9.38 | 0.77 | 8.93 | 0.74 |
| Re-like | 12.39 | 1.19 | 11.58 | 1.06 | 10.90 | 0.99 | 10.30 | 0.94 | 9.78 | 0.90 | 9.31 | 0.87 | 8.89 | 0.85 |
| W-like | 12.11 | 1.22 | 11.39 | 1.15 | 10.77 | 1.09 | 10.21 | 1.05 | 9.72 | 1.01 | 9.27 | 0.98 | 8.87 | 0.96 |
| Ta-like | 11.93 | 1.29 | 11.28 | 1.24 | 10.69 | 1.19 | 10.17 | 1.14 | 9.70 | 1.11 | 9.27 | 1.01 | 8.88 | 1.05 |
| Hf-like | 11.84 | 1.36 | 11.23 | 1.30 | 10.68 | 1.27 | 10.18 | 1.23 | 9.72 | 1.18 | 9.31 | 1.15 | 8.93 | 1.12 |
| Lu-like | 11.81 | 1.38 | 11.23 | 1.32 | 10.72 | 1.29 | 10.24 | 1.26 | 9.78 | 1.22 | 9.38 | 1.18 | 9.00 | 1.14 |
| Yb-like | 11.86 | 1.27 | 11.28 | 1.22 | 10.77 | 1.17 | 10.28 | 1.12 | 9.83 | 1.08 | 9.43 | 1.06 | 9.06 | 1.04 |
| Tm-like | 11.93 | 0.90 | 11.34 | 0.89 | 10.81 | 0.87 | 10.33 | 0.86 | 9.88 | 0.85 | 9.48 | 0.84 | 9.11 | 0.83 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Kilbane, D.; Dunne, P.; Wang, X.; O’Sullivan, G. Configuration Interaction Effects in Unresolved 5p65dN+1−5p55dN+2+5p65dN5f1 Transition Arrays in Ions Z = 79–92. Atoms 2017, 5, 20. https://doi.org/10.3390/atoms5020020
Liu L, Kilbane D, Dunne P, Wang X, O’Sullivan G. Configuration Interaction Effects in Unresolved 5p65dN+1−5p55dN+2+5p65dN5f1 Transition Arrays in Ions Z = 79–92. Atoms. 2017; 5(2):20. https://doi.org/10.3390/atoms5020020
Chicago/Turabian StyleLiu, Luning, Deirdre Kilbane, Padraig Dunne, Xinbing Wang, and Gerry O’Sullivan. 2017. "Configuration Interaction Effects in Unresolved 5p65dN+1−5p55dN+2+5p65dN5f1 Transition Arrays in Ions Z = 79–92" Atoms 5, no. 2: 20. https://doi.org/10.3390/atoms5020020
APA StyleLiu, L., Kilbane, D., Dunne, P., Wang, X., & O’Sullivan, G. (2017). Configuration Interaction Effects in Unresolved 5p65dN+1−5p55dN+2+5p65dN5f1 Transition Arrays in Ions Z = 79–92. Atoms, 5(2), 20. https://doi.org/10.3390/atoms5020020






