You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Atoms
Download PDF
  • Article
  • Open Access

13 June 2017

The Third Spectrum of Indium: In III

and
Physics Department, Aligarh Muslim University, Aligarh 202002, India
*
Author to whom correspondence should be addressed.
Atoms2017, 5(2), 23;https://doi.org/10.3390/atoms5020023
This article belongs to the Special Issue Spectra of Ionized Atoms: From Laboratory to Space
Version Notes
Order Reprints

Abstract

The present investigation reports on the extended study of the third spectrum of indium (In III). This spectrum was previously analyzed in many articles, but, nevertheless, this study represents a significant extension of the previous analyses. The main new contribution is connected to the observation of transitions involving core-excited configurations. Previous data are critically evaluated and in some cases are corrected. The spectra were recorded on 3-m as well as on 10.7-m normal incidence spectrographs using a triggered spark source. Theoretical calculations were made with Cowan’s code. The analysis results in the identifications of 70 spectral lines and determination of 24 new energy levels. In addition, the manuscript represents a compilation of all presently available data on In III.

1. Introduction

The third spectrum of indium (In III) belongs to the Ag I isoelectronic sequence with the ground state [Kr] 4d105s 2S1/2. The outer electronic excitation gives rise to the [Kr] 4d10nℓ (n ≥ 5, for ℓ ≤ 2; n ≥ ℓ + 1 otherwise) type of configurations with a simple doublet structure, while core excitation involving the configurations such as 4d95s (5p + 4f), 4d95s2 and 4d95p2 makes a complex three-electron system having both doublet and quartet terms.
Several authors studied the In III spectrum, and it is appropriate to summarize their work briefly. The first work on the third spectrum of indium was done by Rao et al. [], followed by Lang [], Douglas [] and Nodwell []. Rao et al. [] identified 12 lines in the wavelength region 2983–5918 Å and established 13 levels belonging to the 4d10(5s, 6s, 7s, 5p, 6p, 5d, 6d, 4f, 5f and 5g) configurations. However, only six of those levels could be verified by later workers [,,]. Nodwell [] studied the indium spectrum in more detail. He recorded the indium spectra on a 2-m vacuum grating spectrograph and identified 56 lines of In III in the wavelength region 685–6198 Å. He established 27 energy levels including six doubtful. This work is listed in the Atomic Energy Levels (AEL) compilation []. Bhatia [] investigated the In III spectrum more comprehensively using a 3-m normal incidence vacuum spectrograph in the range 340–2300 Å with a 1200 lines/mm grating giving a reciprocal dispersion of 2.775 Å/mm and a prism spectrograph in the region 2300 Å to 9500 Å with a disruptive electrodeless discharge. He revised and extended the earlier analysis and established the levels of the 4d10ns (n = 5–12), 4d10np (n = 5–9), 4d10nd (n = 5–9), 4d10nf (n = 4–7), 4d10ng (n = 5–9), 4d10nh (n = 6–9), 4d95s2, and 4d95s5p configurations. Kaufman et al. [] studied the core-excited transition array 4d105s–4d95s5p in the isoelectronic sequence from In III to Te VI. The spectra were recorded on 10.7-m normal and grazing incidence spectrographs using a sliding spark source. Out of 23 possible levels of the 4d95s5p configuration, they reported only 10 that can combine with the ground level 4d105s 2S1/2. Kilbane et al. [] studied photoabsorption spectra of In II–IV with a dual laser plasma (DLP) technique. They reported the 4d105s–{4d95snp (n = 6–11) + 4d95snf (n = 4–11)} transition array. They could not observe the 4d105s–4d95s5p transitions as they lie beyond the region of their investigation. Recently, Ryabtsev et al. [] added a new configuration 4d95p2 to the In III-Te VI sequence and observed the 4d105p–4d95p2 transition array in the range 250–600 Å using a 6.65-m normal incidence spectrograph equipped with a 1200 lines/mm grating giving a reciprocal linear dispersion of 1.25 Å/mm. They were able to determine only 13 levels out of 28 levels of the 4d95p2 configuration. Skočić et al. [] studied Stark shifts of some prominent lines of In III (6s–6p, 6p–6d, and 4f–5d).
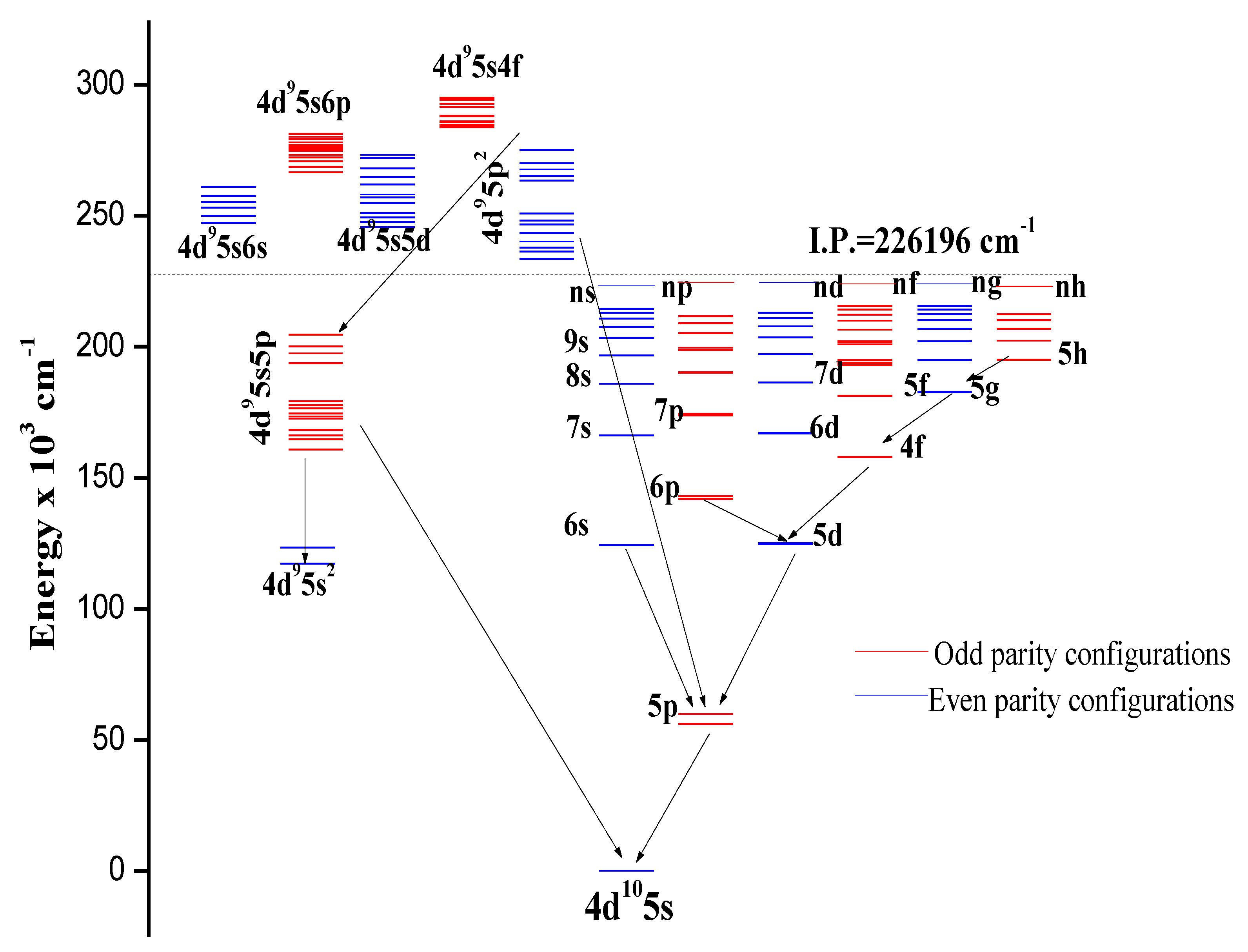
As mentioned above, a number of publications on In III appeared in the literature [,,,,,,,,,,]. Among these, Bhatia’s [] analysis was the most comprehensive and contained a large number of one-electron configurations. However, after careful examination of these results, a number of irregularities were noticed in Bhatia’s results, for example, many lines classified did not match the In III characteristics on our recorded spectra and 17 reported lines have incorrect conversion between wavenumbers and wavelengths. Moreover, the levels of the 4d95s5p configuration reported by Kaufman et al. [] and the levels of 4d95p2 configuration established by Ryabtsev et al. [] are still incomplete. These facts prompted us to re-investigate the In III spectrum in detail. A Grotrian energy level diagram of In III is illustrated in Figure 1 showing the basic configurations and possible transition between them.
Figure 1. Grotrian diagram of In III. “I.P.” denotes the ionization potential (see Section 6). Arrows denote the observed transition arrays.

2. Experiment Detail

The spectra were recorded at two different places. A 3-m vacuum spectrograph equipped with 2400 lines per mm holographic grating was employed at Antigonish laboratory in Nova Scotia, Canada with a triggered spark source to cover the wavelength region 350–2080 Å. This spectrograph gives the first order inverse dispersion of 1.385 Å/mm. For ionization separation of the spectral lines, either the charging potential of the source was varied or an inductance with a varying number of turns was inserted in series in the circuit. The charging unit was a 14.5 µF low inductance fast charging capacitor and the charging potential was varied between 2 and 6 kV. Y.N. Joshi of St. Francis Xavier University, Antigonish (Canada) provided the indium spectra that were recorded on the 10.7-m normal incidence vacuum spectrograph of the National Institute of Standards and Technology (NIST) also using a triggered spark source. The NIST spectrograph was equipped with 1200 lines/mm grating with an inverse dispersion 0.78 Å/mm. The spectrograms were measured either on an Abbec comparator at Aligarh or on a semi-automatic Grant’s comparator in Antigonish, Canada. Known standard lines of oxygen, carbon, aluminium and silicon [] were used as internal standards for the calibration of wavelengths. We estimated our measurements uncertainty for sharp and unblended lines to be within ±0.006 Å for wavelength below 900 Å and ±0.008 Å above that.

3. Theoretical Calculations

The ab initio calculations were performed by the Hartree–Fock method with relativistic corrections using Cowan code [] with superposition of configurations including 4d10ns (n = 5–12), 4d10nd (n = 5–9), 4d10ng (n = 5–9), 4d9(5s2 + 5p2), 4d95s(5d + 6s) configurations for the even parity system and 4d10np (n = 5–9), 4d10nf (n = 4–7), 4d10nh (n = 6–9), 4d95snp (n = 5–11), 4d95snf (n = 4–12), 4d85s25p for the odd parity matrix involving a total of 52 configurations in our calculations. The initial scaling of the Slater energy parameters was kept at 100% of the Hartree–Fock values for Eav and ζnl, 85% for Fk, and 80% for the Gk as well as Rk integrals. These parameters were more refined at a later stage as least squares fitted parametric calculations were performed. The main output from these programs includes the values of energy levels, wavelengths, weighted transition rates and weighted oscillator strengths. The transition probability of lines depends on the line strength and is greatly affected by the cancellation factor [], is also calculated by Cowan’s code programs []. The Hartree–Fock (HFR) and least-squares-fitted (LSF) energy parameters used in the present calculations are given in Table 1 along with their scaling factor (ratio of the LSF value to the HFR value) of the parameters. The standard deviations for the even and odd parity systems are 172 cm−1 and 216 cm−1, respectively.
Table 1. Least Square Fitted (LSF) Energy Parameters (in cm−1) for In III.

4. Spectrum Analysis

The initial approach of the analysis was to identify In III lines with correct ionization character. A computer code FIND3 [] was useful in the analysis to search for new levels. A total of 91 levels have been established, of which 24 are new; they are assembled in Table 2 along with least squares fitted values and LS percentage composition. Two hundred fifty-one lines have been classified in In III and they are given in Table 3 along with their transition probabilities. In the present analysis, apart from the one- electron spectrum 4d10nℓ, the configurations involving inner-shell excitation, such as 4d95s (5p + 4f), 4d95s2 and 4d95p2 have also been studied extensively. The following sections describe them in detail.
Table 2. Optimized energy levels of in III.
Table 3. List of classified lines in In III spectrum.

4.1. The 4d105s– [4d10np] Transition Array

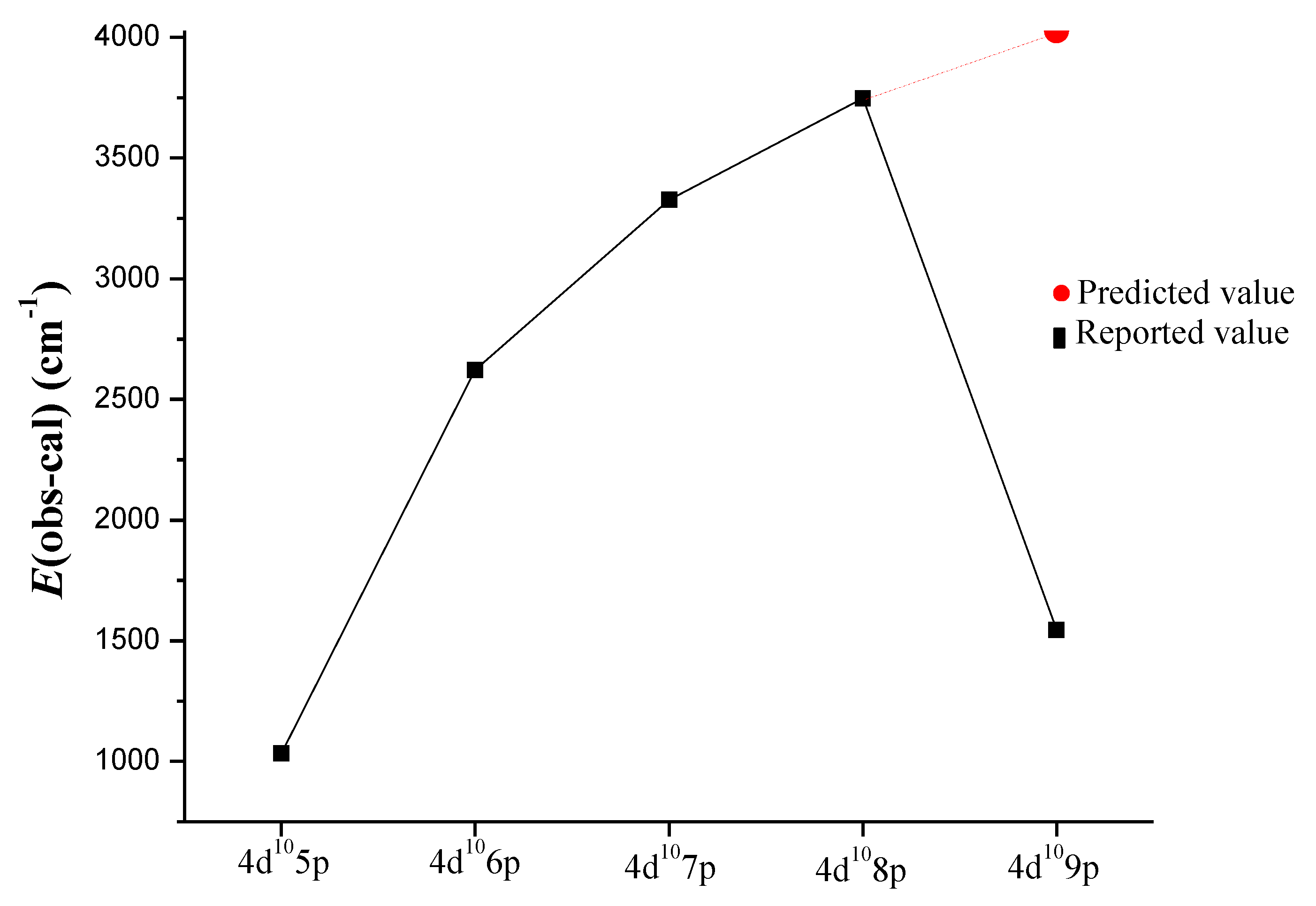
The resonance transitions 4d105s–4d105p were first reported by Rao [], and confirmed by all other workers [,,,]. We observed these two lines in our indium spectra with high intensity. They were the main reference in establishing the In III ionization characteristics. Bhatia [] reported the levels of 4d10np (n = 5–9). We agreed with Bhatia’s analysis only up to 4d108p. The 4d105s–4d109p transitions could not be seen in our spectra. The reported level value of 4d109p 2P3/2,1/2 at 201,180.3 cm−1 did not fit in our least squares fitted parametric calculations. Our predicted values were found to be at 203,388.5 cm−1 and 203,556.3 cm−1 for 2P3/2 and 2P1/2, respectively. A plot of the energy differences between observed and Hartree–Fock (HF) calculated values of 4d10np (n = 5–9) 2P3/2 series is shown in Figure 2, and it is evident from this figure that the reported value for 4d109p levels shows an irregular behavior. Therefore, this reported level seems to be doubtful. We did not find any alternative value as 4d109p transitions were too weak to be observed on our plates.
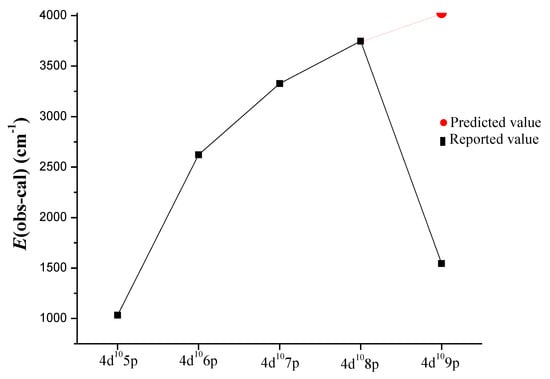
Figure 2. A plot of the observed and calculated energy difference in 4d10np series of In III.

4.2. The 4d10np–[4d10 {ns + nd} + 4d95s2] Transition Array

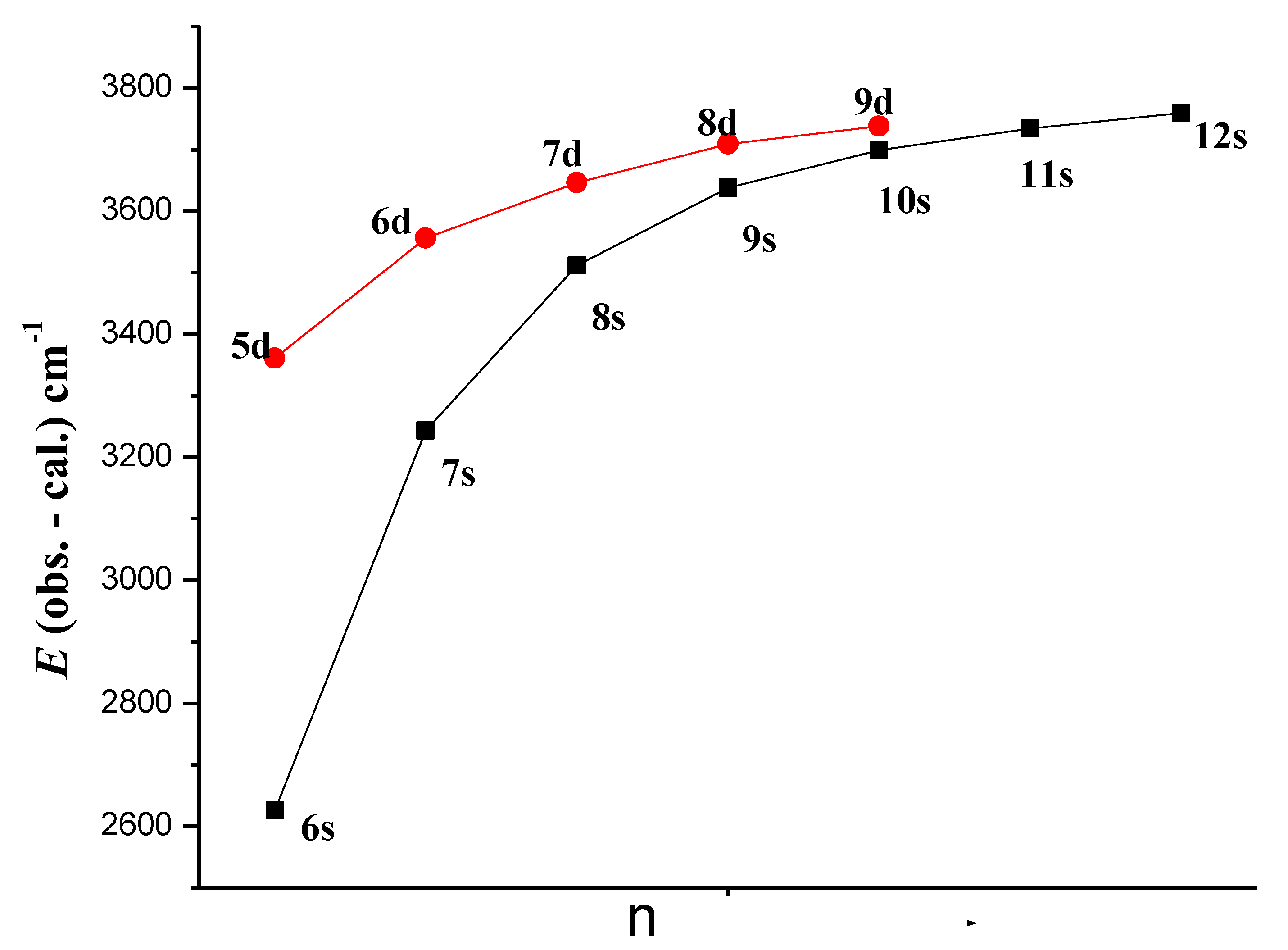
The second excitation, 4d105p–[4d10(6s + 5d) + 4d95s2] transitions, is also observed to be quite strong. In the 4d10ns series, we observed transitions 4d105p–4d10 ns (n = 6–8) and 4d106p–4d10ns (n = 9–12), and, in the 4d10nd series, three transitions are possible between each of the 4d10np–4d10nd configurations out of which two transitions, namely 2P1/2–2D3/2 and 2P3/2–2D5/2, were observed to be quite strong, while the third transition, 2P3/2–2D3/2, was predicted to be weak in the series. All these three transitions were observed in 4d10[5p–nd (n = 5–7)]. Thus, we confirmed the levels of the 4d10ns (n = 6–12) and 4d10nd (n = 5–7) configurations. The transitions from 4d10nd (n = 8, 9) to 4d105p were not observed on our plates. However, these transitions were reported by Bhatia []. We examined these levels and found their scaling factor to be quite regular. Secondly, a similar plot as in Figure 2 with the average energy difference between the calculated and observed values shows a regular behavior for the 4d10ns and 4d10nd series (Figure 3). Although we could not confirm the levels of the 4d10nd (n = 8, 9) configurations, on the basis of their regularity, we included them in Table 2 for the sake of completeness.
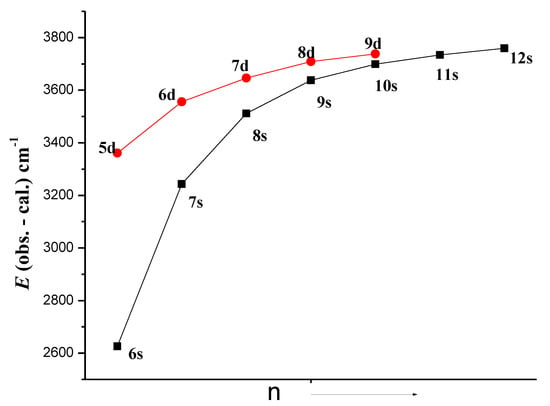
Figure 3. A plot E(obs-cal) for the 4d10ns and 4d10nd series in In III.
The other configuration 4d95s2 in even parity system has two inverted 2D levels having the same energy range as the 4d105d 2D levels. Both 2D levels of these two configurations interact with each other. As a result of this interaction, 4d105p–4d95s2 transitions are observed. Further confirmation of these two levels was made by the observed transitions from the levels of the 4d95s5p configuration that will be discussed later.

4.3 The 4d10(nf + ng + nh) Configurations

The 4d105d–4d104f transitions lie beyond our wavelength region of investigation (above 2080 Å); therefore, we could not confirm them experimentally in the present work. However, these levels were well established by Nodwell [] along with levels of the 4d10ng (n = 5–7) series by observing transitions from 4d104f. The repeated appearance of the 4d104f 2F5/2,7/2 interval in transitions from the 4d10(5g, 6g and 7g) 2G7/2,9/2 levels confirms the correctness of the 4d104f levels. The latter were compiled in AEL [] and were later confirmed by Bhatia []. The 4d105d–4d105f transitions lie in our wavelength region. We observed a pair of lines from 4d105d 2D3/2 and 2D5/2, and two transitions from 4d95s2 2D5/2,3/2, thus confirming 4d105f 2F5/2. The other level 4d105f 2F7/2 is also expected to gives two transitions, one from 4d105d 2D5/2 and the other from 4d95s2 2D5/2; both were in fact found. Furthermore, the level positions agree well with theoretical prediction of an inverted doublet. The 4d106f 2F5/2,7/2 levels are strongly mixed with the 4d95s5p 2F5/2,7/2 levels. Bhatia [] reported only the 4d106f 2F5/2 level at 198,499.3 cm−1, but our least squares fitted calculation predicted at 191,337 cm−1. This large deviation does not seem to be right. Bhatia [] reported unresolved 4d107f levels, but we did not find his identified lines on our line list. Therefore, his 4d106f and 4d107f levels could not be confirmed.
Neither the 4d104f–4d10ng (n = 5–7) nor 4d105g–4d10nh (n = 7–9) transitions lie in our wavelength region. Therefore, they could not be confirmed in the present work. However, we have compared Bhatia’s experimental results [] with theoretical calculations for the known spectra in the isoelectronic sequence from Ag I–Sn IV [], and they appear to be regular. The 4d104f–(8g + 9g) transitions do lie in our wavelength region, but they are too weak to be verified. However, we have included them in our LSF calculations for the sake of completeness.

4.4 The 4d95s5p Configuration

This configuration arises due to core excitation of the ground level configuration 4d105s. A number of levels from this configuration were reported by Bhatia []. Kaufman et al. [] revised three levels of this configuration by observing transitions from the ground level 4d105s 2S1/2, thus connecting only J = 1/2 and 3/2 levels. The remaining levels of Bhatia (with J = 5/2, 7/2 and 9/2) still remain to be verified. In the present investigation, we agreed with six levels of Kaufman et al. [] but revised four levels. The ionization separation on our recorded spectrum in this wavelength region was quite clear, thus new levels could be found with full confidence. The level 2P1/2 reported by Bhatia [] at 199,561.2 cm−1 was revised by Kaufman et al. [] to a new position at 197,081 cm−1. The line (507.406 Å) used by Kaufman et al. [] for this transition actually belongs to O III (507.391 Å) [] and the line used by Bhatia was not found on our spectrograms. We found an unclassified In III line with moderate intensity at 504.080 Å that has been assigned to this transition, yielding the level value at 198,382.2 cm−1 that also fits well in the least squares calculations.
Kaufman et al. [] had revised another J = 1/2 level of Bhatia [] and re-designated it as a J = 3/2 level at 170,888 cm−1 based on Bhatia’s line list as they did not observe the corresponding lines. We also could not find the lines associated with this level in our line list. Therefore, this level was rejected. According to our analysis, we found that the lowest J = 1/2 level reported by Kaufman et al. [] at 170,812 cm−1 is in fact a J = 3/2 level and the replacement for the lowest J = 1/2 level is found at 171,315.7 cm−1. The lowest J = 3/2 level of this configuration reported by Kaufman et al. [] at 167,079 cm−1 is in fact based on an In IV line (598.526 Å) [,]. However, Bhatia [] had reported this level at 167,339.1 cm−1, which was based on a correct In III line at (597.589 Å), and we agree with this identification. Moreover, it also gives two transitions from the recently found 4d95p2 configuration [] that confirm the identification of this level.
The highest J = 3/2 level was not found by Kaufman et al. [] because calculations predict a weak transition to the ground level. However, Bhatia [] had reported this level at 202,132.3 cm−1. We found two strong lines with correct In III ionization characteristics, which we classified as transitions from 4d95s2 levels to the level in question. Thus, we confirmed Bhatia’s level value. Table 4 shows the summary of the J = 1/2 and 3/2 levels of the 4d95s5p configuration given by previous researchers [,] and the present analysis.
Table 4. Energy level values (J = 1/2 & 3/2 Levels) of 4d95s5p Configuration.
The remaining 12 levels of this configuration with higher J values (5/2–9/2) were considered next. These levels have only been reported by Bhatia [] through the transitions from 4d95s2. We found lines corresponding to transitions from the J = 5/2 level at 194,902.6 cm−1 and confirmed only this level in Bhatia’s list. We were successful in locating 10 remaining levels of J = 5/2 and 7/2 from transitions to 4d95s2 and 4d95p2 levels. The level with the highest J value (9/2) does not connect to any other known configuration except 4d95p2, which was partially known. We extended that configuration to include J = 7/2 levels. This paved the way for the establishment of the J = 9/2 level. We found three transitions placing the J = 9/2 level at 168,947.6 cm−1. All 23 levels of 4d95s5p configuration are now known experimentally.

4.5. The 4d95s (nf + np) Configurations

These are the configurations that arise due to the core excitation. The 4d95s4f configuration has a large energy spread and contains 39 levels. Since the ground configuration contains only the 2S1/2 level, only J = 1/2 and 3/2 levels of the 4d95s4f configuration can decay to the ground configuration. Kilbane et al. [] have studied the 4d95snf (n = 4–12) and 4d95snp (n = 6–11) configurations using a photoabsorption technique. They reported 10 levels of 4d95s4f and seven levels of 4d95s6p belonging to J = 1/2 and 3/2. In our spectra, these transitions lie in the shorter wavelength region, where reflectivity of the grating falls considerably in the normal incidence setting. Therefore, these transitions appeared with very weak intensity on our spectrograms. Secondly, a large number of In V [] and In VI [] transitions overlap in this region. Therefore, it was very difficult to identify confidently In III lines of this array. Moreover, these levels lie above the ionization limit and consequently have a very small population. Therefore, these levels could not be located in the present work. However, we performed least squares fitted parametric calculations to provide a precise prediction of the remaining levels of the 4d95snf (n = 4–7) and 4d95snp (n = 6–7) configurations based on the identification made in reference [].

4.6. The 4d95p2 Configuration

The first attempt to study the low-lying autoionizing configuration 4d95p2 in the sequence In III–Te VI was made by Ryabtsev et al. [], connecting this configuration with 4d105p. It is important to note that all the levels of this configuration lie above the ionization limit. It was difficult to arrange experimental conditions providing for a reasonable population above the ionization limit. Certainly it was advantageous to identify the broad lines due to continuum effect, but only the strongest transitions could be observed. Not many pairs connecting to both 4d105p 2P1/2,3/2 were found to confirm these levels. However, the lines used to locate these levels have a definite In III characteristic and show continuum broadening effect. Out of 28 levels of 4d95p2, only 13 levels with J = 1/2, 3/2 and 5/2 were reported by Ryabtsev et al. []. We should point out that two levels (1D) 2S1/2 and (1D) 2P3/2 were reported by Ryabtsev et al. [] with the same energy level values. They were based on the double classification of the same pair of lines (555.669 Å and 569.421 Å). We agreed with assignments of these lines to (1D) 2P3/2 giving the level value at 237,145.6 cm−1 as both transitions are predicted to be of the comparable intensity. However, the (1D) 2S1/2 level is predicted to have one strong and one weak transition, and we found one unclassified line on our plate at 555.501 Å, which we used to establish this level at 237,201.7 cm−1. Several levels have also been confirmed through transitions to the 4d95s5p configuration. The higher J values of 4d95p2 configuration (J = 7/2 and 9/2) could only be established through transitions from 4d95s5p. We were successful in establishing three J = 7/2 and one J = 9/2 levels. One J = 9/2 and two J = 7/2 levels remain unknown. The study of the 4d95p2 and 4d95s5p configurations together complemented each other. The other even parity configuration 4d95s5d lies above the ionization limit and partially overlaps the 4d95p2 configuration. It has also been incorporated in the least squares fitted parametric calculation to interpret the results.

5. Optimization of the Energy Levels

The transition wavelengths observed for this spectrum were used to derive the energy level values. For this purpose, a least-squares level optimization code LOPT [] was used. The essential factors for the level optimization procedure are the correct identification of the spectral lines and estimation of their uncertainties. The wavelength uncertainty is determined by the combined effect of the statistical deviation of the line position measured on the comparator and systematic uncertainty of reference wavelengths used in the fitting. Ryabtsev et al. [] reported the uncertainty of autoionized lines to be ±0.006 Å. Our wavelength accuracy for sharp and unblended lines is estimated to be within ±0.006 Å and ±0.008 Å below and above 900 Å. We estimated the uncertainty of Bhatia’s lines to be ±0.008 Å for lines below 2000 Å with the comparison of our measurement and Kaufman et al. [] for sharp and unblended lines. Bhatia mentioned in his paper that the prism lines are not accurate to more than 0.01 Å. However, he gave wavelengths above 2000 Å with only two places after the decimal point implying that the uncertainty is at least 0.02 Å or higher. In our level optimization with Bhatia’s lines [], we noticed several lines showing a deviation around 0.22 Å for the region 2000–4000 Å from their Ritz values. The deviation increases up to 0.8 Å for the longer-wavelength region 4000–6500 Å. We, therefore, did not use these lines with large deviation in the level optimization. All of the lines used in the optimization of the level values were given an estimated uncertainty to find the final optimized energy level values with an estimated uncertainty for each level. Since the level 4d105p (1S) 2P3/2 connects with the largest number of observed transitions, it was adopted as the base level, hence all the level uncertainties in Table 2 are given with respect to this level. All the given uncertainties are taken to be at the level of one standard deviation.

6. Ionization Potential

Since more than one series with three members are known in In III, its ionization potential can be determined with good accuracy. The value of ionization potential of In III given in AEL [] at 226,100 cm−1 was derived by Catalan and Rico [] by comparison of the third spectra from Y to In. Bhatia [] improved the value of ionization potential by using 4d10ng (n = 5–9) and 4d10nh (n = 6–9) in frames of the polarization theory []. He calculated the In III limit at 226,191 cm−1; this value is listed in the NIST Atomic Spectra Database []. We have calculated the ionization potential from two series, ns (n = 5–12) and ng (n = 5–9) using the Ritz quantum defect extrapolation method with the aid of the RITZPL code []. However, the non-penetrating (4d10ng) series is certainly expected to give more accurate value. The value of IP obtained using the three-parameter extended Ritz formula [] for the 4d10ns (n = 5–12) series is 226,196.58 cm−1, while the values obtained by fitting the two-parameter extended Ritz formula for the two 4d10ng 2G7/2,9/2 (n = 5–9) series are 226,197.00 cm−1 and 226,195.08 cm−1, respectively. The limits calculated by the POLAR code [] for the ng (n = 5–9) 2G7/2, 9/2 series were found to be 226,197.28 and 226,195.35cm−1, respectively. The adopted value is the average of these calculations at 226,196.3 cm−1 ± 1.0 cm−1 (28.0448 ± 0.0001 eV) differing by 5 cm−1 from Bhatia’s value.

7. Conclusions

A total of 91 energy levels have been established, among which three levels are revised and 21 are new. All of these levels were based on the identification of 218 spectral transitions, 70 being new. The results were interpreted using Cowan’s codes and the least square fitted parametric theory. The optimized energy levels and their calculated values are given in Table 2 along with the level uncertainty, LS-percentage compositions and number of connecting transitions. All of the classified transitions are given in Table 3 along with their weighted transition probabilities (gA) obtained with least squares fitted energy parameters. This table also contains the Ritz wavelengths of all transitions with their uncertainties obtained by using the level optimization code (LOPT).

Author Contributions

All authors contributed equally to this work.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rao, K.R. On the Spectra of Doubly-Ionised Gallium and Indium. Proc. Phys. Soc. 1927, 39, 150–160. [Google Scholar] [CrossRef]
  2. Lang, R.J. On the Spectra of Zn II, Cd II, In III and Sn IV. Proc. Natl. Acad. Sci. USA 1929, 15, 414–418. [Google Scholar] [CrossRef] [PubMed]
  3. Archer, D.H. The Spectra of Indium. Master’s Thesis, University of British Columbia, Vancouve, BC, Canada, 1948. [Google Scholar]
  4. Nodwell, R.A. A Study of Spark Spectrum of Indium. Ph.D. Thesis, University of British Columbia, Vancouve, BC, Canada, 1956. [Google Scholar]
  5. Moore, C.E. Atomic Energy Levels, National Bureau of Standards Circular 467; US Govt. Printing Office: Washington, DC, USA, 1958; Volume III.
  6. Bhatia, K.S. Spectrum of Doubly Ionised Indium. J. Phys. B At. Mol. Phys. 1978, 11, 2421–2434. [Google Scholar] [CrossRef]
  7. Kaufman, V.; Sugar, J.; VanKleef, T.A.M.; Joshi, Y.N. Resonance transition 4d105s-4d95s5p in the Ag I sequence of In III, Sn IV, Sb V, and Te VI. J. Opt. Soc. Am. B 1985, 2, 426–429. [Google Scholar] [CrossRef]
  8. Kilbane, D.; Mosnier, J.-P.; Kennedy, E.T.; Costello, J.T.; van Kampen, P. 4d Photoabsorption Spectra of Indium (In II–In IV). J. Opt. Soc. Am. B Opt. Phys. 2006, 39, 773–782. [Google Scholar] [CrossRef]
  9. Ryabtsev, A.; Churilov, S.S.; Kononov, É.Y. 4d95p2 Configuration in the Spectra of In III–Te VI. Opt. Spectrosc. 2007, 102, 354–362. [Google Scholar] [CrossRef]
  10. Skočić, M.; Burger, M.; Bukvić, S.; Djeniže, S. Line intensity and broadening in the In III spectrum. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 225701. [Google Scholar] [CrossRef]
  11. Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database, v. 5.4, National Institute of Standards and Technology, Gaithersburg, MD, USA. 2016. Available online: http://physics.nist.gov/ASD (access on 7 June 2017).
  12. Cowan, R.D. The Theory of Atomic Structure and Spectra; University California Press: Berkeley, CA, USA, 1981. [Google Scholar]
  13. Kramida, A. Critically Evaluated Energy Levels and Spectral Lines of Singly Ionized Indium (In II). J. Res. Natl. Inst. Tech. 2013, 118, 52–104. [Google Scholar] [CrossRef] [PubMed]
  14. van het Hof, G.J. A Computer Program—FIND3, for Searching the Levels; Zeeman Lab: Amsterdam, The Netherland, 1994. [Google Scholar]
  15. Kramida, A.E. The program LOPT for least-squares optimization of energy levels. Comput. Phys. Commun. 2011, 182, 419–434. [Google Scholar] [CrossRef]
  16. Ryabtsev, A.N.; Kononov, E.Y. High Lying Configurations in the Spectrum of Three Times Ionized Indium (In IV). J. Quant. Spectrosc. Radiat. Transf. 2016, 168, 89–101. [Google Scholar] [CrossRef]
  17. Swapnil; Tauheed, A. Revised and Extended Analysis of the Fourth Spectrum of Indium: In IV. J. Quant. Spectrosc. Radiat. Transf. 2013, 129, 31–47. [Google Scholar] [CrossRef]
  18. Joshi, Y.N.; VanKleef, T.A.M.; Kushawaha, V.S. The Fifth Spectrum of Indium: In V. Can. J. Phys. 1976, 54, 889–894. [Google Scholar] [CrossRef]
  19. Joshi, Y.N.; VanKleef, T.A.M. Sixth Spectrum of Indium: In VI. J. Opt. Soc. Am. 1982, 72, 259–267. [Google Scholar] [CrossRef]
  20. Catalán, M.A.; Rico, F.R. Series y potenciales de ionizacion en los espectros III de los elementos del grupo del paladio. An. Fis. Quim. Ser. A 1957, 53, 85. [Google Scholar]
  21. Edlen, B. Wavelength measurements in the vacuum ultra-violet. Rep. Prog. Phys. 1963, 26, 181. [Google Scholar] [CrossRef]
  22. Sansonetti, C.J.; (National Institute of Standards and Technology, Gaithersburg, ML, USA). Computer Programs RITZPL and POLAR. Private Communication, 2005. [Google Scholar]

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Detailed Opacity Calculations for Astrophysical Applications
Previous
Spectrum of Singly Charged Uranium (U II) : Theoretical Interpretation of Energy Levels, Partition Function and Classified Ultraviolet Lines
Next