1. Introduction
The theoretical investigation on hydrogen and hydrogen/helium plasmas is of great interest for many different technological applications, from fusion [
1,
2] to astrophysical [
3] and aerospace [
4] research. These plasmo-chemical systems, though characterized by widely different conditions, share a fundamental feature that governs their behavior and dictates the level of knowledge required in the dynamical information for elementary processes. In fact, the distributions of internal levels of atoms and molecules exhibit a non equilibrium character, quite pronounced in some cases, that affects the chemical kinetics through the microscopic collision dynamics and also the macroscopic quantities. The kinetic equations for the temporal evolution of chemical species are also self-consistently coupled to the free electron kinetics and to radiation transport in the system. The theoretical framework for the reliable description of this complex phenomenology is the state-to-state approach [
5,
6] that treats electronic states and, for molecules, also rovibrationally-excited states as independent species. The critical issue in this approach is represented by the accuracy in the description of the dynamics of relevant elementary processes, occurring at the microscopic level in the plasma and characterized by the knowledge of the appropriate collisional quantities constituting the basic input data of the theoretical model. These include the electron-impact-induced processes, promoting vibrational pumping, excitation, dissociation and ionization in molecular targets, the vibration-translation (VT) energy transfer and dissociation in atom-diatom collisions and the recombination at the surface, significantly affecting the kinetics leading to non-equilibrium nascent rovibrational distributions. The main channels are identified and studied by selecting the most suitable theoretical approach for the calculation of the related scattering cross-sections and surface recombination probabilities, allowing the derivation of complete datasets and balancing accuracy and computational load.
In this paper, the more recent results obtained in the plasma-chemistry group in Bari are reviewed. The results comprise the fundamental studies on the collisional dynamics for the three classes of elementary processes, discussed individually in
Section 2,
Section 3 and
Section 4, obtaining complete datasets for hydrogen/helium system. In particular, the resonant vibrational excitation of the H
molecule has been investigated focusing on the role of the rotational excitation of the target in
Section 2. This process represents the main vibrational pumping mechanism induced by low-energy electrons, while the indirect mechanism of excitation to singlets followed by radiative decay (EV processes) governs the vibrational excitation by the collision with high-energy electrons [
7,
8]. Furthermore, the dissociative excitation by electron impact in the He
system has been recently investigated [
9]. The complete set of rate coefficients for the VT energy transfer and dissociation channels in H
-He collisions is presented in
Section 3, demonstrating the reliability of the adopted quasi-classical trajectory (QCT) approach and briefly discussing its complementarity with the quantum method [
10]. The recombination, through the Eley–Rideal mechanism, of atomic hydrogen on tungsten and graphite surface, relevant to the kinetic simulation of wall effects in negative ion sources and the divertor region of the TOKAMAK fusion reactor [
2,
11,
12], has been investigated in
Section 4, shedding light on the role of the chemical nature of the surface in affecting the dynamics.
Section 5, though not yet including all of the recently calculated processes discussed in the previous sections, shows the fundamental role of these advanced chemical-physical models in a state-to-state kinetic code, allowing the description of the temporal evolution of the plasma as determined by the collisional and reaction dynamics occurring at a microscopic level. The results presented are relevant to the investigation of the shock tube in hydrogen [
13] and demonstrate not only the importance of a complete and accurate chemical model, but also the necessity of a self-consistent kinetic approach to reliably simulate the non-local effects due to the coupling of level and free-electron kinetics with radiation.
Finally,
Section 6 is devoted to the characterization of dense hydrogen plasma. The thermodynamics and transport properties in the case of dense, weakly-ionized Debye hydrogen plasma have been frequently investigated in the literature [
14,
15,
16,
17,
18,
19], due to the necessity of properly accounting for the non-ideal effects of the multi-body interaction. The complexity of the rigorous approach led to the development of simplified models, able to include the neighbor effects on the isolated system though remaining consistent with the traditional approaches. The present results show a possible enhancement of the pressure ionization phenomenon, also affecting the electrical conductivity behavior.
The content of the present paper partially reports the results presented and discussed during the meetings of the Coordinated Research Project (CRP) on “Atomic and Molecular Data for Hydrogen and Helium in Fusion Plasma” organized by the International Atomic Energy Agency-Atomic and Molecular Data Unit (Vienna, 2011–2015).
2. Dependence of Electron-Impact Vibrational Excitation Cross-Sections on the Initial Rotational Level of the H Molecule
Extensive experimental and theoretical studies have been devoted to the resonant vibrational excitation (RVE) of vibrationally-excited H
molecules by electron impact, and large sets of cross-sections data are now available for the plasma community [
4]. On the other hand, a comprehensive investigation of the role played by the initial rotational excitation state of the hydrogen molecule in affecting the resonant processes, extended to a wide range of electron collision energies and including all possible rotational levels, to the best of our knowledge, has never been performed [
1,
20]. In this section, we present a complete set of cross-section data for resonant vibrational excitation, occurring through the formation of the ground
electronic state of H
molecular ion, involving initially rotationally-excited H
molecules, according to the process,
In this reaction, a free electron impacts on a target H
molecule, which is initially found in one of the accessible vibro-rotational levels of its ground electronic state
, denoted by the quantum numbers
. The impinging electron is then momentarily trapped by the molecule, and a transient negative molecular compound, H
, in the
electronic state, is formed. This resonant state can re-emit the extra electron so that the H
molecule is restored in a different vibro-rotational level
. The cross-sections for the process in (
1) can be calculated by resorting to the standard local complex-potential model for resonant collisions, whose formulation can be found in the literature [
21,
22]. In the following, we give only a brief summary of the main equations of the method.
The cross-sections for the RVE process can be obtained once the resonant wave function
, associated to the nuclear motions of the H
molecule and depending on the internuclear distance
R, is known. It can be calculated by solving the inhomogeneous Schrödinger-like equation [
21,
The first term in the brackets is the nuclear kinetic energy operator, where
is the reduced mass of the nuclei, while the second term represents the centrifugal energy operator.
is the real part of the potential energy for the
resonant state, and
is its width.
E is the total energy of the electron-molecule system, and
is expressed as
, where
m is the electron mass and
the potential energy of the target ground electronic state
.
, finally, is the wave function for the
initial rovibrational level of the H
molecule. All of the quantities involved in Equation (
2) have been taken from [
23].
Once Equation (
2) is solved and the resonant wave function
obtained, the cross-section can be calculated by [
23,
24,
25]:
where
is the incident electron energy and
. The cross-sections were computed for all of the initial and final vibrational levels (
) and for all of the allowed values of the rotational quantum numbers
j, as shown in
Table 1. Some results are discussed below.
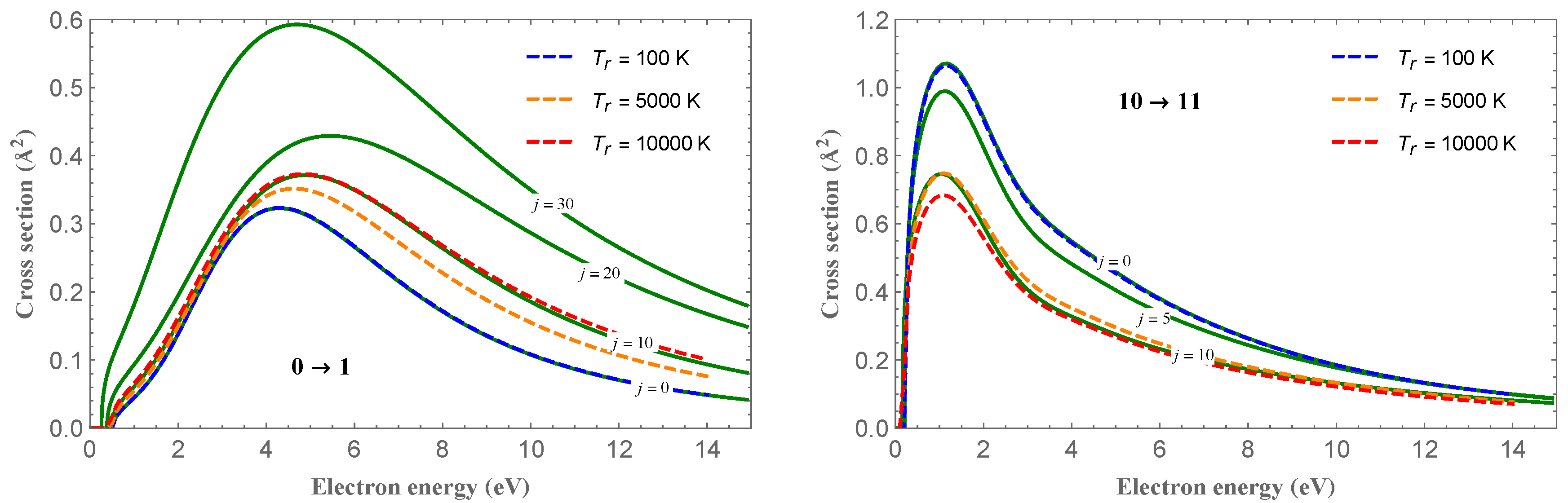
Figure 1 shows the cross-section for the one-quantum vibrational transitions,
, for
and different
j values, as indicated in the plots. For the
transition (left panel), the cross-section peaks follow the trend of the increasing value of the cross-section with increasing
j. An opposite behavior is observed for the
case (right panel). In
Figure 1 are also shown the cross-sections thermally averaged over an equilibrium Boltzmann distribution of the rotational states for different temperatures, according to the equation:
where
is the Boltzmann constant and
is the usual partition function [
26]. The figure also shows that, for the averaged cross-sections, an opposite trend with increasing temperatures is observed for the two
and
vibrational transitions.
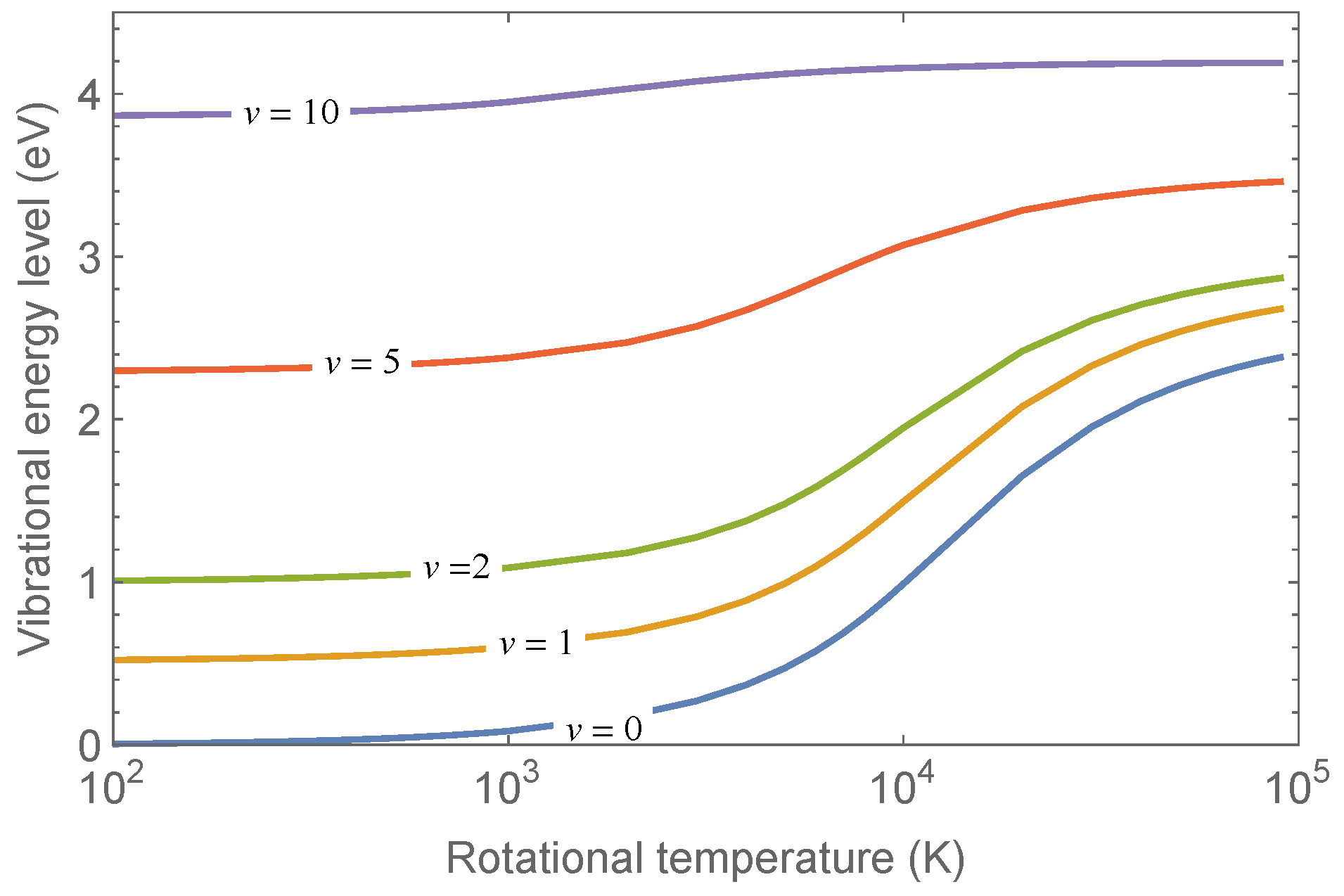
In
Figure 2 are shown the rotationally-averaged vibrational energy values as a function of the rotational temperatures calculated according to the equation:
which gives the mean energy of a given vibrational level when the rotational spectrum is not resolved.
For the processes occurring through the
resonant state, the rotational cross-sections for all possible
transitions and for all of the allowed rotational states are available in [
27] for the H
molecules. The cross-sections for the other hydrogen isotope variants and for different resonant states of H
molecule will be the topics of a future paper, currently in preparation by our group. This future paper will be aimed at extending and upgrading the whole existing electron-H
cross-section database.
3. VT Energy Transfer and Dissociation in H-He Collisions
In the modelization of plasmas of astrophysical interest [
3], as well as of plasmas for energy production in nuclear fusion [
1] or entry into planetary atmospheres [
4], there is a need for detailed data concerning rovibrational energy exchange and dissociation in molecular collisions. Typically, the range of energies/temperatures involved is quite large: for example, in a probe entry into Jovian atmosphere, the range of temperatures extends from 200 K to more than 20,000 K [
28,
29]. This is a challenge for any computational method for molecular dynamics. An accurate quantum mechanical method is surely the right choice in the low energy regime, but it becomes rapidly unfeasible as the total energy increases. On the contrary, the quasi-classical method is not reliable at very low energies, but it becomes rapidly accurate as the total energy increases. A very clear result concerning these opposite and complementary trends has been obtained in [
10], where the reaction:
has been treated by both the exact quantum mechanical method (QM) and the quasi-classical trajectories (QCT) method. The matching of QM and QCT cross-sections from the HeH
ground vibrational state with increasing initial rotation is excellent for a collision energy higher than about 0.1 eV. The agreement is significantly better with respect to the results obtained using other quantum mechanical methods [
30,
31] with the same potential energy surface (PES). The almost coincident results from exact QM and QCT methods are confirmed for higher initial states of reactants, as well, starting from a collision energy decreasing with increasing initial internal energy. This double QM/QCT approach has the fundamental feature of being perfectly sustainable for large-scale calculations, because the QM method is computationally fast at low energies (where the QCT is indeed very expensive, due to very long trajectories to be integrated), while the quasi-classical method reaches its maximum efficiency at high collision energies. A similar approach could successfully be adopted even for He + H
collisions. The collision of helium with molecular hydrogen in their respective electronic ground states is a non-reactive system that has attracted much interest over the years because of its relative simplicity (low number of electrons, light masses, low number of rotational states to be managed in a quantum mechanical treatment) and being indeed attractive also from an applicative point of view [
32]. In this last case, two processes are particularly relevant:
Concerning experimental results, thermal data (without any specification of initial and final states) are available concerning vibrational relaxation [
33], while thermal dissociation is available only in an indirect way [
34]. On the contrary, the detailed calculation of these processes is feasible by quantum, as well as quasi-classical methods. The aim of these calculations is to produce a complete set of cross-sections with respect to the hydrogen rovibrational ladder in a range of collision energy as wide as possible, in order to use these data in models. Large-scale calculations have been performed by one of us (F.E.) using a quasi-classical code written by the same author, developed for efficiently exploiting grid computational resources [
32]. The most recent PES for this collisional system is the one of Boothroyd, Martin and Peterson, known as BMP [
35]. Unfortunately, an accurate comparison in the literature by Lee et al. [
36] with experiments and with calculations on the less recent PES of Muchnick and Russek (MR PES) [
37] shows that the BMP PES has some fitting problems that can have important effects on the state-to-state cross-section calculations. For this reason, we adopted the MR PES in this work. The whole sets of cross-sections for non-reactive rovibrational energy exchange and dissociation were calculated in the translational energy range 0.001–10 eV, including quasi-bound states, with a density of 50,000 trajectories per eV and per Angstrom of impact parameter. A total number of about six billion trajectories was calculated, using about 9.5 years of CPU. The whole set of results will be published shortly.
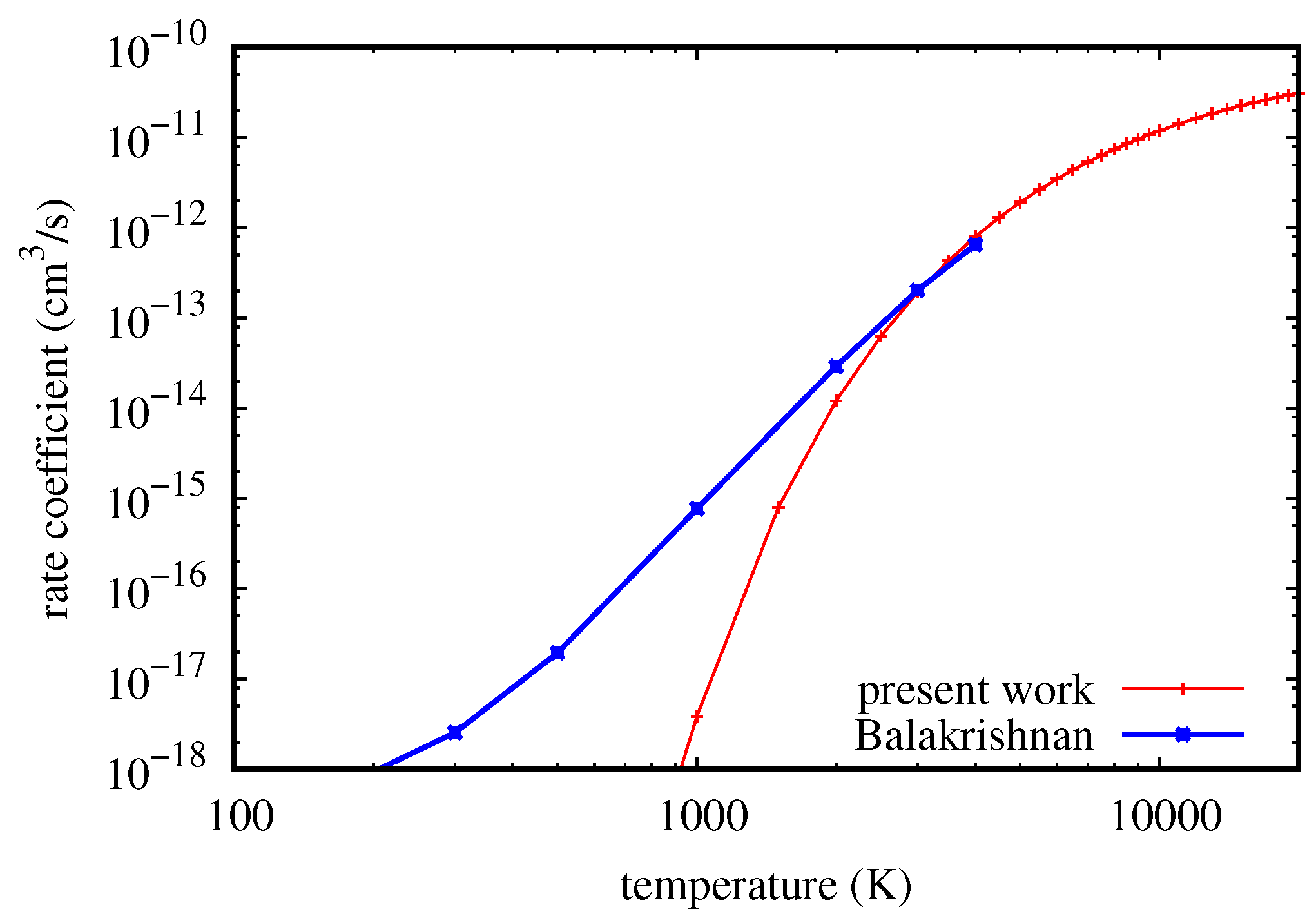
Concerning rovibrational energy transfer, a comparison is shown in
Figure 3 between rate coefficients for the transition (
v = 2,
j = 0) → (
= 1,
= 8) as obtained in this work and by Balakrishnan et al. [
38] using the accurate QM close-coupling method. It is clear that there is a complete disagreement at low temperature, as well as a convergence of the QCT result to the QM one for temperature values greater than 2000 K, as expected. These results are globally confirmed also for all of the other transitions considered in the QM calculations in [
38]. As a consequence, also in this case, the double-approach QM/QCT could be very efficient in calculating the rate coefficients for a complete set of rovibrational transitions for applicative purposes, merging the results from QM and QCT methods. A purely non-reactive case is more challenging for quasi-classical calculations than a case including reaction [
39]; in fact, the difficulty of the QCT method in treating non-reactive transitions at low collision energy [
40] is well known, due to the classically forbidden nature of the process [
41]. This has nothing to do with quantum mechanical tunneling through potential barriers or with resonances; it consists of the failure of QCT method in correctly detecting the final rovibrational actions of molecular products when the exchanged energy is comparable to one quantum in a non-reactive process. On the contrary, when collision energy is sufficiently higher than the transition energy (independently of the exothermicity of the process), the QCT is able to correctly calculate the final product rovibrational state, as implicitly shown also by
Figure 3, and it continues smoothly to exact QM results with increasing computational efficiency. Concerning the dissociation process, two possible channels should be considered (see [
42] for details). The first one is the three body dissociation, obtained directly from quasi-classical calculations. The second one is the rovibrational energy transfer to quasi-bound states (resonances), i.e., states classically bound but with a finite quantum-mechanical lifetime. The fraction of dissociation obtained from this last process depends on kinetic parameters (typically the mean collision time), and therefore, it is useful to consider it separately from the three body contribution. Concerning this last one, in
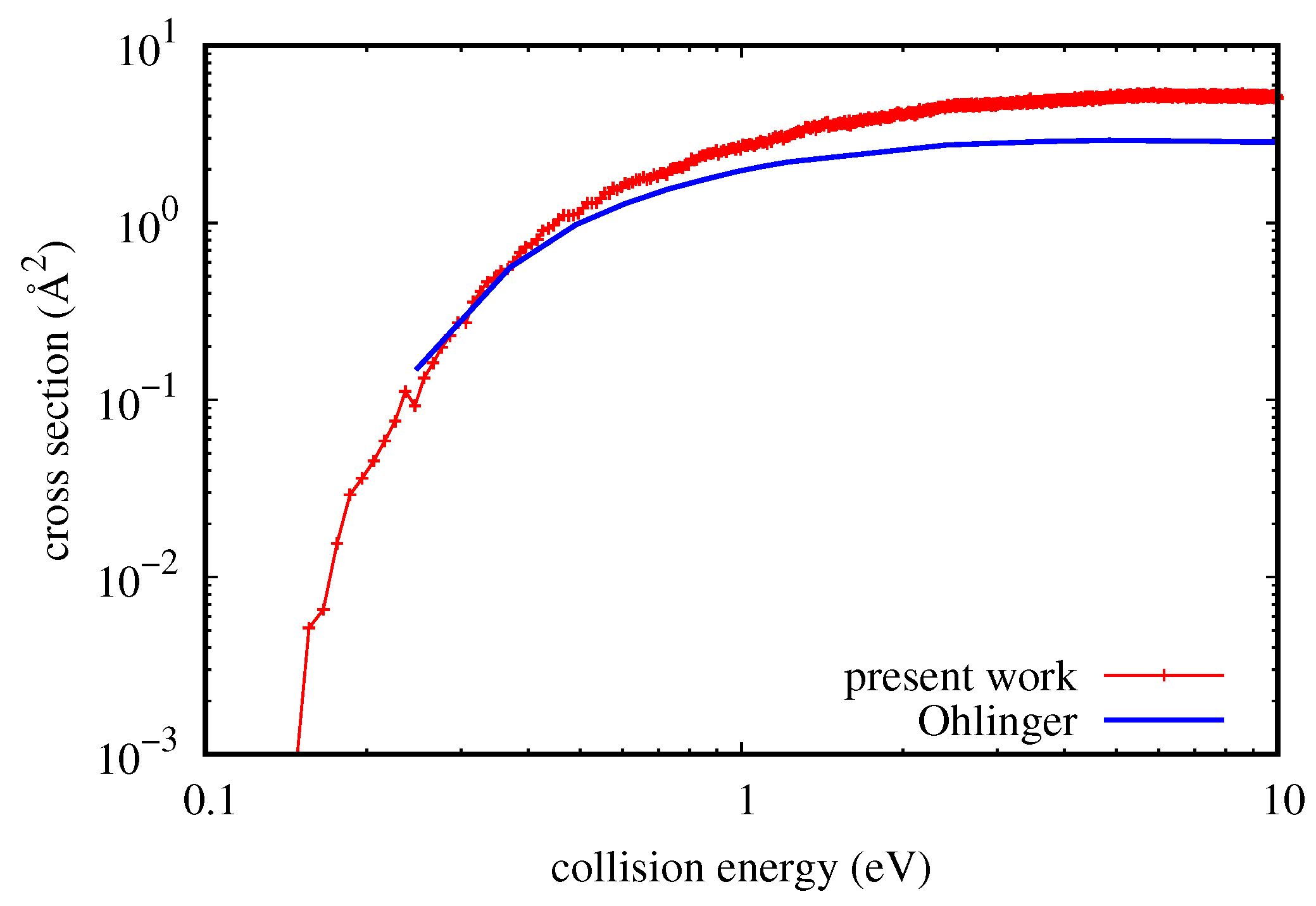
Figure 4, there is a comparison of cross-sections with the QM results of Ohlinger et al. [
43], obtained with a modification of a non-reactive QM code. In that case, dissociation is considered as a rovibrational energy transfer to continuum states and to quasi-bound states. Continuum states are approximated by considering positive energy pseudo-states limited by a sufficiently large artificial boundary.
Unfortunately, just the most interesting part of QM result at low energy has not been calculated in [
43], and therefore, it is impossible to know the probably more reliable trend of the QM curve near the threshold of the process (as low as 26 meV). On the other hand, it is clear that the QCT and QM trends are the same, with quantitative agreement well under 0.3 eV. For higher collision energy values, the quasi-classical result is higher by at most a factor of 1.8. However, considering the approximations introduced in the QM calculation (including coupled states for the calculation) and the quite high collision energy, it would not be surprising to discover with more accurate calculations that the quasi-classical result is the most reliable. Similar results were obtained also by comparing resonance dissociation and will be presented in a more comprehensive study of dissociation/recombination about this system.
It is important to stress that using any quantum mechanical method for calculating dynamical data is not a guarantee that these results will be superior to the quasi-classical calculations under any condition. It depends on the system and on the specific approximations involved. The best strategy for light systems, including helium and hydrogen, is to use a QM method as free as possible from approximations for low total energy values and match the computation with quasi-classical approach, as shown by the actual calculations reported here.
4. H Atoms’ Recombination on Tungsten and Graphite as a Source of Vibrationally-Excited Molecules
The interaction of H atoms with tungsten and graphite surface is of central importance in various areas of fundamental and technological interest, such as the chemistry of plasma fusion devices [
44,
45], negative H-ion sources (volume sources and surface conversion sources) [
2,
11], chemical-physics of divertor region in plasma reactors [
11,
12], etc. Here, the dynamics of the Eley–Rideal (E-R) recombination reaction of hydrogen atoms, a sources of rovibrationally-excited H
molecules, is compared in light of the results obtained in the last few years for two heterogeneous systems: H on tungsten and H on graphite. The E-R reaction is a two-step mechanism:
a H atom is adsorbed on the surface (
) in a specific active surface site:
a H atom approaching the surface from the gas-phase reacts with the adsorbed atom in a single, direct collision:
thus forming a molecule in a specific rovibrational state (
). Here,
is the energy released in the recombination process. The energy released in the reaction can be shared among the degrees of freedom of the newly-formed H
molecules (rotations, vibrations, translation and, possibly, electronic) and the degrees of freedom of the substrate (phonons and, possibly, electrons). The chemistry of H
molecules’ formation on the W(110) at surface temperature
= 700 K via E-R reaction, for two different specific adsorption sites on the surface, is investigated and compared with H
formation on a graphite surface. The W(110) surface exhibits three chemisorption sites: the 3F site (in the center of triangle formed by three W atoms), the T site (corresponding to a W atom) and the B site (placed in the middle between two adjacent W atoms). In the case of a graphite surface, the active sites are: T (corresponding to a C atom), B (placed in the middle between two adjacent C atoms) and C (the center of hexagonal unitary cell). In this work, we compare the results obtained on the T and 3F site on W(110) and on the T site on graphite. The complete set of results obtained for the two heterogeneous systems are discussed in [
46,
47]. The dynamics of the E-R recombination reaction of H atoms on W(110) and graphite (0001) has been investigated by using a time-dependent semiclassical method. The method, fully described in [
48], gives a coherent description of elementary molecular surface processes, and it is able to describe some of the most important features of surface reactions and surface phenomena, including the energy exchange mechanism between the molecules or atoms interacting with the surface and the phonons and/or electrons of the substrate. The recombination probability as a function of the kinetic energy of the impinging H atom for H
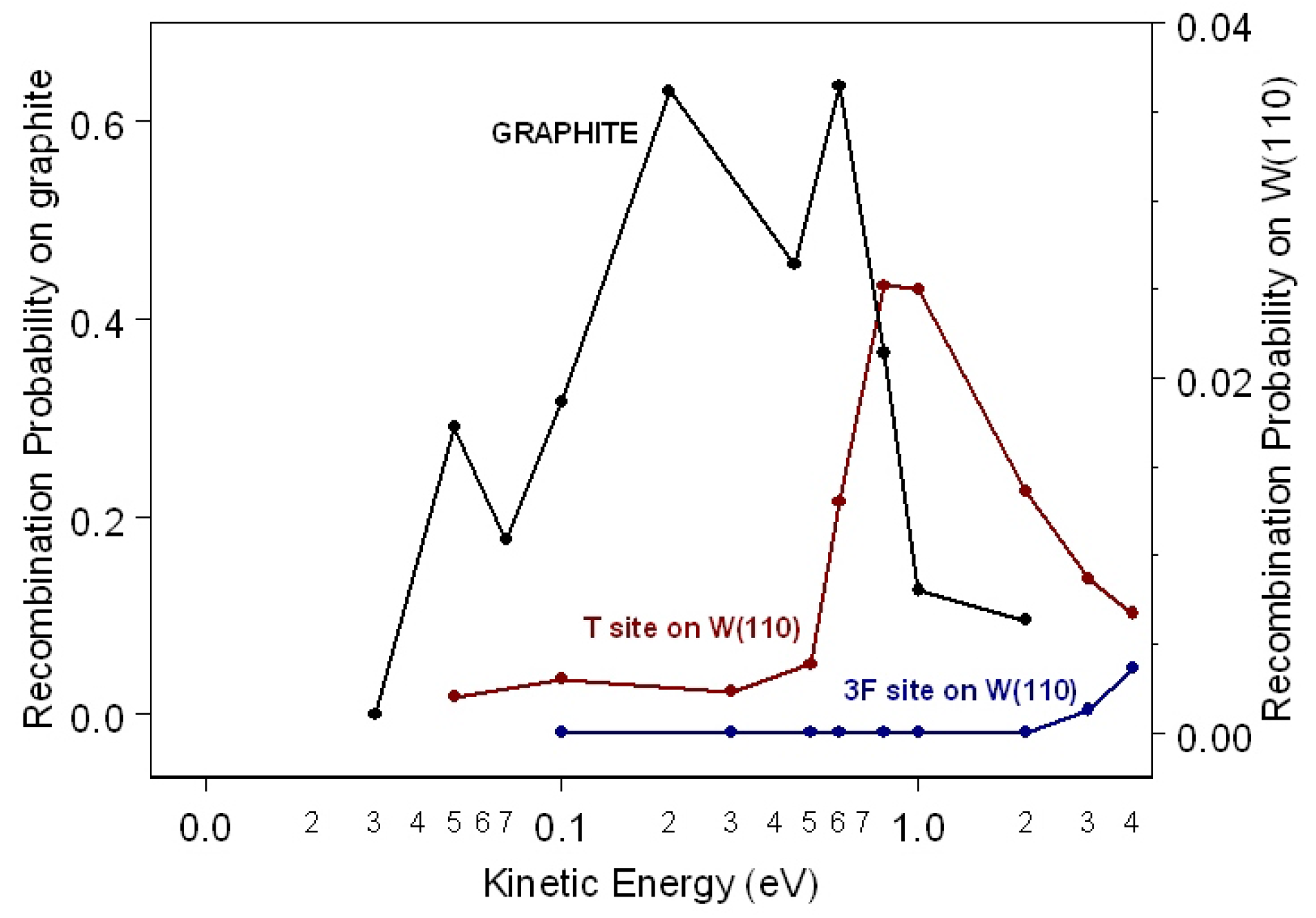
on the T and 3F site on W(110) is shown in
Figure 5 and compared with the probability obtained for recombination on the T site on graphite (
= 800 K).
Looking at
Figure 5, we can infer that for the W(110) surface, the recombination probability for the T site is higher than the probability for the 3F site. In fact, while for the former site, the recombination probability rises at the maximum value of 2.5 × 10
for
= 1.0 eV and then decreases for higher collisional energies, for the latter, it is very small for collisional energy lower that 2.0 eV increasing very fast for higher
values. This interesting adsorption site effect on the interaction dynamics is due to the close correlation and competition between recombination reaction and inelastic processes. In fact, in the case of the T site, the most dominant inelastic processes are the adsorption/desorption, in which the adsorbed atom remains adsorbed and the impinging atom is backscattered in the gas phase after the interaction and the adsorption of both atoms as separated atoms. However, for the 3F site, the most dominant processes are the adsorption/desorption process and the adsorption of both atoms as the H
molecule.
The maximum of the recombination probability on the T site on graphite, occurring at
eV, is more than 20-times higher than that obtained for the T site on W(110) that assumes a maximum value of 0.025 at 0.8 eV. We note that graphite exhibits a higher catalytic activity in the complete range of collisional energies considered. As said above, the reaction mechanism considered here is a source of vibrationally-excited molecules. The final vibrational distributions for the H
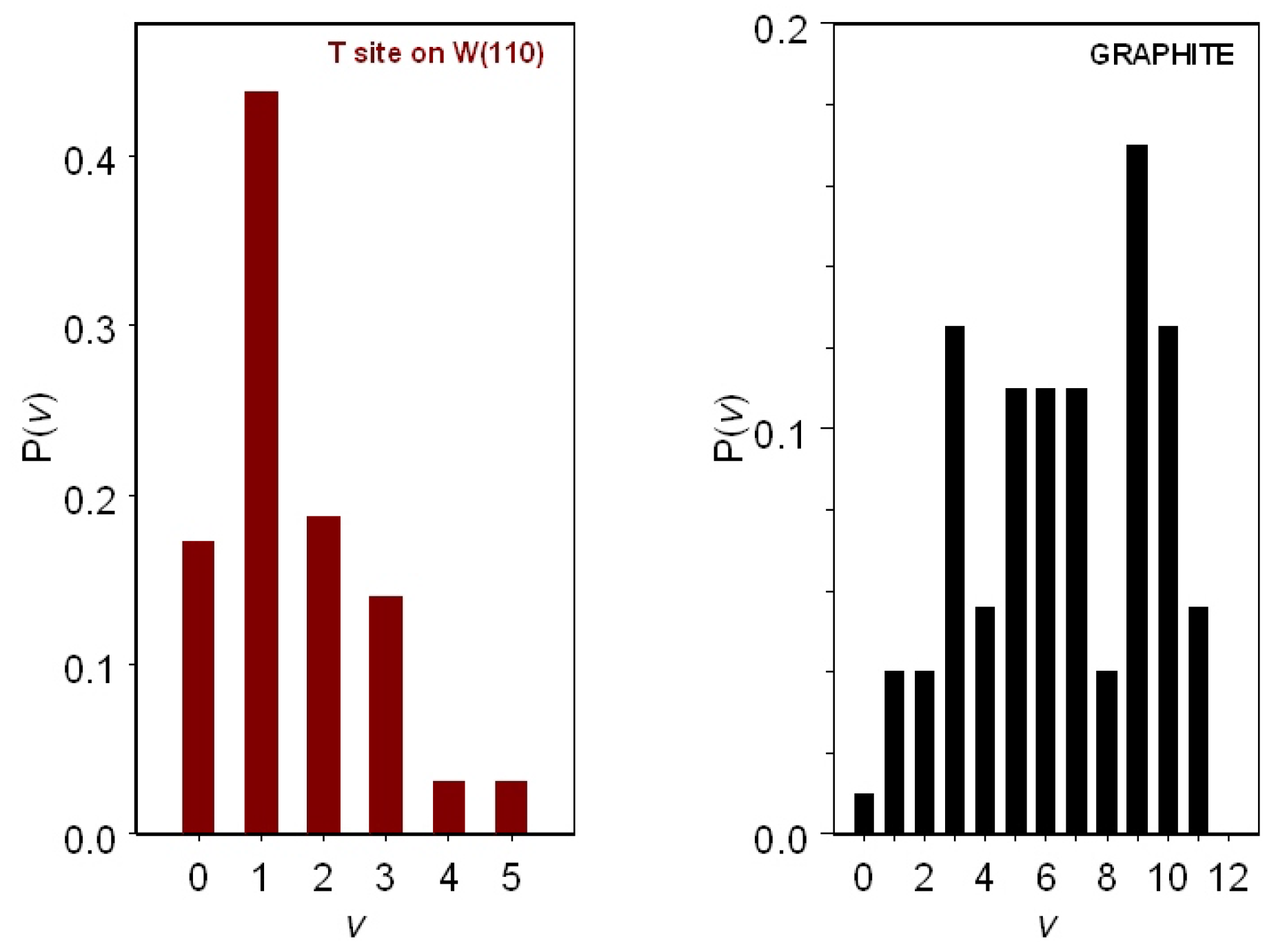
formed, assuming that the impinging atom has a kinetic energy of 0.8 eV and H
is placed on the T site on W(110) and on graphite, are reported in
Figure 6. It appears that molecules formed on graphite populate the complete vibrational ladder with a main peak in
v = 9 and two secondary peaks in
v = 3 and
v = 10, respectively. On the contrary, molecules formed on W(110) populate only the first five levels with a maximum population in
v = 1. Therefore, graphite, being more reactive, represents an effective substrate for the formation of vibrationally-pumped H
molecules.
The most remarkable feature of vibrational distributions is their non-Boltzmann character. This behavior is also observed for the 3F site on W(110), but when we considered the E-R recombination on W(001), the vibrational distributions obtained for the 4F site exhibit a quasi-Boltzmann behavior [
49]. Therefore, vibrational populations exhibit drastic differences, according to the surface orientation and surface site where the interaction occurs. This is the result of various factors, in primis the different binding energy, but also a different energy shared between the internal degrees of the formed molecule and the surface phonons.
5. H and H/He Processes in Kinetic Modeling
The interest in high enthalpy flows in hydrogen and hydrogen/helium mixtures has been growing in view of the future NASA mission
JUNO [
50,
51] dedicated to Jupiter exploration. Nevertheless, research in supersonic hydrogen flows was also developed for practical applications, such as SCRAMJET thrusters for hypersonic vehicles [
52,
53].
In Jupiter atmospheric entry, radiative heating gives a relevant contribution [
54,
55], especially in regions not exposed to conductive and convective heating. At the same time, the ionization degree is sufficiently high to have appreciable effects of free electrons on flow properties. As a consequence, the flow around the hypersonic vehicle is in strong non-equilibrium conditions [
28,
29].
To properly investigate this system, a self-consistent kinetic scheme [
13] is considered, coupling chemical kinetics with that of internal excited states of molecules (vibrational and electronic [
56,
57]) and atoms (electronic [
5,
58]) and of free electrons (Boltzmann equation) [
59,
60]. The main drawback of the state-to-state approach is the large number of chemical variables considered, limiting the applications only to 1D geometries [
61], with a few exceptions [
62,
63].
In recent years, the state-to-state model has been applied to investigate shock tubes in pure hydrogen, considering also radiation transport modeled by the ray-tracing method, coupled self-consistently with level and electron kinetics [
29]. The kinetic scheme included the traditional vibrational kinetics for H
, with internal transitions and dissociation/recombination induced by collisions with heavy particles:
atom-atom collisions:
electron-induced processes with complete sets of cross-sections:
and the collisional radiative model for hydrogen atoms [
58]:
All of the sketched processes are inelastic in the sense that internal energy is not conserved, and the excess (or defect) of energy is exchanged with the translational degrees of freedom. The total energy is assured in the Euler equations by the proper continuity equation.
In a shock tube, the gas is accelerated to supersonic speed and is reflected at the end of the tube, creating a shock wave traveling in the direction opposite to the supersonic flow. The gas crossing the shock front is compressed and warmed up to very high temperature almost instantly (in a space interval of the order of few mean free paths), leaving unchanged its internal degrees of freedom, which relax toward equilibrium moving further from the shock front. To model this system, 1D Euler equations are solved relative to the shock front, giving a steady state profile of the relevant quantities. In the state-to-state approach, the fluid equations are closed by the continuity equations for each species in each level, giving at the same time the gas composition and internal distributions. From internal distributions, it is possible to determine the energy accumulated in the relative degree of freedom, as well as the internal temperature,
, estimated as the temperature of the Boltzmann distribution representing the first excited level, i.e.,
where
,
and
are respectively the energy, population and statistical weight of the
i-th level in the
s-th species. The index zero refers to the ground state and one to the first excited state. To consider non-equilibrium in the electron energy distribution (EEDF), the Boltzmann equation for free electrons [
59,
60] is coupled self-consistently with the level kinetics.
We have applied this model to a shock tube filled with pure hydrogen [
29] or with hydrogen/helium mixture [
28]. Here, we report theoretical results obtained for a pure hydrogen gas with the following free stream conditions:
K,
atm, Mach 20. Just after the shock, the gas temperature reaches
24,000 K and the pressure
atm, while the gas is still formed by molecules with vibrational temperature
K. Under these conditions, collisions among heavy particles excite vibrational states (see the processes in Equation (
11)) and induce dissociation, reducing the gas temperature. When atomic concentration is high enough (about 5 mm from the shock front), atom-atom collisions (see Equation (
12)) activate ionization and atomic excitation, increasing the contribution of electron-induced processes (see Equations (
13) and (
14)) and radiative decay (Equation (
15)). Electron-induced processes are more effective than atom-atom collisions, the latter being important to produce the first electrons. Without atom-atom processes, the non-equilibrium region becomes anomalously long [
64]. All of the temperatures reach equilibrium with the gas temperature in about 5 cm at
K, with the exception of the internal temperature of atomic hydrogen, which reaches equilibrium after 3 m.
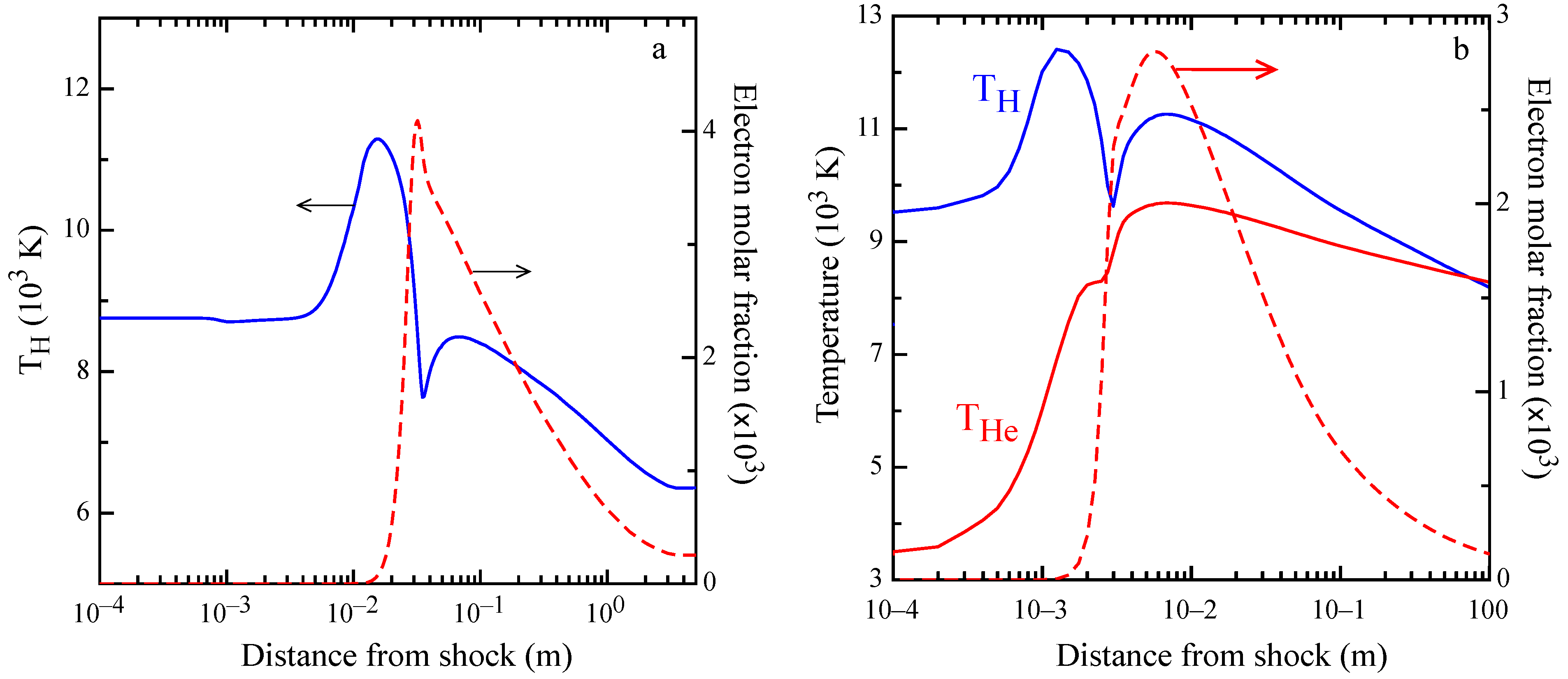
This behavior can be observed in the profile of atomic temperature
and of free electron molar fraction, reported in
Figure 7a. The electron temperature is heated up to 11,000 K at
mm and, after the combination of radiative decay and ionization from excited atomic states, overcomes the excitation, making
decrease as the electron density increases. At about 30 mm, there is the maximum of the electron molar fraction, while at
mm, the minimum of
is observed, followed by a maximum at
mm. It should be noted that in correspondence with the minimum of
, there is a change in the slope of the electron molar fraction. This behavior can be explained by electron-proton recombination in electronically-excited states, which slows down the recombination process sustaining ionization, not only because this process has a smaller threshold from H (
n≥ 2), but also for the heating of the tail of the electron energy distribution due to superelastic collisions, transferring energy from excited states to electrons. Similar behaviors are observed in the shock simulation of the Jupiter atmosphere, as displayed in
Figure 7b, showing higher maxima in the electron molar fraction and in H temperature peaks, due to the higher free stream Mach number.
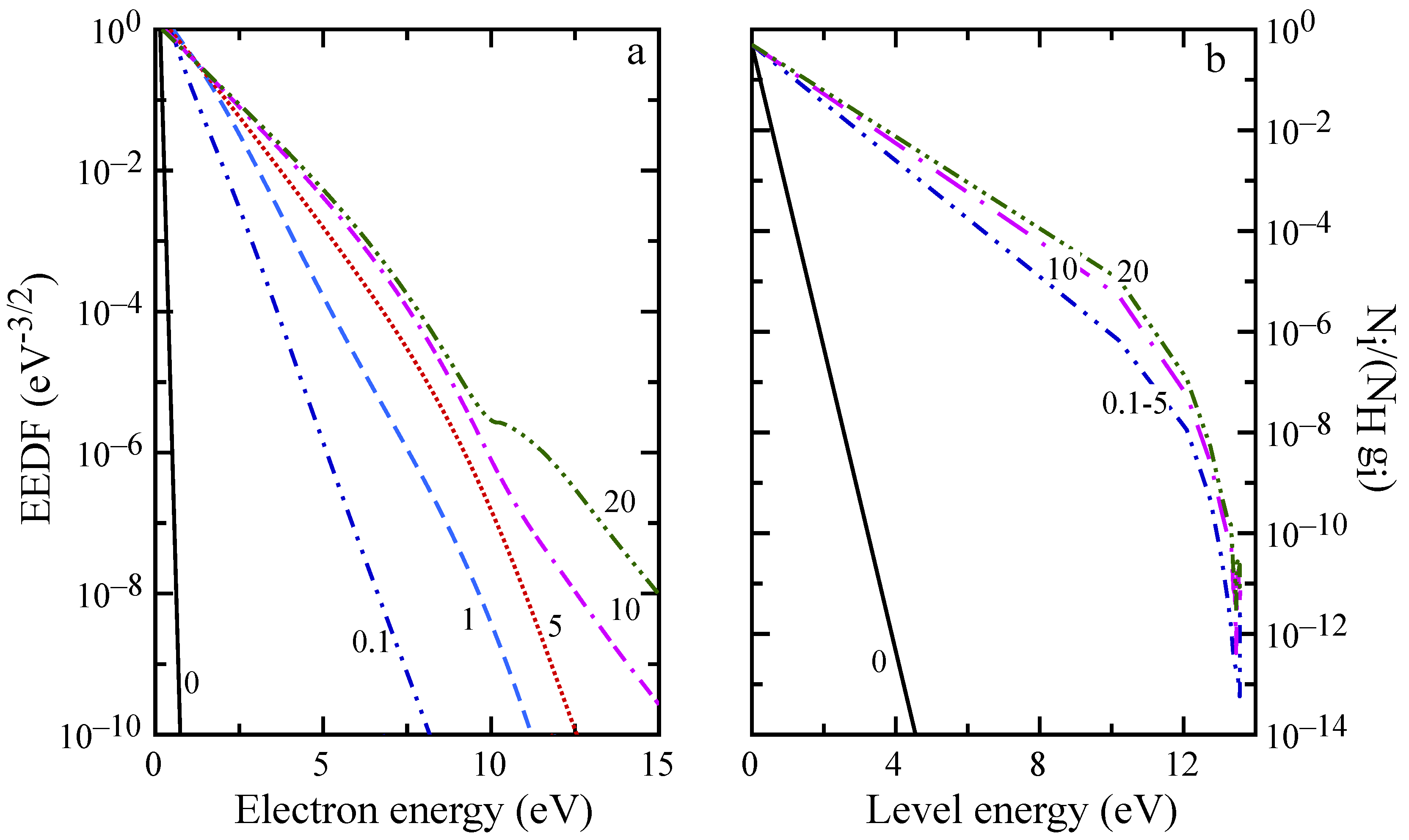
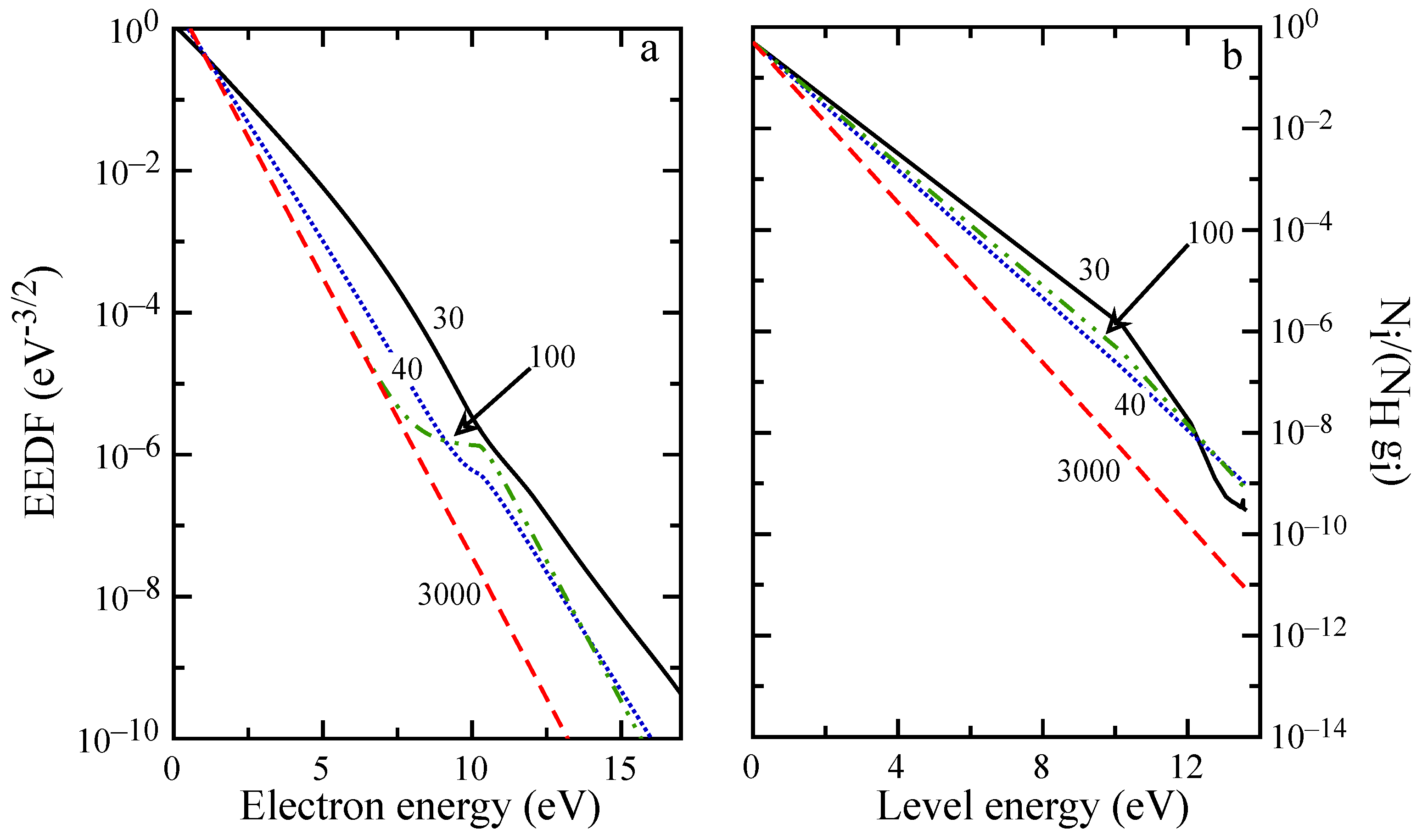
The evolution of macroscopic quantities is reflected also in the distributions, as can be observed in
Figure 8 and
Figure 9. For distances below 5 mm, the EEDF and internal level distribution presents the characteristic shape observed in the ionization regime [
58] with high energy electrons depleted by inelastic processes, while high energy atomic levels are underpopulated because of ionization. EEDF deviates from this behavior already at
mm, due to superelastic collisions, which sustain the distribution tail also at
mm (see the plateau in
Figure 9a), even if the low energy distribution is already in equilibrium. After 20 mm (see
Figure 9b), recombination repopulates the higher energy levels while the population of first excited states is decreasing because of radiative processes and superelastic collisions.
Another aspect that is worthy of discussion is the abnormally high atomic temperature at a short distance from the shock (below 1 mm; see
Figure 7 and
Figure 8), a trend that can be explained only by photons emitted in the hot region and reabsorbed in proximity of the shock front. All of these behaviors can be explained only with self-consistent coupling of radiation transport with level and free electron kinetics.
6. Thermodynamic and Transport of High-Density Hydrogen Plasma
The thermodynamic properties and the electrical conductivity of non-ideal, high-density hydrogen plasma have been investigated, accounting for quantum effects due to the change in the energy spectrum of atomic hydrogen when the electron-proton interaction is affected by the screening due to the plasma environment. High-density conditions have been simulated assuming atomic hydrogen subject to an effective screened Coulomb potential:
characterized by the Debye length
. The influence of the plasma, accounted for including the Debye-Hückel correction, produces a lowering of the ionization energy that for the hydrogen atom corresponds to the so-called self-energy shift,
, thus leading to an effective value [
16,
65,
66]
, where
is the ionization potential of the isolated, unperturbed hydrogen atom. Actually, an additional lowering is due to the effect of the presence of a screened Debye potential on the eigenvalues for electronic levels, obtained solving the Schrödinger equation. In fact, the spectrum of electronic levels characterizing the hydrogen atom, derived solving the eigenvalue problem with a finite difference approach, is modified as the Debye length decreases, and in very high-density regimes, quantum effects act moving the bound (negative) levels to the continuum edge (Mott effect) [
16], reducing the number of terms in the internal partition function of the atomic hydrogen, thus decreasing the ionization potential.
In the frame of the statistical mechanics and adopting a self-consistent cutoff, including all of the bound (negative) levels compatible with the
value [
65], the equilibrium constant for the ionization process has been estimated with the Saha equation.
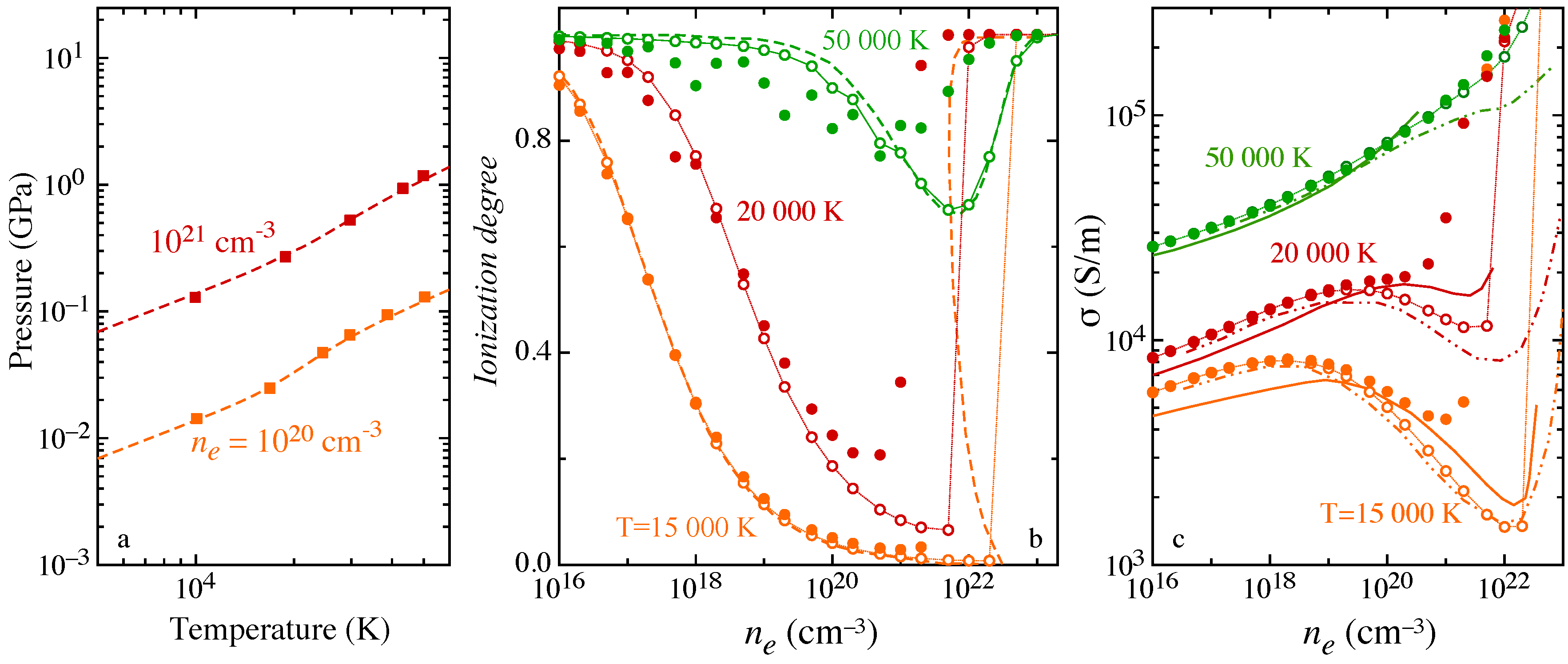
Non-ideality is accounted for by including the Debye-Hückel correction for the lowering of ionization potential and the actual ensemble of levels consistent with the Debye length value, affecting the internal partition function of H atom and the effective ionization potential. The pressure isochors (
Figure 10a) compare rather satisfactorily with the results obtained in [
67] performing a direct path integral Monte Carlo simulation, i.e., estimating the internal partition function from configurational integrals that includes simultaneously the different interactions. The ionization degree
has been calculated at constant total electron density
, i.e., electrons bound in the atomic system plus free electrons formed in ionization, over the explored temperature. The isotherms (
Figure 10b) exhibit the phenomenon of pressure ionization [
16,
65], i.e., the rapid increase of
attaining the high-density regime, where non-ideal effects dominate. The results obtained including or neglecting the effect on atomic electronic levels due to the screened Coulomb potential have been compared for different temperatures to results in [
16]. In the high-density region, the change, usually neglected, in the spectrum of levels is effective in emphasizing the pressure ionization.
The effects of non-ideality on transport properties have been investigated in the frame of the Chapman–Enskog theory [
70,
71], assuming the collision integrals for
e-H interaction unaffected, while charged-particle interactions modeled with accurate Debye-length-dependent collision integrals by Mason [
72,
73], recently fitted in a wide temperature range in [
74]. The electrical conductivity of Debye plasma (
Figure 10c) exhibits a dependence on the total electron density that is affected by the pressure ionization, i.e., the minimum behavior of the conductivity and the Mott transition, merging to the fully-ionized regime. The present results have been compared with results in the literature, obtained in the frame of different theories. In particular, in [
68], the two-term Boltzmann equation is solved including in the collisional terms accurate elastic transport cross sections for
e-
e and
e-H interactions, re-evaluated so as to account for the additional screened Coulomb potential in the first Born approximation, while in [
69], the linear response theory is used for transport. Both [
68,
69] neglect the contribution of excited levels in the atomic internal partition function, one dealing with the ground-state approximation and the second using the Planck–Larkin approach to avoid divergence.
Significant differences are observed when the effect of the Debye screening on atomic electronic levels, and in turn on the internal partition function, is considered, while a satisfactory agreement is found neglecting the change in the level ensemble.
7. Conclusions
The consistent and accurate knowledge of the dynamics of elementary processes involving H and He represents the fundamental information for the kinetic modeling of fusion plasmas and also of the atmosphere-entry condition of aerospace vehicles. In the present paper, complete datasets of state-specific cross-sections and rate coefficients for selected channels, i.e., electron-impact-induced H resonant vibrational excitation, H-He collision-induced VT energy transfer and dissociation and heterogeneous H recombination on tungsten and graphite, are reported.
In particular, cross-sections calculated by using the local complex potential model for electron scattering, occurring through the H
resonant state and involving vibro-rotationally-excited H
molecules, are presented. Thermally-averaged cross-sections for
one-quantum transitions and rotationally-averaged vibrational eigenvalues are also discussed. The obtained compete set of rotational cross-sections is available for the plasma community in [
27].
The theoretical determination by using the QCT method, of the He-H collision cross-sections for the rovibrational energy exchange and dissociation of H molecules, is illustrated. A detailed discussion on the performance of the QCT method, compared with the QM approach, for dissociation and rotational excitations shows that for atom-molecule collisions, the QM method, for light systems, can be considered appropriate close to the process threshold, while the QCT method can be more confidently used for larger energies.
Recombination processes of H atoms on the tungsten and graphite surface, leading to H vibrationally-excited molecules, are discussed. The Eley–Rideal recombination mechanism is illustrated, and recombination coefficients for H on W and graphite are reported. The calculated nascent vibrational distribution of the H molecule shows an outstanding peak for the level in the case of the W surface, while for the graphite, the highest level density is reached at , with secondary peaks observed for the levels and 10.
Moreover, the state-to-state kinetic simulation of H plasma evolution in a shock-tube, obtained accounting for the self-consistent coupling among chemical kinetics, free-electron kinetics and radiation transport, is presented. Calculated spatial profiles of H and He internal temperatures, along with the electron molar fraction, are reported for pure hydrogen and H/He mixture typical of Jupiter’s atmosphere. The analysis of the results for pure hydrogen shows that below 5 mm from the shock front, the heavy particle collisions vibrationally excite the H molecules up to dissociation. The formation of H atoms enhances the role of the H-H collisions, which induces ionization. The production of free electrons leads to a radiative decay process, which deactivates the atom-atom collisions, till the equilibrium is reached. Electron energy distribution function and hydrogen atomic level population are also reported for ionization and recombination regimes and different shock wave distances.
Finally, the thermodynamics and transport properties of dense, non-ideal plasmas are discussed for their relevance in the characterization of technological and inertial fusion plasmas. In particular, the pressure-temperature profile, as well as ionization degree and electrical conductivity, as a function of the total electron density, are reported. The calculated ionization degree exhibits the pressure ionization phenomenon, consisting of its rapid increase at high electron density where the non-ideal conditions dominate. Non-ideal effects influence also the electrical conductivity, which, as shown by the calculated profiles, is affected by the pressure ionization at high electron density. The comparison with the literature results is also discussed.