Multiconfiguration Dirac-Hartree-Fock Calculations with Spectroscopic Accuracy: Applications to Astrophysics
Abstract
:1. Introduction
2. Multiconfiguration Methods
2.1. Multiconfiguration Dirac-Hartree-Fock
2.2. Configuration Interaction
2.3. Managing Large Expansions
2.4. Labelling
2.5. Transition Properties
3. General Computational Methodology: The SD-MR Approach
3.1. Multireference and Gross Features of the Wave Functions
3.2. Including Electron Correlation and Determining an Orbital Set
3.3. Final Configuration Interaction Calculations Including the Breit Interaction and QED Effects
4. Excitation Energies
4.1. Energies for , and States in the B-, C-, N-, O- and F-Like Sequences
4.2. Energies of the and States in the Ne-Like Sequence
4.3. Energies for Higher States in the B-, C-, N-, O-, F- and Ne-Like Sequences
4.4. Energies for Higher Lying States in the Mg-, Al- and Si-Like Sequences
5. Transition Probabilities
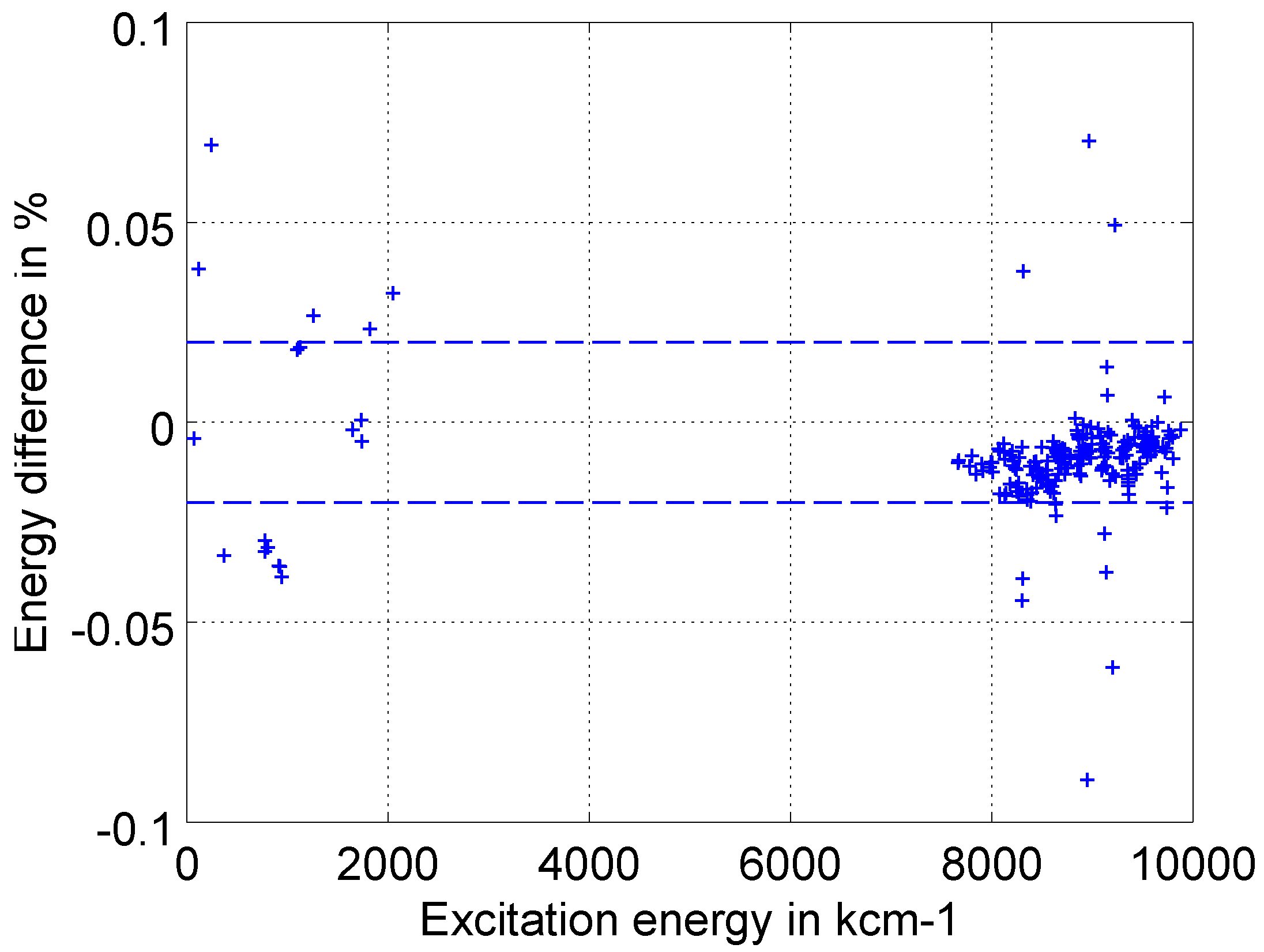
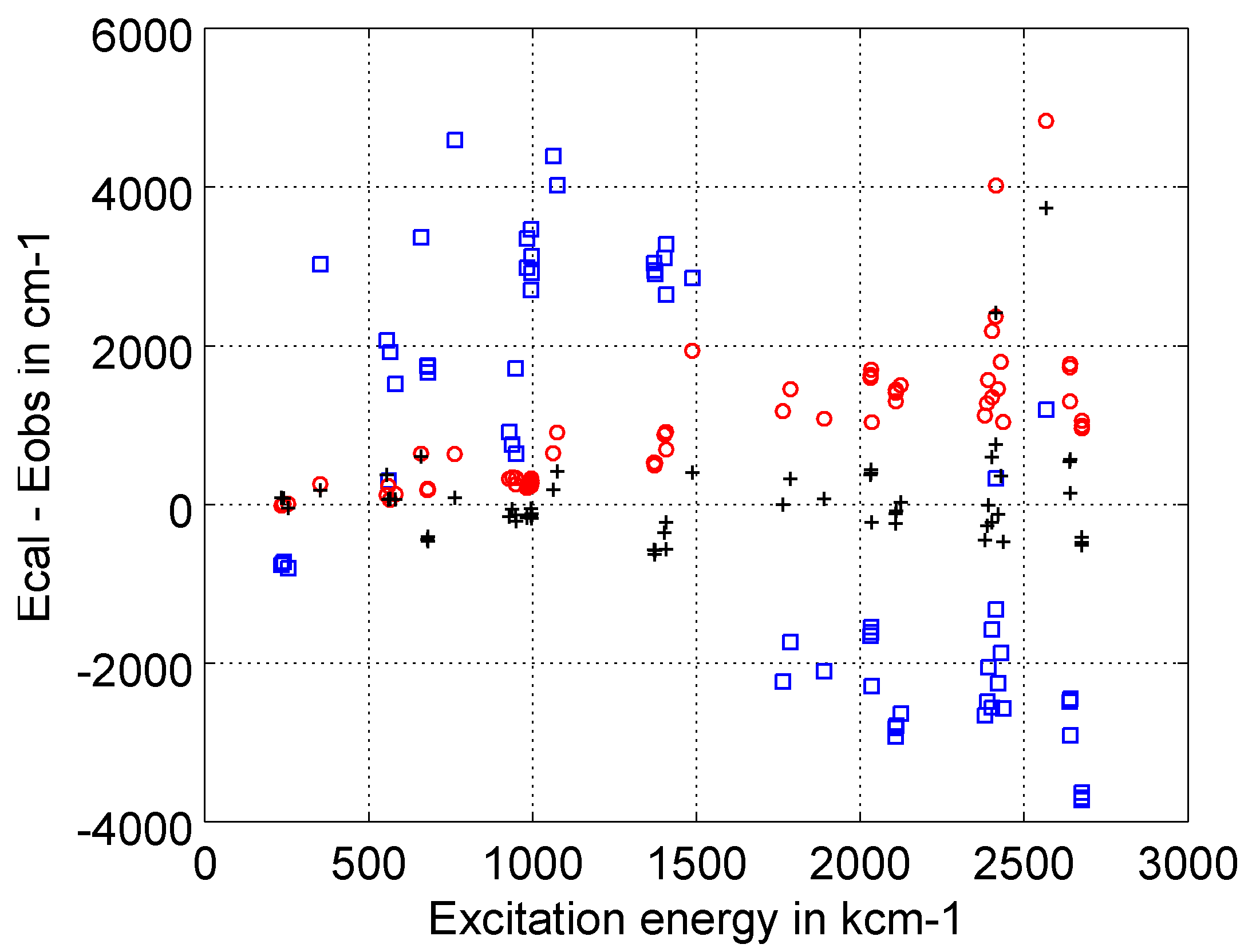
5.1. Internal Validation and Uncertainty Estimates
5.2. Transition Rates for the B- to Si-Like Sequences
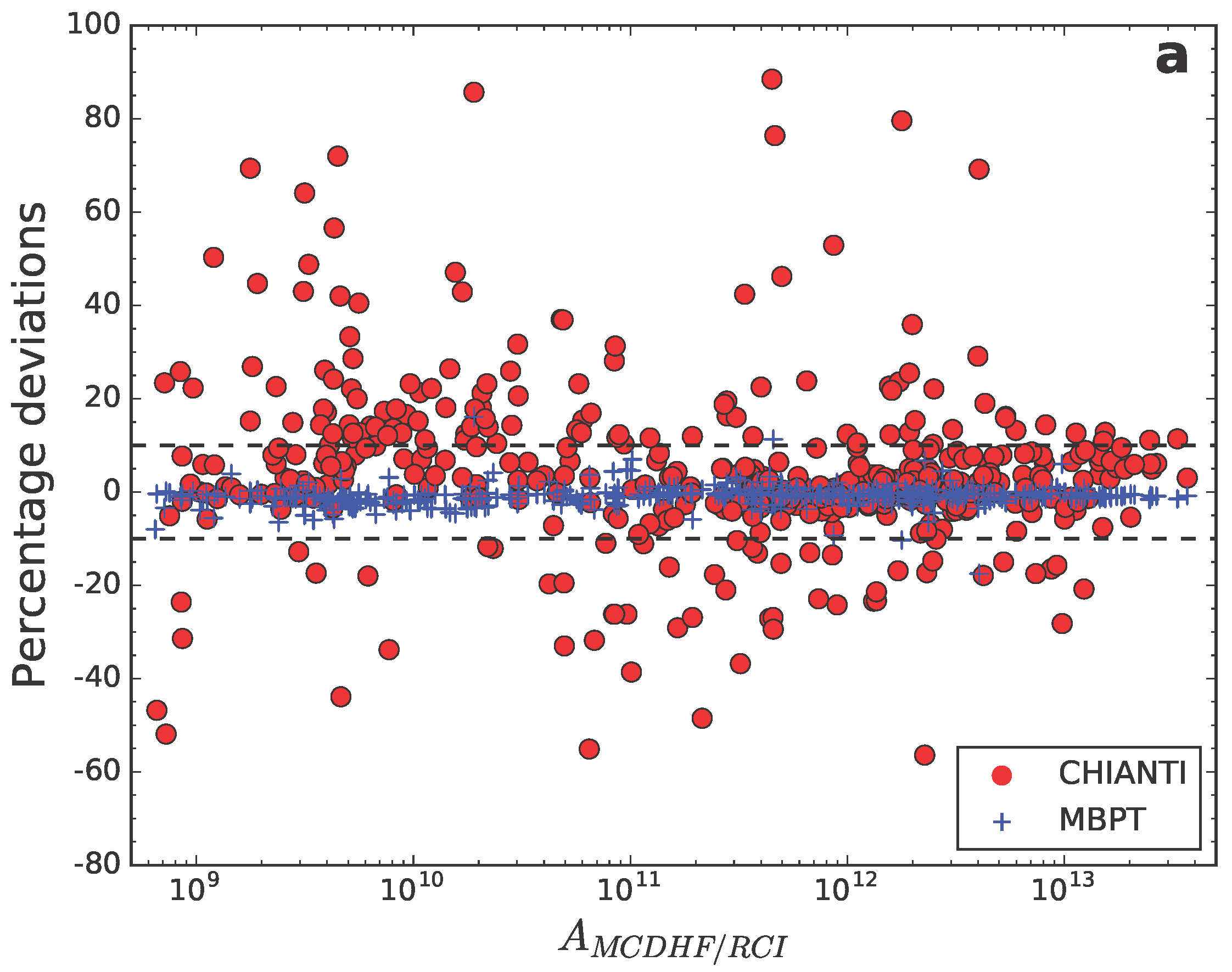
5.3. Systematic Comparisons between Methods
6. Conclusions
7. Further Developments and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Editorial. Nailing fingerprints in the stars. Nature 2013, 437, 503. [Google Scholar]
- Pradhan, A.K.; Nahar, S.N. Atomic Astrophysics and Spectroscopy; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Dere, K.P.; Landi, E.; Mason, H.E.; Monsignori Fossi, B.C.; Young, P.R. CHIANTI—An atomic database for emission lines—Paper I: wavelengths greater than 50 Å (Version 1). Astron. Astrophys. Suppl. Ser. 1997, 125, 149–173. [Google Scholar] [CrossRef]
- Landi, E.; Young, P.R.; Dere, K.P.; Del Zanna, G.; Mason, H.E. CHIANTI—An atomic database for emission lines. XIII. Soft X-ray improvements and other changes: Version 7.1 of the database. Astrophys. J. 2013, 763, 86. [Google Scholar] [CrossRef]
- Del Zanna, G. Benchmarking atomic data for astrophysics: A first look at the soft X-ray lines. Astron. Astrophys. 2012, 546, A97. [Google Scholar] [CrossRef]
- Edlén, B. Atomic Spectra. In Encyclopedia of Physics; Flügge, S., Ed.; Springer-Verlag: Berlin, Germany, 1964. [Google Scholar]
- Froese Fischer, C.; Godefroid, M.; Brage, T.; Jönsson, P.; Gaigalas, G. Advanced multiconfiguration methods for complex atoms: Part I—Energies and wave functions. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 182004. [Google Scholar] [CrossRef]
- Froese Fischer, C.; Brage, T.; Jönsson, P. Computational Atomic Structure—An MCHF Approach; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Kozlov, M.G.; Porsev, S.G.; Safronova, M.S.; Tupitsyn, I.I. CI-MBPT: A package of programs for relativistic atomic calculations based on a method combining configuration interaction and many-body perturbation theory. Comput. Phys. Commun. 2015, 195, 199–213. [Google Scholar] [CrossRef]
- Verdebout, S.; Rynkun, P.; Jönsson, P.; Gaigalas, G.; Froese Fischer, C.; Godefroid, M. A partitioned correlation function interaction approach for describing electron correlation in atoms. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 085003. [Google Scholar] [CrossRef]
- Dzuba, V.A.; Berengut, J.; Harabati, C.; Flambaum, V.V. Combining configuration interaction with perturbation theory for atoms with large number of valence electrons. Phys. Rev. A 2016, 95, 012503. [Google Scholar] [CrossRef]
- Gustafsson, S.; Jönsson, P.; Froese Fischer, C.; Grant, I.P. Combining Multiconfiguration and Perturbation Methods: Perturbative Estimates of Core–Core Electron Correlation Contributions to Excitation Energies in Mg-Like Iron. Atoms 2017, 5, 3. [Google Scholar] [CrossRef]
- Radžiūtė, L.; Gaigalas, G.; Kato, D.; Jönsson, P.; Rynkun, P.; Kučas, S.; Jonauskas, V.; Matulianec, R. Energy level structure of Er3+. J. Quant. Spectrosc. Radiat. Transf. 2015, 152, 94–106. [Google Scholar]
- Jönsson, P.; Gaigalas, G.; Bieroń, J.; Froese Fischer, C.; Grant, I.P. New Version: grasp2K relativistic atomic structure package. Comput. Phys. Commun. 2013, 184, 2197–2203. [Google Scholar] [CrossRef]
- Grant, I.P. Relativistic Quantum Theory of Atoms and Molecules; Springer: New York, NY, USA; 2007. [Google Scholar]
- Dyall, K.G.; Grant, I.P.; Johnson, C.T.; Parpia, F.A.; Plummer, E.P. GRASP: A general-purpose relativistic atomic structure program. Comput. Phys. Commun. 1989, 55, 425–456. [Google Scholar] [CrossRef]
- Grant, I.P.; Pyper, N.C. Breit-interaction in multi-configuration relativistic atomic calculations. J. Phys. B 1976, 9, 761–774. [Google Scholar] [CrossRef]
- Gaigalas, G.; Žalandauskas, T.; Rudzikas, Z. LS-jj transformation matrices for a shell of equivalent electrons. At. Data Nucl. Data Tables 2003, 84, 99–190. [Google Scholar] [CrossRef]
- Froese Fischer, C.; Tachiev, G. Breit-Pauli energy levels, lifetimes, and transition probabilities for the beryllium-like to neon-like sequences. At. Data Nucl. Data Tables 2004, 87, 1–184. [Google Scholar] [CrossRef]
- Froese Fischer, C.; Gaigalas, G. Multiconfiguration Dirac-Hartree-Fock energy levels and transition probabilities for W XXXVIII. Phys. Rev. A 2012, 85, 042501. [Google Scholar] [CrossRef]
- Gaigalas, G.; Froese Fischer, C.; Rynkun, P.; Jönsson, P. JJ2LSJ transformation and unique labeling for energy levels. Atoms 2017, 5, 6. [Google Scholar] [CrossRef]
- Gaigalas, G.; Rudzikas, Z.; Froese Fischer, C. An efficient approach for spin-angular integrations in atomic structure calculations. J. Phys. B At. Mol. Opt. Phys. 1997, 30, 3747–3771. [Google Scholar] [CrossRef]
- Gaigalas, G.; Fritzsche, S.; Grant, I.P. Program to calculate pure angular momentum coefficients in jj-coupling. Comput. Phys. Commun. 2001, 139, 263–278. [Google Scholar] [CrossRef]
- Olsen, J.; Godefroid, M.; Jönsson, P.; Malmqvist, P.Å.; Froese Fischer, C. Transition probability calculations for atoms using nonorthogonal orbitals. Phys. Rev. E 1995, 52, 4499–4508. [Google Scholar] [CrossRef]
- Jönsson, P.; Froese Fischer, C. Multiconfiguration Dirac-Fock calculations of the 2s2 1S0 − 2s2p 3P1 intercombination transition in C III. Phys. Rev. A 1998, 57, 4967–4970. [Google Scholar] [CrossRef]
- Grant, I.P. Gauge invariance and relativistic radiative transitions. J. Phys. B At. Mol. Phys. 1974, 7, 1458–1475. [Google Scholar] [CrossRef]
- Froese Fischer, C.; Gaigalas, G.; Jönsson, P. Core effects on transition energies for 3dk configurations in Tungsten ions. Atoms 2017, 5, 7. [Google Scholar] [CrossRef]
- Rynkun, P.; Jönsson, P.; Gaigalas, G. Energies and E1, M1, E2, M2 transition rates for states of the 2s22p, 2s2p2, and 2p3 configurations in boron-like ions between N III and Zn XXVI. At. Data Nucl. Data Tables 2012, 98, 481–556. [Google Scholar] [CrossRef]
- Jönsson, P.; Rynkun, P.; Gaigalas, G. Energies, E1, M1, and E2 transition rates, hyperfine structures, and Landé gJ factors for the states of the 2s22p2, 2s2p3, and 2p4 configurations in carbon-like ions between F IV and Ni XXIII. At. Data Nucl. Data Tables 2011, 97, 648–691. [Google Scholar] [CrossRef]
- Rynkun, P.; Jönsson, P.; Gaigalas, G.; Froese Fischer, C. Energies and E1, M1, E2, and M2 transition rates for states of the 2s22p3, 2s2p4, and 2p5 configurations in nitrogen-like ions between F III and Kr XXX. At. Data Nucl. Data Tables 2014, 100, 315–402. [Google Scholar] [CrossRef]
- Rynkun, P.; Jönsson, P.; Gaigalas, G.; Froese Fischer, C. Energies and E1, M1, E2, and M2 transition rates for states of the 2s22p4, 2s2p5, and 2p6 configurations in oxygen-like ions between F II and Kr XXIX. Astron. Astrophys. 2013, 557, A136. [Google Scholar] [CrossRef]
- Jönsson, P.; Alkauskas, A.; Gaigalas, G. Energies and E1, M1, E2 transition rates for states of the 2s22p5 and 2s2p6 configurations in fluorine-like ions between Si VI and W LXVI. At. Data Nucl. Data Tables 2013, 99, 431–446. [Google Scholar] [CrossRef]
- Nazé, C.; Verdebout, S.; Rynkun, P.; Gaigalas, G.; Godefroid, M.; Jönsson, P. Isotope shifts in beryllium-, boron-, carbon-, and nitrogen-like ions from relativistic configuration interaction calculations. At. Data Nucl. Data Tables 2014, 100, 1197–1249. [Google Scholar] [CrossRef]
- Verdebout, S.; Nazé, C.; Jönsson, P.; Rynkun, P.; Godefroid, M.; Gaigalas, G. Hyperfine structures and Landé gJ-factors for n = 2 states in beryllium-, boron-, carbon-, and nitrogen-like ions from relativistic configuration interaction calculations. At. Data Nucl. Data Tables 2014, 100, 1111–1155. [Google Scholar] [CrossRef]
- Kelly, R.L. Atomic and Ionic Spectrum Lines Below 2000 Angstroms: Hydrogen Through Krypton. J. Phys. Chem. Ref. Data Suppl. 1987, 16, 1–1698. [Google Scholar]
- Edlén, B. Comparison of Theoretical and Experimental Level Values of the n = 2 Complex in Ions Isoelectronic with Li, Be, O and F. Phys. Scr. 1983, 28, 51–67. [Google Scholar] [CrossRef]
- Kramida, A.E.; Ralchenko, Y.; Reader, J.; NIST ASD Team (2015). NIST Atomic Spectra Database (ver. 5.3). National Institute of Standards and Technology: Gaithersburg, MD. Available online: http://physics.nist.gov/asd (accessed on 28 December 2016).
- Vilkas, M.J.; Ishikawa, Y.; Koc, K. Relativistic multireference many-body perturbation theory for quasidegenerate systems: Energy levels of ions of the oxygen isoelectronic sequence. Phys. Rev. A 1999, 60, 2808–2821. [Google Scholar] [CrossRef]
- Gaigalas, G.; Kaniauskas, J.; Kisielius, R.; Merkelis, G.; Vilkas, M.J. Second-order MBPT results for the oxygen isoelectronic sequence. Phys. Scr. 1994, 49, 135–147. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Thomas, R.J.; Landi, E. Atomic data and spectral line intensities for Ne III. At. Data Nucl. Data Tables 2003, 83, 113–152. [Google Scholar] [CrossRef]
- Jonauskas, V.; Keenan, F.P.; Foord, M.E.; Heeter, R.F.; Rose, S.J.; Ferland, G.J.; Kisielius, R.; van Hoof, P.A.M.; Norrington, P.H. Dirac-Fock energy levels and transition probabilities for oxygen-like Fe XIX. Astron. Astrophys. 2004, 424, 363–369. [Google Scholar] [CrossRef]
- Landi, E.; Gu, M.F. Atomic Data for High-Energy Configurations in Fe XVII-XXIII. Astrophys. J. 2006, 640, 1171–1179. [Google Scholar] [CrossRef]
- Jönsson, P.; Bengtsson, P.; Ekman, J.; Gustafsson, S.; Karlsson, L.B.; Gaigalas, G.; Froese Fischer, C.; Kato, D.; Murakami, I.; Sakaue, H.A.; et al. Relativistic CI calculations of spectroscopic data for the 2p6 and 2p53l configurations in Ne-like ions between Mg III and Kr XXVII. At. Data Nucl. Data Tables 2014, 100, 1–154. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Lopez Encarnacion, J.M.; Träbert, E. N = 3 − 3 transitions of Ne-like ions in the iron group, especially Ca10+ and Ti12+. Phys. Scr. 2009, 79, 025301. [Google Scholar] [CrossRef]
- Jönsson, P.; Ekman, J.; Gustafsson, S.; Hartman, H.; Karlsson, L.B.; du Rietz, R.; Gaigalas, G.; Godefroid, M.R.; Froese Fischer, C. Energy levels and transition rates for the boron isoelectronic sequence: Si X, Ti XVIII – Cu XXV. Astron. Astrophys. 2013, 559, A100. [Google Scholar] [CrossRef]
- Jönsson, P.; Ekman, J.; Träbert, E. MCDHF Calculations and Beam-Foil EUV Spectra of Boron-like Sodium Ions (Na VII). Atoms 2015, 3, 195–259. [Google Scholar] [CrossRef]
- Ekman, J.; Jönsson, P.; Gustafsson, S.; Hartman, H.; Gaigalas, G.; Godefroid, M.R.; Froese Fischer, C. Calculations with spectroscopic accuracy: Energies, Landé gJ-factors, and transition rates in the carbon isoelectronic sequence from Ar XIII to Zn XXV. Astron. Astrophys. 2014, 564, A24. [Google Scholar] [CrossRef]
- Radžiūtė, L.; Ekman, J.; Jönsson, P.; Gaigalas, G. Extended calculations of level and transition properties in the nitrogen isoelectronic sequence: Cr XVIII, Fe XX, Ni XXII, and Zn XXIV. Astron. Astrophys. 2015, 582, A61. [Google Scholar] [CrossRef]
- Wang, K.; Guo, X.L.; Li, S.; Si, R.; Dang, W.; Chen, Z.B.; Jönsson, P.; Hutton, R.; Chen, C.Y.; Yan, J. Calculations with spectroscopic accuracy: Energies and transition rates in the nitrogen isoelectronic sequence from Ar XII to Zn XXIV. Astrophys. J. Suppl. 2016, 223, 3. [Google Scholar]
- Wang, K.; Jönsson, P.; Ekman, J.; Gaigalas, G.; Godefroid, M.R.; So, R.; Chen, Z.B.; Li, S.; Chen, C.Y.; Yan, J. Extended Calculations of Spectroscopic Data Energy Levels, Lifetimes and Transition Rates for O-like Ions from Cr XVII to Zn XXIII. Astrophys. J. Suppl. 2017, 229, 37. [Google Scholar] [CrossRef]
- Si, R.; Li, S.; Guo, X.L.; Chen, Z.B.; Brage, T.; Jönsson, P.; Wang, K.; Yan, J.; Chen, C.Y.; Zou, Y.M. Extended calculations with spectroscopic accuracy: energy levels and transition properties for the fluorine isoelectronic sequence with Z = 24 − 30. Astrophys. J. Suppl. 2016, 227, 16. [Google Scholar] [CrossRef]
- Wang, K.; Chen, Z.B.; Si, R.; Jönsson, P.; Ekman, J.; Guo, X.L.; Li, S.; Long, F.Y.; Dang, W.; Zhao, X.H.; et al. Extended relativistic configuration interaction and many-body perturbation calculations of spectroscopic data for the n ≤ 6 configurations in Ne-like ions between Cr XV and Kr XXVII. Astrophys. J. Suppl. 2016, 226, 14. [Google Scholar] [CrossRef]
- Gu, M.F. Wavelengths of 2l → 3l′ transitions in L-shell ions of iron and nickel: A combined configuration interaction and many-body perturbation approach. Astrophys. J. Suppl. 2005, 156, 105–110. [Google Scholar] [CrossRef]
- Gustafsson, S.; Jönsson, P.; Froese Fischer, C.; Grant, I.P. MCDHF and RCI calculations of energy levels, lifetimes and transition rates for 3l3l′, 3l4l′ and 3s5l states in Ca IX—As XXII and Kr XXV. Astron. Astrophy 2017, 505, A76. [Google Scholar] [CrossRef]
- Ekman, J.; Jönsson, P.; Radžiūtė, L.; Gaigalas, G.; Del Zanna, G.; Grant, I.P. Large-scale calculations of atomic level and transition properties in the aluminium isoelectronic sequence from Ti X through Kr XXIV, Xe XLII, and W LXII. At. Data Nucl. Data Tables 2017. submitted. [Google Scholar]
- Jönsson, P.; Radžiūtė, L.; Gaigalas, G.; Godefroid, M.R.; Marques, J.P.; Brage, T.; Froese Fischer, C.; Grant, I.P. Accurate multiconfiguration calculations of energy levels, lifetimes and transition rates for the silicon isoelectronic sequence: Ti IX—Ge XIX, Sr XXV, Zr XXVII, Mo XXIX. Astron. Astrophys. 2016, 585, A26. [Google Scholar] [CrossRef]
- Del Zanna, G. Benchmarking atomic data for astrophysics: Fe XIII EUV lines. Astron. Astrophys. 2011, 533, A12. [Google Scholar] [CrossRef]
- Vilkas, M.J.; Ishikawa, Y. High-accuracy calculations of term energies and lifetimes of silicon-like ions with nuclear charges Z = 24 − 30. J. Phys. B At. Mol. Opt. Phys. 2004, 37, 1803–1816. [Google Scholar] [CrossRef]
- Träbert, E. Critical Assessment of Theoretical Calculations of Atomic Structure and Transition Probabilities: An Experimenter’s View. Atoms 2014, 2, 15–85. [Google Scholar] [CrossRef]
- Träbert, E.; Curtis, L.J. Isoelectronic trends of line strength data in the Li and Be isoelectronic sequences. Phys. Scr. 2006, 74, C46–C54. [Google Scholar] [CrossRef]
- Froese Fischer, C. Evaluating the accuracy of theoretical transition data. Phys. Scr. 2009, 134, 014019. [Google Scholar] [CrossRef]
- Ekman, J.; Godefroid, M.R.; Hartman, H. Validation and Implementation of Uncertainty Estimates of Calculated Transition Rates. Atoms 2014, 2, 215–224. [Google Scholar] [CrossRef]
- Ynnerman, A.; Froese Fischer, C. Multiconfigurational-Dirac-Fock calculation of the 2s 1S0 − 2s2p 3P1 spin-forbidden transition for the Be-like isoelectronic sequence. Phys. Rev. A 1995, 51, 2020–2030. [Google Scholar] [CrossRef] [PubMed]
- Hibbert, A.; Ledourneuf, M.; Mohan, M. Energies, Oscillator Strengths, and Lifetimes for Neon-like Ions Up to Kr XXVII. At. Data Nucl. Data Tables 1993, 53, 23–112. [Google Scholar] [CrossRef]
- Froese Fischer, C.; Jönsson, P. MCHF calculations for atomic properties. Comput. Phys. Commun. 1994, 84, 37–58. [Google Scholar] [CrossRef]
- Pagel, B.E.J. Nucleosynthesis and Chemical Evolution of Galaxies; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
| 1. | Transitions between two states for which the configurations differ by more than one electron. These transitions are zero in the lowest approximation and are induced by CSFs that enter the calculation to correct for electron correlation effects. |
| Configuration | MR for RMCDHF | MR for RCI | Active Set | |
|---|---|---|---|---|
| boron-like, N III to Zn XXVI | ||||
| 200 100 | ||||
| 360 100 | ||||
| 300 100 | ||||
| carbon-like, F IV to Ni XXIII | ||||
| 340 100 | ||||
| 340 100 | ||||
| 1 000 100 | ||||
| nitrogen-like, F III to Kr XXX | ||||
| 698 100 | ||||
| 382 100 | ||||
| 680 100 | ||||
| oxygen-like, F II to Kr XXIX | ||||
| 709 690 | ||||
| 67 375 | ||||
| 702 892 | ||||
| fluorine-like, Si VI to WLXVI | ||||
| 73 000 | ||||
| 15 000 | ||||
| Ne III | |||||||
| Level | |||||||
| 2 | 0 | 0 (0.00) | 0 (0.00) | 0 (0.00) | 0 (0.00) | 0 (0.00) | |
| 1 | 643 | 645 (0.31) | 638 (0.77) | 645 (0.31) | 628 (2.33) | 744 (15.70) | |
| 0 | 921 | 923 (0.21) | 912 (0.97) | 926 (0.54) | 899 (2.38) | 1 069 (16.06) | |
| 2 | 25 841 | 25 954 (0.43) | 26 097 (0.99) | 25 573 (1.03) | 25 759 (0.31) | 29 219 (13.07) | |
| 0 | 55 753 | 56 058 (0.54) | 55 772 (0.03) | 55 459 (0.52) | 55 382 (0.66) | 72 484 (30.00) | |
| 2 | 204 290 | 204 608 (0.15) | 204 718 (0.20) | 200 686 (1.76) | 204 635 (0.16) | 215 348 (5.41) | |
| 1 | 204 873 | 205 200 (0.15) | 205 297 (0.20) | 201 276 (1.75) | 205 236 (0.17) | 216 008 (5.43) | |
| 0 | 205 194 | 205 603 (0.19) | 205 617 (0.20) | 201 598 (1.75) | 205 539 (0.16) | 216 367 (5.44) | |
| 1 | 289 479 | 290 315 (0.28) | 290 703 (0.42) | 288 219 (0.43) | 291 659 (0.75) | 315 511 (8.99) | |
| Fe XIX | |||||||
| Level | |||||||
| 2 | 0 | 0 (0.000) | 0 (0.000) | 0 (0.00) | 0 (0.00) | 0 (0.00) | |
| 0 | 75 250 | 75 313 (0.083) | 75 218 (0.042) | 74 742 (0.67) | 75 446 (0.26) | 75 198 (0.06) | |
| 1 | 89 441 | 89 434 (0.007) | 89 251 (0.212) | 87 559 (2.10) | 88 791 (0.72) | 88 821 (0.69) | |
| 2 | 168 852 | 168 985 (0.078) | 168 792 (0.035) | 167 881 (0.57) | 170 847 (1.18) | 170 578 (1.02) | |
| 0 | 325 140 | 325 417 (0.085) | 324 949 (0.058) | 321 124 (1.23) | 326 536 (0.42) | 325 421 (0.08) | |
| 2 | 922 890 | 923 044 (0.016) | 922 855 (0.003) | 917 435 (0.59) | 933 081 (1.10) | 929 231 (0.68) | |
| 1 | 984 740 | 984 920 (0.018) | 984 791 (0.005) | 978 242 (0.65) | 995 006 (1.04) | 991 246 (0.66) | |
| 0 | 1030 020 | 1030 199 (0.017) | 1029 992 (0.002) | 1022 753 (0.70) | 1039 692 (0.93) | 1036 058 (0.58) | |
| 1 | 1267 600 | 1268 093 (0.038) | 1267 771 (0.013) | 1258 927 (0.68) | 1287 773 (1.59) | 1282 914 (1.20) | |
| 0 | 2134 180 | 2134 958 (0.036) | 2132 810 (0.064) | 2120 211 (0.65) | 2175 645 (1.94) | 2160 701 (1.24) | |
| Level | J | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 218 800 | 153 478 | 151 954 | −66 846 | −1524 | 15 2035 | −66 765 | −1443 | |
| 1 | 379 800 | 371 663 | 371 606 | −8 194 | −57 | 37 1858 | −7 942 | 195 | |
| 2 | 483 040 | 470 699 | 470 643 | −12 397 | −56 | 47 0804 | −12 236 | 105 | |
| 0 | 944 150 | 912 501 | 911 968 | −32 182 | -533 | 91 2282 | −31 868 | −219 | |
| 2 | 1 579 903 | 1 579 537 | −366 | 1 580 945 | 1042 | ||||
| 1 | 1 755 028 | 1 755 196 | 168 | 1 756 684 | 1656 | ||||
| 0 | 1 986 274 | 1 985 784 | −490 | 1 987 396 | 1122 | ||||
| 1 | 2 229 358 | 2 230 149 | 791 | 2 231 636 | 2278 | ||||
| 0 | 3 573 416 | 3 575 415 | 1999 | 3 579 486 | 6070 |
| Level | Composition | ||||
|---|---|---|---|---|---|
| Ca XI | |||||
| 1.00 | 0 | 0 | 0 | ||
| 0.99 | 2 801 989 | 2 801 819 | |||
| 2 810 900 | 2 810 834 (0.0023) | 2 810 588 (0.011) | |||
| 0.99 | 2 831 800 | 2 831 670 | |||
| 2 839 900 | 2 839 662 (0.0084) | 2 839 386 (0.018) | |||
| 0.92 | 2 953 791 | 2 953 594 | |||
| 2 978 410 | 2 977 968 | ||||
| 1.00 | 2 978 650 | 2 978 276 | |||
| 2 986 908 | 2 986 513 | ||||
| 2 993 760 | 2 993 336 | ||||
| 3 007 301 | 3 006 932 | ||||
| 0.98 | 3 009 345 | 3 009 000 | |||
| 3 016 749 | 3 016 378 | ||||
| 3 017 175 | 3 016 845 | ||||
| 0.98 | 3 101 166 | 3 098 308 | |||
| 0.99 | 3 196 075 | 3 195 830 | |||
| 0.95 | 3 199 300 | 3 199 045 (0.0080) | 3 198 902 (0.012) | ||
| 0.85 | 3 205 278 | 3 205 169 | |||
| 1.00 | 3 208 351 | 3 208 165 | |||
| 3 212 392 | 3 212 144 | ||||
| 3 219 655 | 3 219 428 | ||||
| 3 224 394 | 3 224 078 | ||||
| 0.89 | 3 239 700 | 3 239 502 (0.0061) | 3 239 308 (0.012) | ||
| 3 244 348 | 3 244 161 | ||||
| 3 248 017 | 3 247 805 | ||||
| 3 248 345 | 3 248 099 | ||||
| 0.91 | 3 284 300 | 3 284 444 (0.0044) | 3 283 473 (0.025) | ||
| Fe XVII | |||||
| 1.00 | 0 | 0 | 0 | ||
| 1.00 | 5 849 490 | 5 849 108 (0.0065) | 5 848 891 (0.0102) | ||
| 5 864 760 | 5 864 469 (0.0049) | 5 864 138 (0.0106) | |||
| 1.00 | 5 951 478 | 5 951 003 (0.0079) | 5 950 877 (0.0100) | ||
| 5 961 022 | 5 960 633 (0.0065) | 5 960 410 (0.0102) | |||
| 6 093 568 | 6 093 573 (0.0000) | 6 093 209 (0.0058) | |||
| 6 121 756 | 6 121 769 (0.0002) | 6 121 253 (0.0082) | |||
| 1.00 | 6 134 815 | 6 134 794 (0.0003) | 6 134 360 (0.0074) | ||
| 6 143 897 | 6 143 898 (0.0000) | 6 143 431 (0.0075) | |||
| 6 158 540 | 6 158 481 (0.0009) | 6 158 010 (0.0086) | |||
| 0.94 | 6 202 620 | 6 202 542 (0.0012) | 6 202 238 (0.0061) | ||
| 6 219 266 | 6 219 185 (0.0013) | 6 218 795 (0.0075) | |||
| 6 245 490 | 6 245 346 (0.0023) | 6 245 018 (0.0075) | |||
| 6 248 530 | 6 248 390 (0.0022) | 6 248 024 (0.0080) | |||
| 0.93 | 6 353 356 | 6 353 605 (0.0039) | 6 351 136 (0.0349) | ||
| 0.99 | 6 464 095 | 6 463 913 (0.0028) | 6 463 611 (0.0074) | ||
| 0.91 | 6 471 233 | 6 471 519 (0.0044) | 6 471 317 (0.0012) | ||
| 6 486 440 | 6 486 166 (0.0042) | 6 485 977 (0.0071) | |||
| 1.00 | 6 487 000 | 6 486 745 (0.0039) | 6 486 514 (0.0074) | ||
| 6 492 924 | 6 492 689 (0.0036) | 6 492 387 (0.0082) | |||
| 6 506 808 | 6 506 561 (0.0037) | 6 506 276 (0.0081) | |||
| 6 515 479 | 6 515 276 (0.0031) | 6 514 936 (0.0083) | |||
| 6 552 221 | 6 552 697 (0.0072) | 6 552 491 (0.0041) | |||
| 6 594 617 | 6 594 260 (0.0054) | 6 594 099 (0.0078) | |||
| 6 601 210 | 6 600 855 (0.0053) | 6 600 688 (0.0079) | |||
| 6 605 469 | 6 605 078 (0.0059) | 6 604 858 (0.0092) | |||
| 6 660 894 | 6 661 101 (0.0031) | 6 660 232 (0.0099) | |||
| Sequence | Ions | Configurations | N | Ref. |
|---|---|---|---|---|
| B-like | Si, Ti-Cu | , , , , , , , , | 291 | [45] |
| B-like | Na | , , , , , , , | 133 | [46] |
| C-like | Ar-Zn | , , , , , , | 262 | [47] |
| N-like | Cr, Fe, Ni, Zn | , , , , , | 272 | [48] |
| N-like | Ar-Zn | , , , , , , | 359 | [49] |
| O-like | Cr-Zn | , , , , | 200 | [50] |
| F-like | Cr-Zn | , , , , , | 200 | [51] |
| Ne-like | Cr-Kr | , , , , , | 201 | [52] |
| No. | Level | |||||
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 73 864 | 73 867 | 73 041 | 73 851 | 73 851 | |
| 3 | 117 417 | 117 372 | 117 146 | 117 354 | 117 367 | |
| 4 | 244 751 | 244 581 | 245 710 | 244 561 | 244 568 | |
| 5 | 372 137 | 372 261 | 373 060 | 371 980 | 371 744 | |
| 6 | 486 584 | 487 683 | 479 658 | 486 950 | 486 991 | |
| 7 | 776 775 | 777 005 | 779 724 | 776 690 | 776 685 | |
| 8 | 777 404 | 777 655 | 779 963 | 777 340 | 777 367 | |
| 9 | 803 618 | 803 869 | 805 768 | 803 540 | 803 553 | |
| 10 | 916 444 | 916 773 | 920 272 | 916 330 | 916 333 | |
| 11 | 925 074 | 925 408 | 928 822 | 924 920 | 924 920 | |
| 12 | 942 621 | 942 986 | 946 135 | 942 430 | 942 364 | |
| 13 | 1 096 019 | 1 095 820 | 1 105 578 | 1 095 670 | 1 095 679 | |
| 14 | 1 127 672 | 1 127 460 | 1 137 533 | 1 127 240 | 1 127 250 | |
| 15 | 1 261 577 | 1 261 240 | 1 272 627 | 1 261 140 | 1 260 902 | |
| 16 | 1 646 437 | 1 646 467 | 1 657 411 | 1 646 300 | 1 646 409 | |
| 17 | 1 735 823 | 1 735 813 | 1 747 301 | 1 735 700 | 1 735 715 | |
| 18 | 1 740 623 | 1 740 707 | 1 750 848 | 1 740 500 | 1 740 453 | |
| 19 | 1 817 786 | 1 817 362 | 1 832 102 | 1 817 100 | 1 817 041 | |
| 20 | 2 048 512 | 2 047 850 | 2 066 463 | 2 048 200 | 2 048 056 | |
| 21 | 7 663 283 | 7 664 054 | 7 654 119 | |||
| 22 | 7 671 971 | 7 672 703 | 7 663 398 | 7 661 883 | ||
| 23 | 7 780 298 | 7 781 147 | 7 770 895 | |||
| 24 | 7 803 764 | 7 804 419 | 7 796 397 | |||
| 25 | 7 841 903 | 7 842 922 | 7 834 847 | |||
| 26 | 7 898 154 | 7 898 974 | 7 891 978 | |||
| 27 | 7 901 553 | 7 902 378 | 7 895 497 | |||
| 28 | 7 914 849 | 7 915 811 | 7 909 434 | 7 915 463 | ||
| 29 | 7 983 446 | 7 984 350 | 7 977 011 | |||
| 30 | 7 994 588 | 7 995 388 | 7 987 318 | |||
| 31 | 8 004 987 | 8 005 793 | 7 998 341 | |||
| 32 | 8 007 326 | 8 008 319 | 8 002 052 | |||
| 33 | 8 068 537 | 8 069 071 | 8 065 382 | |||
| 34 | 8 078 540 | 8 079 119 | 8 072 911 | 8 074 160 | ||
| 35 | 8 080 551 | 8 082 001 | 8 070 805 | |||
| 36 | 8 116 048 | 8 116 480 | 8 111 336 | 8 101 400 | 8 118 008 | |
| 37 | 8 121 922 | 8 122 529 | 8 118 025 | 8 124 085 | ||
| 38 | 8 128 645 | 8 129 396 | 8 126 192 | 8 143 710 | ||
| 39 | 8 131 973 | 8 133 460 | 8 121 258 | |||
| 40 | 8 139 290 | 8 140 735 | 8 135 992 | 8 140 000 | 8 141 785 | |
| 41 | 8 181 331 | 8 182 599 | 8 170 876 | |||
| 42 | 8 182 172 | 8 182 844 | 8 179 292 | 8 180 254 | ||
| 43 | 8 202 073 | 8 202 670 | 8 195 771 | |||
| 44 | 8 208 705 | 8 209 597 | 8 204 329 | |||
| 45 | 8 222 156 | 8 222 948 | 8 217 390 | |||
| 46 | 8 230 918 | 8 231 868 | 8 227 144 | (8 195 000) | 8 229 642 | |
| 47 | 8 245 453 | 8 246 428 | 8 241 436 | 8 230 900 | 8 229 642 | |
| 48 | 8 245 737 | 8 247 075 | 8 241 557 | |||
| 49 | 8 247 732 | 8 249 164 | 8 243 033 | |||
| 50 | 8 267 963 | 8 269 220 | 8 259 742 | |||
| 51 | 8 270 558 | 8 272 088 | 8 262 373 | |||
| 52 | 8 274 704 | 8 275 427 | 8 270 235 | |||
| 53 | 8 300 618 | 8 301 128 | 8 301 379 | 8 313 600 | ||
| 54 | 8 303 730 | 8 307 428 | 8 305 376 | 8 293 900 | 8 293 791 | |
| 55 | 8 305 917 | 8 309 162 | 8 297 457 | |||
| 56 | 8 312 499 | 8 309 359 | 8 300 070 | |||
| 57 | 8 349 456 | 8 350 857 | 8 342 324 | 8 350 731 | ||
| 58 | 8 351 775 | 8 353 277 | 8 342 522 | |||
| 59 | 8 352 117 | 8 353 731 | 8 343 801 | |||
| 60 | 8 379 967 | 8 380 890 | 8 373 689 | 8 376 741 | ||
| 61 | 8 388 634 | 8 390 292 | 8 380 281 | |||
| 62 | 8 399 557 | 8 401 039 | 8 390 478 | |||
| 63 | 8 410 077 | 8 411 182 | 8 404 386 | |||
| 64 | 8 420 588 | 8 421 426 | 8 420 569 | |||
| 65 | 8 428 405 | 8 429 248 | 8 428 172 | |||
| 66 | 8 440 926 | 8 441 758 | 8 437 725 | |||
| 67 | 8 442 813 | 8 443 776 | 8 438 241 | |||
| 68 | 8 443 646 | 8 445 037 | 8 440 027 | |||
| 69 | 8 462 365 | 8 463 510 | 8 456 502 | |||
| 70 | 8 467 690 | 8 468 680 | 8 462 413 | |||
| 71 | 8 470 871 | 8 471 913 | 8 466 158 | |||
| 72 | 8 480 620 | 8 481 735 | 8 471 575 | |||
| 73 | 8 488 782 | 8 489 971 | 8 479 898 | 8 486 331 | ||
| 74 | 8 496 990 | 8 497 512 | 8 498 660 | |||
| 75 | 8 506 111 | 8 507 343 | 8 497 311 | 8 511 385 | ||
| 76 | 8 544 575 | 8 545 928 | 8 534 831 | |||
| 77 | 8 545 485 | 8 546 507 | 8 544 603 | |||
| 78 | 8 553 885 | 8 554 716 | 8 545 420 | |||
| 79 | 8 554 798 | 8 555 918 | 8 546 365 | |||
| 80 | 8 555 297 | 8 556 534 | 8 547 553 | |||
| 81 | 8 555 491 | 8 556 850 | 8 558 611 | |||
| 82 | 8 561 662 | 8 562 969 | 8 552 789 | 8 564 535 | ||
| 83 | 8 581 274 | 8 582 755 | 8 576 965 | 8 575 780 | ||
| 84 | 8 586 636 | 8 588 014 | 8 577 151 | |||
| 85 | 8 597 735 | 8 599 106 | 8 588 388 | |||
| 86 | 8 606 110 | 8 606 654 | 8 607 148 | 8 605 427 | ||
| 87 | 8 611 432 | 8 611 843 | 8 608 283 | |||
| 88 | 8 619 312 | 8 620 847 | 8 611 148 | |||
| ⋮ | ||||||
| 228 | 9 735 480 | 9 736 111 | 9 746 771 | |||
| 229 | 9 740 645 | 9 742 719 | 9 754 847 | |||
| 230 | 9 748 184 | 9 749 774 | 9 758 859 | |||
| 231 | 9 757 890 | 9 758 107 | 9 770 963 | |||
| 232 | 9 765 663 | 9 766 056 | 9 781 499 | |||
| 233 | 9 780 738 | 9 781 044 | 9 794 389 | |||
| 234 | 9 800 368 | 9 800 742 | 9 819 206 | |||
| 235 | 9 800 852 | 9 801 738 | 9 819 939 | |||
| 236 | 9 879 471 | 9 879 655 | 9 902 175 | |||
| 237 | 10 368 077 | 10 362 393 | ||||
| 238 | 10 371 121 | 10 365 585 | 10 380 000 | |||
| 239 | 10 442 616 | 10 437 633 | ||||
| 240 | 10 466 102 | 10 460 676 | ||||
| 241 | 10 468 322 | 10 462 978 | ||||
| 242 | 10 470 990 | 10 465 993 | ||||
| 243 | 10 485 597 | 10 479 693 | ||||
| 244 | 10 492 966 | 10 487 317 | ||||
| 245 | 10 532 099 | 10 526 459 | ||||
| 246 | 10 548 542 | 10 542 323 | (10 547 000) | 10 547 249 | ||
| 247 | 10 549 480 | 10 543 488 | 10 548 000 | 10 548 160 | ||
| 248 | 10 554 447 | 10 548 345 | 10 553 000 | 10 553 955 | ||
| 249 | 10 568 810 | 10 563 327 | ||||
| 250 | 10 574 912 | 10 569 412 | 10 664 000 | |||
| 251 | 10 575 111 | 10 569 433 | ||||
| 252 | 10 578 203 | 10 572 657 | ||||
| 253 | 10 597 862 | |||||
| 254 | 10 619 563 | |||||
| 255 | 10 652 979 | |||||
| 256 | 10 653 631 | 10 675 000 | ||||
| 257 | 10 660 593 | |||||
| 258 | 10 666 807 | |||||
| 259 | 10 666 946 | 10 688 000 | ||||
| 260 | 10 667 948 | |||||
| 261 | 10 683 984 | 10 681 000 | ||||
| 262 | 10 687 400 |
| Sequence | Ions | Configurations | N | Ref. |
|---|---|---|---|---|
| Mg-like | Ca-As, Kr | , , | 146 | [54] |
| Al-like | Ti-Kr, Xe, W | , , , | 360 | [55] |
| , , , | ||||
| Si-like | Ti-Ge, Sr, Zr, Mo | , , | 27 | [56] |
| Fe XIII | |||
|---|---|---|---|
| Level | |||
| 0 | 0 | 0 | |
| 9281 (0.237) | 9295 (0.086) | 9303.1 | |
| 18553 (0.048) | 18576 (0.075) | 18561.7 | |
| 48236 (0.344) | 47985 (1.077) | 48069.7 | |
| 91839 (0.357) | 91508 (0.003) | 91511.0 | |
| 214152 (0.220) | 214540 (0.039) | 214624.0 | |
| 287123 (0.028) | 287199 (0.002) | 287205.0 | |
| 287270 (0.029) | 287348 (0.002) | 287356.0 | |
| 290095 (0.029) | 290179 (0.000) | 290180.0 | |
| 328974 (0.014) | 328980 (0.016) | 328927.0 | |
| 329689 (0.015) | 329702 (0.019) | 329637.0 | |
| 330323 (0.012) | 330334 (0.015) | 330282.0 | |
| 362482 (0.020) | 362416 (0.002) | 362407.0 | |
| 415577 (0.027) | 415519 (0.013) | 415462.0 | |
| 430277 (0.035) | 430129 (0.001) | 430124.0 | |
| 437064 (0.033) | 436905 (0.003) | 436919.0 | |
| 438365 (0.063) | 438005 (0.018) | 438086.0 | |
| 447134 (0.029) | 446959 (0.009) | 447001.0 | |
| 486542 (0.037) | 486403 (0.009) | 486358.0 | |
| 495102 (0.032) | 495242 (0.060) | 494942.0 | |
| 499060 (0.038) | 498925 (0.011) | 498870.0 | |
| 501676 (0.032) | 501667 (0.030) | 501514.0 | |
| 506661 (0.030) | 506681 (0.034) | 506505.0 | |
| 509303 (0.024) | 509479 (0.059) | 509176.0 | |
| 509394 (0.028) | 509441 (0.037) | 509250.0 | |
| 557432 (0.093) | 557303 (0.070) | 556911.0 | |
| 571376 (0.110) | 571187 (0.077) | 570743.0 | |
| Upper | Lower | A | |
|---|---|---|---|
| Fe XXI | |||
| 776750 (0.049) | 1.156E+10 (0.00) | ||
| 925023 (0.120) | 4.213E+09 (0.07) | ||
| 1096012 (0.089) | 9.460E+09 (0.16) | ||
| 1261529 (0.205) | 2.850E+07 (1.82) | ||
| 412701 (0.293) | 3.597E+07 (8.72) | ||
| 702930 (0.049) | 7.606E+08 (1.64) | ||
| 703550 (0.048) | 9.240E+09 (0.66) | ||
| 842581 (0.122) | 2.200E+10 (0.31) | ||
| 851203 (0.119) | 1.602E+10 (0.12) | ||
| 868735 (0.120) | 3.820E+08 (1.85) | ||
| 1022191 (0.133) | 2.533E+10 (0.11) | ||
| 1053811 (0.089) | 3.907E+08 (1.68) | ||
| 1187709 (0.205) | 4.909E+09 (0.34) | ||
| 369157 (0.293) | 3.272E+07 (11.61) | ||
| 659387 (0.050) | 8.335E+07 (6.39) | ||
| 660006 (0.050) | 4.535E+06 (22.51) | ||
| 686197 (0.050) | 6.105E+09 (0.80) | ||
| 807659 (0.120) | 2.681E+09 (1.30) | ||
| 825192 (0.121) | 2.038E+10 (0.04) | ||
| 978647 (0.134) | 6.104E+10 (0.24) | ||
| 1010267 (0.090) | 8.020E+09 (0.39) | ||
| 1144165 (0.206) | 2.491E+08 (0.16) | ||
| 241853 (0.714) | 1.307E+06 (19.51) | ||
| 532083 (0.048) | 1.808E+08 (6.63) | ||
| 532703 (0.048) | 3.827E+07 (6.27) | ||
| 558894 (0.049) | 9.767E+08 (3.61) | ||
| 680356 (0.051) | 2.577E+08 (2.44) | ||
| 697888 (0.052) | 1.435E+08 (4.80) | ||
| 851344 (0.084) | 3.607E+08 (3.16) | ||
| 882963 (0.037) | 4.485E+10 (0.37) | ||
| 1016862 (0.170) | 6.583E+10 (0.15) | ||
| 404698 (0.165) | 4.070E+07 (2.97) | ||
| 552971 (0.014) | 1.492E+08 (7.10) | ||
| 723959 (0.008) | 6.511E+08 (2.13) | ||
| 889477 (0.147) | 1.727E+10 (0.52) | ||
| 1159940 (0.180) | 1.422E+09 (2.39) | ||
| 1254085 (0.181) | 2.381E+08 (3.65) | ||
| 1331255 (0.201) | 5.282E+07 (2.48) | ||
| 869710 (0.102) | 3.455E+09 (0.75) | ||
| 959080 (0.137) | 3.474E+10 (0.43) | ||
| 963855 (0.102) | 1.434E+10 (0.27) | ||
| 1041025 (0.103) | 4.033E+06 (20.67) | ||
| 1271738 (0.137) | 2.331E+08 (1.32) | ||
| 869090 (0.103) | 1.335E+10 (0.00) | ||
| 963235 (0.104) | 2.124E+10 (0.28) | ||
| 1040406 (0.106) | 7.878E+08 (0.20) | ||
| 842899 (0.137) | 2.822E+10 (0.53) | ||
| 1014215 (0.260) | 5.622E+09 (0.85) | ||
| 824204 (0.038) | 4.813E+09 (0.02) | ||
| 721437 (0.039) | 3.678E+09 (0.32) | ||
| 810807 (0.040) | 1.827E+10 (0.93) | ||
| 815582 (0.043) | 1.273E+08 (3.29) | ||
| 892752 (0.085) | 1.241E+09 (1.85) | ||
| 1123465 (0.233) | 4.222E+09 (1.30) | ||
| 703905 (0.039) | 3.629E+09 (0.88) | ||
| 798050 (0.040) | 1.598E+10 (0.75) | ||
| 875220 (0.085) | 2.512E+09 (1.79) | ||
| 550450 (0.021) | 6.005E+09 (0.76) | ||
| 639819 (0.020) | 1.733E+10 (0.28) | ||
| 644594 (0.049) | 1.290E+10 (0.00) | ||
| 721764 (0.059) | 7.002E+06 (0.68) | ||
| 952477 (0.060) | 5.111E+09 (0.25) | ||
| 518830 (0.065) | 7.538E+08 (1.85) | ||
| 612975 (0.124) | 3.767E+08 (3.31) | ||
| 690145 (0.311) | 3.182E+10 (0.28) | ||
| 384932 (0.274) | 8.409E+07 (3.44) | ||
| 474302 (0.271) | 9.885E+06 (20.99) | ||
| 479076 (0.265) | 6.387E+08 (1.58) | ||
| 556247 (0.139) | 4.499E+09 (1.15) | ||
| 786959 (0.156) | 7.549E+10 (0.09) | ||
| States | (cm−1) | Type | ||||
|---|---|---|---|---|---|---|
| Upper | Lower | |||||
| S VII | ||||||
| 1371667 | M2 | 7.638E+02 | 7.617E+02 | |||
| 1376084 | E1 | 1.855E+10 | 1.816E+10 | 1.989E+10 | ||
| 1388242 | E1 | 8.421E+10 | 8.507E+10 | 8.777E+10 | ||
| 1484530 | E2 | 3.021E+06 | 2.964E+06 | |||
| 1492576 | E2 | 8.028E+06 | 8.008E+06 | |||
| 1624769 | E1 | 2.160E+09 | 2.182E+09 | 2.312E+09 | ||
| 1627240 | M2 | 1.710E+04 | 1.728E+04 | |||
| 1644545 | E1 | 6.122E+10 | 6.206E+10 | 6.230E+10 | ||
| 1662346 | E1 | 9.452E+11 | 9.448E+11 | 9.087E+11 | ||
| 4417 | M1 | 1.587E+00 | 1.601E+00 | |||
| 16575 | M1 | 1.849E+01 | 1.867E+01 | |||
| 95373 | E1 | 6.393E+08 | 6.504E+08 | 6.480E+08 | ||
| 111609 | E1 | 1.566E+09 | 1.608E+09 | 1.594E+09 | ||
| 112863 | E1 | 6.439E+08 | 6.627E+08 | 6.418E+08 | ||
| 116432 | E1 | 1.994E+08 | 2.060E+08 | 2.023E+08 | ||
| 120909 | E1 | 1.000E+09 | 1.031E+09 | 1.006E+09 | ||
| 124214 | E1 | 7.124E+07 | 7.315E+07 | 6.807E+07 | ||
| 127448 | E1 | 2.464E+08 | 2.501E+08 | 2.832E+08 | ||
| 78797 | E1 | 1.188E+07 | 1.206E+07 | 1.253E+07 | ||
| 96287 | E1 | 6.945E+06 | 7.197E+06 | 5.508E+06 | ||
| 99856 | E1 | 3.825E+06 | 4.290E+06 | 4.536E+06 | ||
| 104333 | E1 | 2.932E+08 | 2.977E+08 | 3.152E+08 | ||
| 107638 | E1 | 7.415E+08 | 7.625E+08 | 7.557E+08 | ||
| 110460 | E1 | 1.908E+08 | 1.974E+08 | 2.006E+08 | ||
| 110872 | E1 | 1.206E+09 | 1.243E+09 | 1.199E+09 | ||
| 112070 | E1 | 7.082E+08 | 7.307E+08 | 7.000E+08 | ||
| 112070 | M2 | 1.139E−01 | 1.191E−01 | |||
| 165149 | E1 | 5.082E+09 | 5.118E+09 | 5.073E+09 | ||
| 125654 | E1 | 1.229E+08 | 1.235E+08 | 1.323E+08 | ||
| 128125 | E1 | 3.010E+08 | 3.017E+08 | 3.358E+08 | ||
| 128125 | M2 | 1.161E−01 | 1.175E−01 | |||
| 132832 | E1 | 1.471E+06 | 1.472E+06 | 1.078E+06 | ||
| 136157 | E1 | 1.190E+06 | 1.370E+06 | 1.643E+06 | ||
| 138763 | E1 | 1.511E+08 | 1.519E+08 | 1.131E+08 | ||
| 145430 | E1 | 3.071E+06 | 3.159E+06 | 1.717E+06 | ||
| 145447 | E1 | 6.172E+08 | 6.286E+08 | 6.276E+08 | ||
| 146716 | E1 | 4.030E+09 | 4.093E+09 | 4.183E+09 | ||
| 146716 | M2 | 1.029E+00 | 1.054E+00 | |||
| 147358 | E1 | 1.521E+08 | 1.531E+08 | 1.489E+08 | ||
| 163231 | E1 | 4.854E+07 | 4.851E+07 | 5.550E+07 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jönsson, P.; Gaigalas, G.; Rynkun, P.; Radžiūtė, L.; Ekman, J.; Gustafsson, S.; Hartman, H.; Wang, K.; Godefroid, M.; Froese Fischer, C.; et al. Multiconfiguration Dirac-Hartree-Fock Calculations with Spectroscopic Accuracy: Applications to Astrophysics. Atoms 2017, 5, 16. https://doi.org/10.3390/atoms5020016
Jönsson P, Gaigalas G, Rynkun P, Radžiūtė L, Ekman J, Gustafsson S, Hartman H, Wang K, Godefroid M, Froese Fischer C, et al. Multiconfiguration Dirac-Hartree-Fock Calculations with Spectroscopic Accuracy: Applications to Astrophysics. Atoms. 2017; 5(2):16. https://doi.org/10.3390/atoms5020016
Chicago/Turabian StyleJönsson, Per, Gediminas Gaigalas, Pavel Rynkun, Laima Radžiūtė, Jörgen Ekman, Stefan Gustafsson, Henrik Hartman, Kai Wang, Michel Godefroid, Charlotte Froese Fischer, and et al. 2017. "Multiconfiguration Dirac-Hartree-Fock Calculations with Spectroscopic Accuracy: Applications to Astrophysics" Atoms 5, no. 2: 16. https://doi.org/10.3390/atoms5020016
APA StyleJönsson, P., Gaigalas, G., Rynkun, P., Radžiūtė, L., Ekman, J., Gustafsson, S., Hartman, H., Wang, K., Godefroid, M., Froese Fischer, C., Grant, I., Brage, T., & Del Zanna, G. (2017). Multiconfiguration Dirac-Hartree-Fock Calculations with Spectroscopic Accuracy: Applications to Astrophysics. Atoms, 5(2), 16. https://doi.org/10.3390/atoms5020016









