Shannon Information Entropy in Position Space for the Ground and Singly Excited States of Helium with Finite Confinements
Abstract
:1. Introduction
2. Theoretical Method
3. Calculations and Results
3.1. Shannon Entropy for the Ground State and the 1s2s 1Se Excited State of He without Confinement
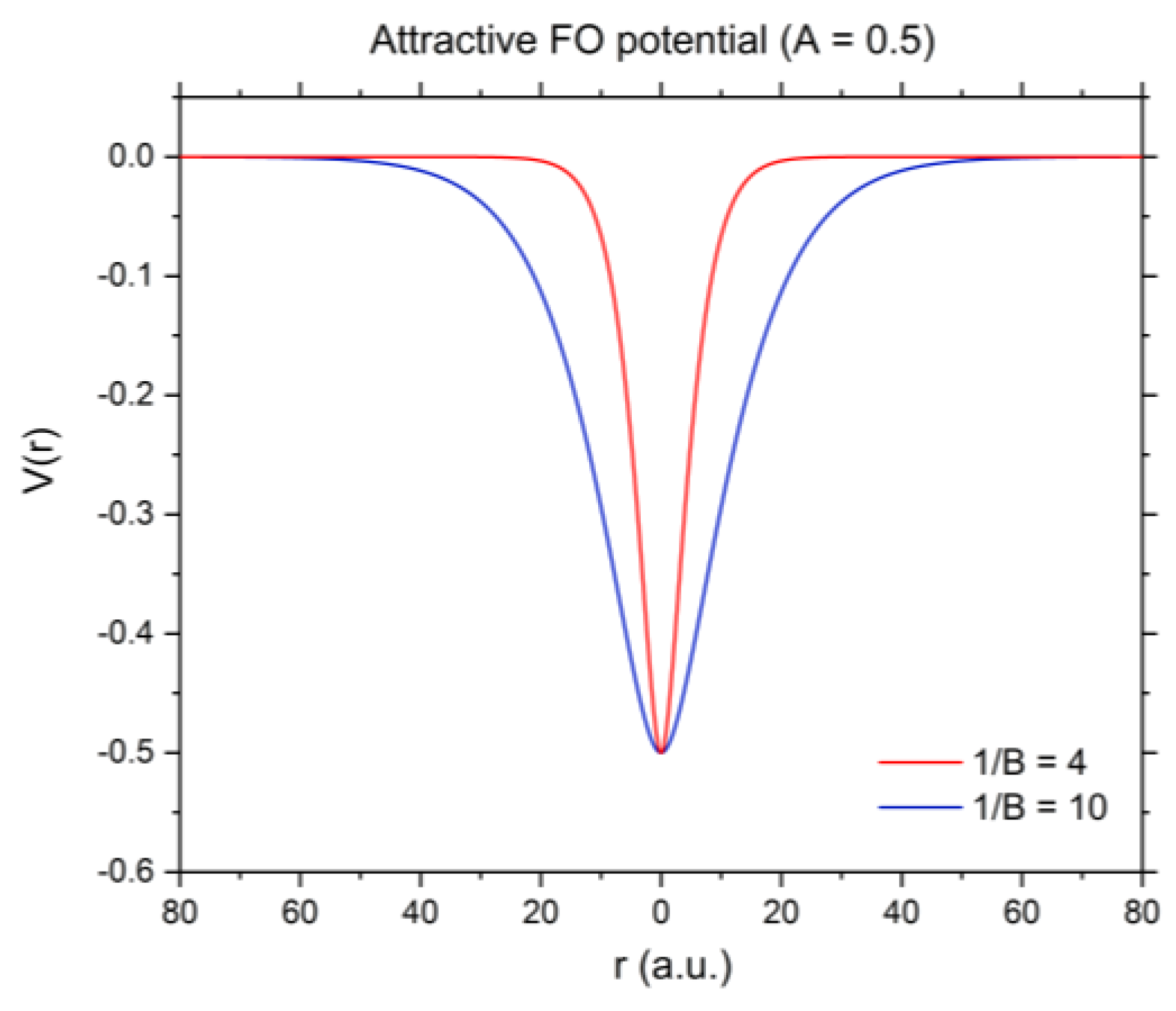
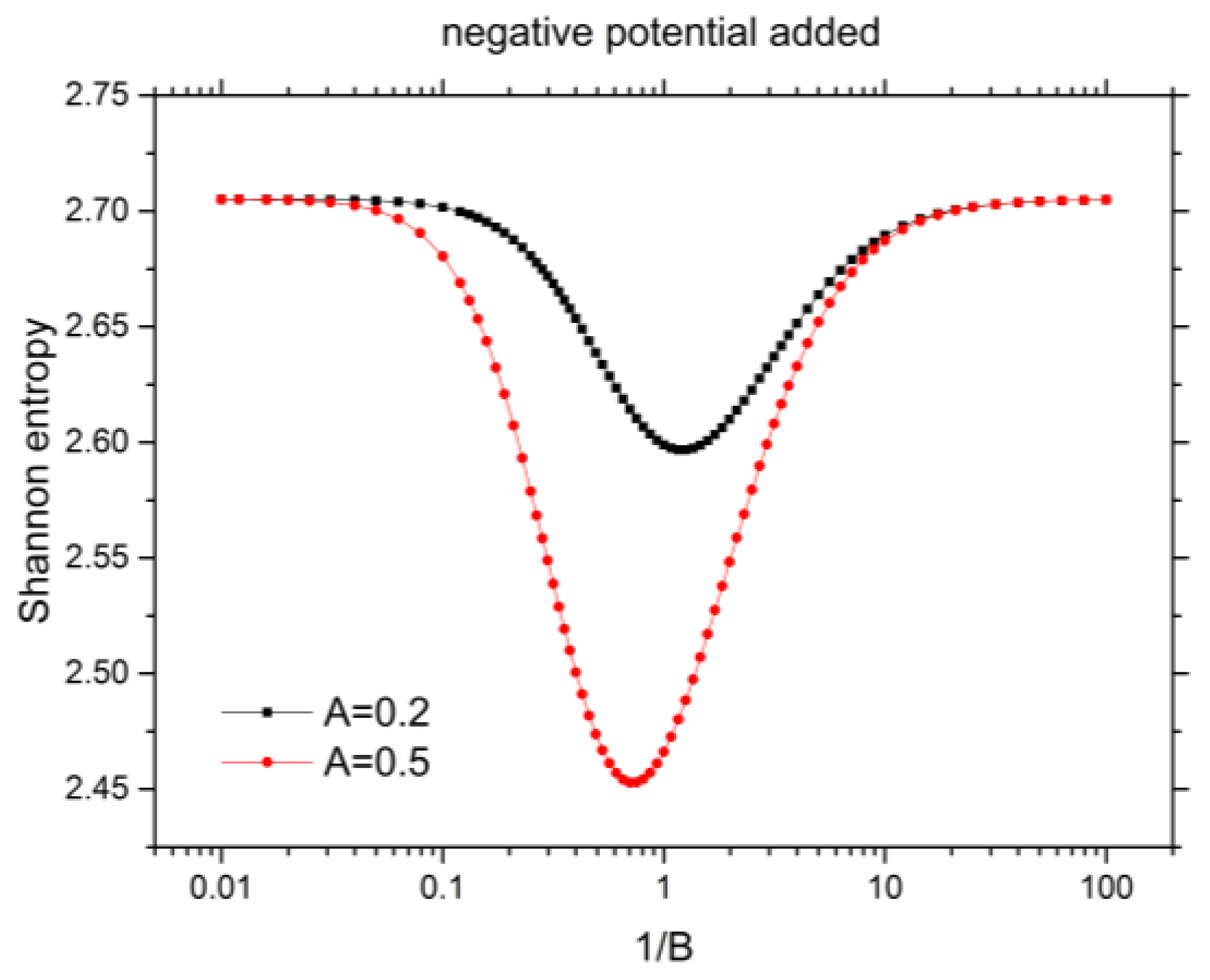
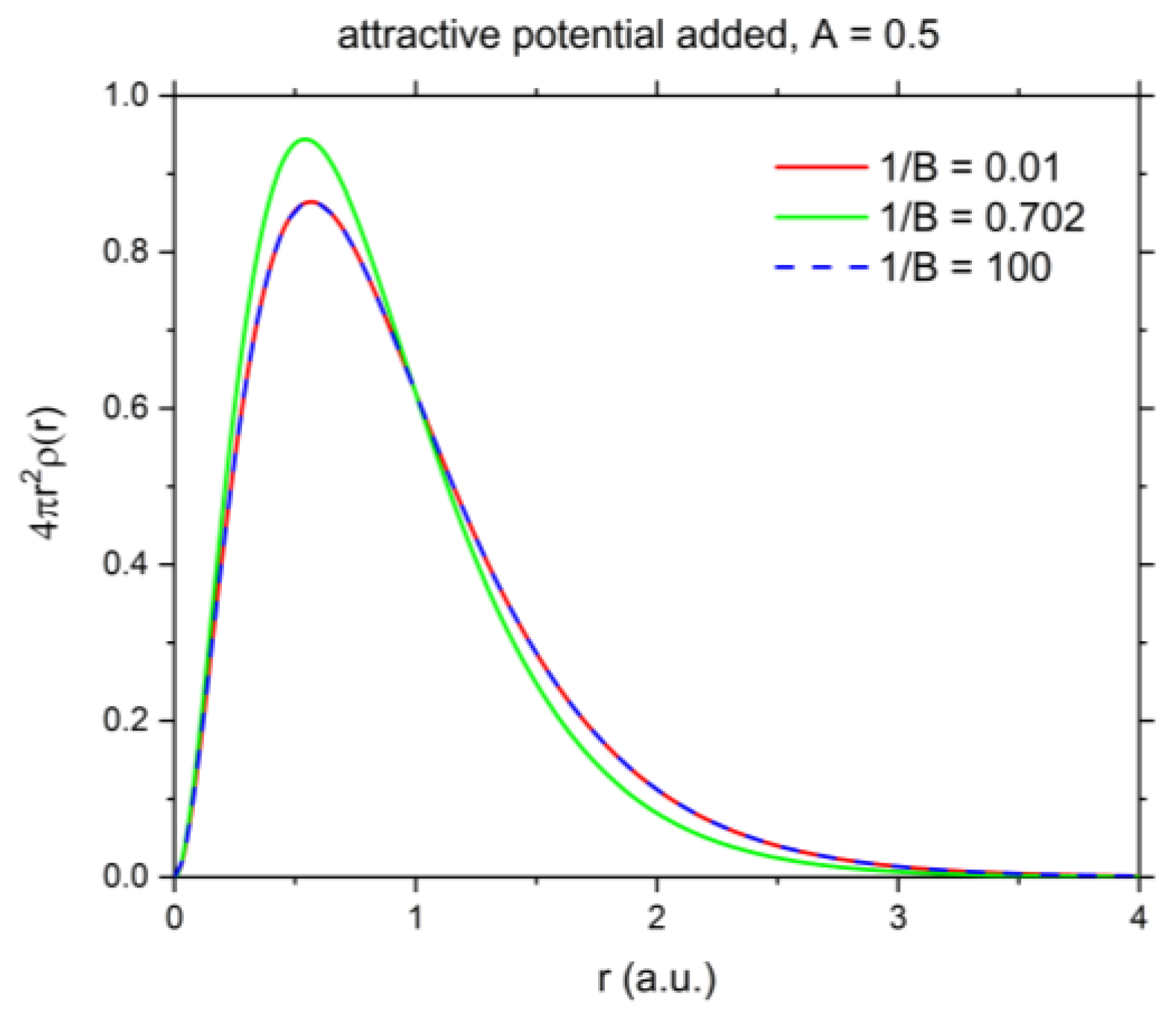
3.2. Shannon Entropy for Ground State He under Confinement with Attractive Potential
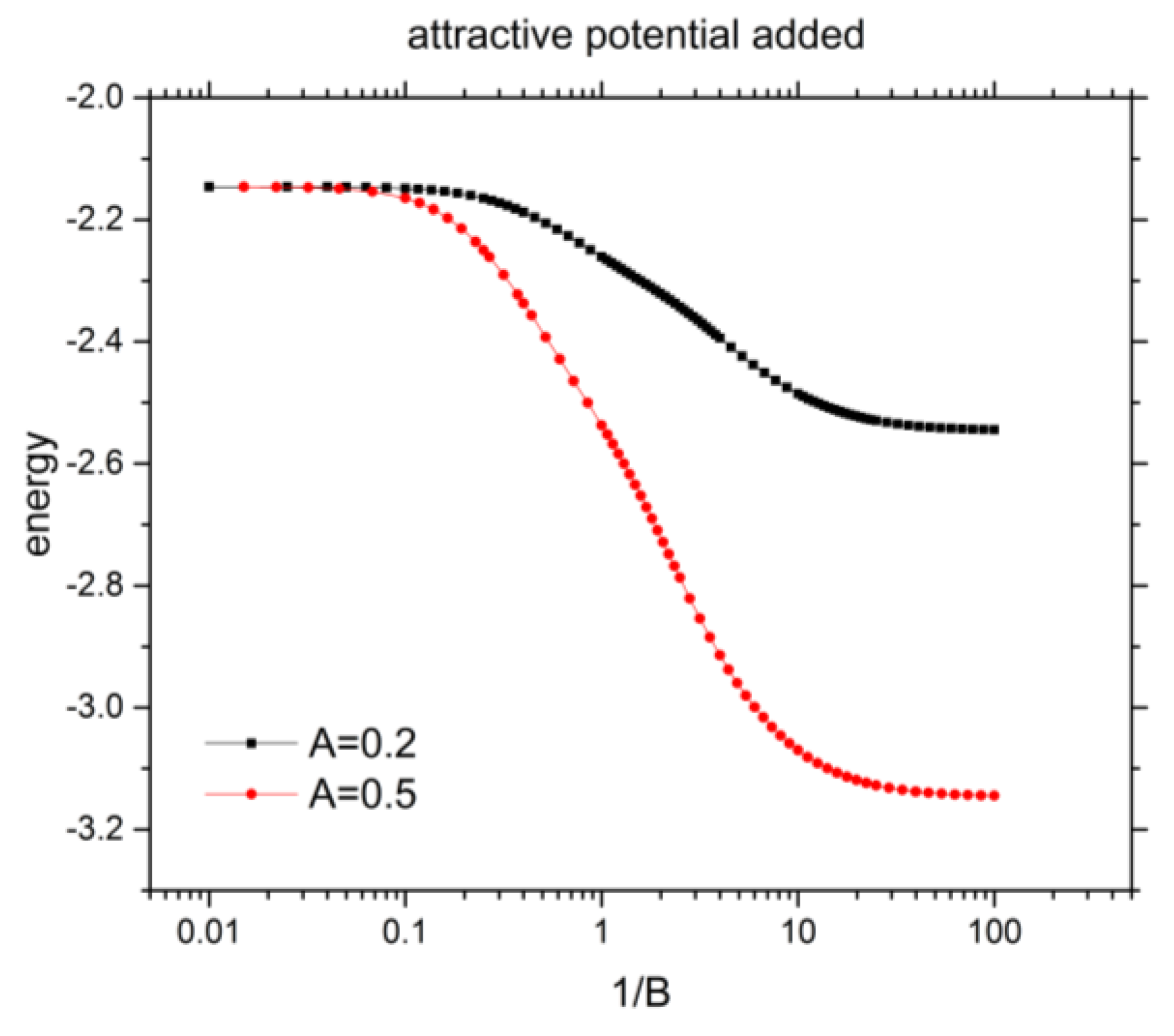
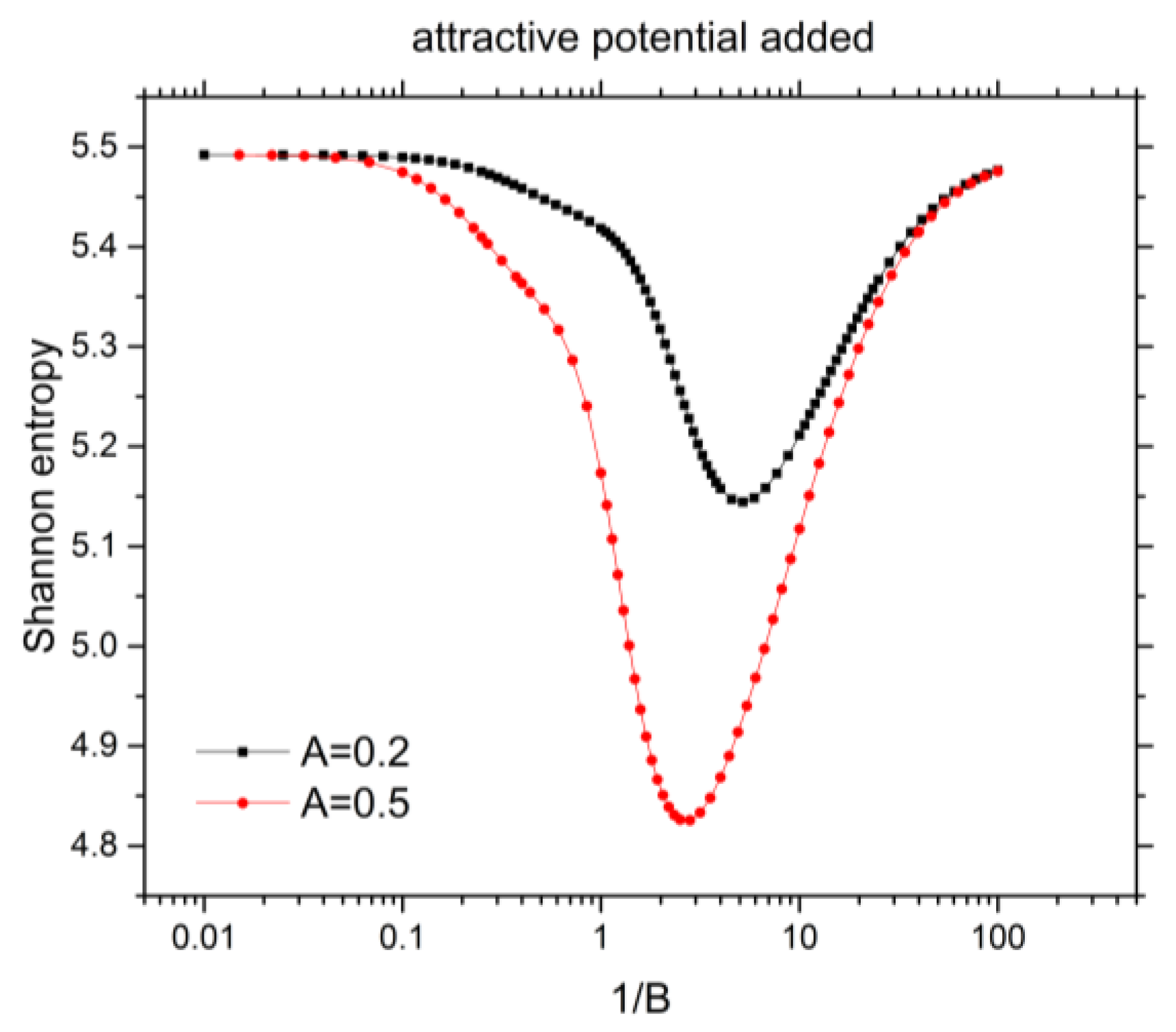
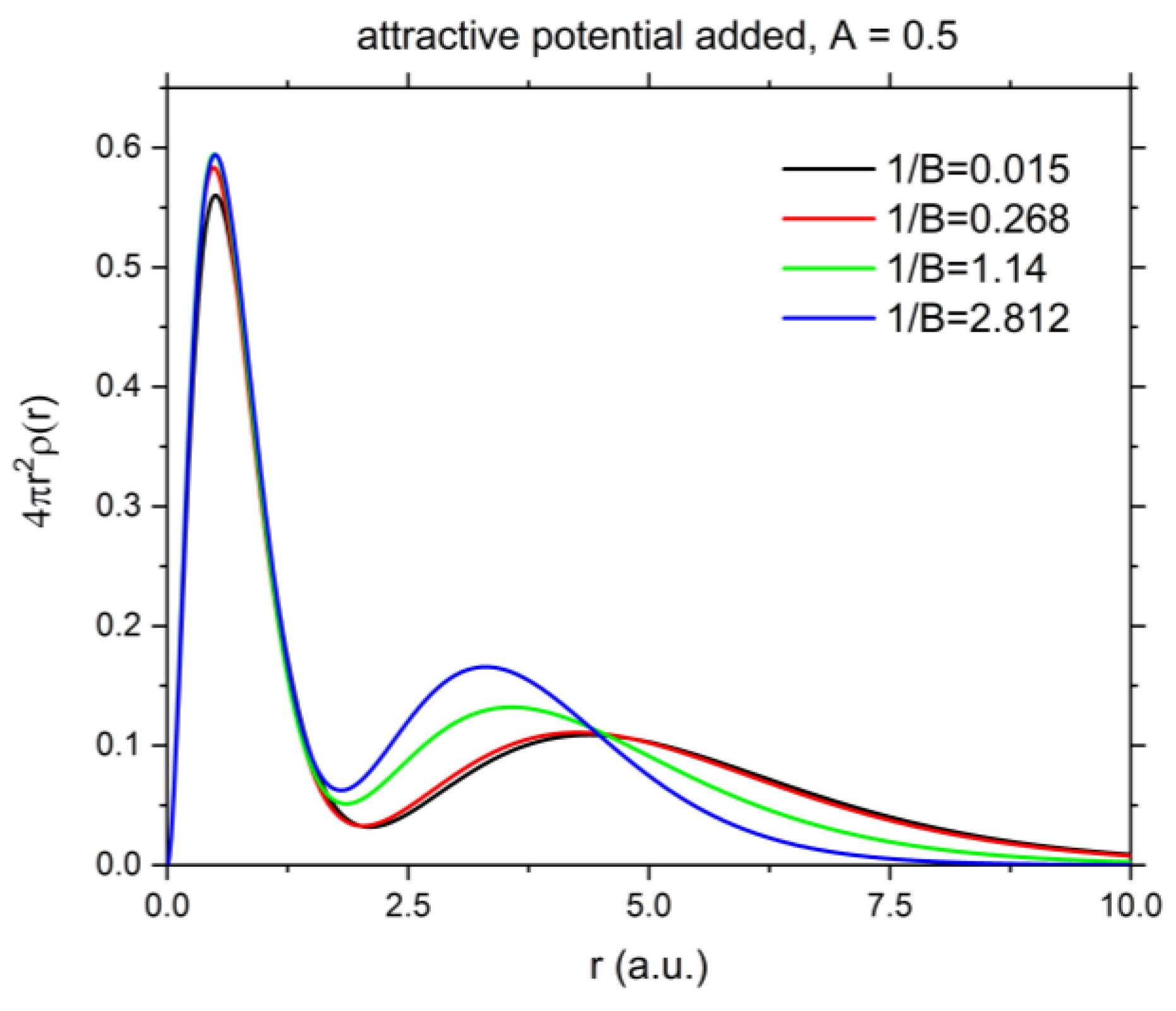
3.3. Shannon Entropy for the 1s2s 1Se Excited State of He under Confinement with Attractive Potential
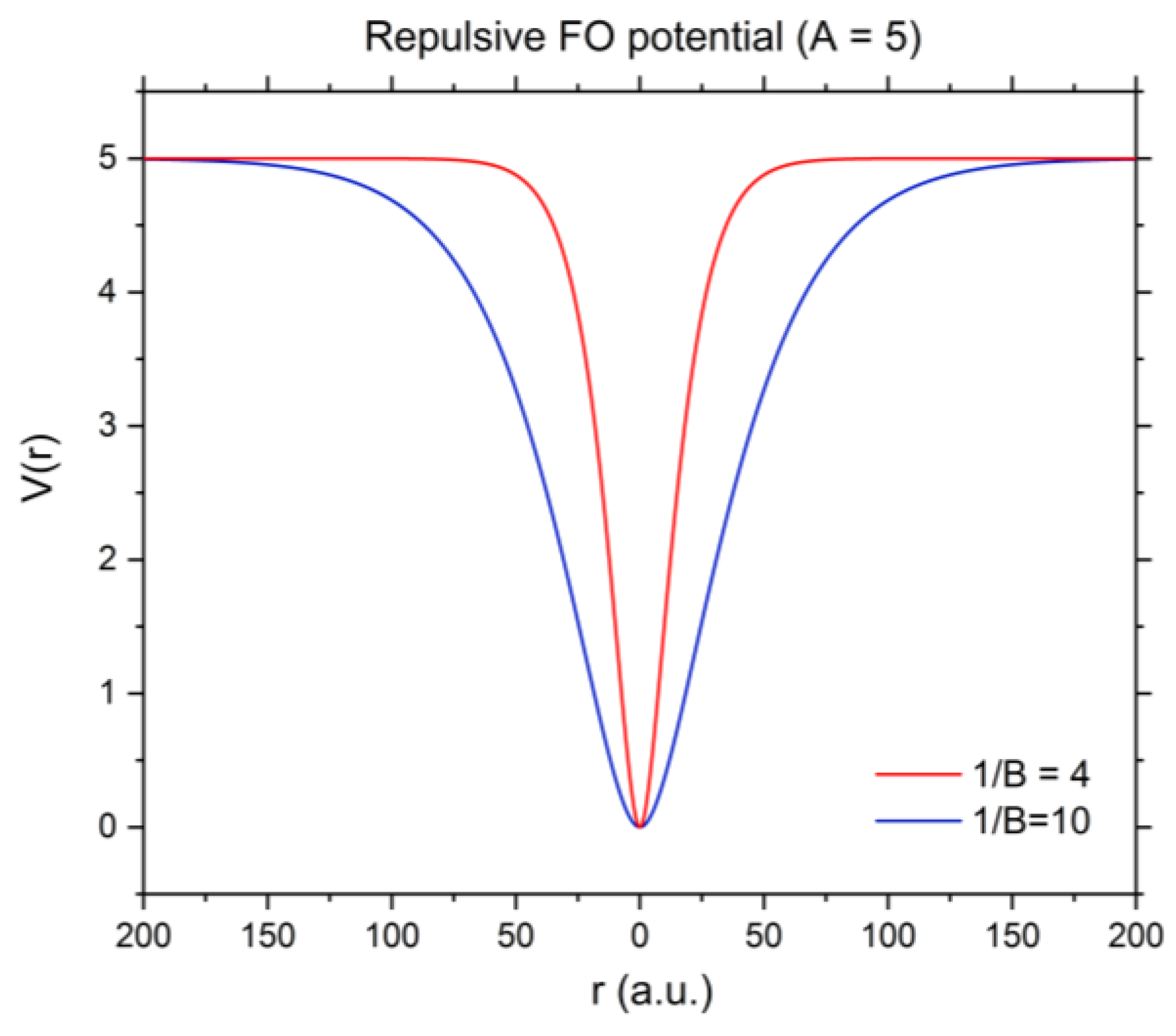
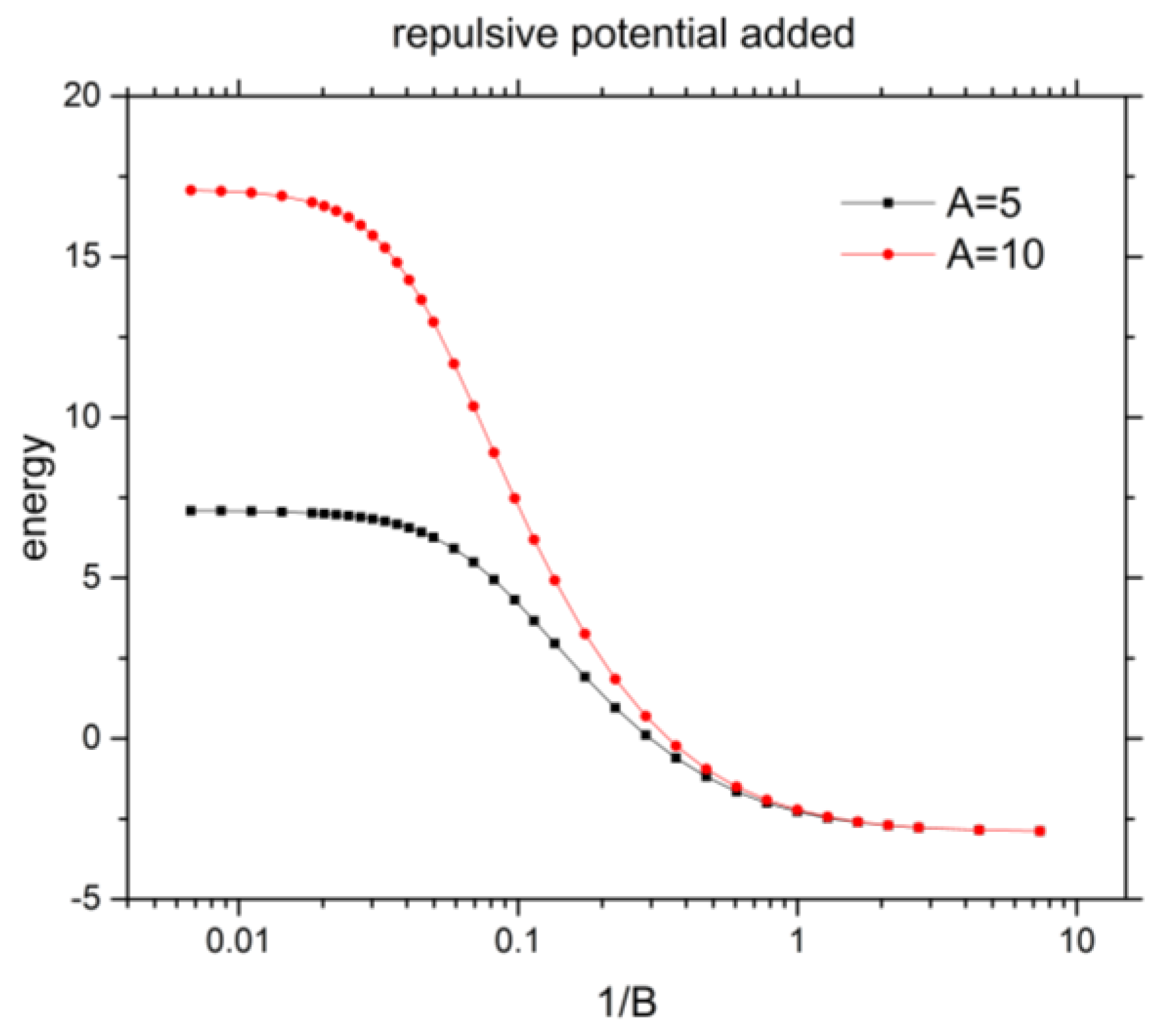
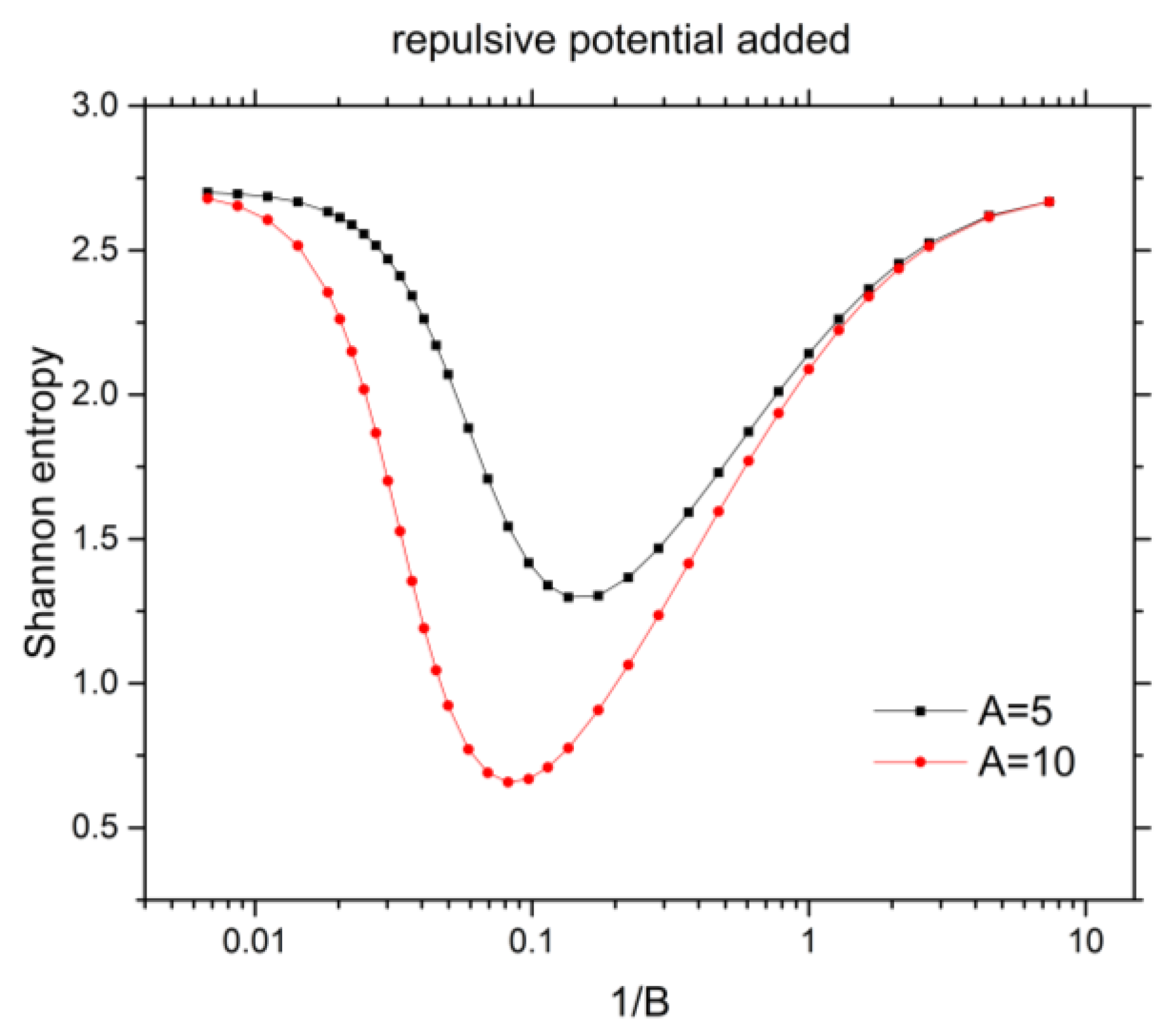
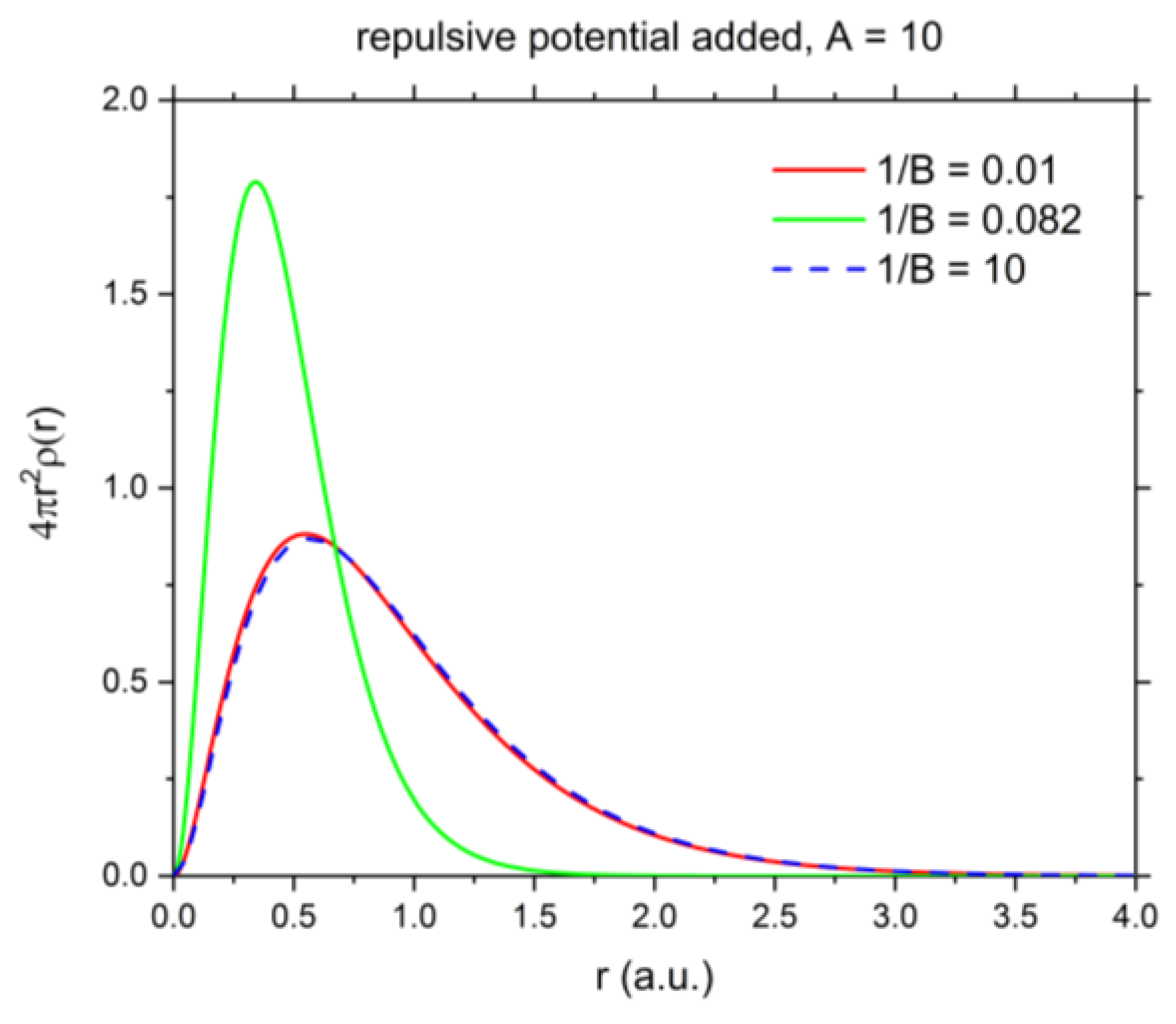
3.4. Shannon Entropy for Ground State of He under Confinement with Repulsive Potential
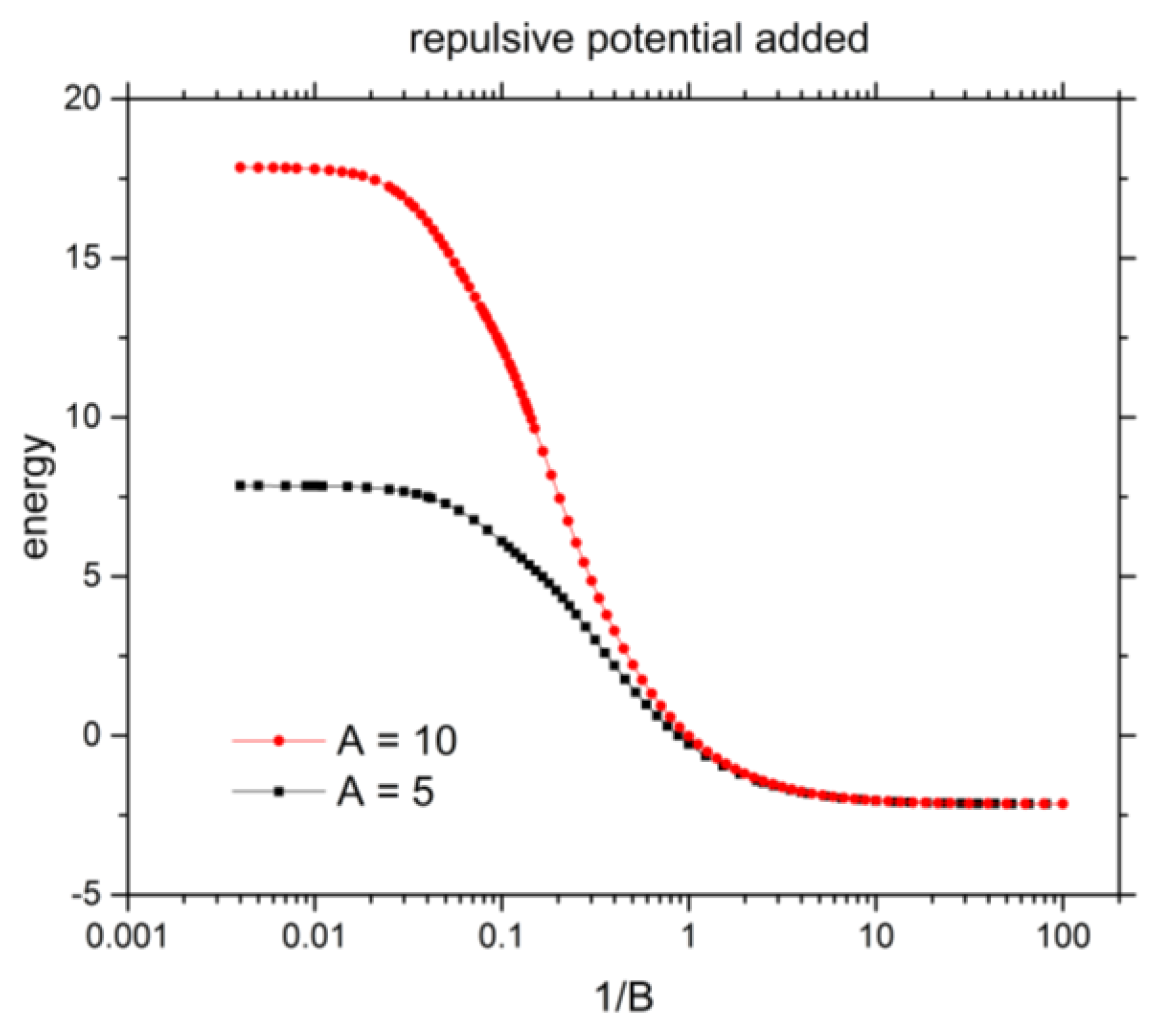
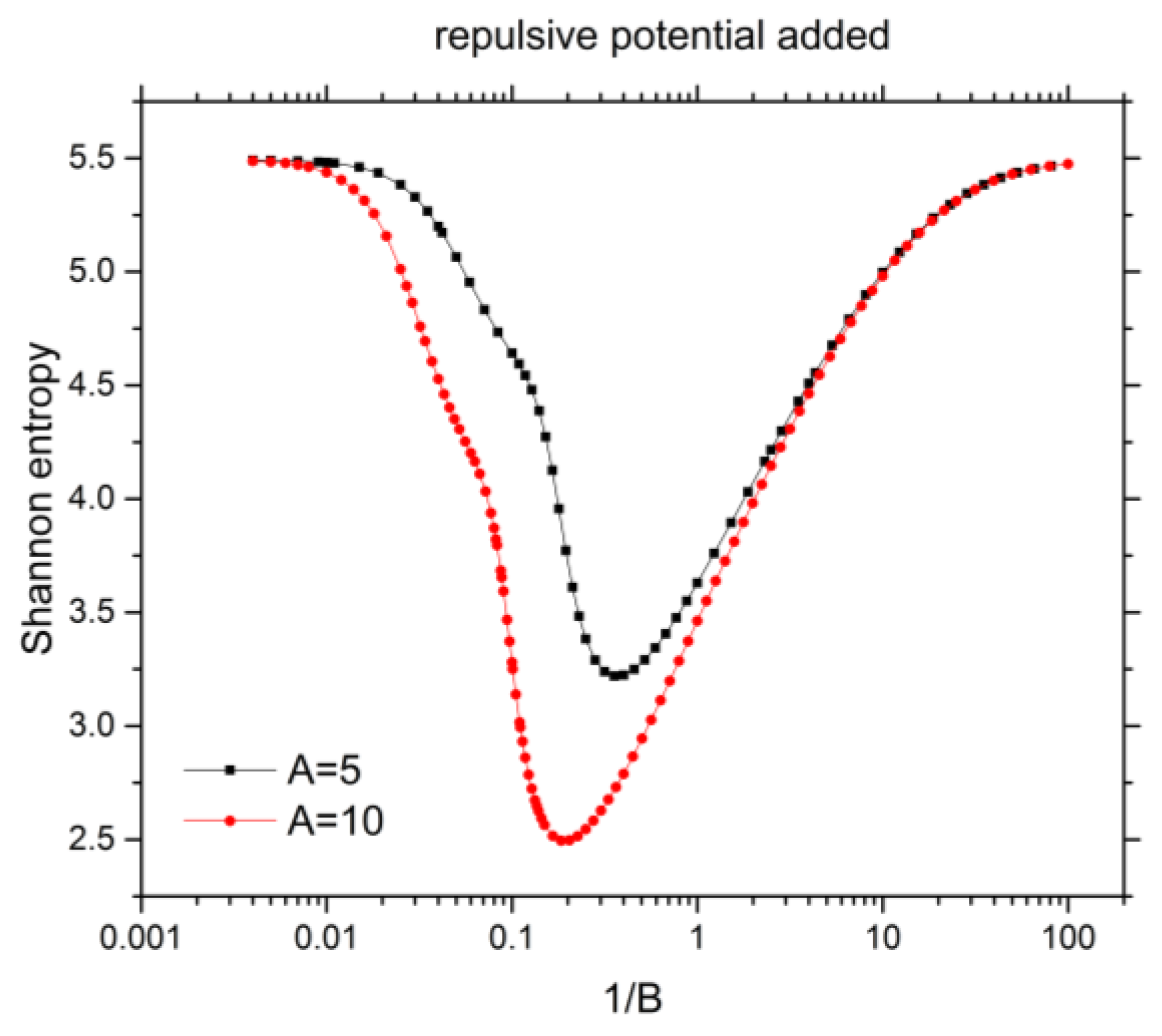
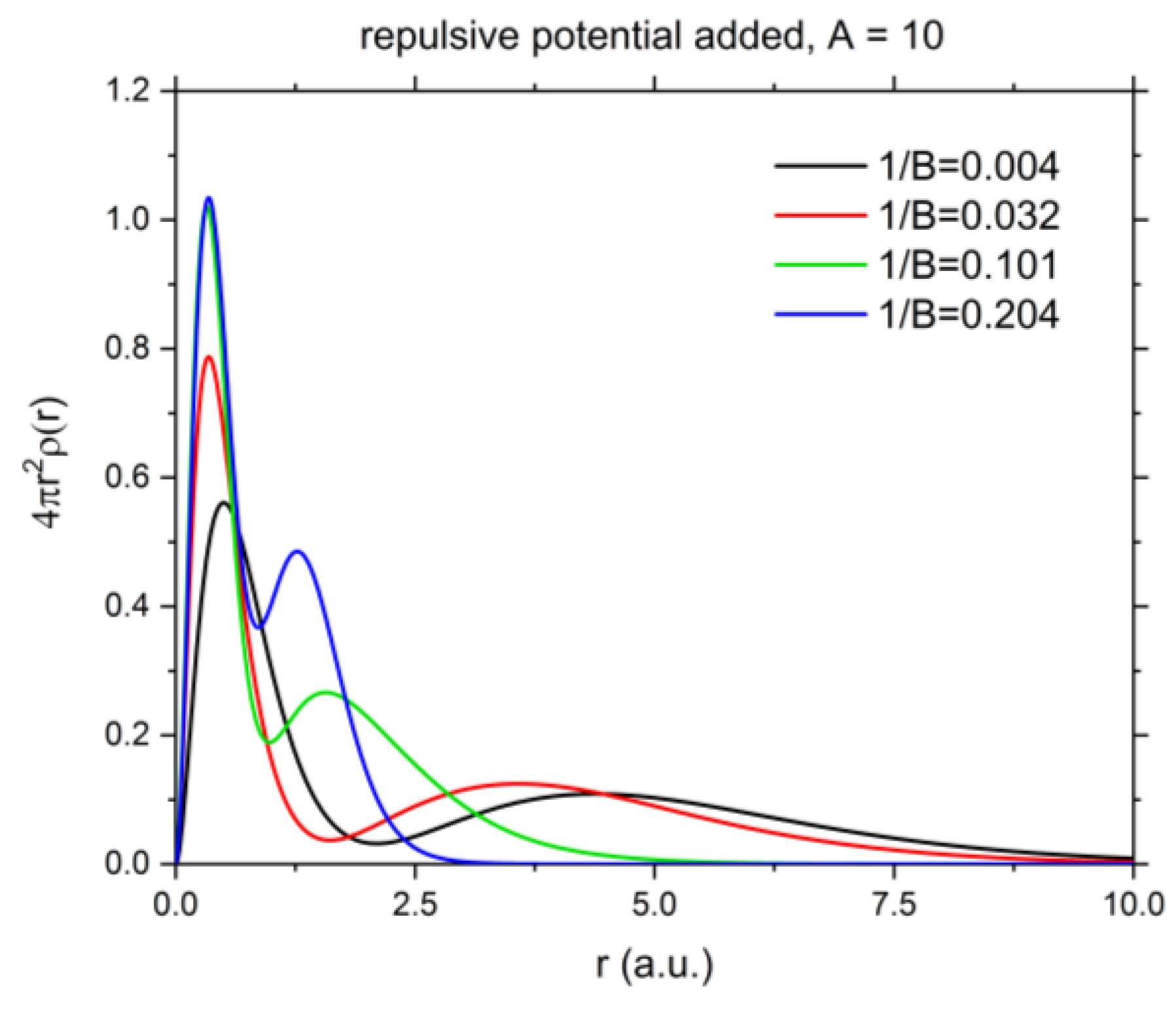
3.5. Shannon Entropy for 1s2s 1Se Excited State of He under Confinement with Repulsive Potential
4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Dehesa, J.S.; Koga, T.; Yanez, R.J.; Plastino, A.R.; Esquivel, R.O. Quantum entanglement in helium. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 015504. [Google Scholar] [CrossRef]
- Dehesa, J.S.; Koga, T.; Yanez, R.J.; Plastino, A.R.; Esquivel, R.O. Corrigendum: Quantum entanglement in helium. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 239501. [Google Scholar]
- Benenti, G.; Siccardi, S.; Strini, G. Entanglement in helium. Eur. Phys. J. D 2013, 67, 1. [Google Scholar] [CrossRef]
- Koscik, P. Entanglement in S states of two-electron quantum dots with Coulomb impurities at the center. Phys. Lett. A 2013, 377, 2393. [Google Scholar] [CrossRef]
- Koscik, P.; Okopiska, A. Entanglement Entropies in the Ground States of Helium-Like Atoms. Few-Body Syst. 2014, 55, 1151–1157. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, H.; Kais, S. Entanglement and Electron Correlation in Quantum Chemistry Calculations. J. Mod. Opt. 2006, 53, 2543–2558. [Google Scholar]
- Hofer, H.T. On the basis set convergence of electron-electron entanglement measures: Helium-like systems. Front. Chem. 2013, 1, 24. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Rosa, S.; Esquivel, R.O.; Plastino, A.R.; Dehesa, J.S. Quantum entanglement of helium-like systems with varying-Z: Compact state-of-the-art CI wave functions. J. Phys. B 2015, 48, 175002. [Google Scholar]
- Restrepo Cuartas, J.P.; Sanz-Vicario, J.L. Information and entanglement measures applied to the analysis of complexity in doubly excited states of helium. Phys. Rev. A 2015, 91, 052301. [Google Scholar] [CrossRef]
- Peng, H.-T.; Ho, Y.K. Statistical Correlations of the N-particle Moshinsky Model. Entropy 2015, 17, 1882–1895. [Google Scholar] [CrossRef]
- Peng, H.T.; Ho, Y.K. Entanglement for excited states of ultracold bosonic atoms in one-dimensional harmonic traps with contact interaction. Mod. Phys. Lett. B 2015, 29, 1550189. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Lin, C.-Y.; Ho, Y.K. Spatial entanglement in two-electron atomic systems. Phys. Rev. A 2013, 87, 022316. [Google Scholar] [CrossRef]
- Lin, Y.C.; Ho, Y.K. Quantum entanglement for two electrons in the excited states of helium-like systems. Can. J. Phys. 2015, 93, 646–653. [Google Scholar] [CrossRef]
- Lin, C.H.; Lin, Y.C.; Ho, Y.K. Quantification of linear entropy for quantum entanglement in He, H− and Ps− ions using highly-correlated Hylleraas functions. Few-Body Syst. 2013, 54, 2147–2153. [Google Scholar] [CrossRef]
- Lin, C.H.; Ho, Y.K. Quantification of entanglement entropy in helium by the Schmidt-Slater decomposition method. Few-Body Syst. 2014, 55, 1141–1149. [Google Scholar] [CrossRef]
- Lin, C.H.; Ho, Y.K. Calculation of von Neumann entropy for hydrogen and positronium negative ions. Phys. Lett. A 2014, 378, 2861–2865. [Google Scholar] [CrossRef]
- Lin, C.H.; Ho, Y.K. Quantification of entanglement entropies for doubly excited states in Helium. Few-Body Syst. 2015, 56, 157. [Google Scholar] [CrossRef]
- Lin, C.H.; Ho, Y.K. Quantum Entanglement and Shannon Information Entropy for the Doubly Excited Resonance State in Positronium Negative Ion. Atoms 2015, 3, 422–432. [Google Scholar] [CrossRef]
- Lin, Y.C.; Fang, T.K.; Ho, Y.K. Quantum entanglement for helium atom in the Debye plasmas. Phys. Plasmas 2015, 22, 032113. [Google Scholar]
- Lin, C.H.; Ho, Y.K. Shannon information entropy in position space for two-electron systems. Chem. Phys. Lett. 2015, 633, 261–264. [Google Scholar] [CrossRef]
- Sen, K.D. Characteristic features of Shannon information entropy of confined atoms. J. Chem. Phys. 2005, 123, 074110. [Google Scholar] [CrossRef] [PubMed]
- Koscik, P.; Saha, J.K. Entanglement in helium atom confined in an impenetrable cavity. Eur. Phys. J. D 2015, 69, 250. [Google Scholar] [CrossRef]
- Koscik, P.; Saha, J.K. Ground-State Entanglement Properties of Helium Atom in a Finite Spherical Cavity. Few-Body Syst. 2015, 56, 645–649. [Google Scholar] [CrossRef]
- Sil, A.N.; Canuto, S.; Mukherjee, P.K. Spectroscopy of confined atomic systems: Effect of plasma. Adv. Quantum Chem. 2009, 58, 115. [Google Scholar]
- Sen, K.D. (Ed.) Electronic Structure of Quantum Confined Atoms and Molecules; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Kimani, P.; Jones, P.; Winkler, P. Correlation studies in weakly confining quantum dot potential. Int. J. Quantum Chem. 2008, 108, 2763. [Google Scholar] [CrossRef]
- Chakraborty, S.; Ho, Y.K. Autoionization resonance states of two electron atomic systems with finite spherical confinement. Phys. Rev. A 2011, 84, 032515. [Google Scholar] [CrossRef]
- Jiao, L.G.; Ho, Y.K. Bound and Resonant States in Confined Atoms. In Electronic Structure of Quantum Confined Atoms and Molecules; Sen, K.D., Ed.; Springer: Cham, Switzerland, 2014; p. 145. [Google Scholar]
- Lin, C.Y.; Ho, Y.K. Photoionization cross sections of hydrogen impurities in spherical quantum dots using the finite-element discrete-variable representation. Phys. Rev. A 2011, 84, 023407. [Google Scholar] [CrossRef]
- Lin, C.Y.; Ho, Y.K. Photoionization of endohedral atoms in fullerene cages. Few-Body Syst. 2013, 54, 425–429. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Nagy, A.; Liu, S.B. Local wave-vector, Shannon and Fisher information. Phys. Lett. A 2008, 372, 1654. [Google Scholar] [CrossRef]
- Guevara, N.L.; Sagar, R.P.; Esquivel, R.O. Shannon-information entropy sum as a correlation measure in atomic systems. Phys. Rev. A 2003, 67, 012507. [Google Scholar] [CrossRef]
- Sagar, R.P.; Laguna, H.G.; Guevara, N.L. Conditional entropies and position-momentum correlations in atomic systems. Mol. Phys. 2009, 107, 2071–2080. [Google Scholar] [CrossRef]
- Gadre, S. Information entropy and Thomas–Fermi theory. Phys. Rev. A 1984, 30, 620–621. [Google Scholar]
- Gadre, S.; Sears, S.; Chakravorty, S.; Bendale, R. Some novel characteristics of atomic information entropies. Phys. Rev. A 1985, 32, 2602–2606. [Google Scholar] [CrossRef]
- Yánez, R.J.; Van Assche, W.; Dehesa, J.S. Position and momentum information entropies of the D-dimensional harmonic oscillator and hydrogen atom. Phys. Rev. A 1994, 50, 3065–3079. [Google Scholar] [CrossRef] [PubMed]
- Drake, G.W.F. Atomic, Molecular, and Optical Physics Handbook; AIP Press: New York, NY, USA, 2006; Chapter 11. [Google Scholar]
- March, N.; Angilella, G.; Pucci, R. Natural Orbitals in Relation to Quantum Information Theory: From Model Light Atoms through to Emergent Metallic Properties. Int. J. Mod. Phys. B 2013, 27, 1330021. [Google Scholar]
- Amovilli, C.; March, N.H. Quantum information: Jaynes and Shannon entropies in a two-electron entangled artificial atom. Phys. Rev. A 2004, 69, 054302. [Google Scholar] [CrossRef]
- Amovilli, C.; March, N.H. Density matrices in direct and momentum space for a model of the He-like sequence of atomic ions. Phys. Rev. A 2005, 72, 042504. [Google Scholar]
- Howard, I.; March, N.H. Towards a differential equation for the nonrelativistic ground-state electron density of the He-like sequence of atomic ions. Phys. Rev. A 2005, 71, 042501. [Google Scholar] [CrossRef]
- Amovilli, C.; Howard, I.; March, N.H. Analytic inhomogeneous electron liquid and its density for model spin-compensated two-electron atomic ions with Coulomb confinement: An exact nonrelativistic Hamiltonian. Phys. Chem. Liq. 2008, 46, 238–241. [Google Scholar] [CrossRef]
- Guevara, N.L.; Sagar, R.P.; Esquivel, R.O. Information uncertainty-type inequalities in atomic systems. J. Chem. Phys. 2003, 119, 7030–7036. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 1975, 44, 12. [Google Scholar] [CrossRef]
- Majernik, V.; Opatrný, T. Entropic uncertainty relations for a quantum oscillator. J. Phys. Math. Gen. 1996, 29, 2187–2197. [Google Scholar] [CrossRef]
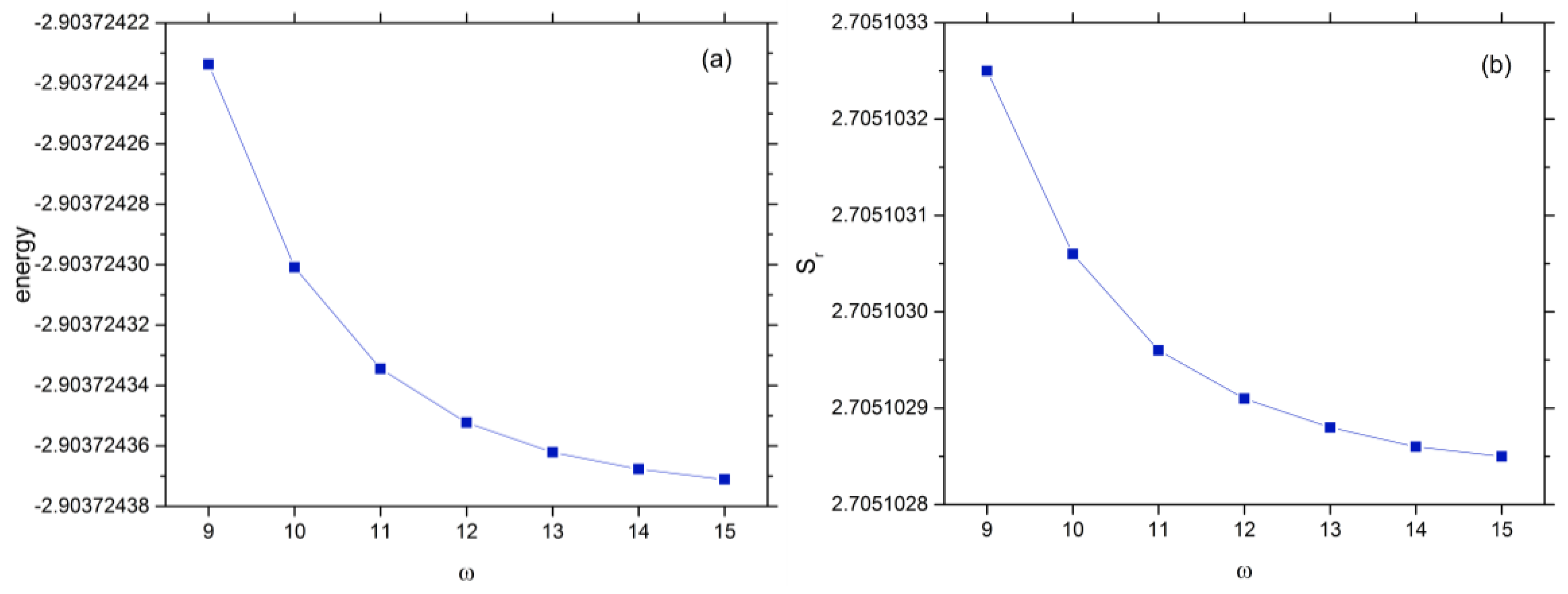

| ω | N | Ground State | 1s2s 1Se Excited State | ||
|---|---|---|---|---|---|
| Energy | Shannon Entropy | Energy | Shannon Entropy | ||
| 9 | 125 | −2.903724233 | 2.70510325 | −2.145945902 | 5.4877391 |
| 10 | 161 | −2.903724300 | 2.70510306 | −2.145968846 | 5.4908525 |
| 11 | 203 | −2.903724334 | 2.70510296 | −2.145972626 | 5.4916522 |
| 12 | 252 | −2.903724352 | 2.70510291 | −2.145973707 | 5.49189461 |
| 13 | 308 | −2.903724362 | 2.70510288 | −2.145973920 | 5.49195037 |
| 14 | 372 | −2.903724367 | 2.70510286 | −2.145973988 | 5.49196539 |
| 15 | 444 | −2.903724371 | 2.70510285 | −2.145974012 | 5.49196837 |
| Ref. [21] | −2.9037243768 | 2.7051028 | |||
| Ref. [39] | −2.9037243770341195 | −2.145974046054419 | |||
| 1/B | Energy | Shannon Entropy | ||
|---|---|---|---|---|
| A = 0.2 | A = 0.5 | A = 0.2 | A = 0.5 | |
| 0.01 | −2.903730428 | −2.903782320 | 2.7050970 | 2.7050463 |
| 0.04 | −2.904046799 | −2.906501450 | 2.7047890 | 2.7024115 |
| 0.1 | −2.907290165 | −2.930040819 −2.93004 † | 2.7016791 | 2.6804318 |
| 0.25 | −2.930892544 | −3.059472114 | 2.6806153 | 2.5789191 |
| 0.4 | −2.965954073 | −3.206030252 | 2.6536356 | 2.5005110 |
| 1 | −3.093344574 | −3.564904622 −3.56490 † | 2.5989837 | 2.4661404 |
| 2.5 | −3.222312613 | −3.798189998 | 2.6227726 | 2.5795868 |
| 4 | −3.261404222 | −3.853009590 | 2.6514702 | 2.6329358 |
| 10 | −3.294341118 | −3.893533087 −3.89353 † | 2.6895775 | 2.6872398 |
| 5 | −3.301992742 | −3.901931164 | 2.7018817 | 2.7016811 |
| 40 | −3.303022766 | −3.903007067 | 2.7037593 | 2.7037067 |
| 100 | −3.303607882 | −3.903606833 −3.90361 † | 2.7048735 | 2.7048699 |
| 1/B | Energy | Shannon Entropy | ||
|---|---|---|---|---|
| A = 0.2 | A = 0.5 | A = 0.2 | A = 0.5 | |
| 0.01 | −2.145978326 | 5.4919460 | ||
| 0.015 | −2.146108395 | 5.4918183 | ||
| 0.1 | −2.148528796 | −2.164613565 | 5.4895009 | 5.4745971 |
| 0.25 | −2.164822224 | −2.249875684 | 5.4752129 | 5.4097138 |
| 0.4 | −2.187604871 | −2.337051173 | 5.4583644 | 5.3631936 |
| 1 | −2.260693038 | −2.537147708 | 5.4182621 | 5.1733749 |
| 2.5 | −2.342674793 | −2.786896138 | 5.2556723 | 4.8262175 |
| 4 | −2.394029709 | −2.914053557 | 5.1576614 | 4.8685244 |
| 10 | −2.485237303 | −3.069904076 | 5.2113530 | 5.1173708 |
| 25 | −2.529366979 | −3.127321718 | 5.3667965 | 5.3446117 |
| 40 | −3.137714313 | 5.4151191 | ||
| 41.38 | −2.538783608 | 5.4270311 | ||
| 100 | −2.544528698 | −3.144476898 | 5.4764372 | 5.4755194 |
| 1/B | Energy | Shannon Entropy | ||
|---|---|---|---|---|
| A = 5 | A = 10 | A = 5 | A = 10 | |
| 0.00674 | 7.091236423 | 17.069559224 | 2.7001966 | 2.6792466 |
| 0.01 † | 7.0812417 † | |||
| 0.01832 | 7.021102846 | 16.698608554 | 2.6337371 | 2.3544713 |
| 0.03020 | 6.832858941 | 15.666363291 | 2.4689643 | 1.7010882 |
| 0.04979 | 6.263771914 | 12.967893252 | 2.0698118 | 0.9227337 |
| 0.08208 | 4.942856089 | 8.899547096 | 1.5435377 | 0.6579720 |
| 0.13534 | 2.957446733 | 4.922590104 | 1.2982587 | 0.7762660 |
| 0.22313 | 0.958092058 | 1.847458176 | 1.3664833 | 1.0640238 |
| 0.36788 | −0.605490789 | −0.229055013 | 1.5923907 | 1.4152561 |
| 0.60653 | −1.651154473 | −1.502227403 | 1.8716883 | 1.7702336 |
| 1.0 | −2.274776743 | −2.220316341 | 2.1423955 | 2.0879127 |
| −2.2747767 † | ||||
| 2.71828 | −2.777381939 | −2.771925145 | 2.5244420 | 2.5135970 |
| 7.38906 | −2.883566744 | −2.883194130 | 2.6685314 | 2.6674284 |
| 1000 † | −2.9037227 † | |||
| 1/B | Energy | Shannon Entropy | ||
|---|---|---|---|---|
| A = 5 | A = 10 | A = 5 | A = 10 | |
| 0.004 | 7.853198946 | 17.849560882 | 5.4911371 | 5.4875642 |
| 0.01 | 7.843185873 | 17.797383638 | 5.4813847 | 5.4376764 |
| 0.025 | 7.736312535 | 17.238747505 | 5.3837869 | 5.0114612 |
| 0.04 | 7.499987880 | 16.12763973 | 5.1996113 | 4.5276297 |
| 0.1 | 6.106023017 | 12.21540359 | 4.6418609 | 3.2801230 |
| 0.25 | 3.806886884 | 6.058810732 | 3.3829537 | 2.5449126 |
| 0.4 | 2.201153744 | 3.294161749 | 3.2239305 | 2.7892007 |
| 1 | −0.268402783 | −0.022735449 | 3.6292016 | 3.4623643 |
| 2.5 | −1.479882907 | −1.429647473 | 4.2163710 | 4.1451505 |
| 4 | −1.780154947 | −1.758998575 | 4.5086622 | 4.4631793 |
| 10 | −2.047704730 | −2.044347012 | 4.9971967 | 4.9805825 |
| 39.685 | −2.136636813 | 5.4009833 | ||
| 43.288 | −2.138141127 | 5.41429737 | ||
| 81.113 | −2.143623958 | 5.46598441 | ||
| 100 | −2.144404056 | 5.4742044 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, J.-H.; Ho, Y.K. Shannon Information Entropy in Position Space for the Ground and Singly Excited States of Helium with Finite Confinements. Atoms 2017, 5, 15. https://doi.org/10.3390/atoms5020015
Ou J-H, Ho YK. Shannon Information Entropy in Position Space for the Ground and Singly Excited States of Helium with Finite Confinements. Atoms. 2017; 5(2):15. https://doi.org/10.3390/atoms5020015
Chicago/Turabian StyleOu, Jen-Hao, and Yew Kam Ho. 2017. "Shannon Information Entropy in Position Space for the Ground and Singly Excited States of Helium with Finite Confinements" Atoms 5, no. 2: 15. https://doi.org/10.3390/atoms5020015
APA StyleOu, J.-H., & Ho, Y. K. (2017). Shannon Information Entropy in Position Space for the Ground and Singly Excited States of Helium with Finite Confinements. Atoms, 5(2), 15. https://doi.org/10.3390/atoms5020015






