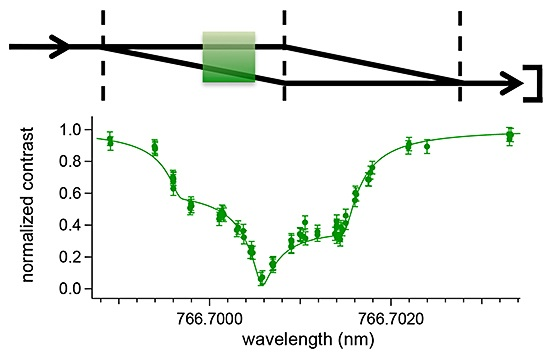
Decoherence Spectroscopy for Atom Interferometry
Abstract
:1. Introduction
2. Motivation
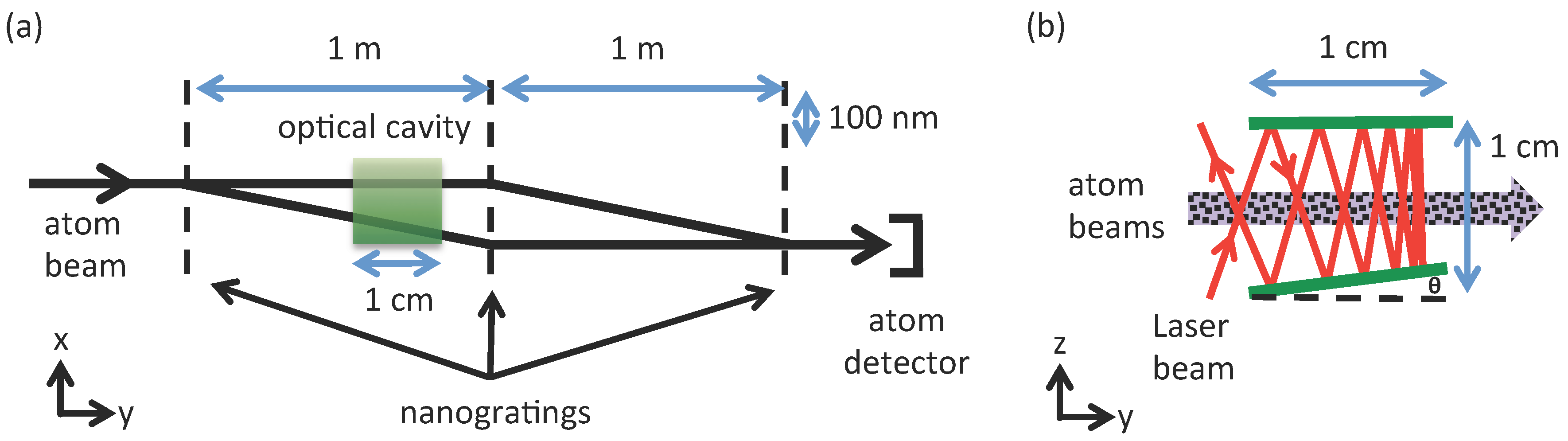
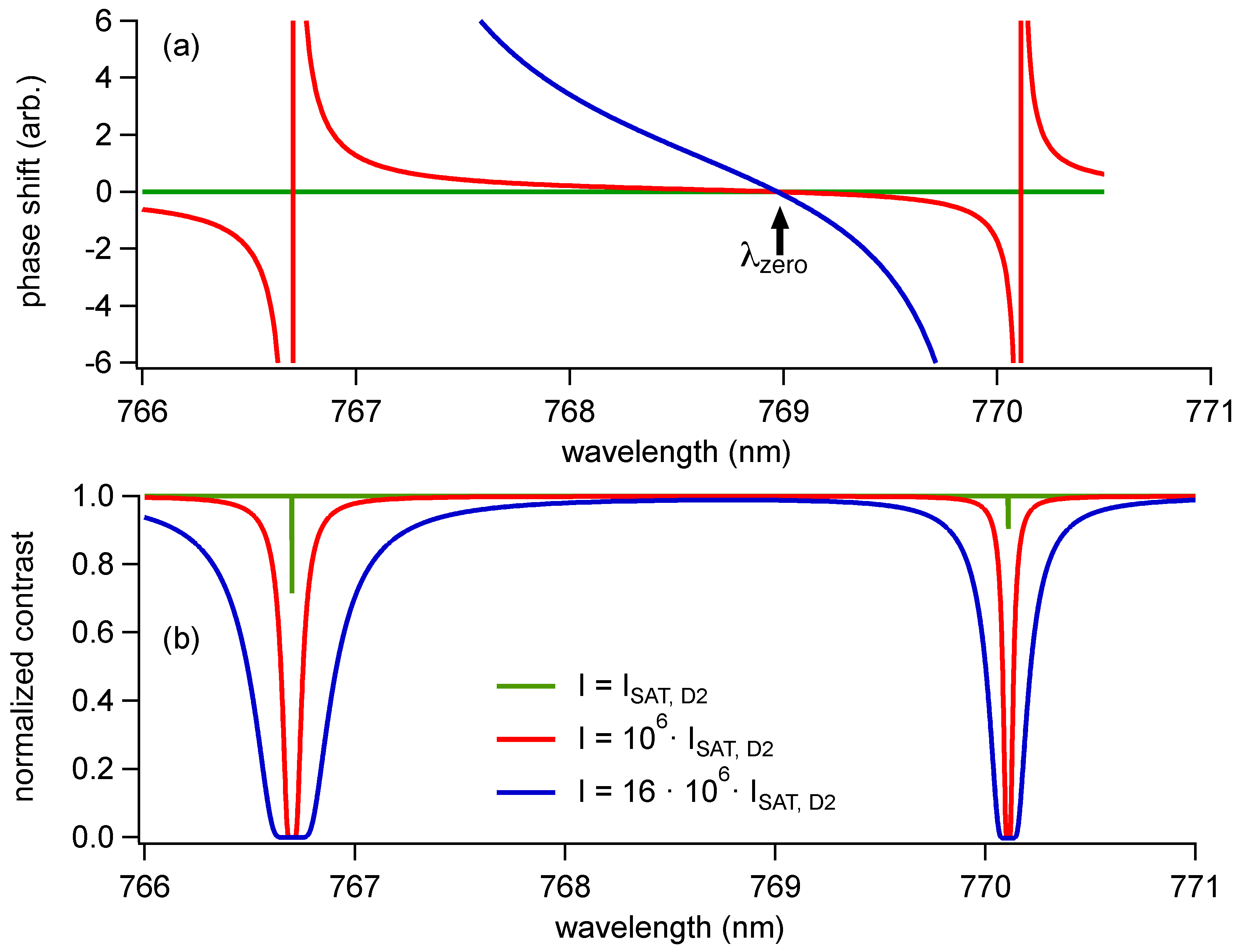
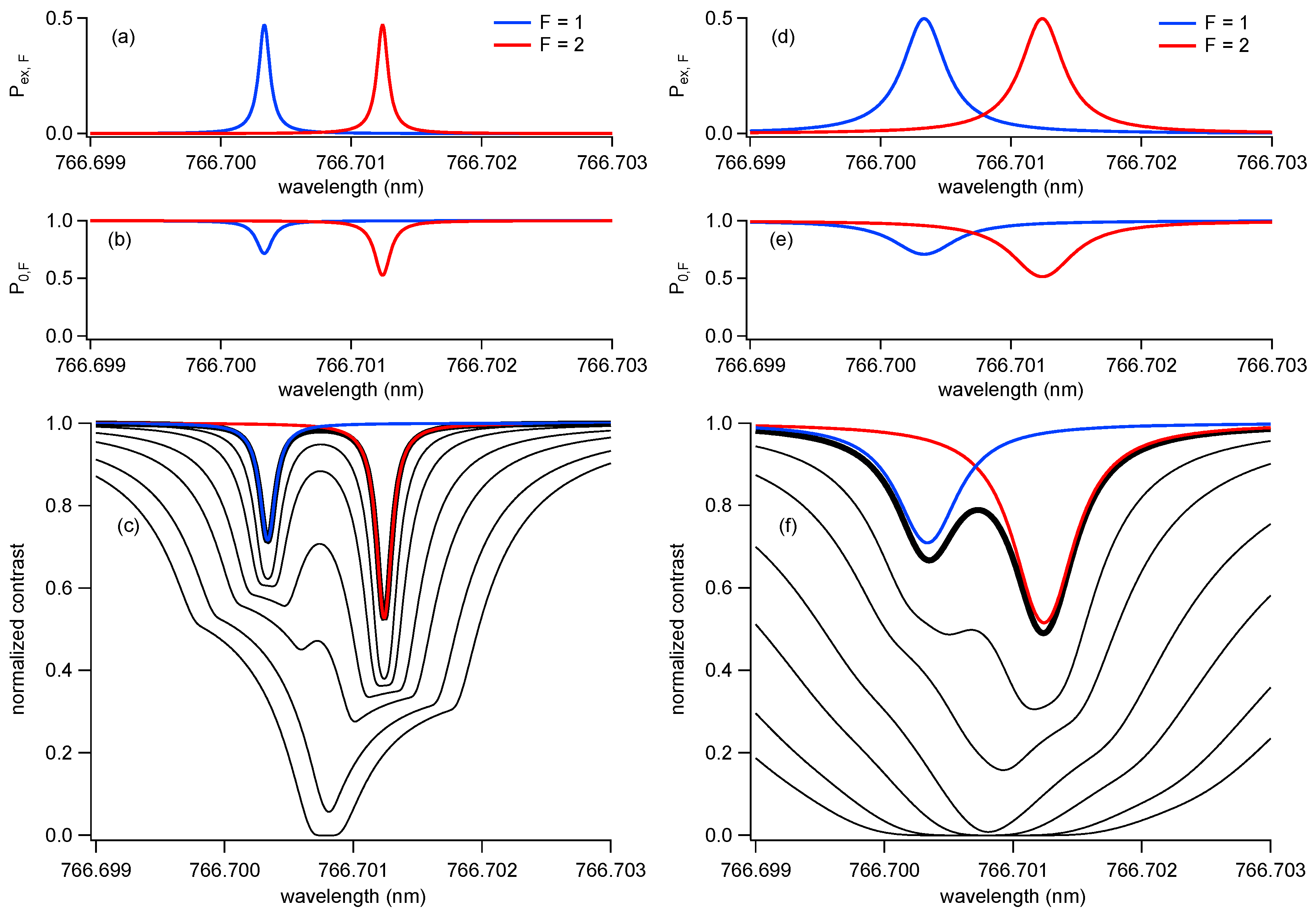
3. Decoherence Spectroscopy Model
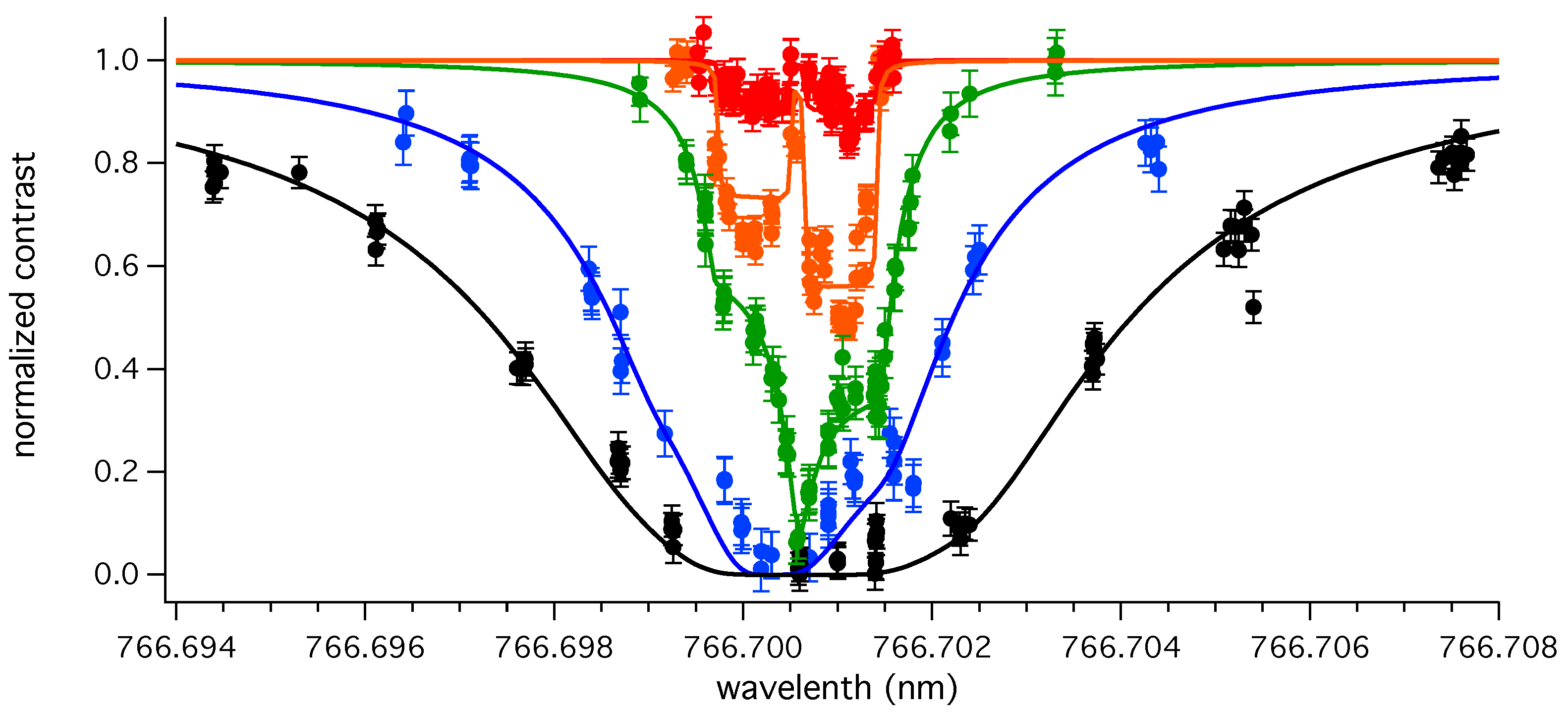
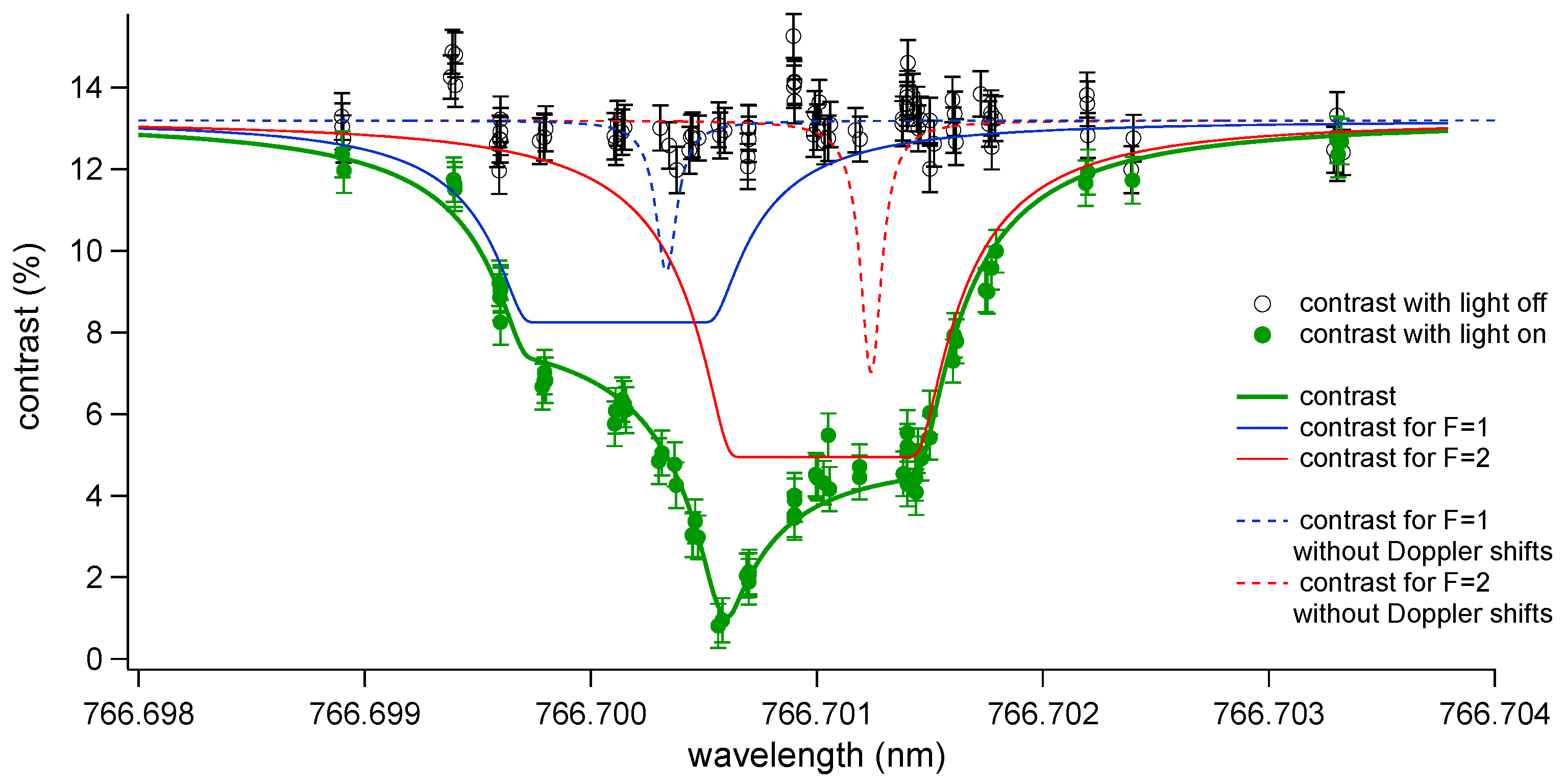
4. Decoherence Spectroscopy Data
5. Discussion
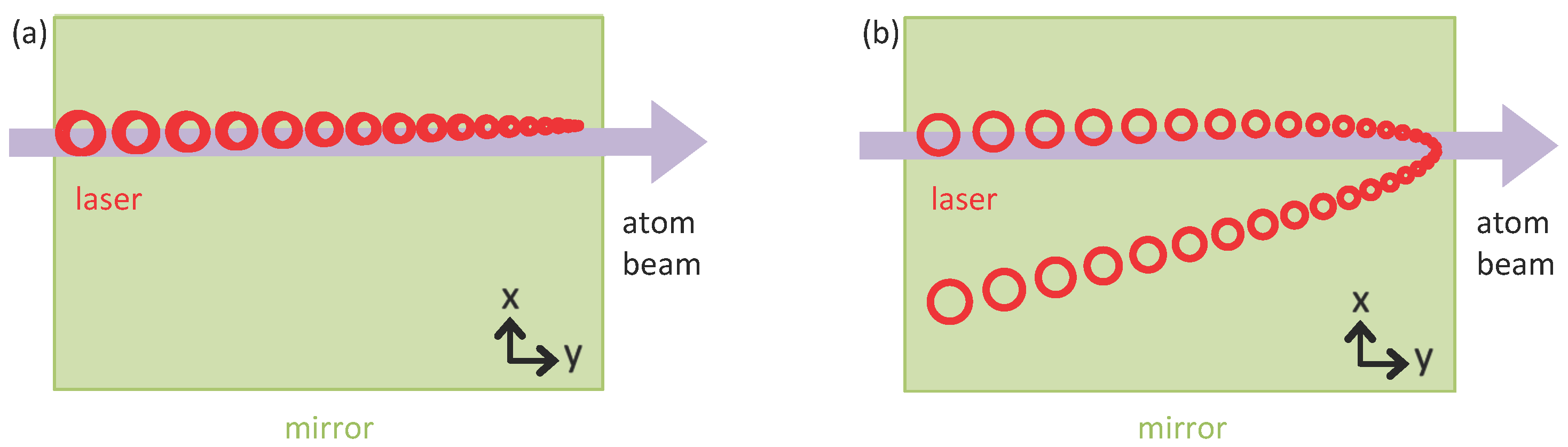
5.1. Complications and Suggested Improvements to Decoherence Spectroscopy Model
5.2. Contrast Loss Mechanisms: Decoherence versus Dephasing
5.3. Comparison with Other Methods and Limits in Precision
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zurek, W.H. Environment-induced superselection rules. Phys. Rev. D 1982, 26, 1862–1880. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence and the transition from quantum to classical. Phys. Today 1991, 44, 36–44. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Joos, E.; Zeh, H.D. The emergence of classical properties through interaction with the environment. Z. Phys. B Condens. Matter 1985, 59, 223–243. [Google Scholar] [CrossRef]
- Caldeira, A.O.; Leggett, A.J. Influence of damping on quantum interference: An exactly soluble model. Phys. Rev. A 1985, 31, 1059–1066. [Google Scholar] [CrossRef]
- Joos, E.; Zeh, H.D.; Kiefer, C.; Giulini, D.J.; Kupsch, J.; Stamatescu, I.O. Decoherence and the Appearance of a Classical World in Quantum Theory; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Chapman, M.S.; Hammond, T.D.; Lenef, A.; Schmiedmayer, J.; Rubenstein, R.A.; Smith, E.; Pritchard, D.E. Photon scattering from atoms in an atom interferometer: Coherence lost and regained. Phys. Rev. Lett. 1995, 75, 3783–3787. [Google Scholar] [CrossRef] [PubMed]
- Kokorowski, D.A.; Cronin, A.D.; Roberts, T.D.; Pritchard, D.E. From single- to multiple-photon decoherence in an atom interferometer. Phys. Rev. Lett. 2001, 86, 2191–2195. [Google Scholar] [CrossRef] [PubMed]
- Uys, H.; Perreault, J.D.; Cronin, A.D. Matter-wave decoherence due to a gas environment in an atom interferometer. Phys. Rev. Lett. 2005, 95, 150403. [Google Scholar] [CrossRef] [PubMed]
- Hornberger, K.; Uttenthaler, S.; Brezger, B.; Hackermüller, L.; Arndt, M.; Zeilinger, A. Collisional decoherence observed in matter wave interferometry. Phys. Rev. Lett. 2003, 90, 160401. [Google Scholar] [CrossRef] [PubMed]
- Hackermüller, L.; Hornberger, K.; Brezger, B.; Zeilinger, A.; Arndt, M. Decoherence of matter waves by thermal emission of radiation. Nature 2004, 427, 711–714. [Google Scholar] [CrossRef] [PubMed]
- Myatt, C.J.; King, B.E.; Turchette, Q.A.; Sackett, C.A.; Kielpinski, D.; Itano, W.M.; Monroe, C.; Wineland, D.J. Decoherence of quantum superpositions through coupling to engineered reservoirs. Nature 2000, 403, 269–273. [Google Scholar] [PubMed]
- Haroche, S. Entanglement, decoherence and the quantum/classical boundary. Phys. Today 1998, 51, 36–42. [Google Scholar] [CrossRef]
- Martinis, J.M.; Nam, S.; Aumentado, J.; Lang, K.M.; Urbina, C. Decoherence of a superconducting qubit due to bias noise. Phys. Rev. B 2003, 67, 094510. [Google Scholar] [CrossRef]
- Wang, H.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Lucero, E.; Neeley, M.; O’Connell, A.D.; Sank, D.; Weides, M.; Wenner, J.; et al. Decoherence dynamics of complex photon states in a superconducting Circuit. Phys. Rev. Lett. 2009, 103, 200404. [Google Scholar] [CrossRef] [PubMed]
- Roszak, K.; Filip, R.; Novotný, T. Decoherence control by quantum decoherence itself. Sci. Rep. 2015, 5, 9796. [Google Scholar] [CrossRef] [PubMed]
- Roszak, K.; Machnikowski, P. A which path decoherence in quantum dot experiments. Phys. Lett. A 2006, 351, 251–256. [Google Scholar] [CrossRef]
- Clauser, J.F.; Li, S. “Heisenberg microscope” decoherence atom interferometry. Phys. Rev. A 1994, 50, 2430–2433. [Google Scholar] [CrossRef] [PubMed]
- Kunze, S.; Dieckmann, K.; Rempe, G. Diffraction of atoms from a measurement induced grating. Phys. Rev. Lett. 1997, 78, 2038–2041. [Google Scholar] [CrossRef]
- Gupta, S.; Dieckmann, K.; Hadzibabic, Z.; Pritchard, D. Contrast interferometry using Bose-Einstein condensates to measure h/m and α. Phys. Rev. Lett. 2002, 89, 140401. [Google Scholar] [CrossRef] [PubMed]
- Eibenberger, S.; Cheng, X.; Cotter, J.P.; Arndt, M. Absolute absorption cross sections from photon recoil in a matter-wave interferometer. Phys. Rev. Lett. 2014, 112, 250402. [Google Scholar] [CrossRef] [PubMed]
- LeBlanc, L.J.; Thywissen, J.H. Species-specific optical lattices. Phys. Rev. A 2007, 75, 053612. [Google Scholar] [CrossRef]
- Safronova, M.; Williams, C.J.; Clark, C.W. Relativistic many-body calculations of electric-dipole matrix elements, lifetimes, and polarizabilities in rubidium. Phys. Rev. A 2004, 69, 022509. [Google Scholar] [CrossRef]
- Arora, B.; Safronova, M.S.; Clark, C.W. Tune-out wavelengths of alkali-metal atoms and their applications. Phys. Rev. A 2011, 84, 043401. [Google Scholar] [CrossRef]
- Topcu, T.; Derevianko, A. Tune-out wavelengths and landscape-modulated polarizabilities of alkali-metal Rydberg atoms in infrared optical lattices. Phys. Rev. A 2013, 88, 053406. [Google Scholar] [CrossRef]
- Mitroy, J.; Tang, L.Y. Tune-out wavelengths for metastable helium. Phys. Rev. A 2013, 88, 052515. [Google Scholar] [CrossRef]
- Le Kien, F.; Schneeweiss, P.; Rauschenbeutel, A. Dynamical polarizability of atoms in arbitrary light fields: General theory and application to cesium. Eur. Phys. J. D 2013, 67, 1–16. [Google Scholar] [CrossRef]
- Jiang, J.; Mitroy, J. Hyperfine effects on potassium tune-out wavelengths and polarizabilities. Phys. Rev. A 2013, 88, 032505. [Google Scholar] [CrossRef]
- Jiang, J.; Tang, L.Y.; Mitroy, J. Tune-out wavelengths for potassium. Phys. Rev. A 2013, 87, 032518. [Google Scholar] [CrossRef]
- Cheng, Y.; Jiang, J.; Mitroy, J. Tune-out wavelengths for the alkaline-earth-metal atoms. Phys. Rev. A 2013, 88, 022511. [Google Scholar] [CrossRef]
- Safronova, M.S.; Zuhrianda, Z.; Safronova, U.I.; Clark, C.W. The magic road to precision. ArXiv e-prints 2015. [Google Scholar]
- Yu, W.W.; Yu, R.M.; Cheng, Y.J. Tune-out wavelengths for the Rb atom. Chin. Phys. Lett. 2015, 32, 123102. [Google Scholar] [CrossRef]
- Chamakhi, R.; Ahlers, H.; Telmini, M.; Schubert, C.; Rasel, E.; Gaaloul, N. Species-selective lattice launch for precision atom interferometry. New J. Phys. 2015, 17, 123002. [Google Scholar] [CrossRef]
- Herold, C.D.; Vaidya, V.D.; Li, X.; Rolston, S.L.; Porto, J.V.; Safronova, M.S. Precision measurement of transition matrix elements via light shift cancellation. Phys. Rev. Lett. 2012, 109, 243003. [Google Scholar] [CrossRef] [PubMed]
- Holmgren, W.F.; Trubko, R.; Hromada, I.; Cronin, A.D. Measurement of a wavelength of light for which the energy shift for an atom vanishes. Phys. Rev. Lett. 2012, 109, 243004. [Google Scholar] [CrossRef] [PubMed]
- Leonard, R.H.; Fallon, A.J.; Sackett, C.A.; Safronova, M.S. High-precision measurements of the 87RbD-line tune-out wavelength. Phys. Rev. A 2015, 92, 052501. [Google Scholar] [CrossRef]
- Keith, D.W.; Ekstrom, C.R.; Turchette, Q.A.; Pritchard, D.E. An interferometer for atoms. Phys. Rev. Lett. 1991, 66, 2693–2696. [Google Scholar] [CrossRef] [PubMed]
- Berman, P. Atom Interferometry; Academic Press: San Diego, CA, USA, 1997. [Google Scholar]
- Cronin, A.D.; Schmiedmayer, J.; Pritchard, D.E. Optics and interferometry with atoms and molecules. Rev. Mod. Phys. 2009, 81, 1051–1129. [Google Scholar] [CrossRef]
- Metcalf, H.J.; van Straten, P. Laser Cooling and Trapping; Springer: New York, NY, USA, 1999. [Google Scholar]
- Foot, C.J. Atomic Physics; OUP Oxford: Oxford, UK, 2004. [Google Scholar]
| Observable in Presence of Laser | Dependence on I | Dependence on Δ | Dependence on v |
|---|---|---|---|
| C loss from decoherence | I | ||
| C loss from dephasing | |||
| light induced ϕ |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trubko, R.; Cronin, A.D. Decoherence Spectroscopy for Atom Interferometry. Atoms 2016, 4, 25. https://doi.org/10.3390/atoms4030025
Trubko R, Cronin AD. Decoherence Spectroscopy for Atom Interferometry. Atoms. 2016; 4(3):25. https://doi.org/10.3390/atoms4030025
Chicago/Turabian StyleTrubko, Raisa, and Alexander D. Cronin. 2016. "Decoherence Spectroscopy for Atom Interferometry" Atoms 4, no. 3: 25. https://doi.org/10.3390/atoms4030025
APA StyleTrubko, R., & Cronin, A. D. (2016). Decoherence Spectroscopy for Atom Interferometry. Atoms, 4(3), 25. https://doi.org/10.3390/atoms4030025