Natural and Unnatural Parity Resonance States in the Positron-Hydrogen System with Screened Coulomb Interactions
Abstract
:1. Introduction
2. Theory
3. Results and Discussion
3.1. D-Wave Resonances with Natural Parity
| D | Er (a.u.) | Γ/2 (a.u.) | ET | H or Ps State | |
|---|---|---|---|---|---|
| H(2d-1) | ∞ | −0.1250332 | 4.781(−6) | −0.125 | H(2p) |
| ∞ | −0.12504795 a | 7.0(−7) a | |||
| ∞ | −0.125047 b | 1.6(−6) b | |||
| 200 | −0.1200768 | 4.847(−6) | −0.120061 | ||
| 100 | −0.115221 | 5.636(−6) | −0.115245 | ||
| 80 | −0.1128364 | 6.481(−6) | −0.112881 | ||
| 60 | −0.1089288 | 8.862(−6) | −0.109006 | ||
| 55 | −0.1075296 | 1.0132(−5) | −0.107616 | ||
| 50 | −0.1058663 | 1.2060(−5) | −0.105963 | ||
| 45 | −0.1038578 | 1.6244(−5) | −0.103962 | ||
| Ps(2d-1) | ∞ | −0.071965 | 8.4198(−5) | −0.0625 | Ps(2p) |
| ∞ | −0.07196495 a | 8.42(−5) a | |||
| ∞ | −0.071943 b | 8.35(−6) b | |||
| 100 | −0.0621949 | 8.3738(−5) | −0.052981 | ||
| 50 | −0.0529684 | 8.1573(−5) | −0.043647 | ||
| 40 | −0.048588 | 7.9652(−5) | −0.04037 | ||
| 30 | −0.0416585 | 7.5121(−5) | −0.03439 | ||
| 25 | −0.0364629 | 7.0354(−5) | −0.029556 | ||
| Ps(2d-2) | ∞ | −0.0644753 | 3.5391(−5) | −0.0625 | Ps(2p) |
| ∞ | −0.064475256 a | 3.48(−5) a | −0.052981 | ||
| ∞ | −0.064470 b | 3.43(−5) b | |||
| 100 | −0.0547611 | 3.4798(−5) | |||
| 50 | −0.0457653 | 3.1925(−5) | −0.043647 | ||
| 40 | −0.041582 | 3.0033(−5) | −0.04037 | ||
| H(3d-1) | ∞ | −0.0572622 | 2.3161(−4) | −0.0555555 | H(3d) |
| ∞ | −0.0572625 a | 2.32(−4) a | |||
| ∞ | −0.057245 b | 2.18(−4) b | |||
| 100 | −0.0475678 | 2.2505(−4) | −0.0460615 | ||
| 50 | −0.0387025 | 1.9549(−4) | −0.0375151 | ||
| 40 | −0.0346464 | 1.6929(−4) | −0.0335731 | ||
| 30 | −0.0285223 | 1.3558(−4) | −0.0274683 | ||
| H(3d-2) | ∞ | −0.0558526 | 4.9653(−5) | −0.0555555 | H(3d) |
| ∞ | −0.055825 a | 3.75(−5) a | |||
| ∞ | −0.055825 b | 3.94(−5) b | |||
| 100 | −0.046236 | 4.8893(−5) | −0.0460615 | ||
| H (3d-shape) | ∞ | −0.055537 | 1.0938(−4) | −0.0555555 | H(3d) |
| ∞ | −0.055542 b | 5.81(−5) b | |||
| 100 | −0.0459933 | 1.1978(−4) | −0.0460615 | ||
| 50 | −0.0374707 | 1.6170(−4) | −0.0375151 | ||
| 40 | −0.0336156 | 2.5161(−4) | −0.0335731 | ||
| 30 | −0.0278024 | 5.0496(−4) | −0.0274683 | ||
| H(4d-1) | ∞ | −0.0378252 | 3.0243(−5) | −0.03125 | H(4d) |
| ∞ | −0.0378252 a | 3.025(−5) a | |||
| ∞ | −0.037689 b | 3.12(−5) b | |||
| 100 | −0.0282273 | 2.9930(−5) | −0.0222278 | ||
| 50 | −0.0197682 | 2.6997(−5) | −0.0149401 | ||
| 40 | −0.0160542 | 2.4349(−5) | −0.0118705 | ||
| 30 | −0.0106871 | 1.8529(−5) | −0.0075338 | ||
| H(4d-2) | ∞ | −0.0349288 | 3.6679(−5) | −0.03125 | H(4d) |
| ∞ | −0.03492875 a | 3.67(−5) a | |||
| ∞ | −0.034 689 b | 3.71(−5) b | |||
| 100 | −0.0255062 | 3.5656(−5) | −0.0222278 | ||
| 50 | −0.0173876 | 3.1467(−5) | −0.0149401 | ||
| 40 | −0.0138584 | 2.8036(−5) | −0.0118705 | ||
| 30 | −0.0088013 | 2.1274(−5) | −0.0075338 | ||
| H(4d-3) | ∞ | −0.0334566 | 2.4389(−5) | −0.03125 | H(4d) |
| ∞ | −0.0334564 a | 2.44(−5) a | |||
| ∞ | −0.033 342 b | 2.47(−5) b | |||
| 100 | −0.0239507 | 2.3450(−5) | −0.0222278 | ||
| 50 | −0.0159279 | 1.7544(−5) | −0.0149401 |
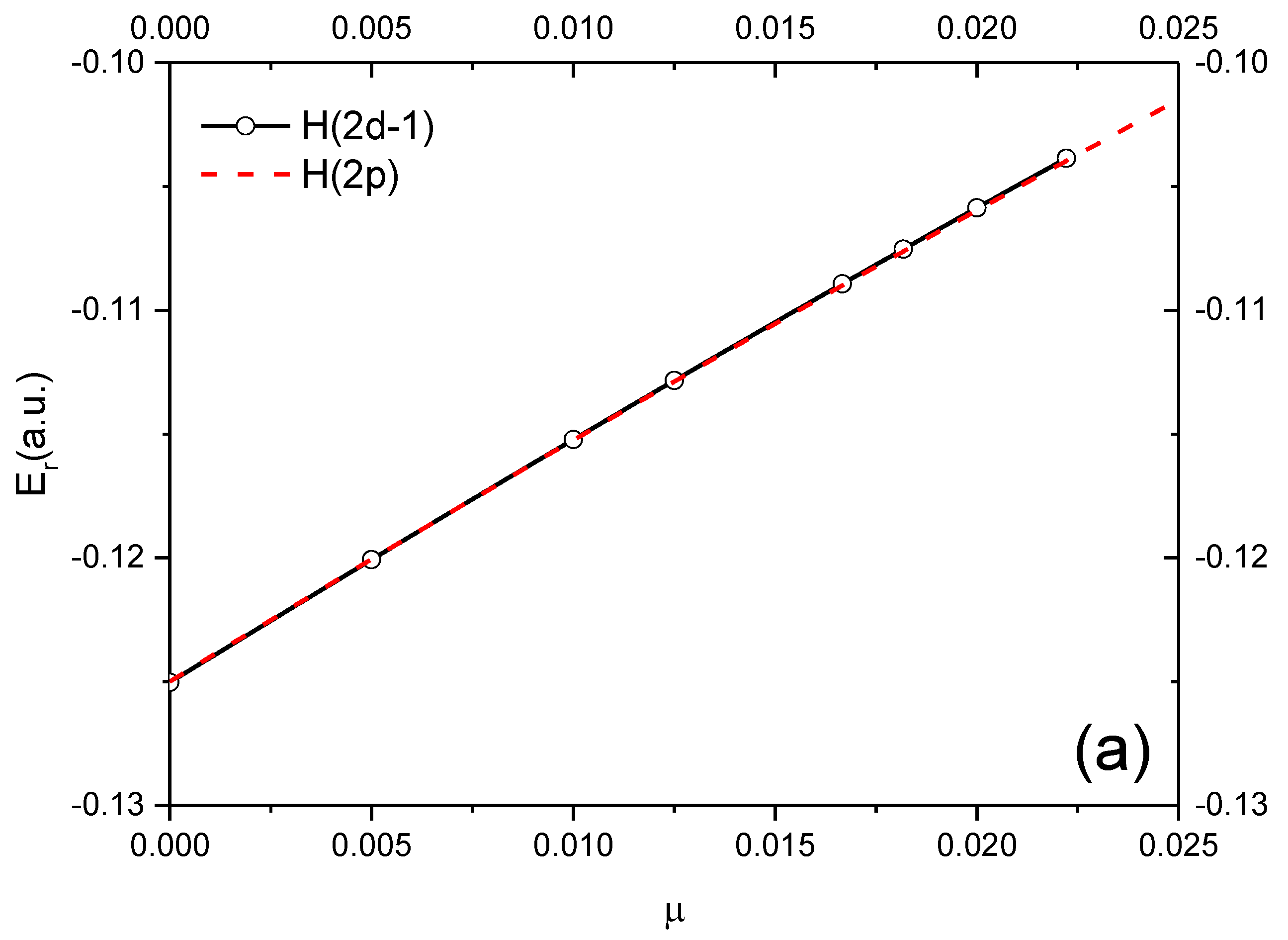
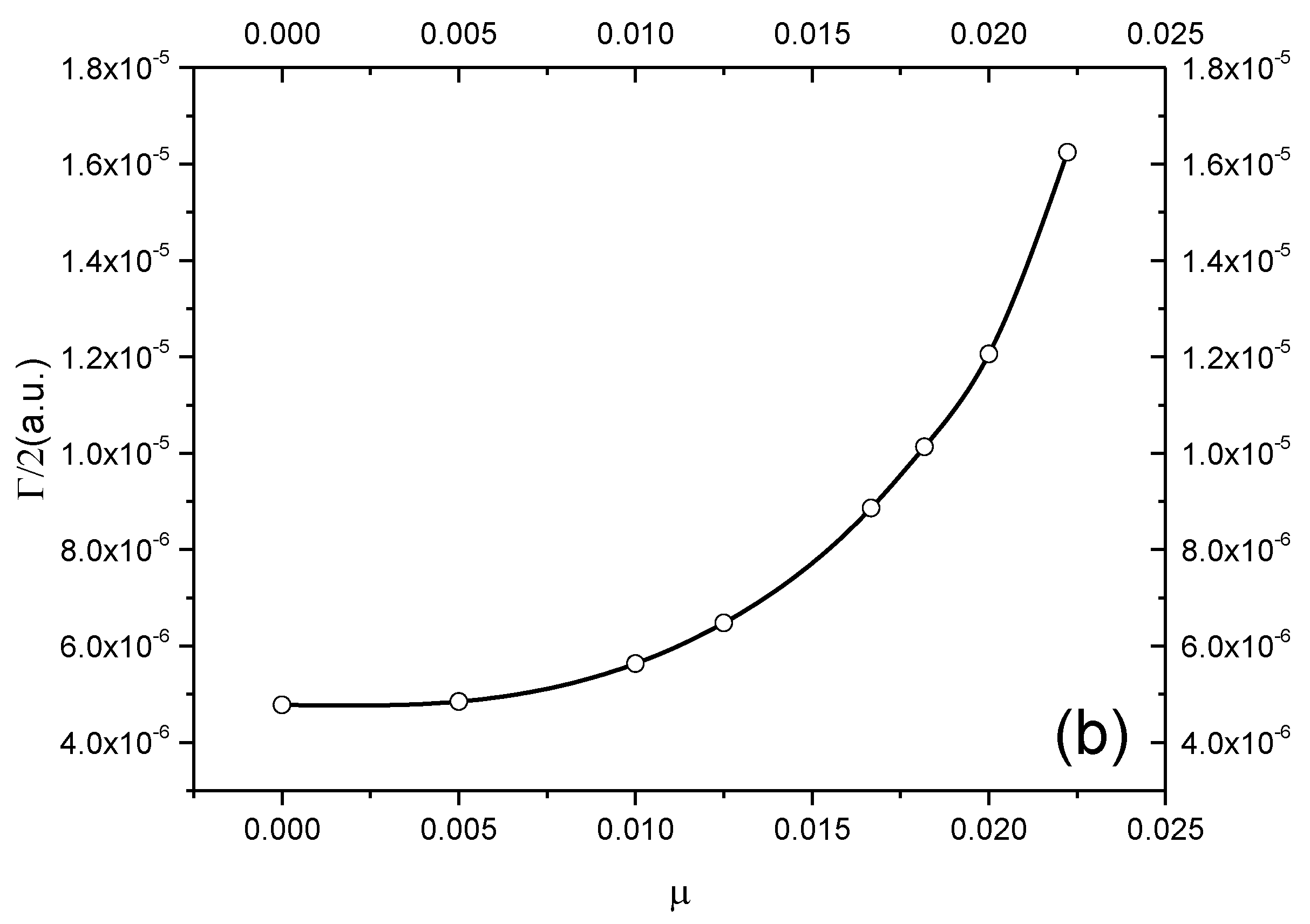
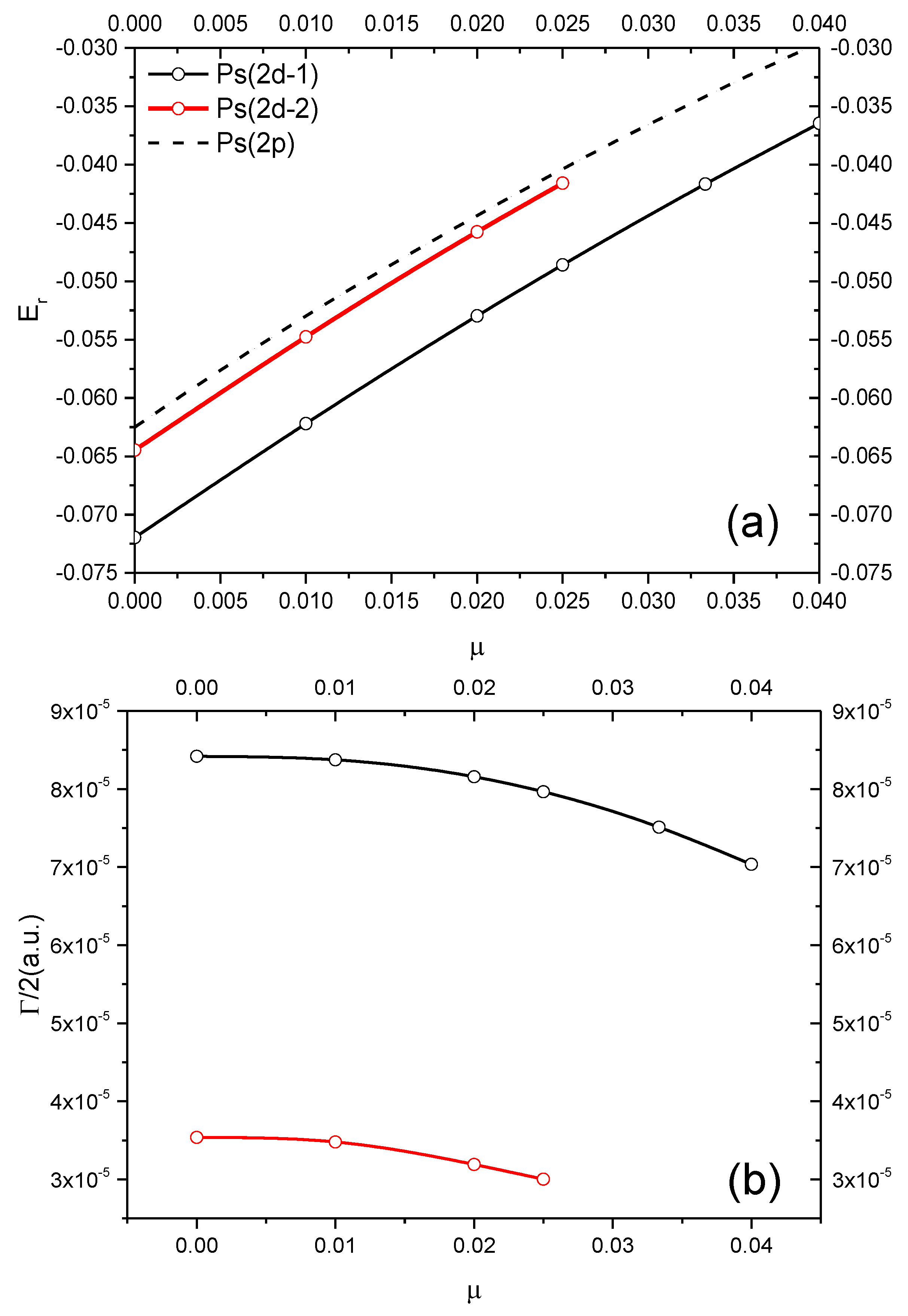
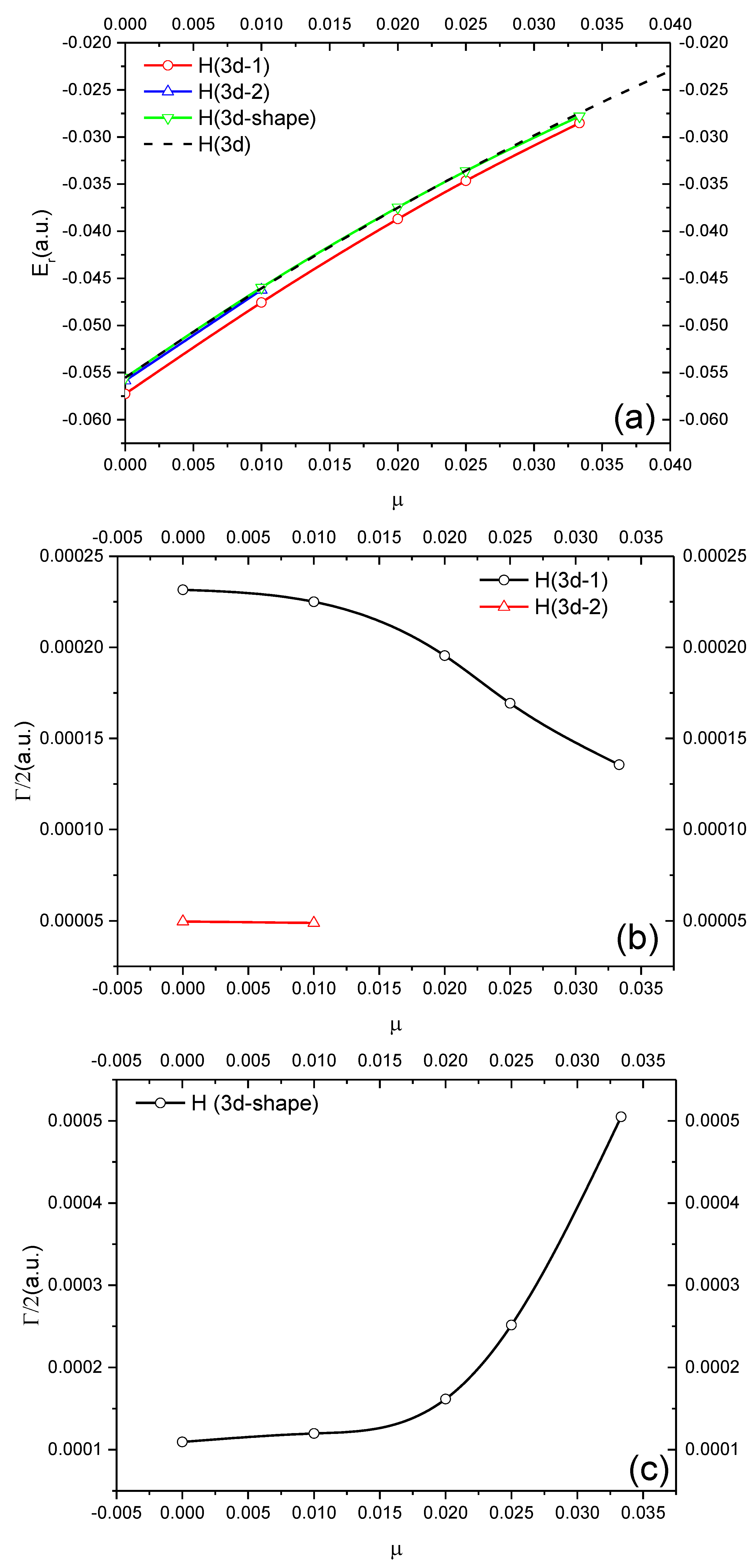
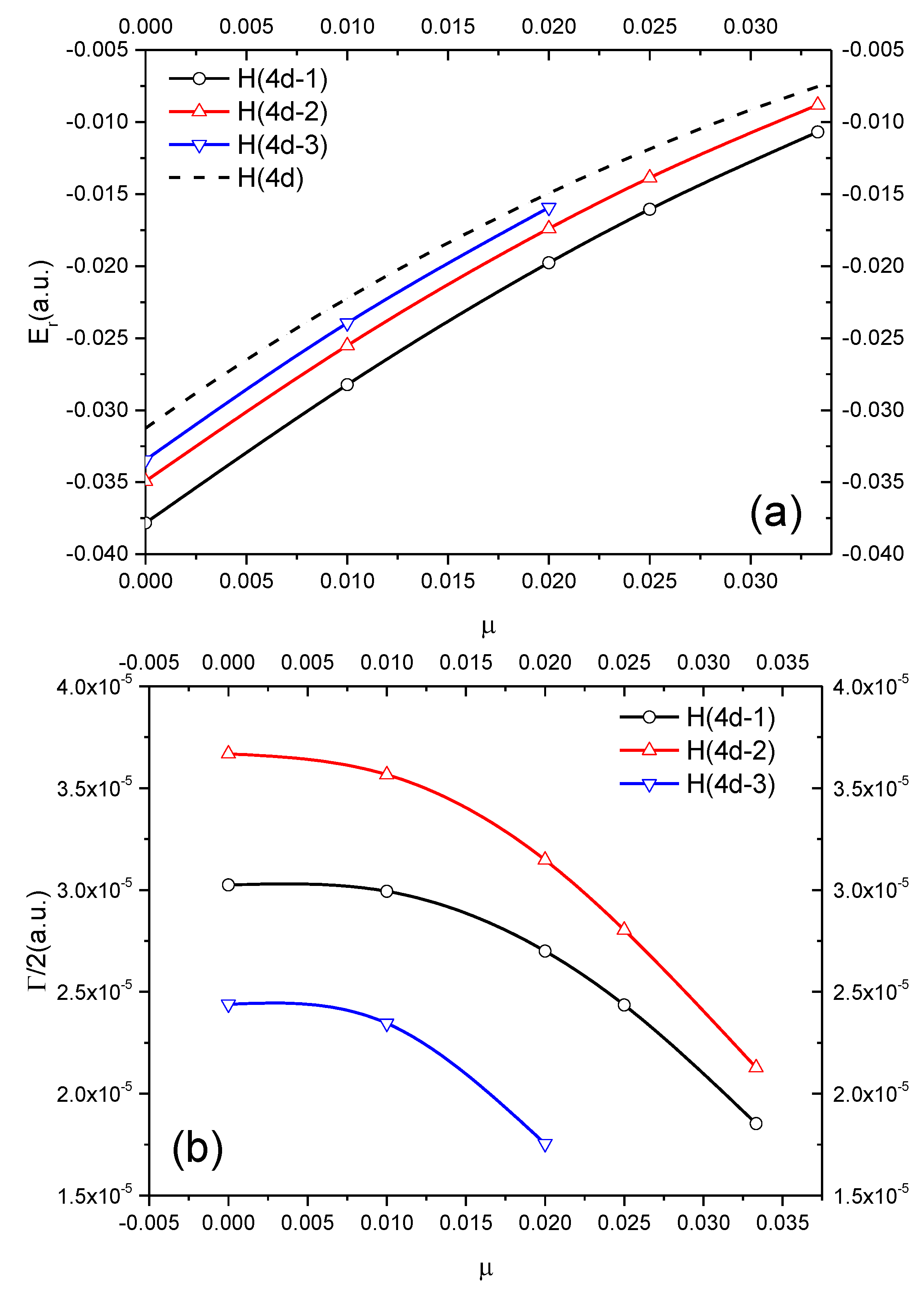
3.2. P-Wave Resonances with Unnatural Parity
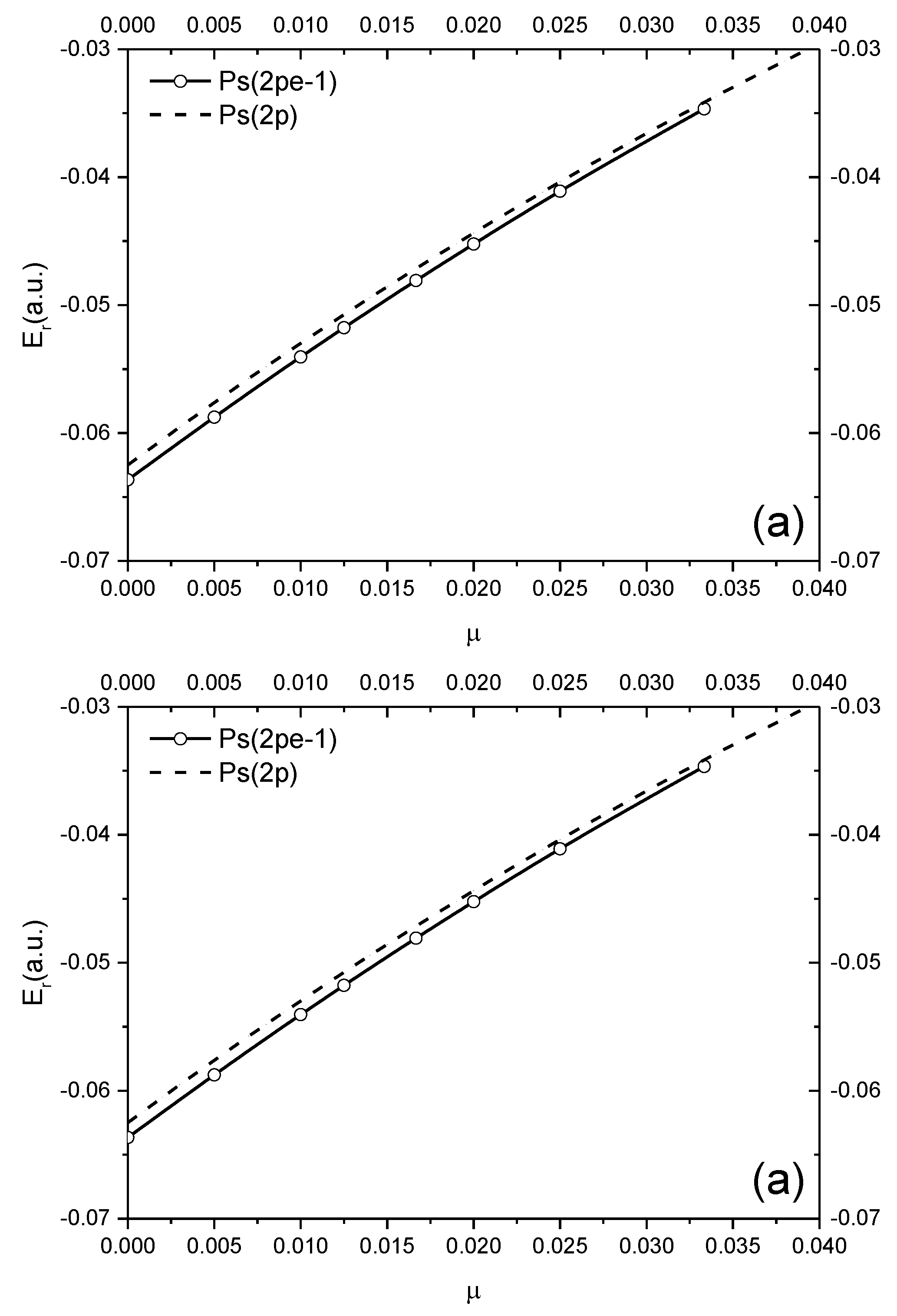
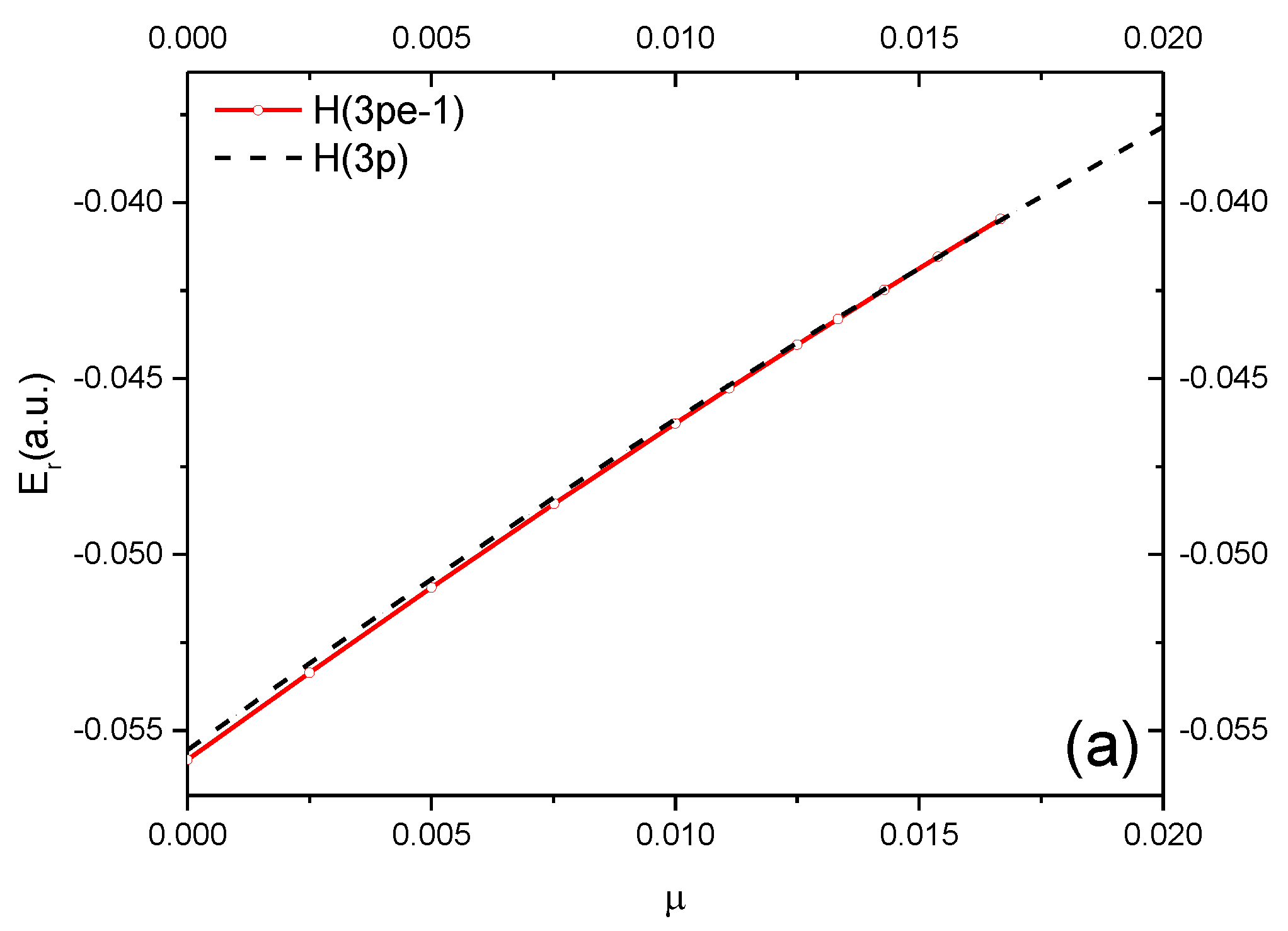
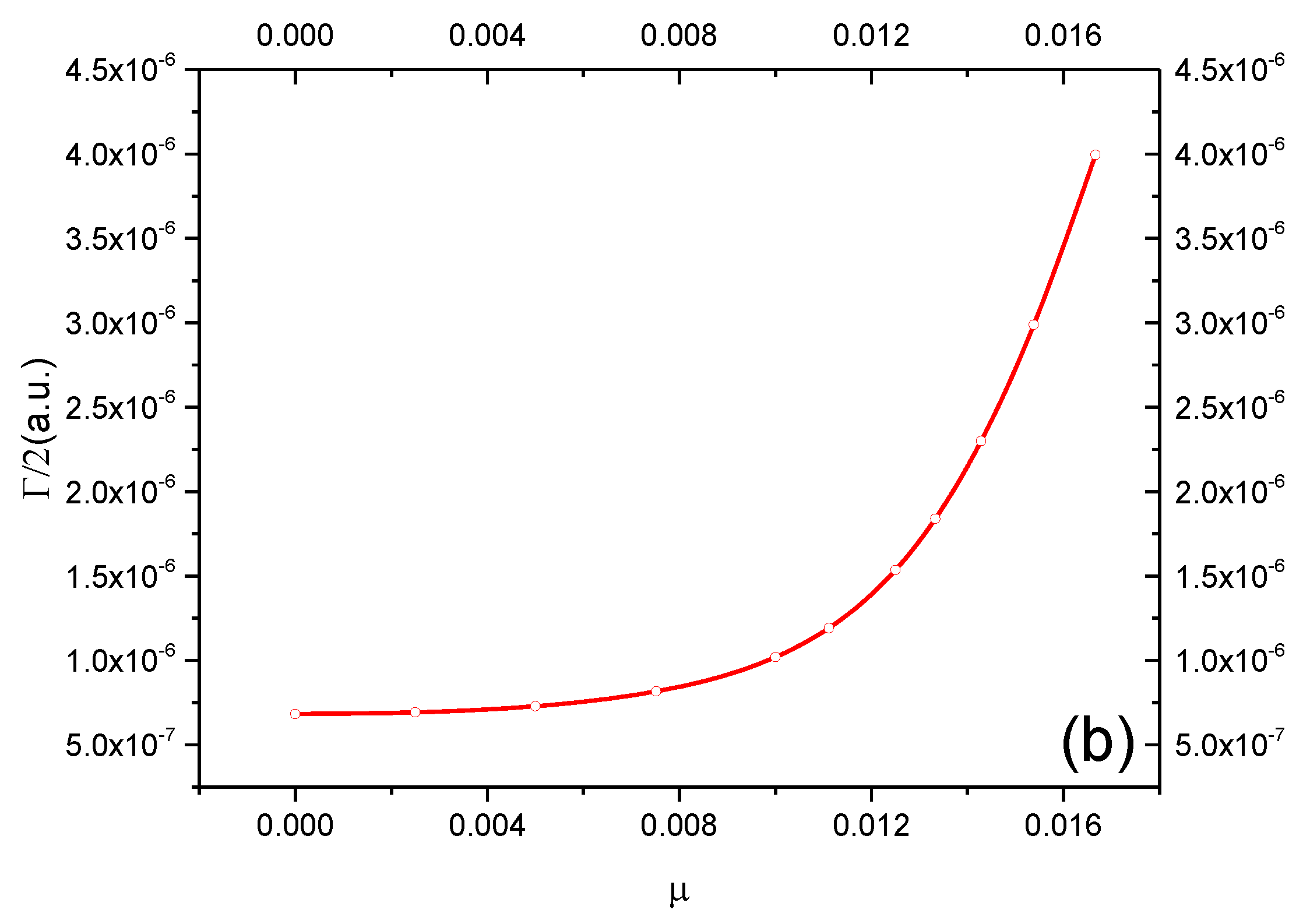
| D | Er (a.u.) | Γ/2 (a.u.) | ET | H or Ps State | |
|---|---|---|---|---|---|
| Ps(2pe-1) | ∞ | −0.0636595 | 2.0486(−7) | −0.0625 | Ps(2p) |
| ∞ | −0.06366 a | 2.05(−6) a | |||
| ∞ | −0.06366 b | 2.06(−7) b | |||
| 200 | −0.0587580 | 2.0717(−7) | −0.057622 | ||
| 100 | −0.0540528 | 2.1353(−7) | −0.052981 | ||
| 80 | −0.0517734 | 2.1794(−7) | −0.050746 | ||
| 60 | −0.0480825 | 2.2669(−7) | −0.047141 | ||
| 50 | −0.0452267 | 2.3461(−7) | −0.044363 | ||
| 40 | −0.0411039 | 2.4891(−7) | −0.04034 | ||
| 30 | −0.0346595 | 2.8003(−7) | −0.03439 | ||
| H(3pe-1) | ∞ | −0.0558317 | 6.8305(−7) | −0.0555555 | H(3p) |
| ∞ | −0.05583 a | 6.0(−7) a | |||
| ∞ | −0.05583 b | 7.04(−7) b | |||
| 200 | −0.0509363 | 7.2906(−7) | −0.0507082 | ||
| 100 | −0.0462736 | 1.0203(−6) | −0.046153 | ||
| 80 | −0.0440384 | 1.5356 (−6) | −0.0439795 | ||
| 60 | −0.0404682 | 3.9950(−6) | −0.0405044 | ||
| 50 | −0.0377501 | 1.4440(−5) | −0.037852 | ||
| H(4pe-1) | ∞ | −0.0355781 | 2.3006(−5) | −0.03125 | H(4p) |
| ∞ | −0.03558 a | 2.3(−5) a | |||
| ∞ | −0.03557 b | 2.30(−5) b | |||
| 100 | −0.0261443 | 2.2093(−5) | −0.0222278 | ||
| 50 | −0.0179889 | 1.8826(−5) | −0.0149401 | ||
| 40 | −0.0144318 | 1.6415(−5) | −0.0118705 | ||
| 30 | −0.0093060 | 1.0714(−5) | −0.0075338 | ||
| H(4pe-2) | ∞ | −0.03214774 | 9.5498(−6) | −0.03125 | H(4p) |
| ∞ | −0.03215 a | 9.5(−6) a | |||
| ∞ | −0.03214 b | 1.25(−5) b | |||
| 100 | −0.0228160 | 8.2815(−6) | −0.0222278 | ||
| 80 | −0.0207323 | 7.3668(−6) | −0.0203829 | ||
| 60 | −0.0175160 | 5.4189(−6) | −0.0174078 |
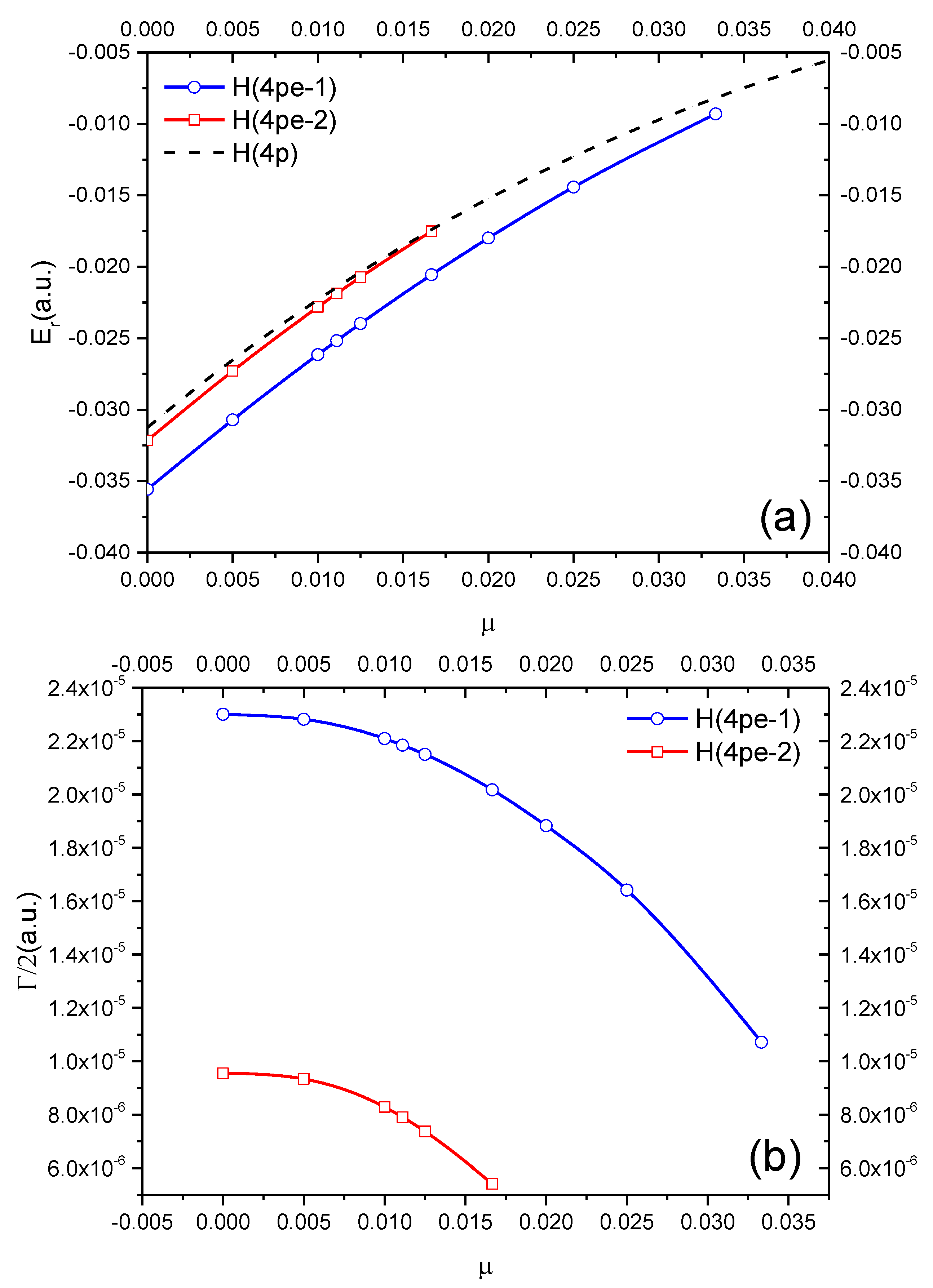
3.3. D-Wave Resonances with Unnatural Parity
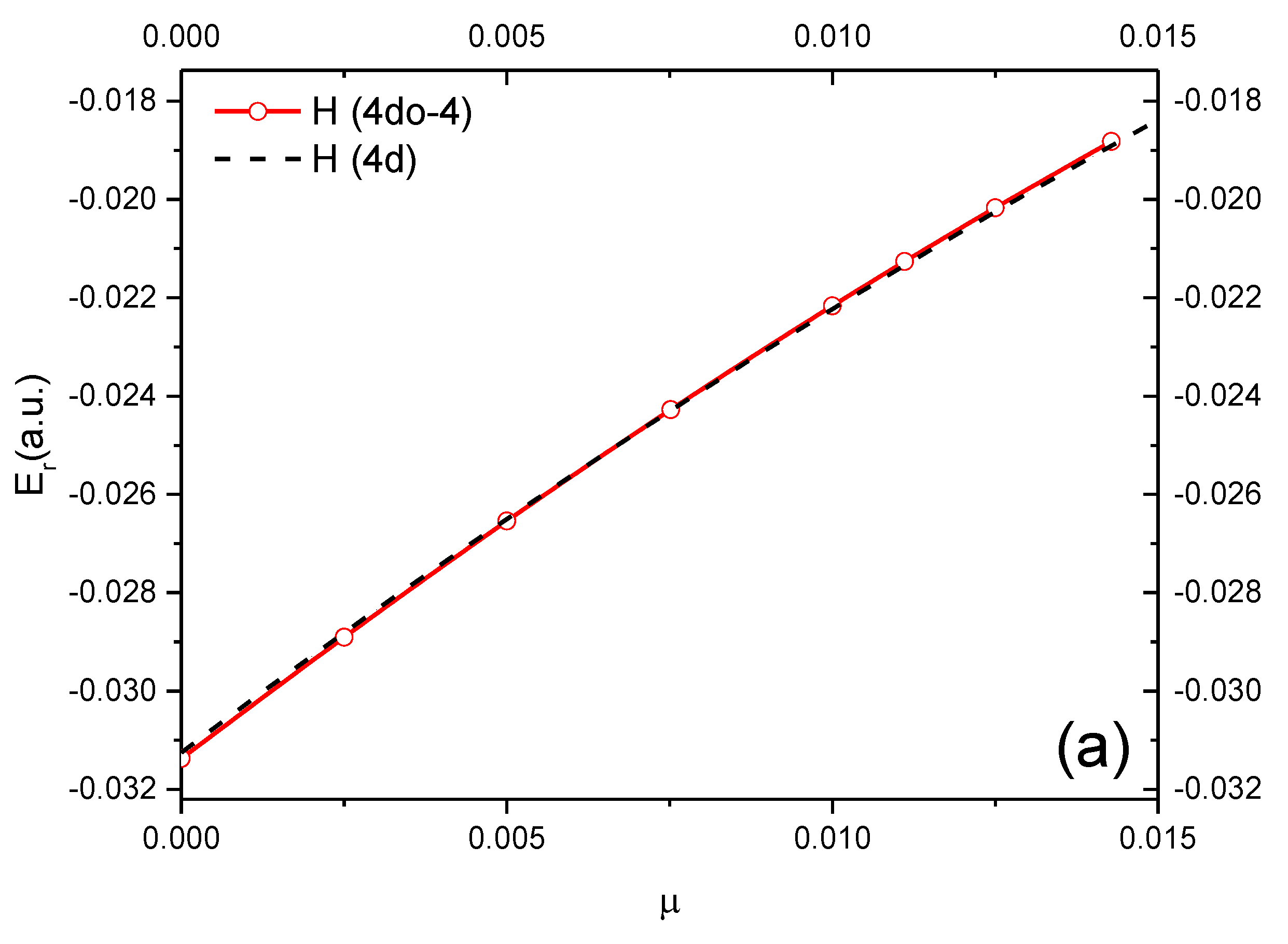
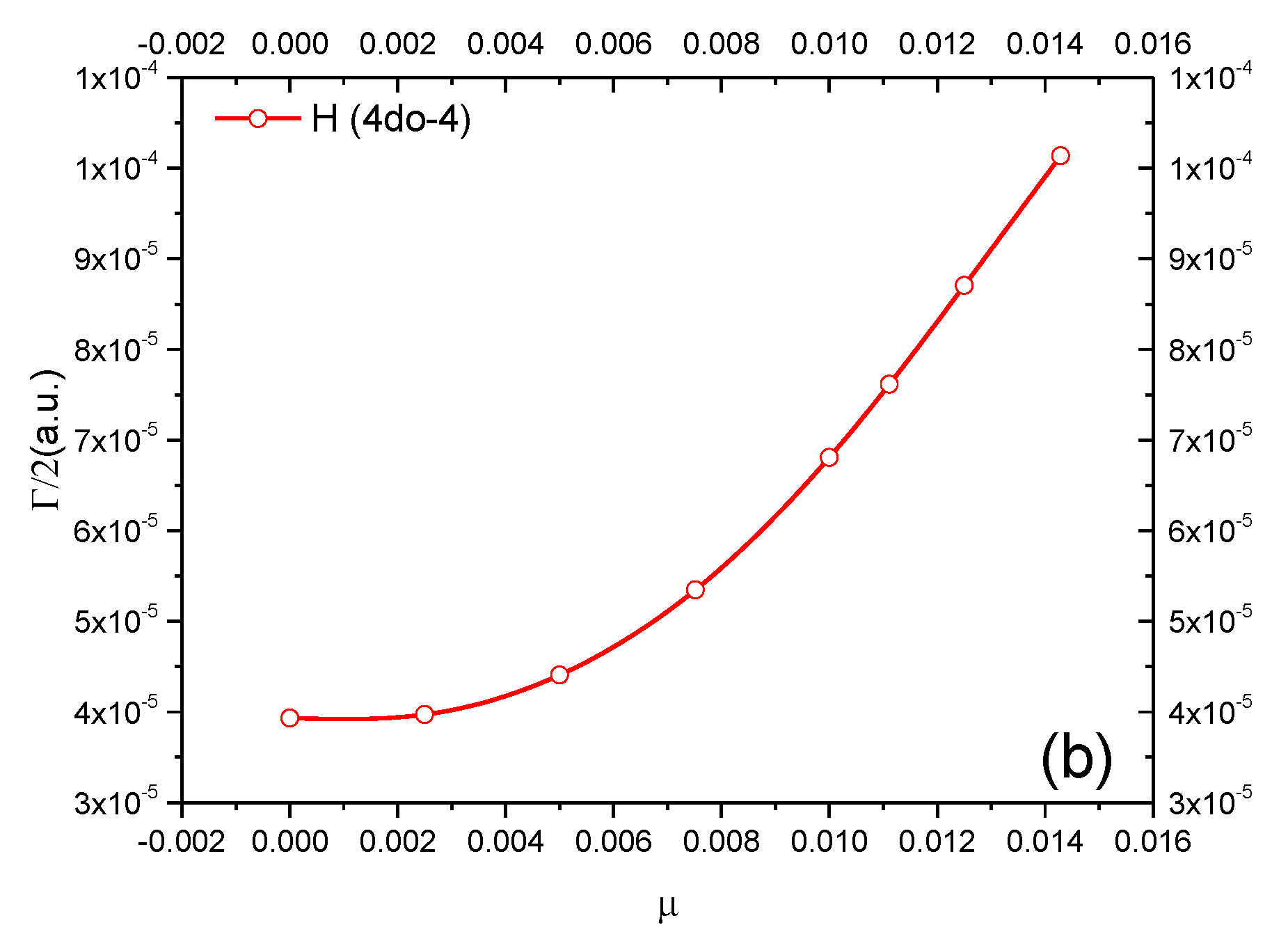
| D | Er (a.u.) | Γ/2 (a.u.) | ET | H or Ps State | |
|---|---|---|---|---|---|
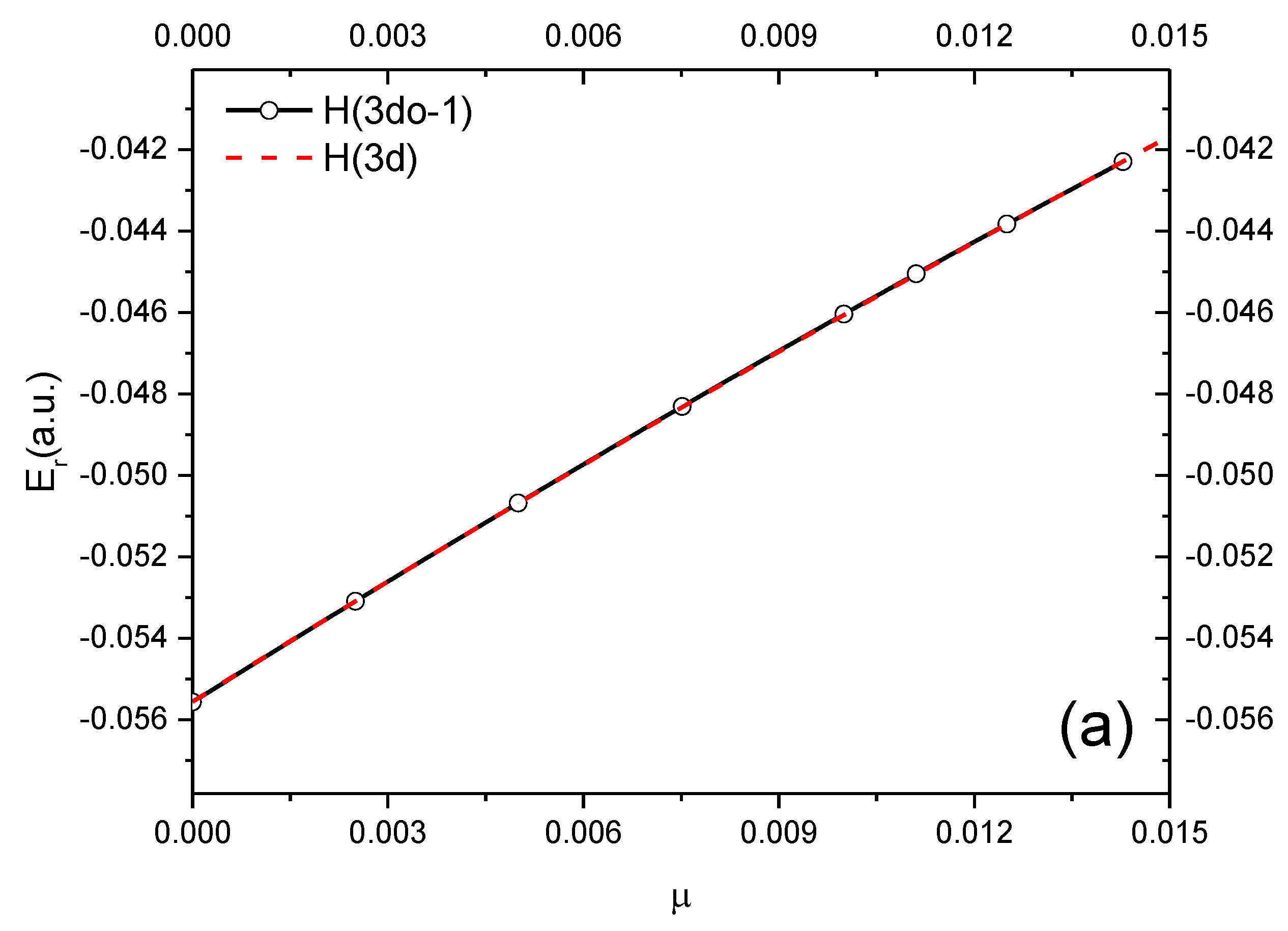
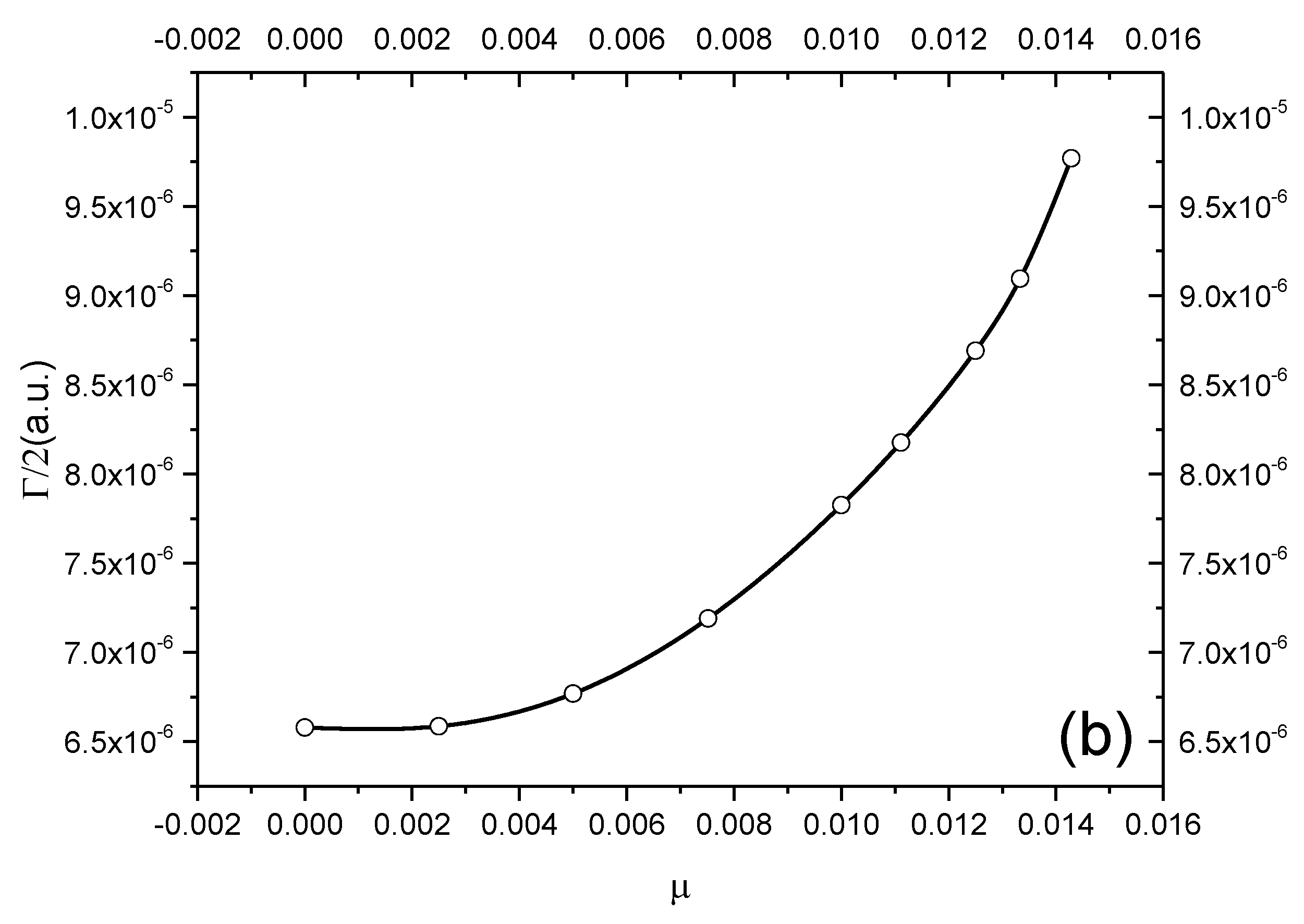
| H(3d°-1) | ∞ | −0.0555696 | 6.5795(−6) | −0.0555555 | H(3d) |
| ∞ | −0.05557 a | 5.0(−7) a | |||
| ∞ | −0.05558 b | 4.46(−6) b | |||
| 400 | −0.053096 | 6.5869(−6) | −0.0530880 | ||
| 200 | −0.050681 | 6.7693(−6) | −0.0506843 | ||
| 133 | −0.0483112 | 7.1902(−6) | −0.0483252 | ||
| 100 | −0.0460441 | 7.8265(−6) | −0.0460614 | ||
| 80 | −0.0438323 | 8.6915(−6) | −0.0438393 | ||
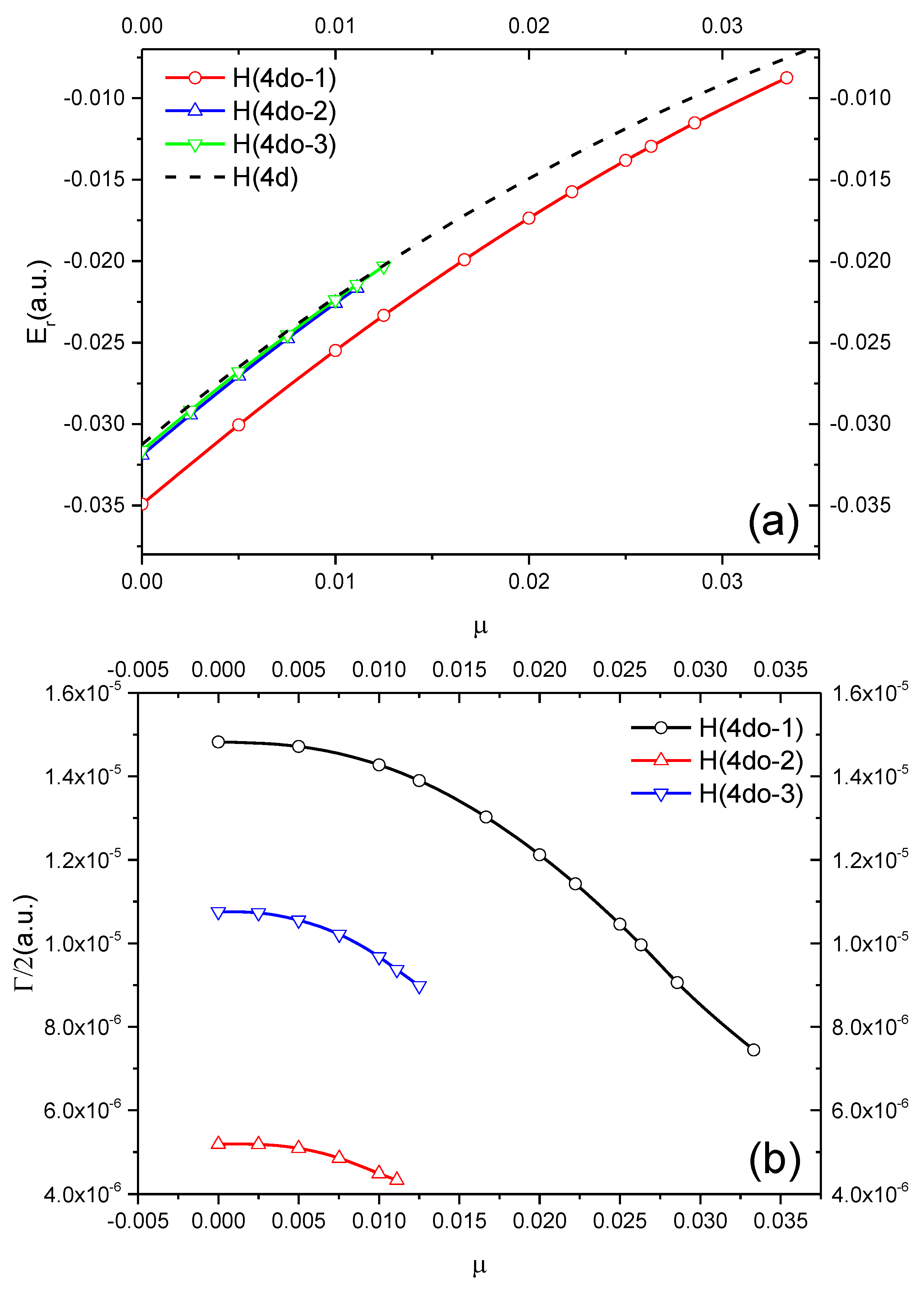
| H(4d°-1) | ∞ | −0.03491874 | 1.4823 (−5) | −0.03125 | H(4d) |
| ∞ | −0.03492 a | 1.5(−5) a | |||
| ∞ | −0.03487 b | 1.52(−5) b | |||
| 200 | −0.0300559 | 1.4717(−5) | −0.0265028 | ||
| 100 | −0.0233321 | 1.3897(−5) | −0.0222277 | ||
| 50 | −0.0173629 | 1.2121(−5) | −0.0149400 | ||
| 40 | −0.0138259 | 1.0457(−5) | −0.0118704 | ||
| 30 | −0.0087534 | 7.4452(−6) | −0.0075337 | ||
| H(4d°-2) | ∞ | −0.03189629 | 5.1879(−6) | −0.03125 | H(4d) |
| ∞ | −0.03190 a | 5.0(−6) a | |||
| ∞ | −0.03187 b | 5.5(−6) b | |||
| 200 | −0.0270512 | 5.0904(−6) | −0.0265028 | ||
| 100 | −0.0225821 | 4.4915(−6) | −0.0222277 | ||
| 80 | −0.0205107 | 4.2532(−6) | −0.0202541 | ||
| H(4d°-3) | ∞ | −0.0316152 | 1.0755(−5) | −0.03125 | H(4d) |
| ∞ | −0.03162 a | 1.1(−5) a | |||
| ∞ | −0.03157 b | 1.09(−5) b | |||
| 200 | −0.0268033 | 1.0556(−5) | −0.0265028 | ||
| 100 | −0.0223763 | 9.6732(−6) | −0.0222277 | ||
| 80 | −0.0203119 | 8.9832(−6) | −0.0202541 | ||
| H(4d°-4) | ∞ | −0.0313742 | 3.9334(−5) | −0.03125 | H(4d) |
| ∞ | −0.03138 a | 2.5(−6) a | |||
| ∞ | −0.03134 b | 1.29(−5) b | |||
| 200 | −0.0265396 | 4.4088(−5) | −0.0265028 | ||
| 100 | −0.0221649 | 6.8085(−5) | −0.0222277 | ||
| 80 | −0.0201687 | 8.7066(−5) | −0.0202541 | ||
| 70 | −0.0188192 | 1.0138(−4) | −0.0189080 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mittleman, M.H. Resonances in proton-hydrogen and positron-hydrogen scattering. Phys. Rev. 1966, 152, 76. [Google Scholar] [CrossRef]
- Doolen, G.D.; Nuttall, J.; Wherry, C.J. Evidence for a resonance in e+-H S-wave scattering. Phys. Rev. Lett. 1978, 40, 313. [Google Scholar] [CrossRef]
- Ho, Y.K.; Greene, C.H. On the positron-hydrogen resonances associated with the N = 2 positronium and N = 3 hydrogen thresholds. Phys. Rev. A 1987, 35, 3169–3171. [Google Scholar] [CrossRef] [PubMed]
- Ho, Y.K. Positron-hydrogen resonances associated with the N = 3 positronium and N = 4 hydrogen thresholds. Phys. Rev. A 1988, 38, 6424–6425. [Google Scholar] [CrossRef] [PubMed]
- Bhatia, A.K.; Drachman, R.J. Search for resonances in positron-atom systems. Phys. Rev. A 1990, 42, 5117. [Google Scholar] [CrossRef] [PubMed]
- Ho, Y.K. P-wave resonances in positron-hydrogen scattering. J. Phys. B 1990, 23, L419–L422. [Google Scholar] [CrossRef]
- Yan, Z.C.; Ho, Y.K. D-wave resonances in e+-H scattering. J. Phys. B At. Mol. Phys. 2002, 35, 1875. [Google Scholar] [CrossRef]
- Ho, Y.K.; Yan, Z.C. High partial wave resonances in positron hydrogen scattering. Phys. Rev. A 2004, 70, 032716. [Google Scholar] [CrossRef]
- Yan, Z.C.; Ho, Y.K. Resonances with unnatural parities in the positron-hydrogen system. Phys. Rev. A 2008, 77, 030701. [Google Scholar] [CrossRef]
- Shimamura, I.; Wakimoto, H.; Igarashi, A. Resonance states of unnatural parity in positronic atoms. Phys. Rev. A 2009, 80, 032708. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, Y.J.; Wang, Y.C. Unnatural parity resonance states in positron-excited hydrogen scattering. Chin. Phys. B 2012, 21, 123403. [Google Scholar] [CrossRef]
- Yu, R.M.; Cheng, Y.J.; Jiao, L.G.; Zhou, Y.J. Resonances in positron hydrogen scattering above the H (n = 2) Threshold. Chin. Phys. Lett. 2012, 29, 053401. [Google Scholar] [CrossRef]
- Umair, M.; Jonsel, S. Natural and unnatural parity resonance states in positron–hydrogen scattering. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 225001. [Google Scholar] [CrossRef]
- Ho, Y.K.; Yan, Z.C. High-angular momentum resonances in e+-He+ scattering. Phys. Rev. A 2002, 66, 062705. [Google Scholar] [CrossRef]
- Roy, U.; Ho, Y.K. S-wave resonances in positron-lithium scattering. J. Phys. B 2002, 35, 1875–1883. [Google Scholar] [CrossRef]
- Roy, U.; Ho, Y.K. P-wave resonances in e+-Li scattering. Nucl. Instrum. Methods B 2004, 221, 36–40. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K. S-wave resonances in e+-He scattering below the Ps (n = 2) excitation threshold. J. Phys. B 2004, 37, 3177–3186. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K. S-wave resonances in positron scattering from Na and K. Eur. Phys. J. D 2005, 35, 453. [Google Scholar] [CrossRef]
- Han, H.L.; Zhong, Z.X.; Zhang, X.Z.; Shi, T.Y. S-wave resonances in positron-lithium scattering below the Li (n = 4) thresholds. Phys. Rev. A 2008, 78, 044701. [Google Scholar] [CrossRef]
- Umair, M.; Jonsell, S. Resonances with natural and unnatural parities in positron-sodium scattering. Phys. Rev. A 2015, 92, 012706. [Google Scholar] [CrossRef]
- Ren, Z.Z.; Han, H.L.; Shi, T.Y. S-wave resonances in the positron–helium scattering. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 065204. [Google Scholar] [CrossRef]
- Ho, Y.K. The method of complex coordinate rotation and its applications to atomic collision processes. Phys. Rep. 1983, 99, 1. [Google Scholar] [CrossRef]
- Ho, Y.K. Resonances in positron-atom scattering. Hyperfine Interact. 1992, 73, 109–130. [Google Scholar]
- Ho, Y.K. Resonances in three-body atomic systems involving positrons. Chin. J. Phys. 1997, 35, 97. [Google Scholar]
- Ho, Y.K. Atomic resonances involving positrons. Nucl. Instrum. Methods Phys. Res. B 2008, 266, 516–521. [Google Scholar] [CrossRef]
- Ho, Y.K. Recent Advances in the theoretical methods and computational schemes for Investigations of resonances in few-body atomic systems. Few-Body Syst. 2013, 54, 31–37. [Google Scholar] [CrossRef]
- Debye, P.; Hückel, E. The theory of electrolytes. I. Lowering of freezing point and related phenomena. Phys. Z. 1923, 24, 185–206. [Google Scholar]
- Salzman, D. Atomic Physics in Hot Plasmas; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Ichimarn, S. Strongly coupled plasmas: High-density classical plasmas and degenerate electron liquids. Rev. Mod. Phys. 1982, 54, 1017. [Google Scholar] [CrossRef]
- Sil, A.N.; Canuto, S.; Mukherjee, P.K. Spectroscopy of confined atomic systems: Effect of plasma. Adv. Quantum Chem. 2009, 58, 115. [Google Scholar]
- Paul, S.; Ho, Y.K. Combined effect of Debye plasma environment and external electric field on hydrogen atom. Phys. Plasmas 2010, 17, 082704. [Google Scholar] [CrossRef]
- Lin, Y.C.; Lin, C.Y.; Ho, Y.K. Spectral data of helium atoms with screened Coulomb potentials using the B-spline approach. Phys. Rev. A 2012, 85, 042516. [Google Scholar] [CrossRef]
- Pandey, M.K.; Lin, Y.C.; Ho, Y.K. Investigation of charge transfer and ionization in He-like systems (Li+, Be2+, B3+, C4+, N5+, O6+)-hydrogen atom collisions in Debye plasmas. Phys. Plasmas 2013, 20, 022104. [Google Scholar] [CrossRef]
- Chang, T.N.; Fang, T.K.; Ho, Y.K. One- and two-photon ionization of hydrogen atom embedded in Debye plasmas. Phys. Plasmas 2013, 20, 092110. [Google Scholar] [CrossRef]
- Lin, Y.C.; Fang, T.K.; Ho, Y.K. Quantum entanglement for helium atom in the Debye plasmas. Phys. Plasmas 2015, 22, 032113. [Google Scholar]
- Pandey, M.K.; Lin, Y.C.; Ho, Y.K. An investigation of antiprotons collisions with positronium atom in Debye plasma environments. Phys. Plasmas 2015, 22, 052104. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K. Autoionizing 1Se resonance of H− in Debye plasma environments. Phys. Rev. E 2004, 70, 066411. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Ho, Y.K. Complex-scaling treatment for high-lying doubly excited resonances for screened Coulomb helium atom. Eur. Phys. J. D 2008, 49, 59–65. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Doubly excited resonance states of helium in exponential cosine-screened Coulomb potentials. Phys. Rev. A 2009, 79, 062514. [Google Scholar] [CrossRef]
- Jiao, L.G.; Ho, Y.K. Shape resonances in the electron-hydrogen system with screened Coulomb potentials. Phys. Rev. A 2013, 87, 052508. [Google Scholar] [CrossRef]
- Jiao, L.G.; Ho, Y.K. Doubly excited P-wave resonance states of H− in Debye plasmas. Phys. Plasmas 2013, 20, 083303. [Google Scholar] [CrossRef]
- Jiao, L.G.; Ho, Y.K. Doubly-excited 2p2 3Pe state of the hydrogen negative ion in Debye plasmas. J. Quant. Spectrosc. Radiat. Transf. 2014, 144, 27–35. [Google Scholar] [CrossRef]
- Jiang, P.; Kar, S.; Zhou, Y. Doubly excited states of the hydrogen negative ion and helium in astrophysical plasmas. Phys. Plasmas 2013, 20, 012126. [Google Scholar] [CrossRef]
- Rej, P.; Ghoshal, A. Positron impact excitations of hydrogen atom embedded in weakly coupled plasmas: Formation of Rydberg atoms. Phys. Plasmas 2014, 21, 093507. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Kamali, M.Z.M.; Ghoshal1, A.; Ratnavelu, K. Positron scattering from hydrogen atom embedded in dense quantum plasma. Phys. Plasmas 2013, 20, 083514. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, Y.; Wang, Y.C.; Zhou, Y. Positronium formation in positron-hydrogen collisions with Debye potentials. Phys. Plasmas 2012, 19, 063303. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K. S-wave resonances in the positron–hydrogen system with screened Coulomb potentials. J. Phys. B 2005, 38, 3299. [Google Scholar] [CrossRef]
- Chakraborty, S.; Ho, Y.K. Determination of resonance parameters for the e+-H system in Debye plasma environments using the complex-coordinate-rotation method. Phys. Rev. A 2008, 77, 014502. [Google Scholar] [CrossRef]
- Ning, Y.; Yan, Z.C.; Ho, Y.K. An investigation of resonances in e+-H scattering embedded in Debye plasm. Phys. Plasmas 2015, 22, 013302. [Google Scholar] [CrossRef]
- Jiang, Z.S.; Zhang, Y.Z.; Kar, S. Resonances in positron-hydrogen scattering in dense quantum plasmas. Phys. Plasmas 2015, 22, 052105. [Google Scholar] [CrossRef]
- Yan, Z.C.; Drake, G.W.F. On the evaluation of 2-electron integrals in Hylleraas coordinates. Chem. Phys. Lett. 1996, 259, 96. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, Y.; Yan, Z.-C.; Ho, Y.K. Natural and Unnatural Parity Resonance States in the Positron-Hydrogen System with Screened Coulomb Interactions. Atoms 2016, 4, 3. https://doi.org/10.3390/atoms4010003
Ning Y, Yan Z-C, Ho YK. Natural and Unnatural Parity Resonance States in the Positron-Hydrogen System with Screened Coulomb Interactions. Atoms. 2016; 4(1):3. https://doi.org/10.3390/atoms4010003
Chicago/Turabian StyleNing, Ye, Zong-Chao Yan, and Yew Kam Ho. 2016. "Natural and Unnatural Parity Resonance States in the Positron-Hydrogen System with Screened Coulomb Interactions" Atoms 4, no. 1: 3. https://doi.org/10.3390/atoms4010003
APA StyleNing, Y., Yan, Z.-C., & Ho, Y. K. (2016). Natural and Unnatural Parity Resonance States in the Positron-Hydrogen System with Screened Coulomb Interactions. Atoms, 4(1), 3. https://doi.org/10.3390/atoms4010003






