Quantum Entanglement and Shannon Information Entropy for the Doubly Excited Resonance State in Positronium Negative Ion
Abstract
:1. Introduction
2. Theoretical Method
2.1. The Stabilization Method
2.2. Von Neumann and Linear Entropies
2.3. Shannon Information Entropy
3. Results and Discussion
3.1. Resonance Energy, Width and Wave Function
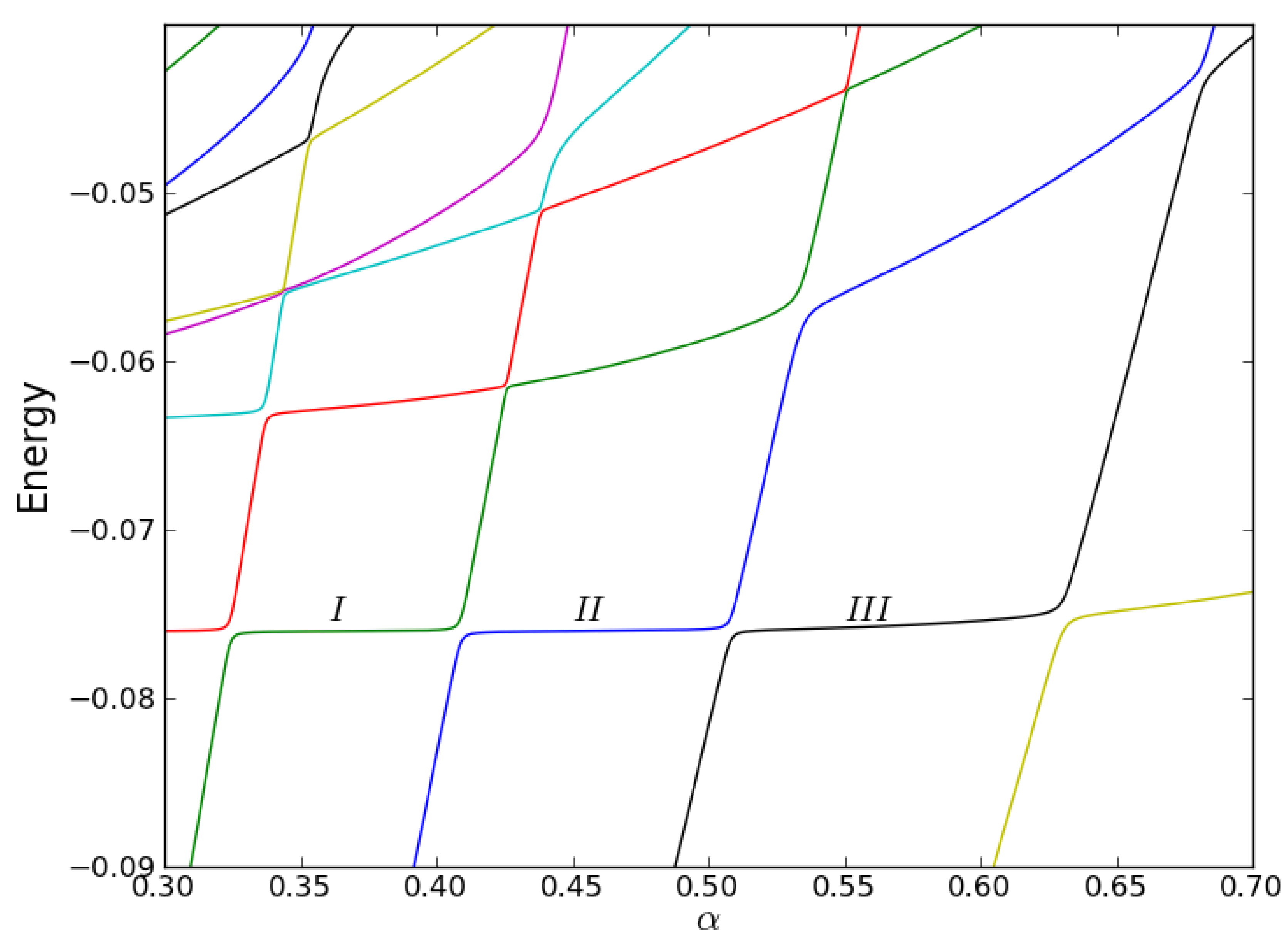
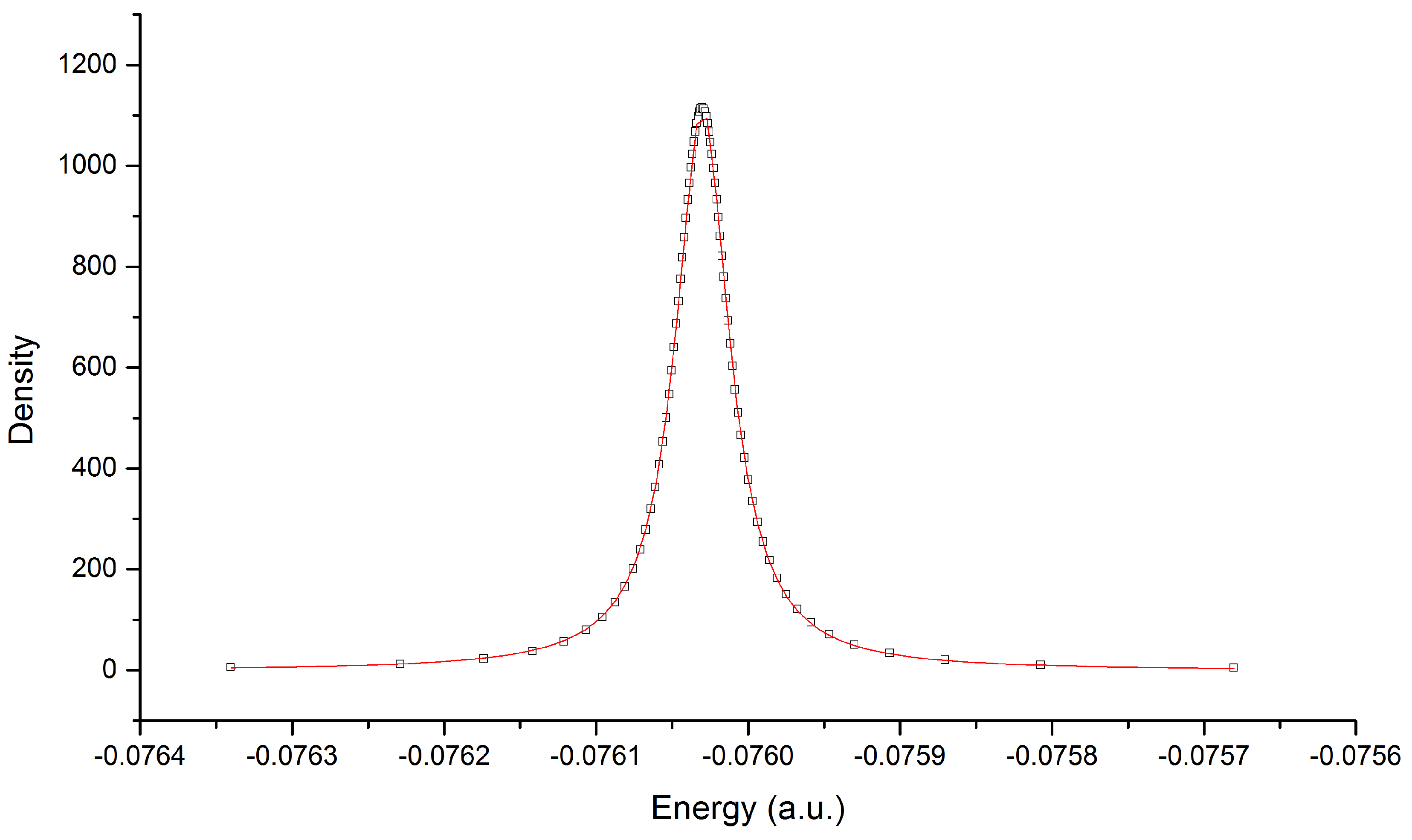
| Wave function | (a.u.) | (a.u.) | |||
|---|---|---|---|---|---|
| Reference [46] | −0.07603044 | 0.00004303 | |||
| Section I | −0.07603006 | 0.00004310 | 0.9999715 | 0.516517 | 1.684376 |
| Section II | −0.07602959 | 0.00004421 | 0.9997358 | 0.516568 | 1.684917 |
| Section III | −0.07602008 | 0.00008226 | 0.9831704 | 0.517067 | 1.686998 |
3.2. von Neumann Entropy and Linear Entropy
3.3. Shannon Entropy for Doubly Excited State of Ps
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dehesa, J.S.; Koga, T.; Yanez, R.J.; Plastino, A.R.; Esquivel, R.O. Quantum entanglement in helium. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 015504. [Google Scholar] [CrossRef]
- Dehesa, J.S.; Koga, T.; Yanez, R.J.; Plastino, A.R.; Esquivel, R.O. Corrigendum: Quantum entanglement in helium. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 239501. [Google Scholar] [CrossRef]
- Benenti, G.; Siccardi, S.; Strini, G. Entanglement in helium. Euro. Phys. J. D 2013, 67, 83. [Google Scholar] [CrossRef]
- Koscik, P. Entanglement in S states of two-electron quantum dots with Coulomb impurities at the center. Phys. Lett. A 2013, 377, 2393–2397. [Google Scholar] [CrossRef]
- Koscik, P.; Okopinska, A. Entanglement Entropies in the Ground States of Helium-Like Atoms. Few-Body Syst. 2014, 55, 1151–1157. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, H.; Kais, S. Entanglement and Electron Correlation in Quantum Chemistry Calculations. J. Mod. Opt. 2006, 53, 2543–2558. [Google Scholar] [CrossRef]
- Hofer, T.S. On the basis set convergence of electron-electron entanglement measures: Helium-like systems. Front. Chem. 2003. [Google Scholar] [CrossRef] [PubMed]
- Tichy, M.C.; Mintert, F.; Buchleitner, A. Essential entanglement for atomic and molecular physics. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 192001. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Peng, H.T.; Ho, Y.K. Entanglement for Excited States of Ultracold Bosonic Atoms in One-Dimensional Harmonic Traps with Contact Interaction. Mod. Phys. Lett. B 2015, in press. [Google Scholar]
- Peng, H.T.; Ho, Y.K. Statistical Correlations of the N-particle Moshinsky Model. Entropy 2015, 17, 1882–1895. [Google Scholar] [CrossRef]
- Lin, Y.C.; Lin, C.Y.; Ho, Y.K. Spatial entanglement in two-electron atomic systems. Phys. Rev. A 2013, 87, 022316. [Google Scholar] [CrossRef]
- Lin, Y.C.; Ho, Y.K. Quantum entanglement for two electrons in the excited states of helium-like systems. Can. J. Phys. 2015, 93, 646–653. [Google Scholar] [CrossRef]
- Lin, C.H.; Lin, Y.C.; Ho, Y.K. Quantification of linear entropy for quantum entanglement in He, H− and Ps− ions using highly-correlated Hylleraas functions. Few-Body Syst. 2013, 54, 2147–2153. [Google Scholar] [CrossRef]
- Lin, C.H.; Ho, Y.K. Quantification of entanglement entropy in helium by the Schmidt-Slater decomposition method. Few-Body Syst. 2014, 55, 1141–1149. [Google Scholar] [CrossRef]
- Lin, C.H.; Ho, Y.K. Calculation of von Neumann entropy for hydrogen and positronium negative ions. Phys. Lett. A 2014, 378, 2861–2865. [Google Scholar] [CrossRef]
- Lin, C.H.; Ho, Y.K. Quantification of entanglement entropies for doubly excited states in Helium. Few-Body Syst. 2015, 56, 157–163. [Google Scholar] [CrossRef]
- Lin, C.H.; Ho, Y.K. Shannon information entropy in position space for two-electron atomic systems. Chem. Phys. Lett. 2015, 633, 261–264. [Google Scholar] [CrossRef]
- Lin, Y.C.; Fang, T.K.; Ho, Y.K. Quantum entanglement for helium atom in the Debye plasmas. Phys. Plasmas 2015, 22, 032113. [Google Scholar] [CrossRef]
- Cuartas, J.P.R.; Sanz-Vicario, J.L. Information and entanglement measures applied to the analysis of complexity in doubly excited states of helium. Phys. Rev. A 2015, 91, 052301. [Google Scholar] [CrossRef]
- Kuros, A.; Okopinska, A. Entanglement Properties of the Two-Electron Quasi-One Dimensional Gaussian Quantum Dot. Few-Body Syst. 2015. [Google Scholar] [CrossRef]
- Wheeler, J.A. Polyelectrons. Ann. N. Y. Acad. Sci. 1946, 48, 219–238. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Drachman, R.J. Polarizabilities of the Ps negative ion. Phys. Rev. A 2007, 75, 062510. [Google Scholar] [CrossRef]
- Frolov, A.M. Annihilation, bound state properties and photodetachment of the positronium negatively charged ion. Chem. Phys. Lett. 2015, 626, 49–54. [Google Scholar] [CrossRef]
- Ho, Y.K.; Kar, S. Complex-scaling calculations for doubly excited resonances in Ps− interacting with screened coulomb (Yukawa) potentials. Few-Body Syst. 2012, 53, 437–443. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K. Shape resonance in the Ps− system. Phys. Rev. A 2012, 86, 014501. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Autoionization states of the positronium negative ion in exponential cosine-screened Coulomb potentials. Euro. Phys. J. D 2010, 56, 151–156. [Google Scholar] [CrossRef]
- Ho, Y.K. Doubly excited states of positronium negative ions. Hyperfine Interactions 1994, 89, 401–406. [Google Scholar] [CrossRef]
- Ho, Y.K. Resonances in positronium negative ions. In Proceedings of the Temkin-Drachman Retirement Symposium, Greenbelt, MD, USA, 18 November 2005; Bhatia, A.K., Ed.; p. 111.
- Ho, Y.K. Atomic resonances involving positrons. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2008, 266, 516–521. [Google Scholar] [CrossRef]
- Mills, A.P., Jr. Observation of the positronium negative ion. Phys. Rev. Lett. 1981, 46, 717–720. [Google Scholar] [CrossRef]
- Nagashima, Y. Experiments on positronium negative ions. Phys. Rep. 2014, 545, 95–123. [Google Scholar] [CrossRef]
- Ho, Y.K. Autoionization states of the positronium negative ion. Phys. Rev. A 1979, 19, 2347–2352. [Google Scholar] [CrossRef]
- Hu, C.Y.; Kvitsinsky, A.A. Resonances in e−-Ps elastic scattering via a direct solution of the three-body scattering problem. Phys. Rev. A 1994, 50, 1924–1926. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Shakeshaft, R. S-wave resonances of the negative positronium ion and stability of a system of two electrons and an arbitrary positive charge. Phys. Rev. A 2005, 71, 052505. [Google Scholar] [CrossRef]
- Mills, A.P., Jr. Cross section for photoionization of the positronium negative ion at the lowest Feshbach resonance. Can. J. Phys. 2013, 91, 751–755. [Google Scholar] [CrossRef]
- Mandelshtam, V.; Ravuri, T.; Taylor, H. Calculation of the density of resonance states using the stabilization method. Phys. Rev. Lett. 1993, 70, 1932–1935. [Google Scholar] [CrossRef] [PubMed]
- Tan, S.; Ho, Y.K. Determination of Resonance Energy and Width by Calculation of the Density of Resonance States Using the Stabilisation Met hod. Chin. J. Phys. 1998, 35, 701–707. [Google Scholar]
- Chakraborty, S.; Ho, Y.K. Autoionization resonance states of two-electron atomic systems with finite spherical confinement. Phys. Rev. A 2011, 84, 032515. [Google Scholar] [CrossRef]
- Ho, Y.K. Recent advances in the theoretical methods and computational schemes for investigations of resonances in few-body atomic systems. Few-Body Syst. 2013, 54, 31–37. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Nagy, A.; Liu, S. Local wave-vector, Shannon and Fisher information. Phys. Lett. A 2008, 372, 1654–1656. [Google Scholar] [CrossRef]
- Guevara, N.L.; Sagar, R.P.; Esquivel, R.O. Shannon-information entropy sum as a correlation measure in atomic systems. Phys. Rev. A 2003, 67, 012507. [Google Scholar] [CrossRef]
- Sen, K.D. Characteristic features of Shannon information entropy of confined atoms. J. Chem. Phys. 2005. [Google Scholar] [CrossRef] [PubMed]
- Bialynicki-Birula, I.; Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Commun. Mathematical Phys. 1975, 44, 129–132. [Google Scholar] [CrossRef]
- Ho, Y.K. Resonances in three-body atomic systems involving positrons. Chin. J. Phys. 1997, 35, 97–120. [Google Scholar]
- Ho, Y.K. The method of complex coordinate rotation and its applications to atomic collision processes. Phys. Rept. 1983, 99, 1–68. [Google Scholar] [CrossRef]
- Cooper, J.W.; Fano, U.; Prats, F. Classification of Two-Electron Excitation Levels of Helium. Phys. Rev. Lett. 1963, 10, 518–521. [Google Scholar] [CrossRef]
- Herrick, D.R.; Sinanoglu, O. Comparison of doubly-excited helium energy levels, isoelectronic series, autoionization lifetimes, and group-theoretical configuration-mixing predictions with large-configuration-interaction calculations and experimental spectra. Phys. Rev. A 1975, 11, 97–110. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-H.; Ho, Y.K. Quantum Entanglement and Shannon Information Entropy for the Doubly Excited Resonance State in Positronium Negative Ion. Atoms 2015, 3, 422-432. https://doi.org/10.3390/atoms3030422
Lin C-H, Ho YK. Quantum Entanglement and Shannon Information Entropy for the Doubly Excited Resonance State in Positronium Negative Ion. Atoms. 2015; 3(3):422-432. https://doi.org/10.3390/atoms3030422
Chicago/Turabian StyleLin, Chien-Hao, and Yew Kam Ho. 2015. "Quantum Entanglement and Shannon Information Entropy for the Doubly Excited Resonance State in Positronium Negative Ion" Atoms 3, no. 3: 422-432. https://doi.org/10.3390/atoms3030422
APA StyleLin, C.-H., & Ho, Y. K. (2015). Quantum Entanglement and Shannon Information Entropy for the Doubly Excited Resonance State in Positronium Negative Ion. Atoms, 3(3), 422-432. https://doi.org/10.3390/atoms3030422






