Validation and Implementation of Uncertainty Estimates of Calculated Transition Rates
Abstract
:1. Introduction
2. Theoretical Background
2.1. Transition Rates and Line Strengths
2.2. Accuracy Estimates
3. Statistical Analysis of Calculated Transition Rates in O IV
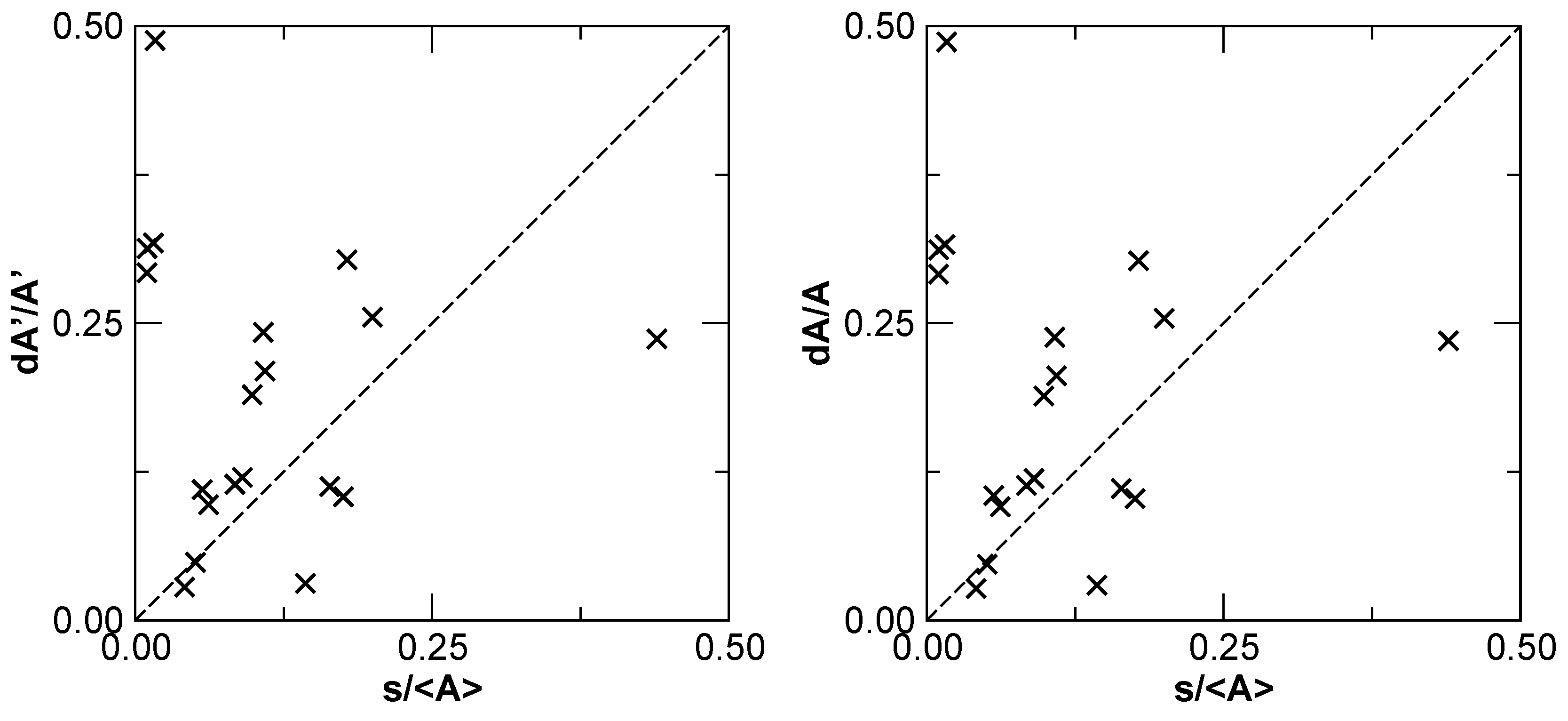
3.1. -Allowed Transitions

3.2. Intercombination Transitions
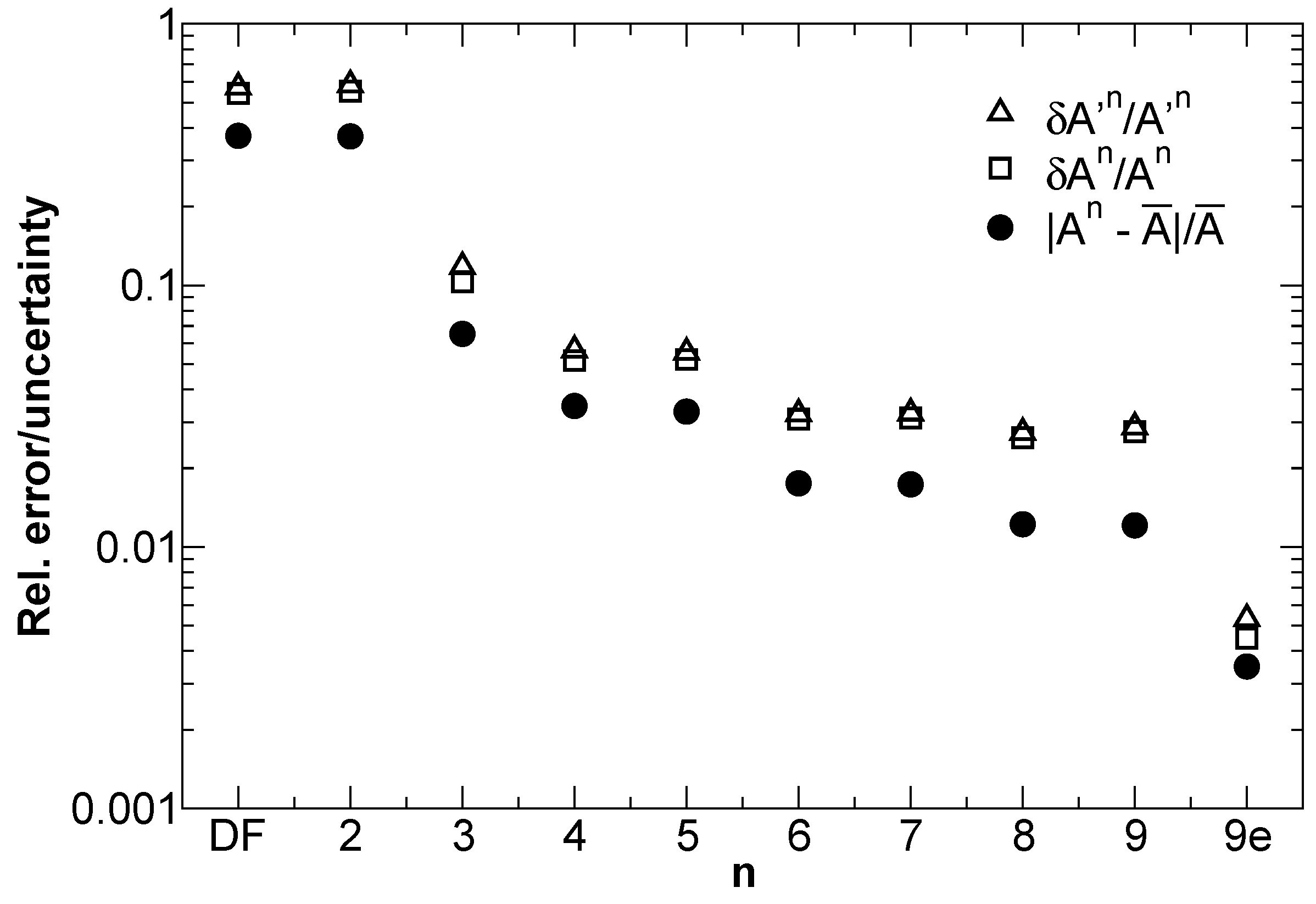
4. Uncertainty Analysis of Calculated Transition Rates for Increasing Orbital Sets in O IV
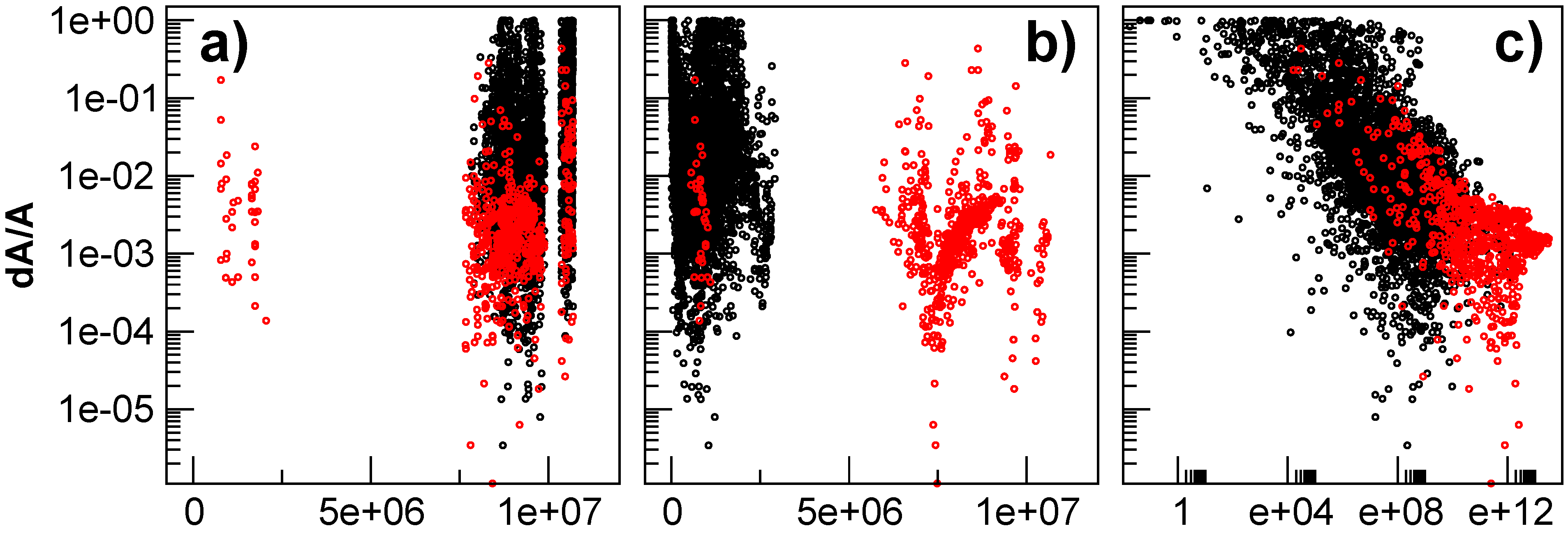
5. Implementation of Uncertainty Estimates in Carbon-Like Fe XXI
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ekman, J.; Jönsson, P.; Gustafsson, S.; Hartman, H.; Gaigalas, G.; Godefroid, M.R.; Froese Fischer, C. Calculations with spectroscopic accuracy: Energies, transition rates, and Landé gJ-factors in the carbon isoelectronic sequence from Ar XIII to Zn XXV. Astron. Astrophys. 2014, 564, A24. [Google Scholar] [CrossRef]
- Jönsson, P.; Ekman, J.; Gustafsson, S.; Hartman, H.; Karlsson, L.B.; du Rietz, R.; Gaigalas, G.; Godefroid, M.R.; Froese Fischer, C. Energy levels and transition rates for the boron isoelectronic sequence: Si X, Ti XVIII–Cu XXV. Astron. Astrophys. 2013, 559, A100. [Google Scholar] [CrossRef]
- Froese Fischer, C.; Verdebout, S.; Godefroid, M.; Rynkun, P.; Jönsson, P.; Gaigalas, G. Doublet-quartet energy separation in boron: A partitioned-correlation-function-interaction method. Phys. Rev. A 2013, 88, 062506. [Google Scholar] [CrossRef]
- Kramida, A.E.; Brown, C.M.; Feldman, U.; Reader, J. Extended EUV and UV spectrum of Ne II. Phys. Scr. 2006, 74, 156–167. [Google Scholar] [CrossRef]
- Veza, D.; Sansonetti, C.J.; Salit, M.L.; Travis, J.C. Wave numbers and pressure-induced shifts of Ar I atomic lines measured by Fourier transform spectroscopy. J. Phys. B-At. Mol. Opt. Phys. 2012, 45, 115001. [Google Scholar] [CrossRef]
- Amaro, P.; Schlesser, S.; Guerra, M.; le Bigot, E.-O.; Isac, J.-M.; Travers, P.; Santos, J.P.; Szabo Csilla, I.; Gumberidze, A.; Indelicato, P. Absolute measurement of the relativistic magnetic dipole transition energy in heliumlike argon. Phys. Rev. Lett. 2012, 109, 043005. [Google Scholar] [CrossRef] [PubMed]
- Niering, M.; Holzwarth, R.; Reichert, J.; Pokasov, P.; Udem, Th.; Weitz, M.; Hansch, T.W.; Lemonde, P.; Santarelli, G.; Abgrall, M.; et al. Measurement of the hydrogen 1S-2S transition frequency by phase coherent comparison with a microwave cesium fountain Clock. Phys. Rev. Lett. 2000, 84, 5496–5499. [Google Scholar] [CrossRef] [PubMed]
- Young, P.R.; Feldman, U.; Lobel, A. Forbidden and intercombination lines of RR telescopii: Wavelength measurements and energy levels. Astrophys. J. 2011, 196, 23. [Google Scholar] [CrossRef]
- Weinhold, F. Calculation of upper and lower bounds to oscillator strengths. J. Chem. Phys. 1971, 54, 1874–1880. [Google Scholar] [CrossRef]
- Roginsky, D.V.I.; Weiss, A.W. Calculation of tighter error bounds for theoretical atomic-oscillator strengths. Phys. Rev. A 1988, 38, 1760–1766. [Google Scholar] [CrossRef] [PubMed]
- Sims, J.S.; Hagstrom, S.A.; Rumble, J.R., Jr. Upper and lower bounds to atomic properties. III. Li oscillator strengths for various 2S-2P transitions. Phys. Rev. A 1976, 13, 242. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Yu.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (version 5.1), [Online]; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013. Available online: http://physics.nist.gov/asd (accessed on 27 January 2014).
- Froese Fischer, C.; Brage, T.; Jönsson, P. Computational Atomic Structure: An MCHF Approach; Institute of Physics Publishing: Bristol and Philadelphia, UK and USA, 1997. [Google Scholar]
- Grant, I.P. Relativistic Quantum Theory of Atoms and Molecules: Theory and Computation; Springer: New York, USA, 2007. [Google Scholar]
- Froese Fischer, C.; Godefroid, M.R. Programs for computing LS and LSJ transitions from MCHF wave functions. Comput. Phys. Commun. 1991, 64, 501–519. [Google Scholar] [CrossRef]
- Grant, I.P. Gauge invariance and relativistic radiative transitions. J. Phys. B-At. Mol. Opt. Phys. 1974, 7, 1458. [Google Scholar] [CrossRef]
- Froese Fischer, C. Evaluating the accuracy of theoretical transition data. Phys. Scr. 2009. [Google Scholar] [CrossRef]
- Froese Fischer, C.; Tachiev, G. MCHF/MCDHF Collection, Version 2, Ref. No. 3, 40, National Institute of Standards and Technology, 2011. Available online: http://physics.nist.gov/mchf (accessed on 12 May 2014).
- Corrégé, G.; Hibbert, A. Transitions in C II, N III, and O IV. At. Data Nucl. Data Tables 2004, 86, 19–34. [Google Scholar] [CrossRef]
- Koc, K. Ab initio calculation of 1s22ℓ3ℓ′4ℓ′′ energy levels and E1 transition probabilities for O3+. J. Phys. B-At. Mol. Opt. Phys. 2004, 37, 3821–3835. [Google Scholar] [CrossRef]
- Rynkun, P.; Jönsson, P.; Gaigalas, G.; Froese Fischer, C. Energies and E1, M1, E2, M2 transition rates for states of the 2s22p, 2s2p2, and 2p3 configurations in boron-like ions between N III and Zn XXVI. At. Data and Nucl. Data Tables 2012, 98, 481–556. [Google Scholar] [CrossRef]
- Tayal, S.S. Breit-Pauli R-matrix calculation for electron collision rates in O IV. ApJS 2006, 166, 634–649. [Google Scholar] [CrossRef]
- Aggarwal, K.M.; Keenan, F.P. Energy levels, radiative rates, and excitation rates for transitions in O IV. Astron. Astrophys. 2008, 486, 1053–1067. [Google Scholar] [CrossRef]
- Liang, G.Y.; Badnell, N.R.; Zhao, G. R-matrix elecron-impact excitation data for the B-like iso-electronic sequence. Astron. Astrophys. 2012, 547, A87. [Google Scholar] [CrossRef]
- Drake, G.W.F. Relativistic corrections to spin-forbidden electric-dipole transitions. J. Phys. B-At. Mol. Phys. 1976, 9, L169–L171. [Google Scholar] [CrossRef]
- Pachucki, K. Theory of forbidden transitions in light atoms. Phys. Rev. A 2003, 67, 012504. [Google Scholar] [CrossRef]
- Jönsson, P.; Gaigalas, G.; Bieroń, J.; Froese Fischer, C.; Grant, I.P. New version: Grasp2K relativistic atomic structure package. Comput. Phys. Commun. 2013, 184, 2197–2203. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ekman, J.; Godefroid, M.R.; Hartman, H. Validation and Implementation of Uncertainty Estimates of Calculated Transition Rates. Atoms 2014, 2, 215-224. https://doi.org/10.3390/atoms2020215
Ekman J, Godefroid MR, Hartman H. Validation and Implementation of Uncertainty Estimates of Calculated Transition Rates. Atoms. 2014; 2(2):215-224. https://doi.org/10.3390/atoms2020215
Chicago/Turabian StyleEkman, Jörgen, Michel R. Godefroid, and Henrik Hartman. 2014. "Validation and Implementation of Uncertainty Estimates of Calculated Transition Rates" Atoms 2, no. 2: 215-224. https://doi.org/10.3390/atoms2020215
APA StyleEkman, J., Godefroid, M. R., & Hartman, H. (2014). Validation and Implementation of Uncertainty Estimates of Calculated Transition Rates. Atoms, 2(2), 215-224. https://doi.org/10.3390/atoms2020215



