Abstract
In exotic atomic systems with hadronic constituent particles, it is notoriously difficult to estimate the strong-interaction correction to energy levels. It is well known that, due to the strength of the nuclear interaction, the problem cannot be solved using Wigner–Brillouin perturbation theory alone. Recently, high-angular-momentum Rydberg states of exotic atomic systems with hadronic constituents have been identified as promising candidates in the search for new physics in the low-energy sector of the Standard Model. We thus derive a generalized Deser–Trueman formula for the induced energy shift for a general hydrogenic bound state with principal quantum number n and orbital angular momentum quantum number ℓ, and we find that the energy shift is given by the formula , where , , , is the Hartree energy, is the hadronic radius and is the generalized Bohr radius. The square of the double factorial, , in the denominator implies a drastic suppression of the effect for higher angular momenta.
1. Introduction
Recently, the non-S Rydberg states of exotic hadronic atomic systems have been proposed as candidates in the search for new physics effects as additions to the low-energy sector [1,2]. Hence, the focus in the current work is on the strong-interaction energy correction for bound states of hadronic bound systems with nonvanishing angular momenta, where the strong-interaction shift is so small that it is otherwise neglected in many treatments of exotic systems (see Section 5 of Ref. [3]). However, in the search for new physics, it is still necessary to estimate the strong-interaction shift because it can be an obstacle to the detection of new physics effects in the extreme electromagnetic fields encountered in exotic hadronic bound systems [1,2].
Examples of exotic bound systems (see also the comprehensive discussion in Appendix A) addressed in the literature include antiprotonic atoms [1]; K-mesic atoms (see Ref. [4]) such as those involving a negatively charged K meson and a proton (–p) or deuteron (–d); and protonium, the bound system of a proton and its antiparticle (see Refs. [5,6,7]). The DIRAC collaboration at CERN has focused on the ground-state lifetime of pionium (the atom; see Refs. [8,9]) and the bound pion–kaon system [10]. The pionic hydrogen collaboration at the Paul Scherrer Institute (PSI) has focused on pionic hydrogen measurements (see Ref. [11]) and pionic deuterium (Ref. [12]). The DEAR (DAΦNE Exotic Atom Research) collaboration at LNF/INFN has investigated kaonic hydrogen [13], including transitions of kaonic hydrogen from states of higher excitation to the ground state (the so-called , and lines; see Ref. [13]). In general, the search for new physics effects [14] on the basis of Rydberg states of two-body exotic hadronic atomic systems is very promising because the extreme field strengths experienced at a distance equal to the generalized Bohr radius can exceed the Schwinger critical field strength (for muonic bound systems, see Figure 3 of Ref. [15]). Thus, while the term “Rydberg state” can, strictly speaking, refer to any excited state of a bound Coulomb quantum system, we focus the present study on states with nonvanishing angular momenta; in particular, we have in mind so-called “circular Rydberg states” with the maximum angular momentum for a given principal quantum number, and nearly circular states. Indeed, the new approach outlined in Refs. [1,2] focuses on non-S states that provide us with an almost ideal scenario of extreme electric field strength, combined with greatly reduced nuclear-size and strong-interaction effects. It is of crucial importance to estimate the effects of the strong interaction for non-S states. The strong interaction becomes dominant at distances commensurate with . A universally applicable, approximate formula for the estimation of the strong-interaction effects [4,5,6,7] is thus highly desirable. This necessitates a generalization of the Deser–Trueman formulas [4,16,17,18] for arbitrary excited states, which is the subject of the current paper.
According to Section 3 of Ref. [7], a suitable approximation for the incorporation of strong-interaction effects into the discussion of energy levels of electromagnetically bound particle–antiparticle systems consists of the addition of an intense, short-range (radius ) potential, which can be assumed to approximate a hard-sphere potential for . Such intense, short-range hard-sphere (infinitely intense) potentials, when added to a long-range Coulomb potential, cannot be described on the basis of Wigner–Brillouin perturbation theory (for a recent overview, see Chap. 5 of Ref. [19]). This is because the expectation value of a hard-sphere potential (which assumes an infinite value inside the core) is infinite for any bound state in a Coulomb potential. Rather, one needs to apply so-called radius perturbation theory where the expansion parameter is the ratio of the radius of the hard-sphere potential to the Bohr radius .
The calculation of the shift due to the hard-sphere potential has been considered by Deser et al. (see Ref. [16]) and Trueman (see Ref. [4]), and the result is therefore commonly referred to as the Deser–Trueman formula (see Refs. [20,21,22,23,24,25,26,27]. It is generally assumed [see, e.g., Equation (3.69) of Ref. [7] that the energy perturbation takes the form
where remains to be determined.
The problem of the calculation of arises in hadronic bound systems such as protonium [5,6,7,28] and in other bound systems where hadrons are the constituent particles. (The concept of the Bohr radius finds a natural generalization in these systems as , where is the reduced mass of the two-body bound quantum system.) It is well known that the nucleon–antinucleon potential is more attractive than the nucleon–nucleon potential, in view of the fact that the -meson exchange reverses its sign and becomes attractive [29]. For Coulombic bound systems where the constituent particles are hadrons and annihilation is involved, this means that, for a very close approach , the strong interaction leads to immediate annihilation of the particles. The wave function of the Coulombic bound system thus needs to vanish inside the range of the strong interaction, typically assumed to be on the order of . Therefore, the strong-interaction potential, on the scale of the Bohr radius, acts, somewhat counterintuitively, as a hard-sphere potential. One thus needs to calculate the perturbed energies under the assumption that the wave functions vanish for , as induced by the potential . Hence, again, somewhat counterintuitively, the strong-interaction correction shifts the bound-state energies of protonium upwards in energy, i.e., it reduces the modulus of the binding energy.
The need to calculate was recognized in the early days of the analysis of mesic atoms [4,7,16,18,28]. Our goals here are to derive a formula for that is valid for general quantum numbers n and ℓ and to verify the result based on numerical calculations (see Section 2.2). The latter require the use of extended-precision arithmetic because, for higher ℓ, the perturbation becomes very small as a result of scaling with (see Section 3). Conclusions are drawn in Section 4.
2. Derivation
2.1. Mathematical Foundations
Let us now discuss the mathematical details; these are straightforward but worth reviewing for reference. We consider the physical system where a short-range hard-sphere potential perturbs an attractive Coulomb potential ,
Here, e is the electron charge, is the vacuum permittivity, c is the speed of light, and ℏ is Planck’s unit of action. Notably, by contrast, the perturbative potentials induced by the nuclear finite-size effect remain finite near the origin and allow a perturbative treatment (see Chap. 5 of Ref. [19]). The infinite character of the potential makes the current treatment more challenging. The (generalized) Hartree energy is , and is the Bohr radius as defined earlier. It is interesting to note that discontinuities in binding potentials, such as the one encountered for at , are not unique to strong-interaction corrections but also occur in the context of spherical quantum reflection traps [30]. For an exotic two-body bound state, the Bohr energy levels are given by
The bound-state wave functions are well known to have the form , where is the spherical harmonic and the radial wave function depends on the principal quantum number n and the orbital angular momentum ℓ as follows (we recall the formula for convenience):
Here, is the associated Laguerre polynomial. Problems arise because the expectation value diverges for any quantum numbers n, ℓ and m, which occurs because, even for higher ℓ, the wave functions do not completely vanish inside the hard-sphere radius , no matter how small is. Hence, ordinary perturbation theory is not applicable. A suitable expansion parameter is the ratio of the radius of the hard core to the Bohr radius (see Refs. [4,5,6,7,16,17,18,28]).
2.2. Radius Perturbation Theory
After we recognize that any nonrelativistic hydrogenic bound-state wave function necessarily has the form , we can reduce the problem to the calculation of a bound-state solution that fulfills the matching condition and approximates the solution (4) of the radial wave equation. We start from the representation of the radial function given in Equation (4) in terms of a Whittaker W function [31,32],
The task is to adjust the principal quantum number n from its integer value, which is obtained from the unperturbed Schrödinger–Coulomb problem, to a non-integer , chosen so that after we find , close to n, the wave function vanishes when ,
and the energy shift is given by
where is the unperturbed energy given in Equation (3). By carefully considering the shift in the short-range asymptotics of the Whittaker function [31,32,33] in Equation (5) upon a departure of n from its initial integer value, one finds the compact result
where is the Hartree energy and , consistent with the identification of an empty product as being equal to one. The square of the double factorial, , in the denominator of Equation (8) leads to a useful suppression of the strong-interaction shift for Rydberg states with high angular momenta. Corrections to Equation (8) are one power of the ratio higher than the leading order [4]. In view of the fact that the generalized Bohr radius is proportional to , the corrections can be expressed, as explained in Ref. [3], in powers of .
Our result can easily be expressed in terms of a quantum defect , where the bound-state energy shifts to a value , with a shifted principal quantum number ,
Notably, quantum defect theory is often used in order to describe energy shifts due to “core” potentials [34].
2.3. Comparison to the Literature
For S states with orbital angular momentum , Equation (8) specializes to the formula
where is the Schrödinger–Coulomb energy given in Equation (3). This is in agreement with Equation (1.1) of Ref. [4] if one identifies the hadronic size with the S-wave scattering length used in Ref. [4]. For P states (), Equation (8) implies that
which is also in agreement with Ref. [4], but it takes some additional work to verify this conclusion. Namely, one needs to realize that the quantity defined in Equation (2.11) of Ref. [4], which parameterizes the phase shift according to Equation (2.13) of Ref. [4], actually diverges for a hard-sphere potential. This is easily seen if one takes into account that the complete radial wave function (in the notation of Ref. [4]) vanishes at the boundary of the hard-sphere potential, and hence, the logarithmic derivative of the radial wave function, , diverges at the boundary of the hard-sphere potential. One then combines Equations (4.4) and (5.7) of Ref. [4], realizing that R in the notation of Ref. [4] is our , while B in the notation of Ref. [4] is our ; one can then show the agreement of Trueman’s paper [4] with our analysis for P states.
For D states (), which were not thoroughly considered in Refs. [4,5,6,7], we obtain
While the scaling with is in agreement with the basic assumption given in Equation (1), the prefactor is nontrivial and drastically reduces the magnitude of the effect for Rydberg D states. For example, the value of the 3D protonium energy shift (expected to be roughly similar to the imaginary part of the shift), from Table 3.4 of Ref. [7], was estimated as , while our formula with the prefactor gives the significantly smaller shift .
3. Numerical Verification
The use of exponential numerical grids for the calculation of Schrödinger–Coulomb energy eigenvalues was pioneered in Ref. [35]. The use of extended-precision arithmetic [36,37] facilitates the calculation of precise eigenvalues even under extreme conditions where the perturbations of a binding potential (here, a Coulomb potential) are minute. In the current section, we thus ask the academic question of whether lattice methods can be optimized to the point where our analytic result can be verified against numerical calculations even in parameter ranges where the numerical shifts are not detectable by standard-precision arithmetic. For our calculations, as an academic check, we thus use a lattice with N = 20,000 points, a maximum radial distance , and a minimum distance , where the lattice spacing parameter is . Lattice points are distributed according to the formula
Numerically, we approximate the potential as vanishing for , while inside the hard sphere, we assign a numerical value of
as an approximation of an infinite value. We use extended-precision arithmetic of 1024 decimal digits in order to overcome numerical instability problems, and we determine the energy eigenvalues by inverse iteration [38,39]. In order to verify Equation (8), we vary with a reference lattice point , where s is a lattice index chosen so that is in the range of to . This parameter range serves as a testing ground for numerical lattice methods. For reference F states, because the energy displacement is proportional to , this means that needs to be determined with an accuracy of up to 47 decimal places in order to discern the effect of the hard-sphere correction to the Coulomb potential. We rewrite the second derivative with respect to the radial coordinate, which is inherent to the radial Schrödinger–Coulomb eigenvalue equation, in terms of a derivative with respect to the lattice index i, and we use an 11-point finite-difference approximation in the numerical calculations (see Chap. 20 of Ref. [40]).
We have carried out extensive numerical checks of the result (8) for all hydrogenic states with principal quantum numbers . Here, we concentrate on states with a maximum angular momentum quantum number ℓ for a given principal quantum number n (see Figure 1). Let us add a numerical example. For (we have chosen this value in order to illustrate the high precision achieved using our numerics) and a reference state, we obtain
in excellent agreement with Equation (8), which implies that
Notably, the energy shift cannot be numerically determined with standard arithmetic, which is typically limited to 32 decimal digits in Fortran quadruple precision [41].
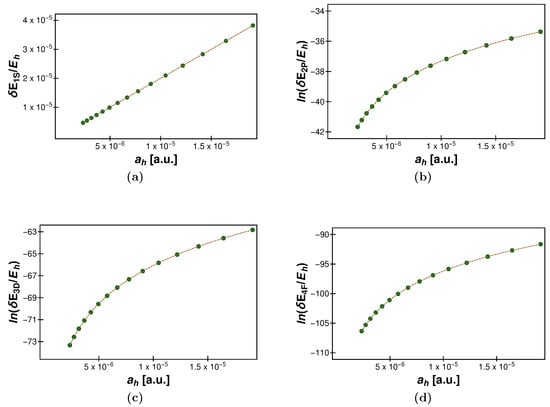
Figure 1.
Numerical values for the energy shift induced by a hard-sphere potential of radius are plotted as a function of for a reference hydrogenic state [panel (a)], state [panel (b)], state [panel (c)], and state [panel (d)]. The dots are from the numerical approach outlined in Section 2.2, while the dashed curve represents the analytic result given in Equation (8). Logarithmic scales are chosen for the ordinate axes in panels (b–d). By “a.u.”, we refer to atomic units, i.e., the radius is given in units of .
4. Conclusions
The problem treated in the current article possesses a compact formulation but, nevertheless, has quite far-reaching consequences. Let us emphasize that the analytic and numerical calculations were performed for a hydrogenic reference system (in the non-recoil limit of an infinite mass of the nucleus) for definiteness and ease of notation. In order to expand them to two-body bound systems in general (for example, protonium), one sets equal to the generalized Bohr radius , where is the reduced mass. The formula (8) remains valid provided one reinterprets in terms of the generalized Hartree energy . For systems with constituent particles of charge numbers and , one generalizes the result with the replacement .
We note that the Deser–Trueman formula reproduces measured strong-interaction energy shifts reasonably well. For protonium 1S states, the formula gives a shift of 0.867 keV, compared to the measured value of 0.72(4) keV from Table 6.3 of Ref. [7]. Furthermore, for systems not composed of particles and antiparticles, the Deser–Trueman formula with (approximating the S-wave scattering length with a hard-sphere radius of ) still gives a rough estimate. For example, for kaonic hydrogen (), the formula suggests a strong interaction shift of 0.41 keV, while the measured shift is 0.19(4) keV (from Table I of Ref. [23]). The validity of our formulas for the estimation of the strong-interaction correction for more general hadronic bound systems is supported by comparatively recent investigations indicating that the scattering length relative to that of protonium is a decreasing function of the atomic weight (see the conclusions of Ref. [42]).
A few remarks might be in order regarding the literature on the Deser–Trueman formula. As already mentioned, the parameter finds a natural generalization as the S-wave scattering length in the absence of a Coulomb field. With this idea in mind, it has been stressed [4,7] that the energy shift (8), for reference P states, can be assumed to be proportional to a scattering “volume”, namely, to the third power of a parameter , which is commensurate with the scattering length [see also Equation (5.7) of Ref. [4]. For reference D and F states, the energy shift is then proportional to the scattering “hyper-volumes”, i.e., proportional to and , respectively. These assumptions are confirmed in Equations (11) and (12). Our general result, given in Equation (8), possesses a highly nontrivial prefactor, which leads to a drastic suppression of the effect for high angular momenta, beyond simple scaling with .
Thus, our result allows for a reliable estimate of the strong-interaction correction to non-S Rydberg levels of electromagnetically bound systems containing hadronic constituent particles, and it is thus essential for the reliability of theoretical predictions for corresponding experiments involving exotic hadronic atoms. Our investigations here focus on the estimation of the numerically small strong-interaction correction for high-precision experiments in exotic, hadronic bound systems involving non-S states (see also Appendix A), where the presence of numerically small but nonvanishing strong-interaction shifts can be an obstacle to the detection of new physics effects [1,2]. Our general-purpose formula, given in Equation (8), addresses the issue.
Author Contributions
Conceptualization, G.S.A. and U.D.J., investigation, G.S.A. and U.D.J., writing, G.S.A. and U.D.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Science Foundation through Grants PHY-2308792 (G.S.A.), PHY-2110294 and PHY-2513220 (U.D.J.) and by the National Institute of Standards and Technology through Grant 60NANB23D230 (G.S.A.).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions and formulas presented in this study are included in the article. Further inquiries can be directed to the authors.
Acknowledgments
The authors acknowledge insightful discussions with Jean-Marc Richard.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Strong-Interaction Shifts: S Versus Non-S States
The focus in our current work is on Rydberg states with manifestly nonvanishing angular momenta. This approach constitutes a departure from previous investigations of exotic bound systems, which have primarily focused on measurements of the ground-state parameters (energy and lifetime) and their relation to S-wave scattering lengths (see the comprehensive discussion in Refs. [3,43]). Over the last three decades, there have been remarkable efforts by the DIRAC collaboration at CERN in regard to the ground-state lifetime of pionium (the atom; see Refs. [8,9]), and other bound states such as bound pion–kaon systems [10]. The pionic hydrogen collaboration at the Paul Scherrer Institute (PSI) has focused on pionic hydrogen measurements (see Refs. [11,44,45]) and pionic deuterium (Ref. [12]), focusing primarily on ground-state properties in each case. The DEAR collaboration has determined ground-state properties of kaonic hydrogen [13], but has also, quite remarkably, observed transitions of kaonic hydrogen from states of higher excitation to the ground state (the so-called , and lines; see Ref. [13]). Conversely, from the theoretical side, many efforts have been undertaken to understand the strong-interaction energy shift of the ground state of these exotic systems and the contribution of the strong interaction to the ground-state lifetime [3,43,46,47,48,49,50,51,52,53,54,55,56]). The properties of the ground states of exotic Coulomb systems offer tremendous insights into the contributions of the strong interaction to the effective Lagrangian describing the exotic bound systems. These contributions can be absorbed, to a good approximation, in contact terms, such as the last term on the right-hand side of Equation (4.2) of Ref. [3]. However, if one focuses on S states of exotic systems, then one overlooks the fact that the Rydberg states (notably, those with nonvanishing angular momenta) offer an almost ideal combination of very strong electromagnetic fields that approach the Schwinger limit (see also the pertinent discussion in Ref. [2]), while being largely free of strong-interaction effects. They are thus very attractive candidates in the search for new physics [1]. For the latter states (Rydberg states with nonvanishing angular momenta), the strong-interaction effects are small and, in fact, vanishing within the approximations considered in the treatment following Equation (5.27) of Ref. [3]. However, if one would like to consider highly excited non-S Rydberg states of exotic bound states, then the approach based on contact terms involving coordinate-space Dirac terms in the effective Lagrangian (specifically, contact terms not involving derivatives) is not applicable because the wave functions of states with high angular momenta vanish at the origin, while the strong-interaction correction does not vanish but is parametrically suppressed for the non-S states. For this reason, one needs an estimate of the strong-interaction shift in order to discern possible minute energy shifts due to residual strong-interaction shifts from putative new physics effects in prospective measurements of Rydberg-state transitions in heavy exotic systems [1,2]. This is the issue addressed in the current investigation.
For S states, within the approximation of treating the strong-interaction correction as a hard-sphere potential (see Section 3 of Ref. [7]), our approach is consistent with but less precise than the one chosen in Refs. [3,43,46,47,49,50,51,52,53,54,55,56]. Furthermore, it should be clearly stated that our approach cannot, in principle, describe the spin-dependent terms of the nucleon–nucleon interaction [57,58,59,60,61,62,63,64,65]. However, we reemphasize that it is our goal to present a universally applicable approximation of the strong-interaction correction for non-S Rydberg states, where the strong-interaction correction is numerically so small that it is otherwise mostly ignored in the literature, and utmost accuracy is not required for the treatment of the strong-interaction correction [see the discussion following Equation (5.27) of Ref. [3]. As a last remark, the imaginary part of the S-wave scattering length is found to be commensurate with its real part for all exotic systems considered in Refs. [3,43,46,47,49,50,51,52,53,54,55,56]). While our hard-sphere approach only yields the real part of the energy correction for the non-S Rydberg states, which are at the focus of our interests, we can thus reliably estimate the imaginary part of the strong-interaction energy correction for the non-S Rydberg states to be commensurate with its real part. In this context, it is useful to recall that the scattering lengths used for S-state calculations are manifestly complex rather than real quantities (see Tables 7 and 8 of Ref. [3]). For P states, the scattering volumes obtained using optical nucleon–nucleon potentials are, likewise, complex rather than real (for example calculations, see Table 1 of Ref. [65]). For reference, it is worth noting that the radiative photon-emission decay widths of excited atomic states (due to spontaneous emission of photons and dipole-allowed transitions to energetically lower atomic bound states) are well known to be of order (see Ref. [19]), uniformly for any orbital angular momentum. For P states, the photon-emission decay width is thus of the same order in as the hadronic decay widths described by the imaginary part of the strong-interaction correction for P states (also of order ). For excited S states, the strong-interaction decay width dominates (order ), while for D states and higher angular momenta, the strong-interaction decay width (order and higher) is parametrically suppressed in comparison to the photon-emission decay width.
References
- Baptista, G.; Rathi, S.; Roosa, M.; Senetaire, Q.; Sommerfeldt, J.; Azuma, T.; Becker, D.; Butin, F.; Eizenberg, O.; Fowler, J.; et al. Towards Precision Spectroscopy of Antiprotonic Atoms for Probing Strong-field QED. arXiv 2025, arXiv:2501.08893. [Google Scholar] [CrossRef]
- Adkins, G.S.; Jentschura, U.D. Bound Deuteron–Antideuteron System (Deuteronium): Leading Radiative and Internal–Structure Corrections to Bound-State Energies. arXiv 2025, arXiv:2506.15974v1 [hep-ph]. [Google Scholar]
- Gasser, J.; Lyubovitskij, V.E.; Rusetsky, A. Hadronic atoms in QCD + QED. Phys. Rep. 2008, 456, 167–251. [Google Scholar] [CrossRef]
- Trueman, T.L. Energy level shifts in atomic states of strongly-interacting particles. Nucl. Phys. 1961, 26, 57–67. [Google Scholar] [CrossRef]
- Carbonell, J.; Richard, J.-M.; Wycech, S. On the relation between protonium level shifts and nucleon–antinucleon scattering amplitudes. Z. Phys. A 1992, 343, 325–329. [Google Scholar] [CrossRef]
- Batty, C.J.; Friedman, E.; Gal, A. Unified optical-model approach to low-energy antiproton annihilation on nuclei and to antiprotonic atoms. Nucl. Phys. A 2001, 689, 721–740. [Google Scholar] [CrossRef]
- Klempt, E.; Bradamante, F.; Martin, A.; Richard, J.-M. Antinucleon–nucleon interaction at low energy: Scattering and protonium. Phys. Rep. 2002, 368, 119–316. [Google Scholar] [CrossRef]
- Adeva, B.; Afanasyev, L.; Benayoun, M.; Benelli, A.; Berka, Z.; Brekhovskikh, V.; Caragheorgheopol, G.; Cechak, T.; Chiba, M.; Constantinescu, S.; et al. First measurement of the π+π− atom lifetime. Phys. Lett. B 2005, 619, 50–60. [Google Scholar] [CrossRef]
- DIRAC Collaboration. First observation of long-lived π+π− atoms. arXiv 2015, arXiv:1508.04712. [Google Scholar] [CrossRef]
- Adeva, B.; Afanasyev, L.; Allkofer, Y.; Amsler, C.; Anania, A.; Aogaki, S.; Benelli, A.; Brekhovskikh, V.; Cechak, T.; Chiba, M.; et al. Measurement of the πK atom lifetime and the πK scattering length. Phys. Rev. D 2017, 96, 052002. [Google Scholar] [CrossRef]
- Pionic Hydrogen Collaboration at PSI. Available online: http://pihydrogen.web.psi.ch (accessed on 1 September 2025).
- Hauser, P.; Kirch, K.; Simons, L.M.; Borchert, G.; Gotta, D.; Siems, T.; El-Khoury, P.; Indelicato, P.; Augsburger, M.; Chatellard, D.; et al. New precision measurement of the pionic s-wave strong interaction parameters. Phys. Rev. D 1998, 58, 1869(R)–1872(R). [Google Scholar] [CrossRef]
- Beer, G.; Bragadireanu, A.M.; Cargnelli, M.; Curceanu-Petrascu, C.; Egger, J.-P.; Fuhrmann, H.; Guaraldo, C.; Iliescu, M.; Ishiwatari, T.; Itahashi, K.; et al. Measurement of the Kaonic Hydrogen X–Ray Spectrum. Phys. Rev. Lett. 2005, 94, 212302. [Google Scholar] [CrossRef] [PubMed]
- Safronova, M.S.; Budker, D.; DeMille, D.; Kimball, D.F.J.; Derevianko, A.; Clark, C.W. Search for new physics with atoms and molecules. Rev. Mod. Phys. 2018, 90, 025008. [Google Scholar] [CrossRef]
- Jentschura, U.D. Muonic Bound Systems, Strong–Field Quantum Electrodynamics and Proton Radius. Phys. Rev. A 2015, 92, 012123. [Google Scholar] [CrossRef]
- Deser, S.; Goldberger, M.L.; Baumann, K.; Thirring, W. Energy level displacements in pi-mesonic atoms. Phys. Rev. 1954, 96, 774–776. [Google Scholar] [CrossRef]
- Bethe, H.A.; de Hoffmann, F. Mesons and Fields; Row, Peterson and Co.: Evanston, IL, USA, 1955; Volume 2. [Google Scholar]
- Byers, N. Interactions of low-energy negative pions with nuclei. Phys. Rev. 1957, 107, 843–849. [Google Scholar] [CrossRef]
- Jentschura, U.D.; Adkins, G.S. Quantum Electrodynamics: Atoms, Lasers and Gravity; World Scientific: Singapore, 2022. [Google Scholar]
- Barrett, R.C.; Deloff, A. Strong interaction effects in kaonic deuterium. Phys. Rev. C 1999, 60, 025201. [Google Scholar] [CrossRef]
- Mitroy, J.; Ivallov, I.A. Quantum defect theory for the study of hadronic atoms. J. Phys. G 2001, 27, 1421–1433. [Google Scholar] [CrossRef]
- Deloff, A. Determination of π N scattering lengths from pionic hydrogen and pionic deuterium data. Phys. Rev. C 2001, 64, 065205. [Google Scholar] [CrossRef]
- Yan, Y.; Nualchimplee, C.; Suebka, P.; Kobdaj, C.; Khosonthogkee, K. Accurate evaluation of wave functions of pionium and kaonium. Mod. Phys. Lett. A 2009, 24, 901–906. [Google Scholar] [CrossRef]
- Nualchimplee, C.; Suebka, P.; Yan, Y.; Faessler, A. Accurate evaluation of the 1s wave functions of kaonic hydrogen. Hyp. Int. 2009, 193, 97–102. [Google Scholar] [CrossRef]
- Bobeth, C.; Hiller, G.; van Dyk, D. The benefits of B¯→K¯*l+l− decay at low recoil. J. High Energy Phys. 2010, 1007, 098. [Google Scholar] [CrossRef]
- Richard, J.-M.; Fayard, C. Level rearrangement in exotic-atom-like three-body systems. Phys. Lett. A 2017, 381, 3217–3221. [Google Scholar] [CrossRef][Green Version]
- Moriya, H.; Horiuchi, W.; Richard, J.-M. Three-body correlations in mesonic-atom-like systems. SciPost Phys. Proc. 2020, 3, 051. [Google Scholar] [CrossRef]
- Batty, C.J. Antiprotonoic-hydrogen atoms. Rep. Prog. Phys. 1989, 52, 1165–1216. [Google Scholar] [CrossRef]
- Richard, J.-M. Antiproton Physics. Front. Phys. 2020, 8, 6. [Google Scholar] [CrossRef]
- Jurisch, A.; Rost, J.-M. Trapping cold atoms by quantum reflection. Phys. Rev. A 2008, 77, 043603. [Google Scholar] [CrossRef]
- Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Bateman, H. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1953; Volume 1. [Google Scholar]
- Lambert, E. Fonction de portée effective et déplacement en énergie des états liés en présence d’un potential coulombien modifié. Helv. Phys. Acta 1969, 42, 667–677. [Google Scholar]
- Greene, C.; Fano, U.; Strinatio, G. General form of the quantum defect theory. Phys. Rev. A 1979, 19, 1485–1509. [Google Scholar] [CrossRef]
- Salomonson, S.; Öster, P. Solution of the pair equation using a finite discrete spectrum. Phys. Rev. A 1989, 40, 5559–5567. [Google Scholar] [CrossRef]
- Available online: https://julialang.org (accessed on 1 September 2025).
- Balbaert, I. Getting Started with Julia Programming; Packt Publishing: Birmingham, UK, 2015. [Google Scholar]
- Pohlhausen, E. Berechnung der Eigenschwingungen statisch-bestimmter Fachwerke. ZAMM—Z. Angew. Math. 1921, 1, 28–42. [Google Scholar] [CrossRef]
- Trefethen, L.N.; Bau, D. Numerical Linear Algebra; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1997. [Google Scholar]
- Kong, Q.; Siauw, T.; Bayen, A. Python Programming and Numerical Methods; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- IBM. XL Fortran for Linux, Compiler Reference; IBM Corporation: Armonk, NY, USA, 2012. [Google Scholar]
- Protasov, K.V.; Bonomi, G.; Rizzini, E.L.; Zenoni, A. Antiproton annihilation on light nuclei at very low energies. Eur. Phys. J. A 2000, 7, 429–434. [Google Scholar] [CrossRef][Green Version]
- Gasser, J.; Lyubovitskij, V.E.; Rusetsky, A. Hadronic Atoms. Annu. Rev. Nucl. Part. Sci. 2009, 59, 169–190. [Google Scholar] [CrossRef]
- Hennebach, M.; Anagnostopoulos, D.F.; Dax, A.; Fuhrmann, H.; Gotta, D.; Gruber, A.; Hirtl, A.; Indelicato, P.; Liu, Y.-W.; Manil, B.; et al. Hadronic shift in pionic hydrogen. Eur. Phys. J. A 2014, 50, 190. [Google Scholar] [CrossRef]
- Hirtl, A.; Anagnostopoulos, D.F.; Covita, D.S.; Fuhrmann, H.; Gorke, H.; Gotta, D.; Gruber, A.; Hennebach, M.; Indelicato, P.; Jensen, T.S.; et al. Redetermination of the strong-interaction width in pionic hydrogen. Eur. Phys. J. A 2021, 57, 70. [Google Scholar] [CrossRef]
- Lyubovitskij, V.; Rusetsky, A. Lifetime of (π+π−) atom: Analysis of the role of strong interactions. Phys. Lett. B 1996, 389, 181–186. [Google Scholar] [CrossRef]
- Gall, A.; Gasser, J.; Lyubovitskij, V.E.; Rusetsky, A. On the lifetime of the π+π− atom. Phys. Lett. B 1999, 462, 335–340. [Google Scholar] [CrossRef]
- Gall, A.; Gasser, J.; Lyubovitskij, V.E.; Rusetsky, A. π−p atom in ChPT: Strong energy-level shift. Phys. Lett. B 2000, 494, 9–18. [Google Scholar]
- Kong, X.; Ravndal, F. Relativistic corrections to the pionium lifetime. Phys. Rev. D 2000, 61, 077506. [Google Scholar] [CrossRef]
- Gasser, J.; Lyubovitskij, V.E.; Rusetsky, A.; Gall, A. Decays of π+π− atom. Phys. Rev. D 2001, 64, 016008. [Google Scholar] [CrossRef]
- Lipartia, E.; Lyubovitskij, V.E.; Rusetsky, A. Hadronic potentials from effective field theories. Phys. Lett. B 2002, 533, 285–293. [Google Scholar] [CrossRef][Green Version]
- Gasser, J.; Ivanov, M.A.; Lipartia, E.; Mojzis, M.; Rusetsky, A. Ground-state energy of pionic hydrogen to one loop. Eur. Phys. J. C 2002, 26, 13–34. [Google Scholar] [CrossRef]
- Meissner, U.-G.; Raha, U.; Rusetsky, A. Spectrum and decays of kaonic hydrogen. Eur. Phys. J. C 2004, 35, 349–357. [Google Scholar] [CrossRef]
- Meissner, U.-G.; Raha, U.; Rusetsky, A. The pion-nucleon scattering lengths from pionic deuterium. Eur. Phys. J. C 2005, 41, 213–232. [Google Scholar] [CrossRef]
- Meissner, U.-G.; Raha, U.; Rusetsky, A. Kaon–nucleon scattering lengths from kaonic deuterium experiments. Eur. Phys. J. C 2006, 47, 473–480. [Google Scholar] [CrossRef][Green Version]
- Döring, M.; Meissner, U.-G. Kaon–nucleon scattering lengths from kaonic deuterium experiments revisited. Phys. Lett. B 2011, 704, 663–666. [Google Scholar] [CrossRef]
- Dover, C.B.; Richard, J.-M. Elastic, charge exchange, and inelastic p cross sections in the optical model. Phys. Rev. C 1980, 21, 1466–1471. [Google Scholar] [CrossRef]
- Kohno, M.; Weise, W. Proton-antiproton scattering and annihilation into two mesons. Nucl. Phys. A 1986, 454, 429–452. [Google Scholar] [CrossRef]
- Malfliet, R.A.; Tjon, J.A. Solution of the Faddeev Equations for the Triton Problem using Two–Particle Interactions. Nucl. Phys. A 1969, 127, 161–168. [Google Scholar] [CrossRef]
- Payne, G.L.; Friar, J.L.; Gibson, B.F. Configuration space Faddeev continuum calculations. I. n-d scattering length. Phys. Rev. C 1982, 26, 1385–1398. [Google Scholar] [CrossRef]
- Wycech, S.; Green, A.M.; Niskanen, J.A. On the energy levels in antiprotonic deuterium. Phys. Lett. B 1985, 152, 308–312. [Google Scholar] [CrossRef]
- Yan, Y.; Khosonthongkee, K.; Kobdaj, C.; Suebka, P. D atoms in realistic potentials. Phys. Lett. B 2008, 659, 555. [Google Scholar] [CrossRef][Green Version]
- Lazauskas, R.; Carbonell, J. Antiproton-deuteron hydrogenic states in optical models. Phys. Lett. B 2021, 820, 136573. [Google Scholar] [CrossRef]
- Duerinck, P.-Y.; Lazauskas, R.; Carbonell, J. Corrigendum to “Antiproton-deuteron hydrogenic states in optical models” [Phys. Lett. B 820 (2021) 136573]. Phys. Lett. B 2023, 841, 137936. [Google Scholar] [CrossRef]
- Duerinck, P.-Y.; Lazauskas, R.; Dohet-Eraly, J. Antiproton-deuteron hydrogenic states from a coupled-channel approach. Phys. Rev. C 2023, 108, 054003. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).