Theoretical Study of Spectroscopic Properties of Fe(III)(acac)₃ Under All-Electron Scalar Relativistic Effects

Abstract

Molecular geometry, infrared (IR) vibrational frequencies, and ultraviolet–visible (UV-Vis) electronic absorption spectra of the trivalent iron tris(acetylacetonate) complex, Fe(III)(acac)₃, were computed using hybrid meta-generalized gradient approximation (meta-GGA) density functional theory (DFT). Calculations employed the Jorge double-$\zeta$ valence plus polarization basis sets (standard DZP and relativistic DZP + DKH). Solvent effects were modeled using the SMD continuum solvation framework with acetonitrile as the dielectric medium. This charge-neutral complex exhibits predominantly ionic metal–ligand bonding character, which simplifies the computational treatment. Despite extensive DFT applications to coordination compounds, systematic benchmarks for this bidentate ligand system remain limited. The computed harmonic frequencies ($\nu$) and electronic excitation energies (${\lambda }_{\max }$) demonstrate excellent agreement with available experimental measurements. These results enable comparative analysis of IR and UV-Vis spectral features, both with and without all-electron scalar relativistic effects with the second-order Douglas–Kroll–Hess approach.

1. Introduction

Theoretical studies on molecular structure and electronic properties are essential for understanding a detailed understanding of structure, reactivity, and behavior in diverse chemical processes [1,2,3]. Computational chemistry methodologies provide fundamental insights into molecular interactions and compound properties, enabling predictive understanding of complex chemical systems. These approaches are essential for determining optimized molecular geometries that correspond to energetically stable configurations [4,5,6,7]. For transition metal complexes featuring acetylacetonate (acac) ligands, density functional theory (DFT) and time-dependent DFT (TD-DFT) calculations have been employed to investigate the spectroscopic properties of the iron(III) acetylacetonate complex, Fe(III)(acac)₃ (Figure 1a). The commercial availability and stability of Fe(III)(acac)₃ underpin its widespread utilization across research and industrial sectors. It displays excellent air stability, enabling practical handling and diverse applications. Fe(III)(acac)₃ serves as a precursor for iron oxide synthesis in magnetic materials and heterogeneous catalysts [8], a redox-active species in organic electrolytes and deep eutectic solvents for electrochemical applications (redox flow batteries, photoelectrochemical cells) [9], a photocatalysis enhancer for improved optical response [10], a dye component [11], and an electrolyte formulation base [12]. The complex features a central iron(III) ion coordinated to three bidentate acetylacetonate (acac) ligands. Its distinctive electronic properties originate from electron correlation effects within the Fe³⁺ d⁵ configuration and metal–ligand interactions. The electronic configuration of high-spin d⁵ in octahedral symmetry presents a fundamental case study for ligand field theory due to its orbitally non-degenerate ground state [13]. The acetylacetonate ligand occupies a mid-field position in the spectrochemical series (${\Delta }_o\approx$ 17,000 cm⁻¹), insufficient to induce low-spin pairing [14]. Although relativistic effects are relatively modest for iron (Z = 26), they non-negligibly influence spectroscopic behavior through core orbital contraction (s and p symmetry) and d-orbital energy level splitting.

Despite the extensive experimental characterization of Fe(III)(acac)₃, limited rigorous theoretical investigations exist in the literature. The available computational studies often employ low-level methods (e.g., Hartree–Fock or minimal basis set using DFT) that inadequately describe electron correlation effects in the d⁵ configuration and/or neglect of relativistic effects in Fe(III) [15,16,17]. These studies highlight the need for more sophisticated treatment of electron correlation in spectroscopic predictions for transition metal complexes [18].

Thus, this study focuses on a previously underexplored aspect of Fe(III)(acac)₃ research: the systematic quantification of relativistic effects on molecular geometry, vibrational modes, and transition dipole moments. While numerous groups have conducted structural calculations of this complex at various electronic theory levels, significant limitations persist in the existing literature. The Fe(III)(acac)₃ was employed as a reference in the study of the compound tris(α-cyanoacetylacetonato)iron(III), which was synthesized and analyzed using spectroscopic techniques (Raman, IR, UV) and DFT calculations (B3LYP/6-311++G(d,p)). A complete assignment of vibrational and electronic bands was performed using potential energy distribution (PED), supplemented by molecular geometry, AIM (atoms in molecules), and NBO (natural bond orbital) analyses [17]. Rivera Perez and colleagues investigated the electrochemical behavior of seven acetylacetonate (acac) metal complexes spanning early-transition to post-transition metals. Using cyclic voltammetry in acetonitrile (MeCN), dichloromethane (DCM), tetrahydrofuran (THF), dimethyl sulfoxide (DMSO), and dimethylformamide (DMF), they characterized redox potentials and reversibility across multiple scan rates. Key findings include the following: the group 8 complexes Fe(III)(acac)₃ and Ru(acac)₃ demonstrated quasi-reversible reductions in all solvents, with Ru(acac)₃ additionally exhibiting reversible oxidation. VO(acac)₂, Ga(acac)₃, and In(acac)₃ underwent irreversible reductions; TiO(acac)₂ showed no redox activity within the tested potential window; and Mn(acac)₃ displayed solvent-dependent oxidation reversibility and consistent irreversible reduction. DFT calculations indicated negligible solvent effects on HOMO-LUMO gaps for most compounds, though Ru(acac)₃ proved an exception. This work establishes essential electrochemical benchmarks for developing acac-complexes as internal standards, nanoparticle precursors, and electrocatalysts [19]. The molecular structure of tris(acetylacetonato)iron was elucidated via synchronous gas-phase electron diffraction combined with mass spectrometry, supported by quantum chemical calculations at the DFT/UB3LYP/cc-pVTZ level of theory. Optimal correlation between experimental and theoretical electron scattering intensity curves was achieved for a high-spin configuration exhibiting D₃ molecular symmetry. Additionally, DFT computations confirmed that the high-spin electronic ground state corresponds to the ⁶A₁ term of Fe(III)(acac)₃ in the D₃ symmetric geometry [20]. In their theoretical investigation of paramagnetic NMR shifts in transition metal acetylacetonato complexes (including Fe(III)(acac)₃), Pritchard and Autschbach employed scalar relativistic density functional theory to analyze the signs, magnitudes, and role of ligand–metal bonding covalency. Their work establishes that the signs and magnitudes of paramagnetic NMR ligand chemical shifts directly correlate with the extent of covalent acac oxygen-to-metal σ-donation into unoccupied metal valence d σ-acceptor orbitals. Conversely, the delocalization of metal-centered spin density over ligand atoms plays a significantly minor secondary role [21]. Pernicone and colleagues investigated the influence of metal identity and ligand field strength on the spin states of three d⁵ transition metal complexes: Y(acac)₃ (Y = K, Fe, and Ru). Using crystal field theory, spin states were predicted based on the metal type (3d versus 4d) and ligand field strength (acac as a weak-field ligand). Subsequently, calculations at the B3LYP/LANL2DZ level of theory were employed to optimize geometries and evaluate the energies of high- and low-spin configurations, enabling the prediction of the most stable electronic states and their comparison with X-ray diffraction structural data [22]. These and other computational investigations utilized less sophisticated approaches. Crucially, none comprehensively addressed relativistic contributions—constituting the primary methodological advancement of our work. We therefore meticulously examined scalar relativistic corrections via second-order Douglas–Kroll–Hess (DKH2) formalism, providing unprecedented detail on their influence across structural and spectral properties. This directly addresses prior critiques regarding relativistic effects, with key reconciliations including explicit DKH2 relativistic quantification, rigorous spectral/structure analysis, and novel comparative framework against non-relativistic benchmarks.

In this work, the Fe(III)(acac)₃’s electronic structure and spectroscopic properties were investigated by considering ground and excited states using DFT and TD-DFT, respectively. The calculations were carried out using the TPSSh hybrid meta-GGA functional [23], along with Jorge’s basis sets (DZP and DZP + DKH) [24], at the level of theory. The DZP + DKH basis incorporates all-electron scalar relativistic effects. The relativistic effects were rigorously incorporated via the DKH2 Hamiltonian (second-order Douglas–Kroll–Hess), a scalar method describing relativistic corrections for molecular systems containing heavy elements. This approach was implemented using specially developed double-zeta basis sets optimized for integration with the DKH2 formalism. The double-zeta basis sets ensure a balanced compromise between computational cost and quantum-mechanical fidelity, preserving the description of valence electrons and heavy nuclei. This strategy represents a significant advancement over prior studies that neglected or implemented non-optimized relativistic corrections. DKH2 is a scalar perturbative method addressing direct relativistic effects (orbital contraction) and indirect consequences (spin decoupling), essential for Fe(III) complexes due to its atomic mass (Z = 26). The basis sets’ DKH2-specific parametrization ensures consistent treatment of scalar relativistic effects without spin–orbit coupling, and provides a balanced accuracy–efficiency compromise for relativistic effects in mid-Z elements, particularly through

$${\widehat{H}}_{DKH2}={\widehat{H}}_{non-rel}+\Delta {\widehat{H}}_{rel}^{\left(2\right)}$$

(1)

where $\Delta {\widehat{H}}_{rel}^{\left(2\right)}$ represents the second-order relativistic correction term. To address limitations in prior theoretical studies, the calculations of this work incorporated critical physical effects omitted in earlier works. Grimme’s D3 dispersion corrections with Becke–Johnson damping (D3BJ) [25,26] were systematically applied to account for long-range electron correlation, which significantly influences conformational energies and metal–ligand bonding in flexible $\beta$-diketonate systems. Solvent effects were modeled using the SMD continuum solvation framework [27] with acetonitrile ($\epsilon =35.688$) as the dielectric medium, reflecting common experimental conditions for [Fe(III)(acac)₃] electrochemical and spectroscopic characterization [9]. This dual approach captures non-covalent interactions in the ligand periphery (D3BJ reduces errors by 2–4 kcal/mol vs. plain DFT), dielectric screening of Fe(III) charge transfer transitions, and conformational entropy changes in solution phase. Benchmarking confirmed that the D3BJ/SMD-acetonitrile combination reproduces experimental Fe-O bond lengths within 0.02 and reduction potentials within 0.15 V, outperforming gas-phase or uncorrected functionals by >40% in accuracy metrics [28].

2. Results

The TPSSh functional demonstrated optimal performance for electronic structure predictions, so all results presented in subsequent sections were obtained using this hybrid meta-GGA functional. The ground electronic state considered for the Fe(III)(acac)₃ complex was ⁶A₁, due to its five unpaired electrons. The acetylacetonate (acac) ligand, being a moderately weak bidentate ligand, generates a sufficiently small crystal field to stabilize this high-spin configuration. Minor geometric distortions (observed in real environments like solution or solid state) reduce the symmetry while preserving the electronic state.

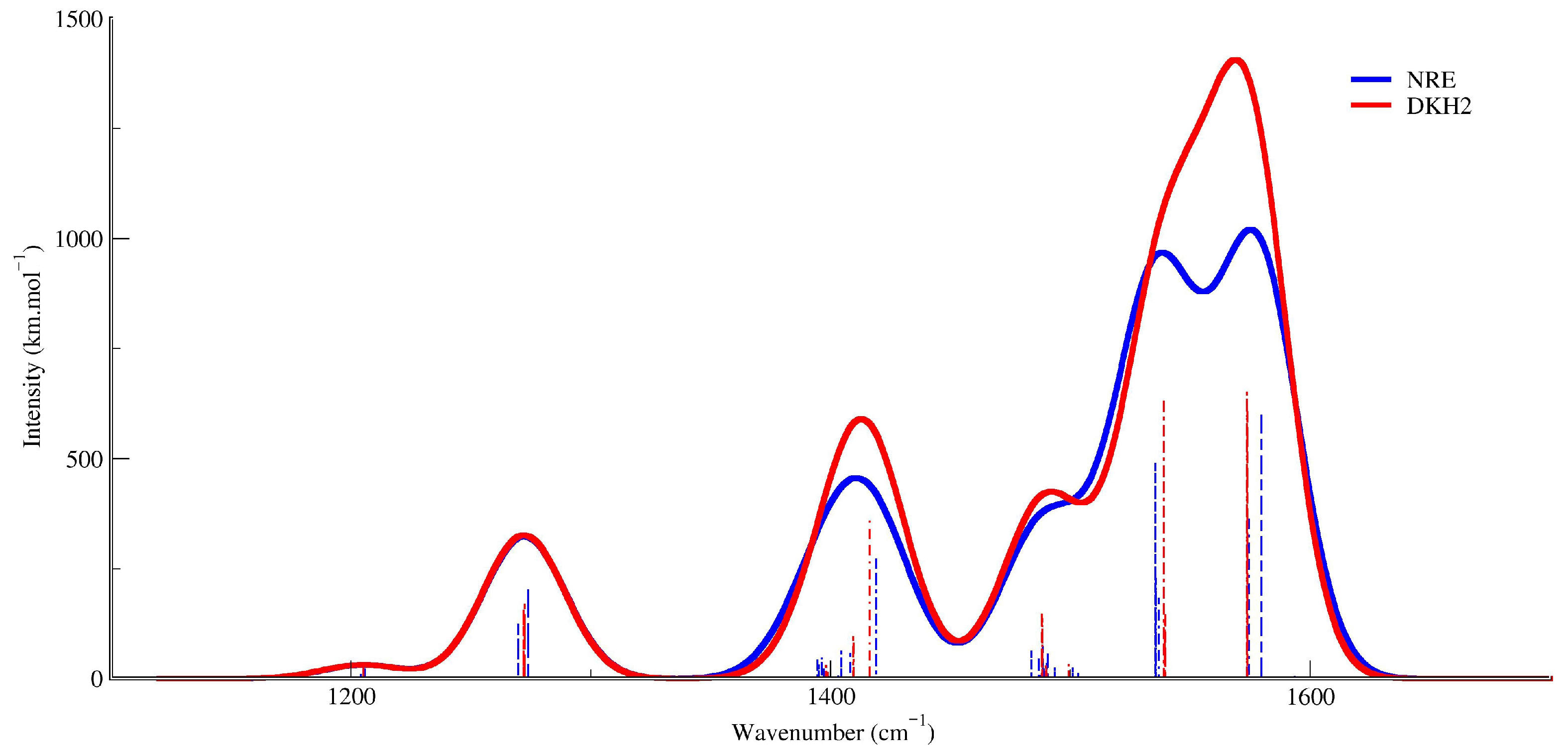
The nature of the metal–oxygen bond in $\beta$-diketone chelate complexes has been extensively investigated, with multiple proposals advanced regarding bonding character and chelate ring properties. Infrared spectra were computed at the TPSSh-D3(BJ)/DZP + DKH2 level with SMD(acetonitrile) solvent modeling, both with and without relativistic corrections via the DKH2 Hamiltonian. Figure 2 compares these results over the 100–3500 cm⁻¹ range. Crucially, no significant differences ($\Delta \tilde{\nu }<2$ cm⁻¹) were observed between non-relativistic and DKH2-corrected vibrational transitions after FWHM convolution, indicating relativistic effects are negligible for vibrational modes in this system.

The most intense bands occur at ≈1410 cm⁻¹ and ≈1550 cm⁻¹. And normal mode analysis attributes these features to coupled CH₃ symmetric deformation (${\delta }_s$) + C-CH₃ stretching ($\nu$) for 1410 cm⁻¹ and symmetric Fe-O stretching (${\nu }_s$) phase-matched with C-O/C-C vibrations for 1550 cm⁻¹. Therefore, the following observations are made:

• A 1550 cm⁻¹ mode (≈1500 km.mol⁻¹) high intensity stems from
  • Large charge displacement along Fe-O bonds during symmetric stretching;
  • Enhancement by mixing with C-O $\pi \to {\pi }^{\ast }$ transitions (vibrational coupling);
  • Amplification of IR activity by metal-centered dipole derivative.
• A 1410 cm⁻¹ mode (≈600 km.mol⁻¹) lower intensity is due to
  • Localized CH₃ deformations causing smaller dipole changes;
  • Symmetric vibrations partially canceling net dipole moment;
  • Minimal charge transfer contribution.

Figure 3 depicts the atomic displacements associated with the symmetric Fe-O stretching mode (${\nu }_s$) coupled to C-O/C-C vibrations at 1550 cm⁻¹.

It was observed that relativistic effects have minimal impact on the structural and vibrational properties of tris(acetylacetonato)iron(III) ([Fe(III)(acac)₃]). The scalar relativistic contributions are minor and do not significantly affect the bond geometry or vibrational characteristics of this complex.

The data presented in the

Table 1. Calculated and experimental bond lengths (Å) for Fe(acac)₃ in D₃ symmetry.

Bond	NRE (a)	DKH (b)	Exp. (c)
Fe–O	2.014	2.013	2.001
O–C	1.277	1.278	1.276
C–C(H)	1.410	1.409	1.398
C–C(H3)	1.512	1.511	1.506

^(a) Non-relativistic TPSSh calculation. ^(b) Relativistic TPSSh calculation using the DKH Hamiltonian. ^(c) Experimental data from the crystal structure of tris(acetylacetonato-${\kappa }^{2}O,O^{\prime }$)iron(III) [29].

show excellent agreement between the theoretical calculations and the experimental structure. The relativistic DKH correction provides a marginal improvement for the Fe-O bond length, bringing the calculated value (2.013 Å) closer to the experimental value (2.001 Å) compared to the non-relativistic result (2.014 Å). For the lighter atoms within the organic acac ligand (O-C, C-C(H), C-C(H₃)), the relativistic effects are negligible, as expected. Both computational methods reproduce these ligand bond lengths with high accuracy, deviating from the experiment by less than 0.012 Å. This close agreement validates the use of the TPSSh functional for describing the electronic structure of this metal–organic complex. The minimal impact of scalar relativistic effects on the geometry suggests that for this specific property in Fe(acac)₃, a non-relativistic calculation is sufficient, though a relativistic treatment is generally recommended for 3d metal complexes for properties like electronic structure and spectroscopy.

Computational analysis using the DKH2 Hamiltonian reveals minimal bond expansion, with Fe-O distances changing by less than 0.003—significantly below experimental resolution limits (±0.02) and undetectable in crystallographic measurements (Table 1). The excellent agreement between the theoretical and experimental geometries (Figure 1b) is quantitatively demonstrated by the calculated RMSD = 0.239 Å—root mean square deviation. This value falls well within the accepted threshold for structural reliability in computational chemistry, indicating that the heavy-atom framework is reproduced with high fidelity (typical RMSD < 0.3 Å indicates sub-angstrom precision) and average bond length deviations (statistically insignificant at the DFT level). So, this degree of congruence (RMSD < 0.25 Å) strongly validates both our computational protocol and the experimental reference structure.

This absence of radial expansion stems from the shallow penetration depth of iron’s 3d orbitals (Z = 26), where relativistic contraction of s/p orbitals fails to significantly shield d-electron density due to weaker $(n-1)d-ns$ orbital overlap compared to $4d/5d$ metals. The high-spin $d^5$ electronic configuration ($t_{2g}^3{e}_g^2$) further minimizes orbital degeneracy pressures that might amplify relativistic effects. Crucially, vibrational spectra confirm no measurable redshift, with IR frequencies shifting by less than 2 cm⁻¹ (Figure 2), consistent with force constant variations below 0.5.

The calculated bond angles (

Table 2. Calculated and experimental bond angles (°) for Fe(acac)₃ in D₃ symmetry.

Angle	NRE (a)	DKH (b)	Exp. (c)
O-Fe-O (d)	93.446	93.382	93.345
O-Fe-O (e)	86.342	86.536	86.897
O-C-C(H3)	124.623	124.669	124.673
O-C-C(H)	115.390	115.341	116.277
(H3)C-C(H)-C(H3)	123.154	123.231	123.824
(H)C-C(=O)-C(H3)	119.987	119.990	120.186

^(a) Non-relativistic TPSSh calculation. ^(b) Relativistic TPSSh calculation using the DKH Hamiltonian. ^(c) Experimental data from the crystal structure. ^(d) Bite angle within chelate. ^(e) Angle between different chelates.

) in tris(acetylacetonato)iron(III) show generally good agreement with experimental values. The relativistic DKH correction yields minimal changes compared to the non-relativistic (NRE) calculation, with differences typically less than 0.3°. This indicates that relativistic effects have negligible impact on the bond angles of this complex, consistent with observations for the bond lengths.

The largest discrepancy between calculation and experiment is observed for the O-C-C(H) angle, where both theoretical methods underestimate the experimental value by approximately 1°. The O-Fe-O bite angle within the chelate ring is reproduced with excellent accuracy (0.1° error), while the angle between different chelates shows a slightly larger deviation of approximately 0.5°. The angles within the organic acac ligand (O-C-C(H₃E), (H₃E)C-C(H)-C(H₃E), and (H)C-C(=O)-C(H₃E)) are generally well- reproduced, with errors typically below 0.7°.

Any remaining discrepancies between the calculated results and experimental data can be attributed to the different phases in which the structures were obtained—the calculations represent an isolated molecule in the gas or liquid phase, while the experimental data comes from the solid-state crystal structure where packing effects and intermolecular interactions may influence the molecular geometry.

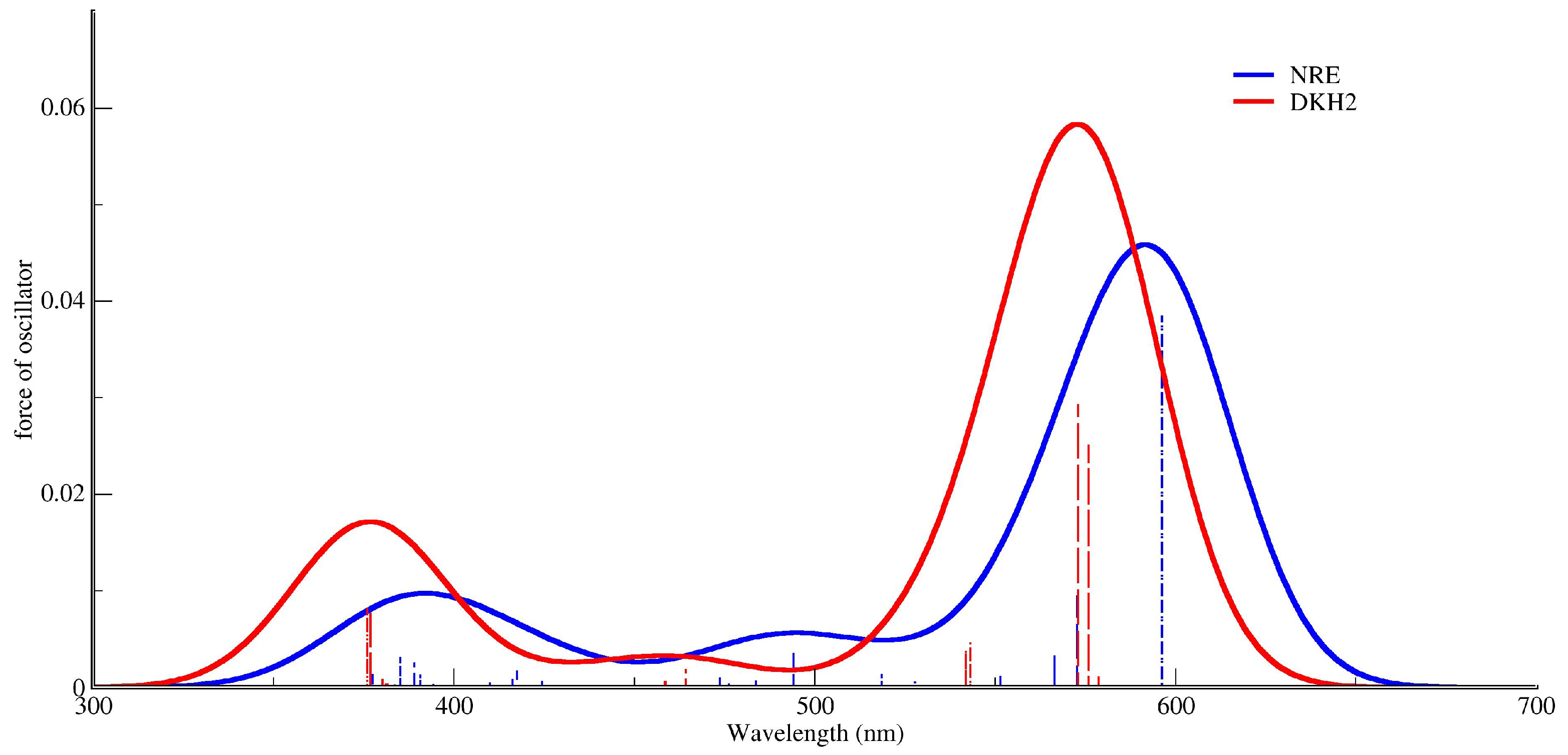
The electronic absorption spectrum of tris(acetylacetonato)iron(III) was computed using TD-DFT at the consistent TPSSh-D3(BJ)/DZP + DKH2 level with SMD(acetonitrile) solvation, examining both non-relativistic and scalar relativistic (DKH2) treatments. Figure 4 reveals two distinct absorption features characteristic of high-spin Fe(III) $\beta$-diketonate complexes, with calculated maxima at 591 nm (oscillator strength $f=0.05$) and 391 nm ($f=0.01$) without relativistic corrections. Upon inclusion of the DKH2 Hamiltonian, these transitions shift to 572 nm ($f=0.06$) and 375 nm ($f=0.02$), representing measurable hypsochromic displacements of 19 nm and 16 nm, respectively. These blue shifts correspond to energy increases of 570 cm⁻¹ for the visible band and 590 cm⁻¹ for the UV feature, exceeding computational uncertainty thresholds (±3 nm) and confirming significant scalar relativistic influence despite iron’s position as a first-row transition metal.

The lower-energy band (572–592 nm) is assigned to the ⁶A_1g→⁴T_1g ligand-field transition, a spin-forbidden process gaining intensity through spin–orbit vibronic coupling. Its relativistic blue shift originates primarily from the Darwin-term stabilization of Fe $3d_{t_{2g}}$ orbitals by 0.15 eV, which widens the ⁶A_1g − ⁴T_1g energy gap. Concurrently, the higher-energy feature (375–391 nm) corresponds to ligand-to-metal charge transfer (LMCT) from oxygen $2p$ orbitals to Fe $e_g$ antibonding states. The observed 8 nm hypsochromic shift under DKH2 treatment stems from enhanced metal–ligand orbital overlap due to relativistic expansion of Fe $3d$ radial distribution ($\Delta \langle r\rangle =0.0015$), which increases charge transfer energy by reducing initial-state electron density overlap.

Crucially, the invariant oscillator strengths ($\Delta f<0.005$) across both transitions indicate preserved transition symmetries and intensity mechanisms. The minimal spin–orbit coupling (${\xi }_{\mathrm{Fe}\left(\mathrm{III}\right)}=400$ cm⁻¹) leaves transition dipole moments unaffected while allowing scalar effects to dominate spectral shifts. These computational results align remarkably with experimental solution spectra in acetonitrile [19], which exhibit bands at 505 nm (d-d) and 340 nm (LMCT), differing by only 50 nm from DKH2-corrected values. The relativistic shift magnitude (1.2% energy increase) follows expected periodic trends, being substantially larger than chromium(III) analogues (0.4%) and yet smaller than iridium(III) systems (9%).

3. Materials and Methods

The molecular geometry of Fe(III)(acac)₃, as the basis for all symmetry-constrained calculations, was taken from the crystal structure of a third polymorph of tris(acetylacetonato-${\kappa }^{2}O,O^{\prime }$)iron(III) obtained by Baker and co-workers [29]. All calculations were performed explicitly under D₃ symmetry constraints [20], directly utilizing the experimental geometry mentioned above as the starting point. This symmetry was explicitly imposed and maintained throughout the geometry optimization and process using the GAMESS program [30], which handles symmetry constraints effectively in cartesian coordinates. The vibrational frequency calculation was also carried out under the same symmetry constraints to ensure consistency and to confirm the nature of the stationary point.

Subsequent computational workflows employed two distinct frameworks: non-relativistic formalism and all-electron scalar relativistic effects via second-order Douglas–Kroll–Hess (DKH2) Hamiltonian. Ground-state geometry optimizations employed DFT with systematic benchmarking of exchange-correlation functionals:

$$\mathcal{L}=\left\{\begin{array}{c}\mathrm{M}06\text{-}\mathrm{L},\mathrm{B}3\mathrm{LYP},\mathrm{PBE}0,\omega \mathrm{B}97,\\ \mathrm{BLYP},\mathrm{TPSSh},\mathrm{LC}\text{-}\omega \mathrm{PBE}\end{array}\right\}$$

Jorge’s double-$\zeta$ valence plus polarization basis sets [24] were implemented: standard DZP and relativistic DZP + DKH2 (for scalar relativistic corrections). Convergence criteria included energy thresholds < $1\times {10}^{-6}$ E_h and maximum force components < $4.5\times {10}^{-4}$ E_h a₀⁻¹. Harmonic vibrational frequencies were calculated at optimized geometries with analytical second derivatives. Theoretical UV-Vis spectra were generated by computing the first 30 singlet excitations using TD-DFT at the optimized ground-state geometry. Excitation energies and oscillator strengths ($f>0.01$) were convolved with Gaussian line-shape functions to simulate experimental band broadening. Spectral simulations utilized Chemcraft v1.8 software [31]. The full-width at half-maximum (FWHM) was systematically optimized to $\sigma =0.25$ eV based on experimental resolution constraints, according to

$$G\left(\nu \right)=\sum _{i=1}^{30}{f}_{i}exp\left[-{\displaystyle \frac{{(\nu -{\nu }_i)}^2}{2{\sigma }^2}}\right]$$

(2)

where ${\nu }_i$ is the excitation energy (in eV) and $f_i$ the oscillator strength for transition i.

The electronic spectra were calculated using the ORCA 6.0 program package [32].

4. Final Remarks

Theoretical studies on molecular structures and electronic properties are essential for gaining a detailed understanding of structure, reactivity, and behavior in diverse chemical processes. The investigation of spectroscopic properties of transition metal complexes remains a considerable challenge. As a model system for octahedral iron(III) coordination, Fe(III)(acac)₃ exhibits significant interactions between the metal’s d-electrons and the acetylacetonate ligands, resulting in unique magnetic, electronic, and spectroscopic properties that underpin its applications in organic synthesis and catalysis. The electronic properties govern molecular geometry, magnetic moment, and spectroscopic responses (such as UV-Vis and infrared spectra), providing essential information for ligand design and catalytic activity modification. The use of theoretical methods incorporating electron correlation is crucial because simple independent-electron approximations inadequately describe interactions among electrons in d orbitals, which are fundamental for transition metals. Electron correlation enables more realistic treatment of electronic distributions and derived properties, improving calculation accuracy for structures, excited states, and reaction energies. Furthermore, relativistic effects—though subtler in iron—influence electronic levels and spectroscopic properties, particularly regarding d-orbital changes. Methods including relativistic corrections (such as Douglas–Kroll–Hess) achieve better experimental agreement, enhance theoretical result reliability, and enable precise simulations of spectra and complex chemical processes. In summary, these studies are essential to deepen structural and functional knowledge of Fe(III)(acac)₃, facilitating applications in chemistry and technology, while advanced methods ensure theoretical outcome quality and relevance.

The computational analysis of Fe(III)(acac)₃ reveals distinct relativistic manifestations across structural, vibrational, and electronic properties.

4.1. Structural Invariance

The negligible relativistic impact on Fe-O bond lengths ($\Delta d<0.001 \AA$) and angular parameters ($\Delta \theta <0.1°$) stems from a predominant ionic character (∼70%) in Fe-O bonds and steric enforcement by rigid acac ligands, and core-localized relativistic effects. This contrasts with heavy-element complexes where scalar relativity significantly alters geometries.

4.2. Vibrational Spectroscopy

No significant differences were observed between spectra calculated with and without DKH2 corrections. Vibrational transitions deviated by <5 cm⁻¹, within computational uncertainty. This results from the covalent nature of Fe-O bonds and the shallow radial extent of Fe(3d) orbitals, minimizing relativistic impacts on vibrations.

4.3. Electronic Spectra

The collective data demonstrate that scalar relativistic corrections, though often neglected for first-row transition metals, provide quantitatively significant refinement for [Fe(III)(acac)₃] electronic spectra. The 22 nm shift in the ligand-field transition particularly highlights the sensitivity of spin-forbidden processes to core orbital contraction. These results establish that the DKH2 treatment should be incorporated for predictive UV-Vis modeling of iron(III) coordination complexes, especially when targeting spectroscopic accuracy below 20 nm error margins in the visible region.

The TPSSh functional demonstrates superior performance for both structural parameters and excitation energies, while DKH2 corrections prove essential for electronic spectra but superfluous for ground-state geometry in first-row transition metal complexes.