Curvature Effects on the Regimes of the Lateral van der Waals Force
Abstract
1. Introduction
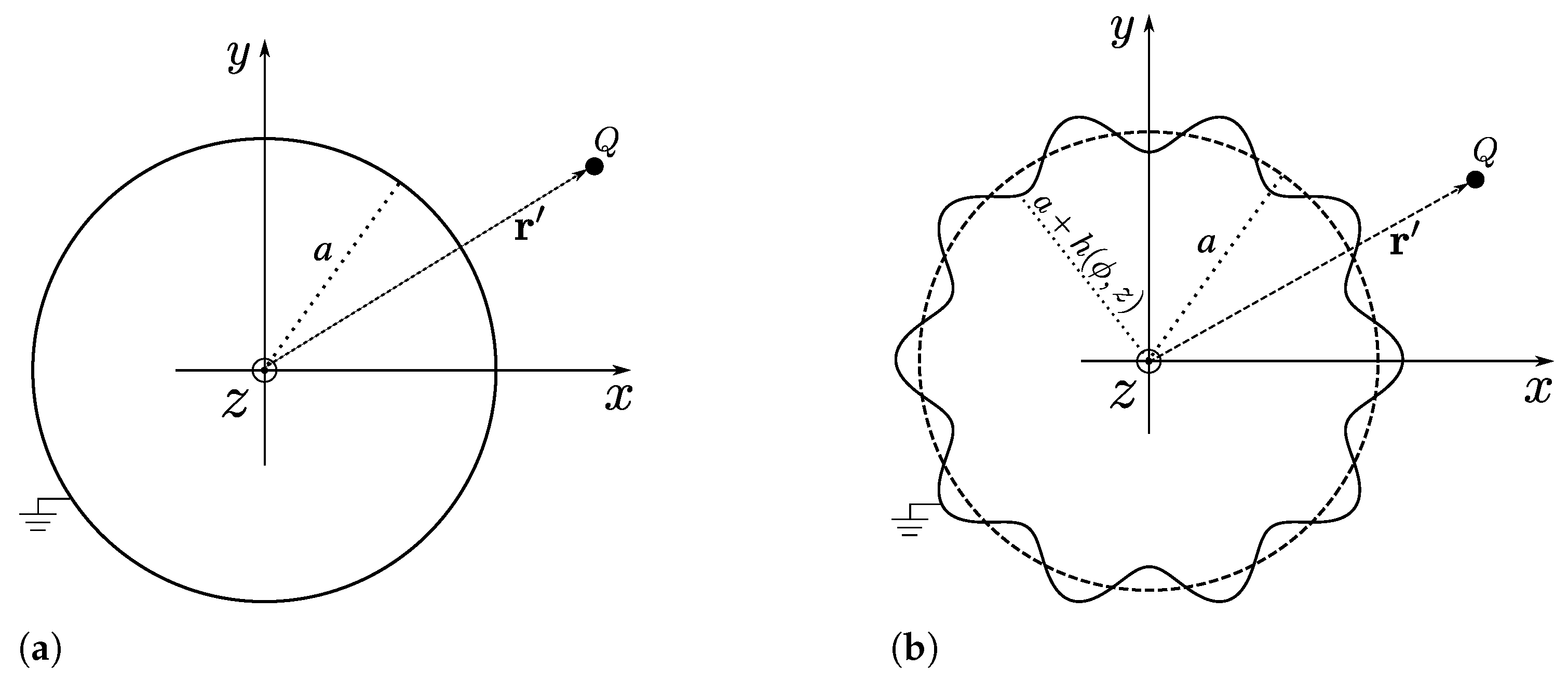
2. Point Charge in the Presence of a Corrugated Cylinder
2.1. The Solution of the Poisson’s Equation
2.2. Electrostatic Interaction Energy Between a Point Charge and a General Corrugated Cylinder
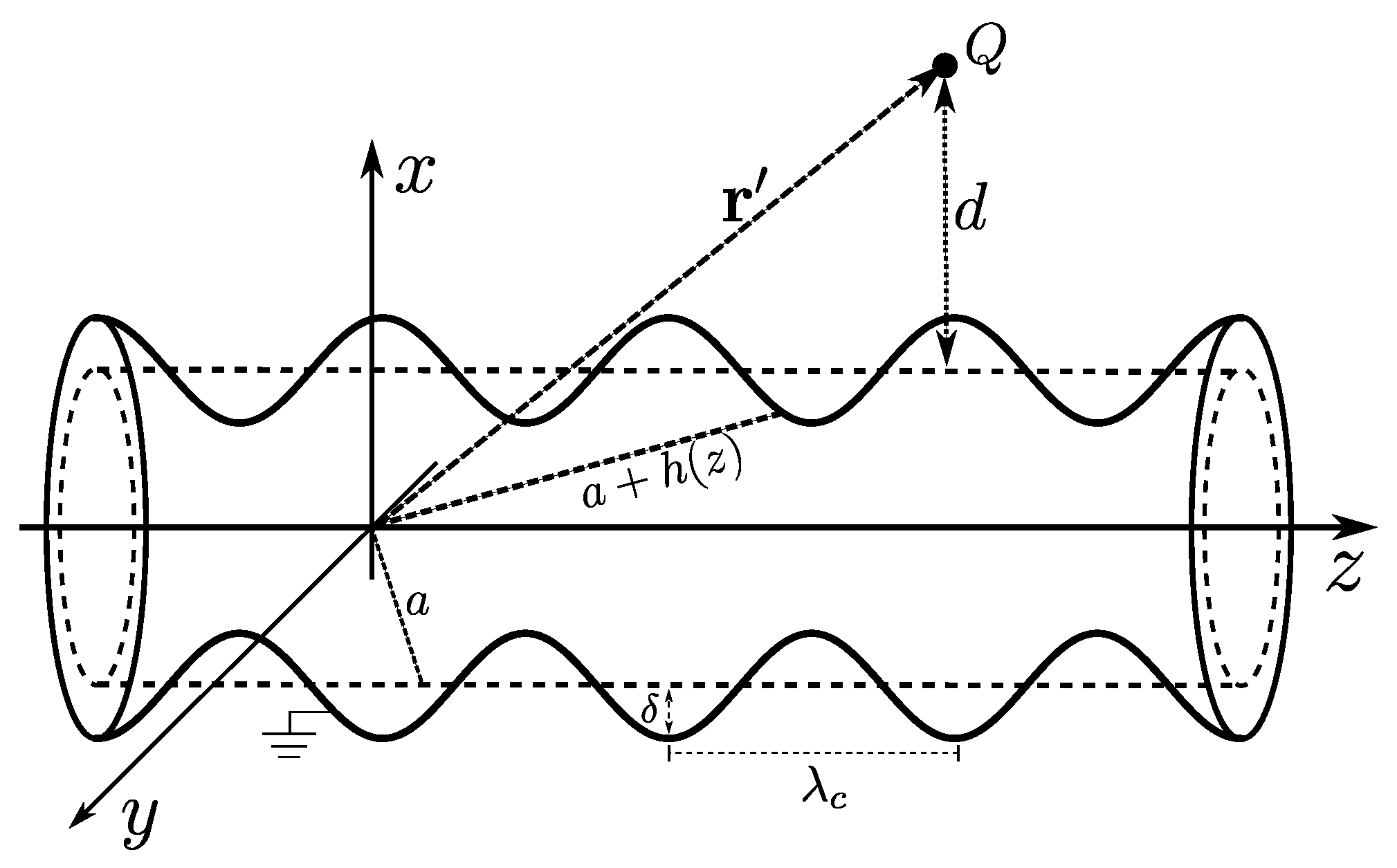
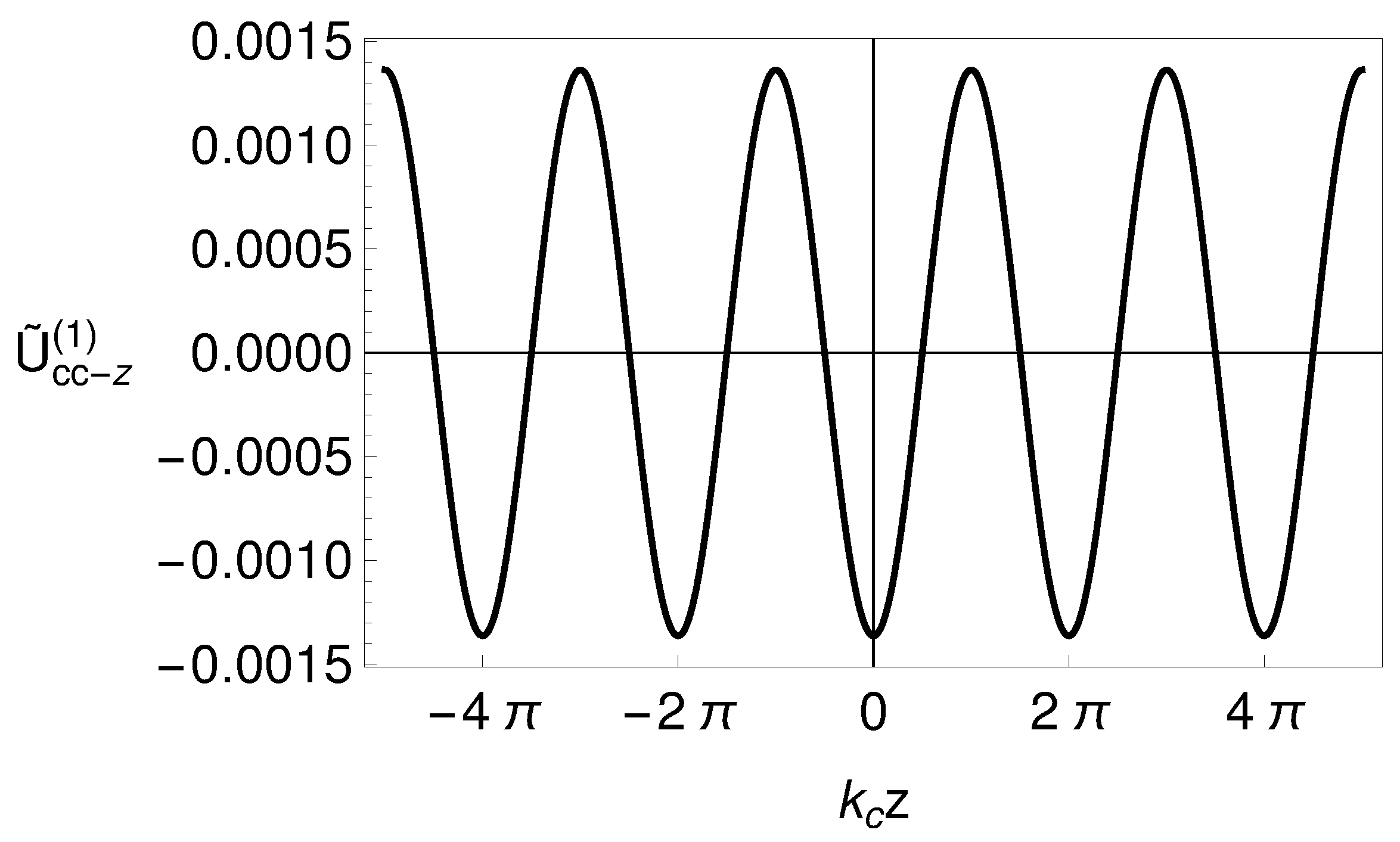
2.3. Electrostatic Interaction Energy for a Cylinder with a Sinusoidal Corrugation Along the z-Direction
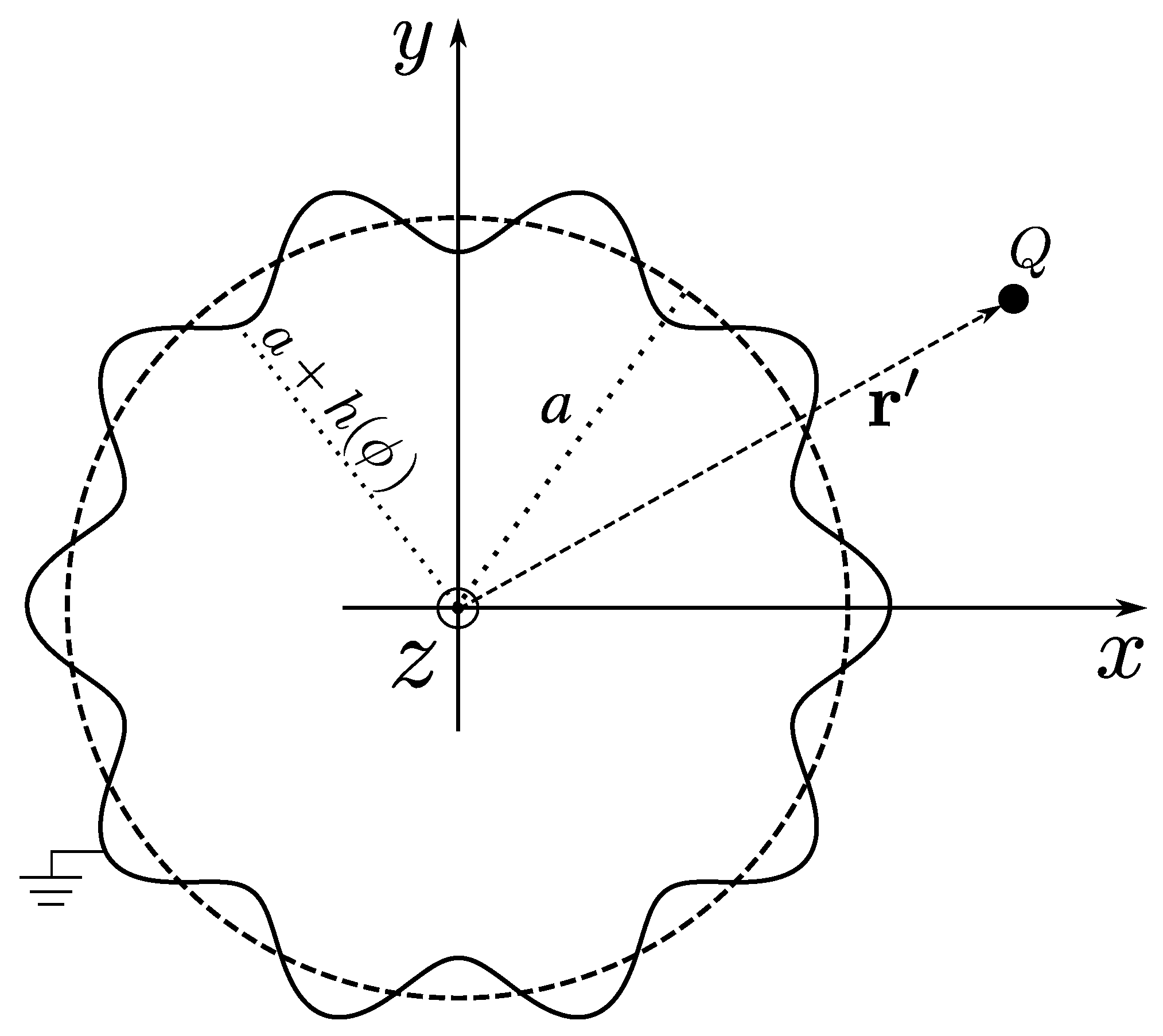
2.4. Electrostatic Interaction Energy for a Cylinder with a Sinusoidal Corrugation Along the -Direction
3. The van der Waals Interaction Between a Polarizable Point Particle and a Corrugated Cylinder
3.1. Interaction Energy for a General Corrugated Cylinder
3.2. Interaction Energy for a Cylinder with a Sinusoidal Corrugation Along the z-Direction
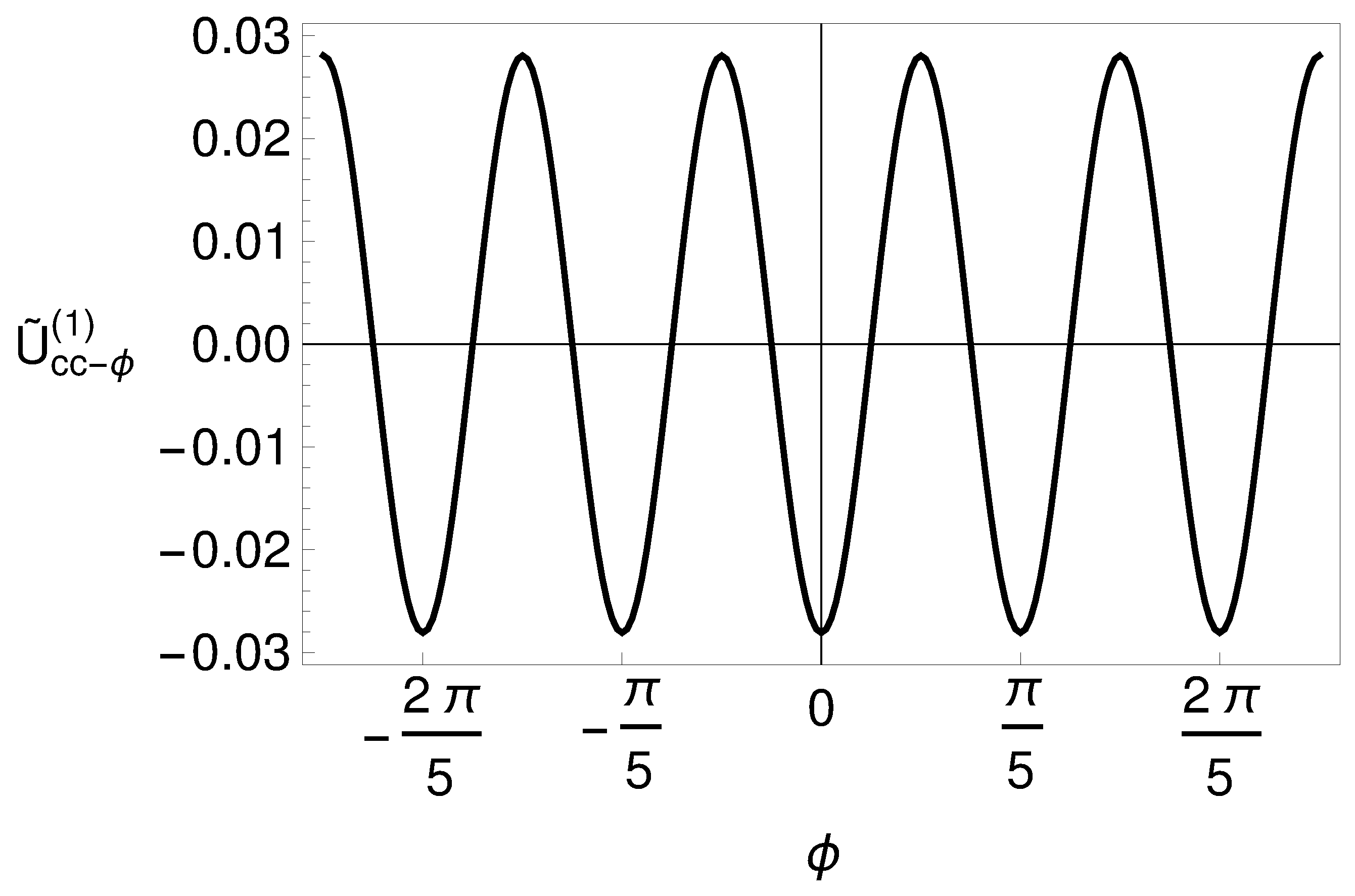
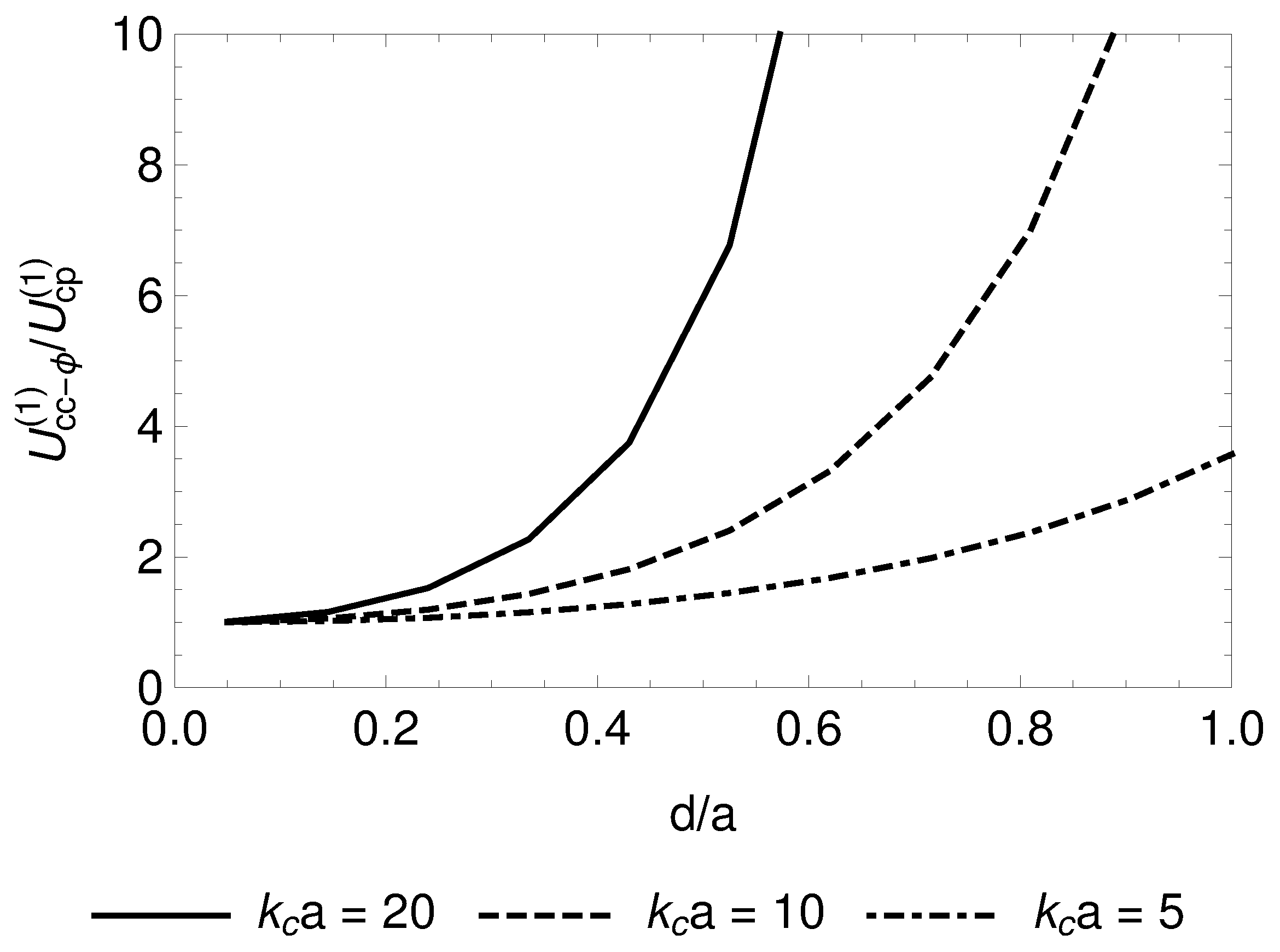
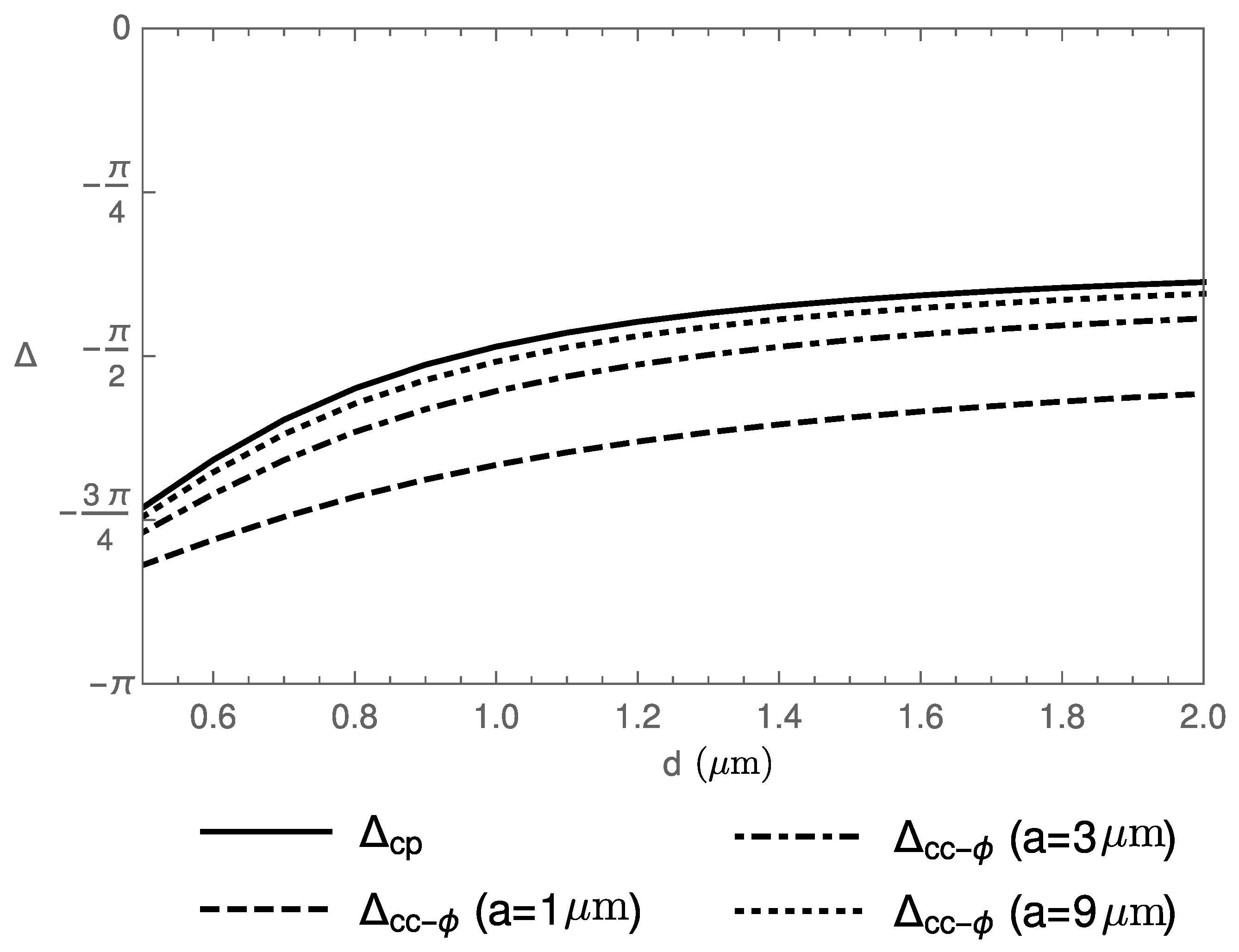
3.3. Interaction Energy for a Cylinder with a Sinusoidal Corrugation Along the -Direction
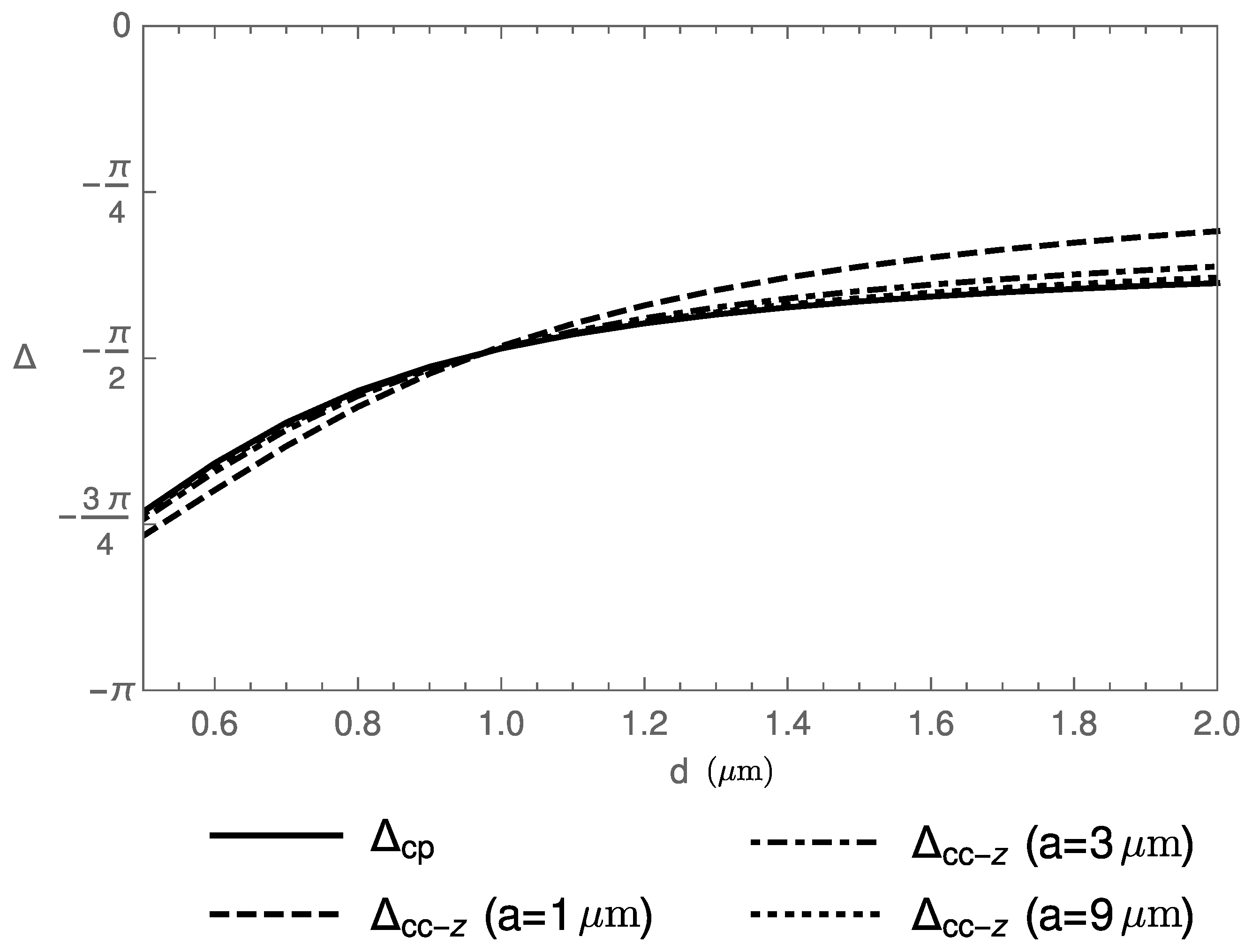
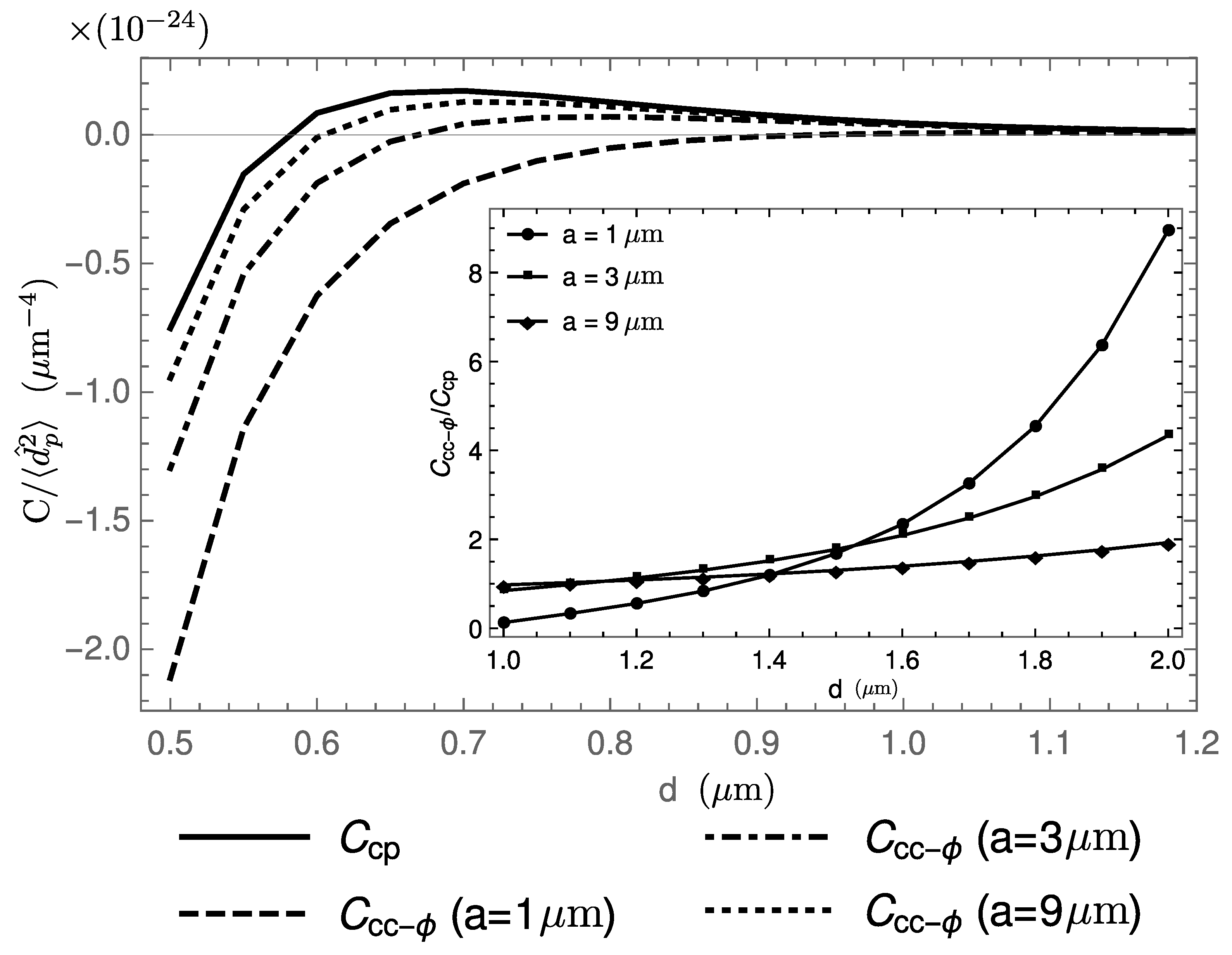
4. Final Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Casimir, H.B.G.; Polder, D. The Influence of Retardation on the London-van der Waals Forces. Phys. Rev. 1948, 73, 360–372. [Google Scholar] [CrossRef]
- Buhmann, S.Y. Dispersion Forces I. In Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 2012; Volume 247. [Google Scholar] [CrossRef]
- Buhmann, S.Y. Dispersion Forces II. In Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 2012; Volume 248. [Google Scholar] [CrossRef]
- Milonni, P.W. The Quantum Vacuum. An Introduction to Quantum Electrodynamics; Academic Press: San Diego, CA, USA, 1994. [Google Scholar]
- Parsegian, A.V. Van der Waals Forces. A Handbook for Biologists, Chemists, Engineers, and Physicists; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Woods, L.M.; Dalvit, D.A.R.; Tkatchenko, A.; Rodriguez-Lopez, P.; Rodriguez, A.W.; Podgornik, R. Materials perspective on Casimir and van der Waals interactions. Rev. Mod. Phys. 2016, 88, 045003. [Google Scholar] [CrossRef]
- Valchev, G.S.; Djondjorov, P.A.; Vassilev, V.M.; Dantchev, D.M. Van der Waals interactions between planar substrate and tubular lipid membranes undergoing pearling instability. AIP Conf. Proc. 2017, 1895, 090002. [Google Scholar] [CrossRef]
- Sukenik, C.I.; Boshier, M.G.; Cho, D.; Sandoghdar, V.; Hinds, E.A. Measurement of the Casimir-Polder force. Phys. Rev. Lett. 1993, 70, 560–563. [Google Scholar] [CrossRef] [PubMed]
- Druzhinina, V.; DeKieviet, M. Experimental Observation of Quantum Reflection far from Threshold. Phys. Rev. Lett. 2003, 91, 193202. [Google Scholar] [CrossRef]
- Obrecht, J.M.; Wild, R.J.; Antezza, M.; Pitaevskii, L.P.; Stringari, S.; Cornell, E.A. Measurement of the Temperature Dependence of the Casimir-Polder Force. Phys. Rev. Lett. 2007, 98, 063201. [Google Scholar] [CrossRef]
- Zhao, B.S.; Schulz, S.A.; Meek, S.A.; Meijer, G.; Schöllkopf, W. Quantum reflection of helium atom beams from a microstructured grating. Phys. Rev. A 2008, 78, 010902. [Google Scholar] [CrossRef]
- Bender, H.; Courteille, P.W.; Marzok, C.; Zimmermann, C.; Slama, S. Direct Measurement of Intermediate-Range Casimir-Polder Potentials. Phys. Rev. Lett. 2010, 104, 083201. [Google Scholar] [CrossRef]
- Rance, G.A.; Marsh, D.H.; Bourne, S.J.; Reade, T.J.; Khlobystov, A.N. van der Waals Interactions between Nanotubes and Nanoparticles for Controlled Assembly of Composite Nanostructures. ACS Nano 2010, 4, 4920–4928. [Google Scholar] [CrossRef]
- Schneeweiss, P.; Gierling, M.; Visanescu, G.; Kern, D.P.; Judd, T.E.; Günther, A.; Fortágh, J. Dispersion forces between ultracold atoms and a carbon nanotube. Nat. Nanotechnol. 2012, 7, 515–519. [Google Scholar] [CrossRef]
- Chang, D.E.; Sinha, K.; Taylor, J.M.; Kimble, H.J. Trapping atoms using nanoscale quantum vacuum forces. Nat. Commun. 2014, 5, 4343. [Google Scholar] [CrossRef]
- Bender, H.; Stehle, C.; Zimmermann, C.; Slama, S.; Fiedler, J.; Scheel, S.; Buhmann, S.Y.; Marachevsky, V.N. Probing Atom-Surface Interactions by Diffraction of Bose-Einstein Condensates. Phys. Rev. X 2014, 4, 011029. [Google Scholar] [CrossRef]
- Laliotis, A.; de Silans, T.P.; Maurin, I.; Ducloy, M.; Bloch, D. Casimir–Polder interactions in the presence of thermally excited surface modes. Nat. Commun. 2014, 5, 4364. [Google Scholar] [CrossRef]
- Chan, E.A.; Aljunid, S.A.; Adamo, G.; Laliotis, A.; Ducloy, M.; Wilkowski, D. Tailoring optical metamaterials to tune the atom-surface Casimir-Polder interaction. Sci. Adv. 2018, 4, eaao4223. [Google Scholar] [CrossRef] [PubMed]
- Kundu, A.; Paul, S.; Banerjee, S.; Banerjee, A. Measurement of Van der Waals force using oscillating optical tweezers. Appl. Phys. Lett. 2019, 115, 123701. [Google Scholar] [CrossRef]
- Dalvit, D.A.R.; Neto, P.A.M.; Lambrecht, A.; Reynaud, S. Probing Quantum-Vacuum Geometrical Effects with Cold Atoms. Phys. Rev. Lett. 2008, 100, 040405. [Google Scholar] [CrossRef] [PubMed]
- Dalvit, D.A.R.; Neto, P.A.M.; Lambrecht, A.; Reynaud, S. Lateral Casimir-Polder force with corrugated surfaces. J. Phys. A Math. Theor. 2008, 41, 164028. [Google Scholar] [CrossRef]
- Messina, R.; Dalvit, D.A.R.; Neto, P.A.M.; Lambrecht, A.; Reynaud, S. Dispersive interactions between atoms and nonplanar surfaces. Phys. Rev. A 2009, 80, 022119. [Google Scholar] [CrossRef]
- Döbrich, B.; DeKieviet, M.; Gies, H. Scalar Casimir-Polder forces for uniaxial corrugations. Phys. Rev. D 2008, 78, 125022. [Google Scholar] [CrossRef]
- Nogueira, E.C.M.; Queiroz, L.; Alves, D.T. Peak, valley, and intermediate regimes in the lateral van der Waals force. Phys. Rev. A 2021, 104, 012816. [Google Scholar] [CrossRef]
- Queiroz, L.; Nogueira, E.C.M.; Alves, D.T. Regimes of the lateral van der Waals force in the presence of dielectrics. Phys. Rev. A 2021, 104, 062802. [Google Scholar] [CrossRef]
- Queiroz, L. Influence of retardation and dispersive surfaces on the regimes of the lateral Casimir-Polder force. Phys. Rev. A 2024, 109, 032824. [Google Scholar] [CrossRef]
- Yi, W.; Huang, H.; Lai, C.; He, T.; Wang, Z.; Dai, X.; Shi, Y.; Cheng, X. Optical Forces on Chiral Particles: Science and Applications. Micromachines 2024, 15, 1267. [Google Scholar] [CrossRef]
- Nogueira, E.C.M.; Queiroz, L.; Alves, D.T. Sign inversion in the lateral van der Waals force. Phys. Rev. A 2022, 105, 062816. [Google Scholar] [CrossRef]
- Alves, D.T.; Queiroz, L.; Nogueira, E.C.M.; Peres, N.M.R. Curvature-induced repulsive effect on the lateral Casimir-Polder–van der Waals force. Phys. Rev. A 2023, 107, 062821. [Google Scholar] [CrossRef]
- Queiroz, L.; Nogueira, E.C.M.; Alves, D.T. Sign inversion in the lateral van der Waals force between an anisotropic particle and a plane with a hemispherical protuberance: An exact calculation. J. Phys. A Math. Theor. 2023, 56, 115301. [Google Scholar] [CrossRef]
- Clinton, W.L.; Esrick, M.A.; Sacks, W.S. Image potential for nonplanar metal surfaces. Phys. Rev. B 1985, 31, 7540–7549. [Google Scholar] [CrossRef]
- Costa, A.P.; Queiroz, L.; Nogueira, E.C.M.; Alves, D.T. Introducing corrugated surfaces in electrostatic problems via a perturbative approach. Am. J. Phys. 2023, 91, 629–636. [Google Scholar] [CrossRef]
- Eberlein, C.; Zietal, R. Force on a neutral atom near conducting microstructures. Phys. Rev. A 2007, 75, 032516. [Google Scholar] [CrossRef]
- Rosenfeld, J.; Wasan, D. The London force contribution to the van der Waals force between a sphere and a cylinder. J. Colloid Interface Sci. 1974, 47, 27–31. [Google Scholar] [CrossRef]
- Gu, Y.; Li, D. The van der Waals Interaction between a Spherical Particle and a Cylinder. J. Colloid Interface Sci. 1999, 217, 60–69. [Google Scholar] [CrossRef]
- Kirsch, V. Calculation of the van der Waals force between a spherical particle and an infinite cylinder. Adv. Colloid Interface Sci. 2003, 104, 311–324. [Google Scholar] [CrossRef] [PubMed]
- Blagov, E.V.; Klimchitskaya, G.L.; Mostepanenko, V.M. Van der Waals interaction between microparticle and uniaxial crystal with application to hydrogen atoms and multiwall carbon nanotubes. Phys. Rev. B 2005, 71, 235401. [Google Scholar] [CrossRef]
- Eberlein, C.; Zietal, R. Retarded Casimir-Polder force on an atom near reflecting microstructures. Phys. Rev. A 2009, 80, 012504. [Google Scholar] [CrossRef]
- Afanasiev, A.; Minogin, V. van der Waals interaction of an atom with the internal surface of a hollow submicrometer-size cylinder. Phys. Rev. A 2010, 82, 052903. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Bezerra de Mello, E.R.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Saharian, A.A. Exact Casimir–Polder potential between a particle and an ideal metal cylindrical shell and the proximity force approximation. Eur. Phys. J. C 2011, 71, 1614. [Google Scholar] [CrossRef]
- Frawley, M.C.; Nic Chormaic, S.; Minogin, V.G. The van der Waals interaction of an atom with the convex surface of a nanocylinder. Phys. Scr. 2012, 85, 058103. [Google Scholar] [CrossRef]
- Dung Chinh, N. van der Waals interaction of an atom near a fiber tip. Eur. Phys. J. D 2018, 72, 164. [Google Scholar] [CrossRef]
- Hernandes, J.A.; Assis, A.K.T. Electric potential due to an infinite conducting cylinder with internal or external point charge. J. Electrost. 2005, 63, 1115–1131. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Schwinger, J.; Milton, K.A.; DeRaad, L.L.; Tsai, W. Classical Eletrodynamics, 1st ed.; Perseus Books: New York, NY, USA, 1998. [Google Scholar]
- Contreras Reyes, A.M.; Eberlein, C. Casimir-Polder interaction between an atom and a dielectric slab. Phys. Rev. A 2009, 80, 032901. [Google Scholar] [CrossRef]
- Eberlein, C.; Zietal, R. Casimir-Polder interaction between a polarizable particle and a plate with a hole. Phys. Rev. A 2011, 83, 052514. [Google Scholar] [CrossRef]
- de Melo e Souza, R.; Kort-Kamp, W.J.M.; Sigaud, C.; Farina, C. Finite-size effects and nonadditivity in the van der Waals interaction. Phys. Rev. A 2011, 84, 052513. [Google Scholar] [CrossRef]
- Abrantes, P.P.; França, Y.; da Rosa, F.S.S.; Farina, C.; de Melo e Souza, R. Repulsive van der Waals interaction between a quantum particle and a conducting toroid. Phys. Rev. A 2018, 98, 012511. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, A.P.; Queiroz, L.; Alves, D.T. Curvature Effects on the Regimes of the Lateral van der Waals Force. Atoms 2025, 13, 61. https://doi.org/10.3390/atoms13070061
Costa AP, Queiroz L, Alves DT. Curvature Effects on the Regimes of the Lateral van der Waals Force. Atoms. 2025; 13(7):61. https://doi.org/10.3390/atoms13070061
Chicago/Turabian StyleCosta, Alexandre P., Lucas Queiroz, and Danilo T. Alves. 2025. "Curvature Effects on the Regimes of the Lateral van der Waals Force" Atoms 13, no. 7: 61. https://doi.org/10.3390/atoms13070061
APA StyleCosta, A. P., Queiroz, L., & Alves, D. T. (2025). Curvature Effects on the Regimes of the Lateral van der Waals Force. Atoms, 13(7), 61. https://doi.org/10.3390/atoms13070061






