g-Factor Isotopic Shifts: Theoretical Limits on New Physics Search
Abstract
1. Introduction
2. Fifth-Force Model
3. Nuclear Size and Polarization Effects
3.1. Radii Uncertainty
3.2. Nuclear Model Uncertainty
3.3. Nuclear Polarization
3.4. Field Shift Correction and Uncertainties
4. Nuclear Recoil Effect
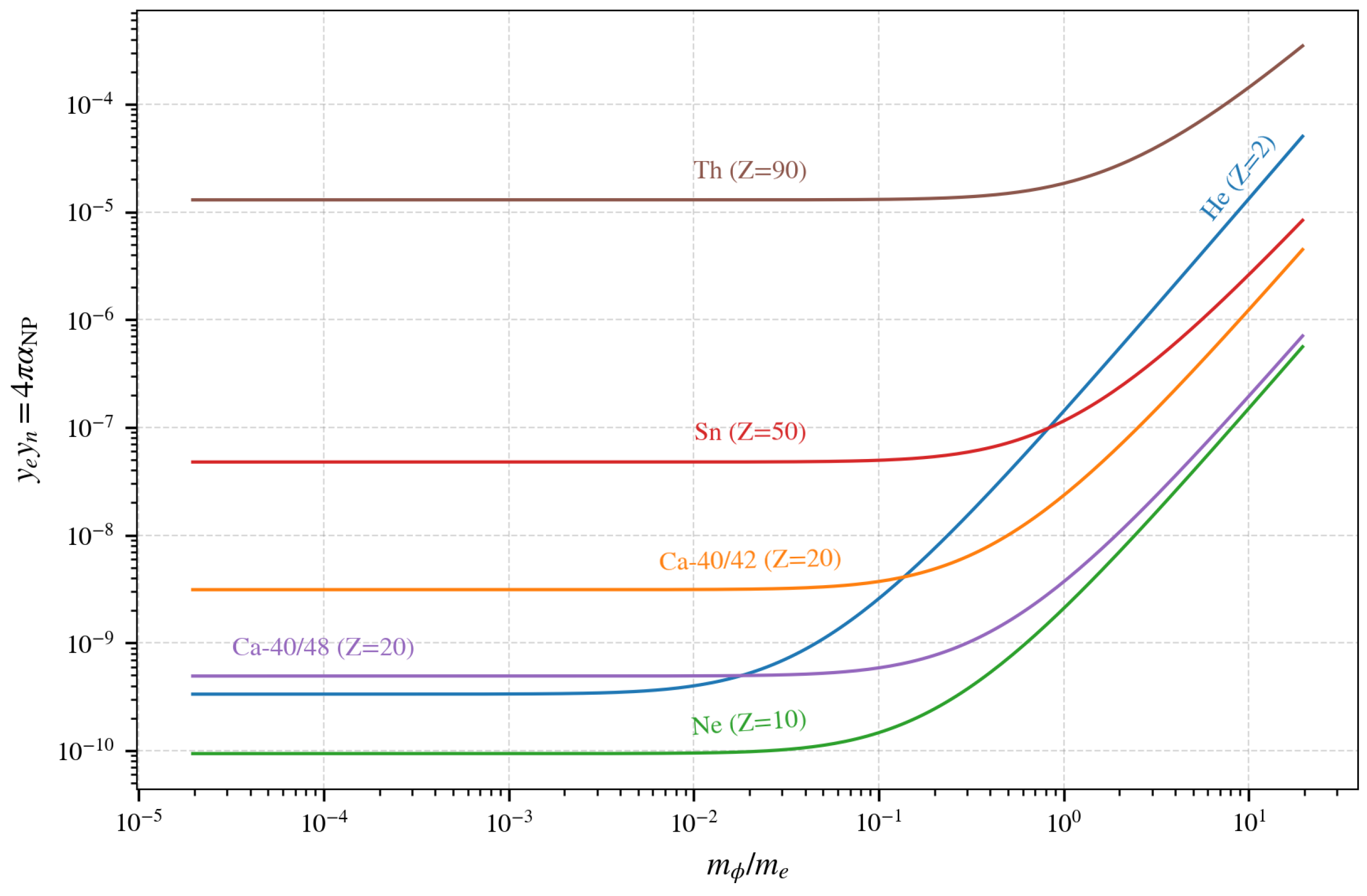
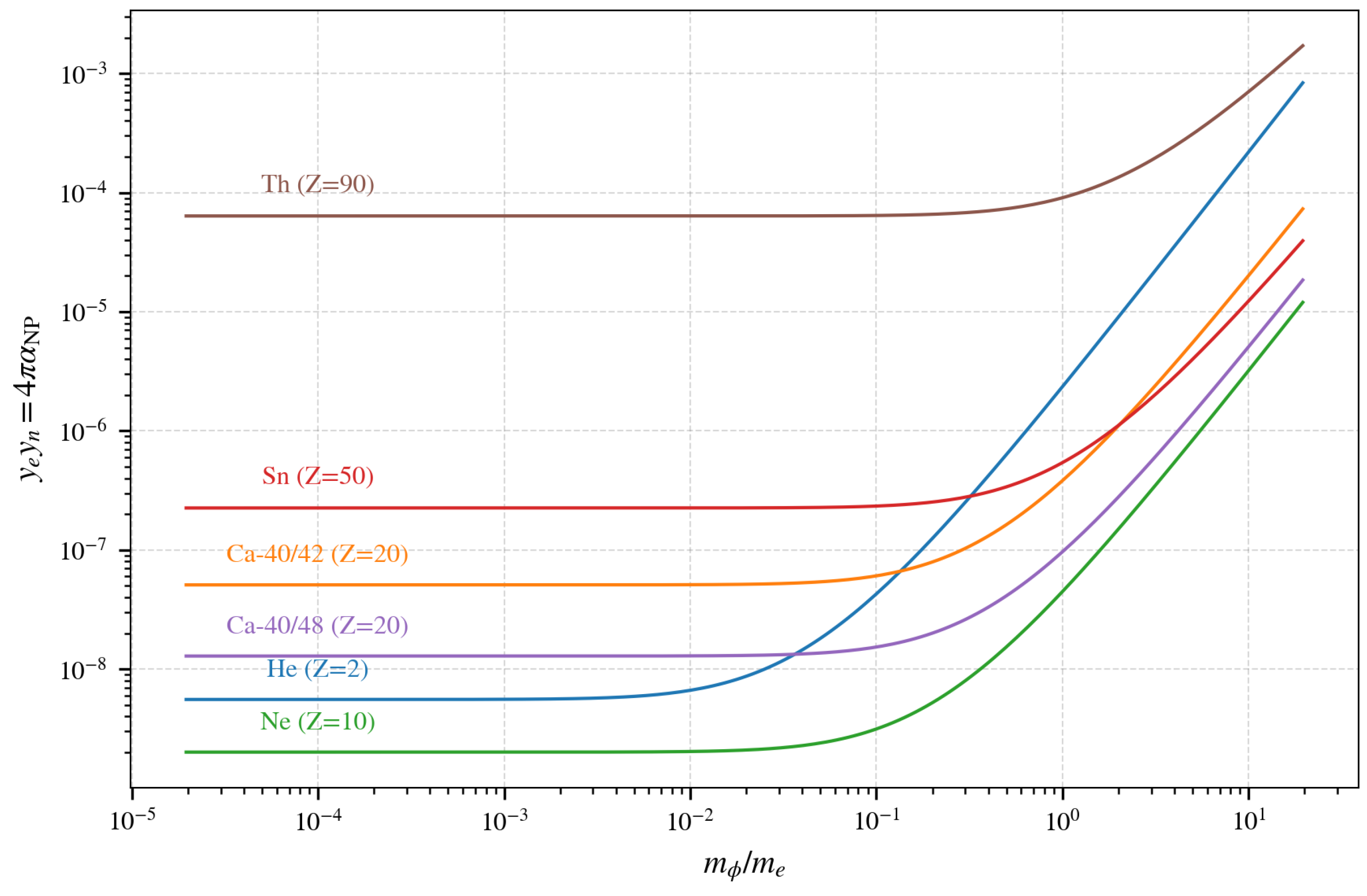
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aoyama, T.; Kinoshita, T.; Nio, M. Theory of the Anomalous Magnetic Moment of the Electron. Atoms 2019, 7, 28. [Google Scholar] [CrossRef]
- Fan, X.; Myers, T.G.; Sukra, B.A.D.; Gabrielse, G. Measurement of the Electron Magnetic Moment. Phys. Rev. Lett. 2023, 130, 071801. [Google Scholar] [CrossRef]
- Sturm, S.; Köhler, F.; Zatorski, J.; Wagner, A.; Harman, Z.; Werth, G.; Quint, W.; Keitel, C.H.; Blaum, K. High-precision measurement of the atomic mass of the electron. Nature 2014, 506, 467. [Google Scholar] [CrossRef]
- Arapoglou, I.; Egl, A.; Höcker, M.; Sailer, T.; Tu, B.; Weigel, A.; Wolf, R.; Cakir, H.; Yerokhin, V.A.; Oreshkina, N.S.; et al. The g-factor of Boronlike Argon 40Ar13+. Phys. Rev. Lett. 2019, 122, 253001. [Google Scholar] [CrossRef]
- Glazov, D.A.; Köhler-Langes, F.; Volotka, A.V.; Blaum, K.; Heiße, F.; Plunien, G.; Quint, W.; Rau, S.; Shabaev, V.M.; Sturm, S.; et al. g Factor of Lithiumlike Silicon: New Challenge to Bound-State QED. Phys. Rev. Lett. 2019, 123, 173001. [Google Scholar] [CrossRef]
- Micke, P.; Leopold, T.; King, S.A.; Benkler, E.; Spieß, L.; Schmöger, L.; Schwarz, M.; Crespo López-Urrutia, J.R.; Schmidt, P.O. Coherent Laser Spectroscopy of Highly Charged Ions Using Quantum Logic. Nature 2020, 578, 60–65. [Google Scholar] [CrossRef]
- Köhler, F.; Blaum, K.; Block, M.; Chenmarev, S.; Eliseev, S.; Glazov, D.A.; Goncharov, M.; Hou, J.; Kracke, A.; Nesterenko, D.A.; et al. Isotope dependence of the Zeeman effect in lithium-like calcium. Nat. Commun. 2016, 7, 10246. [Google Scholar] [CrossRef]
- Blaum, K.; Eliseev, S.; Sturm, S. High-Precision Mass Measurements and Their Impact on Fundamental Constants and Tests of the Standard Model. Quantum Sci. Technol. 2021, 6, 014002. [Google Scholar] [CrossRef]
- Morgner, J.; Tu, B.; König, C.; Sailer, T.; Heiße, F.; Bekker, H.; Sikora, B.; Lyu, C.; Yerokhin, V.A.; Harman, Z.; et al. Stringent test of QED with hydrogen-like tin. Nature 2023, 622, 53–57. [Google Scholar] [CrossRef]
- Morgner, J.; Tu, B.; Moretti, M.; König, C.M.; Heiße, F.; Sailer, T.; Yerokhin, V.A.; Sikora, B.; Oreshkina, N.S.; Harman, Z.; et al. g Factor of Boronlike Tin. Phys. Rev. Lett. 2025, 134, 123201. [Google Scholar] [CrossRef]
- Sailer, T.; Debierre, V.; Harman, Z.; Heiße, F.; König, C.; Morgner, J.; Tu, B.; Volotka, A.V.; Keitel, C.H.; Blaum, K.; et al. Measurement of the bound-electron g-factor difference in coupled ions. Nature 2022, 606, 479–483. [Google Scholar] [CrossRef] [PubMed]
- Glazov, D.; Zinenko, D.; Agababaev, V.; Moshkin, A.; Tryapitsyna, E.; Volchkova, A.; Volotka, A. g Factor of Few-Electron Highly Charged Ions. Atoms 2023, 11, 119. [Google Scholar] [CrossRef]
- Shabaev, V.M.; Glazov, D.A.; Plunien, G.; Volotka, A.V. Theory of bound-electron g factor in highly charged ions. J. Phys. Chem. Ref. Data 2015, 44, 031205. [Google Scholar] [CrossRef]
- Volotka, A.V.; Plunien, G. Nuclear Polarization Study: New Frontiers for Tests of QED in Heavy Highly Charged Ions. Phys. Rev. Lett. 2014, 113, 023002. [Google Scholar] [CrossRef]
- Mohr, P.J.; Plunien, G.; Soff, G. QED corrections in heavy atoms. Phys. Rep. 1998, 293, 227–369. [Google Scholar] [CrossRef]
- Nefiodov, A.V.; Plunien, G.; Soff, G. Nuclear-polarization correction to the bound-electron g factor in heavy hydrogenlike ions. Phys. Rev. Lett. 2002, 89, 081802. [Google Scholar] [CrossRef]
- Rinker, G.A.; Speth, J. Nuclear polarization in muonic atoms. Nucl. Phys. A 1978, 306, 397–405. [Google Scholar] [CrossRef]
- Kozhedub, Y.S.; Andreev, O.V.; Shabaev, V.M.; Tupitsyn, I.I.; Brandau, C.; Kozhuharov, C.; Plunien, G.; Stöhlker, T. Nuclear Deformation Effect on the Binding Energies in Heavy Ions. Phys. Rev. A 2008, 77, 032501. [Google Scholar] [CrossRef]
- Sun, Z.; Valuev, I.A.; Oreshkina, N.S. Nuclear Deformation Effects in the Spectra of Highly Charged Ions. Phys. Rev. Res. 2024, 6, 023327. [Google Scholar] [CrossRef]
- Glazov, D.A.; Shabaev, V.M. Finite nuclear size correction to the bound-electron g factor in a hydrogenlike atom. Phys. Lett. A 2002, 297, 408–411. [Google Scholar] [CrossRef]
- Zwicky, F. Die Rotverschiebung von extragalaktischen Nebeln. Helv. Phys. Acta 1933, 6, 110–127. [Google Scholar] [CrossRef]
- Graham, P.W.; Kaplan, D.E.; Rajendran, S. Cosmological Relaxation of the Electroweak Scale. Phys. Rev. Lett. 2015, 115, 221801. [Google Scholar] [CrossRef] [PubMed]
- Sakharov, A.D. Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe. JETP Lett. 1967, 5, 32–35. [Google Scholar]
- Debierre, V.; Keitel, C.H.; Harman, Z. Fifth-force search with the bound-electron g factor. Phys. Lett. B 2020, 807, 135527. [Google Scholar] [CrossRef]
- Debierre, V.; Oreshkina, N.S.; Valuev, I.A.; Harman, Z.; Keitel, C.H. Testing standard-model extensions with isotope shifts in few-electron ions. Phys. Rev. A 2022, 106, 062801. [Google Scholar] [CrossRef]
- Shabaev, V.M.; Glazov, D.A.; Malyshev, A.V.; Tupitsyn, I.I. Recoil Effect on the g Factor of Li-Like Ions. Phys. Rev. Lett. 2017, 119, 263001. [Google Scholar] [CrossRef]
- Shabaev, V.M.; Glazov, D.A.; Malyshev, A.V.; Tupitsyn, I.I. Nuclear recoil effect on the g factor of highly charged Li-like ions. Phys. Rev. A 2018, 98, 032512. [Google Scholar] [CrossRef]
- Shabaev, V.M.; Yerokhin, V.A. Recoil correction to the bound-electron g factor in H-like atoms to all orders in αZ. Phys. Rev. Lett. 2002, 88, 091801. [Google Scholar] [CrossRef]
- Arcadi, G.; Djouadi, A.; Raidal, M. Dark Matter through the Higgs portal. Phys. Rep. 2020, 842, 1–180. [Google Scholar] [CrossRef]
- Shabaev, V.M.; Tupitsyn, I.I.; Yerokhin, V.A.; Plunien, G.; Soff, G. Dual Kinetic Balance Approach to Basis-Set Expansions for the Dirac Equation. Phys. Rev. Lett. 2004, 93, 130405. [Google Scholar] [CrossRef]
- Angeli, I.; Marinova, K.P. Table of experimental nuclear ground state charge radii: An update. At. Data Nucl. Data Tables 2013, 99, 69–95. [Google Scholar] [CrossRef]
- Fricke, G.; Heilig, K. Nuclear Charge Radii; Springer: Berlin/Heidelberg, Germany, 2004; pp. 18–350. [Google Scholar] [CrossRef]
- Mårtensson-Pendrill, A.M.; Ynnerman, A.; Warston, H.; Vermeeren, L.; Silverans, R.E.; Klein, A.; Neugart, R.; Schulz, C.; Lievens, P. The ISOLDE Collaboration. Isotope Shifts and Nuclear-Charge Radii in Singly Ionized 40–48Ca. Phys. Rev. A 1992, 45, 4675–4681. [Google Scholar] [CrossRef] [PubMed]
- De Vries, H.; De Jager, C.W.; De Vries, C. Nuclear Charge-Density-Distribution Parameters from Elastic Electron Scattering. At. Data Nucl. Data Tables 1987, 36, 495–536. [Google Scholar] [CrossRef]
- Pieper, S.C.; Wiringa, R.B. Quantum Monte Carlo Calculations of Light Nuclei. Annu. Rev. Nucl. Part. Sci. 2001, 51, 53–90. [Google Scholar] [CrossRef]
- Friar, J.L.; Schwieger, J.; Faessler, A.; Kosmas, T.S. Nuclear Size Effects in Light Atoms. Phys. Rev. C 1997, 56, 2830–2835. [Google Scholar] [CrossRef]
- Johnson, W.R.; Blundell, S.A.; Sapirstein, J. Finite basis sets for the Dirac equation constructed from B splines. Phys. Rev. A 1988, 37, 307–315. [Google Scholar] [CrossRef]
- Shabaev, V.M. QED theory of the nuclear recoil effect on the atomic g factor. Phys. Rev. A 2001, 64, 052104. [Google Scholar] [CrossRef]
- Grotch, H.; Hegstrom, R.A. Hydrogenic Atoms in a Magnetic Field. Phys. Rev. A 1971, 4, 59–69. [Google Scholar] [CrossRef]
- Pachucki, K. Nuclear mass correction to the magnetic interaction of atomic systems. Phys. Rev. A 2008, 78, 012504. [Google Scholar] [CrossRef]
- Close, F.E.; Osborn, H. Relativistic extension of the electromagnetic current for composite systems. Phys. Lett. B 1971, 34, 400–404. [Google Scholar] [CrossRef]
- Eides, M.I.; Grotch, H. Gyromagnetic Ratios of Bound Particles. Ann. Phys. 1997, 260, 191–200. [Google Scholar] [CrossRef]
- Eides, M.I.; Martin, T.J.S. Universal Binding and Recoil Corrections to Bound State g Factors in Hydrogenlike Ions. Phys. Rev. Lett. 2010, 105, 100402. [Google Scholar] [CrossRef] [PubMed]

| Contribution | ||||||
|---|---|---|---|---|---|---|
| −0.019 | 0.224 | −181 | ||||
| −0.019 | 2.57 | 4.84 | ||||
| −0.02 | 1.78 | −0.258 | ||||
| 0.033 | 181 |
| Contribution | ||||||
|---|---|---|---|---|---|---|
| 0.017 | 0.03 | 1.53 | 1.55 | 9560 |
| Contribution | ||||||
|---|---|---|---|---|---|---|
| 19.9 | 2180 |
| Contribution | ||||||
|---|---|---|---|---|---|---|
| FNS | 0.17 | −1.99 | −332 | −4720 | ||
| NP | ≤10−6 | −0.136 | 59.3 |
| Contribution | ||||||
|---|---|---|---|---|---|---|
| ≤0.0001 | ≤0.0001 | 29.64 | ||||
| 0.033 | 181 | |||||
| 19.9 | 2180 |
| Contribution | ||||||
|---|---|---|---|---|---|---|
Non-QED | 9.780 | 13.276 | 13.882 | 48.622 | 54.49 | 7.3 |
QED | 0.0005 | 0.0436 | 0.2598 | 0.9100 | 10.4496 | 10.939 |
| −0.0076 | −0.0103 | −0.0108 | −0.0377 | −0.043 | −0.007 | |
| −0.0067 | −0.0077 | −0.0078 | −0.0257 | −0.025 | −0.004 | |
| 9.7662 | 13.3012 | 14.1232 | 49.4686 | 64.8716 | 18.228 |
| Contribution | ||||||
|---|---|---|---|---|---|---|
| ≤0.0001 | ≤0.0001 | ≤0.0001 | ≤0.0001 | 0.01 | 0.5 | |
| ≤0.0001 | ≤0.0001 | ≤0.0001 | ≤0.0001 | 0.0002 | 0.003 | |
| ≤0.0001 | ≤0.0001 | 0.0002 | 0.0008 | 0.006 | 0.003 | |
| ≤0.0001 | ≤0.0001 | 0.0002 | 0.0005 | 0.003 | 0.002 | |
| ≤0.0001 | ≤0.0001 | 0.0004 | 0.0013 | 0.0192 | 0.508 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akulov, D.S.; Abdullin, R.R.; Chubukov, D.V.; Glazov, D.A.; Volotka, A.V. g-Factor Isotopic Shifts: Theoretical Limits on New Physics Search. Atoms 2025, 13, 52. https://doi.org/10.3390/atoms13060052
Akulov DS, Abdullin RR, Chubukov DV, Glazov DA, Volotka AV. g-Factor Isotopic Shifts: Theoretical Limits on New Physics Search. Atoms. 2025; 13(6):52. https://doi.org/10.3390/atoms13060052
Chicago/Turabian StyleAkulov, Dmitry S., Rinat R. Abdullin, Dmitry V. Chubukov, Dmitry A. Glazov, and Andrey V. Volotka. 2025. "g-Factor Isotopic Shifts: Theoretical Limits on New Physics Search" Atoms 13, no. 6: 52. https://doi.org/10.3390/atoms13060052
APA StyleAkulov, D. S., Abdullin, R. R., Chubukov, D. V., Glazov, D. A., & Volotka, A. V. (2025). g-Factor Isotopic Shifts: Theoretical Limits on New Physics Search. Atoms, 13(6), 52. https://doi.org/10.3390/atoms13060052








