UK APAP R-Matrix Electron-Impact Excitation Cross-Sections for Modelling Laboratory and Astrophysical Plasma
Abstract
1. Introduction
2. Methods
3. Atomic Data
3.1. H-like and He-like Ions
3.2. Li-like Ions
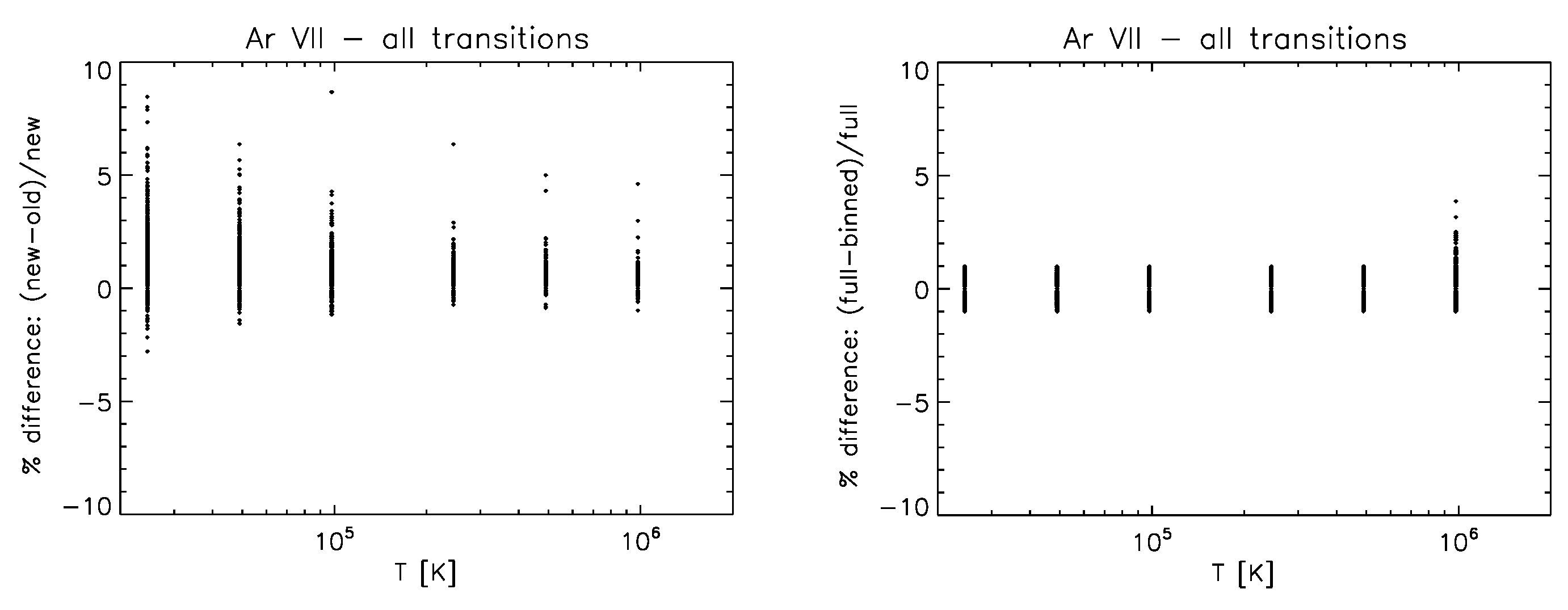
3.3. Be-like Ions
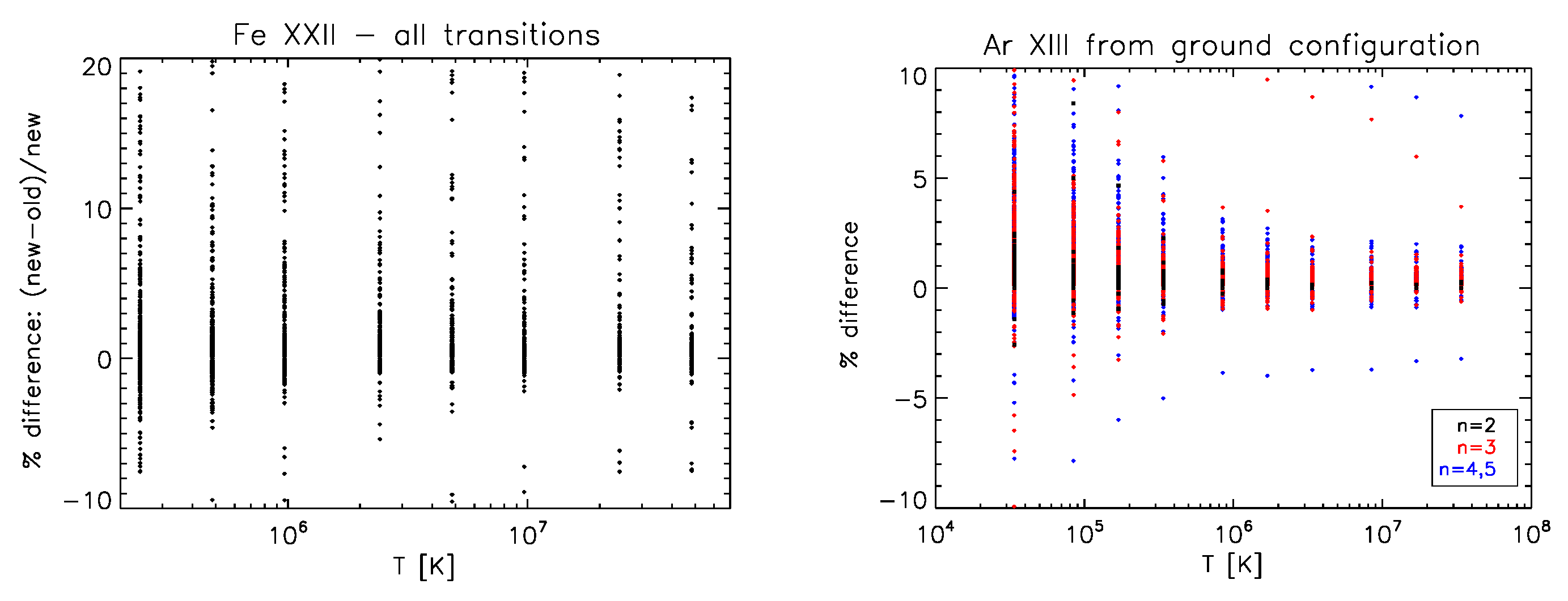
3.4. B-like Ions
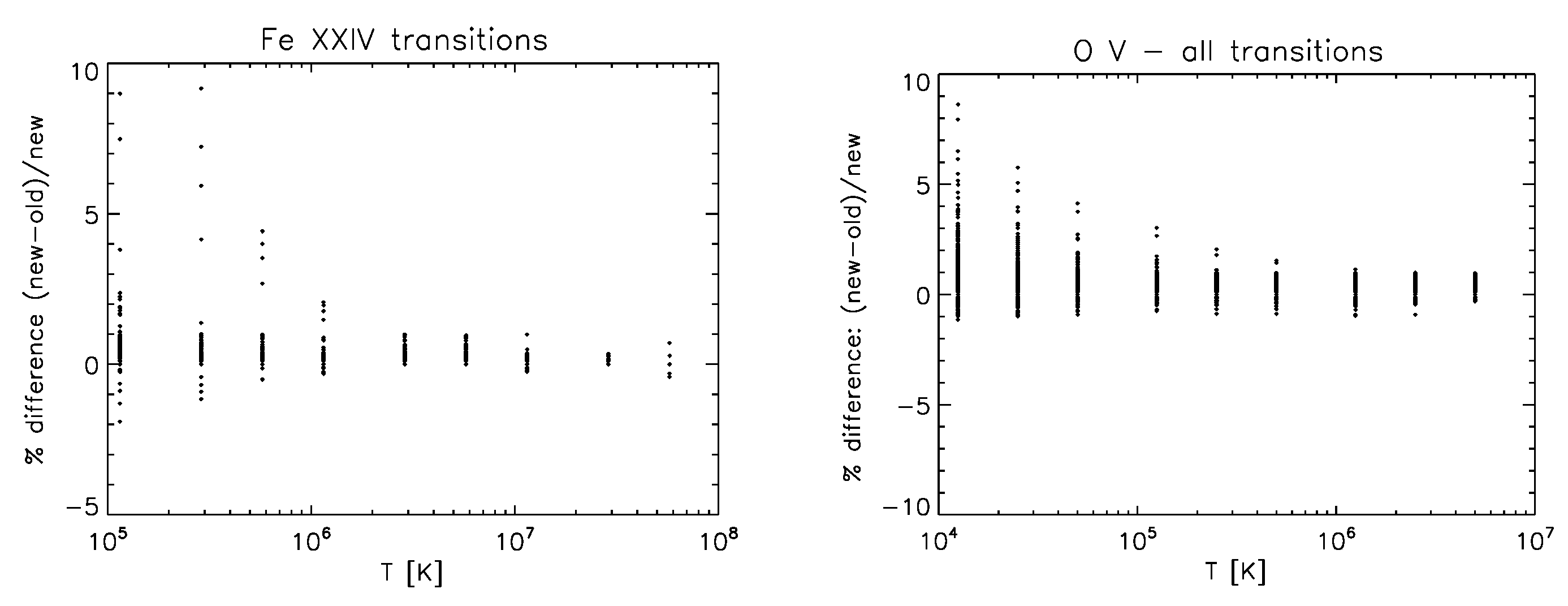
3.5. C-like Ions
3.6. N-like Ions
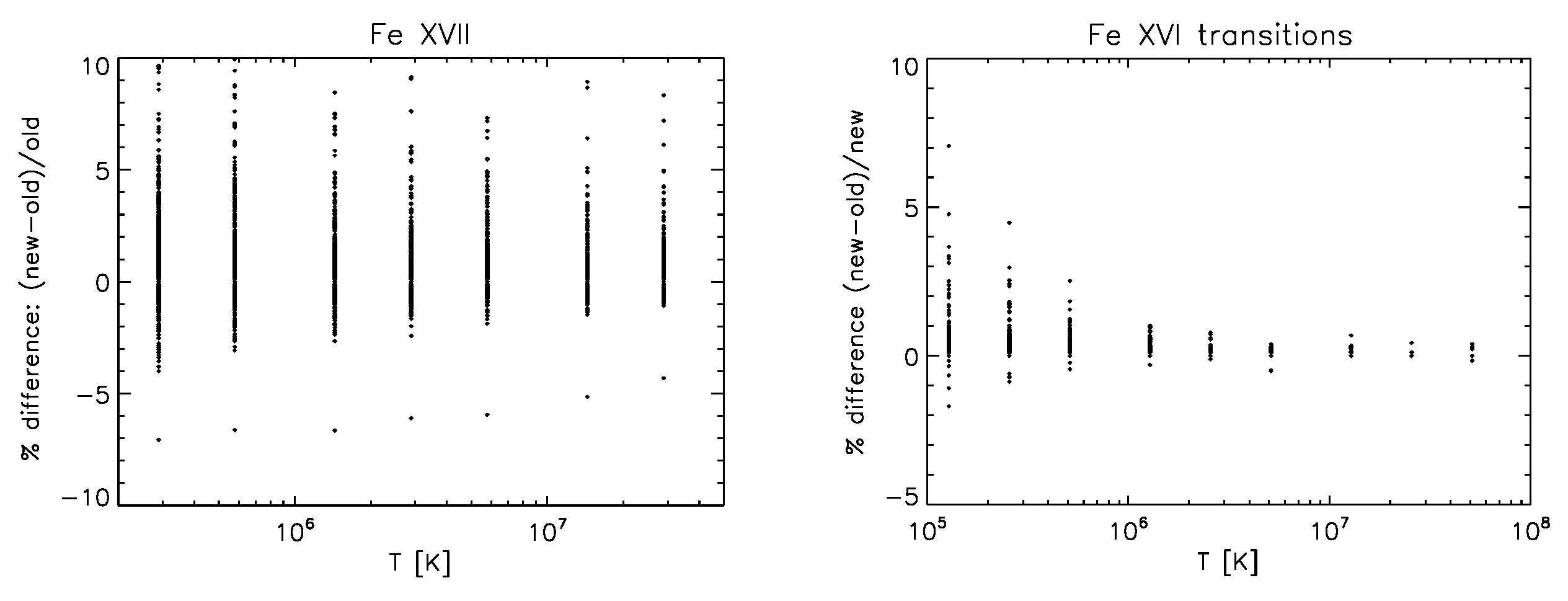
3.7. O-like Ions
3.8. Ne-like Ions
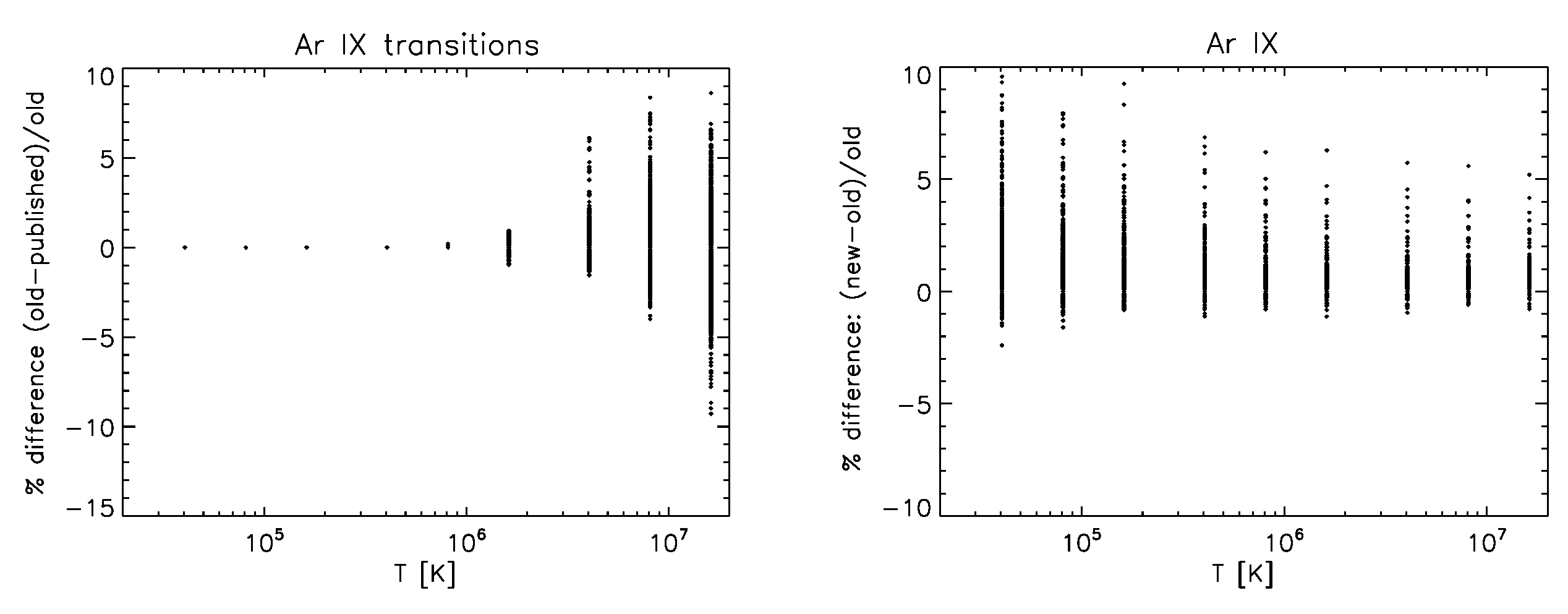
3.9. Na-like Ions
3.10. Mg-like Ions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |
References
- Seaton, M.J. Atomic data for opacity calculations. I. General description. J. Phys. B At. Mol. Phys. 1987, 20, 6363–6378. [Google Scholar] [CrossRef]
- Hummer, D.G.; Berrington, K.A.; Eissner, W.; Pradhan, A.K.; Saraph, H.E.; Tully, J.A. Atomic data from the IRON project. I. Goals and methods. Astron. Astrophys. 1993, 279, 298–309. [Google Scholar]
- Badnell, N.R. A perturbative approach to the coupled outer-region equations for the electron-impact excitation of neutral atoms. J. Phys. B At. Mol. Phys. 1999, 32, 5583–5591. [Google Scholar] [CrossRef]
- Badnell, N.R. A Breit-Pauli distorted wave implementation for AUTOSTRUCTURE. Comput. Phys. Commun. 2011, 182, 1528–1535. [Google Scholar] [CrossRef]
- Chidichimo, M.C.; Badnell, N.R.; Tully, J.A. Atomic data from the IRON Project. LII. Electron excitation of Ni+24. Astron. Astrophys. 2003, 401, 1177–1183. [Google Scholar] [CrossRef]
- Chidichimo, M.C.; Del Zanna, G.; Mason, H.E.; Badnell, N.R.; Tully, J.A.; Berrington, K.A. Atomic data from the IRON Project = 2, 3, 4 configurations. LVI. Electron excitation of Be-like Fe XXIII for the n = 2,3,4 configurations. Astron. Astrophys. 2005, 430, 331–341. [Google Scholar] [CrossRef]
- Del Zanna, G.; Mason, H.E. Solar UV and X-ray spectral diagnostics. Living Rev. Sol. Phys. 2018, 15, 5. [Google Scholar] [CrossRef]
- Badnell, N.R.; Del Zanna, G.; Fernández-Menchero, L.; Giunta, A.S.; Liang, G.Y.; Mason, H.E.; Storey, P.J. Atomic processes for astrophysical plasmas. J. Phys. B At. Mol. Phys. 2016, 49, 094001. [Google Scholar] [CrossRef]
- Del Zanna, G.; Dere, K.P.; Young, P.R.; Landi, E.; Mason, H.E. CHIANTI—An atomic database for emission lines. Version 8. Astron. Astrophys. 2015, 582, A56. [Google Scholar] [CrossRef]
- Del Zanna, G.; Dere, K.P.; Young, P.R.; Landi, E. CHIANTI—An Atomic Database for Emission Lines. XVI. Version 10, Further Extensions. Astrophys. J. 2021, 909, 38. [Google Scholar] [CrossRef]
- Ljepojevic, N.N.; Burgess, A. Calculation of the electron velocity distribution function in a plasma slab with large temperature and density gradients. Proc. R. Soc. Lond. Ser. A 1990, 428, 71–111. [Google Scholar] [CrossRef]
- Dudík, J.; Dzifčáková, E.; Meyer-Vernet, N.; Del Zanna, G.; Young, P.R.; Giunta, A.; Sylwester, B.; Sylwester, J.; Oka, M.; Mason, H.E. Nonequilibrium Processes in the Solar Corona, Transition Region, Flares, and Solar Wind (Invited Review). Sol. Phys. 2017, 292, 100. [Google Scholar] [CrossRef]
- Lörinčík, J.; Dudík, J.; Del Zanna, G.; Dzifčáková, E.; Mason, H.E. Plasma Diagnostics from Active Region and Quiet-Sun Spectra Observed by Hinode/EIS: Quantifying the Departures from a Maxwellian Distribution. Astrophys. J. 2020, 893, 34. [Google Scholar] [CrossRef]
- Del Zanna, G.; Polito, V.; Dudík, J.; Testa, P.; Mason, H.E.; Dzifčáková, E. Diagnostics of Non-Maxwellian Electron Distributions in Solar Active Regions from Fe XII Lines Observed by the Hinode Extreme Ultraviolet Imaging Spectrometer and Interface Region Imaging Spectrograph. Astrophys. J. 2022, 930, 61. [Google Scholar] [CrossRef]
- Nicholls, D.C.; Dopita, M.A.; Sutherland, R.S. Resolving the Electron Temperature Discrepancies in H II Regions and Planetary Nebulae: κ-distributed Electrons. Astrophys. J. 2012, 752, 148. [Google Scholar] [CrossRef]
- Storey, P.J.; Sochi, T. Effective collision strengths for excitation and de-excitation of nebular [O III] optical and infrared lines with κ distributed electron energies. Mon. Not. R. Astron. Soc. 2015, 449, 2974–2979. [Google Scholar] [CrossRef][Green Version]
- Griffin, D.C.; Badnell, N.R.; Pindzola, M.S. R-matrix electron-impact excitation cross sections in intermediate coupling: An MQDT transformation approach. J. Phys. B At. Mol. Phys. 1998, 31, 3713–3727. [Google Scholar] [CrossRef]
- Berrington, K.A.; Eissner, W.B.; Norrington, P.H. RMATRX1: Belfast atomic R-matrix codes. Comput. Phys. Commun. 1995, 92, 290–420. [Google Scholar] [CrossRef]
- Zatsarinny, O. BSR: B-spline atomic R-matrix codes. Comput. Phys. Commun. 2006, 174, 273–356. [Google Scholar] [CrossRef]
- Norrington, P.H.; Grant, I.P. Electron scattering from Ne II using the relativistic R-matrix method. J. Phys. B At. Mol. Phys. 1981, 14, L261–L267. [Google Scholar] [CrossRef]
- Fernández-Menchero, L.; Zatsarinny, O.; Bartschat, K. Electron impact excitation of N3+ using the B-spline R-matrix method: Importance of the target structure description and the size of the close-coupling expansion. J. Phys. B At. Mol. Phys. 2017, 50, 065203. [Google Scholar] [CrossRef]
- Del Zanna, G.; Fernández-Menchero, L.; Badnell, N.R. Uncertainties on atomic data. A case study: N IV. Mon. Not. R. Astron. Soc. 2019, 484, 4754–4759. [Google Scholar] [CrossRef]
- Burgess, A.; Chidichimo, M.C.; Tully, J.A. High-energy Born collision strengths for optically forbidden transitions. J. Phys. B At. Mol. Phys. 1997, 30, 33–57. [Google Scholar] [CrossRef]
- Burgess, A.; Tully, J.A. On the Analysis of Collision Strengths and Rate Coefficients. Astron. Astrophys. 1992, 254, 436. [Google Scholar]
- Whiteford, A.D.; Badnell, N.R.; Ballance, C.P.; O’Mullane, M.G.; Summers, H.P.; Thomas, A.L. A radiation-damped R-matrix approach to the electron-impact excitation of helium-like ions for diagnostic application to fusion and astrophysical plasmas. J. Phys. B At. Mol. Phys. 2001, 34, 3179–3191. [Google Scholar] [CrossRef]
- Mao, J.; Del Zanna, G.; Gu, L.; Zhang, C.Y.; Badnell, N.R. R-matrix Electron-impact Excitation Data for the H- and He-like Ions with Z = 6-30. Astrophys. J. Suppl. 2022, 263, 35. [Google Scholar] [CrossRef]
- Gorczyca, T.W.; Badnell, N.R. LETTER TO THE EDITOR: Radiation damping in highly charged ions: An R-matrix approach. J. Phys. B At. Mol. Phys. 1996, 29, L283–L290. [Google Scholar] [CrossRef]
- Griffin, D.C.; Ballance, C.P. Relativistic radiatively damped R-matrix calculations of the electron-impact excitation of helium-like iron and krypton. J. Phys. B At. Mol. Phys. 2009, 42, 235201. [Google Scholar] [CrossRef]
- Fernández-Menchero, L.; Del Zanna, G.; Badnell, N.R. Scaling of collision strengths for highly-excited states of ions of the H- and He-like sequences. Astron. Astrophys. 2016, 592, A135. [Google Scholar] [CrossRef]
- Liang, G.Y.; Badnell, N.R. R-matrix electron-impact excitation data for the Li-like iso-electronic sequence including Auger and radiation damping. Astron. Astrophys. 2011, 528, A69. [Google Scholar] [CrossRef]
- Del Zanna, G.; Rozum, I.; Badnell, N. Electron-impact excitation of Be-like Mg. Astron. Astrophys. 2008, 487, 1203–1208. [Google Scholar] [CrossRef]
- Fernández-Menchero, L.; Del Zanna, G.; Badnell, N.R. R-matrix electron-impact excitation data for the Be-like iso-electronic sequence. Astron. Astrophys. 2014, 566, A104. [Google Scholar] [CrossRef]
- Liang, G.Y.; Badnell, N.R.; Zhao, G. R-matrix electron-impact excitation data for the B-like iso-electronic sequence. Astron. Astrophys. 2012, 547, A87. [Google Scholar] [CrossRef]
- Badnell, N.R.; Griffin, D.C.; Mitnik, D.M. Electron-impact excitation of Fe21+, including n = 4 levels. J. Phys. B At. Mol. Phys. 2001, 34, 5071–5085. [Google Scholar] [CrossRef]
- Fernández-Menchero, L.; Giunta, A.S.; Del Zanna, G.; Badnell, N.R. Importance of the completeness of the configuration interaction and close coupling expansions in R-matrix calculations for highly charged ions: Electron-impact excitation of Fe20+. J. Phys. B At. Mol. Phys. 2016, 49, 085203. [Google Scholar] [CrossRef]
- Mao, J.; Badnell, N.R.; Del Zanna, G. R-matrix electron-impact excitation data for the C-like iso-electronic sequence. Astron. Astrophys. 2020, 634, A7. [Google Scholar] [CrossRef]
- Witthoeft, M.C.; Whiteford, A.D.; Badnell, N.R. R-matrix electron-impact excitation calculations along the F-like iso-electronic sequence. J. Phys. B At. Mol. Phys. 2007, 40, 2969–2993. [Google Scholar] [CrossRef]
- Mao, J.; Badnell, N.R.; Del Zanna, G. R-matrix electron-impact excitation data for the N-like iso-electronic sequence. Astron. Astrophys. 2020, 643, A95. [Google Scholar] [CrossRef]
- Butler, K.; Badnell, N.R. Atomic data from the IRON project. LXVI. Electron impact excitation of Fe18+. Astron. Astrophys. 2008, 489, 1369–1376. [Google Scholar] [CrossRef][Green Version]
- Mao, J.; Badnell, N.R.; Del Zanna, G. R-matrix electron-impact excitation data for the O-like iso-electronic sequence. Astron. Astrophys. 2021, 653, A81. [Google Scholar] [CrossRef]
- Liang, G.Y.; Badnell, N.R. R-matrix electron-impact excitation data for the Ne-like iso-electronic sequence. Astron. Astrophys. 2010, 518, A64. [Google Scholar] [CrossRef]
- Del Zanna, G. Benchmarking atomic data for astrophysics: Fe XVII X-ray lines. Astron. Astrophys. 2011, 536, A59. [Google Scholar] [CrossRef]
- Loch, S.D.; Pindzola, M.S.; Ballance, C.P.; Griffin, D.C. The effects of radiative cascades on the X-ray diagnostic lines of Fe16+. J. Phys. B At. Mol. Phys. 2006, 39, 85–104. [Google Scholar] [CrossRef]
- Liang, G.Y.; Whiteford, A.D.; Badnell, N.R. R-matrix electron-impact excitation data for the Na-like iso-electronic sequence. Astron. Astrophys. 2009, 500, 1263–1269. [Google Scholar] [CrossRef]
- Liang, G.Y.; Whiteford, A.D.; Badnell, N.R. R-matrix inner-shell electron-impact excitation of the Na-like iso-electronic sequence. J. Phys. B At. Mol. Phys. 2009, 42, 225002. [Google Scholar] [CrossRef]
- Fernández-Menchero, L.; Del Zanna, G.; Badnell, N.R. R-matrix electron-impact excitation data for the Mg-like iso-electronic sequence. Astron. Astrophys. 2014, 572, A115. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Del Zanna, G.; Liang, G.; Mao, J.; Badnell, N.R. UK APAP R-Matrix Electron-Impact Excitation Cross-Sections for Modelling Laboratory and Astrophysical Plasma. Atoms 2025, 13, 44. https://doi.org/10.3390/atoms13050044
Del Zanna G, Liang G, Mao J, Badnell NR. UK APAP R-Matrix Electron-Impact Excitation Cross-Sections for Modelling Laboratory and Astrophysical Plasma. Atoms. 2025; 13(5):44. https://doi.org/10.3390/atoms13050044
Chicago/Turabian StyleDel Zanna, Giulio, Guiyun Liang, Junjie Mao, and Nigel R. Badnell. 2025. "UK APAP R-Matrix Electron-Impact Excitation Cross-Sections for Modelling Laboratory and Astrophysical Plasma" Atoms 13, no. 5: 44. https://doi.org/10.3390/atoms13050044
APA StyleDel Zanna, G., Liang, G., Mao, J., & Badnell, N. R. (2025). UK APAP R-Matrix Electron-Impact Excitation Cross-Sections for Modelling Laboratory and Astrophysical Plasma. Atoms, 13(5), 44. https://doi.org/10.3390/atoms13050044





