Abstract
Triple-differential cross-sections for the positron impact ionization of argon were calculated using a distorted-wave Born approximation (DWBA) convoluted to the experimental uncertainties. In almost all of the cases studied, our results agree well with the positions and heights of the experimental peaks.
1. Introduction
Triple-differential cross-sections (TDCSs) are obtained in experiments in which all of the energies and directions of the particles involved in the ionization process are determined. Ionization through the impact of electrons has been widely investigated, while studies including the positron projectiles are a relatively new field of investigation. The low positron beam currents available make the experimental TDCSs less reliable. Coincidence techniques that use the same apparatus to determine both electron and positron impact ionization of an atom allow for calibration of the positron impact data. There have been several experimental studies of the ionization of argon () through the impact of electrons and positrons using coincidence techniques [1,2,3]. One determined the TDCS data corresponding to 1000 eV projectiles [1], and another obtained TDCSs corresponding to 200 eV projectiles [2]. In the case studied by de Lucio et al. [2], the energy of the ejected electron energy was 5.4 ± 3 eV, and the positron was scattered at an angle of °. These experimental uncertainties were used in the calculation of the TDCSs using a convoluted continuum-distorted-wave-eikonal-initial-state (CDW-EIS) approximation. This theoretical approach provided data in good agreement with that from the experiment. An analysis of the experimental data of de Lucio et al. [2] was recently modified to obtain improved statistics by DuBois et al. [3]. Their paper studied the ionization of argon using 200 eV incident positrons for six ejected electron energies between 2.6 eV and 19 eV and for three positron scattering angles (2, 3, and 4 degrees).
One of the most popular methods for producing theoretical TDCSs is the distorted-wave Born approximation (DWBA). This theory was compared with the experimental data from ref. [1] by Campeanu et al. [4] and with the experimental data from ref. [2] by Campeanu and Alam [5]. In the present paper, we shall discuss the agreement between the convoluted DWBA and the experimental data from ref. [3]. A similar paper was recently published by Zaidi et al. [6], which used the non-convoluted 3CWZ theoretical approximation.
2. The Theory
The DWBA has been described in detail in several papers, such as that by Campeanu et al. [4] or the review paper dealing with the ionization of molecules by Nagy et al. [7]. The first paper [4] studied the ionization of argon for cases using 1000 eV incident positrons and 26 eV ejected electrons. In this scenario, the positron-distorted waves (incident or scattered) were calculated in the static potential of the atom, and the electron-distorted waves were calculated in the static potential of the Ar+ ion. In the current paper, the incident positrons have lower energies (200 eV), and we have had to use a more precise description of the distorted waves.
The triple-differential cross-section for the ionization of the atom can be written as
Here, the k symbols stand for the momenta of the incident (i) or scattered (f) positron and of the ejected (e) electron, respectively, while is the energy of the ejected electron. The scattering amplitude (or t matrix) in the framework of the DWBA is written as the matrix element of the interaction potential of the positron and the active electron taken between the initial and final states of the two particles.
To calculate the incident positron continuum states, we used a field containing the Hartree–Fock models for the static potential of argon and for the target polarization potential. The dipole polarization potential was calculated inside the atomic charge cloud of the atom using the polarized-orbital method [8], while asymptotically, outside the atomic charge cloud, we have a dependence. We used a Hartree–Fock representation of the bound states of argon , obtained using code similar to that used in [8]. In the final state of the ionization system, in all cases of kinematics considered, the scattered positron is faster than the ejected electron. In these conditions, the positron continuum states were calculated in the same way as they were for the incident positron, while the more slowly ejected electron continuum states were calculated in the Coulomb potential of Ar+, plus a Furness–McCarthy (FM) exchange potential [9]. The continuum states were expanded into partial-wave series. In our current calculations, we used 10 partial waves for the ejected electron and 30 partial waves for the incident and scattered positrons. The wavefunction was obtained by solving the radial Schrödinger equation for the scattering states, using the Numerov numerical integration method.
To account for the post-collision interaction (PCI), we used a Coulomb distortion factor, as in [4]. It can be expressed as [10]
Here, G is the Gamow factor
while is the confluent hypergeometric function, , and is the Sommerfeld parameter. represents the relative velocity of the scattered positron and the ejected electron, while is the reduced mass of the two particles. is parallel to and is the average of the actual ejected electron–projectile distance, . It can be expressed as
where is the total energy of the scattered and ejected particles. Finally, the obtained TDCSs are multiplied by the Coulomb distortion factor.
The experimental papers [2,3] suggested that their data had limited statistics because of the low positron beam current, and for a proper comparison with the theory, convolution of the theoretical calculations for a range of energies is needed. The paper by de Lucio et al. [2] contained an elaborate CDW-EIS calculation [11] that, when convoluted, agreed well with the experimental results. In the present paper, for each case studied, we convoluted the DWBA theory by employing a Gauss–Hermite quadrature over five points around the mean ejected electron energy. The Gaussian width for each ejected electron energy was given in the last column of Table 1 in reference [3].
3. Results and Discussion
The theoretical and experimental results correspond to the single ionization of the orbital of argon by a 200 eV positron impact. The experimental cross-sections of DuBois and de Lucio [3] were not measured on an absolute scale but were normalized to each other because the same setup and techniques were used for all ejection energies and scattering angles. In these conditions, we normalize the experimental data to our calculations by applying the same scaling factor for each kinematic situation. With a scaling factor of 0.6, we have obtained the best fit with our convoluted data for the largest ejection energy, where the relative error in the measurement is the smallest.
In Figure 1, Figure 2 and Figure 3, we show our calculated TDCSs along with the experimental data of DuBois and de Lucio [3] for several energies of the ejected electron and three different scattering angles of the positron: 2, 3, and 4 degrees. Besides the primary results (the blue curve), we also represent the convoluted results (the yellow curve), which take into account the relatively large experimental uncertainties in the determination of the ejection energy of the electron. In the case of the experimental data, the black squares represent the measured signal [3], and the red open circles represent the experimental data with corrected statistics [3]. This correction was not needed at higher energies of the ejected electron. In all cases, our convoluted results are below the primary calculations. However, the shape of the curves did not change significantly.
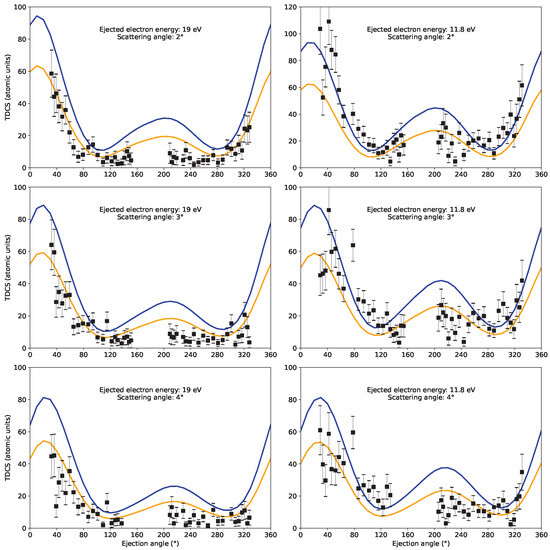
Figure 1.
The variation in the TDCSs with the ejected electron angles when the ejected electron energies are 19 eV (left panel) and 11.8 eV (right panel). The black solid squares show the measured TDCS signals [3]. The two theoretical curves correspond to the DWBA model (the blue curve) and the convoluted DWBA model (the yellow curve).
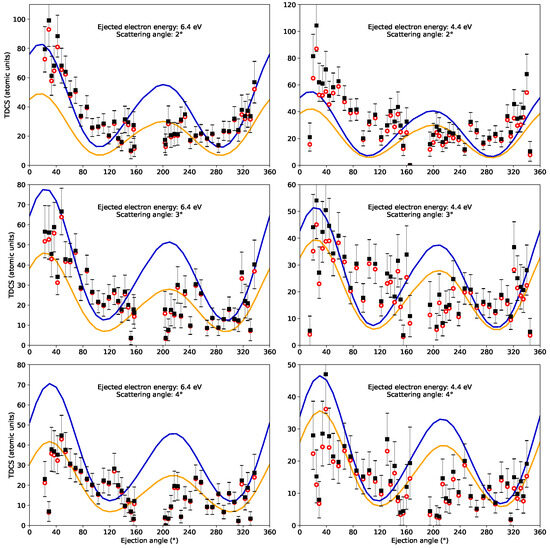
Figure 2.
The variation in the TDCSs with the ejected electron angles when the ejected electron energies are 6.4 eV and 4.4 eV. The black solid squares show the measured TDCS signals, while the red open circles show the values after applying an improved statistical analysis [3]. The two theoretical curves correspond to the DWBA model (the blue curve) and the convoluted DWBA model (the yellow curve).
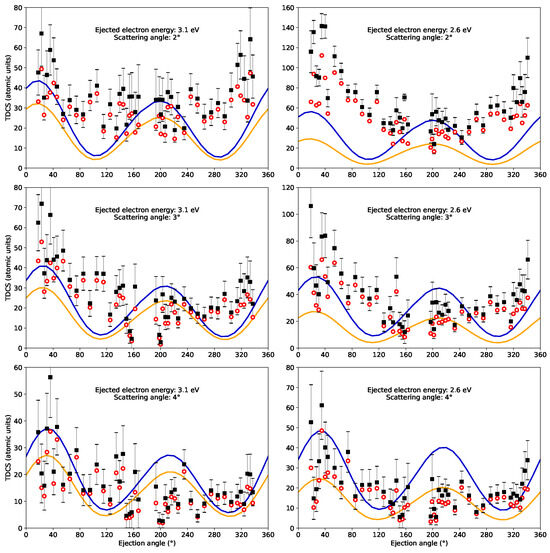
Figure 3.
The same as Figure 2 but for ejected electron energies of 3.1 eV and 2.6 eV.
In Figure 1, the highest two energies of the ejected electrons (19 eV and 11.8 eV) are represented. Our calculations reproduce the binary and recoil peaks detected in the experiment well. For 11.8 eV, the positions of the binary peaks are obtained at slightly smaller angles relative to those in the experiment.
Figure 2 shows graphs for energies of 6.6 eV and 4.4 eV of the ejected electron. Here, in general, we have satisfactory agreement between the experimental data and the corrected statistics (red open circles). However, the quantitative agreement for the smaller angles in our convoluted results with the experimental data is worse, and our binary peak is below that found experimentally for the 2° scattering angle. For a larger scattering angle (4°), the agreement in the recoil peak is worse, but the agreement in the binary peak is quite good.
In Figure 3, we show the results for the lowest ejection energies, 3.1 eV and 2.6 eV. Here, we obtain almost equal binary and recoil peaks. The experimental data have more pronounced binary peaks, and the recoil peak is barely visible. However, in these cases, the data are very scattered, the uncertainty in the ejected electron energy is large, and the comparison with the experiment is not very conclusive. In spite of this problem, we can state that for a 3.1 eV ejection energy, the agreement is fair, as it is even for the larger scattering angles at a 2.6 eV energy. For the lowest, the 2° scattering angle, the agreement is the worst.
4. Conclusions
We have presented theoretical calculations for the TDCSs of argon under ionization using a 200 eV positron impact and compared them with the experimental data [3]. All of our theoretical calculations used the DWBA. We also applied convolution to our calculations for a range of energies around the mean ejected electron energy, accounting for the experimental resolution. When we compared our results with the experiment, we used a single normalization factor. Consequently, we obtained a few cases in which the agreement between the theory and the experiment was not very good, but in most cases, it was quite satisfactory. Our convoluted and unconvoluted DWBA results correctly predicted the positions of the peaks in the binary and recoil regions. The difference between the two calculations is in the height of the predicted peaks, and convolution reduces the value of the cross-sections. The best agreement between the theory and the experiment is achieved using the convoluted DWBA. The only case where the results of the convoluted DWBA are in worse agreement with the experiment than the unconvoluted DWBA results is for 2.6 eV, the lowest ejected electron energy studied in this paper.
Author Contributions
Conceptualization: R.I.C. and L.N. Methodology: R.I.C. and L.N. Software: R.I.C. Investigation: R.I.C. and L.N. Writing—original draft preparation: R.I.C. and L.N. Writing—review and editing: R.I.C., L.N., and Z.B. Visualization: Z.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article; further inquiries can be directed to the corresponding author.
Acknowledgments
We thank R. DuBois for sending us his experimental cross-sections.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CDW-EIS | Continuum-distorted-wave–eikonal-initial-state |
| DWBA | Distorted-wave Born approximation |
| PCI | Post-collision interaction |
| TDCS | Triple-differential cross section |
References
- Gavin, J.; de Lucio, O.G.; DuBois, R.D. Triply differential measurements of single ionization of argon by 1-keV positron and electron impact. Phys. Rev. A 2017, 95, 062703. [Google Scholar] [CrossRef]
- de Lucio, O.G.; Otrano, S.; Olson, R.E.; DuBois, R.D. Triply Differential Single Ionization of Argon: Charge Effects for Positron and Electron Impact. Phys. Rev. Lett. 2010, 104, 163201. [Google Scholar] [CrossRef] [PubMed]
- DuBois, R.D.; de Lucio, O.G. Triply Differential Positron and Electron Impact Ionization of Argon: Systematic Features and Scaling. Atoms 2021, 9, 78. [Google Scholar] [CrossRef]
- Campeanu, R.I.; Walters, H.R.J.; Whelan, C.T. Electron- and positron-impact ionization of inert gases. Phys. Rev. A 2018, 97, 062702. [Google Scholar] [CrossRef]
- Campeanu, R.I.; Alam, M. DWBA calculation of positron impact ionization of argon. J. Phys. Conf. Ser. 2011, 262, 012010. [Google Scholar] [CrossRef]
- Zaidi, O.; Mansouri, A.; Houamer, S.; Tamin, A.; Khatir, T.; Dal Cappello, C. Ionization of argon atom by positron and electron impact. Eur. J. Phys. D 2024, 78, 140. [Google Scholar] [CrossRef]
- Nagy, L.; Tóth, I.; Campeanu, R.I. Electron and Positron Impact Ionization of Molecules. Atoms 2024, 12, 38. [Google Scholar] [CrossRef]
- McEachran, R.P.; Ryman, A.G.; Stauffer, A.D.; Morgan, D.L. Positron scattering from noble gases. J. Phys. B 1977, 10, 663. [Google Scholar] [CrossRef]
- Furness, J.B.; Carthy, I.E.M. Semiphenomenological optical model for electron scattering on atoms. J. Phys. B Atom. Mol. Phys. 1973, 78, 140. [Google Scholar] [CrossRef]
- Ward, S.J.; Macek, J.H. Wave functions for continuum states of charged fragments. Phys. Rev. A 1994, 49, 1049–1056. [Google Scholar] [CrossRef] [PubMed]
- Otranto, S. Initial-state correlation in the electron-impact ionization of argon. Phys. Rev. A 2009, 79, 012705. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).