Revisiting the Influence of Neutron Transfer Coupling on Surface Diffuseness Parameters for Carbon-Induced Fusion Reactions

Abstract

The influence of neutron transfer coupling on surface diffuseness has been thoroughly investigated in the study of carbon-induced fusion reactions. Through analysis of experimental measurements using advanced coupled-channel computational frameworks, we have examined how neutron exchange processes modify nuclear interaction potentials with a particular focus on surface diffuseness parameters. The findings reveal that neutron transfer mechanisms substantially contribute to reducing surface diffuseness values, with this effect being particularly pronounced in reactions involving neutron-rich isotopic combinations. This research highlights the critical importance of incorporating neutron transfer pathways when modeling fusion cross-sections, offering valuable perspectives for subsequent investigations of nuclear reaction dynamics.

1. Introduction

When atomic nuclei collide at energies close to the Coulomb barrier, their internal constituent significantly influences how they interact. During these collisions, the interplay between relative motion and nuclear properties (including excitation states and particle transfers) transforms what would be a single energy barrier into multiple distributed barriers. One can analyze these barrier distributions (BDs) by calculating the second derivative of the energy-weighted fusion cross-section. This mathematical approach reveals intricate details about nuclear structure, making fusion reactions an effective tool for examining nuclear properties, much like using a microscope to study atomic structures through quantum tunneling effects. Though fusion cross-sections offer crucial insights into the dynamic behavior of nuclei during fusion processes, experimental measurements alone do not fully explain the intricate mechanisms governing nuclear interactions [1,2,3]. This limitation necessitates the application of theoretical models, such as coupled-channel (CC) calculations, to capture the interaction between nuclear structure and reaction dynamics. These calculations link relative motion with nuclei’s intrinsic properties, offering key insights into fusion processes when compared with experiments [4,5]. The coupled-channels approach has thus become essential for reconstructing fusion dynamics, with the nuclear interaction potential representation being a critical element. Nuclear potentials can be represented through multiple parameterization approaches, including double-folding models and the commonly employed Woods–Saxon potential. The Woods–Saxon formulation relies on three key parameters: depth ($V_0$), radius ($r_0$), and surface diffuseness ($a_0$) [6,7]. The nuclear potential’s surface diffuseness parameter requires independent determination, unlike depth and radius, which can be calibrated to match the Coulomb barrier. This parameter critically shapes nuclear interactions by controlling the gradual transition at the surface region. Multiple experimental methods exist to determine surface diffuseness, including elastic scattering measurements and high-precision fusion cross-section measurements (requiring larger values for deformed nuclei). Studies indicate surface diffuseness increases with the charge product of reaction partners. Backward-angle quasi-elastic scattering provides another approach, particularly at sub-Coulomb barrier energies. Research shows rotational couplings significantly influence the diffuseness parameter, while vibrational couplings have minimal impact, as demonstrated by Washiyama et al. [8] in their analysis of QE scattering for O-16, S-32,34 + Pb-208 systems. Accurate determination of this parameter is essential for reliable theoretical predictions of nuclear reactions, especially near the Coulomb barrier.

Heavy ion-induced fusion reactions, particularly those involving light projectiles like ¹²C and ¹³C, have been extensively studied to elucidate nuclear reaction mechanisms and dynamics. These investigations often center around sub-barrier fusion, where quantum tunneling is pivotal, and the role of nuclear structure, notably neutron transfer, in influencing fusion probabilities. For example, Hagino et al. [9] explored the fusion of ¹²C with ²⁸Si, offering valuable insights into the interaction potential and fusion dynamics at near-barrier energies. Similarly, Kolata et al. [10] examined the fusion of ¹³C with ²⁰⁸Pb, underscoring the effect of the additional neutron in ¹³C to enhance fusion likelihood. Jiang et al. [11] analyzed the light system ¹²C + ¹⁶O, emphasizing the nuclear structure’s impact on fusion outcomes. Research on sub-barrier fusion has further illuminated the critical role of neutron transfer. Sargsyan et al. [12] demonstrated its influence in the ¹³C + ²⁰⁸Pb system, while Keeley et al. [13] investigated this effect in the nearly symmetric ^12,13,15C + ²⁰⁸Pb systems. A study by Canto et al. [14] clarified the mechanisms by which neutron transfer enhances sub-barrier fusion. In another theoretical approach to understanding C-induced fusion in the sub-barrier region, the effect of nuclear polarization was presented within the Feynman path integral framework, where it was inferred that the friction of collective modes related to the pre-equilibrium nucleon flux in the neck region plays a dominant role in fusion reactions [15]. Together, these studies deepen the understanding of heavy ion-induced fusion, highlighting the interplay between projectile, target selection, and neutron transfer in shaping fusion dynamics, with significant implications for fundamental nuclear physics and astrophysical applications.

Other existing studies are focused on quasi-elastic scattering data collected at a laboratory frame angle for the ¹²C + ^105,106Pd and ¹³C + ^105,106Pd reaction systems, as documented in previous experimental investigations. To maintain methodological consistency and enable direct comparison with these measurements, all theoretical calculations are configured to match this specific scattering geometry.

When analyzing backward-angle scattering data, the relationship between the energy and the scattering angle introduces complex centrifugal effects that can complicate direct comparisons between theories and experiments. To address this issue, the following equation implements an energy transformation framework using the effective energy parameter ($E_{\mathrm{eff}}$), defined by Hagino et al. as follows [6,7,9]:

$$E_{\mathrm{eff}}={\displaystyle \frac{2E_{\mathrm{c}.\mathrm{m}.}}{1+{\cos \mathrm{ec}}^2{\theta }_{\mathrm{c}.\mathrm{m}.}}}.$$

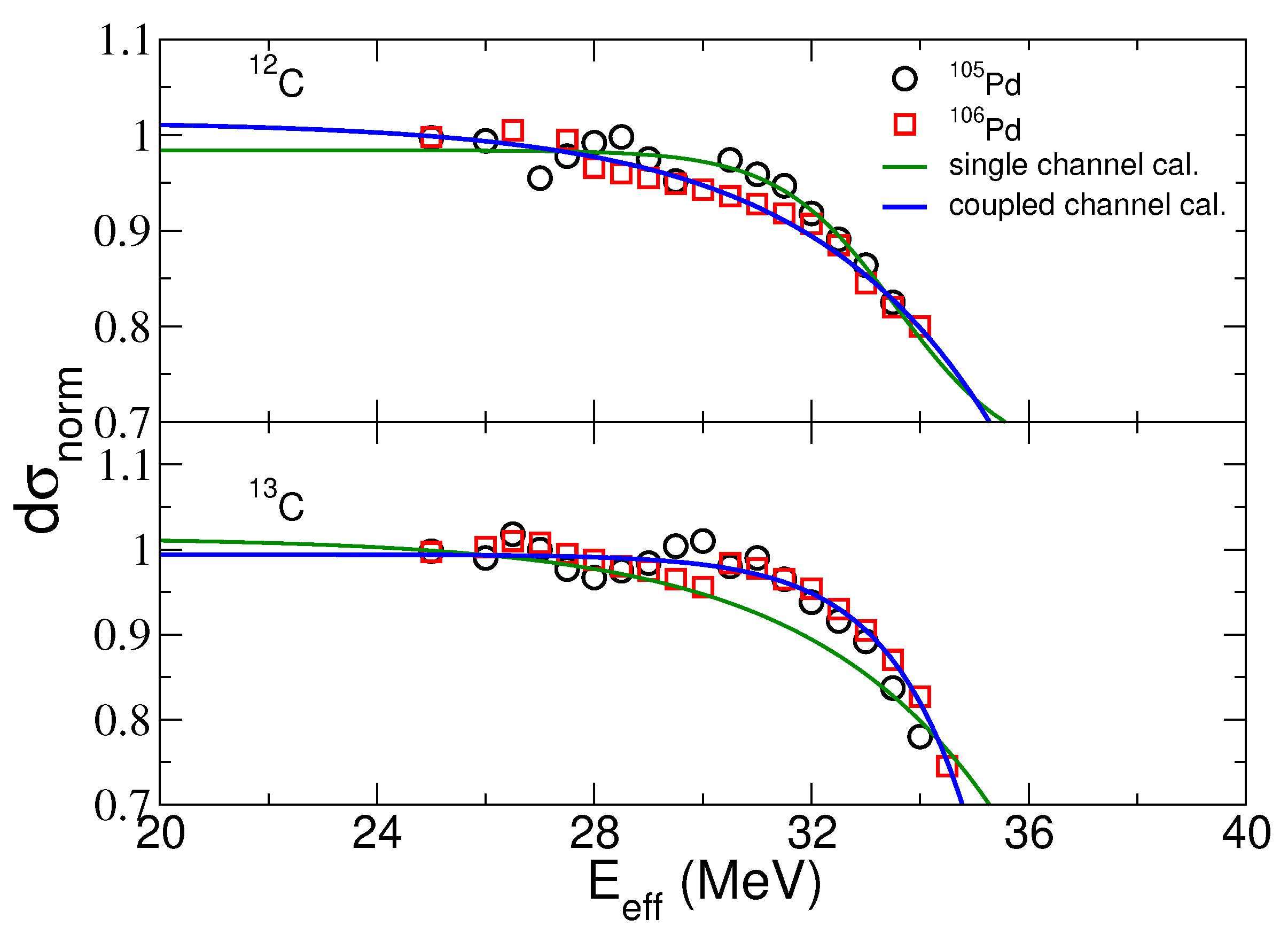
The calculated and plotted ratio of quasi-elastic to Rutherford cross-sections as functions of effective energy is shown in Figure 1. This normalized representation provides a more physically intuitive visualization of barrier penetration effects and enhances the sensitivity of the analysis to the surface diffuseness parameter that primarily governs interaction dynamics near the Coulomb barrier.

As shown in Figure 1, recent studies by Gurpreet and colleagues [16] have examined how channel coupling affects the surface properties of internuclear potentials in heavy-ion reactions by considering the experimental data of Capurro et al. [17]. Their work presents experimental quasielastic cross-section measurements for the ¹²C + ^105,106Pd and ¹³C + ^105,106Pd systems.

Figure 1. The single-channel and coupled-channel calculations for the quasi-elastic excitation function are compared using a surface diffuseness parameter ($a_0=0.8$) in the nuclear potential. The upper panels correspond to the ¹²C + ¹⁰⁵Pd and ¹²C + ¹⁰⁶Pd systems, while the lower panels correspond to the ¹³C + ¹⁰⁵Pd and ¹³C + ¹⁰⁶Pd systems. The solid green curve represents ¹²C and ¹³C on ¹⁰⁵Pd, while the blue curve represents the coupled-channel calculation for ¹²C and ¹³C on ¹⁰⁶Pd. Experimental data are taken from the works of Capurro et al. [17].

Figure 1. The single-channel and coupled-channel calculations for the quasi-elastic excitation function are compared using a surface diffuseness parameter ($a_0=0.8$) in the nuclear potential. The upper panels correspond to the ¹²C + ¹⁰⁵Pd and ¹²C + ¹⁰⁶Pd systems, while the lower panels correspond to the ¹³C + ¹⁰⁵Pd and ¹³C + ¹⁰⁶Pd systems. The solid green curve represents ¹²C and ¹³C on ¹⁰⁵Pd, while the blue curve represents the coupled-channel calculation for ¹²C and ¹³C on ¹⁰⁶Pd. Experimental data are taken from the works of Capurro et al. [17].

Using a coupled-channels approach that incorporates vibrational excitations in the target nuclei, they observed notable results. While previous studies of spherical nuclear systems suggested minimal impact of vibrational excitation on the surface diffuseness parameter, the ^12,13C + Pd systems demonstrate a considerable effect. The systematic investigation further reveals that transfer coupling mechanisms substantially influence the surface diffuseness parameter. These findings contribute to the evolving understanding of nuclear interaction dynamics and highlight the importance of including transfer channels when modeling heavy-ion reaction potentials. Thus, the surface diffuseness parameter in heavy-ion nuclear potentials is significantly influenced by neutron transfer coupling effects. Despite numerous investigations, the comprehensive understanding of these effects remains incomplete.

Thus, in this study, we revisit the influence of neutron transfer on surface diffuseness in carbon-induced fusion reactions, considering ^12,13C + ^105,106Pd systems as an example, which offer neutron transfer Q-values. These systems provide an excellent opportunity to investigate how neutron transfer coupling impacts surface diffuseness.

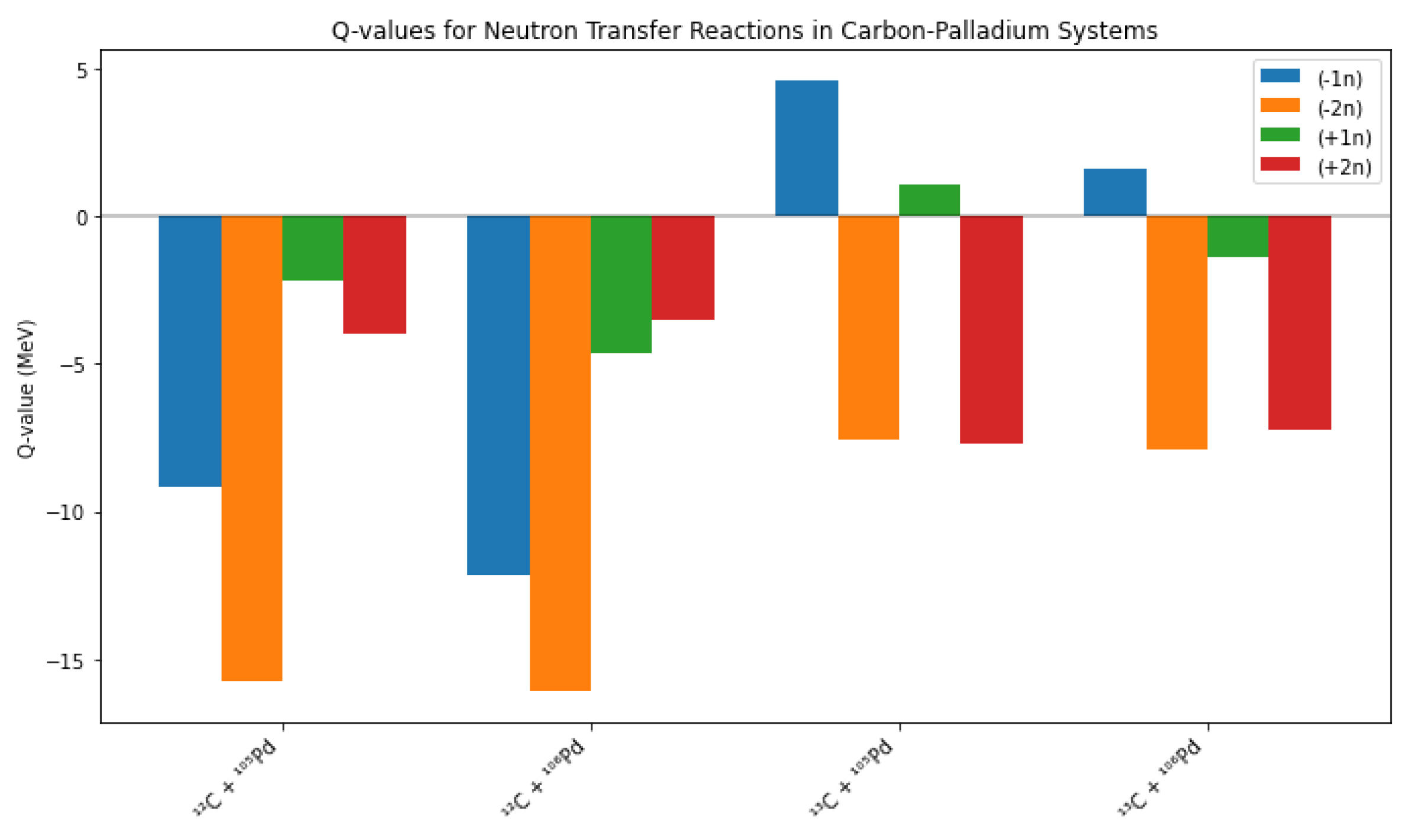
The present study revisits and extends previous work on the initial ^12,13C-induced fusion reaction. We implement advanced coupled-channel computational frameworks that incorporate both structural excitations and nucleon transfer pathways. The calculations explicitly model vibrational modes (characteristic of near-spherical nuclei), rotational excitations (prominent in deformed systems), and critically, neutron transfer channels. We provide a comprehensive analysis of energetically favorable neutron exchange processes through Q-value calculations for single and double neutron transfers between these specific isotopic combinations, presented in Figure 2. This study focuses on the fundamental question of how neutron transfer mechanisms modify effective diffuseness parameters, potentially offering a theoretical reconciliation for the divergent experimental results observed through different measurement techniques.

2. Results and Discussion

For this investigation, we employed both single-channel and coupled-channel computational approaches using a modified scattering version of the CCFULL code. The coupled-channel framework incorporated double quadrupole phonon excitations within target nuclei, operating under the harmonic oscillator approximation. For the ¹⁰⁶Pd nucleus, we utilized established spectroscopic parameters with a deformation value of $\beta =0.229$ and excitation energy of $E^{*}=0.523$ MeV. When modeling the odd-mass ¹⁰⁵Pd nucleus, we implemented an averaging technique using data from neighboring even–even isotopes (¹⁰⁴Pd and ¹⁰⁶Pd), resulting in parameters of $\beta =0.219$ and $E^{*}=0.534$ MeV.

Interaction potential in calculations features both real and imaginary Woods–Saxon components. The imaginary term functions to represent compound nucleus formation processes. We calibrated its strength parameters to ensure complete absorption of incoming flux once the Coulomb barrier is penetrated. Specifically, the imaginary potential was configured with a depth of 34 MeV, a radius parameter of 1.0 fm, and diffuseness of 0.35 fm. This parameterization effectively confines the imaginary potential to regions well inside the Coulomb barrier, with negligible contribution at the nuclear surface. We verified through sensitivity tests that the results remain stable against reasonable variations in the imaginary potential parameters, provided the absorption remains primarily within the barrier region.

For the real components of nuclear potential, we followed the previously mentioned fixed depth parameter ($V_0$) of 185 MeV across all calculations. To maintain consistent physical conditions between systems with different diffuseness values, we implemented a systematic procedure where the radius parameter ($r_0$) was individually adjusted for each diffuseness value. This adjustment ensured that the calculated Coulomb barrier height ($V_B$) consistently matched the reference values from the Bass potential model for each isotopic combination. This calibration approach is physically justified because variations in potential depth and radius parameters produce compensatory effects in the surface region, allowing for consistent barrier properties across different parameterizations. To ensure that the barrier height for both the single-channel and coupled-channel calculations was consistent, we slightly adjusted the potential parameters for the coupled-channel calculations using fusion cross-sections at energies above the barrier.

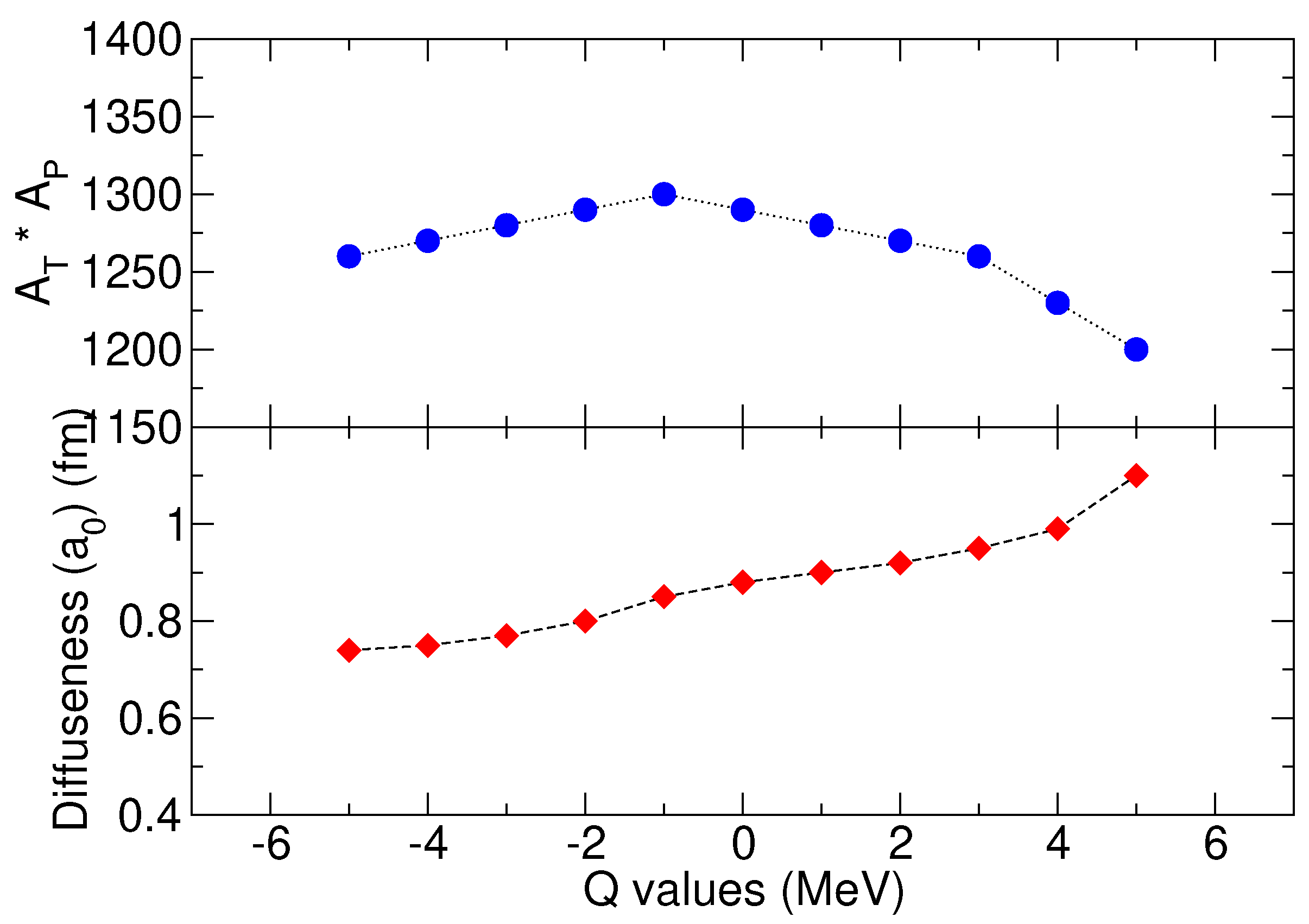
The analysis revealed a significant correlation between the neutron transfer Q-value and the product of colliding partner masses ($A_p\times A_T$) across carbon-induced systems. For example, as shown in the upper panel of Figure 3, this relationship illustrates how the Q-value systematically varies with the combined mass of the interacting nuclei in these reactions. Complementing this observation, the lower panel demonstrates the clear dependence of surface diffuseness parameters on neutron transfer Q-values for ^12,13C + ^105,106Pd reaction systems. This visualization captures the inverse relationship we discovered between diffuseness parameters and Q-values, providing strong evidence that neutron transfer coupling mechanisms directly influence nuclear potential surface properties.

The investigation employed a methodical parameter determination protocol with several distinct phases. Initially, we considered a reference potential depth ($V_0=185$ MeV) across all systems [17]. For each diffuseness value ($a_0$) under examination, we conducted iterative numerical searches to identify the specific radius parameter ($r_0$) that generates a Coulomb barrier precisely matching the established Bass barrier prediction. This calibration established consistent energetic landmarks for comparative analyses across parameter configurations.

Subsequently, we generated baseline reaction profiles by performing fundamental single-channel calculations that excluded structural coupling effects. These calculations yielded reference fusion cross-sections (${\sigma }_{\mathrm{fus}}^{\mathrm{sc}}$) that served as control measurements for quantifying coupling-induced modifications.

This study involved coupled-channel calculations that incorporated the complete spectrum of relevant nuclear excitation modes. These calculations produced structure-enhanced fusion cross-sections (${\sigma }_{\mathrm{fus}}^{\mathrm{cc}}$) that exhibited characteristic deviations from single-channel predictions due to dynamic barrier modifications. To achieve physically consistent parameter sets, we implemented targeted refinements to the radius parameter until coupled-channel fusion predictions at energies substantially exceeding the barrier demonstrated convergence with single-channel results. This convergence criterion ensured that the parameter sets ($V_0$, $r_0$, $a_0$) accurately reflected both the static barrier properties and dynamic coupling effects.

In the final stage, we calculated quasi-elastic cross-sections using both computational frameworks. In the simplified single-channel approach, quasi-elastic scattering was identical to pure elastic scattering. Conversely, the coupled-channel framework generated quasi-elastic cross-sections that incorporated the combined contributions from elastic scattering and all inelastic excitation pathways included in the coupling scheme, providing reaction observables directly comparable to experimental measurements.

Further, we adopted a custom statistical framework based on QP (Poisson chi-square (${\chi }_P^2$)) principles to evaluate diffuseness parameters with enhanced statistical validity. The modified statistical estimator we implemented takes the following form:

$${\chi }_P^2=2\sum _i\left[M_i-E_i+E_{i}ln\left({\displaystyle \frac{E_i}{M_i}}\right)\right],$$

(1)

where $M_i$ represents the model prediction, and $E_i$ denotes the experimental measurement for observation i. This formulation addresses the inherent counting statistics of nuclear detection systems and appropriately weights measurements according to their statistical reliability.

The data validation protocol identified a significant trend: when the ratio between quasi-elastic and Rutherford cross-sections exceeds the unity, i.e.,

$$R_i={\displaystyle \frac{{\sigma }_{\mathrm{qe},i}}{{\sigma }_{R,i}}}>1,$$

(2)

systematic deviations emerge between observations and theoretical frameworks. This pattern primarily occurs at energies significantly below the Coulomb barrier region ($E\ll E_C$), where the analysis suggests additional reaction channels, including nucleon exchange processes and non-equilibrium dynamics, become relevant but fall outside standard coupled-channels calculations. These data points were omitted from the quantitative analysis while being preserved in visual presentations for comprehensive evaluation.

For statistical uncertainty estimation, we constructed a confidence boundary defined by the following:

$${\chi }_{\mathrm{bound}}^2={\chi }_{\mathrm{opt}}^2+{\displaystyle \frac{{\chi }_{\mathrm{opt}}^2}{N_{\mathrm{eff}}}},$$

(3)

where ${\chi }_{\mathrm{opt}}^2$ represents the optimized chi-square value, and $N_{\mathrm{eff}}$ signifies the effective statistical weight calculated as follows:

$$N_{\mathrm{eff}}=N_{\mathrm{valid}}-p,$$

(4)

with $N_{\mathrm{valid}}$ representing the count of validated experimental points and p denoting the dimensionality of the parameter space.

Through systematic parameter sampling across the diffuseness domain, we generated a comprehensive ${\chi }^2$ response surface and determined intersection coordinates with the following confidence boundary:

$${\chi }^2\left(a\right)={\chi }_{\mathrm{bound}}^2,$$

(5)

where a represents the diffuseness parameter. The resulting boundary values ($a_{\mathrm{lower}}$ and $a_{\mathrm{upper}}$) establish the confidence region as follows:

$$a_{\mathrm{best}}={\displaystyle \frac{a_{\mathrm{lower}}+a_{\mathrm{upper}}}{2}}\pm {\displaystyle \frac{a_{\mathrm{upper}}-a_{\mathrm{lower}}}{2}}.$$

(6)

This integrated approach produces more robust parameter constraints than traditional methods that typically under-represent uncertainties by failing to account for theoretical approximations and inter-parameter correlations.

Single-Channel and Coupled-Channel Calculations

Through the systematic analysis framework, we determined diffuseness parameters with enhanced precision by directly comparing theoretical calculations with experimental quasi-elastic scattering data. We began by establishing baseline parameters using simplified single-channel calculations that omitted structural excitations. By applying the statistical optimization procedures outlined in the methodology, we derived diffuseness values for the ¹²C + ¹⁰⁵Pd and ¹²C + ¹⁰⁶Pd systems of $1.0\pm 0.07$ fm and $1.05\pm 0.17$ fm, respectively. These values exceed those reported by Gurpreet and colleagues by approximately 25 percent [16], highlighting significant differences in the present approach.

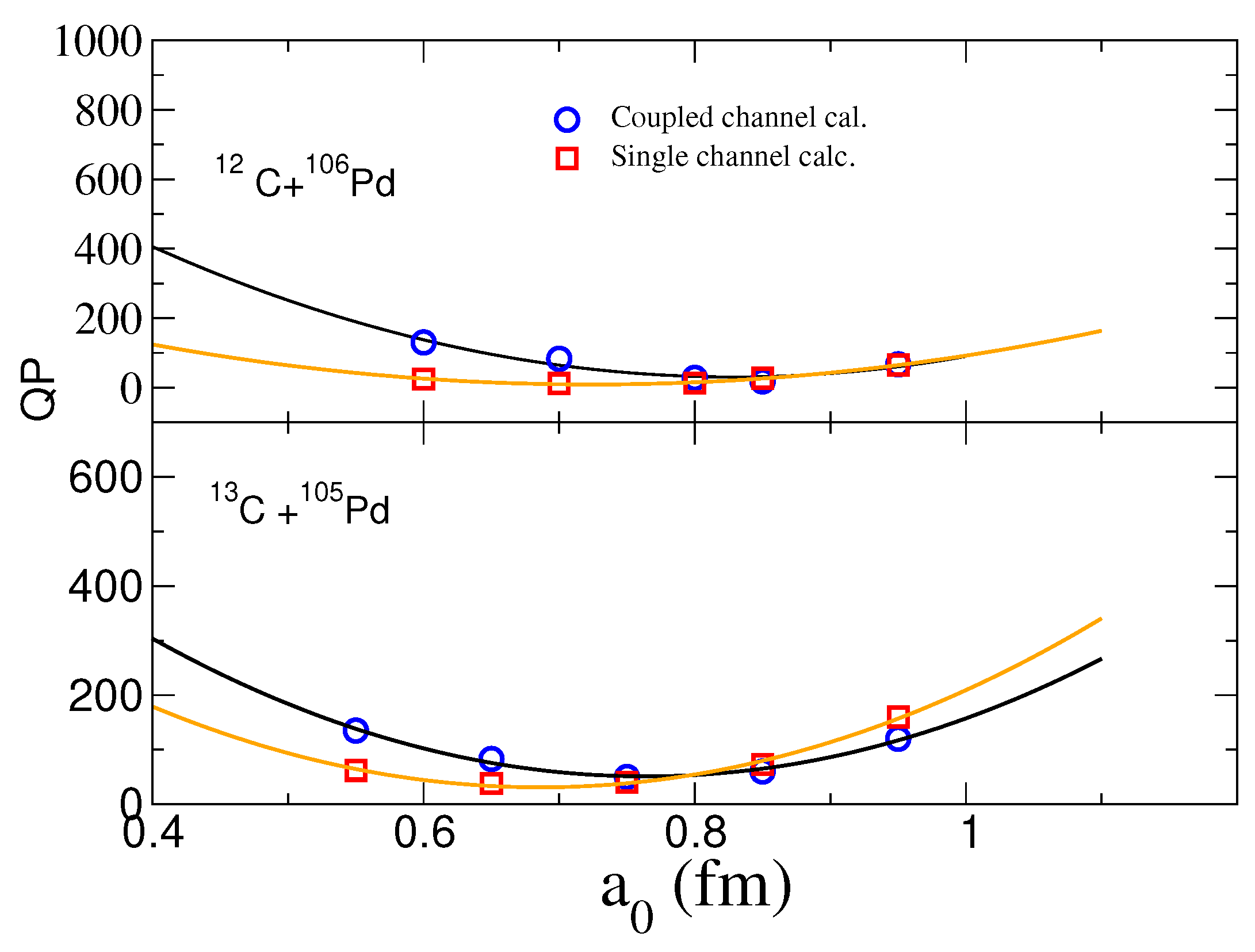
Extended coupled-channel calculations uncovered a notable systematic trend: systems with ¹³C projectiles consistently exhibited smaller diffuseness parameters compared to their ¹²C counterparts. This finding carries important theoretical significance, suggesting that the valence neutron configuration in ¹³C substantially modifies effective nuclear interaction in the surface region.

We identified this pattern through two independent isotopic comparisons. When examining reactions with identical target nuclei but different carbon isotopes as projectiles (¹²C versus ¹³C), we observed a consistent reduction in the diffuseness parameter. Similarly, when comparing systems with the same projectile but different palladium isotopes (even–even ¹⁰⁶Pd versus odd–even ¹⁰⁵Pd), we again found reduced diffuseness values. This consistent behavior across different isotopic variations strongly indicates a common underlying physical mechanism.

Conventional nuclear reaction theory would suggest relatively uniform diffuseness parameters across closely related isotopic systems in the absence of specific coupling effects. The results challenge this expectation as we measured variations in diffuseness comparable to those typically produced by strong collective mode couplings. This unexpected similarity suggests additional reaction pathways beyond the standard quadrupole vibrational modes explicitly incorporated in the calculations. The considerable deformation parameter ($\beta$) of these palladium isotopes enhances coupling-induced effects on surface properties, making these particular nuclear combinations especially valuable for investigating subtle reaction dynamics that modify effective interaction potentials.

Finally, as shown in Figure 4, the comparative results highlight the significant impact of vibrational excitation on the surface diffuseness parameter despite the target nuclei being spherical. These findings underscore the importance of incorporating neutron transfer coupling into models that predict fusion cross-sections. Failure to account for this coupling could lead to overestimated diffuseness parameters, especially in systems involving neutron-rich isotopes. Further research should focus on expanding the analysis to other reaction systems and improving the accuracy of coupled-channel models.

3. Summary

As an example, we considered Gurpreet et al.’s [16] theoretical work by identifying variations in diffuseness parameters across different isotopic combinations of projectile and target systems. Through the methodology, we performed a systematic reduction in surface diffuseness when transitioning from ¹²C to ¹³C projectiles or from ¹⁰⁶Pd to ¹⁰⁵Pd targets, a pattern not fully characterized in previous analyses. Where Gurpreet et al. [16] proposed initial indications of structural influences on diffuseness parameters, the quantitative analysis offers yielding absolute diffuseness values approximately 25% higher than their reported measurements. Particularly noteworthy is the substantial diffuseness decrease observed with ¹³C projectiles relative to ¹²C systems, a phenomenon insufficiently addressed in earlier research that strongly indicates transfer coupling contributions.

In contrast to Gurpreet et al.’s [16] proposition of negligible vibrational coupling effects, a detailed examination of backward-angle quasi-elastic scattering revealed substantial diffuseness modifications occurring when the coupling strength surpassed specific intensity thresholds. This observation necessitates a re-evaluation of their earlier conclusion, restricting significant diffuseness alterations exclusively to rotational coupling mechanisms. We additionally identified a previously unrecognized inverse relationship between transfer Q-values and diffuseness parameters, where increased Q-values consistently corresponded with reduced diffuseness parameters. This new correlation establishes a theoretical framework for subsequent research into the complex inter-relationship between collective nuclear excitations and transfer processes extending beyond the parameters examined in Gurpreet et al.’s [16] initial investigation.