Statistics of Quantum Numbers for Non-Equivalent Fermions in Single-j Shells
Abstract
1. Introduction
2. Characterization of the Magnetic Quantum Number Distribution
2.1. Generalities
2.2. Binomial Coefficients and the Sunko Algorithm
2.3. Connection with Elementary Symmetric Functions
2.4. Link with Cyclotomic Polynomials
3. Expressions Involving Multinomial Coefficients
3.1. Integral Representation from Group Theory
3.2. Expression Using Multinomial Coefficients: A New Sum Rule
4. Expression in Terms of Pascal Triangles
Case of Different Angular Momenta
5. Special Cases
6. Sum Rules
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
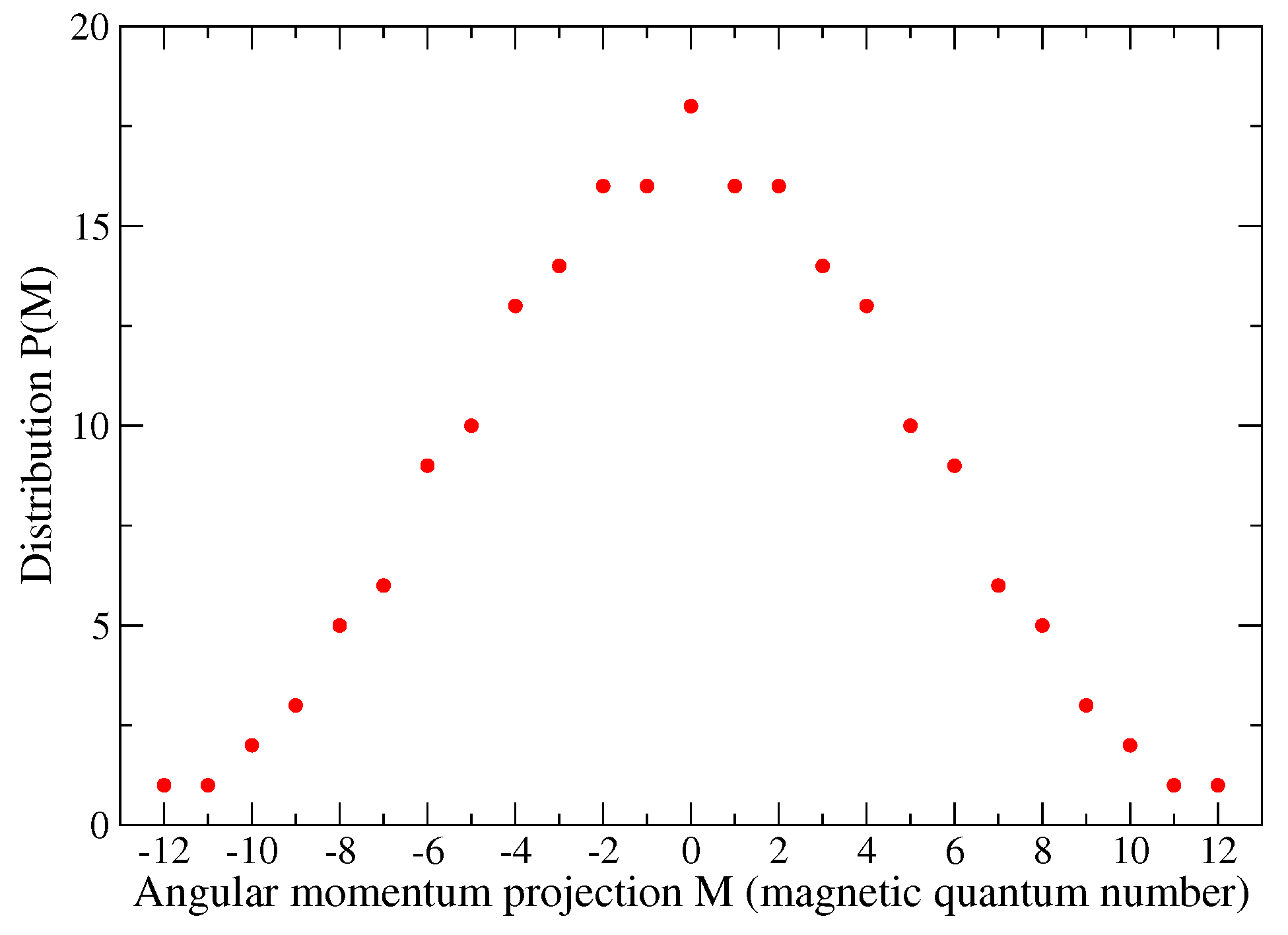
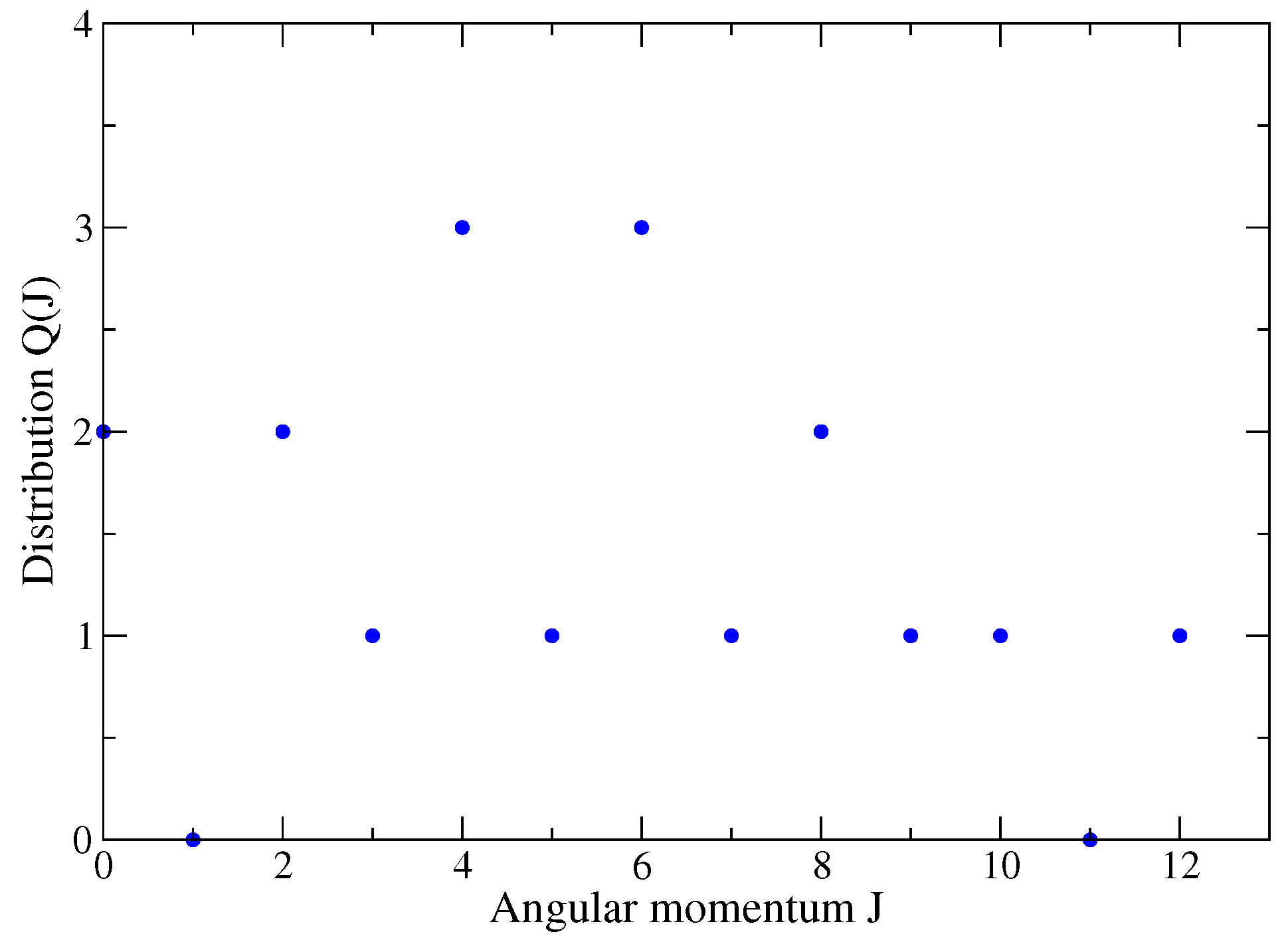
Appendix A. Distributions P(M) and Q(J) for a j Shell with N = 4 Fermions
Appendix B. SO(3) and SU(2)
Appendix C. Total Number of J Levels, Restricted Partitions and q−Binomial Coefficients
- Pt[n_,k_]:=Length[IntegerPartitions[Floor[n*k/2],n,Range[k]]];
- j = …;
- Flatten[Table[Pt[2j+1-k,k],{k,0,2j+1}]]
| N | |
|---|---|
| 1 | 1 |
| 2 | 5 |
| 3 | 10 |
| 4 | 18 |
| 5 | 20 |
| 6 | 18 |
| 7 | 10 |
| 8 | 5 |
| 9 | 1 |
| 10 | 1 |
| N | |
|---|---|
| 1 | 1 |
| 2 | 6 |
| 3 | 15 |
| 4 | 33 |
| 5 | 49 |
| 6 | 58 |
| 7 | 49 |
| 8 | 33 |
| 9 | 15 |
| 10 | 6 |
| 11 | 1 |
| 12 | 1 |
| / | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1/2 | 1 | 2 | 3 | 6 | 10 | 20 | 35 | 70 | 126 |
| 3/2 | 1 | 4 | 12 | 44 | 155 | 580 | 2128 | 8092 | 30,276 |
| 5/2 | 1 | 6 | 27 | 146 | 780 | 4332 | 24,017 | 135,954 | 767,394 |
| 7/2 | 1 | 8 | 48 | 344 | 2460 | 18,152 | 134,512 | 1,012,664 | 7,635,987 |
| 9/2 | 1 | 10 | 75 | 670 | 6000 | 55,252 | 512,365 | 4,816,030 | 45,433,800 |
| 11/2 | 1 | 12 | 108 | 1156 | 12,435 | 137,292 | 1,528,688 | 17,232,084 | 195,170,310 |
Appendix D. Deriving Multiplicities from the Knowledge of Molien Functions
References
- Bethe, H.A. An attempt to calculate the number of energy levels of a heavy nucleus. Phys. Rev. 1936, 50, 332–341. [Google Scholar] [CrossRef]
- Talmi, I. Simple Models of Complex Nuclei; Harwood: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Zamick, L.; Van Isacker, P. Partial dynamical symmetries in the shell: Progress and puzzles. Phys. Rev. C 2008, 78, 044327. [Google Scholar]
- Zhao, Y.M.; Arima, A.; Yoshinaga, N. Many-body systems interacting via a two-body random ensemble. I. Angular momentum distribution in the ground states. Phys. Rev. C 2002, 66, 064322. [Google Scholar]
- Mulhall, D.; Volya, A.; Zelzvinsky, V. Geometric chaoticity leads to ordered spectra for randomly interacting fermions. Phys. Rev. Lett. 2000, 85, 4016–4019. [Google Scholar] [CrossRef]
- Fu, G.J.; Zhao, Y.M.; Arima, A. Nucleon-pair approximation of the shell model with isospin symmetry. Phys. Rev. C 2013, 88, 054303. [Google Scholar] [CrossRef]
- Zamick, L.; Escuderos, A. Odd-J pairing in nuclei. Phys. Rev. C 2013, 87, 044302. [Google Scholar] [CrossRef]
- Ginocchio, J.N.; Haxton, W.C. Symmetries in Science VI: From the Rotation Group to Quantum Algebras; Gruber, B., Ed.; Plenum: New York, NY, USA, 1993; p. 263. [Google Scholar]
- Zhao, Y.M.; Arima, A. Number of states with a given angular momentum for identical fermions and bosons. Phys. Rev. C 2003, 68, 044310. [Google Scholar] [CrossRef]
- Zamick, L.; Escuderos, A. Alternate derivation of Ginocchio-Haxton relation [(2j + 3)/6]. Phys. Rev. C 2005, 71, 054308. [Google Scholar]
- Talmi, I. Number of states with given spin J of n fermions in a j orbit. Phys. Rev. C 2005, 72, 037302. [Google Scholar] [CrossRef]
- Zamick, L.; Escuderos, A. Companion problems in quasispin and isospin. Phys. Rev. C 2005, 71, 014315. [Google Scholar] [CrossRef]
- Zamick, L.; Escuderos, A. Isospin relations for four nucleons in a single j shell. Phys. Rev. C 2005, 72, 044317. [Google Scholar]
- Zhao, Y.M.; Arima, A. Number of states for nucleons in a single-j shell. Phys. Rev. C 2005, 72, 064333. [Google Scholar]
- Zamick, L.; Robinson, S.J.Q. Zeros of 6-j symbols: Atoms, nuclei, and bosons. Phys. Rev. C 2011, 84, 044325. [Google Scholar]
- Qi, C.; Wang, X.B.; Xu, Z.X.; Liotta, R.J.; Wyss, R.; Xu, F.R. Alternate proof of the Rowe-Rosensteel proposition and seniority conservation. Phys. Rev. C 2010, 82, 014304. [Google Scholar]
- Wang, X.B.; Xu, F.R. Special relations of coefficients of fractional parentage and partial dynamical symmetries in j = 9/2 shells. Phys. Rev. C 2012, 85, 034304. [Google Scholar]
- Zamick, L.; Escuderos, A. Large-j limit for certain 9-j symbols: Power law behavior. Phys. Rev. C 2013, 88, 014326. [Google Scholar] [CrossRef]
- Kleszyk, B.; Zamick, L. Analytical and numerical calculations for the asymptotic behavior of unitary 9j coefficients. Phys. Rev. C 2014, 89, 044322. [Google Scholar] [CrossRef]
- Hertz-Kintish, D.; Zamick, L.; Kleszyk, B. Asymptotics of the 3j and 9j coefficients. Phys. Rev. C 2014, 90, 027302. [Google Scholar]
- Redmond, P.J. An explicit formula for the calculation of fractional parentage coefficients. Proc. Roy. Soc. A 1954, 222, 84. [Google Scholar]
- Rosensteel, G.; Rowe, D.J. Seniority-conserving forces and Usp(2j + 1) partial dynamical symmetry. Phys. Rev. C 2003, 67, 014303. [Google Scholar]
- Bao, M.; Zhao, Y.M.; Arima, A. Number of states for identical particles. Phys. Rev. C 2016, 93, 014307. [Google Scholar]
- Pain, J.-C. Special six-j and nine-j symbols for a single-j shell. Phys. Rev. C 2011, 84, 047303. [Google Scholar]
- Pain, J.-C. Number of spin-J states and odd-even staggering for identical particles in a single-j shell. Phys. Rev. C 2018, 97, 064311. [Google Scholar]
- Poirier, M.; Pain, J.-C. Angular momentum distribution in a relativistic configuration: Magnetic quantum number analysis. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 145002. [Google Scholar]
- Poirier, M.; Pain, J.-C. Distribution of the total angular momentum in relativistic configurations. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 145006. [Google Scholar]
- Pain, J.-C. Total number of J levels for identical particles in a single-j shell using coefficients of fractional parentage. Phys. Rev. C 2019, 99, 054321. [Google Scholar]
- Karazija, R. Sums of Atomic Quantities and Mean Characteristics of Spectra; Mokslas: Vilnius, Lithuania, 1992. (In Russian) [Google Scholar]
- Bauche, J.; Bauche-Arnoult, C.; Peyrusse, O. Atomic Properties in Hot Plasmas; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Kucˇas, S.; Karazija, R.; Jonauskas, V.; Aksela, S. Global characteristics of atomic spectra and their use for the analysis of spectra. III. Auger spectra. Phys. Scr. 1995, 52, 639–648. [Google Scholar]
- Poirier, M.; Pain, J.-C. Exact expressions for the number of levels in single-j orbits for three, four, and five fermions. Phys. Rev. C 2021, 104, 064324. [Google Scholar]
- Poirier, M.; Pain, J.-C. Exact expressions of the distributions of total magnetic quantum number and angular momentum in single-j orbits: A general technique for any number of fermions. Phys. Rev. C 2024, 109, 024306. [Google Scholar]
- Sunko, D.K. Rapid calculation of exact spin distributions of multilevel configurations. Phys. Rev. C 1986, 33, 1811–1813. [Google Scholar]
- Sunko, D.K.; Svrtan, D. Generating function for angular momentum multiplicities. Phys. Rev. C 1985, 31, 1929–1933. [Google Scholar] [CrossRef] [PubMed]
- Andrews, G.E. The Theory of Partitions, Encyclopedia of Mathematics and Its Applications; Cambridge University Press, Cambridge, UK, 1984.
- Schroeder, M. Cyclotomic polynomials. In Number Theory in Science and Communication: With Applications in Cryptography, Physics, Digital Information, Computing, and Self-Similarity; Springer: Berlin/Heidelberg, Germany, 2009; pp. 289–304. [Google Scholar]
- Mendonça, J.R.G. Exact eigenspectrum of the symmetric simple exclusion process on the complete, complete bipartite and related graphs. J. Phys. A Math. Theor. 2013, 46, 295001. [Google Scholar]
- Gyamfi, J.A.; Barone, V. On the composition of an arbitrary collection of SU(2) spins: An enumerative combinatoric approach. J. Phys. A Math. Theor. 2018, 51, 105202. [Google Scholar]
- Klapisch, M.; Krasnitz, A.; Mandelbaum, P.; Bauche-Arnoult, C.; Bauche, J. New results of the unresolved transition arrays method, Eight International Colloquium on Ultraviolet and X-ray Spectroscopy of Astrophysical and Laboratory Plasmas. In Proceedings of the IAU Colloq. 86, Washington, DC, USA, 27–29 August 1984; Naval Research Laboratory: Washington, DC, USA, 1984; p. 114. [Google Scholar]
- Faà di Bruno, F. Einleitung in Die Theorie der Binären Formen; B. G. Teubner: Leipzig, Germany, 1881; p. 126. [Google Scholar]
- Hamermesh, M. Group Theory and Its Applications to Physical Problems; Addison-Wesley: Reading, MA, USA, 1962. [Google Scholar]
- Murnaghan, F.D. The Theory of Group Representations; Dover Publications: Dover, NY, USA, 1963. [Google Scholar]
- Rashid, M.A. Addition of arbitrary number of identical angular momenta. J. Phys. A Math. Gen. 1977, 10, L135–L137. [Google Scholar]
- Ramadevi, P.; Dubey, V. Group Theory for Physicists: With Applications; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Szegö, G. Ch. 4 in Orthogonal Polynomials. In Jacobi Polynomials, 4th ed.; American Mathematical Society: Providence, RI, USA, 1975. [Google Scholar]
- Iyanaga, S.; Kawada, Y. (Eds.) Jacobi Polynomials. Appendix A, Table 20.V in Encyclopedic Dictionary of Mathematics; MIT Press: Cambridge, MA, USA, 1980; p. 1480. [Google Scholar]
- Talman, J.D. Special Functions: A Group Theoretic Approach; Based on Lectures by Eugene P. Wigner; Mathematical Physics Monograph Series; Benjamin: New York, NY, USA; Amsterdam, The Netherlands, 1968. [Google Scholar]
- Nikiforov, A.F.; Uvarov, V.B. Special Functions of Mathematical Physics: A Unified Introduction with Applications; Birkhäuser: Boston, MA, USA, 2013. [Google Scholar]
- Mason, J.C.; Handscomb, D.C. Chebyshev Polynomials, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- Vilenkin, N.J. Special Functions and Theory of Group Representations; Izdat. “Nauka”, Moscow, 1965, Transl. Math. Monographs; American Mathematical Society: Providence, RI, USA, 1968; Volume 22. [Google Scholar]
- Vilenkin, N.J.; Klimyk, A.U. Representation of Lie Groups and Special Functions, Recent Advances; Mathematics and its Applications 316; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Haettel, T.; Was, M. Fonctions Spéciales et Théorie des Représentations de Groupes. Available online: https://imag.umontpellier.fr/~haettel/Memoire%20Maitrise.pdf (accessed on 24 March 2025). (In French).
- Bollinger, R.C. Extended Pascal Triangles. Math. Mag. 1993, 66, 87–94. [Google Scholar]
- Takhtadzhyan, L.A.; Fadeev, L.D. Spectrum and scattering of excitations in the one-dimensional isotropic Heisenberg model. J. Sov. Math. 1984, 24, 241–267. [Google Scholar]
- Kirrilov, A.N. Combinatorial identities, and completeness of eigenstates of the Heisenberg magnet. J. Math. Sci. 1985, 30, 2298–2310. [Google Scholar]
- Crance, M. A statistical description for multiphoton stripping of atoms. J. Phys. B At. Mol. Opt. Phys. 1984, 17, 4333–4341. [Google Scholar]
- Poirier, M.; Pain, J.-C. Analytical and numerical expressions for the number of atomic configurations contained in a supershell. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 115002. [Google Scholar]
- Mikhailov, V.V. Addition of a large number of identical angular momenta. Statistical distributions. J. Phys. A Math. Gen. 1979, 12, 2329–2335. [Google Scholar]
- Mikhailov, V.V. Addition of an arbitrary number of different spins. Phys. Lett. 1980, 6A, 229–230. [Google Scholar] [CrossRef]
- Condon, E.U.; Shortley, G.H. The Theory of Atomic Spectra; Cambridge University Press: Cambridge, UK, 1935. [Google Scholar]
- Curtright, T.L.; Van Kortryk, T.S.; Zachos, C.K. Spin multiplicities. Phys. Lett. A 2017, 381, 422–427. [Google Scholar] [CrossRef]
- Wolfram Research, Inc. Mathematica, Version 11.3; Wolfram Research: Champaign, IL, USA, 2018.
- Polychronakos, A.P.; Sfetsos, K. Composition of many spins, random walks and statistics. Nucl. Phys. B 2016, 913, 664–693. [Google Scholar] [CrossRef]
- Cornwell, J.F. The double crystallographic point groups. In Group Theory in Physics; Academic Press: Cambridge, MA, USA, 1984; Volume I, pp. 342–355. [Google Scholar]
- Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions (Reidel, Dordrecht, 1974); Translation of Analyse Combinatoire; Presses Universitaires de France: Paris, France, 1970. [Google Scholar]
- Asherova, R.M.; Zhilinsky, B.I.; Pavlov-Verevkin, V.B.; Smirnov, Y.F. Preprint IFT-88-70P; Institute for Theoretical Physics: Kiev, Ukraine, 1988. [Google Scholar]
- Raychev, P.P.; Smirnov, Y.F. On the generalization of Molien functions to supergroups. J. Phys. A Math. Gen. 1990, 23, 4417–4425. [Google Scholar] [CrossRef]
- Dhont, G.; Cassam-Chenaï, P.; Patras, F. Molien generating functions and integrity bases for the action of the SO(3) and O(3) groups on a set of vectors. J. Math. Chem. 2021, 10, 2294–2326. [Google Scholar] [CrossRef]
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| / | 1 | 3 | 4 | 3 | 1 | 0 | −6 | |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 6 |
| J | 1/2 | 3/2 | 5/2 | 7/2 | 9/2 | 11/2 | 13/2 | 15/2 |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| / | 4 | 8 | 7 | 8 | −1 | −1 | −3 | 0 | −2 | −7 | |
| 1 | 4 | 12 | 29 | 62 | 119 | 211 | 349 | 545 | 808 | 1144 |
| k | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 4 | −1 | 4 | 1 | 2 | 0 | 4 | −10 | 4 | −7 | |
| 1553 | 2028 | 2554 | 3108 | 3661 | 4179 | 4628 | 4975 | 5195 | 5270 |
| J | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 75 | 220 | 347 | 449 | 518 | 553 | 554 | 526 | 475 | 409 | 336 |
| J | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 263 | 196 | 138 | 92 | 57 | 33 | 17 | 8 | 3 | 1 |
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| / | 4 | 12 | 4 | 8 | −1 | 0 | −3 | 0 | −5 | −3 | |
| 1 | 4 | 14 | 36 | 84 | 171 | 324 | 565 | 932 | 1449 | 2153 |
| k | 11 | 12 | 13 | 14 | 15 |
| 4 | −4 | 4 | 5 | −1 | |
| 3054 | 4168 | 5472 | 6943 | 8515 |
| k | 16 | 17 | 18 | 19 | 20 | 21 |
| 0 | 4 | −9 | 4 | −7 | −3 | |
| 10,123 | 11,668 | 13,062 | 14,204 | 15,018 | 15,440 |
| J | 1/2 | 3/2 | 5/2 | 7/2 | 9/2 | 11/2 | 13/2 | 15/2 | 17/2 | 19/2 | 21/2 |
| 422 | 814 | 1142 | 1394 | 1545 | 1608 | 1572 | 1471 | 1304 | 1114 | 901 |
| J | 23/2 | 25/2 | 27/2 | 29/2 | 31/2 | 33/2 | 35/2 | 37/2 | 39/2 | 41/2 | 43/2 |
| 704 | 517 | 367 | 241 | 153 | 87 | 48 | 22 | 10 | 3 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pain, J.-C. Statistics of Quantum Numbers for Non-Equivalent Fermions in Single-j Shells. Atoms 2025, 13, 25. https://doi.org/10.3390/atoms13040025
Pain J-C. Statistics of Quantum Numbers for Non-Equivalent Fermions in Single-j Shells. Atoms. 2025; 13(4):25. https://doi.org/10.3390/atoms13040025
Chicago/Turabian StylePain, Jean-Christophe. 2025. "Statistics of Quantum Numbers for Non-Equivalent Fermions in Single-j Shells" Atoms 13, no. 4: 25. https://doi.org/10.3390/atoms13040025
APA StylePain, J.-C. (2025). Statistics of Quantum Numbers for Non-Equivalent Fermions in Single-j Shells. Atoms, 13(4), 25. https://doi.org/10.3390/atoms13040025






