High-Resolution Fourier Transform Spectra of Atomic Sulfur: Testing of Modified Quantum Defect Theory
Abstract
1. Introduction
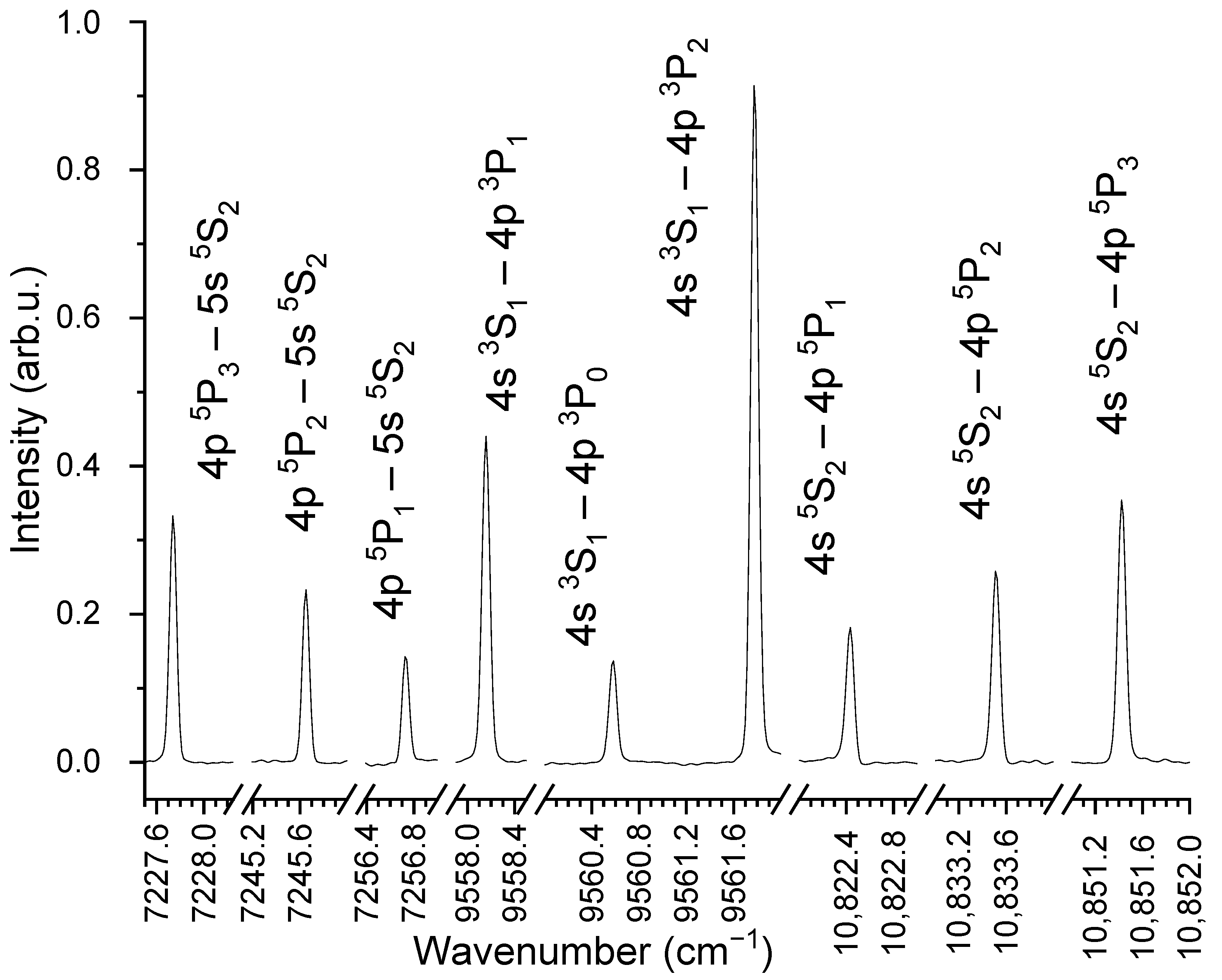
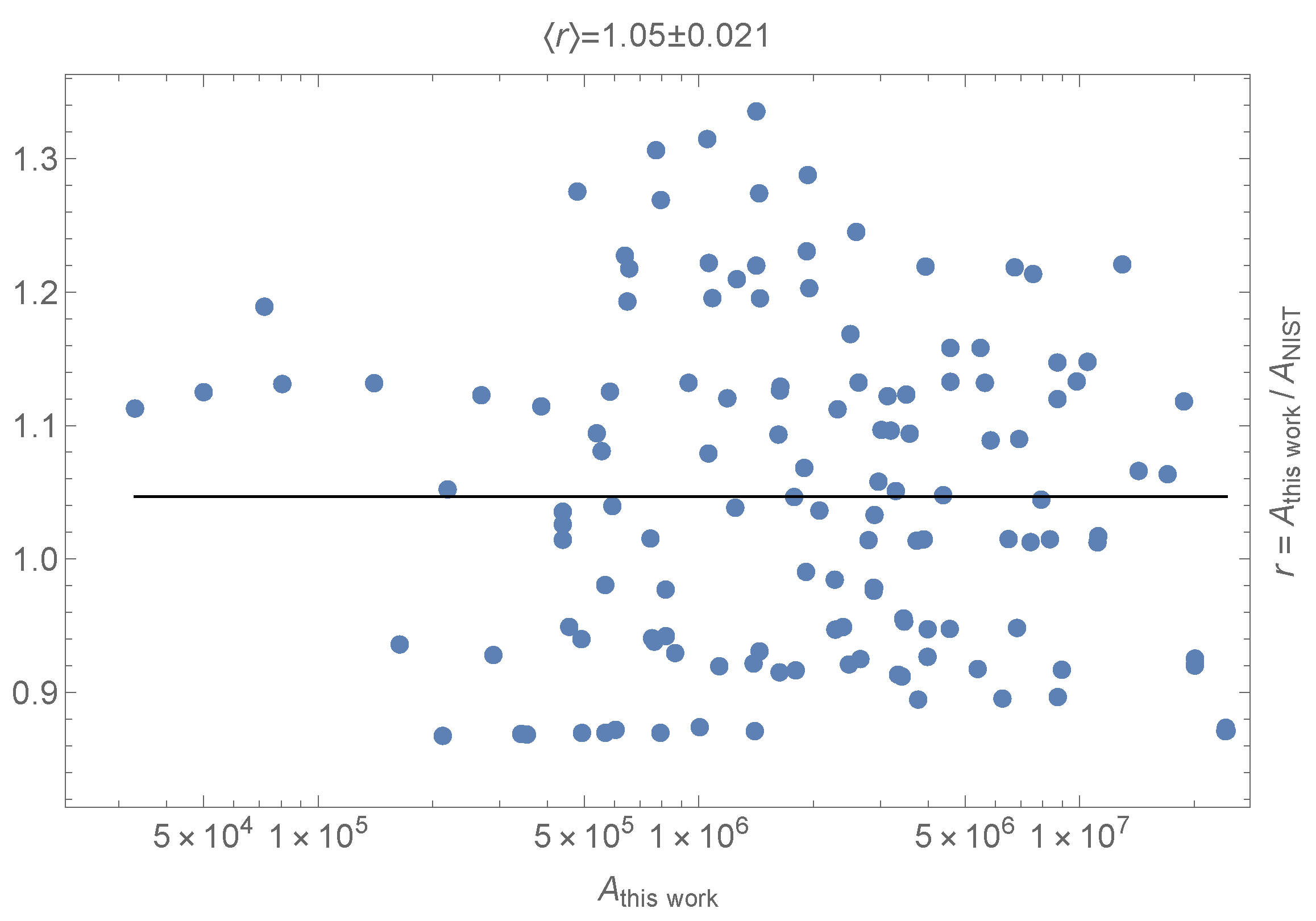
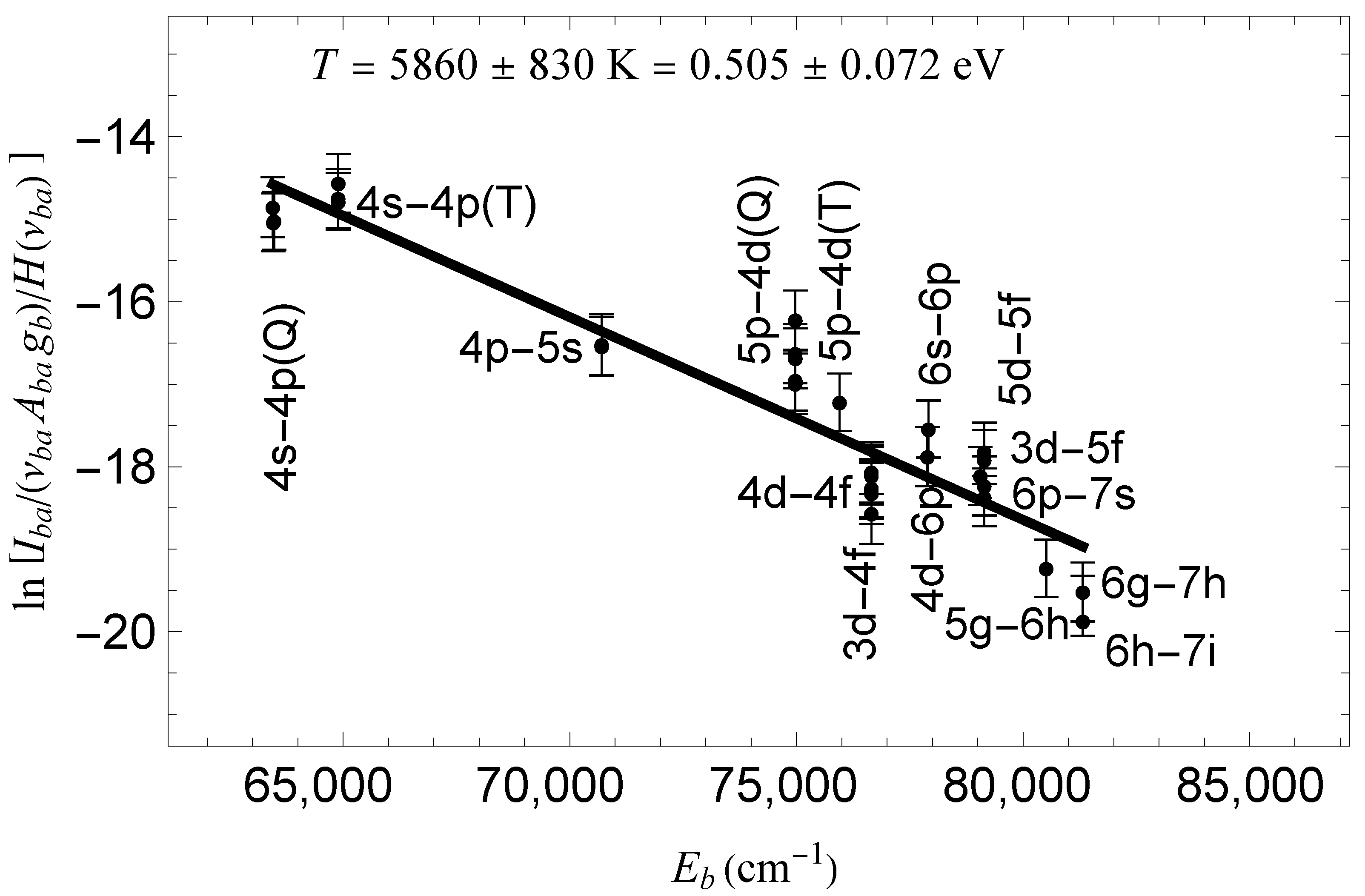
2. Results and Discussion
3. Methods
3.1. Theory
3.2. Experiment
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FTS | Fourier transform spectroscopy |
| GF | Green’s function |
| IP | Ionization potential |
| IR | Infrared |
| LTE | Local thermodynamic equilibrium |
| QD | Quantum defect (see (1)) |
| QDT | Quantum defect theory |
| RAGF | Reduced-added Green’s function (see [45]) |
| SNR | Signal-to-noise ratio |
References
- Maillard, J.P. Infrared astronomy beyond JWST: The Moon perspective. Phil. Trans. R. Soc. A 2024, 382, 20230070. [Google Scholar] [CrossRef] [PubMed]
- Pickering, J.; Blackwell-Whitehead, R.; Thorne, A.; Ruffoni, M.; Holmes, C. Laboratory measurements of oscillator strengths and their astrophysical applications. Can. J. Phys. 2011, 89, 387–393. [Google Scholar] [CrossRef]
- Bhatia, A.K. Scattering and Its Applications to Various Atomic Processes: Elastic Scattering, Resonances, Photoabsorption, Rydberg States, and Opacity of the Atmosphere of the Sun and Stellar Objects. Atoms 2020, 8, 78. [Google Scholar] [CrossRef]
- Srećković, V.A.; Ignjatović, L.M.; Dimitrijević, M.S. Symmetric Atom–Atom and Ion–Atom Processes in Stellar Atmospheres. Atoms 2018, 6, 1. [Google Scholar] [CrossRef]
- Hillier, D.J. Photoionization and Electron–Ion Recombination in Astrophysical Plasmas. Atoms 2023, 11, 54. [Google Scholar] [CrossRef]
- Nave, G.; Nahar, S.; Zhao, G. Division B Commission 14 Working Group: Atomic Data. Trans. IAU 2015, 11, 103–119. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Sahal-Bréchot, S. On the Application of Stark Broadening Data Determined with a Semiclassical Perturbation Approach. Atoms 2014, 2, 357–377. [Google Scholar] [CrossRef]
- Alexiou, S. Effects of Spiralling Trajectories on White Dwarf Spectra: High Rydberg States. Atoms 2023, 11, 141. [Google Scholar] [CrossRef]
- Papoulia, A.; Ekman, J.; Gaigalas, G.; Godefroid, M.; Gustafsson, S.; Hartman, H.; Li, W.; Radžiūtė, L.; Rynkun, P.; Schiffmann, S.; et al. Coulomb (Velocity) Gauge Recommended in Multiconfiguration Calculations of Transition Data Involving Rydberg Series. Atoms 2019, 7, 106. [Google Scholar] [CrossRef]
- Seaton, M.J. Quantum defect theory. Rep. Prog. Phys. 1983, 46, 167–257. [Google Scholar] [CrossRef]
- Letunov, A.Y.; Lisitsa, V.S. Review of Rydberg Spectral Line Formation in Plasmas. Atoms 2023, 11, 133. [Google Scholar] [CrossRef]
- Lee, C.W. Inter-Series Interactions on the Atomic Photoionization Spectra Studied by the Phase-Shifted Multichannel-Quantum Defect Theory. Atoms 2017, 5, 21. [Google Scholar] [CrossRef]
- Baig, M.A. Measurement of Photoionization Cross-Section for the Excited States of Atoms: A Review. Atoms 2022, 10, 39. [Google Scholar] [CrossRef]
- Gning, M.T.; Sakho, I. Photoionization Study of Neutral Chlorine Atom. Atoms 2023, 11, 152. [Google Scholar] [CrossRef]
- Khuskivadze, A.A.; Chibisov, M.I.; Fabrikant, I.I. Adiabatic energy levels and electric dipole moments of Rydberg states of Rb2 and Cs2 dimers. Phys. Rev. A 2002, 66, 042709. [Google Scholar] [CrossRef]
- Narits, A.; Kislov, K.; Lebedev, V. Electron-Impact Excitation and Dissociation of Heavy Rare Gas Heteronuclear Ions via Transitions to Charge Transfer States. Atoms 2023, 11, 60. [Google Scholar] [CrossRef]
- Pazyuk, E.; Revina, E.; Stolyarov, A. Ab Initio Long-Range Stud. Electron. Transit. Dipole Moments Low-Lying States Rb2 Cs2 Mol. J. Quant. Spectrosc. Radiat. Transf. 2016, 177, 283–290. [Google Scholar] [CrossRef]
- Li, H.; Li, M.; Makrides, C.; Petrov, A.; Kotochigova, S. Universal Scattering of Ultracold Atoms and Molecules in Optical Potentials. Atoms 2019, 7, 36. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Srećković, V.A.; Zalam, A.A.; Bezuglov, N.N.; Klyucharev, A.N. Dynamic Instability of Rydberg Atomic Complexes. Atoms 2019, 7, 22. [Google Scholar] [CrossRef]
- Simons, G. New procedure for generating valence and Rydberg orbitals. I. Atomic oscillator strengths. J. Chem. Phys. 1974, 60, 645–649. [Google Scholar] [CrossRef]
- Manakov, N.L.; Ovsiannikov, V.D.; Rapoport, L.P. Atoms in a laser field. Phys. Rep. 1986, 141, 320–433. [Google Scholar] [CrossRef]
- Il’inova, E.Y.; Ovsyannikov, V.D. Modified Fues potential for many-electron atoms. Opt. Spectrosc. 2008, 105, 647–656. [Google Scholar] [CrossRef]
- Zon, B.A.; Manakov, N.L.; Rapoport, L.P. Semiphenomenological Green’s Function of the Optical Electron in a Complex Atom. Sov. Phys. Dokl. 1970, 14, 904. [Google Scholar]
- Chernov, V.; Manakov, N.; Starace, A. Exact analytic relation between quantum defects and scattering phases with applications to Green’s functions in quantum defect theory. Eur. Phys. J. D 2000, 8, 347–359. [Google Scholar] [CrossRef]
- Walsh, C. The Chemical Biology of Sulfur; Royal Society of Chemistry: London, UK, 2020. [Google Scholar] [CrossRef]
- Turrini, D.; Schisano, E.; Fonte, S.; Molinari, S.; Politi, R.; Fedele, D.; Panic, O.; Kama, M.; Changeat, Q.; Tinetti, G. Tracing the Formation History of Giant Planets in Protoplanetary Disks with Carbon, Oxygen, Nitrogen, and Sulfur. Astrophys. J. 2021, 909, 40. [Google Scholar] [CrossRef]
- Bernard-Salas, J.; Pottasch, S.R.; Gutenkunst, S.; Morris, P.W.; Houck, J.R. Neon and Sulfur Abundances of Planetary Nebulae in the Magellanic Clouds. Astrophys. J. 2008, 672, 274. [Google Scholar] [CrossRef][Green Version]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database, version 5.10; NIST: Gaithersburg, MD, USA, 2022. [Google Scholar] [CrossRef]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; Los Alamos Series in Basic and Applied Sciences; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Kramida, A. Cowan Code: 50 Years of Growing Impact on Atomic Physics. Atoms 2019, 7, 64. [Google Scholar] [CrossRef]
- Glukhov, I.L.; Mokhnenko, S.N.; Nikitina, E.A.; Ovsiannikov, V.D. Natural widths and blackbody radiation induced shift and broadening of Rydberg levels in magnesium ions. Eur. Phys. J. D 2015, 69, 1. [Google Scholar] [CrossRef]
- Glukhov, I.L.; Kamenski, A.A.; Ovsiannikov, V.D.; Palchikov, V.G. Precision Spectroscopy of Radiation Transitions between Singlet Rydberg States of the Group IIb and Yb Atoms. Photonics 2023, 10, 1153. [Google Scholar] [CrossRef]
- Veselov, M.G.; Shtoff, A.V. Calculation of oscillator strengths of principal series of lithium in adiabatic approximation. Opt. Spectrosc. 1969, 26, 177. [Google Scholar]
- Beigman, I.L.; A., V.L.; Shevelko, V.P. Effect of polarization of atomic core on oscillator strengths and photoionization cross-sections of alkali element atoms. Opt. Spectrosc. 1970, 28, 229. [Google Scholar]
- Chichkov, B.N.; Shevelko, V.P. Dipole Transitions in Atoms and Ions With One Valence Electron. Phys. Scr. 1981, 23, 1055–1065. [Google Scholar] [CrossRef]
- Astapenko, V.A.; Bureeva, L.A.; Lisitsa, V.S. Polarization effects in atomic transitions. Phys. Uspekhi 2002, 45, 149–184. [Google Scholar] [CrossRef]
- Kramida, A. Critical Evaluation of Data on Atomic Energy Levels, Wavelengths, and Transition Probabilities. Fusion Sci. Technol. 2013, 63, 313–323. [Google Scholar] [CrossRef]
- Derevianko, A.; Ovsiannikov, V.D.; Pal’chikov, V.G.; Johnson, W.R.; Plante, D.R.; von Oppen, G. Higher-order Stark effect on an excited helium atom. Phys. Rev. A 1999, 60, 986–995. [Google Scholar] [CrossRef]
- Romanov, A.A.; Silaev, A.A.; Vvedenskii, N.V.; Breev, I.V.; Flegel, A.V.; Frolov, M.V. Second-harmonic generation of a short XUV pulse interacting with an IR-laser-dressed atom. Phys. Rev. A 2022, 106, 063101. [Google Scholar] [CrossRef]
- Romanov, A.A.; Silaev, A.A.; Sarantseva, T.S.; Flegel, A.V.; Vvedenskii, N.V.; Frolov, M.V. Channel separation of secondary generated radiation induced by orthogonal XUV and IR pulses. Opt. Lett. 2023, 48, 3583–3586. [Google Scholar] [CrossRef] [PubMed]
- Norman, G.E. Basis for the Quantum Defect Method. Opt. Spectrosc. (USSR) 1962, 12, 183. [Google Scholar]
- Davydkin, V.A.; Rapoport, L.P. The two-photon ionization of . J. Phys. B At. Mol. Opt. Phys. 1974, 7, 1101–1108. [Google Scholar] [CrossRef]
- Davydkin, V.A.; Zon, B.A. Radiation And Polarization Characteristics Of Rydberg Atomic States. Part I. Opt. Spectrosc. (USSR) 1981, 51, 13–150. [Google Scholar]
- Alcheev, P.G.; Buenker, R.J.; Chernov, V.E.; Zon, B.A. Oscillator strengths for Rydberg states in ArH calculated in QDT approximation. J. Mol. Spectrosc. 2003, 218, 190–196. [Google Scholar] [CrossRef]
- Chernov, V.E.; Dorofeev, D.L.; Kretinin, I.Y.; Zon, B.A. Method of the reduced-added Green function in the calculation of atomic polarizabilities. Phys. Rev. A 2005, 71, 022505. [Google Scholar] [CrossRef]
- Bateman, H.; Erdélyi, A. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
- Martin, W.; Wiese, W. Atomic, Molecular, and Optical Physics Handbook (Version 2.2); Springer: New York, NY, USA, 2002. [Google Scholar]
- Drake, G.W.F. (Ed.) Springer Handbook of Atomic, Molecular, and Optical Physics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Sobelman, I.I. Atomic Spectra and Radiative Transitions; Springer Series in Chemical Physics; Springer: Berlin/Heidelberg, Germany, 1979; Volume 1. [Google Scholar]
- Gordon, I.; Rothman, L.; Hargreaves, R.; Hashemi, R.; Karlovets, E.; Skinner, F.; Conway, E.; Hill, C.; Kochanov, R.; Tan, Y.; et al. The HITRAN2020 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107949. [Google Scholar] [CrossRef]
- Civiš, S.; Kubelík, P.; Ferus, M.; Chernov, V.E.; Zanozina, E.M.; Juha, L. Laser ablation of an indium target: Time-resolved Fourier-transform infrared spectra of In I in the 700–7700 cm−1 range. J. Anal. At. Spectrom. 2014, 29, 2275–2283. [Google Scholar] [CrossRef]
- Civiš, S.; Ferus, M.; Chernov, V.E.; Zanozina, E.M.; Juha, L. Zn I spectra in the 1300–6500 cm−1 range. J. Quant. Spectrosc. Radiat. Transf. 2014, 134, 64–73. [Google Scholar] [CrossRef]
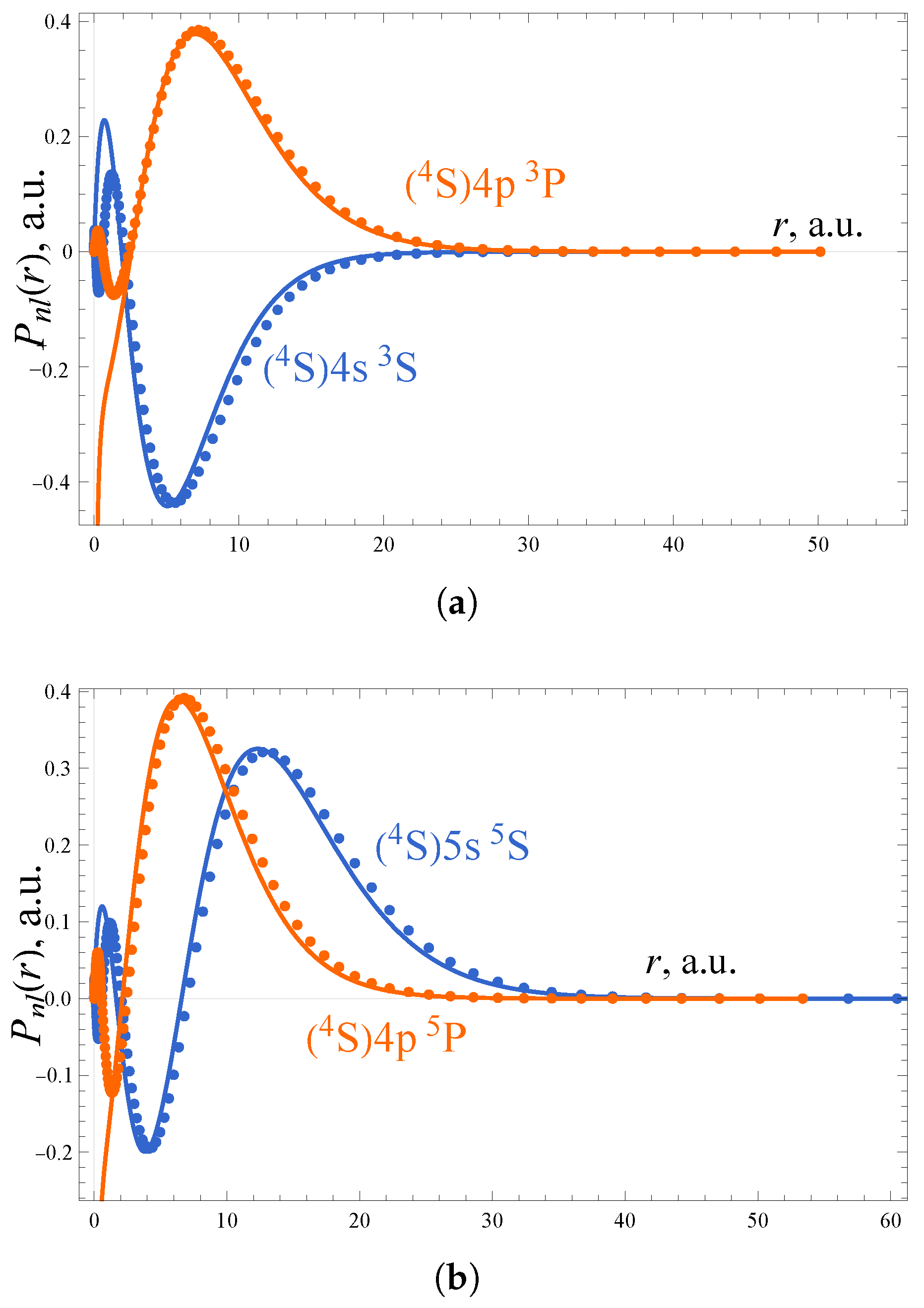
| Term | n | l | ||||
|---|---|---|---|---|---|---|
| 4 | 0 | 1.972 | 2.028 | 1 | −0.02835 | |
| 4 | 0 | 1.883 | 2.117 | 1 | −0.1166 | |
| 4 | 1 | 2.425 | 1.575 | 0 | 1.425 | |
| 4 | 1 | 2.337 | 1.663 | 0 | 1.337 | |
| 4 | 2 | 3.799 | 0.2014 | 1 | 1.799 | |
| 4 | 2 | 3.575 | 0.4247 | 1 | 1.575 | |
| 5 | 0 | 2.998 | 2.002 | 2 | −0.001832 | |
| 5 | 0 | 2.922 | 2.078 | 2 | −0.07844 | |
| 5 | 1 | 3.437 | 1.563 | 1 | 1.437 | |
| 5 | 1 | 3.374 | 1.626 | 1 | 1.374 | |
| 6 | 0 | 4.006 | 1.994 | 3 | 0.005860 | |
| 6 | 0 | 3.933 | 2.067 | 3 | −0.06727 | |
| 6 | 1 | 4.403 | 1.597 | 2 | 1.403 | |
| 6 | 1 | 4.386 | 1.614 | 2 | 1.386 |
| Wavenumber () | Lower Level a | Upper Level b | () | |
|---|---|---|---|---|
| This Work | NIST | |||
| 3567.46 | ||||
| 3567.46 | ||||
| 3567.12 | ||||
| 3567.12 | ||||
| 3566.79 | ||||
| 3566.79 | ||||
| 3527.40 | ||||
| 3525.89 | ||||
| 3525.87 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chernov, V.E.; Manakov, N.L.; Meremianin, A.V.; Naskidashvili, A.V.; Civiš, S.; Ferus, M.; Kubelík, P.; Zanozina, E.M.; Zetkina, O.V. High-Resolution Fourier Transform Spectra of Atomic Sulfur: Testing of Modified Quantum Defect Theory. Atoms 2025, 13, 16. https://doi.org/10.3390/atoms13020016
Chernov VE, Manakov NL, Meremianin AV, Naskidashvili AV, Civiš S, Ferus M, Kubelík P, Zanozina EM, Zetkina OV. High-Resolution Fourier Transform Spectra of Atomic Sulfur: Testing of Modified Quantum Defect Theory. Atoms. 2025; 13(2):16. https://doi.org/10.3390/atoms13020016
Chicago/Turabian StyleChernov, Vladislav E., Nikolai L. Manakov, Alexei V. Meremianin, Alexander V. Naskidashvili, Svatopluk Civiš, Martin Ferus, Petr Kubelík, Ekaterina M. Zanozina, and Oxana V. Zetkina. 2025. "High-Resolution Fourier Transform Spectra of Atomic Sulfur: Testing of Modified Quantum Defect Theory" Atoms 13, no. 2: 16. https://doi.org/10.3390/atoms13020016
APA StyleChernov, V. E., Manakov, N. L., Meremianin, A. V., Naskidashvili, A. V., Civiš, S., Ferus, M., Kubelík, P., Zanozina, E. M., & Zetkina, O. V. (2025). High-Resolution Fourier Transform Spectra of Atomic Sulfur: Testing of Modified Quantum Defect Theory. Atoms, 13(2), 16. https://doi.org/10.3390/atoms13020016






