Diagnostics of Spin-Polarized Ions at Storage Rings
Abstract
1. Introduction
2. Theoretical Background
2.1. Density Matrix Approach
2.2. RR Cross Section
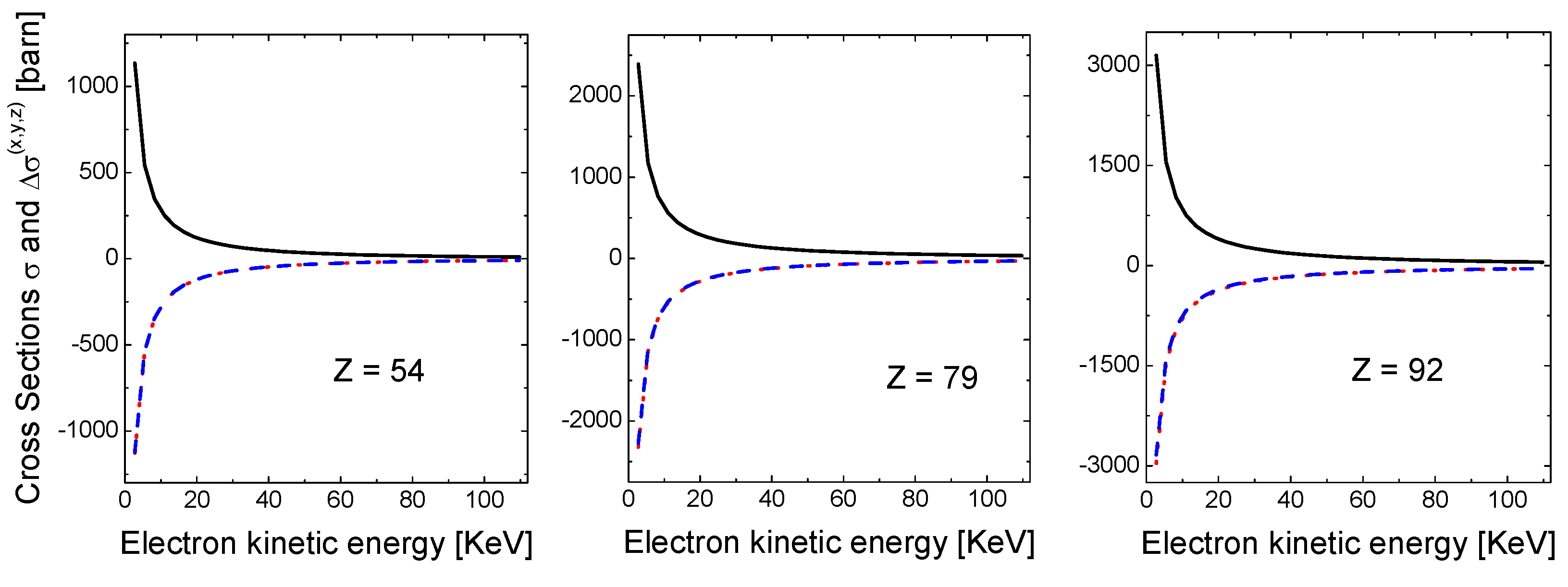
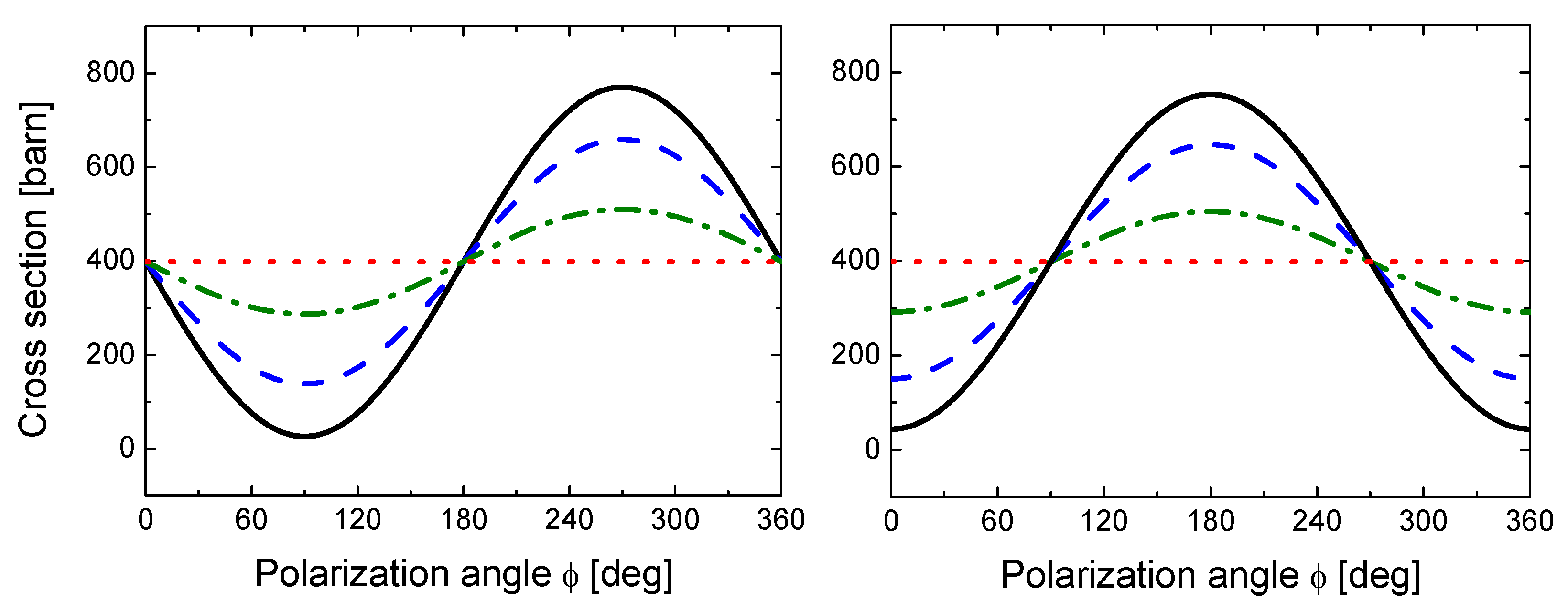
3. Results and Discussion
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khriplovich, I. Feasibility of search for nuclear electric dipole moments at ion storage rings. Phys. Lett. B 1998, 444, 98–102. [Google Scholar] [CrossRef]
- Labzowsky, L.N.; Nefiodov, A.V.; Plunien, G.; Soff, G.; Marrus, R.; Liesen, D. Parity-violation effect in heliumlike gadolinium and europium. Phys. Rev. A 2001, 63, 054105. [Google Scholar] [CrossRef]
- Klasnikov, A.E.; Artemyev, A.N.; Beier, T.; Eichler, J.; Shabaev, V.M.; Yerokhin, V.A. Spin-flip process in radiative recombination of an electron with H- and Li-like uranium. Phys. Rev. A 2002, 66, 042711. [Google Scholar] [CrossRef]
- Maiorova, A.; Pavlova, O.; Shabaev, V.; Kozhuharov, C.; Plunien, G.; Stöhlker, T. Parity nonconservation in the radiative recombination of electrons with heavy hydrogen-like ions. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 205002. [Google Scholar] [CrossRef]
- Lenisa, P.; Maiorova, A.; Nass, A.; Pretz, J.; Rathmann, F.; Stöhlker, T.; Bondarev, A.; Engels, R.; Fritzsche, S.; Gebel, R.; et al. Towards experiments with polarized beams and targets at the GSI/FAIR storage rings. PoS 2023, PSTP2022, 028. [Google Scholar] [CrossRef]
- Prozorov, A.; Labzowsky, L.; Liesen, D.; Bosch, F. Schemes for radiative polarization of ion beams in storage rings. Phys. Lett. B 2003, 574, 180–185. [Google Scholar] [CrossRef]
- Bondarevskaya, A.; Prozorov, A.; Labzowsky, L.; Plunien, G.; Liesen, D.; Bosch, F. Theory of the polarization of highly charged ions in storage rings: Production, preservation, observation and application to the search for a violation of the fundamental symmetries. Phys. Rep. 2011, 507, 1–42. [Google Scholar] [CrossRef]
- Surzhykov, A.; Fritzsche, S.; Stöhlker, T.; Tashenov, S. Application of Radiative Electron Capture for the Diagnostics of Spin-Polarized Ion Beams at Storage Rings. Phys. Rev. Lett. 2005, 94, 203202. [Google Scholar] [CrossRef]
- Middents, W.; Weber, G.; Spillmann, U.; Krings, T.; Vockert, M.; Volotka, A.; Surzhykov, A.; Stöhlker, T. Possible Polarization Measurements in Elastic Scattering at the Gamma Factory Utilizing a 2D Sensitive Strip Detector as Dedicated Compton Polarimeter. Ann. Phys. 2022, 534, 2100285. [Google Scholar] [CrossRef]
- Fritzsche, S.; Surzhykov, A.; Stöhlker, T. Radiative recombination into high-Z few-electron ions: Cross sections and angular distributions. Phys. Rev. A 2005, 72, 012704. [Google Scholar] [CrossRef]
- Maiorova, A.V.; Fritzsche, S.; Surzhykov, A.; Stöhlker, T. Radiative recombination of highly charged ions with polarized electrons. Phys. Rev. A 2023, 107, 042814. [Google Scholar] [CrossRef]
- Eichler, J.; Meyerhof, W. Relativistic Atomic Collisions; Academic Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Shabaev, V.M. Two-time Green’s function method in quantum electrodynamics of high-Z few-electron atoms. Phys. Rep. 2002, 356, 119. [Google Scholar] [CrossRef]
- Eichler, J. Lectures on Ion-Atom Collisions: From Nonrelativistic to Relativistic Velocities; North-Holland Personal Library; Elsevier: Boston, MA, USA, 2005. [Google Scholar]
- Fano, U.; Racah, G. Irreducible Tensorial Sets; Academic Press: Cambridge, MA, USA, 1959. [Google Scholar]
- Blum, K. Density Matrix Theory and Applications, 3rd ed.; Springer Series on Atomic Optical and Plasma Physics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Balashov, V.V.; Grum-Grzhimailo, A.N.; Kabachnik, N.M. Polarization and Correlation Phenomena in Atomic Collisions; Kluwer Academic/Plenum: New York, NY, USA, 2000. [Google Scholar]
- Varshalovich, D.A.; Moskalev, A.N.; Khersonskii, V.K. Quantum Theory of Angular Momentum; World Scientific Publishing Company: Singapore, 1988. [Google Scholar] [CrossRef]
- Eichler, J.; Ichihara, A.; Shirai, T. Photon angular distributions from radiative electron capture in relativistic atomic collisions. Phys. Rev. A 1995, 51, 3027–3035. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maiorova, A.; Fritzsche, S.; Surzhykov, A.; Stöhlker, T. Diagnostics of Spin-Polarized Ions at Storage Rings. Atoms 2025, 13, 15. https://doi.org/10.3390/atoms13020015
Maiorova A, Fritzsche S, Surzhykov A, Stöhlker T. Diagnostics of Spin-Polarized Ions at Storage Rings. Atoms. 2025; 13(2):15. https://doi.org/10.3390/atoms13020015
Chicago/Turabian StyleMaiorova, Anna, Stephan Fritzsche, Andrey Surzhykov, and Thomas Stöhlker. 2025. "Diagnostics of Spin-Polarized Ions at Storage Rings" Atoms 13, no. 2: 15. https://doi.org/10.3390/atoms13020015
APA StyleMaiorova, A., Fritzsche, S., Surzhykov, A., & Stöhlker, T. (2025). Diagnostics of Spin-Polarized Ions at Storage Rings. Atoms, 13(2), 15. https://doi.org/10.3390/atoms13020015





