Antiprotonic Atoms as Gateways to HCI

Abstract

The present study investigates the production of highly charged ions (HCIs) through the novel application of antiprotonic atoms and explores their potential for studying atomic and nuclear structures. Utilizing the Geant4 simulation toolkit, comprehensive simulations were conducted for all known isotopes with atomic numbers below 100. These simulations recorded key parameters of the resulting nuclear fragments, including mass, momentum, charge, and yield. The results obtained from this study offer valuable insights into the mechanisms of HCI production and provide a foundation for planning and analyzing future experimental investigations. This work demonstrates the feasibility of using antiprotonic atoms to advance nuclear and atomic physics research.

1. Antiprotonic Atoms

Exotic atoms contain particles other than electrons, neutrons, or protons. Antiprotonic atoms are a type of exotic atom that contains antiprotons. An ‘ordinary’ atom is composed of a positively charged nucleus that interacts electromagnetically with electrons, resulting in a bound atomic state. Antiprotonic atoms are similar systems where there is a negatively charged antiproton instead of an electron. Figure 1 schematically depicts antiprotonic helium.

De-Excitation X-Rays Spectra

Exotic atoms are produced by stopping negatively charged particles, other than electrons, in matter. Generally, it is assumed that the stopped particle replaces an electron of an ordinary atom. Energies of atomic level (${\mathrm{E}}_{\mathrm{n}}$) and corresponding orbital radius (${\mathrm{r}}_{\mathrm{n}}$) of such an antiproton attached to the nucleus could be calculated similarly to the electron, written as follows:

$${\mathrm{E}}_{\mathrm{n}}=-{\displaystyle \frac{\mu {\mathrm{c}}^2}{2}}\ast {\left({\displaystyle \frac{\mathrm{Z}\alpha }{\mathrm{n}}}\right)}^2$$

(1)

$${\mathrm{r}}_{\mathrm{n}}={\displaystyle \frac{{\mathrm{h}}^2}{\mu {\mathrm{e}}^2}}{\displaystyle \frac{{\mathrm{n}}^2}{\mathrm{Z}}}$$

(2)

where n is the principal quantum number describing a bound state, c is the speed of light, $\alpha$ is the fine structure constant, h is the Planck constant, Z is the atomic number, and e is the elemental charge. The difference in mass is taken into account by $\mu$, which is the reduced particle-nucleus mass.

On account of this difference in mass between the electron and the heavier particle, the same radius of the orbit corresponds to different energy levels. Assuming the non-resonant interaction of an antiproton with an electron with a Bohr radius ${\mathrm{r}}_{\mathrm{b}}$, the exotic atom that would be created would have an antiproton at the same radius, and it would be excited with energy level ${\mathrm{n}}_{\overline{\mathrm{p}}}$, calculated as follows:

$${\mathrm{n}}_{\overline{\mathrm{p}}}={\mathrm{n}}_{\mathrm{el}}{\left({\displaystyle \frac{{\mathrm{m}}_{\overline{\mathrm{p}}}}{{\mathrm{m}}_{\mathrm{el}}}}\right)}^{1/2}$$

(3)

where ${\mathrm{m}}_{\mathrm{el}}$ is mass of electron and ${\mathrm{m}}_{\overline{\mathrm{p}}}$ is mass of antiproton. If this were an atom of helium in its ground state, one of the K-shell (principle quantum number of electron ${\mathrm{n}}_{\mathrm{el}}=1$), resulting in the principle quantum number of the antiproton ${\mathrm{n}}_{\overline{\mathrm{p}}}=43$. When an antiproton replaces a K-shell electron, it begins a cascade down to its ground state ${\mathrm{n}}_{\overline{\mathrm{p}}}=1$ from a highly excited state relative to the antiproton atomic level scheme. The entire atomic cascade occurs within the electron cloud; therefore, the influence of electrons could be omitted. The de-excitation of the atom into lower states occurs primarily through two processes. In the upper part of the cascade, the dominant deexcitation process is the Auger process. 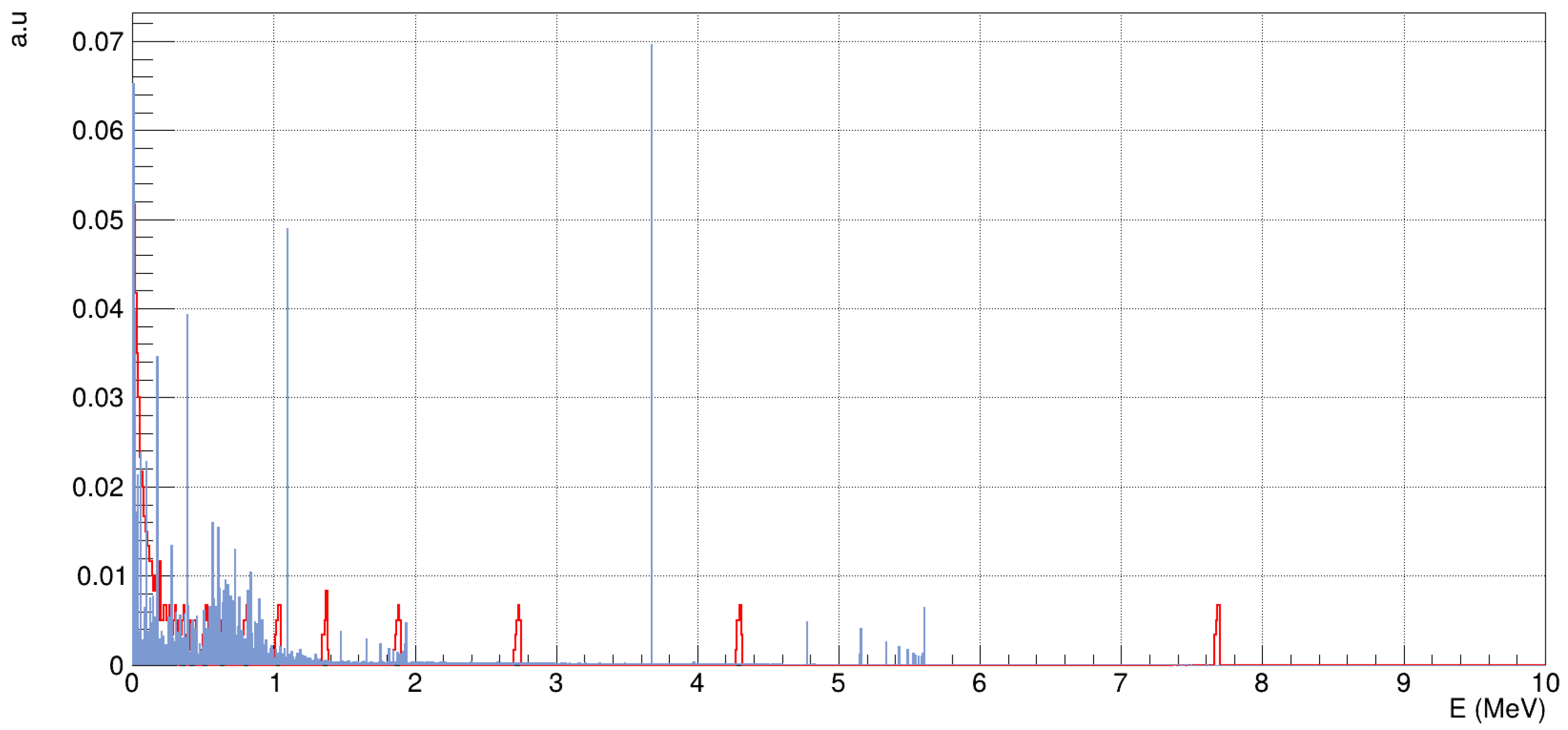During de-excitation to lower levels with increasing energy differences ($\Delta$E) between levels, the X-ray transitions begin to compete and finally take over completely. A histogram with gamma photons simulated by Geant4 during de-excitation and annihilation on isotope I125 is presented in Figure 2.

A different scenario would be if the initial atom would be if the antiproton is captured at very low energies in a Rydberg state $({\mathrm{n}}_{\mathrm{el}}\approx 30)$, then the electron correlations should be considered. Transitions of $\overline{\mathrm{p}}$ were studied in noble gases in gaseous form at reduced pressure [1]. In an energy range between 1 and 250 keV, results supported the idea that the $\overline{\mathrm{p}}$ is incorporated in the atom far beyond the electronic K shell. In the upper shells, the atom steadily loses its electrons. In diluted gases, refilling of Auger-ejected electrons from neighboring atoms or molecules is very strongly suppressed—which leads to the formation of highly charged ions. However, in the course of the cascade, the remaining electrons are more deeply bound. This can effectively temporarily interrupt the Auger de-excitation. Such levels should be metastable as only radiative transitions could occur at lower levels. Even relatively low-resolution fluorescence spectroscopy of the X-ray transitions at the end of the antiprotonic cascade provided valuable information on the strong interaction or permitted identifying the last state reached in the cascade and from which annihilation occurs [2]. Studies of ${\overline{\mathrm{p}}}^{208}\mathrm{Pb}$ have been the target of spectroscopic observations, where measurement of the fine-structure splitting in X-ray transition allowed determining the magnetic moment of the antiproton at the ‰level [3].

2. Pulsed Production and HCI’s

Different approaches for forming antiprotonic atoms—especially antihydrogen—were implemented in the past. Pulsed production with a charge exchange reaction with positronium was proposed as an alternative to the nested well technique of producing antihydrogen [4]. Positronium Ps is an exotic system—bound by the Coulomb force state of electron and positron—similar to protonium but much lighter and of leptonic nature. By producing Rydberg-excited positronium, it is thus possible to produce large amounts of Rydberg antihydrogen, with the additional benefit of having control of its Rydberg state. Using a similar principle, the pulsed production could be used for obtaining different antiprotonic atoms. As for the pulsed production of antihydrogen, it relies on the resonant-charge exchange reaction with ions in the Rydberg state.

$${\mathrm{A}}^{*}+\overline{\mathrm{p}}\to \overline{\mathrm{p}}{\mathrm{A}}^{*}+{\mathrm{e}}^{-}$$

(4)

where a Rydberg excited atom ${\mathrm{A}}^{*}$ and antiprotons $\overline{\mathrm{p}}$ interact to form the antiprotonic atom $\overline{\mathrm{p}}{\mathrm{A}}^{*}$. An excited Rydberg atom ${\mathrm{A}}^{*}$ is created from excited anions ${\mathrm{A}}^{-}$ via pulsed laser photo-detachment. Anions can be trapped alongside other negative particles—antiprotons and electrons—for electron cooling. Three lasers are then sequentially turned on: first for photodetachment, followed by two laser pulses for Rydberg excitation. At this moment, a resonant exchange reaction happens between the Rydberg atoms and the antiprotons, forming the antiprotonic atoms depicted in [5]. This process lasts for approximately 10 ns and ends with the annihilation of the antiproton on the surface of the nuclei with the production of several pions. The pions can interact with the nucleus, causing antiproton-induced fragmentation.

The remaining nuclei or fragments should be fully or almost fully stripped of electrons [6]. Working within a nested Penning trap as depicted in Figure 3 would allow the trapping of any formed highly charged nuclear fragments [7].

Hollow Rydberg Antiprotonic Atoms

There is a possibility of the creation of subsequent antiprotonic atoms from remaining HCIs if they are trapped with antiprotons and initial Rydberg atoms. A process called charge exchange happens between HCIs and Rydberg atoms. This results in new Rydberg systems that are in a state like the original Rydberg atom [8]:

$${\mathrm{A}}^{\mathrm{Z}+}+{\mathrm{B}}^{*}\to {\mathrm{A}}^{(\mathrm{Z}-1)+\ast }+{\mathrm{B}}^{+\ast }$$

(5)

where excited B-ions are initial ions, and A-ions are HCIs produced from them. Another possibility of creating (hollow) Rydberg ions is interactions of HCI ${\mathrm{A}}^{\mathrm{Z}+}$ with excited positronium ${\mathrm{Ps}}^{*}$, mimicking the pulsed production process of antihydrogen to form the same hollow Rydberg ion ${\mathrm{A}}^{(\mathrm{Z}-1)+\ast }$:

$${\mathrm{A}}^{\mathrm{Z}+}+{\mathrm{Ps}}^{*}\to {\mathrm{A}}^{(\mathrm{Z}-1)+\ast }+{\mathrm{e}}^{+}$$

(6)

After A-ions excite one electron, they could have a charge exchange with antiprotons that are also trapped alongside, leading to the subsequent formation of antiprotonic atoms, annihilation, and formation of new HCIs:

$${\mathrm{A}}^{(\mathrm{Z}-1)+\ast }+\overline{\mathrm{p}}\to \overline{\mathrm{p}}{\mathrm{A}}^{\mathrm{Z}+\ast }+{\mathrm{e}}^{-}$$

(7)

Another possibility would be the exchange process with protonium atoms formed shortly after the production of the ${\mathrm{A}}^{Z\ast }$ fragment from nearby co-trapped ${\mathrm{H}}^{-}$ and ${\overline{\mathrm{p}}}^{-}$. Those Rydberg protonium atoms can then lead, via a second charge exchange process, to the hollow Rydberg antiprotonic atoms consisting of nuclear fragments and the antiproton:

$${\mathrm{A}}^{\mathrm{Z}+}+\overline{\mathrm{p}}\mathrm{p}\to \overline{\mathrm{p}}{\mathrm{A}}^{\mathrm{Z}+\ast }+{\mathrm{e}}^{-}+\mathrm{p}$$

(8)

This process is similar to the interaction between antiprotons and highly charged ions in an electron beam ion trap, which has been found to have a very high cross-section. Before annihilation, these highly charged, trapped, hollow Rydberg ions are heavily charged ions with a single negative particle, an antiproton, in a long-lived Rydberg state, which is not only an interesting system to study on its own but also can lead to further formation of antiprotonic atoms.

3. Geant4 Simulation

The simulations were focusing the annihilation of antiprotons on various nuclei. Simulation applications were developed using Geant4, an open-source toolkit developed at CERN. It is based on the Geant4 basic example B2B.

The geometry proposed in simulations differs from the one that is implemented in experiments. Other than the absence of external magnetic and electric fields in the simulation, we focus on the interaction of a single antiproton with the target, whereas in the experimental design, it would happen as a mixing of clouds of antiprotons, electrons, and ions trapped alongside in a Penning trap. The secondary annihilation discussed in the Section Hollow Rydberg Antiprotonic Atoms which is not implemented in Geant4 might as well influence the quantity of fragments and their energy. Nevertheless, simulations would give a general idea of what to expect.

The “world” in simulation is defined as a cube with a sphere inside. The spherical geometry of the target was proposed for targeting the elastic interaction of antiprotons. The antiproton is released inside a sphere made of a specific isotope. There is a vacuum inside the sphere. The detector is constructed as a thin 0.5 nm sphere of isotope where a particle gun is placed in the middle (Figure 4). FThe material of which the sphere is built is defined in such a way that a bash script could substitute values with data of known isotopes. There is no external magnetic or electric field implemented. One million antiprotons are subsequently created in the center with an energy of 1 keV, which is the lowest energy sustained by Geant4.

After they annihilate, information about produced secondaries with mass, momentum, charge, and quantity is stored, creating a database for known isotopes with Z < 100. Possible products of the capture and annihilation of antiprotons on atoms are as follows:

• Pions: ${\pi }^0,{\pi }^{-},{\pi }^{+}$;
• Kaons: ${\kappa }^0,{\kappa }^{-},{\kappa }^{+}$;
• Light nuclear fragments: proton, neutron, deuteron, triton, ³He, ⁴He;
• Heavier nuclear fragments;
• Gamma—from deexcitation and annihilation;
• Electrons.

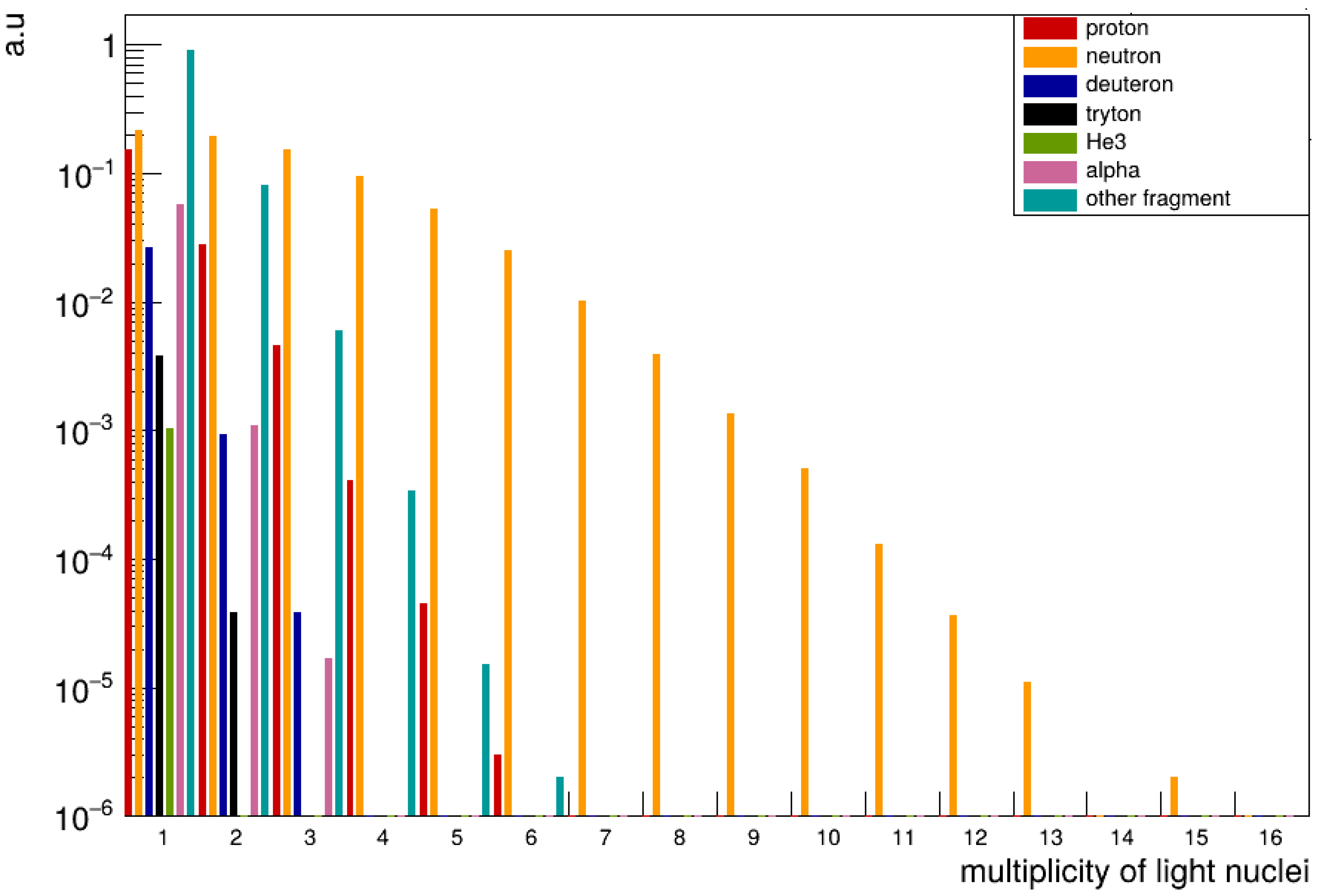
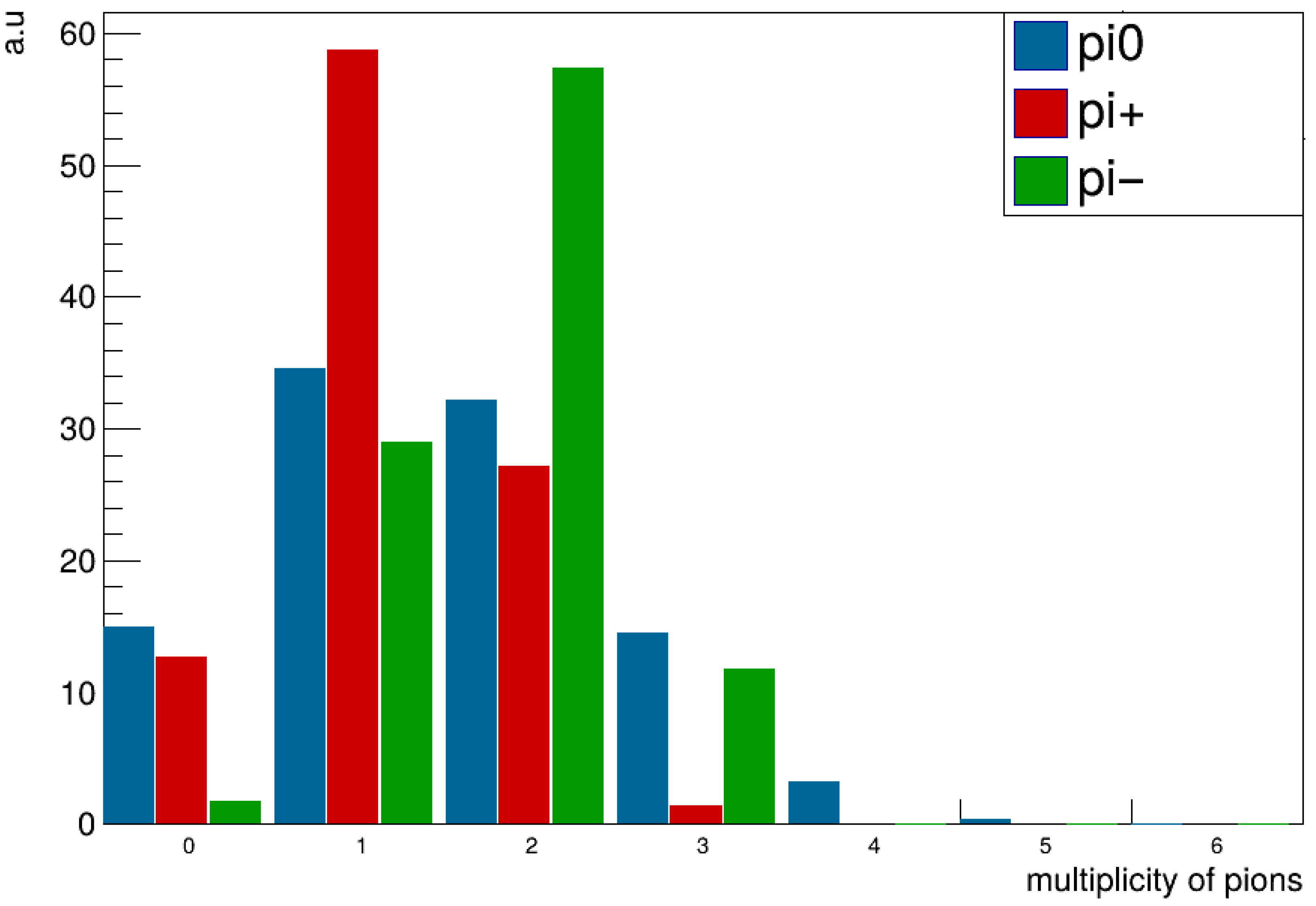
The frequency with which light nuclei are produced during annihilation is shown in Figure 5. It shows how often nuclei are split, fragmented, or emit singular nucleons. Separately, in Figure 6, the frequency of pion production is displayed. Charged pions are an important product, and they could be measured with scintillators. The sum of charges indicates if annihilation took place on a proton or a neutron. The chosen example isotope ¹²⁵I is one of the potential isotopes that might be studied in the AEgIS experiment in the near future.

Even though the antiproton annihilates at rest, the energy of the fragments produced could be much higher. The energy-to-charge ratio could be used to estimate the number of fragments that can be trapped. A histogram of the energy of created fragments from antiproton annihilations on ¹²⁵I is present in Figure 7.

While it is expected that antiprotons will (almost) completely ionize the atom, in Geant4, the target is considered continuous material, which means electrons are distributed freely and the gaps are immediately filled. Therefore, it is assumed that fragments are completely stripped.

In Geant4, stopping and absorption of antiprotons and all anti-nuclei uses the Fritiof (FTF) string model. In this model, the parameterizations of the cross sections implemented in the CHIPS (CHiral Invariant Phase Space) model are used. For nuclear deexcitation, the PreCompound model is used. Coulomb cross-sections are implemented within electromagnetic physics libraries, so the main Coulomb term is excluded from hadron cross-sections. An interference between electromagnetic and strong amplitudes should be taken into account in hadronic physics but in the main models is ignored so far. Nuclear reactions are typically modeled in two stages. The first, fast reaction stage is described by a dynamical model (quantum molecular dynamics, intranuclear cascade, pre-compound, etc.) and often results in the production of one or several excited nuclei. The second reaction stage describes the de-excitation of the excited nuclei, and it is usually handled by statistical de-excitation models. Each hadronic process is derived from the G4Hadronic-Process. Each has a list of cross-section datasets—objects that encapsulate methods and data for calculating total cross-sections for a given process in a certain range. The implementations can be an equation, sophisticated parameterizations, or evaluated data. All cross-section dataset classes are derived from the abstract class G4VCrossSection-DataSet [9].

The class G4HadronicAbsorptionFritiof is responsible for handling anti-proton capture and annihilation. $\mu$—capture is handled by class G4MuonMinusCapture. The capture of low-energy negatively charged particles is a complex process involving the formation of exotic atoms, X-ray cascade and Auger cascade, and nuclear interaction. In the case of $\mu$, there is also a probability of decay from the K-shell of the muonic atom. To handle this, a base process class G4HadronicStoppingProcess is used [10]. It is possible to create a similar dedicated class to the antiprotons class, but for now, it is not available.

4. Nuclear Fragment Production

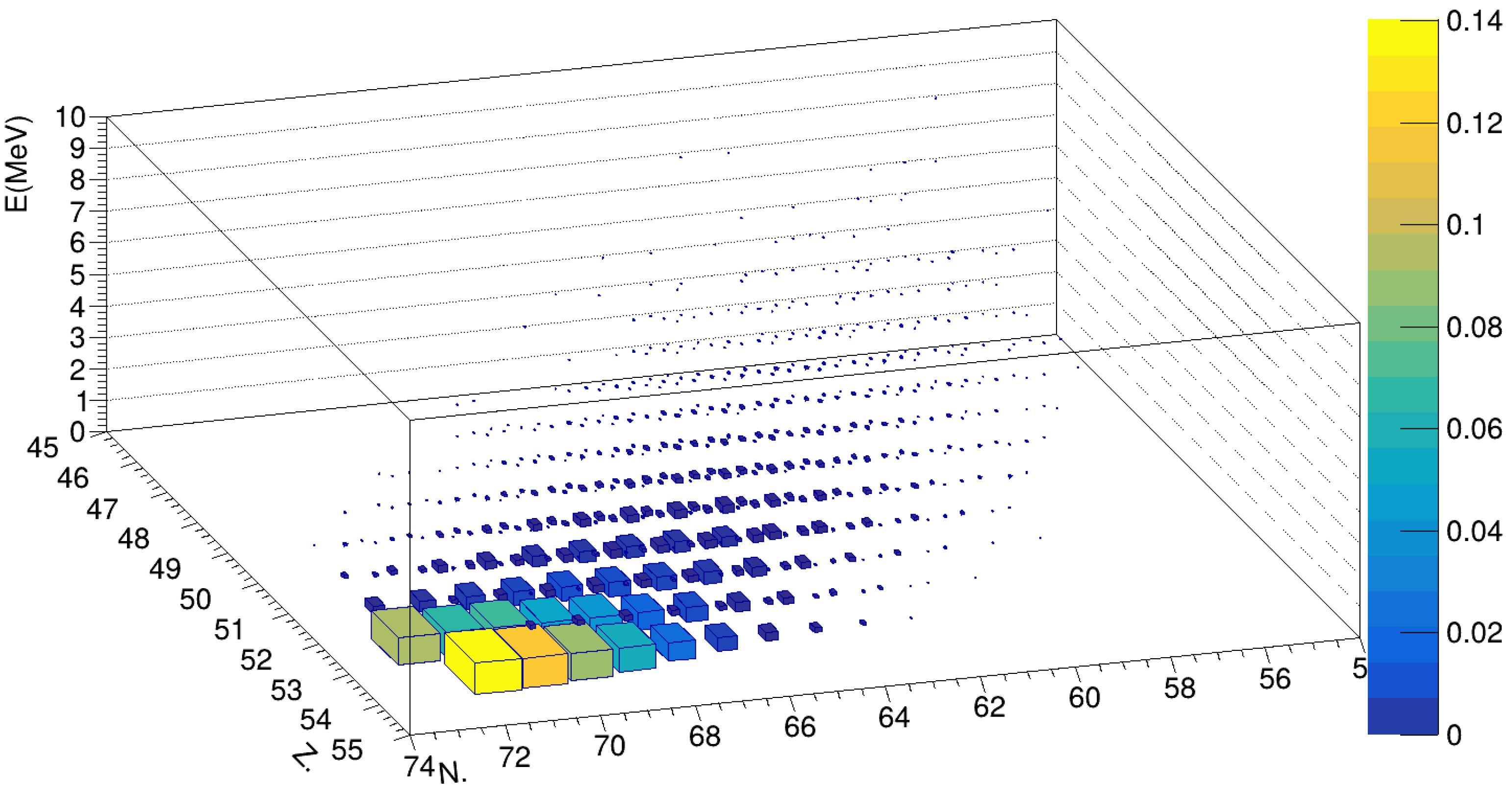
The use of antiprotonic atoms represents an innovative mechanism for producing highly charged ions and difficult-to-obtain radioisotopes, including those of short-lived isotopes. Antiproton-induced fragmentation offers a new approach to generating radioisotopes that are otherwise challenging to produce, extract, or trap. With the AEgIS apparatus, it may be possible to obtain cold, pre-trapped rare radioisotopes, opening new research opportunities. An example of created isotopes from antiproton annihilations on ¹²⁵I is shown in Figure 8. After the antiprotonic cascade and annihilation, the remaining nuclei should be fully or almost fully stripped of electrons. Already cold and trapped HCIs are interesting cases to study. They exhibit extreme electromagnetic properties, which are ideal to test strong field QED. It has an enhanced sensitivity to nuclear structure (QCD). Moreover, electron capture is no longer possible, so radioactive HCIs have suppressed this channel of decay [7].

The formation of HCIs typically requires the removal of electrons from atoms, which can be achieved through collisional processes involving a series of foils or by exposure to an intense current of high-energy electrons. Once the electrons are stripped, the resulting HCIs are trapped and cooled for further investigation. In the case of antiprotonic atoms, for light and mid-heavy nuclei with electron binding energies below 40 keV, electron stripping occurs automatically during the annihilation process. At the moment of antiproton annihilation, the remaining nuclei are left fully or nearly fully stripped of electrons, simplifying the production of HCIs. The resulting cold and trapped HCIs are particularly valuable for scientific exploration. These ions exhibit extreme electromagnetic properties that make them ideal for testing strong-field quantum electrodynamics and studying nuclear structures with enhanced sensitivity, relevant to QCD. Additionally, radioactive HCIs benefit from suppressed electron capture decay channels due to the absence of bound electrons, as shown in recent studies [7].

Currently, the production of radioisotopes relies on several processes, including proton-induced spallation, fragmentation, ablation-fission, Coulomb excitation-fission, multinucleon transfer, and the decay of naturally occurring isotopes. Each method imposes specific constraints on the types of isotopes that can be produced. Antiproton-induced fragmentation could complement these techniques by enabling the creation of radioisotopes that are challenging to produce with existing methods. The lifetimes of the isotopes to be investigated also play a crucial role in limiting possibilities for studies. Short-lived isotopes often could not be studied because the time of production and trapping is shorter than the time of life.

Another exciting possibility is achieving subsequent annihilations. If HCIs, antiprotons, and initial Rydberg atoms are trapped together, the system could facilitate a chain of annihilation events. This process is similar to the interaction between antiprotons and highly charged ions in an electron beam ion trap, which has been found to have a very high cross-section [8]. Before annihilation, these highly charged, trapped, hollow Rydberg ions are heavily charged ions with a single negative particle in a long-lived Rydberg state. First and subsequent annihilations can create a path to reach very exotic and short-lived nuclei starting from a stable isotope. Unlike traditional nuclear physics methods, where exotic nuclei are created in highly energetic states or their production is restricted by their chemical properties, this approach would yield already trapped and cold nuclei. By using antiproton-induced fragmentation and the resulting annihilations, researchers could explore new ways to produce isotopes and study fundamental physics.

5. Path for Exotic Isotopes

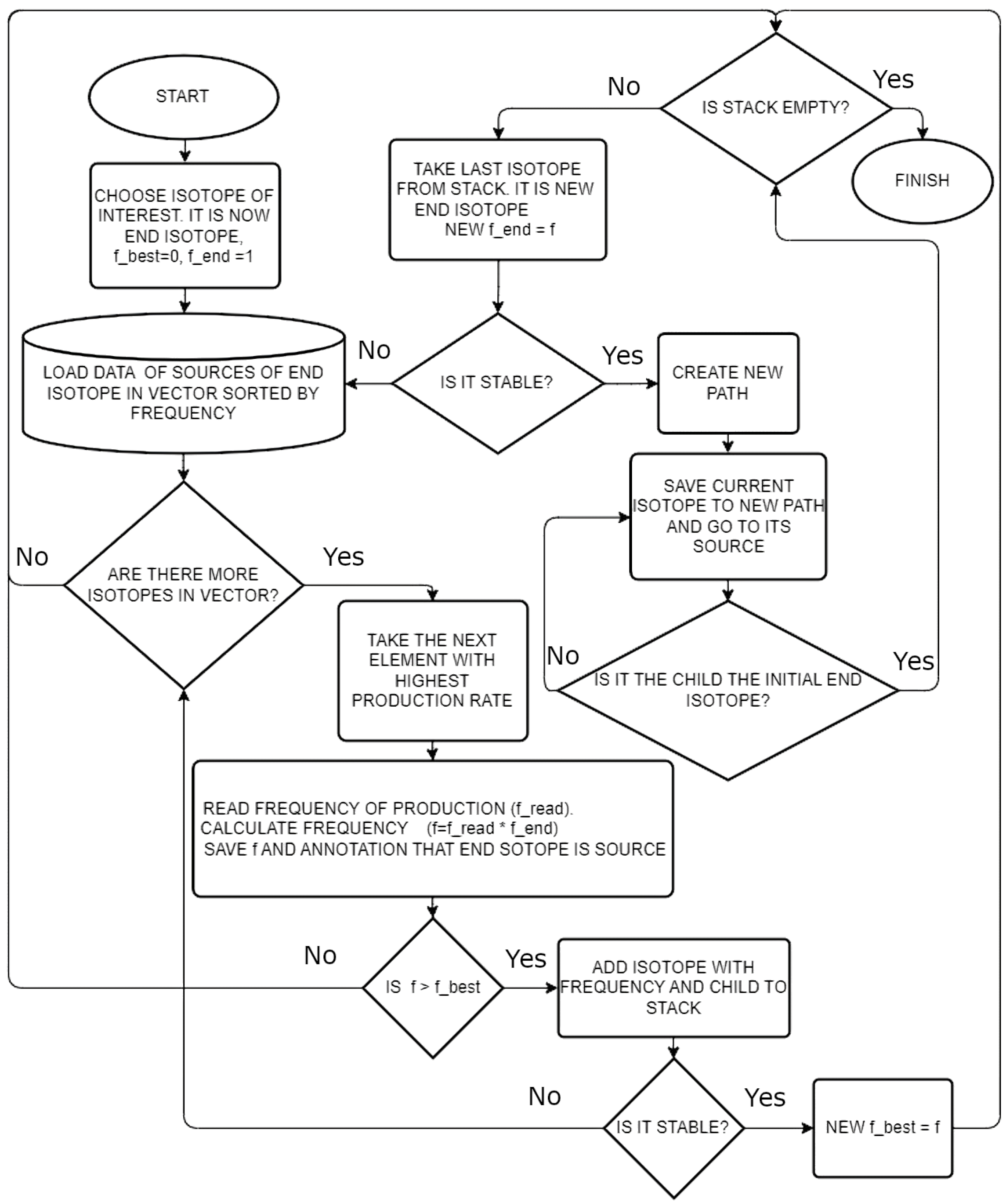
Antiproton capture is simulated with more than 3000 different target-type isotopes, and from each different nuclei are produced. Some of the secondary isotopes that may be interesting for studies are not achievable from stable initial isotopes in satisfying ratios. There is a possibility of accessing them through subsequent annihilation. Based on simulations, it is possible to build a path to any interesting exotic isotope from a stable ion that we can use in the beginning. Determining which path to use is a difficult task, as there are multiple possible paths and multiple starting points. With more than 3000 isotopes, the complete computation of all the possible paths to find the optimum one would take an impractical amount of time. The problem is simplified, and an algorithm is proposed that, for the given resulting nucleus, determines the best starting isotope to produce the largest quantity of said nuclei. The created algorithm is inspired by Dijkstra’s algorithm [11] in a directed weighted graph. Here, the concept is adapted to a nuclear transformation framework, where isotopes represent nodes, and the possible annihilation-induced fragmentation processes are represented as directed edges with weights corresponding to their frequencies. This graph-based approach facilitates efficient navigation through the complex network of nuclear reactions, enabling the identification of optimal pathways in a fraction of the time that brute-force methods would require. It allows finding the most efficient way of producing any isotope from a stable isotope.

Algorithm

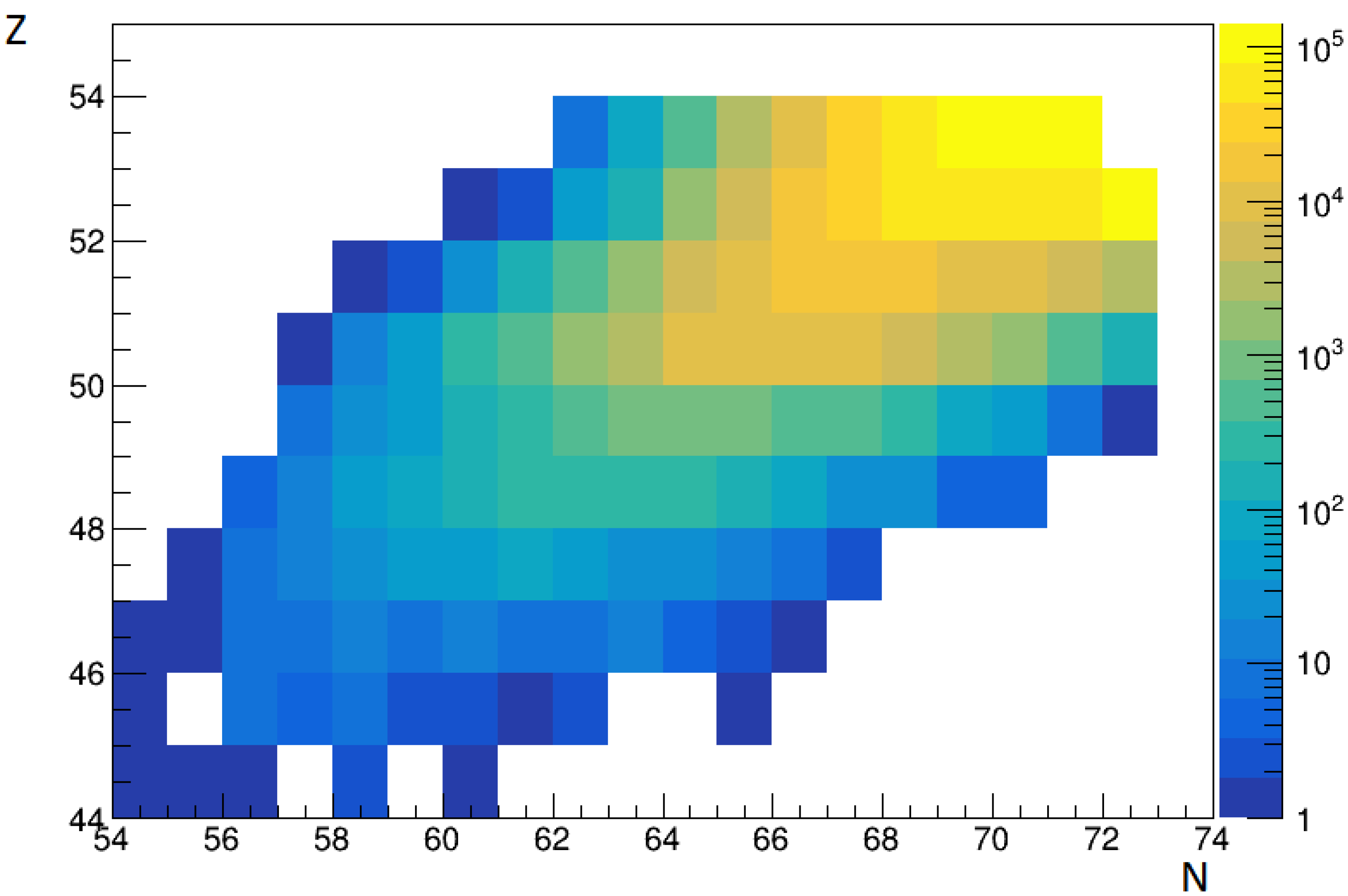
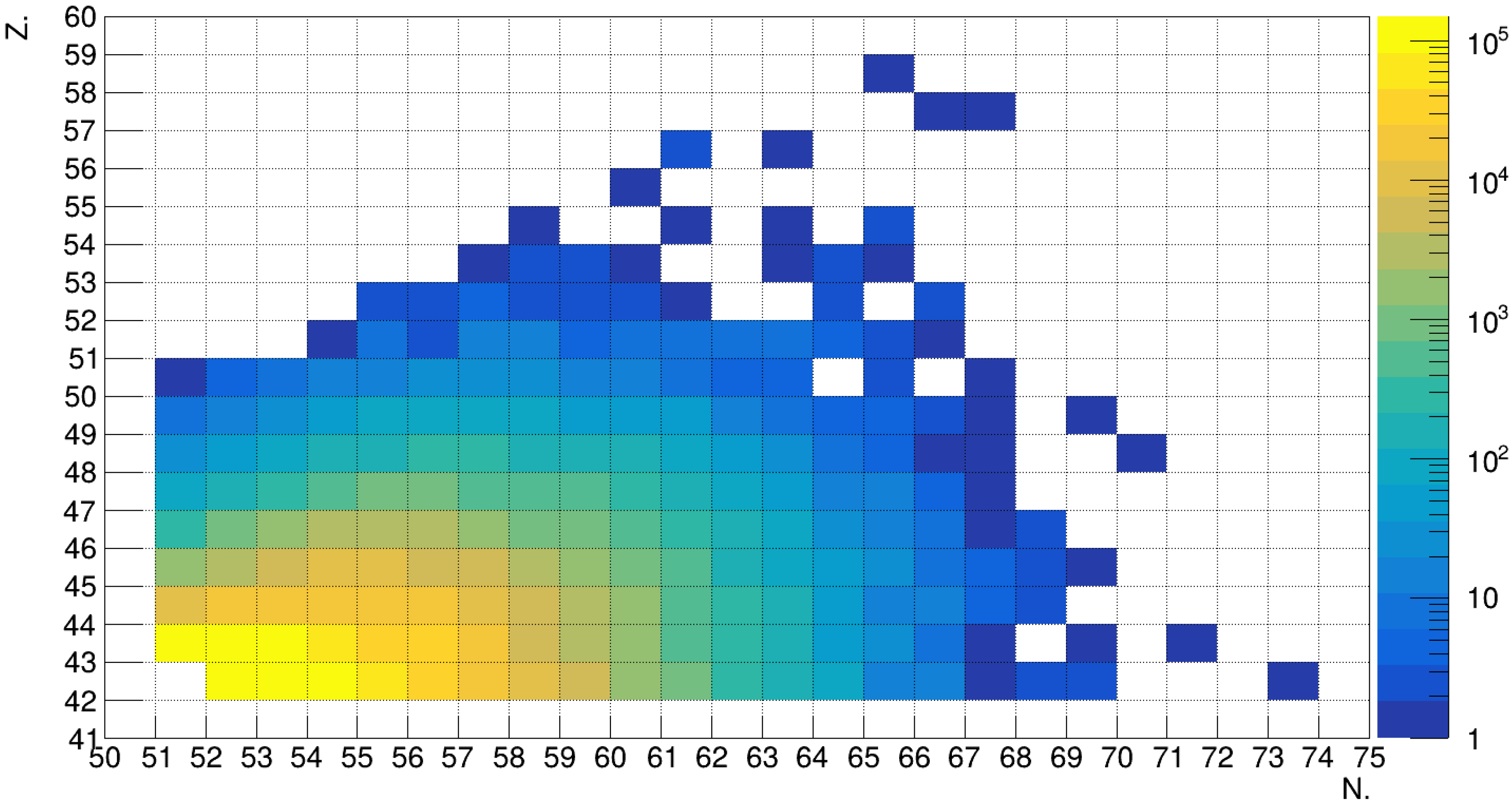
Let us say we want to find the unknown initial isotope Y for isotope X. We consider the available data, which is presented in the form of a histogram with all potential sources capable of yielding the X isotope. In Figure 9 and Figure 10, two exemplary histograms of sources are presented from which ⁹²Nb and ⁹³Mo are created after antiproton annihilation are presented. Those isotopes were chosen, for example, because they have isomer states and could be potentially interesting cases to obtain and study.

These sources can be represented by a vector, organized according to their frequency f. The frequency of a particular isotope X can be calculated as the ratio of the number of atoms from the initial source Y that have transformed into X, expressed as $f={\displaystyle \frac{N_X}{N_Y}}$. The set of isotopes X is represented by the vector $X=[A,B,C,D,\dots ]$ with frequencies $f_A>f_B>f_C>f_D$. Assuming the isotope B is stable, it is possible to create the isotope X from B with frequency $f_B$. This is one possible path. However, isotope A is produced from another set of isotopes $A=[K,L,M,\dots ]$. If K is stable, the desired isotope B could be reached through multiple annihilations K→A→X with a frequency $f=f_A·f_K$. If $f_B<f_A·f_K$, then this longer path would be optimal, producing the majority of the desired isotope X. The algorithm employs an iterative process to identify these pathways. Starting from the last element, the algorithm iteratively examines possible pathways and computes their production frequencies. In the following algorithm, the vector of the desired X isotope was read up to the first stable isotope. Each element of the vector was added to the stack. Then the last element was taken from the stack. The process is repeated for this element. The frequency of production is then checked to see if it is better than the previous best. If not, the algorithm stops following this path. The block scheme for this algorithm is presented in Figure 11.

The algorithm offers a strategic framework for isotope production, particularly in scenarios involving complex nuclear cascades or multiple annihilation steps. This approach is adaptable; it could be easily modified to consider all paths from stable isotopes by getting rid of frequency comparison. The use of algorithms and simulated data allows scientists to tailor experiments to exploit specific nuclear interactions or optimize the production of target isotopes.

6. Summary

This study has explored the production mechanisms of HCIs through interactions involving antiprotonic atoms using the Geant4 simulation toolkit. By systematically analyzing the annihilation of antiprotons with nuclei, this research aimed to understand nuclear fragmentation processes and their implications for the synthesis of exotic isotopes and highly charged systems. The results demonstrate that, according to Geant4 simulations, the structure of atomic nuclei and the interactions of antiparticles with matter could be studied with this technique.

The application of antiprotonic atoms as a tool to generate HCIs is a unique approach for accessing isotopes that are usually difficult to produce or study. By substitution of an electron for an antiproton, these exotic atoms start processes that lead to the stripping of electrons and the formation of HCIs. The annihilation of the antiproton at the nucleus’s surface results in cascading nuclear fragmentation, producing fragments that are almost entirely stripped of electrons. These cold, charged fragments hold significant value for probing QCD and QED in extreme electromagnetic conditions. Additionally, this mechanism opens the way for studying radioisotopes that are either short-lived or challenging to extract through conventional means, broadening the possibilities of research in both nuclear and atomic physics.

The study used Geant4 simulations for the examination of antiproton-induced fragmentation across all isotopes with atomic numbers less than 100. A simulation of one million antiproton interactions for each isotope was made to track the resulting nuclear fragments by cataloging the mass, momentum, charge, and quantity of the fragments. This simulation tool is really important for planning and analyzing future experiments, as it provides a detailed map of potential outcomes and interactions. One of the key things the study did was introduce a way to optimize the production path of specific isotopes. It adapts some ideas from graph theory to help choose the right starting isotopes and reaction pathways, which makes the process more efficient. The algorithm is particularly suited for those that require multiple annihilation steps to achieve the desired outcome. The ability to generate rare trapped isotopes can open new avenues in both fundamental research and practical applications.

In conclusion, this study shows how antiprotonic atoms and their interactions could be used to make highly charged ions and exotic isotopes. The findings improve our understanding of antiproton-induced fragmentation and open up new ways to use this in nuclear physics, atomic physics, and more.