Single Ionization with Dressed Projectiles: An Improved Theory for Both Long- and Short-Range Interactions
Abstract
1. Introduction
2. Theory
2.1. Continuum Distorted Wave Theories
2.2. Hydrogen Molecule Description
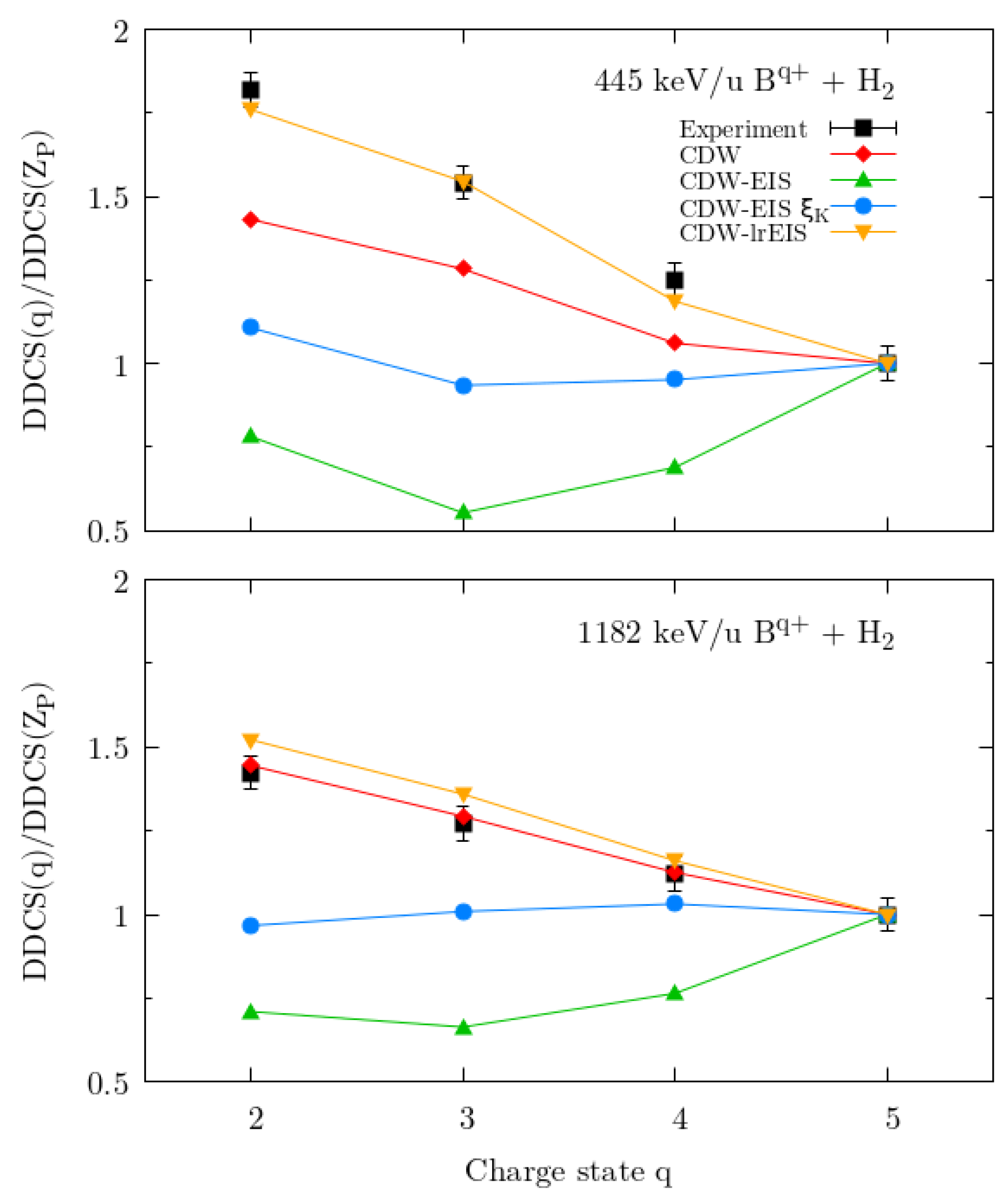
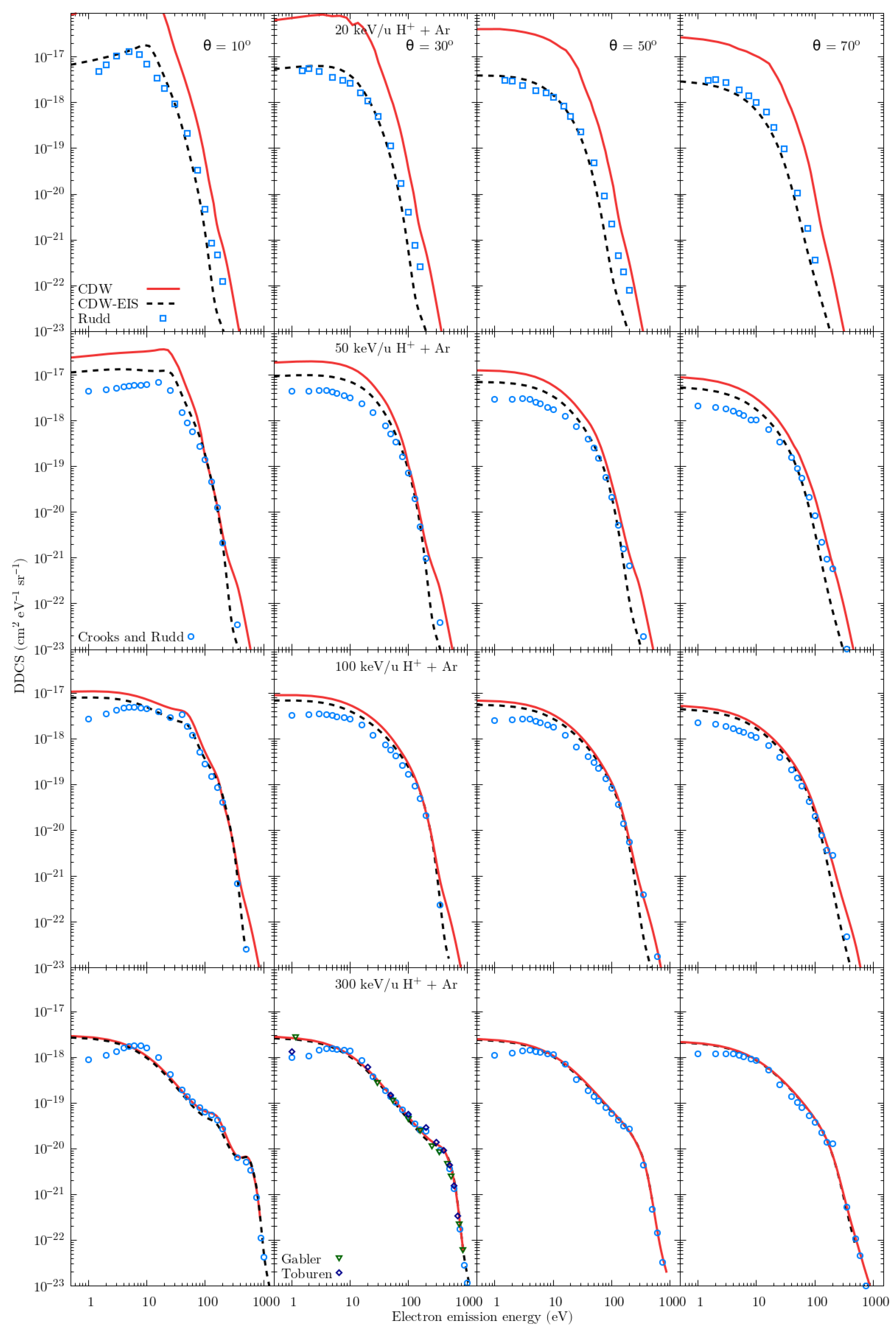
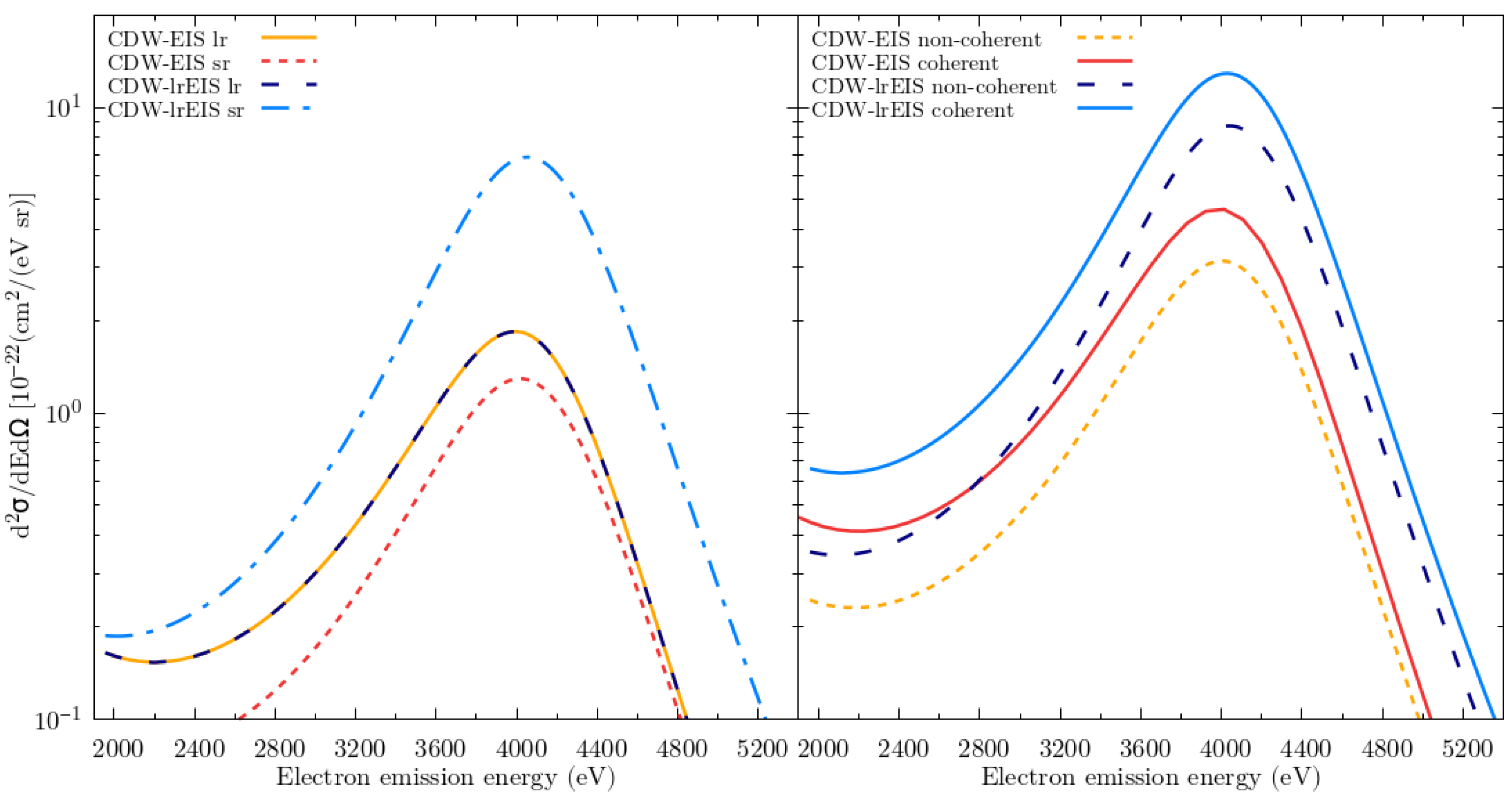
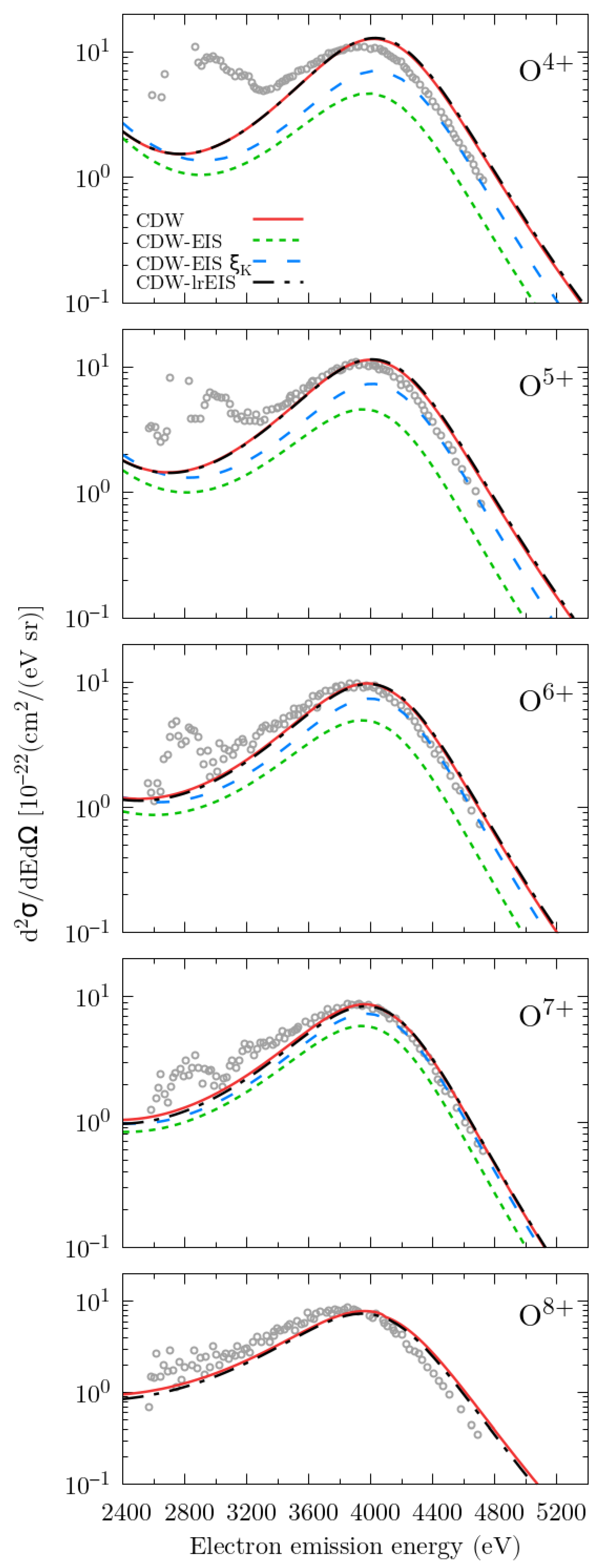
3. Results and Discussion
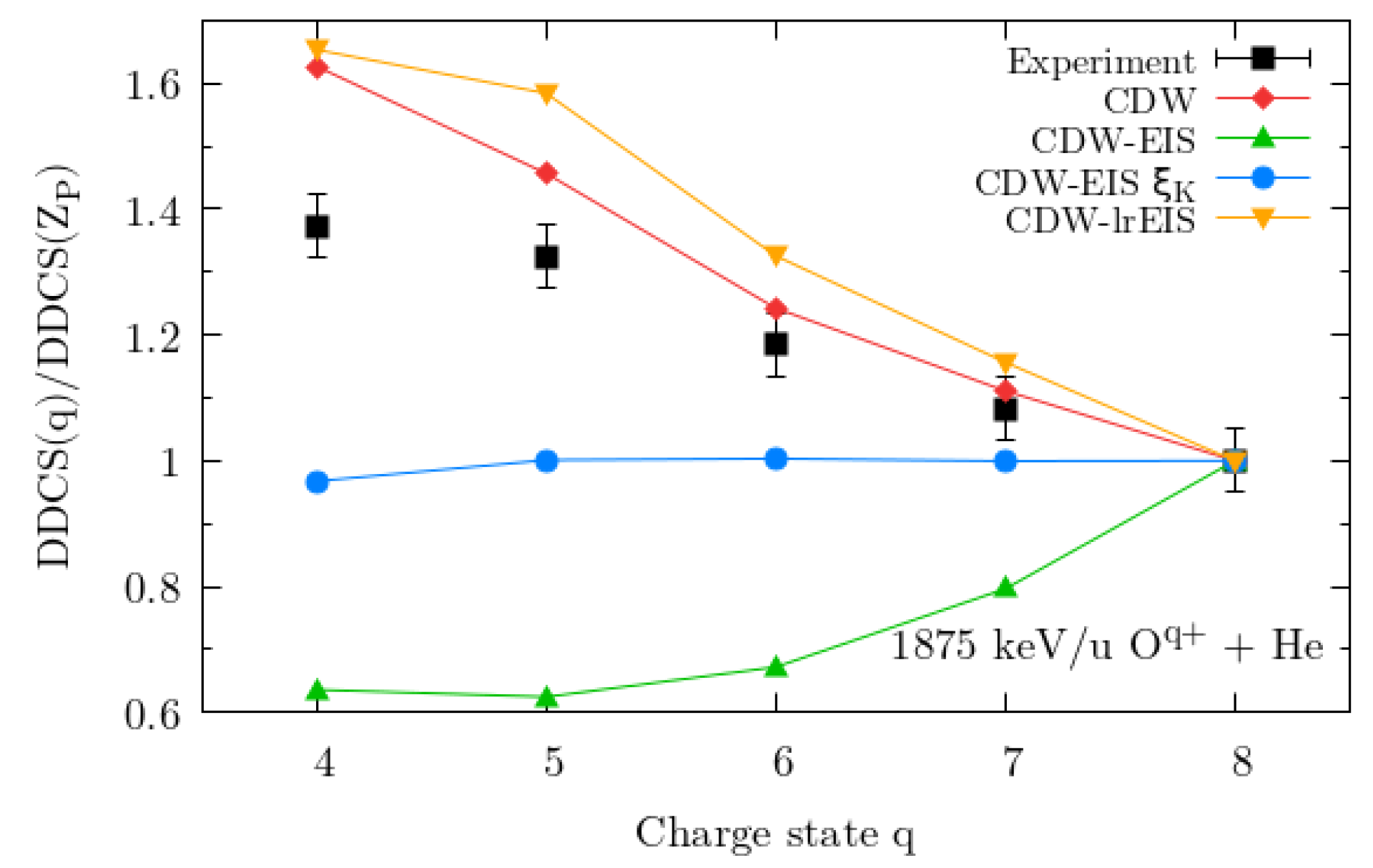
3.1. Helium Target
3.2. Hydrogen Molecule Target
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CDW | Continuum Distorted Wave |
| CDW-EIS | Continuum Distorted Wave-Eikonal Initial State |
| CDW-lrEIS | Continuum Distorted Wave-long-range Eikonal Initial State |
| BEE | Binary-Encounter Emission |
| DDCS | Double-Differential Cross-Sections |
Appendix A. Comparison Between CDW and CDW-EIS
References
- Crothers, D.S.F.; McCann, J.F. Ionisation of atoms by ion impact. J. Phys. B At. Mol. Phys. 1983, 16, 3229–3242. [Google Scholar] [CrossRef]
- Monti, J.M.; Rivarola, R.D.; Fainstein, P.D. Distorted wave theories for dressed-ion-atom collisions with GSZ projectile potentials. J. Phys. B At. Mol. Phys. 2011, 44, 195206. [Google Scholar] [CrossRef]
- Muñoz, A.; Fuss, M.C.; Cortés-Giraldo, M.A.; Incerti, S.; Ivanchenko, V.; Ivanchenko, A.; Quesada, J.M.; Salvat, F.; Champion, C.; Gómez-Tejedor, G.G. Monte Carlo Methods to Model Radiation Interactions and Induced Damage. In Radiation Damage in Biomolecular Systems; García Gómez-Tejedor, G., Fuss, M.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; p. 203. [Google Scholar] [CrossRef]
- Lamour, E.; Fainstein, P.D.; Galassi, M.; Prigent, C.; Ramirez, C.A.; Rivarola, R.D.; Rozet, J.P.; Trassinelli, M.; Vernhet, D. Extension of charge-state-distribution calculations for ion-solid collisions towards low velocities and many-electron ions. Phys. Rev. A 2015, 92, 042703. [Google Scholar] [CrossRef]
- Richards, P.; Lee, D.H.; Zouros, T.J.M.; Sanders, J.M.; Shinpaugh, J.L. Anomalous q dependence of 0’ binary encounter electron production in energetic collisions of Fq+ (q=3-9) with He and H2 targets. J. Phys. B At. Mol. Phys. 1990, 23, L213–L218. [Google Scholar] [CrossRef]
- Hvelplund, P.; Tawara, H.; Komaki, K.i.; Yamazaki, Y.; Kuroki, K.; Watanabe, H.; Kawatsura, K.; Sataka, M.; Imai, M.; Kanai, Y.; et al. Binary Encounter Peaks for 0° Electrons in Collisions between 2 MeV/amu Siq+ and He. J. Phys. Soc. Jpn. 1991, 60, 3675. [Google Scholar] [CrossRef]
- Gonzalez, A.D.; Hvelplund, P.; Petersen, A.G.; Taulbjerg, K. Elastic scattering of quasifree electrons on fully stripped and one-electron ions. J. Phys. B At. Mol. Phys. 1992, 25, L57–L62. [Google Scholar] [CrossRef]
- Wolff, W.; Wolf, H.E.; Shinpaugh, J.L.; Wang, J.; Olson, R.E.; Fainstein, D.; Lencinas, S.; Bechthold, U.; Hermann, R.; Schmidt-Bocking, H. Ionic charge dependence of the zero degree binary encounter peak for partially stripped heavy ions. J. Phys. B At. Mol. Phys. 1993, 26, 4169–4180. [Google Scholar] [CrossRef]
- Hidmi, H.I.; Bhalla, C.P.; Grabbe, S.R.; Sanders, J.M.; Richard, P.; Shingal, R. Effect of exchange on the binary-encounter-electron double-differential cross section in Cq+-H2 collisions at 0.75 MeV/amu. Phys. Rev. A 1993, 47, 2398–2400. [Google Scholar] [CrossRef] [PubMed]
- Hidmi, H.I.; Richard, P.; Sanders, J.M.; Schöne, H.; Giese, J.P.; Lee, D.H.; Zouros, T.J.M.; Varghese, S.L. Charge-state dependence of binary-encounter-electron cross sections and peak energies. Phys. Rev. A 1993, 48, 4421–4428. [Google Scholar] [CrossRef]
- Posthumus, J.H.; Christensen, B.; Glargaard, N.; Madsen, J.N.; Andersen, L.H.; Hvelplund, P.; Grabbe, S.R.; Bhalla, C.P. The enhancement of the binary encounter peak for q=1 to Z in collisions of fast Cq+ and Oq+ on H2. J. Phys. B At. Mol. Phys. 1994, 27, L97–L102. [Google Scholar] [CrossRef]
- Sataka, M.; Imai, M.; Yamazaki, Y.; Komaki, K.; Kawatsura, K.; Kanai, Y.; Tawara, H.; Schultz, D.R.; Reinhold, C.O. Projectile charge state dependence of binary electron production for 1 MeV u-1 Auq+ (q=12-37) ion impact on He. J. Phys. B At. Mol. Phys. 1994, 27, L171–L177. [Google Scholar] [CrossRef]
- Zouros, T.J.M.; Wong, K.L.; Grabbe, S.; Hidmi, H.I.; Richard, P.; Montenegro, E.C.; Sanders, J.M.; Liao, C.; Hagmann, S.; Bhalla, C.P. 0° binary encounter electron production in 30-MeV Oq++H2, He, O2, Ne, and Ar collisions. Phys. Rev. A 1996, 53, 2272–2280. [Google Scholar] [CrossRef]
- Kraft, G. Radiobiological effects of very heavy ions: Inactivation, induction of chromosome aberrations and strand breaks. Nucl. Sci. Appl. 1987, 3, 1–28. [Google Scholar]
- Katz, R. Particle tracks in diverse media. Nucl. Instrum. Methods Phys. Res. B 1989, 40, 1271–1274. [Google Scholar] [CrossRef]
- Toburen, L.H.; Metting, N.F.; Braby, L.A. Spatial patterns of ionization in charged-particle tracks. Nucl. Instrum. Methods Phys. Res. B 1989, 40, 1275–1278. [Google Scholar] [CrossRef]
- Dressendorfer, P.V. Effects of radiation on microelectronics and techniques for hardening. Nucl. Instrum. Methods Phys. Res. B 1989, 40, 1291–1294. [Google Scholar] [CrossRef]
- Schultz, D.R.; Olson, R.E. Binary peak enhancement and structure in partially stripped ion-atom collisions. J. Phys. B At. Mol. Phys. 1991, 24, 3409–3432. [Google Scholar] [CrossRef]
- Olson, R.E.; Reinhold, C.O.; Schultz, D.R. Non-q2 scaling of the ionization cross section near the binary peak. J. Phys. B At. Mol. Phys. 1990, 23, L455–L459. [Google Scholar] [CrossRef]
- Reinhold, C.O.; Schultz, D.R.; Olson, R.E. Theoretical description of the binary peak in clothed ion-atom collisions. J. Phys. B At. Mol. Phys. 1990, 23, L591–L596. [Google Scholar] [CrossRef]
- Shingal, R.; Chen, Z.; Karim, K.R.; Lin, C.D.; Bhalla, C.P. Charge-state dependence of elastic scattering cross sections at large angles between electrons and multiply charged ions. J. Phys. B At. Mol. Phys. 1990, 23, L637–L640. [Google Scholar] [CrossRef][Green Version]
- Taulbjerg, K. The binary-encounter peak in energetic ion-atom collisions. J. Phys. B At. Mol. Phys. 1990, 23, L761–L765. [Google Scholar] [CrossRef]
- Bhalla, C.P.; Shingal, R. Contribution of exchange on charge-state dependence of large-angle electron-ion elastic scattering. J. Phys. B At. Mol. Phys. 1991, 24, 3187–3191. [Google Scholar] [CrossRef]
- Salin, A. The role of exchange for 0∘ binary electrons ejected in clothed ion-atom collisions. J. Phys. B At. Mol. Phys. 1991, 24, L611–L615. [Google Scholar] [CrossRef]
- Monti, J.M.; Quinto, M.A.; Rivarola, R.D. A Complete CDW Theory for the Single Ionization of Multielectronic Atoms by Bare Ion Impact. Atoms 2021, 9, 3. [Google Scholar] [CrossRef]
- Esponda, N.J.; Nanos, S.; Quinto, M.A.; Zouros, T.J.M.; Rivarola, R.D.; Benis, E.P.; Monti, J.M. Binary Encounter Electrons in Fast Dressed-Ion-H2 Collisions: Distorted Wave Theories and Experiment. Atoms 2023, 11, 17. [Google Scholar] [CrossRef]
- Green, A.E.; Sellin, D.L.; Zachor, A.S. Analytic Independent-Particle Model for Atoms. Phys. Rev. 1969, 184, 1–9. [Google Scholar] [CrossRef]
- Szydlik, P.P.; Green, A.E. Independent-particle-model potentials for ions and neutral atoms with Z ≤ 18. Phys. Rev. A 1974, 9, 1885–1894. [Google Scholar] [CrossRef]
- Garvey, R.H.; Jackman, C.H.; Green, A.E.S. Independent-particle-model potentials for atoms and ions with 36 < Z ≤ 54 and a modified Thomas-Fermi atomic energy formula. Phys. Rev. A 1975, 12, 1144–1152. [Google Scholar] [CrossRef]
- Clementi, E.; Roetti, C. Roothaan-Hartree-Fock Atomic Wavefunctions: Basis Functions and Their Coefficients for Ground and Certain Excited States of Neutral and Ionized Atoms, Z ≤ 54. At. Data Nucl. Data Tables 1974, 14, 177. [Google Scholar] [CrossRef]
- Belkić, D.; Gayet, R.; Salin, A. Electron capture in high-energy ion-atom collisions. Phys. Rep. 1979, 56, 279–369. [Google Scholar] [CrossRef]
- Nordsieck, A. Reduction of an Integral in the Theory of Bremsstrahlung. Phys. Rev. 1954, 93, 785–787. [Google Scholar] [CrossRef]
- Gravielle, M.S.; Miraglia, J.E. Some Nordsieck integrals of interest in radiation and atomic collision theories. Comput. Phys. Commun. 1992, 69, 53–58. [Google Scholar] [CrossRef]
- Lühr, A.; Vanne, Y.V.; Saenz, A. Parameter-free one-center model potential for an effective one-electron description of molecular hydrogen. Phys. Rev. A 2008, 78, 042510. [Google Scholar] [CrossRef][Green Version]
- Gulyás, L.; Egri, S.; Kirchner, T. One- and two-center effects in single ionization in high-energy collisions of protons and hydrogen molecules. Phys. Rev. A 2025, 111, 032805. [Google Scholar] [CrossRef]
- Esponda, N.J.; Quinto, M.A.; Rivarola, R.D.; Monti, J.M. Dynamic screening and two-center effects in neutral and partially dressed ion-atom collisions. Phys. Rev. A 2022, 105, 032817. [Google Scholar] [CrossRef]
- Rudd, M.; Toburen, L.; Stolterfoht, N. Differential cross sections for ejection of electrons from argon by protons. At. Data Nucl. Data Tables 1979, 23, 405–442. [Google Scholar] [CrossRef]

| j | ||
|---|---|---|
| 1 | 0.954069 | 1.129807 |
| 2 | 0.067364 | 3.297702 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esponda, N.J.; Quinto, M.A.; Rivarola, R.D.; Monti, J.M. Single Ionization with Dressed Projectiles: An Improved Theory for Both Long- and Short-Range Interactions. Atoms 2025, 13, 88. https://doi.org/10.3390/atoms13110088
Esponda NJ, Quinto MA, Rivarola RD, Monti JM. Single Ionization with Dressed Projectiles: An Improved Theory for Both Long- and Short-Range Interactions. Atoms. 2025; 13(11):88. https://doi.org/10.3390/atoms13110088
Chicago/Turabian StyleEsponda, Nicolás J., Michele A. Quinto, Roberto D. Rivarola, and Juan M. Monti. 2025. "Single Ionization with Dressed Projectiles: An Improved Theory for Both Long- and Short-Range Interactions" Atoms 13, no. 11: 88. https://doi.org/10.3390/atoms13110088
APA StyleEsponda, N. J., Quinto, M. A., Rivarola, R. D., & Monti, J. M. (2025). Single Ionization with Dressed Projectiles: An Improved Theory for Both Long- and Short-Range Interactions. Atoms, 13(11), 88. https://doi.org/10.3390/atoms13110088