First and Second Law of Thermodynamics Constraints in the Lifshitz Theory of Dispersion Forces

Abstract

The presence of dominant interatomic dispersion forces on the nanoscale holds the promise for breakthrough applications in key areas of quantum sensing, such as accelerometry, as well as nano-manipulation and energy storage. In order to do work, nano-machines enabled by dispersion forces must exchange energy with the surrounding environment. Such processes can be described in terms of thermodynamical engine cycles involving individual atoms or material boundaries, separated by possibly empty gaps and interacting via time-dependent dispersion forces. The fundamental strategy indispensable to achieve dispersion force time-modulation, demonstrated experimentally by independent groups on different scales, is based on the illumination of interacting, semiconducting elements by appropriate radiation beams. Here we analyze the operation of ideal nano-engines in the quasi-static regime by means of the Lifshitz theory of dispersion forces involving semiconducting boundary or atom irradiation. Firstly, we verify that the First Law of Thermodynamics is satisfied so that the total energy of the system is rigorously conserved. Secondly, we show that, within this first approximate treatment, the Second Law of Thermodynamics may be violated for extremely small interboundary gap widths. We identify important limitations to be addressed to determine whether this is a reliable conclusion. The technological and historic backdrops are presented, and important topics for future research are identified.

1. Introduction and Historical Context

The first quantitative treatments of dispersion forces represented a remarkable triumph of the revolutionary description of the physical world introduced by the development of the new quantum theory and, soon afterwards, of early quantum electrodynamics (QED). This year, 2025, is being justifiably celebrated by the United Nations as the International Year of Quantum Science and Technology [1], including reflections on the dawn of quantum mechanics [2] and its several intriguing philosophical implications [3]. Perhaps surprisingly, even after one century of intense exploration, quantum theory is being described as an “an unfinished revolution,” whose “…resulting applications in computing, ultra-secure communications, and innovative scientific instruments are still in their nascent stages” [4].

Within this broader context, the goal of the present contribution is to explore an example of such an essential connection of theoretical research to quantum technologies to be deployed in the marketplace. We commence by providing a historical overview to place the appearance of such a “nascent” industry within the framework of crucial developments that are enabling the transfer of technologies derived from fundamental scientific inquiry to applications, with an emphasis on the space industry.

At the inauguration of the Ryerson Physical Laboratory at the University of Chicago, Albert Michelson offered a comment about the status of contemporary science that has been reproduced so often as to have become almost a cliché: “It seems probable that most of the grand underlying principles have been firmly established and that further advances are to be sought chiefly in the rigorous application of these principles to all the phenomena which come under our notice …An eminent physicist has remarked that the future truths of physical science are to be looked for in the sixth place of decimals” [5]. With the benefit of hindsight, we know that, on the contrary, an epochal revolution was about to unfold, replacing Newton’s Second Law of motion with a dramatically different description of mechanics.

The identity of the “eminent physicist” referred to by Michelson above remains unknown [6] and Michelson was later reported to have deeply regretted his now famous remark (Ref. [7] (pp. 23–24)). As to contradict the claimed knowledge of all “underlying principles,” Ludwig Boltzmann was, at that very same time, lamenting the absence of any fundamental understanding of interatomic forces, despite the fashionable speculations of Roger Joseph Boscovich [8] and the development of a successful Theory of Gases [9]: “But this theory agrees in so many respects with the facts that we can hardly doubt that in gases certain entities, the number and size of which can roughly be determined, fly about pell-mell. Can it be seriously expected that they will behave exactly as aggregates of Newtonian centres of force, or as the rigid bodies of our Mechanics?” [10].

Indeed, despite profound early insights, such as those by Lebedev [11] and Debye [12,13,14,15], producing any quantitatively verifiable predictions about forces between, for instance, two hydrogen atoms without permanent electric multipoles by employing classical mechanics and electrodynamics is impossible. This is so because, classically, the time-average of any multipole moment vanishes and the atoms cannot induce any moment on each other (Ref. [16], §4). The answer to Boltzmann’s rhetorical question, therefore, was bound to be strongly in the negative and, as Rowlinson appropriately observes, “not in a way that he or Boscovich would have suspected” [15].

Events unfolded quickly. According to one “probably true” (Ref. [17], p. 311, Note 60) anecdote told by Edmund H. Bauer (Ref. [18], p. 258), the inspiration for the non-relativistic relationship now known as the Schrödinger equation was provided to Schrödinger by Langevin, who shared with him the “speculative thought” (Ref. [19], p. 5) on matter waves developed by his doctoral student, Louis de Broglie, in his doctoral thesis [20].

Schrödinger reportedly rejected those ideas outright as “rubbish” [17]. However, in 1925, the year of submission of the breakthrough Umdeutung (i.e., reinterpretation) paper by Heisenberg [21,22] and of the “three-man paper” (Drei Männer Arbeit) by Born, Heisenberg, and Jordan [23,24], he reconsidered his initially negative view. This was due to Langevin’s insistence and perhaps also to Einstein’s enthusiastic reception. Thus started Schrödinger’s investigation into the foundational equation of wave mechanics [25]. His results appeared in four publications received at the Annalen del Physik between 27 January and 21 June 1926, and all published that same year [26,27,28,29,30].

Speaking about the “phænomena of nature” in the Premise to his Principia, Newton had famously lamented [8,15]: “…for I am induced by many reasons to suspect that they may all depend upon certain forces by which particles of bodies, by some causes hitherto unknown, are either mutually impelled towards each other, and cohere in regular figures, or are repelled and recede from each other; which forces being unknown, philosophers have hitherto attempted the search of nature in vain” [31].

It is impressive to compare such a statement, published in 1687, to the assessment provided in 1928 by George Arthur Tomlinson at the opening of his report on cohesion in quartz, often cited as the earliest experimental attempt of scientific significance in modern dispersion force studies [14,32]: “The amount of well-established knowledge concerning the nature and origin of interatomic forces is very limited …It is generally agreed, however, that the problem of atomic forces has not been solved” [33].

Rowlinson splendidly captures the extreme confusion of the times in his description of Tomlinson’s review of existing theoretical information on interatomic potentials: “He cited different authorities who had maintained, since 1900, that the attractive potential varied with the inverse of the separation to the powers of 1, 2, 3, 4, 5, 7 or 8. The only number missing from this sequence is 6 which was soon to prove to be the right answer. His own attempt to find the correct solution by a direct measurement of the force of adhesion between two quartz fibres was ingenious but not decisive and, as we shall see, had it been successful it would have given a misleading answer” [15].

Just before the introduction of the Schrödinger equation [8], over two centuries after Newton and well over two millennia after the introduction of the concept of atoms through pure philosophical speculation [8], workers were still “not at all in agreement” as to the most basic properties of interatomic forces [33]. After the publication of the Schrödinger equation, it took only one year, till 17 August 1927, for S. C. Wang to follow up on a suggestion from Debye, while visiting Columbia University, to calculate the van der Waals potential energy of two hydrogen atoms at a relatively large distance by employing perturbation theory within Schrödinger’s new mathematical framework [34]. In a later publication submitted to the Physical Review in that same year, Wang developed an approximate treatment valid at all interatomic distances, thus obtaining the effective potential of a hydrogen molecule [35].

These important contributions were soon noticed by several other workers [15], including Fritz London, who cited the latter paper by Wang in his own review on the significance of quantum mechanics in chemistry [36], and again by Eisenschitz and London [37], who cited the earlier paper by Wang and refined the estimates published therein. London proposed a well-known description, based on Drude’s oscillator model of the atom [38], and used the term “dispersion effect” in reference to the dependence of the force on the dynamical atomic polarizability [16].

A fundamental explanation could finally be provided for the fact that forces between neutral, isotropic, polarizable particles are impossible classically but exist quantum mechanically: “However, in quantum mechanics, as is well known, a particle cannot lie absolutely at rest on a certain point. That would contradict the uncertainty relation. According to quantum mechanics our isotropic oscillators, even in their lowest states, make a so-called zero-point motion which one can only describe statistically, for example, by a probability function which defines the probability with which any configuration occurs …We need not know much quantum mechanics in order to discuss our simple model.” (Ref. [16], italics in the original).

In the immediate aftermath of the development of the London theory of van der Waals forces, research efforts were directed at employing those results to calculate and to measure the interactions between macroscopic objects, such as spherical particles and nearby parallel planes. This was not just aimed at identifying feasible fundamental physics experiments to test theoretical predictions, but it was also inextricably connected to and motivated by applications in industrial activities [39,40,41,42].

Discrepancies between the predictions from early theories and industrial data suggested that electrodynamic retardation may play a crucial role [43,44,45]. Within approximately two decades of the development of non-relativistic quantum mechanics, this line of inquiry led Casimir, in 1948, to the prediction that two perfectly conducting, infinitely wide parallel planes separated by an empty gap interact through an attractive force, the so-called Casimir effect [46,47,48,49]. A full treatment of the interaction between two dielectric slabs, accounting for the optical properties of real materials, was formulated by Lifshitz only in 1955, three decades after the appearance of the new quantum theory [50,51].

In what follows, in order to frame the central question of the present investigation, we shall recall the three crucial directions of inquiry that developed somewhat independently only to later become intertwined and converge to the treatment of the nano-engine models we develop below (Section 2.1, Section 2.2 and Section 2.3). We shall then introduce the specific thermodynamical engine cycle adopted to illustrate the challenges to the Laws of Thermodynamics as they initially emerged, including a resolution (Section 3.1). Finally, debates and conclusions are presented.

2. Dispersion Forces, Engineering, and Industry

The different directions of inquiry that developed somewhat independently, before becoming intertwined and converging to applications in the specific devices we analyze below, are, respectively, the discovery of strategies for high-frequency time-modulation of dispersion force magnitude (Section 2.1), the role of dispersion forces in high-density energy storage (Section 2.2), and the use of dispersion forces to mechanically drive nano-device oscillations (Section 2.3).

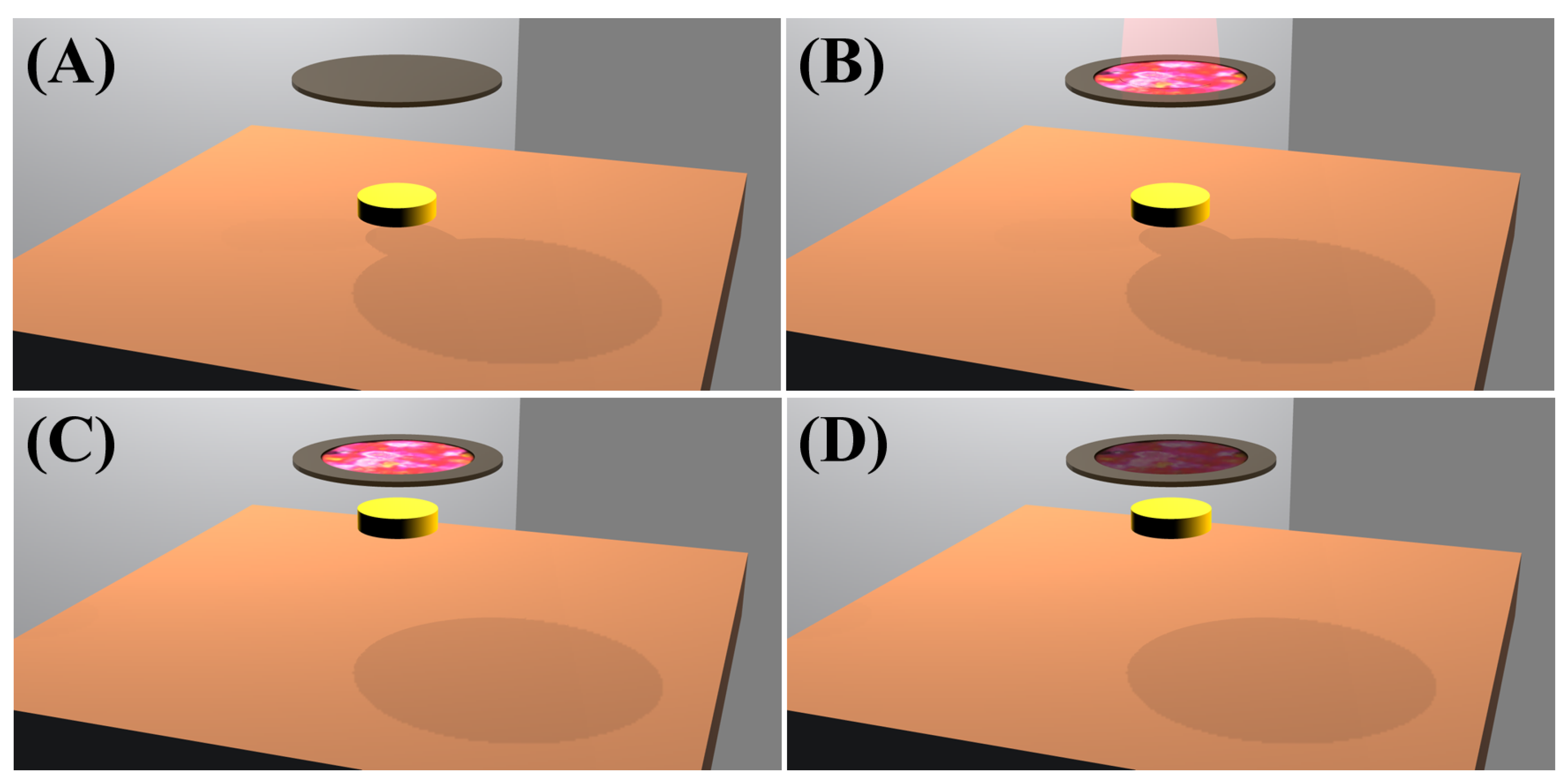
2.1. The Arnold-Hunkinger-Dransfeld Experiment

The first research thrust emerged, somewhat unexpectedly, from the development of a novel approach for accurate dispersion force measurement. This strategy replaced existing, typically static, measurements by dynamical sensing, thereby promising significant improvements over previous results (for instance, see Ref. [52], Section 8.7 and Ref. [53], Sections 18.1-2 for analyses of the earliest attempts). Specifically, the sensing probe was a flat silica disk epoxied to the vibrating membrane of a condenser microphone operating in a vacuum chamber, driven at its resonance frequency by a spherical lens vibrating across an empty gap. By varying the gap width and one or both of the probe and lens materials, it was possible to test the predictions of the Lifshitz theory for various pairs of substances both in the unretarded and retarded regimes [54,55,56].

Almost half a century ago, a remarkable phenomenon was demonstrated by means of this experimental setup. By depositing a semiconducting amorphous silicon layer upon the facing lens, and by back-illuminating it, it was observed that the magnitude of the dispersion force between the flat silica probe and the semiconductor could be modulated [57]. For reasons possibly connected to the use of non-conducting materials, whose work function could not be controlled, and to the presence of residual spurious electrostatic charges, the quantitative results were not in full agreement with all expectations from the Lifshitz theory (see Refs. [53,58,59,60,61] for independent critiques of these experiments from a modern perspective). However, the implications of this fascinating discovery from the standpoint of industrial applications on the nanoscale were later understood to be extremely significant [62,63], and this result must be viewed as a crucial achievement in the development of technologies enabled by dispersion forces.

In a broader context, this experiment demonstrated an original implementation of dispersion force engineering on the nanoscale by means of processes and components typical of the semiconductor industry. As such, this illustrates the potential of “…manipulating dispersion forces to achieve a causally quantifiable success,” [64]. As has been argued by the present author, dispersion force engineering represents an example of an Emerging Enabling General-Purpose Technology (EEGPT) [64]. From the standpoint of fundamental physics, the demonstration of the modulation of dispersion forces in semiconductors [57] is so significant (In what follows, for brevity, we shall specifically refer to the dispersion force modulation demonstration by this group [57] as the AHD experiment, consistently with our previous discussions [62,63]) as to consider it as the first forceful appearance of issues connected to dispersion forces and energy conservation central to this paper [65]. Although any specific questions in this regard remained implicit in the original report [57], the highly original and still cited AHD experiment represented the first viable testbed to directly expose, at least in principle, the interplay between energy associated with the dispersion force field and other forms of energy.

An important follow-up to the AHD experiment has come more recently with an independent verification of the expectations from the Lifshitz theory about Casimir force modulation in semiconductors by means of modern atomic force microscope (AFM) techniques [53,59,60,61,66]. In addition to providing what appears to be a full experimental confirmation of all theoretical expectations, these contributions provide additional useful information about dispersion force engineering as a developing discipline. These authors correctly articulate the fact that “The vital issue in many applications of the Casimir effect is how to control the magnitude of the force by changing the parameters of the system.” [59]. Furthermore, it is clearly stated that “The most suitable method to change the carrier density in semiconductors is through the illumination of the surfaces by laser light.” [59]. Such understanding is unambiguously described as follows: “The proposed effect opens novel opportunities in nanotechnology to actuate the periodic movement in electro- and optomechanical micromachines based entirely on the zero-point oscillations of the quantum vacuum without the action of mechanical springs.”(Ref. [66], Abstract).

2.2. Casimir Force-Enabled Energy Storage

The second research direction having a considerable bearing on the topic of the present paper was the proposal, presented by Robert Forward, to employ dispersion force fields as “batteries,” in which energy could be stored. In a well-known Physical Review paper [67]—a follow-up to two reports written for the US Air Force Rocket Propulsion Laboratory [68,69]—Forward proposed an energy storage system composed of two perfectly conducting, parallel, smooth surfaces attracting each other via the Casimir force while in quasi-equilibrium under the simultaneous action of a slightly smaller, repulsive electrostatic interaction.

In principle, such an idealized system would yield an infinite amount of electrical energy during a transformation commencing at any finite gap width between the two surfaces and ending with a negligible gap width at final contact between the two perfect conductors. In practice, however, due to the numerical values of the natural constants, to the properties of real materials, and to surface roughness, the energy densities available in the system proposed by Forward are frustratingly low [70]. Hence, no practically advantageous devices could be identified, although a now iconic “spiral design” (Ref. [67], Figure 1) was introduced.

Crucial to the present paper, the question as to whether dispersion forces are fundamentally conservative was brought into sharp focus, possibly for the first time. Forward reasoned: “There is no rigorous proof known that the vacuum-fluctuation field is a conservative field such as the gravity field. It is highly probable that it is conservative; otherwise, it would be possible to design machines using the Casimir force that would allow an infinite amount of energy to be extracted from the vacuum.” (Ref. [67], Section III).

Forward recognized that such a constraint does in no way diminish the technological potential of employing Casimir force fields for energy storage, stating: “Even if the vacuum-fluctuation field is a conservative field, that does not mean we cannot use it to obtain energy. The gravity field of the earth is a conservative force field, and yet hydroelectric dams extract energy from the gravity field by using water coming from a region of high gravitational potential.” Hence, at least initially (Section 3.2), Forward presented his conceptual device as a “vacuum-fluctuation battery,” that is, a system that can be discharged but must be first charged, and cannot function as a continuous energy source.

Importantly, although Forward was aware of the AHD study and cited it [67], he failed to recognize the important connection between that experiment and the important question of energy conservation in dispersion force theory he had exposed.

2.3. Casimir Force-Driven Nanodevice Actuation

In his prescient speech, “There’s Plenty of Room at the Bottom,” delivered on 26 December 1959 at Caltech, Feynman had used a characteristically amusing analogy to portray van der Waals forces as a design limitation [71]:

“There is the problem that materials stick together by the molecular (Van der Waals) attractions. It would be like this: After you have made a part and you unscrew the nut from a bolt, it isn’t going to fall down because the gravity isn’t appreciable; it would even be hard to get it off the bolt. It would be like those old movies of a man with his hands full of molasses, trying to get rid of a glass of water. There will be several problems of this nature that we will have to be ready to design for.”

The third research direction relevant to this paper can be identified with the appearance of the oft-cited report by Serry, Walliser, and Maclay [72] (SWM) on micro- (and, later, nano-) electromechanical systems (MEMS/NEMS) as “anharmonic Casimir oscillators” (ACOs). The model devices considered are assumed to be under the simultaneous action of time-independent dispersion, elastic, and, possibly, also electrostatic forces [72]. Therefore, no energy exchange with outside reservoirs can take place, and, strictly from the standpoint of energy conservation considerations, no surprising results can be expected. Remarkably, however, the authors concluded [72]:

“Furthermore, it appears that the attractive force between parallel surfaces may not always have to be dealt with as a nuisance; rather, it may be manipulated to perform useful tasks just as capillary forces have been utilized to actuate MEMS components. Dynamic characteristics of the ACO may be used to design small gap resonators based on the Casimir effect.”

This statement signaled a historic shift in the role to be played by dispersion forces in MEMS/NEMS design (Ref. [64], Section 4), from the cause of a MEMS failure mode anticipated by Feynman to an unprecedented technological opportunity.

The promise held by this novel view of dispersion forces was appreciated quite slowly, as shown by the citation count for the first ten years after publication of the SWM paper [72], provided by IEEE Xplore^®, excluding self-citations: 1995 (0), 1996 (1), 1997 (0), 1998 (0), 1999 (3), 2000 (0), 2001 (4), 2002 (3), 2003 (3), 2004 (5), 2005 (7). Therefore, this important work was cited only four times between 1995 and 1999. However, all those papers were very much forward-looking.

The first citation, chronologically, is in a paper by Ulyanov et al. on “intelligent” nano-robotics, in which a bold connection between dominant dispersion forces and micro-manipulation is explicitly made [73]. The second one is in an extensive nanotechnology review by MacDonald—“Nanostructures in Motion: Micro-Instruments for Moving Nanometer-Scale Objects”—in which the potential use of “micro-instruments” to investigate “nanometer-scale interactions such as the Casimir effect” is stated [74]. The third one is in a mention by Marc Millis, founder of the NASA Breakthrough Propulsion Program [75], during his review of promising technologies with possible applications in future, very advanced spacecraft [76]. Finally, the fourth one is in the paper by the present author [77], in which the energy conservation issues discussed herein are raised for the first time (Section 3).

Following this early reception, while research in the role of the Casimir force in some forms of “stiction,” as anticipated by Feynman, continued to develop [78,79,80], interest in the SWM paper turned more specifically to the suggestion that the Casimir force may be “…utilized to actuate MEMS components.” [72]. Significantly, two of the four citations of 2001 were by Federico Capasso’s group, in their important reports on experimental verification of the highly non-linear dynamical behavior of ACOs [81] and laboratory demonstration of MEMS actuation by Casimir interactions [82].

In an intriguing manifestation of “multiple discovery” (or “simultaneous invention”) [83,84], the demonstration that “adhesion is not always a phenomenon to be avoided in MEMS” [85] was being announced as “the first controlled use of the phenomenon of stiction” [86], and explored theoretically and experimentally by V. Agache et al. [86,87], apparently unaware of other workers:

“Though the stiction phenomenon has been widely investigated leading to its better understanding, it has never intentionally been used in a positive way for MEMS applications.”

In the immediate aftermath of publication, the results by Capasso’s group were hailed as “Quantum stickiness put to use” [88] and were even covered in the New York Times [89]. Independently, the findings by V. Agache et al. were reported as showing that “stiction is starting to be used in a positive way” [90].

3. Dispersion Force-Enabled Thermodynamical Engine Cycles

Within the setting of the three above foundational developments, the present author introduced the topic of thermodynamical engine cycles enabled by the modulation of dispersion forces between semiconducting boundaries in MEMS [77].

This study had the two following separate and independent aims:

A. 

The former was to address Forward’s direct and crucial question [67], that is, whether or not the nature of dispersion forces is conservative. This issue was attacked by investigating whether it is possible, in principle, to achieve a non-zero net energy exchange (“energy extraction”) by introducing appropriately designed dispersion force-enabled engine cycles (Ref. [77], Sections II).

B. 

The latter aim was to explore the possibility of driving MEMS by means of such a dispersion force modulation mechanism as that identified in the AHD experiment. In order to describe the effect of irradiation on dispersion forces, an analytical description of the dielectric functions of the semiconductor boundaries was adopted, appropriate for industrial use (Ref. [77], Sections IV–V).

Although the focus of the present paper is upon the former topic, it is important to stress that the technological opportunity presented by time-dependent dispersion force actuation of MEMS is independent of any conclusions regarding energy conservation.

3.1. Dispersion Forces and Energy Conservation

An example of a typical Otto dispersion force engine cycle is provided in the ($F_{\mathrm{vdW}}$, s)-diagram in Figure 1. Consider a moving semiconducting membrane of area A interacting by a dispersion force $F_{\mathrm{vdW}}$ across an empty gap of width s with a fixed substratum realized from the same semiconducting material. For simplicity, let us model both boundaries as plane parallel surfaces (Figure 4). In realistic implementations, the membrane can be assumed to be acted upon by an elastic force, such as that due to an ideal spring, although such details do not affect the conclusions of the present discussion and shall not be considered further [91,92,93].

The substratum-membrane dispersion force is provided by an expression obtained from the Lifshitz theory [50] in terms of the optical properties of the boundaries, which are described by the dielectric function, $\widetilde{ϵ}\left({\omega }_R\right)$, where $\widetilde{ϵ}$ is the complex dielectric function, $\widetilde{ϵ}={ϵ}_R+i{ϵ}_I$, and ${\omega }_R$ is the angular frequency, assumed real. As is well known, the causality requirement imposed by the Kramers–Kronig relations imply that, in the complex frequency plane, ${\omega }_C={\omega }_R+i{\omega }_I$, the complex dielectric function becomes real on the imaginary frequency axis, that is, $\widetilde{ϵ}\left({\omega }_I\right)\in \mathbb{R}$. As first shown by Lifshitz, this allows one to carry out the calculation as an integral along that same imaginary frequency axis, where the integrand is well-behaved, instead of having to deal with a “particularly difficult” [50] integration caused by oscillations along the real axis.

The strategy of the engine cycle, consistent with the results of the AHD experiment, is based on explicitly writing the dielectric function as a function of the charge carrier density, $N_q$, that is, $\widetilde{ϵ}=\widetilde{ϵ}\left(N_q\right)$ so that, by back-illuminating the semiconducting boundaries, the charge carrier density can be varied, thus causing an increase of the substratum-membrane dispersion force. A corresponding decrease in the dispersion force occurs as the charge carriers decay back to the lower energy band by any available mechanisms, such as radiation emission. Furthermore, the system can do mechanical work by allowing transformations during which the membrane moves towards or away from the substratum. In the analysis of this idealized cycle, we shall assume the charge carrier density to be constant, and therefore no radiation emission to occur, during such adiabatic transformations. For temperatures $T>0$ K, the integral introduced by Lifshitz must be appropriately generalized. However, as assumed in the discussion of the AHD experimental data and also noted during the analysis of the more recent AFM experiment, such a procedure introduces relatively small corrections. Since our conclusions are not altered by such a refinement, throughout the present paper we shall adopt the expressions valid at $T=0$ K and refer to internal energy instead of free energy. Furthermore, since the substratum and, especially, the membrane are not semi-infinite slabs, the expressions to be used should be generalizations of the Lifshitz theory to slabs of finite thickness [94]. Once again, this correction does not change our conclusions and we shall omit it in this paper.

The cycle commences at A with the dispersion force, $F_{\mathrm{vdW}}(N_{q,A},s_A)$, determined by the charge carrier density of the semiconducting materials corresponding, for instance, to its environmental temperature equilibrium value, $T_A$. An amount of energy $\Delta E_{AB}>0$ is transferred to the system by irradiation during an isochoric transformation so as to increase the charge carrier density and, consequently, to also enhance the dispersion force to the value $F_{\mathrm{vdW}}(N_{q,B},s_A)=F_{\mathrm{vdW}}(N_{q,B},s_B)$. The membrane is now allowed to move towards the substratum to $s=s_C$ adiabatically till the force becomes $F_{\mathrm{vdW}}(N_{q,B},s_C)$, so that the charge carrier density can be assumed to be constant. Then, the charge carriers are allowed to decay back by releasing an amount of energy $\Delta E_{CD}<0$, thus returning the semiconductor to its original dielectric function during an isochoric transformation till the force becomes $F_{\mathrm{vdW}}(N_{q,A},s_C)$. Finally, the membrane is allowed to move away from the substratum back to $s=s_A$ again adiabatically till the dispersion force returns to $F_{\mathrm{vdW}}(N_{q,A},s_A)$.

The First Law of Thermodynamics requires the following:

$$\Delta E_{AB}+\Delta E_{CD}=\oint {\mathbf{F}}_{\mathbf{disp}}\left(s\right)·\mathrm{d}\mathbf{s}.$$

(1)

However, since we assumed that the optical properties of the semiconductors be independent of the gap width, the left-hand-side (LHS) of the equation can be assumed to vanish (the carriers re-emit as much energy as was provided to bring them into conduction band, or $|\Delta E_{AB}\left|=\right|\Delta E_{CD}|$). The overall result is that the net work done at right-hand-side (RHS) appears to be energy that was “extracted,” leading to the following contradiction:

$$0=\Delta E_{AB}+\Delta E_{CD}=\oint {\mathbf{F}}_{\mathbf{disp}}\left(s\right)·\mathrm{d}\mathbf{s}\ne 0.$$

(2)

The conclusion that the First Law is violated is independent of any other details describing the cycle or the device under consideration. In the original report [77], in order to provide a term of comparison describing a worst possible case, it was assumed that the re-emitted energy could not be used and the RHS was compared to $\Delta E_{AB}$. In a specific example therein, in which sub-nanometer minimum interboundary separations were assumed, a net energy “excess,” defined in this sense, appeared at the end of the closed engine cycle. Thus the former objective of the analysis suggested that “extraction” was possible in systems of this type.

3.2. Response

The title of Forward’s seminal paper on energy storage—“Extracting electrical energy from the vacuum by cohesion of charged foliated conductors”—stimulated extensive and sometimes controversial research on the relationship between electrodynamical fluctuating fields and thermodynamical concepts aimed at identifying strategies for continuous energy extraction, as Forward himself was later to propose [95].

As first strongly emphasized by London [16,96] and quoted above in the Introduction, the existence of dispersion forces appears to be inextricably connected to the concept of zero-point-energy. This quantity had appeared in Max Planck’s new quantum theory of 1912 [97], had been thus named (“Nullpunktenergie”) by Einstein and Stern in 1913 [52,98,99], and had re-emerged in both Heisenberg’s (ref. [21], Equation (23) therein) and Schrödinger’s (ref. [27], Equation (25’) therein) treatments of the harmonic oscillator problem (see also ref. [24] (pp. 271, 377) and Ref. [30] (pp. 31–32)). In search for a “source,” the debate focused on the ultimate nature of the zero-point field, if any such field physically exists [100,101,102,103,104,105,106,107,108,109], and on the possibility in principle of zero-point-energy (ZPE) “extraction”.

In order to remove difficulties connected to the fact that the zero-point-energy represents a ground state in the quintessentially quantum sense, some workers speculated that energy extraction might be permitted if the zero-point field is a non-thermal, classical entity [110,111,112,113,114,115]. This is physically possible, for instance, within “stochastic electrodynamics” (SED)—a theory proposed [116] as alternative to quantum-electrodynamics (QED) (ref. [52], Section 8.12).

The pervasiveness and intensity of this controversy can be appreciated by considering that, in 1997, Scientific American ran a special Trends in Physics piece exclusively devoted to “Exploiting Zero-Point Energy” [117]. In the same above-cited New York Times piece covering MEMS actuation by Casimir forces [89], the writer felt compelled to report, “The effect cannot be tapped as a continuous power source, though, since pulling the plates apart takes as much energy as is released when they come together.” This refrain in the popular science media—repeated almost verbatim in Ref. [88] and mentioned also in the Scientific American report—is obviously incorrect in light of the results from the AHD experiment (see also Refs. [62,63,64] for broader discussions and additional references). We shall explore this point in detail below (Section 3.3).

The findings from exploration of the latter subtopic (Section 3, B), rooted in the existing experimental evidence, did not arouse particular controversy. In contrast, the former subtopic, which had exposed an apparent violation of the principle of the conservation of energy, became quite controversial and caused the entire study to be received with suspicion by the scientific community (Section 4).

Marco Scandurra insightfully observed: “The silence of the “orthodox” part of the community expresses the deep scepticism on such developments. However the policy of ignoring publications does not contribute to the progress of science. Discussion is always positive as long as it remains on the track of scientific argumentation. We also point out that a rigorous quantum field theoretical analysis of the ideas lying at the basis of the proposed machines is still lacking” (ref. [118], double quotes in the original).

3.3. Resolution

Indeed, the only researcher to openly confront the issue and to propose a possible resolution was Scandurra himself, by considering in detail what he referred to as the “intriguing apparatus” [118] discussed by the present author from the point of view of the thermodynamics of the quantum vacuum. In a lively section entitled “Casimir machines,” which included a very intuitive illustration of the implementation of an engine cycle (Ref. [118], Figure 1, erroneously referred to in the text as Figure 2; see also Ref. [65], p. 288 for additional insights and illustrations), Scandurra reached the following conclusion:

“This is the crucial point. The work we must do to recombine the electrons with the atoms is of course larger when the distance of the plates is small and it is presumably equal to the total energy released by the vacuum during the compression phase.”

[118]

The important consequence of this suggestion is that energy conservation—by itself—demands that the optical properties of two interacting boundaries must depend on their mutual separation and are, therefore, different than those derived from measurements of isolated samples.

The rest of this section is devoted to exploring the implications of this important statement, which is made credible by Scandurra although not rigorously proven and is left as a plausibility argument.

Also, our treatment allows us to meet a crucial challenge of both theoretical and practical importance, formulated by Inui as the closing point of his first paper on this topic: “Probably the power generated by these engines is small, but, it is an interesting problem to calculate the efficiency of heat engine using vacuum fluctuations.” [119].

First, we shall offer a rigorous proof of the conservation of energy in the thermodynamical engine cycles considered (Section 3.3.1) and we shall introduce Second Law of Thermodynamics considerations (Section 3.3.2). After a brief review (Section 3.3.3), in Section 3.3.4 an engine cycle involving a two-state atom in the unretarded regime is discussed, and general conclusions about atom-surface interactions are drawn. This treatment is then further generalized to the interactions of macroscopic boundaries in Section 3.3.5, including possible experimental and engineering implications of the proposed resolution above.

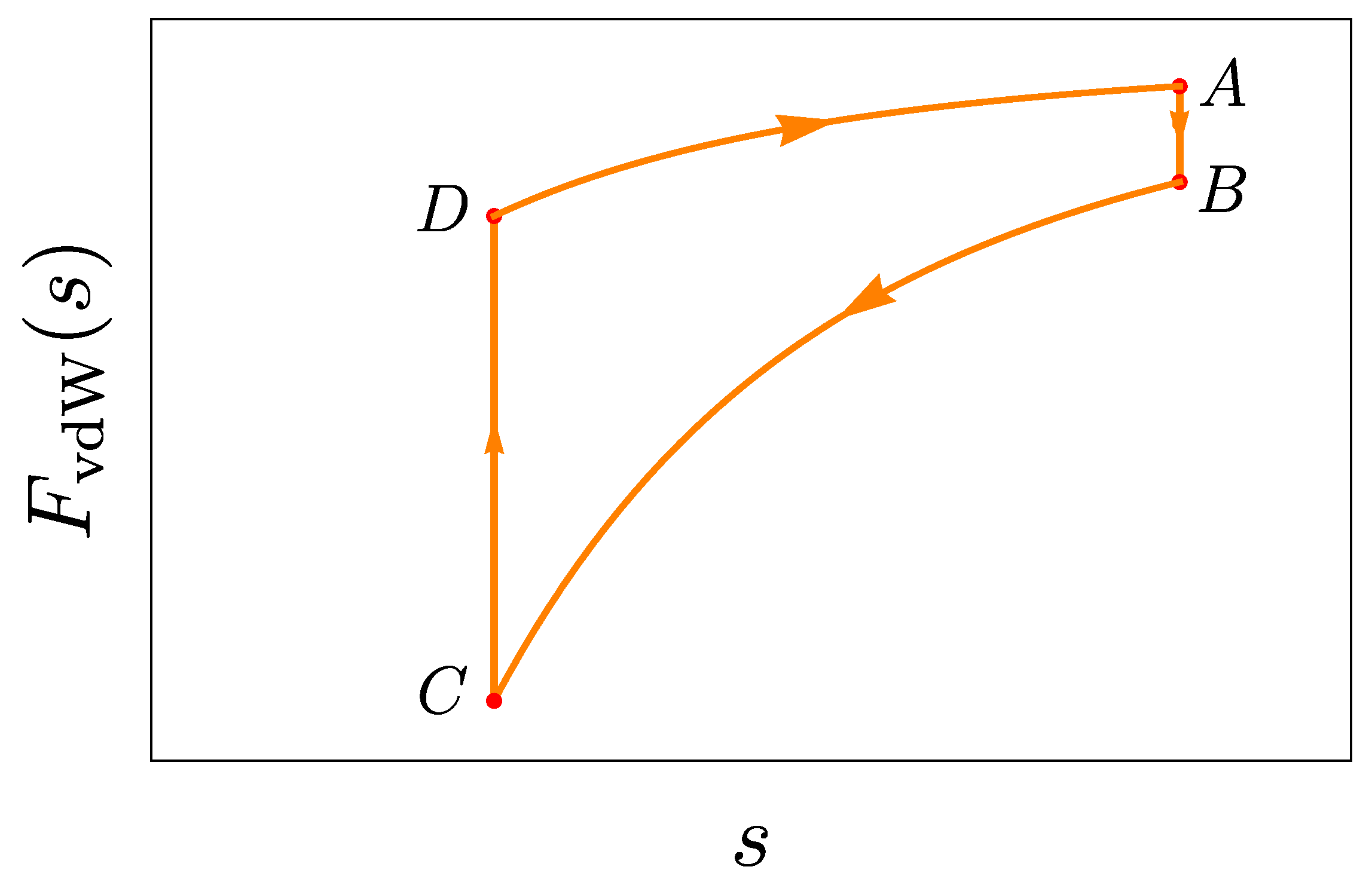
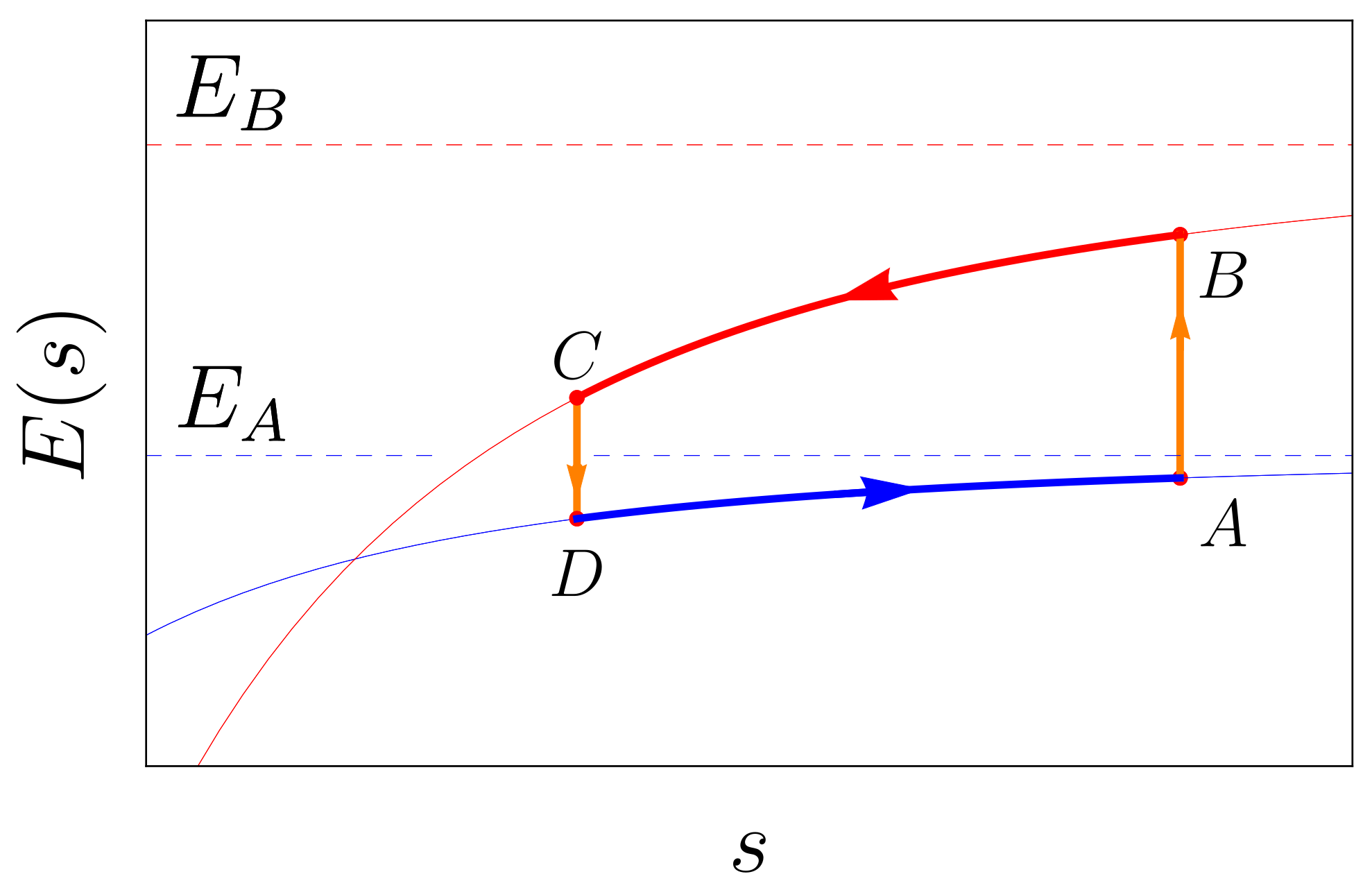
3.3.1. General Results: The First Law of Thermodynamics

In this section, we prove that, regardless of the form of the dispersion force interaction, the First Law of Thermodynamics is never violated in the engine cycles considered, so that the total energy is exactly conserved.

Let us reformulate the implementation of the Otto cycle (excluding the initial intake stroke) [120] presented in Section 3.1, leading to the violation of the First Law (Equation (2)). By paralleling that approach, one proceeds, for instance, by raising the energy of the movable system component, referred to as the ‘piston,’ by providing an amount of energy $\Delta E_{AB}$, isochorically; the piston is then drawn close to the fixed boundary so as to allow the dispersion force, presumed attractive, to do an amount of work $W_{BC}>0$; then the piston releases the same energy received initially, $\Delta E_{CD}=-\Delta E_{AB}$, isochorically; finally the piston returns to its original distance from the fixed boundary so as to cause the dispersion force to do an amount of work $W_{DA}<0$. As already seen in Section 3.1, this approach implies that, at the end of the cycle, a finite amount of mechanical work was done by the dispersion force while no net energy was transferred to the system, thus violating the First Law of Thermodynamics (Equation (2)).

A resolution is now proposed by the following approach. Let us again consider the same above thermodynamical engine cycle in detail (Figure 1). Notice that, in what follows, we shall not appeal to any properties of the zero-point field, but we shall consider an elementary formulation of thermodynamics. However, ordinary concepts are adapted to accommodate the fact that the interactions herein are attractive and that they are not modified by transferring heat to a substance in the cylinder but to the interacting boundaries themselves, so that the interactions appear due to the Uncertainty Principle, as stated by London. It is important to follow the process not only in an ordinary (P, V)-diagram (Figure 2) but also considering the details of all energy transfers (Figure 2).

A → B Isochoric transformation.

While the piston is at a distance $s=s_A=s_B$, an amount of energy $\Delta E_{AB}$ is provided for a transition from state with energy $E_A$ to one of energy $E_B$.

$$\Delta E_{AB}=E_B\left(s_B\right)-E_A\left(s_A\right)>0.$$

(3)

B → C Adiabatic transformation.

While the piston is in the state of energy $E_B$, it is moved to a distance $s_C$, $s=s_B\to s_C<s_B$.

The van der Waals (vdW) dispersion force is given by the following:

$$F_{\mathrm{vdW}}\left(s\right)=-{\displaystyle \frac{\partial E_{\mathrm{vdW}}\left(s\right)}{\partial s}}.$$

(4)

Therefore the work done by the van der Waals force at is as follows:

$$W_{BC}=-{\int }_{s_B}^{s_C}{\displaystyle \frac{\partial E_{\mathrm{vdW}}\left(s\right)}{\partial s}}\mathrm{d}s=E_B\left(s_B\right)-E_C\left(s_C\right).$$

(5)

C → D Isochoric transformation.

While the piston is at a distance $s=s_C=s_D$, energy is removed for a transition from the state with energy $E_C$ to the state with energy $E_D$. The corresponding energy change is as follows:

$$\Delta E_{CD}=E_D\left(s_D\right)-E_C\left(s_C\right)<0.$$

(6)

D → A Adiabatic transformation.

While the piston is in the state of energy $E_D$, it is moved so that $s=s_D\to s_A>s_D$. The work done by the dispersion force is as follows:

$$W_{DA}=-{\int }_{s_D}^{s_A}{\displaystyle \frac{\partial E_{\mathrm{vdW}}\left(s\right)}{\partial s}}\mathrm{d}s=+E_{\mathrm{vdW}}\left(s_D\right)-E_{\mathrm{vdW}}\left(s_A\right).<0.$$

(7)

The First Law of Thermodynamics would require the following:

$$\Delta E_{AB}+\Delta E_{CD}=W_{\mathrm{CP}},$$

(8)

where the total work over the cycle is as follows:

$$W_{\mathrm{CP}}\equiv \oint {\mathbf{F}}_{\mathbf{disp}}\left(s\right)·\mathrm{d}\mathbf{s}.$$

(9)

Now, we have the following, from Equations (3) and (6):

$$\Delta E_{AB}+\Delta E_{CD}=E_B\left(s_B\right)-E_A\left(s_A\right)+E_D\left(s_D\right)-E_C\left(s_C\right),$$

(10)

and, from Equations (5) and (7):

$$W_{\mathrm{CP}}=W_{BC}+W_{DA}=E_B\left(s_B\right)-E_C\left(s_C\right)+E_D\left(s_D\right)-E_A\left(s_A\right).$$

(11)

Therefore, Equations (1) and (8) are satisfied and, with this approach, there is no violation of the First Law of Thermodynamics so that the conflict shown at Equation (2) disappears.

This rigorous proof that energy is conserved confirms the hypothesis advanced by Scandurra, that is, the mechanical work done by the system appears as the difference between the energy provided to the system and the energy released by the system back into the environment (the wording of his statement is somewhat different than the language used here). In particular:

$$|\Delta E_{CD}|=-\Delta E_{CD}=\Delta E_{AB}-W_{\mathrm{CP}}<\Delta E_{AB}.$$

(12)

Notice that the implementation of this resolution is made possible by the fact that the $B\to C$ and $D\to A$ transformations can be assumed to be adiabatic during the lifetimes of the states. Therefore, “…when the applied perturbation changes sufficiently slowly (adiabatically), a system in any non-degenerate stationary state will remain in that state.” (Ref. [121], § 41, italic in the original; see also § 53 therein).

As is evident from our results, the statement reported by the media that “The effect cannot be tapped as a continuous power source, though, since pulling the plates apart takes as much energy as is released when they come together” [89] is obviously incorrect and incompatible with the available experimental data (Section 2.1). Although one may state that the systems we are considering are not a “continuous power source,” in the sense that energy is conserved, it is manifestly incorrect to state that “pulling the plates apart takes as much energy as is released when they come together.” Indeed, the total difference between the energy needed is the mechanical work done by these systems.

Furthermore, the prediction that the energy is conserved, although the mechanical work done causes the energy returned to the environment to be less than the energy absorbed at excitation, has consequences that can be tested experimentally.

3.3.2. General Results: The Second Law of Thermodynamics

An obvious further question is whether the engines considered herein satisfy the Second Law of Thermodynamics. In order to address this issue, we need to estimate the efficiency of the cycle, which requires deriving an expression for $\Delta E_{CD}$ from Equation (12):

$$\begin{array}{cc}\hfill |\Delta E_{CD}| =& E_B\left(s_B\right)-E_A\left(s_A\right)-(E_B\left(s_B\right)-E_C\left(s_C\right)+E_D\left(s_D\right)-E_A\left(s_A\right))=\hfill \\ \hfill & E_{\mathrm{vdW}}\left(s_C\right)-E_{\mathrm{vdW}}\left(s_D\right).\hfill \end{array}$$

(13)

However, this adds no new information.

In order to answer this question, we must provide details about the dispersion forces involved.

3.3.3. Two-Level Atom-Surface Interaction

Here we briefly review the elementary case of the unretarded interaction between an atom and a perfectly conducting wall, first treated by Lennard-Jones [40] by means of the method of images. In order to succinctly present the main point of this paper, we adopt the description developed by London [16], who employed the harmonic oscillator model of the atom introduced by Lorentz (Ref. [122], §116, p. 136 ff.; see Refs. [123,124]), widely reproduced as a tool to recover the essential features of unretarded dispersion interactions [52,94,125,126,127]. A detailed analysis of the application of the harmonic oscillator model to this and closely related problems, including important subtleties [128], has been carried out by Farina’s group [129,130,131].

Let us consider two identical atoms, labeled 1 and 2, each represented by positive nuclear charges $q_n=+\left|e\right|=e$ at a distance $z_{1,2}$ from negative electron charges, $q_e=-\left|e\right|=-e$, of relatively much smaller mass m, bound to the nuclei by a harmonic force of elastic constant $K_{\mathrm{el}}$. In one dimension (1D), the familiar dipole-dipole interaction between these two harmonic oscillators is as follows, in Gaussian units:

$$V_{\mathrm{int}}(R,z_1,z_2)=e^2\left({\displaystyle \frac{1}{R}}+{\displaystyle \frac{1}{R+z_2-z_1}}-{\displaystyle \frac{1}{R-z_1}}-{\displaystyle \frac{1}{R+z_2}}\right),$$

(14)

where R is the distance between the two nuclei. The case of one oscillator, for instance, at $z>0$, and an infinitely wide, perfectly conducting surface, assumed to be at $z=0$, coinciding with the (x, y) plane, can be treated by the classical method of images [40,129,130,131,132]. In our geometry, this is achieved by the customary substitutions, $e^2\to -e^2$, $R\to 2s$, and $z_2\to -z_1$, and by the division of the energy by a factor of 2, which is required and is often overlooked in the literature, even by Lennard-Jones (Ref. [131] and references therein). The atom–wall interaction energy becomes the following:

$$V_{\mathrm{aw}}(R,z_1)=-{\displaystyle \frac{e^2}{4}}\left({\displaystyle \frac{1}{s-z_1}}-{\displaystyle \frac{2}{s-\frac{1}{2}{z}_1}}+{\displaystyle \frac{1}{s}}\right).$$

(15)

By adding to this result the 1D elastic energy, $\frac{1}{2}{K}_{\mathrm{el}}{z}_1^2$, and by expanding to first order in the ratio $z_1/s$, we can see that the natural frequency is shifted as follows:

$${\omega }^{\prime }=\sqrt{{\displaystyle \frac{K_{\mathrm{el}}}{m}}}\left(1-{\displaystyle \frac{e^2}{8K_{\mathrm{el}}{s}^3}}\right),$$

(16)

where ${\omega }_0=\sqrt{K_{\mathrm{el}}/m}$.

This 1D result is consistent with the 3D treatment if the angle between the dipole and the direction perpendicular to the conducting plane vanishes (see [129], Equation (15), with $\theta =0$ therein). From the definition of the classical static polarizability [52,94,125,126,127], ${\alpha }_0\equiv e^2/K_{\mathrm{el}}$, we can write the total perturbed energy of the system as follows:

$${\displaystyle E^{\prime }\left(s\right)=\frac{1}{2}\hslash {\omega }^{\prime }=\frac{1}{2}\hslash {\omega }_0\left(1-\frac{{\alpha }_0}{8s^3}\right).}$$

(17)

We can now identify the dispersion interaction energy with the only term that depends on the atom-boundary gap, s, thus leading to the standard expression (1D case):

$$U_{\mathrm{vdW}}\left(s\right)=-{\displaystyle \frac{\hslash {\omega }_0{\alpha }_0}{16s^3}}.$$

(18)

This result is a particular embodiment of the general definition for the potential energy of a conservative force [133,134,135], which we can write in the present notation as follows:

$$U_{\mathrm{vdW}}(E^{\left(0\right)};s)\equiv U_{\mathrm{vdW}}(E^{\left(0\right)};r_0)-{\int }_{r_0}^s{F}_{\mathrm{vdW}}(E^{\left(0\right)};s)\mathrm{d}s,$$

(19)

where we have made explicit that the potential energy at a distance s will depend on the unperturbed atomic quantum state energy, $E^{\left(0\right)}=\hslash {\omega }_0$, and there exist arbitrary choices of both a reference point $r_0$ (in 1D) and of the value of the potential energy at that point, $U_{\mathrm{vdW}}(E^{\left(0\right)};r_0)$ (see Figure 3 and Section Summary 2).

Regardless of any such arbitrary choices, the dispersion force becomes the following:

$$F_{\mathrm{vdW}}\left(s\right)=-{\displaystyle \frac{\partial U_{\mathrm{vdW}}}{\partial s}}=-{\displaystyle \frac{3\hslash {\omega }_0{\alpha }_0}{16s^4}},$$

(20)

where the energy state dependence is not indicated for brevity.

Summary 1

In this Section, we have obtained the atom–wall potential using the harmonic oscillator approach introduced by London. An important illustrative feature of this result is that it describes the potential not only as a function of the atom–wall distance but also as a function of the atomic state energy. Although advantageous for simplicity of illustration, this expression has inherent limitations, which, however, do not invalidate the main results of this paper. In particular, the above results are valid only at near range, that is, in the unretarded regime, but are perturbative, which, on the contrary, demands the atom–wall separation to not vanish. Brief comments about non-perturbative theories will be given in Section 3.3.7.

3.3.4. Simple Atomic Engine Cycle

By following the treatment seen in Section 3.3.1, now we analyze the following results for the Otto engine cycle with an atom–wall system. Once again, we refer to Figure 2.

A → B Isochoric transformation.

While the atom is at a distance $s=s_A=s_B$, energy is provided for a transition from state with energy $E_A=E_A^{\left(0\right)}+U_{\mathrm{vdW}}(E_A^{\left(0\right)};s_A)$ to energy $E_B=E_B^{\left(0\right)}+U_{\mathrm{vdW}}(E_B^{\left(0\right)};s_B)$, where $E_A^{\left(0\right)}=\frac{1}{2}\hslash {\omega }_{0,A}$ and $E_B^{\left(0\right)}=\frac{1}{2}\hslash {\omega }_{0,B}$. Notice that the polarizability depends on the energy of the state, so that ${\alpha }_0={\alpha }_0\left(E^{\left(0\right)}\right)$ (${\alpha }_0={\alpha }_0\left(E_B^{\left(0\right)}\right)>{\alpha }_0\left(E_A^{\left(0\right)}\right)$). By using the results above, the energy required for this transformation is as follows:

$$\begin{array}{cc}\hfill \Delta E_{AB}& =E_B^{\left(0\right)}+U_{\mathrm{vdW}}(E_B^{\left(0\right)};s_B)-E_A^{\left(0\right)}s-U_{\mathrm{vdW}}(E_A^{\left(0\right)};s_A)\hfill \\ \hfill & =\Delta E_{AB}^{\left(0\right)}+U_{\mathrm{vdW}}(E_B^{\left(0\right)};s_B)-U_{\mathrm{vdW}}(E_A^{\left(0\right)};s_A)>0,\hfill \end{array}$$

(21)

where $\Delta E_{AB}^{\left(0\right)}\equiv E_B^{\left(0\right)}-E_A^{\left(0\right)}>0$ and the ⁽⁰⁾ superscript indicates the state energy unperturbed by the van der Waals potential.

B → C Adiabatic transformation.

While the atom is in the state of energy $E_B$, it is moved to $s=s_B\to s_C<s_B$. The work done by the van der Waals force at Equation (20) is as follows:

$$W_{BC}={\int }_{s_B}^{s_C}{F}_{\mathrm{vdW}}\left(s\right)\mathrm{d}s=+{\displaystyle \frac{\hslash {\omega }_{0,B}}{16}}{\alpha }_0\left(E_B^{\left(0\right)}\right)\left({\displaystyle \frac{1}{s_C^3}}-{\displaystyle \frac{1}{s_B^3}}\right).$$

(22)

C → D Isochoric transformation.

While the atom is at a distance $s=s_C=s_D$, energy is removed for a transition from the state with energy $E_C=E_C^{\left(0\right)}+U_{\mathrm{vdW}}(E_C^{\left(0\right)};s_C)$ to the state with energy $E_D=E_D^{\left(0\right)}+U_{\mathrm{vdW}}(E_D^{\left(0\right)};s_D)$. The corresponding energy change is as follows:

$$\begin{array}{cc}\hfill \Delta E_{CD}& =E_D^{\left(0\right)}+U_{\mathrm{vdW}}(E_D^{\left(0\right)};s_D)-E_C^{\left(0\right)}-U_{\mathrm{vdW}}(E_C^{\left(0\right)};s_C)\hfill \\ \hfill & =\Delta E_{CD}^{\left(0\right)}+U_{\mathrm{vdW}}(E_D^{\left(0\right)};s_D)-U_{\mathrm{vdW}}(E_C^{\left(0\right)};s_C)<0,\hfill \end{array}$$

(23)

where $\Delta E_{CD}^{\left(0\right)}\equiv E_D^{\left(0\right)}-E_C^{\left(0\right)}=-\Delta E_{AB}^{\left(0\right)}<0$.

D → A Adiabatic transformation.

While the atom is in the state of energy $E_D$, it is moved so that $s=s_D\to s_A>s_D$. The work done by the van der Waals force is as follows:

$$W_{DA}={\int }_{s_D}^{s_A}{F}_{\mathrm{vdW}}\left(s\right)\mathrm{d}s=+{\displaystyle \frac{\hslash {\omega }_{0,A}}{16}}{\alpha }_0\left(E_D^{\left(0\right)}\right)\left({\displaystyle \frac{1}{s_A^3}}-{\displaystyle \frac{1}{s_D^3}}\right)<0.$$

(24)

Thus, the First Law of Thermodynamics requires the following:

$$\begin{array}{cc}\hfill \Delta E_{AB}& + \Delta E_{CD}=E_B^{\left(0\right)}+U_{\mathrm{vdW}}(E_B^{\left(0\right)};s_B)-E_A^{\left(0\right)}-U_{\mathrm{vdW}}(E_A^{\left(0\right)};s_A)\hfill \\ \hfill & + E_D^{\left(0\right)}+U_{\mathrm{vdW}}(E_D^{\left(0\right)};s_D)-E_C^{\left(0\right)}-U_{\mathrm{vdW}}(E_C^{\left(0\right)};s_C)\hfill \\ \hfill & = \Delta E_{AB}^{\left(0\right)}+\Delta E_{CD}^{\left(0\right)}+U_{\mathrm{vdW}}(E_B^{\left(0\right)};s_B)-U_{\mathrm{vdW}}(E_A^{\left(0\right)};s_A)\hfill \\ \hfill & + U_{\mathrm{vdW}}(E_D^{\left(0\right)};s_D)-U_{\mathrm{vdW}}(E_C^{\left(0\right)};s_C)=W_{\mathrm{CP}},\hfill \end{array}$$

(25)

where, recalling that, to this perturbative order, $\Delta E_{AB}^{\left(0\right)}+\Delta E_{CD}^{\left(0\right)}=0$, ${\alpha }_0\left(E_A^{\left(0\right)}\right)={\alpha }_0\left(E_D^{\left(0\right)}\right)$ and ${\alpha }_0\left(E_B^{\left(0\right)}\right)={\alpha }_0\left(E_C^{\left(0\right)}\right)$, and with $s_A=s_B$, $s_C=s_D$, the work done by the Casimir-Polder force (in the unretarded regime) is as follows:

$$\begin{array}{cc}\hfill W_{\mathrm{CP}}& =W_{BC}+W_{DA}=\oint {\mathbf{F}}_{\mathbf{disp}}\left(s\right)·\mathrm{d}\mathbf{s}\hfill \\ \hfill & =+{\displaystyle \frac{\hslash {\omega }_{0,B}}{16}}{\alpha }_0\left(E_B^{\left(0\right)}\right)\left({\displaystyle \frac{1}{s_C^3}}-{\displaystyle \frac{1}{s_B^3}}\right)+{\displaystyle \frac{\hslash {\omega }_{0,A}}{16}}{\alpha }_0\left(E_D^{\left(0\right)}\right)\left({\displaystyle \frac{1}{s_A^3}}-{\displaystyle \frac{1}{s_D^3}}\right)=\hfill \\ \hfill & -{\displaystyle \frac{\hslash {\omega }_{0,B}}{16}}{\alpha }_0\left(E_B^{\left(0\right)}\right)\left({\displaystyle \frac{1}{s_A^3}}-{\displaystyle \frac{1}{s_D^3}}\right)+{\displaystyle \frac{\hslash {\omega }_{0,A}}{16}}{\alpha }_0\left(E_A^{\left(0\right)}\right)\left({\displaystyle \frac{1}{s_A^3}}-{\displaystyle \frac{1}{s_D^3}}\right)\hfill \\ \hfill & ={\displaystyle \frac{\hslash }{16}}\left({\omega }_{0,B}{\alpha }_0(E_B^{\left(0\right)})-{\omega }_{0,A}{\alpha }_0(E_A^{\left(0\right)})\right)\left({\displaystyle \frac{1}{s_D^3}}-{\displaystyle \frac{1}{s_A^3}}\right)>0.\hfill \end{array}$$

(26)

Clearly, in this treatment, there is no violation of the First Law of Thermodynamics (Equation (1)).

Let us now find the energy released back into the environment, analogously to what was indicated at Equation (13):

$$|\Delta E_{CD}|=-\Delta E_{CD}=\Delta E_{AB}-W_{\mathrm{CP}}>0.$$

(27)

By using Equations (21), (23) and (26), we find the following:

$$\begin{array}{cc}\hfill |\Delta E_{CD}|=& \Delta E_{AB}^{\left(0\right)}+U_{\mathrm{vdW}}(E_B^{\left(0\right)};s_B)-U_{\mathrm{vdW}}(E_A^{\left(0\right)};s_A)\hfill \\ \hfill & -{\displaystyle \frac{\hslash }{16}}\left({\omega }_{0,B}{\alpha }_0(E_B^{\left(0\right)})-{\omega }_{0,A}{\alpha }_0(E_A^{\left(0\right)})\right)\left({\displaystyle \frac{1}{s_D^3}}-{\displaystyle \frac{1}{s_A^3}}\right)=\hfill \\ \hfill & \Delta E_{AB}^{\left(0\right)}-{\displaystyle \frac{\hslash {\omega }_{0,B}}{16}}{\alpha }_0(E_B^{\left(0\right)}){\displaystyle \frac{1}{s_B^3}}+{\displaystyle \frac{\hslash {\omega }_{0,A}}{16}}{\alpha }_0(E_A^{\left(0\right)}){\displaystyle \frac{1}{s_A^3}}\hfill \\ \hfill & -{\displaystyle \frac{\hslash }{16}}\left({\omega }_{0,B}{\alpha }_0(E_B^{\left(0\right)})-{\omega }_{0,A}{\alpha }_0(E_A^{\left(0\right)})\right)\left({\displaystyle \frac{1}{s_D^3}}-{\displaystyle \frac{1}{s_A^3}}\right)=\hfill \\ \hfill & \Delta E_{AB}^{\left(0\right)}-{\displaystyle \frac{\hslash }{16}}\left({\omega }_{0,B}{\alpha }_0(E_B^{\left(0\right)})-{\omega }_{0,A}{\alpha }_0(E_A^{\left(0\right)})\right){\displaystyle \frac{1}{s_D^3}}<\Delta E_{AB}^{\left(0\right)}.\hfill \end{array}$$

(28)

Finally, for the efficiency, $\eta$, of this engine cycle [136], we obtain the following interesting result:

$$\begin{array}{cc}\hfill \eta & =1-{\displaystyle \frac{|\Delta E_{CD}|}{\Delta E_{AB}}}\hfill \\ \hfill & {\displaystyle =1-\frac{{\displaystyle \Delta E_{AB}^{\left(0\right)}-\frac{\hslash }{16}\left({\omega }_{0,B}{\alpha }_0(E_B^{\left(0\right)})-{\omega }_{0,A}{\alpha }_0(E_A^{\left(0\right)})\right)\frac{1}{s_D^3}}}{{\displaystyle \Delta E_{AB}^{\left(0\right)}-\frac{\hslash }{16}\left({\omega }_{0,B}{\alpha }_0(E_B^{\left(0\right)})-{\omega }_{0,A}{\alpha }_0(E_A^{\left(0\right)})\right)\frac{1}{s_A^3}}}=1-\frac{\Delta E_{AB}^{\left(0\right)}-\Delta U_{\mathrm{vdW},AB}\left(s_D\right)}{\Delta E_{AB}^{\left(0\right)}-\Delta U_{\mathrm{vdW},AB}\left(s_A\right)}<1,}\hfill \end{array}$$

(29)

where $\Delta U_{\mathrm{vdW},AB}\left(s_{A,D}\right)\equiv \left(\hslash /16\right)({\omega }_{0,B}{\alpha }_0\left(E_B^{\left(0\right)}\right)-{\omega }_{0,A}{\alpha }_0\left(E_A^{\left(0\right)}\right))/s_{A,D}^3$. As one might expect, the crucial figure of merit is the minimum approach distance of the atom to the boundary, $s_D$. For instance, in the limit for $s_A\to +\infty$:

$$\eta (s_A,s_D)>\eta (s_A\to +\infty ,s_D)=\frac{\hslash }{16\Delta E_{AB}^{\left(0\right)}}\left({\omega }_{0,B}{\alpha }_0(E_B^{\left(0\right)})-{\omega }_{0,A}{\alpha }_0(E_A^{\left(0\right)})\right)\frac{1}{s_D^3}=\frac{\Delta U_{\mathrm{vdW},AB}\left(s_D\right)}{\Delta E_{AB}^{\left(0\right)}},$$

(30)

which obviously grows without limit for $s_D\to 0$. The implications of this result shall be discussed in Section 3.3.7.

Summary 2

Let us close this section with some useful observations. As can be seen from Equation (20) and from Figure 1, the value of the dispersion force change during the $A\to B$ excitation transition is smaller in magnitude than that during the $C\to D$ decay transition. However, as shown by Equation (17) and in Figure 2, the opposite occurs for energy changes.

Let us consider this behavior diagrammatically. The reason that the energy change is smaller at decay is that the total energy curve diverges more rapidly for high energy-than for low energy states for $s\to 0^{+}$, since the absolute value of the force is indeed the first derivative of the energy. As a visual confirmation, it can be appreciated by inspection in Figure 2 that the slope of the higher energy (red) curve at point C is larger than that of the lower energy (blue) curve at point D.

Although this remains true at excitation, the difference between those slopes is smaller as both energy curves are approaching their asymptotic values. This means that, as s decreases ($s\to s_C$) the energy curve of the excited state will necessarily approach that of the ground state from above. It is clear from Figure 2 that an energy defect at decay must exist, and we have rigorously shown this defect to be exactly equal to the mechanical work done.

This conclusion can be promtply visualized by considering the diagram of Figure 3, showing not only the dispersion force along the engine cycle but also the potential energy definition discussed at Equation (19). For illustration purposes, here we choose $r_0<+\infty$ and $U_{\mathrm{vdW}}(E^{\left(0\right)};r_0)=0$ for all energy levels. Hence, the potential energy $U_{\mathrm{vdW}}(E_A^{\left(0\right)};s_A)$ is the area $S\left(s_{A}A{r}_{DA,0}{r}_0\right)$, shown in yellow in Figure 3a, where S indicates an area and the yellow color indicates the positive contribution, $-U_{\mathrm{vdW}}(E_A^{\left(0\right)};s_A)$, in Equation (25). With reference to Figure 3b, the potential energy contribution, $+U_{\mathrm{vdW}}(E_B^{\left(0\right)};s_B)$, corresponds to the area $\left[S\left(s_{A}B{r}_{CB,0}{r}_0\right)\right]$, where green indicates the negative contribution. By adding these two areas with their signs, we obtain the following negative contribution:

$$S\left[r_0{r}_{DA,0}A{s}_A\right]+S\left[r_0{r}_{CB,0}B{s}_A\right]=S\left[r_{DA,0}{r}_{CB,0}BA\right]<0.$$

(31)

Similarly for Figure 3c,d, we find the following positive contribution:

$$S\left[r_0{r}_{CB,0}C{s}_D\right]+S\left[r_0{r}_{DA,0}D{s}_D\right]=S\left[r_{DA,0}{r}_{CB,0}CD\right]>0.$$

(32)

Finally, by adding the right-hand-sides of the two above equations, we derive an area representation of the third equality in Equation (25):

$$S\left[r_{DA,0}{r}_{CB,0}BA\right]+S\left[r_{DA,0}{r}_{CB,0}CD\right]=S\left[ABCD\right],$$

(33)

which is clearly the work done by the dispersion force along the cycle. These results leave no ambiguity as to the fact that energy is exactly conserved in this system.

The treatment employed in this paper is of limited applicability as $s\to 0^{+}$. For instance, if we naively applied the above procedures in that limit, we should expect the energy of the excited state to become equal to and to even fall below that of the ground state. At crossover, all energy transferred to the system at excitation should be assumed to have been converted to mechanical work with no energy to be released back into the environment at decay, thus violating the Second Law of Thermodynamics. This distance represents another threshold past which the present treatment should be considered invalid and more sophisticated treatments should be used (Section 3.3.7).

Finally, it is important to recall that experimental studies of van der Waals forces with atoms in highly excited Rydberg states have been successfully carried out [137,138], thus indicating that laboratory confirmation of the phenomena described in this section is, in principle, possible (see also Ref. [52], Section 8.8).

3.3.5. Engine Cycles with Macroscopic Boundaries

In order to explore applications involving macroscopic boundaries in which a simple analytical treatment is possible, we start from the derivation of the interaction between two atoms modeled as identical harmonic oscillators used to obtain the atom–wall potential at Section 3.3.3. The classic result for the unretarded atom–atom potential in 3D first derived by Eisenschitz and London [52,94,125,126,127] (Section 1, herein) is:

$$V_{\mathrm{vdW}}\left(s\right)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{\hslash {\omega }_0{\alpha }_0^2}{s^6}},$$

(34)

with the usual meaning of all symbols. Considering now two parallel plane, semi-infinite slabs with densities N of such identical atoms per unit volume, separated by an empty gap of width s, and assuming the interboundary force to be given by the pair-wise additive approximation [41,42,43], we obtain the following:

$$F_{\mathrm{vdW}}\left(s\right)=-{\displaystyle \frac{\pi N^2\hslash {\omega }_0{\alpha }_0^2}{8s^3}}.$$

(35)

By again using Equation (20), the dependence of the corresponding slab–slab van der Waals potential on the gap width s is shown to be $\propto -1/s^2$. Further steps towards an intuitive, approximate decription can be taken by recalling the Clausius-Mossotti relation [139,140,141], which yields the atomic polarizability in terms of the dielectric constant in the media, and by expressing the final result in terms of integrals of the dielectric function over the imaginary frequency axis [52,142,143].

The correct result can be rigorously derived in the limit for small separations of the general equation for the dispersion pressure between two macroscopic, semi-infinite parallel slabs first obtained by Lifshitz (see Ref. [50], Equation (3.4); for accessible derivations, see also Ref. [52], Equation (7.57) and Ref. [144]). In this regime, adapting Krupp’s notation (Refs. [32,145], Equations (17) and (18)) to two slabs of area A and of identical materials of dielectric function $\widetilde{ϵ}\left({\omega }_C\right)$ in the complex frequency plane, we can write ($T=0$ K):

$$F_{\mathrm{vdW}}\left(s\right)=A{P}_{\mathrm{vdW}}\left(s\right)=-{\displaystyle \frac{\hslash \overline{\omega }}{8{\pi }^2{s}^3}}A=-{\displaystyle \frac{\hslash }{8{\pi }^2{s}^3}}A{\int }_0^{+\infty }\mathrm{d}{\omega }_I{\left({\displaystyle \frac{\widetilde{ϵ}\left(i{\omega }_I\right)-1}{\widetilde{ϵ}\left(i{\omega }_I\right)+1}}\right)}^2,$$

(36)

confirming the gap-width dependence found at Equation (35), with the unretarded limit as usually marked by the van der Waals (“vdW”) subscript and the Lifshitz constant, $\hslash \overline{\omega }$, is $\hslash \overline{\omega }=\frac{4}{3}\pi A_{\mathrm{dBH}}$, where $A_{\mathrm{dBH}}$ is the de Boer-Hamaker constant, (Ref. [32], p. 133, footnote (**)). The van der Waals potential energy density, $U_{\mathrm{vdW}}$, again related to the force above as $F_{\mathrm{vdW}}=-\partial U_{\mathrm{vdW}}/\partial s$, is, therefore:

$$U_{\mathrm{vdW}}\left(s\right)=-{\displaystyle \frac{\hslash \overline{\omega }}{16{\pi }^2{s}^2}}A=-{\displaystyle \frac{\hslash }{16{\pi }^2{s}^2}}A{\int }_0^{+\infty }\mathrm{d}{\omega }_I{\left({\displaystyle \frac{\widetilde{ϵ}\left(i{\omega }_I\right)-1}{\widetilde{ϵ}\left(i{\omega }_I\right)+1}}\right)}^2.$$

(37)

The example of engine cycle considered by the present author [77] and recalled above in Section 3.1 is based on altering the free carrier density in semiconductors by irradiation. An estimate of the Lifshitz constant for the contribution of free carriers—for instance, electrons—to the cohesive van der Waals pressure between two identical samples, is given by (Ref. [32], Equations (38) and (51)):

$$\hslash \overline{\omega }=\hslash {\displaystyle \frac{\pi }{8}}\sqrt{{\displaystyle \frac{2e^2}{{ϵ}_0}}{\displaystyle \frac{N_{-}}{m_{\mathrm{eff}}}}}={\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash {\omega }_p,$$

(38)

where $N_{-}$ is the free electron density, ${\omega }_p$ is the plasma frequency:

$${\omega }_p^2={\displaystyle \frac{N_{-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}},$$

(39)

with $m_{\mathrm{eff}}$ the effective electron mass and ${ϵ}_0$ the dielectric permittivity.

We recall that the plasma frequency formally emerges from the Drude model treatment of the equation of motion of free charges under the action of a periodic external electric field [146,147,148]. An intuitive image of this concept is provided by a gas of free electrons of charge $-\left|e\right|$ that, at the initial time, are found displaced along two parallel planes of area A separated by an empty gap of width x, oppositely charged by the excess and defect electrons of total charge $Q=\sigma A$, where $\sigma$ is the surface charge density [149]. The electric field $\mathbf{E}$, perpendicular to the two planes, is that of a capacitor, $\left|\mathbf{E}\right|=-\sigma /{ϵ}_0$, where the negative sign indicates that the oscillating charges are attracted back to their position of equilibrium. The total charge is that originally contained in the space between the planes, $Q=N_{-}xAe$. By differentiating this equation twice with respect to time, using Newton’s second law for every electron, $\ddot{x}=e\left|\mathbf{E}\right|/m$, and substituting the above expression for the electric field, we find a harmonic oscillator equation of angular frequency ${\omega }_p$ for the charge Q, where the plasma frequency is given by Equation (39).

In the treatment of this section, we shall assume that free charge carriers (electrons) with initial number density, $N_{A,-}$, exist at the beginning of the cycle so that irradiation causes a change of that value to $N_{B,-}>N_{A,-}$. The dispersion force in the “dark” state (see Ref. [57], Equation (7)) is neglected in this calculation of the energy exchanged in this engine cycle as it is assumed that such a contribution is not affected by irradiation and it is conservative. Notice also that the initial (“dark”) state serves as the standard state to measure the initial internal energy of the system, as defined in classical thermodynamics [136,150]. This value is arbitrary, and, unlike the simple atomic case, its value need not be known.

Analogously to the assumptions above, in this idealized cycle, the free carrier lifetime is assumed to be infinite, and we estimate the free carrier density change, $\Delta N_{-}$ after the first energy transfer, $\Delta E_{\gamma }^{\uparrow }$, as follows:

$$\Delta N_{-}={\displaystyle \frac{\Delta E_{\gamma }^{\uparrow }}{\hslash {\omega }_{\gamma }}}{\displaystyle \frac{1}{d_{\gamma }{A}_{\gamma }}},$$

(40)

where, in this case, $\Delta E_{\gamma }^{\uparrow }$ is the total energy deposited upon the semiconductor surface, for instance by a laser pulse, resulting in excitation of carriers to the conduction band as indicated by the upward arrow, $\hslash {\omega }_{\gamma }$ is the photon energy, $d_{\gamma }$ is the absorption depth, and $A_{\gamma }$ is the irradiated area (Ref. [57], Section IV.B.3; Ref. [151], Equation (20); Ref. [59], Equation (16)).

The transformations discussed in Section 3.3.4 now become as follows (Figure 4).

A → B: Isochoric transformation.

By indicating the unperturbed initial internal energy as $E^{\left(0\right)}$, we obtain the following:

$$E_A=E_A^{\left(0\right)}-{\displaystyle \frac{\hslash \overline{\omega }}{16{\pi }^2{s}_A^2}}A=E_A^{\left(0\right)}-{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash {\displaystyle \frac{{\omega }_p}{16{\pi }^2{s}_A^2}}A=E_A^{\left(0\right)}-{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash \sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_A^2}}A.$$

(41)

On the other hand, after irradiation, we have the following:

$$E_B=E_B^{\left(0\right)}-{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash \sqrt{{\displaystyle \frac{N_{B,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_B^2}}A.$$

(42)

Therefore:

$$\Delta E_{AB}=E_B^{\left(0\right)}-{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash \sqrt{{\displaystyle \frac{N_{B,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_B^2}}A-E_A^{\left(0\right)}+{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash \sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_A^2}}A>0.$$

(43)

In order to appreciate the significance of this expression, let us rewrite it in the assumption of a relatively small change in the carrier number density, that is the following:

$$N_{B,-}-N_{A,-}=\Delta N_{-}\ll N_{A,-}.$$

(44)

By substituting this into Equation (43) we find, to 1st order in the relative carrier density change, $\Delta N_{-}/N_{A,-}$:

$$\begin{array}{c}\Delta E_{AB}= E_B^{\left(0\right)}-E_A^{\left(0\right)}-{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash \left(\sqrt{N_{A,-}+\Delta N_{-}}-\sqrt{N_{A,-}}\right)\sqrt{{\displaystyle \frac{1}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_A^2}}A\simeq \hfill \\ E_B^{\left(0\right)}-E_A^{\left(0\right)}-{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash \left({\displaystyle \frac{\Delta N_{-}}{2N_{A,-}}}\right)\sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_A^2}}A=\hfill \\ E_B^{\left(0\right)}-E_A^{\left(0\right)}-{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash {\displaystyle \frac{1}{2N_{A,-}}}{\displaystyle \frac{\Delta E_{\gamma }^{\uparrow }}{\hslash {\omega }_{\gamma }}}{\displaystyle \frac{1}{d_{\gamma }}}\sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_A^2}},\hfill \end{array}$$

(45)

where we used Equation (40) with $A_{\gamma }=A$.

B → C: Adiabatic transformation.

Along the adiabatic transformation ($s=s_B\to s_C<s_B$), the number of charge carriers is assumed to be constant, so that $N_{B,-}=N_{C,-}$. Neglecting the “dark” state dispersion force, the work done by the van der Waals force given at Equation (36) is as follows:

$$W_{BC}={\int }_{s_B}^{s_C}{F}_{\mathrm{vdW}}\left(s\right)\mathrm{d}s=+{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash \sqrt{{\displaystyle \frac{N_{B,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2}}\left({\displaystyle \frac{1}{s_C^2}}-{\displaystyle \frac{1}{s_B^2}}\right)>0.$$

(46)

C → D: Isochoric transformation.

While the boundaries are at a distance $s=s_C=s_D$, energy is removed for a transition from the state with energy $E_C=E_C^{\left(0\right)}+U_{\mathrm{vdW}}(N_{C,-};s_C)$ to the state with energy $E_D=E_D^{\left(0\right)}+U_{\mathrm{vdW}}(N_{D,-};s_D)$ with the same initial number of charge carriers as in the dark state ($N_{D,-}=N_{A,-}$). The corresponding energy change is as follows:

$$\Delta E_{CD}=E_D^{\left(0\right)}-{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash \sqrt{{\displaystyle \frac{N_{D,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_D^2}}A-E_C^{\left(0\right)}+{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash \sqrt{{\displaystyle \frac{N_{C,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_C^2}}A<0.$$

(47)

By using the same formalism and approximation as in Equation (45) above, we can write:

$$N_{D,-}-N_{C,-}=-\Delta N_{-}\ll N_{D,-}.$$

(48)

$$\Delta E_{CD}\simeq E_D^{\left(0\right)}-E_C^{\left(0\right)}+{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash {\displaystyle \frac{1}{2N_{C,-}}}{\displaystyle \frac{\Delta E_{\gamma }^{\downarrow }}{\hslash {\omega }_{\gamma }}}{\displaystyle \frac{1}{d_{\gamma }}}\sqrt{{\displaystyle \frac{N_{C,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_C^2}},$$

(49)

where $\Delta E_{\gamma }^{\downarrow }$ indicates that this energy was released by charge carriers decaying back from conduction band.

D → A: Adiabatic transformation.

Along the adiabatic transformation ($s=s_D\to s_A>s_D$), the number of charge carriers is assumed to be constant, so that $N_{D,-}=N_{A,-}$. The work done by the van der Waals force is as follows:

$$W_{DA}={\int }_{s_D}^{s_A}{F}_{\mathrm{vdW}}\left(s\right)\mathrm{d}s=+{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash \sqrt{{\displaystyle \frac{N_{D,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2}}\left({\displaystyle \frac{1}{s_A^2}}-{\displaystyle \frac{1}{s_D^2}}\right)<0.$$

(50)

In this case, the First Law of Thermodynamics requires the following:

$$\begin{array}{cc}\hfill & \Delta E_{AB}+\Delta E_{CD}=\hfill \\ \hfill & E_B^{\left(0\right)}-{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash \sqrt{{\displaystyle \frac{N_{B,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_B^2}}A-E_A^{\left(0\right)}+{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash \sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_A^2}}A\hfill \\ \hfill & +E_D^{\left(0\right)}-{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash \sqrt{{\displaystyle \frac{N_{D,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_D^2}}A-E_C^{\left(0\right)}+{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash \sqrt{{\displaystyle \frac{N_{C,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_C^2}}A=W_{\mathrm{CP}},\hfill \end{array}$$

(51)

where, in this system, the work done by the Casimir-Lifshitz force is as follows:

$$\begin{array}{cc}\hfill W_{\mathrm{CP}}& =W_{BC}+W_{DA}=\oint {\mathbf{F}}_{\mathbf{disp}}\left(s\right)·\mathrm{d}\mathbf{s}=\hfill \\ \hfill & +{\displaystyle \frac{\pi }{4\sqrt{2}}}{\displaystyle \frac{1}{16{\pi }^2}}\hslash \sqrt{{\displaystyle \frac{N_{B,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}\left({\displaystyle \frac{1}{s_C^2}}-{\displaystyle \frac{1}{s_B^2}}\right)A+{\displaystyle \frac{\pi }{4\sqrt{2}}}{\displaystyle \frac{1}{16{\pi }^2}}\hslash \sqrt{{\displaystyle \frac{N_{D,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}\left({\displaystyle \frac{1}{s_A^2}}-{\displaystyle \frac{1}{s_D^2}}\right)A\hfill \\ \hfill & ={\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash {\displaystyle \frac{1}{16{\pi }^2}}\left(\sqrt{{\displaystyle \frac{N_{B,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}-\sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}\right)\left({\displaystyle \frac{1}{s_D^2}}-{\displaystyle \frac{1}{s_A^2}}\right)A.\hfill \end{array}$$

(52)

Therefore, in this case as well, the First Law of Thermodynamics is satisfied.

In order to assess whether the Second Law of Thermodynamcs is satisfied, let us proceed as in the atomic case of Equation (27), by evaluating the energy released back into the environment:

$$\begin{array}{c}|\Delta E_{CD}|=\Delta E_{AB}^{\left(0\right)}-{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash {\displaystyle \frac{1}{16{\pi }^2{s}_A^2}}A\left(\sqrt{{\displaystyle \frac{N_{B,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}-\sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}\right)\hfill \\ -{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash {\displaystyle \frac{1}{16{\pi }^2}}\left(\sqrt{{\displaystyle \frac{N_{B,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}-\sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}\right)\left({\displaystyle \frac{1}{s_D^2}}-{\displaystyle \frac{1}{s_A^2}}\right)A\hfill \\ =\Delta E_{AB}^{\left(0\right)}-{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash {\displaystyle \frac{1}{16{\pi }^2}}\left(\sqrt{{\displaystyle \frac{N_{B,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}-\sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}\right){\displaystyle \frac{1}{s_D^2}}A<\Delta E_{AB}^{\left(0\right)}.\hfill \end{array}$$

(53)

Finally, for the efficiency, we find the following, again in analogy with Equation (29):

$$\begin{array}{l}\eta =1-\frac{\left|\Delta E_{CD}\right|}{\Delta E_{AB}}=1-\frac{{\displaystyle \Delta E_{AB}^{\left(0\right)}-\frac{\pi }{4\sqrt{2}}\hslash \frac{1}{16{\pi }^2}\left(\sqrt{{\displaystyle \frac{N_{B,-}}{m_{\mathrm{eff}}}\frac{e^2}{{ϵ}_0}}}-\sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}\frac{e^2}{{ϵ}_0}}}\right)\frac{1}{s_D^2}A}}{{\displaystyle \Delta E_{AB}^{\left(0\right)}-\frac{\pi }{4\sqrt{2}}\hslash \frac{1}{16{\pi }^2}\left(\sqrt{{\displaystyle \frac{N_{B,-}}{m_{\mathrm{eff}}}\frac{e^2}{{ϵ}_0}}}-\sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}\frac{e^2}{{ϵ}_0}}}\right)\frac{1}{s_A^2}A}}=\\ 1-{\displaystyle \frac{\Delta E_{AB}^{\left(0\right)}-\Delta U_{\mathrm{vdW},BA}\left(s_D\right)}{\Delta E_{AB}^{\left(0\right)}-\Delta U_{\mathrm{vdW},BA}\left(s_A\right)}}<1.\end{array}$$

(54)

Again considering the limit for $s_A\to +\infty$:

$$\begin{array}{c}\eta (s_A,s_D)>\eta (s_A\to +\infty ,s_D)\hfill \\ {\displaystyle =\frac{\pi }{4\sqrt{2}}\hslash \frac{1}{16{\pi }^2}\left(\sqrt{{\displaystyle \frac{N_{B,-}}{m_{\mathrm{eff}}}\frac{e^2}{{ϵ}_0}}}-\sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}\frac{e^2}{{ϵ}_0}}}\right)\frac{1}{s_D^2}A\frac{1}{\Delta E_{AB}^{\left(0\right)}}=\frac{\Delta U_{\mathrm{vdW},BA}\left(s_D\right)}{\Delta E_{AB}^{\left(0\right)}}.}\hfill \end{array}$$

(55)

Let us now rewrite this result to 1st order in $\Delta N_{-}/N_{A,-}$ in the following equivalent forms by means of Equation (45):

$$\begin{array}{c}\eta (s_A\to +\infty ,s_D)\simeq {\displaystyle \frac{\pi }{4\sqrt{2}}}{\displaystyle \frac{1}{16{\pi }^2}}\hslash \left({\displaystyle \frac{\Delta N_{-}}{2N_{A,-}}}\right)\sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{s_D^2}}A{\displaystyle \frac{1}{\Delta E_{AB}^{\left(0\right)}}}\hfill \\ ={\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash {\displaystyle \frac{1}{2N_{A,-}}}{\displaystyle \frac{\Delta E_{\gamma }^{\uparrow }}{\hslash {\omega }_{\gamma }}}{\displaystyle \frac{1}{d_{\gamma }}}\sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{16{\pi }^2{s}_D^2}}{\displaystyle \frac{1}{\Delta E_{AB}^{\left(0\right)}}}\hfill \\ ={\displaystyle \frac{\pi }{8\sqrt{2}}}{\displaystyle \frac{1}{16{\pi }^2}}\left({\displaystyle \frac{\Delta N_{-}}{N_{A,-}}}\right){\displaystyle \frac{\hslash {\omega }_{p,A}}{\Delta E_{AB}^{\left(0\right)}}}{\displaystyle \frac{A}{s_D^2}}.\hfill \end{array}$$

(56)

Assuming that $\Delta E_{\gamma }^{\uparrow }\approx \Delta E_{AB}^{\left(0\right)}$, the middle equation above yields the following:

$$\begin{array}{cc}\hfill \eta (s_A\to +\infty ,s_D)& \simeq {\displaystyle \frac{1}{128\sqrt{2}\pi }}\hslash {\displaystyle \frac{1}{N_{A,-}}}{\displaystyle \frac{1}{\hslash {\omega }_{\gamma }}}{\displaystyle \frac{1}{d_{\gamma }}}\sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}}{\displaystyle \frac{e^2}{{ϵ}_0}}}{\displaystyle \frac{1}{s_D^2}}\hfill \\ \hfill & ={\displaystyle \frac{1}{128\sqrt{2}\pi }}{\displaystyle \frac{1}{N_{A,-}}}{\displaystyle \frac{\hslash {\omega }_{p,A}}{\hslash {\omega }_{\gamma }}}{\displaystyle \frac{1}{d_{\gamma }}}{\displaystyle \frac{1}{s_D^2}}.\hfill \end{array}$$

(57)

All above results are fully consistent with the classical thermodynamics expressions for the Otto cycle [120,152].

Summary 3

In order to summarize the quantitative implications of the results of this Section, let us adopt values of the numerical parameters typical of the AHD experiment: $N_{A,-}={10}^{24}$ m⁻³, $\hslash {\omega }_{p,A}=0.066$ eV, $\hslash {\omega }_{\gamma }=1.5$ eV, $d_{\gamma }\simeq 1/\alpha ={10}^{-6}$ m, $s_D=0.1\times {10}^{-6}$ m, where $\alpha$ is the absorption coefficient. With these choices, the efficiency is $\eta \approx 5\times {10}^{-9}$.

It is useful to notice that, for this system, the breakdown of the expression for the Lifshitz force ($\eta (s_A\to +\infty ,s_D)\gtrsim 1$) occurs for $s_D\lesssim 1$ Å, consistently with the results in [77] (Figure 8, therein). Although the main results obtained herein are not affected by the use of approximate expressions, the several limitations to be addressed to enhance the accuracy of these calculations are described in Section 5.

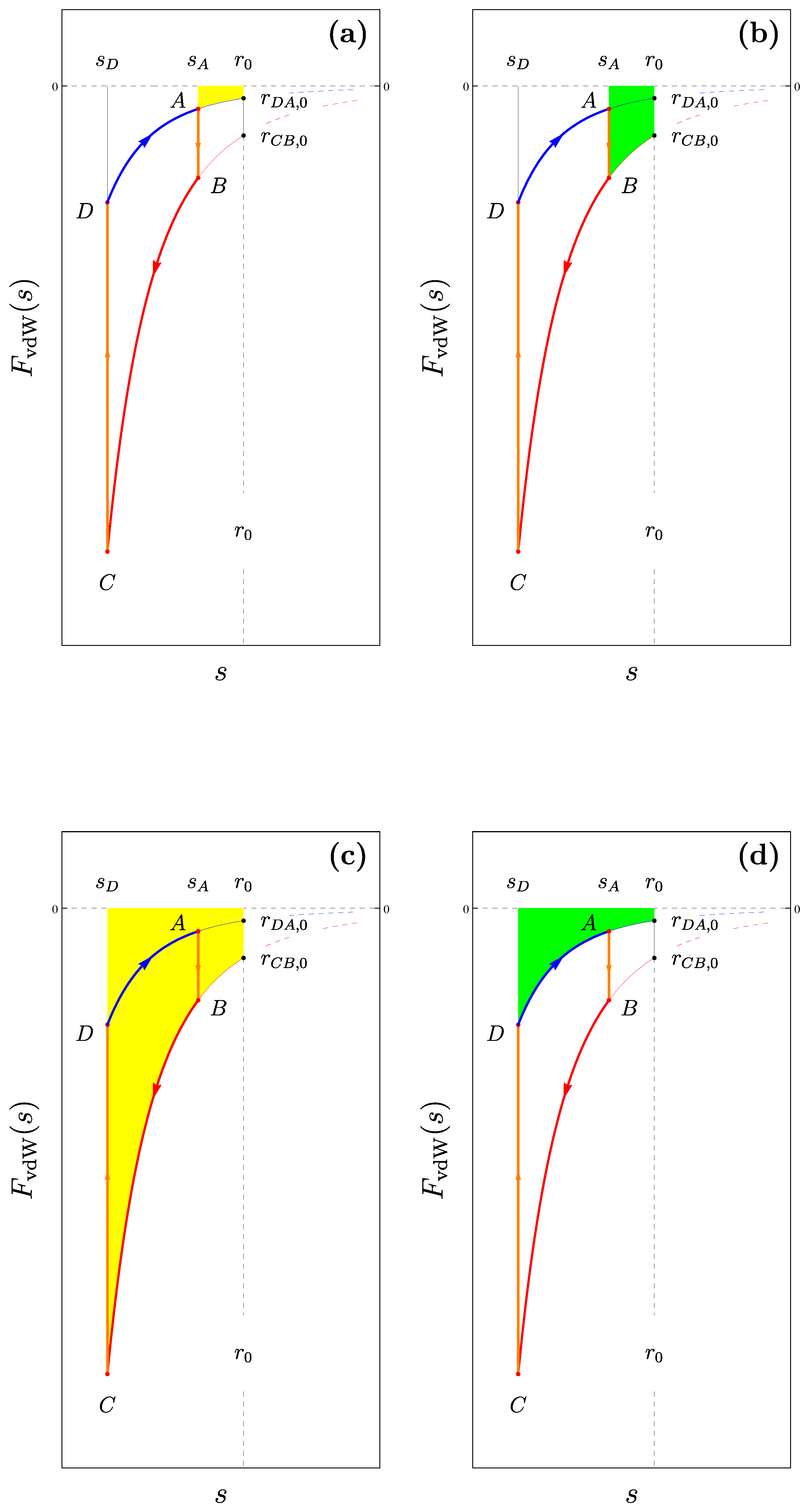
3.3.6. Plane-Sphere Boundaries

As is well known, since the earliest experimental efforts aimed at measuring dispersion forces between macroscopic boundaries [153,154,155,156,157], including also the AHD setup [54,55,56] discussed in Section 2.1, the sphere–plane geometry has been adopted in order to circumvent the parallelism challenges associated to a plane–plane geometry [158]. This was also the approach employed by Lamoreaux in his extensively cited and historically significant demonstration of Casimir force measurement by means of a Cavendish balance (Ref. [159]; see also re-analyses at Refs. [160,161,162], and reviews within a broader context at Refs. [163,164]).

In this Section, we obtain an efficiency expression for an Otto engine cycle carried out with this oft-used arrangement. In order to do so, the expression for the dispersion force obtained by Lifshitz for the archetypal plane–plane system must be generalized to a different geometry. This is well-known to be an extremely challenging problem, only solved recently by means of sophisticated numerical approaches [165,166,167]. In what follows, we shall adopt the Proximity Force Theorem (PFT) [153,155,168,169,170,171] to estimate the dispersion force (Ref. [169], Equation (7)) between a plane and a sphere of radius R with a minimum gap width s and $s\ll R$, under the same assumptions as in Section 3.3.5.

An intuitive justification for the expression obtained by using the PFT is gained by using a “graded boundary” approximation, in which the spherical surface is described by a series of plane, concentric, circular boundaries parallel to the plane substratum facing across the empty gap. Again, by assuming the validity of the additive approach, it is quickly shown that the total force between the “graded” sphere and the plane becomes the following (Ref. [52], Section 8.7):

$$F_{\mathrm{s}-\mathrm{p}}\left(s\right)=2\pi Ru\left(s\right)=-2\pi R{\displaystyle \frac{\hslash \overline{\omega }}{16{\pi }^2{s}^2}}=-2\pi R{\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash {\omega }_p{\displaystyle \frac{1}{16{\pi }^2{s}^2}},$$

(58)

where $u\left(s\right)=U_{\mathrm{vdW}}\left(s\right)/A$ is the energy per unit area of the plane–plane geometry given by Equation (37). The corresponding proximity energy, $U_{\mathrm{s}-\mathrm{p}}\left(s\right)$, such that $F_{\mathrm{s}-\mathrm{p}}\left(s\right)=-\partial U_{\mathrm{s}-\mathrm{p}}\left(s\right)/\partial s$ (Ref. [169], Equation (7)), becomes the following:

$$U_{\mathrm{s}-\mathrm{p}}\left(s\right)=-2\pi {\displaystyle \frac{\pi }{4\sqrt{2}}}\hslash {\omega }_p{\displaystyle \frac{R}{16{\pi }^{2}s}},$$

(59)

where, as always, $R\gg s$. With this result, we can rewrite Equations (54)–(57), within the same approximations therein, as follows:

$${\displaystyle \eta =1-\frac{{\displaystyle \Delta E_{AB}^{\left(0\right)}-\frac{\hslash }{32\sqrt{2}}\left(\sqrt{{\displaystyle \frac{N_{B,-}}{m_{\mathrm{eff}}}\frac{e^2}{{ϵ}_0}}}-\sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}\frac{e^2}{{ϵ}_0}}}\right)\frac{R}{s_D}}}{{\displaystyle \Delta E_{AB}^{\left(0\right)}-\frac{\hslash }{32\sqrt{2}}\left(\sqrt{{\displaystyle \frac{N_{B,-}}{m_{\mathrm{eff}}}\frac{e^2}{{ϵ}_0}}}-\sqrt{{\displaystyle \frac{N_{A,-}}{m_{\mathrm{eff}}}\frac{e^2}{{ϵ}_0}}}\right)\frac{R}{s_A}}}<1;}$$

(60)

$${\displaystyle \eta (s_A\to +\infty ,s_D)\simeq \frac{1}{64\sqrt{2}}\frac{1}{N_{A,-}}\frac{1}{d_{\gamma }{A}_{\gamma }}\frac{R}{s_D}\frac{\hslash {\omega }_{p,A}}{\hslash {\omega }_{\gamma }}.}$$

(61)

By using the same numerical values as above, with also $R=0.25$ m [56] and $A_{\gamma }=\pi r_{\mathrm{a}:\mathrm{Si}}^2$, with the radius of the amorphous silicon deposition, $r_{\mathrm{a}:\mathrm{Si}}={10}^{-3}$ m [57], we find the following, for the efficiency, $\eta \approx 8\times {10}^{-11}$.

Summary 4

In this Section, we focused more closely upon the sphere–plane geometry, with its proven record of successful experimental implementation. Of course, as discussed in the literature provided, results obtained from the PFT approach must be further strengthened by means of accurate numerical calculations.

It is worth noting that, although approximating the energy released at decay as being equal to that absorbed at excitation might appear acceptable due to the very small values of the efficiency obtained in this paper, the frequencies of operation of MEMS (∼10⁴–${10}^5$ Hz) imply that the accumulated absolute energy error can quickly become unacceptably large in simulations of these systems.

3.3.7. Extremely near Range Limit

The expressions obtained above and the comments at the end of Section 3.3.4 show that, if the minimum interboundary gap is $s_D\lesssim 1$ nm, the efficiency of the dispersion force thermodynamical engine cycle we considered might exceed unity. Although, technologically, this is a challenging regime to reach, the question stands as to whether, in principle, these particular systems represent yet another possible example of a quantum engine predicted to violate the Second Law of Thermodynamics (Section 4).

In order to address this issue, we must consider whether the assumptions made to obtain our results are valid at such close range (of course, the onset of retardation requires the use of the full Lifshitz treatment at the opposite large range). We shall mention three issues that affect the treatment of the atom–wall system.

1. 

The real temperatures are $T_K\ne 0$ K so that the present analysis must be repeated using the more general expressions from the Lifshitz theory, involving the free energy.

2. 

The expressions we used for the force are perturbative results. In recent years, several theories have been proposed to obtain the exact, nonperturbative expressions for the Casimir-Polder free energy, including also the effect of a non-zero temperature, for these systems [172,173,174,175,176,177,178]. As expected, the nonperturbative Casimir-Polder force behaves differently than in the perturbative approximation at near range, thus requiring a revision of our expressions.

3. 

The last issue to consider is the effect of extremely short range on atomic states and atomic polarizability, which become therefore also functions of distance (see, for instance, Refs. [179,180,181,182,183] and references therein).

As regards the specific case of two macroscopic boundaries in the plane–plane geometry, it is important to recall that “…the Lifshitz formula is always nonperturbative” [173]. Therefore, only items (1.) and (3.) above must be addressed. In particular, this requires employing an appropriate theory of the dielectric response of semiconductors in close proximity to a boundary for nonzero temperatures.

A full analysis of the consequences of including all such improvements is beyond the scope of the present paper. It remains to be seen whether a vastly refined treatment of the engine cycles we discussed allows one to rule out violations of the Second Law or whether such violations become even more likely.

4. Silence and Debates About Violations of the Laws of Thermodynamics

The ultimate nature of the relationship between dispersion force theory and the First and Second Laws of Thermodynamics is a relatively unexplored topic within the broader research landscape of nano- through mesoscopic system quantum thermodynamics, which has been attracting rapidly growing attention in recent years [184,185,186,187,188,189].

It is helpful to recall unambiguously that conflicts with fundamental laws of thermodynamics usually do not disqualify a topic from discussion within the scientific community. Such issues may arise and still remain even in the treatment of deceptively simple systems.

In addition to quantum thermodynamics, consider an important electrodynamical analog of the system discussed in this paper, that is, a standard idealized capacitor, either empty or possibly filled with a dielectric material. Calculations of the potential energy of capacitors and of the mechanical work done by the electric force on one of the plates, if movable, have been an enduring genre in the scientific literature since the publication of A Treatise on Electricity and Magnetism (Vol. I, Articles 93 a.-3 c.) [190] by Maxwell, whose treatment remains remarkably modern [147,148,191,192]. Additional complications arise if the gap is completely or partially filled by a dielectric and if the dielectric can move transversally between two fixed plates, or if it is fixed to one moving plate [148,193]. Energy budget and energy conservation issues, along with the consequences of considering charging and discharging capacitors as energy radiators [194,195,196], are topics typically treated in the pedagogical literature [197,198].

However, far more challenging thermodynamical interpretations of the energy of a parallel plate capacitor are needed if the gap material has a temperature-dependent dielectric constant [199,200,201,202]. Discussions about the consequences of such treatments for the applicability of the Second Law of Thermodynamics on the microscale [203], including “Exorcising the Demon Within” [204], have been remarkably lively in leading research journals in the last thirty years [205,206].

Studies of the parallel plate capacitor with dielectrics have been motivated by the fact that “the representation of the effect of fields in terms of thermodynamic variables is still not well understood” [207] and “The plate capacitor system facilitates a simple example that illustrates the difference that can exist between field independent and field dependent thermodynamic variables” [208]. More recently, it was stated that “…the effect of field induced changes in temperature, and the exact form of the stored field energy, are not yet known” [209]. Perhaps surprisingly, as recently as early 2025, the status of this area of study is still that “There are some theoretical puzzles in thermodynamics in the presence of electromagnetic fields” [210].

As forcefully stated by D’Abramo: “…over the last 10–15 years an unparalleled number of challenges has been proposed against the status of the Second Law of Thermodynamics. During this period, more than 50 papers have appeared in the refereed scientific literature …together with a monograph entirely devoted to this subject. Moreover, during the same period of time two international conferences on the limit of the Second Law were also held …” [203] (see also [204,211,212,213]). Of course, the fact that the need should be felt to offer such information is a likely indication that a degree of suspicion about the legitimacy of this topic persists.

However, the opposite has occurred with the fascinating Casimir force issues we analyzed herein, which were not investigated by the community with a similar degree of interest. The reasons for this intriguing difference in practitioner community response deserves research in its own right. Here we can only remark that the negative effects of this approach were envisaged by Marco Scandurra (Section 3.2), referring to “The silence of the “orthodox” part of the community” (Ref. [118], double quotes in the original), as he candidly stated that “…the policy of ignoring publications does not contribute to the progress of science.” (notice that his own contribution appeared as a preprint on arXiv).

The specific terminology used by Scandurra deserves comment. Indeed, there exists a significant body of research literature devoted to “orthodoxy” in science and to the adjective “orthodox,” used by Scandurra. This is sometimes introduced as simply meaning “widely accepted” but it may become a juxtaposition to “anarchy” [214]. Such a characterization as “orthodox” is frequent in discussions of various aspects of quantum mechanics. For instance, the Copenhagen interpretation is typically described as the “orthodox view” (Ref. [215], p. 168, Note 15). Some authors even report that “many versions of “the Copenhagen interpretation” are found, from orthodox to liberal,” [216] thus implying the existence of an even more orthodox orthodoxy. Despite the well-known existence of such a practice in science, for some purists [217], the mere mention of the existence of orthodoxy is sufficient reason for inclusion of an author with the “fringe” [218], for mockery [219], and for awarding a paper ‘crank index’ points according to one of several, admittedly humorous, schemes [220,221,222] devised to shame trespassers [223].

However, one needs only to turn to Thomas Kuhn, discussing the upbringing of scientists, to find the rather obvious connection to indoctrination made explicit: “Of course, it is a narrow and rigid education, probably more so than any other except perhaps in orthodox theology. But for normal scientific work, for puzzle-solving within the tradition that the textbooks define, the scientist is almost perfectly equipped. Furthermore, he is well equipped for another task as well—the generation through normal science of significant crises. When they arise, the scientist is not, of course, equally well prepared.” (Ref. [224], p. 166).

The undeniable existence of an enforced orthodoxy naturally raises the issue as to its stultifying effect on the evolution of scientific knowledge, as stated by Scandurra. This process is described by Merton: “Take the issue of “orthodoxy” and “heterodoxy.” Each of us can cite cases where later history has reversed the contemporaneous judgment of the worth of particular people and their works of heterodoxy. Much (not all) innovation is in the nature of the case heterodox, and we all know that the lot of the heterodox innovator is often a most unhappy one.” (Ref. [84], p. 433).

Perhaps the most ferocious attack against orthodoxy in science is by Feyerabend, who advocated his epistemological anarchism, famously demanding an “anything goes” approach to scientific methodology. He states: “The consistency condition demands that new hypotheses agree with accepted theories,” something Feyerabend finds “unreasonable because it preserves the older theory, and not the better theory.” Reflecting on John Stuart Mill’s “account of the gradual transformation of revolutionary ideas into obstacles to thought,” Feyerabend criticizes empiricists such as “some proponents of what has been called the orthodox interpretation of quantum mechanics,” stating, “When a new view is proposed it faces a hostile audience and excellent reasons are needed to gain for it an even moderately fair hearing. The reasons are produced, but they are often disregarded or laughed out of court, and unhappiness is the fate of the bold inventors.” (Ref. [225], Ch. 3).

In light of these observations, two strategies are worth pursuing to foster the advancement of progress in investigations of processes we explored in this paper. The former strategy is continued professional research into the events we discussed—from the standpoint of history, philosophy, scientometrics, and sociology of science [64,84,219,226,227], including the mechanisms by which silence was not only practiced, but imposed in this case [228].

The latter strategy is continued research into the physical processes we explored and their engineering applications. In this regard, it is appropriate to observe that those who both became interested in the original findings by this author and cited that work typically approach it from one of the two angles we identified in Section 3.

On the one hand (A.), investigators in the field of “zero-point energy extraction” considered the proposed thermodynamical engine cycles as carried out in a Gedankenexperiment (thought experiment) [229,230,231], the end result of which appears to be a net energy transfer from “vacuum energy” into, for instance, mechanical or electrical energy [114,232,233,234]. As we have mentioned throughout this paper, this topic has been so controversial as to provide, in part, an explanation for the “silence” Scandurra reports.

In recent years, renewed interest has emerged from some within the quantum thermodynamics community, who have cited previous work on “zero-point energy extraction.”

As to confirm the misgivings of the “orthodox” part of the community” [118], Henriet et al. commence their own work by stating that “The dream of using fluctuations from the quantum vacuum as a limitless power source has inspired many, from science fiction writers to scientists.” (Ref. [185]; see Ref. [64] for references to science fiction and the movie industry). The single work published by the present author on this topic in the last quarter century is amplified, somewhat dramatically, as a “…minority but vocal viewpoint.” [235]. Apparently, in order to not be vocal, one should be completely silent.

Sheehan states the typical opinions from within this community: “While experimental and theoretical evidence abounds for the existence of zero point energy, there is no convincing evidence for its nonconservative extraction.” [235] Although, as mentioned earlier, some workers dispute the existence of a zero-point energy [101,102,105,106,108,109], in the present work we have gone beyond “convincing evidence” by providing the needed proof of conservation independently of the existence of the zero-point energy of the quantum vacuum.

Speculations that the vacuum may have properties opposite than those predicted by the orthodox theory of quantum-electroynamics (QED) has also reappeared to explain early data about the EMDrive obtained at the NASA Johnson Space Center [236], later conclusively contradicted by measurements presented by Tajmar’s group [237]. Recently, widely cited reports of “Extraction of Zero-Point Energy” have also appeared in the pages of Atoms [233].

On the other hand (B.), the thermodynamical engine cycles discussed herein interested researchers seeking a novel strategy for nano-device operation based upon the undisputed experimental evidence available (Section 2.1). Within this latter category, we mention the group led by Raul Esquivel-Sirvent, who were able to look beyond the unresolved energy conservation issue and recognized that the dispersion force modulation thermodynamical engine cycles introduced by the present author [77] represent a promising technology [238,239].

Also, Norio Inui, at the onset of an interesting series of papers on the behavior of irradiated Casimir cavities with semiconducting boundaries [119,151,240,241,242], commented: “From the standpoint of engineering, depending of the Casimir force on several physical properties means that the Casimir force can be controlled by changing them. …Thus the Casimir force may play an important role in microelectromechanical system (MEMS) …Furthermore, Pinto has proposed an engine cycle of an optically controlled vacuum energy transducer …The main purpose of his study was arguing about the possibility of creating free-energy. It is an interesting problem, but, we do not discuss it at all.” [151] Thus, in his work, Inui proceeded to explore implementations of thermodynamical transformations largely within the same mathematical framework proposed by the present author while disregarding any open issues, which were not expected to detract, and never did detract, from the potential of the proposed novel approach to MEMS operation.

5. Conclusions

In this paper, we have generalized the resolution of the apparent inconsistency with the First Law of Thermodynamics that had been reported in an earlier original treatment of dispersion force-driven thermodynamical engine cycles [77], proving that energy is rigorously conserved and further broadening results recently announced by this author [243]. Furthermore, we have shown the need for further analysis to determine the consistency of predictions from the Casimir-Lifshitz theory with the Second Law of Thermodynamics at nonzero temperatures, within possibly necessary non-perturbative treatments, and considering modifications of the optical properties near boundaries throughout the full interboundary distance range till surface contact.

The resolution of the apparent conflict with the First Law of Thermodynamics opens up a wide research landscape holding answers to some of the most exciting questions in the topic of dispersion force-enabled engine cycle applications in nano-devices. We highlight the following issues merely as examples of topics obviously worthy of future investigations:

1. 

The treatments proposed herein must be generalized to the non-vanishing temperature case ($T_K>0$ K), considering distance-dependent optical properties, and, in the atom–wall case, employing nonperturbative results.

2. 

What theoretical predictions can be made about the energy re-emitted at the end of the downstroke and its interactions with the cavity walls? Can such radiation be directly observed?

3. 

The results of this paper must be further generalized to the case of semiconducting multiwalled nanotubes [244,245] and also graphene.

4. 

What is the effect of out-of-equilibrium conditions on the results of this paper?

5. 

What is the effect of fluctuations on the results of this paper?

6. 

To what extent do thermodynamical considerations alone constrain the general mathematical form of any non-perturbative dispersion force law?

7. 

What experiments can be carried out to detect any force law modifications connected to the issues raised in this paper?

8. 

What is the anticipated technological impact on nano-device performance of those same modifications?

9. 

Are there different regimes or systems in which violations of the First and Second Laws of Thermodynamics reappear?

10. 

How can these results valid for illuminated semiconductors be extended to completely different strategies for dispersion force modulation?

Writing in a recent quantum thermodynamics review, Manzano and Zambrini [246] observed:

“From the experimental perspective, …still very few aspects of stochastic quantum thermodynamics have been tested in the laboratory.”

This assessment applies fittingly to our present understanding of Casimir force quantum thermodynamical engine cycles in real nano-machines. Calorimetry studies [247], needed to explore the principles of quantum thermodynamics in such systems, have not yet even been realistically attempted. Indeed, “…there is still not a clear consensus about how to determine what is the work and the heat in a quantum system” [248]. Although the analysis of this paper should finally dispose of any remaining speculations about violations of the First Law, a tremendous amount of both theoretical and experimental work remains to be done to assess issues connected to the Second Law, including theoretical application and laboratory verification of the Jarzynski equality [249,250] in systems of the type we considered. For instance, experimental data on dispersion force fluctuations in Casimir force systems are lacking [251,252,253] and possibly only marginally possible with present-day technology in the atom–wall case [254,255]. In addition to these purely theoretical and experimental efforts, it is appropriate to also point out the crucial role of numerical simulations in exploring the intriguing questions that lie ahead [256,257].

Some technological applications of radiation-driven dispersion force modulation may be especially sensitive to the processes described in this paper. For instance, we have been investigating the use of parametric amplification in possible table-top gravitational wave detectors [258,259,260] and in accelerometers for inertial navigation in space [91,92,93,243]. The sensitivity of these instruments increases dramatically in the limit of small interboundary gap widths, which is also the regime in which the thermodynamical effects discussed herein become important.

As outlined by this author over a quarter century ago, the irradiation of semiconductors represents a strategy for “achieving optical control of Casimir force actuated devices” [77]. The results presented in this report pave the way for the implementation of next-generation thermodynamically consistent multiphysics models of nanodevices operating in the regime in which dispersion forces are both dominant and time-modulated.