Electron and Positron Impact Ionization of Molecules

Abstract

We review our group’s most significant results concerning the collision of positrons and electrons with small molecules. Total and triple differential cross sections for the ionization of these targets were calculated in the distorted wave Born approximation using Gaussian molecular orbitals. Different models were tested. The obtained theoretical results reproduced, in most cases, the features observed in the experimental data.

1. Introduction

The interaction of charged particles with matter is important for the investigation of the fundamental properties of atoms and molecules. The few-body dynamics occurring in these collisions is not yet fully understood because ab initio calculations are possible only for the interaction with small atoms. The collision of electrons and positrons with small molecules is of great interest for some important fields like astrophysics, radiobiology, and medical sciences. For example, the interaction between positrons and small molecules (especially water) is of great importance in medical diagnosis, such as PET (positron emission tomography).

In the last two decades, there was a continuous interest in the interaction of electrons and positrons colliding with molecules, obtaining both total ionization [1,2,3] and differential ionization cross sections [4,5,6,7,8,9,10]. Our group has published a series of articles presenting calculations for the total ionization cross sections [11,12] and differential ionization cross sections [13,14,15,16,17,18] of different small molecules in collision with electrons and positrons. We have adopted a single active electron approximation, calculating the cross sections for the ionization from different occupied orbitals of the molecules. In most of the cases, we have used the distorted-wave Born approximation (DWBA) in different variants, in some situations with corrections for taking into account the post-collision interactions (PCIs). The main task in these studies was the correct description of the initial bound state and the final continuous state of the active electron. The initial state was expressed by a Gaussian wavefunction of the molecular orbital, while for the final state, we calculated the wavefunction in different spherically averaged potentials. Comparing our results with the available experimental data, we could find the best model among these approximations.

In the case of total ionization, cross-sectional comparison is possible between the theoretical results and experimental data for both types of projectiles, electrons, and positrons due to the large number of experimental measurements for both projectiles and several molecular targets. In contrast, triple differential cross section (TDCS) measurements for positron impact are very rare and exist only for some special cases. In this situation, we can compare our theoretical results with the experimental data obtained with electron projectiles. Comparing the TDSCs for positrons and electrons, we can study the dependence of the cross sections on the charge sign of the projectile.

In the present paper, we review our group’s work in the ionization of small molecules by electron and positron impact. We give a relatively simple but efficient method to calculate the cross sections and present some relevant results.

2. Theory

We present a brief description of the theoretical background for the ionization of molecules by charged particles (positron or electron). First, we discuss the calculation of the total cross section (TCS); then, we briefly lay out the steps for the calculation of the triple-differential cross section.

2.1. Total Cross Section

The TCS is obtained by integrating the triple-differential cross section. Based on previous studies [19,20], the TDCS for the ionization process by an electron or a positron impact may be written as

$${\displaystyle \frac{d^3\sigma }{d{\widehat{\mathbf{k}}}_{f}d{\widehat{\mathbf{k}}}_{e}d{E}_e}}=\sum _r{\displaystyle \frac{{\left(2\pi \right)}^4}{E_i}}{\left|f_t^r\right|}^2,$$

(1)

where the summation is performed over the molecular orbitals which are occupied. We denote by ${\widehat{\mathbf{k}}}_f$ and ${\widehat{\mathbf{k}}}_e$ the angles of the momenta of the scattered projectile and the ejected electron, respectively. $E_i$ represents the impact energy of the projectile, while $E_e$ denotes the ejected electron’s energy.

The transition amplitude from the initial to the final state of the system is written as

$${\left|f_t^r\right|}^2={\left|f_d^r\right|}^2+{\left|f_e^r\right|}^2-\alpha \left|f_d^r\right|\left|f_e^r\right|.$$

(2)

Here, we denote by $f_d^r$ and $f_e^r$ the direct and exchange scattering amplitudes, while $\alpha$ is a phase factor, and $\alpha =1$ as in [21] (maximum interference). For the positron impact ionization, only the direct term is present; therefore, we have

$${\left|f_t^r\right|}^2={\left|f_d^r\right|}^2.$$

(3)

The direct and the exchange amplitudes are written in terms of the wavefunctions of the particles involved in the ionization process.

$$\begin{array}{ccc}\hfill f_d^r& =& \langle {\varphi }_f\left({\mathbf{r}}_1\right){\varphi }_e\left({\mathbf{r}}_2\right)\left|V\left(r_{12}\right)\right|{\varphi }_i\left({\mathbf{r}}_1\right){\varphi }_b^r\left({\mathbf{r}}_2\right)\rangle \hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill f_e^r& =& \langle {\varphi }_e\left({\mathbf{r}}_1\right){\varphi }_f\left({\mathbf{r}}_2\right)\left|V\left(r_{12}\right)\right|{\varphi }_i\left({\mathbf{r}}_1\right){\varphi }_b^r\left({\mathbf{r}}_2\right)\rangle \hfill \end{array}$$

(5)

In the direct term, ${\varphi }_f$ and ${\varphi }_e$ stand for the wavefunctions of the scattered projectile and ejected electron, respectively, while ${\varphi }_i$ represents the wavefunction of the incoming particle. ${\mathbf{r}}_1$ is the position vector of the projectile, while ${\mathbf{r}}_2$ stands for the position vector of the active electron. Note that the coordinates are exchanged for ${\varphi }_f$ and ${\varphi }_e$ in the exchange term relative to the direct term, in order to include the exchange interaction, when the electron impact ionization is considered. The initial, bound state of the active electron is ${\varphi }_b^r$.

The bound state of the active electron is written as a linear combination of atomic orbitals, while the atomic orbitals are constructed as a linear combination (contractions) of Gaussian-type functions. We used mostly the STO-3G and STO-6G basis sets [11,19].

The multi-center bound states are further expanded in terms of the Legendre polynomials in the case of the $\sigma$ orbitals of linear molecules.

$${\varphi }_b^r\left({\mathbf{r}}_2\right)=\sum _{l_b}{c}_{l_b}^r(r_2,R)P_{l_b}(cos{\omega }_2),$$

(6)

where

$$c_{l_b}^r(r_2,R)={\displaystyle \frac{2l_b+1}{2}}{\int }_{-1}^{1}d(cos{\omega }_2)P_{l_b}(cos{\omega }_2){\varphi }_b^r\left({\mathbf{r}}_2\right).$$

(7)

Here, R is the mean inter-nuclear distance. The order of the Legendre polynomial, $l_b$, has the meaning of the orbital quantum number of the bound electron, while the angle between the vectors ${\mathbf{r}}_2$ and $\mathbf{R}$ is denoted by ${\omega }_2$. Further, the Legendre polynomials are expanded in terms of the spherical harmonics. With this procedure, we can separate the dependencies on the characteristic angles of the active electron and of the molecular axis. This procedure ensures that the multi-center wavefunctions are expressed as a sum of products between one-center wavefunctions (with a certain $l_b$) and a spherical harmonic, which contains the dependence on the angles of $\mathbf{R}$. The above expansion for $\sigma$ orbitals can be performed directly as shown in [19], but for $\pi$ orbitals, the expansion is preceded by a transformation to the center of mass coordinate system due to the non-cylindrical symmetry of such orbitals.

In the case of molecules with a non-linear nature, the expansion of the bound state is performed in terms of the spherical harmonics expressed in a coordinate system tied to the molecule.

$${\varphi }_b^r\left({\mathbf{r}}_{\mathbf{2}}\right)=\sum _{l_b,\mu }{c}_{l_b\mu }^r\left(r_2\right)Y_{l_b\mu }\left({\widehat{\mathbf{r}}}_{\mathbf{2}}\right)$$

(8)

And the expansion coefficient may be expressed as

$$c_{l_b\mu }^r\left(r_2\right)=\int d{\widehat{r}}_2{Y}_{l_b\mu }\left({\widehat{\mathbf{r}}}_{\mathbf{2}}\right){\varphi }_b^r\left({\mathbf{r}}_{\mathbf{2}}\right)$$

(9)

Both for the $\pi$ orbitals of linear molecules and for orbitals of non-linear molecules, the transformation from the molecular frame to the laboratory frame is performed by the rotation operator $D_{m_b\mu }^{l_b}(\alpha ,\beta ,\gamma )$ as detailed in [20], where $\alpha$, $\beta$, and $\gamma$ are the Euler angles.

In addition to the above-presented expansion of the bound state, we employ a standard partial-wave expansion of the wavefunctions associated with the free particles involved in the process. Also, the interaction potential between the active electron and the projectile is expanded into the multi-pole series.

Since in the experiments the orientation of the molecules is usually not detected, the cross section (1) is averaged over all possible orientations to ensure a comparison with the experimental measurements. The averaging is performed in the case of $\sigma$ orbitals by taking into account the orthogonality properties of the spherical harmonics. As for $\pi$ orbitals of linear molecules and the orbitals of non-linear molecules, the orthogonality properties of the rotation operator are used. Finally, the differential cross section is obtained as a sum of cross sections characterized by a given value of the initial state’s angular momentum.

$${\displaystyle \frac{d^3{\sigma }_{av}}{d{\widehat{\mathbf{k}}}_{f}d{\widehat{\mathbf{k}}}_{e}d{E}_e}}=\sum _r\sum _{l_b,m_b}{\displaystyle \frac{{\left(2\pi \right)}^4}{E_i}}{\left|f_{l_b{m}_b}^r\right|}^2,$$

(10)

The total cross section is obtained from the above differential cross section by integrating over the angles of the scattered and ejected particles and the energy of the ejected electron. In the case of electron impact ionization, the emerging electrons are identical; therefore, by definition, the ejected one is considered the slower one, while the scattered one has greater energy. With this assumption, the integration over the ejected electron energy is performed [21] up to half of the total kinetic energy ($E=E_i-I=E_e+E_f$) of the emerging particles, where E is the sum of the energies of the ejected and scattered particles, while I is the ionization potential of the considered molecular orbital.

2.2. Triple-Differential Cross Section

Here, we define the TDCS in terms of the transition matrix element t for the ionization of a molecular orbital as in [16] for the ${\mathrm{CH}}_4$ molecule.

$${\displaystyle \frac{d^3\sigma }{d{\widehat{\mathbf{k}}}_{f}d{\widehat{\mathbf{k}}}_{e}d{E}_e}}=2{\left(2\pi \right)}^4{\displaystyle \frac{k_f{k}_e}{k_i}}{\left|t\right|}^2,$$

(11)

where the factor 2 accounts for the fact that a molecular orbital is populated by two electrons. Here, $k_i$ is the momentum of the incident projectile. The transition matrix element for the electron projectile is

$${\left|t\right|}^2={\left|t_d\right|}^2+{\left|t_e\right|}^2-\left|t_d\right|\left|t_e\right|,$$

(12)

where $t_d$ is the direct term and $t_e$ is the exchange term. These are essentially identical to (4) and (5).

The detailed calculations for the ${\mathrm{CH}}_4$ molecule are presented in [16] for the direct term of the transition matrix element. Here, we give only the final formula obtained after using the expansions presented above and also in the case of the TCS. The TDCS is written as a sum of cross sections depending on the angular momentum of the bound state.

$${\displaystyle \frac{d^3{\sigma }_{av}}{d{\widehat{\mathbf{k}}}_{f}d{\widehat{\mathbf{k}}}_{e}d{E}_e}}=2{\displaystyle \frac{64\pi }{E_i}}\sum _{l_b{m}_b\nu }{\displaystyle \frac{1}{2l_b+1}}{\left|\sum _{l_f{l}_e{l}_i\lambda }A\left(l_f{l}_e{l}_i\right)\sum _{m_f{m}_e{m}_i\mu }M(l_b{l}_f{l}_e{l}_i\lambda ;m_b{m}_f{m}_e{m}_i\mu ,\nu )\right|}^2.$$

(13)

Here, $E_i=k_i^2/2$ is the impact incident particle’s energy, while

$$A\left(l_f{l}_e{l}_i\right)=i^{l_f}{\mathrm{e}}^{i{\sigma }_{l_f}}{i}^{l_e}{\mathrm{e}}^{i{\sigma }_{l_e}}{(-i)}^{l_i}{\mathrm{e}}^{-i{\sigma }_{l_i}}$$

(14)

is a phase term and

$$\begin{array}{c}\hfill M(l_b{l}_f{l}_e{l}_i\lambda ;m_b{m}_f{m}_e{m}_i\mu ,\nu )=\sqrt{(2l_f+1)(2l_i+1)(2l_e+1)(2l_b+1)}\\ \hfill \times \left(\begin{array}{ccc}{l}_f& \lambda & l_i\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}{l}_e& l_b& \lambda \\ 0& 0& 0\end{array}\right)\\ \hfill \times \int \mathrm{d}{r}_1\mathrm{d}{r}_2{y}_{l_f}\left(r_1\right)y_{l_e}\left(r_2\right){\displaystyle \frac{r_{<}^{\lambda }}{r_{>}^{\lambda +1}}}{y}_{l_b\nu }\left(r_2\right)y_{l_i}\left(r_1\right)\\ \hfill \times {(-1)}^{m_i+\mu }\left(\begin{array}{ccc}{l}_f& \lambda & l_i\\ m_f& \mu & -m_i\end{array}\right)\left(\begin{array}{ccc}{l}_e& l_b& \lambda \\ m_e& m_b& -\mu \end{array}\right)\\ \hfill \times Y_{l_f{m}_f}^{*}\left({\widehat{\mathbf{k}}}_f\right)Y_{l_e{m}_e}^{*}\left({\widehat{\mathbf{k}}}_e\right)Y_{l_i{m}_i}\left({\widehat{\mathbf{k}}}_i\right).\end{array}$$

(15)

Here, the different quantum numbers come from the expansions used in our calculations [16]. The parentheses denote the Wigner $3j$-symbols. The $y_{l_x}$, ($x=f,e$ or i) are obtained by solving the one-electron radial Schrödinger equation for the continuum state, and $y_{l_b\nu }=r_2{c}_{l_b\nu }$.

The TDCS is averaged over all possible orientations of the molecule, using, again, the orthogonality properties of the rotation operator D. We note that these calculations may be adapted to other molecules as well [13,14,15,17,18] using the appropriate expansions and approximations.

2.3. The Models

We developed three models and used them to calculate TCSs and TDCSs in the distorted-wave formalism of the Born approximation. We named these models ES (Electron Screening), TS (Total Screening), and ${\mathrm{TS}}^{*}$, the latter being a modified version of TS. These models differ in the potentials in which the continuum wavefunctions are calculated, as detailed below for electron impact ionization.

In the ES model, the incident and scattered particles move in a zero potential; only the ejected electron is considered to move in the spherically averaged combined potential of the nuclei $V_{nuclei}$ and remaining electrons $V_{electrons}^{-}$:

$$\begin{array}{ccc}\hfill V_i& =& 0\hfill \\ \hfill V_e& =& V_{nuclei}+V_{electrons}^{-}\hfill \\ \hfill V_f& =& 0.\hfill \end{array}$$

(16)

The TS model describes the incident and scattered particles moving in the spherically averaged potential created by the molecule (nuclei and electrons), while the ejected electron experiences the averaged potential of the residual ion:

$$\begin{array}{ccc}\hfill V_i& =& V_{nuclei}+V_{electrons}\hfill \\ \hfill V_e& =& V_{nuclei}+V_{electrons}^{-}\hfill \\ \hfill V_f& =& V_{nuclei}+V_{electrons}.\hfill \end{array}$$

(17)

In these models, the ejected electron is slower than the scattered one. If this is not the case, the scattered particle moves in the field of the residual ion, and the ejected electron in the field of the neutral molecule.

The ${\mathrm{TS}}^{*}$ model is a modified version of TS; it describes differently the scattered electron. Here, both emerging particles move in the potential of the residual ion:

$$\begin{array}{ccc}\hfill V_i& =& V_{nuclei}+V_{electrons}\hfill \\ \hfill V_e& =& V_{nuclei}+V_{electrons}^{-}\hfill \\ \hfill V_f& =& V_{nuclei}+V_{electrons}^{-}.\hfill \end{array}$$

(18)

The detailed description of these models is provided in [11] for positron impact ionization and in several other studies for electron projectiles. See, for example, [14,15,16,17].

The averaging of the potentials is described in [11]. Since the recoil peak of the TDCS is influenced mainly by the nuclear potential, we briefly describe the method for the ${\mathrm{CH}}_4$ molecule. The charges of the hydrogen nuclei are distributed on a sphere with the center in the C nucleus and radius equal to the C-H ($r_{CH}$) distance. Similar considerations may be employed for other molecules by taking into account their geometry.

However, this spherically averaged nuclear potential does not lead to a proper description of the recoil peak when calculating the TDCS. The recoil peak is a result of a strong interaction between the ejected electron and the nucleus. The averaged nuclear potential is weaker because of the uniform charge distribution on a sphere. In order to increase the intensity of the electric field created by the nuclei, we also used a model in which the nuclear charge is distributed on a sphere with smaller radius.

Our simple DWBA does not include the post collision interaction between the two outgoing particles. This is particularly important in the situations when the two emerging particles move approximately in the same direction with similar velocities. In order to also obtain reliable results for these kinematic conditions, we included in some of our calculations the Coulomb distortion factor of [22]

$$CDF=G{\left|{}_{1}F_1(i\gamma ,1,-2i{k}_{fe}{r}_{fe}^{ave})\right|}^2.$$

(19)

Here, G is called the Gamow factor.

$$G=2\pi \gamma {\displaystyle \frac{exp(-2\pi \gamma )}{[1-exp(-2\pi \gamma \left)\right]}}.$$

(20)

In the above equations, ${}_{1}F_1$ is the confluent hypergeometric function, $k_{fe}=\mu v_{fe}$, and $\gamma =\pm 1/v_{fe}$ is the Sommerfeld parameter. $v_{fe}$ represents the relative velocity of the scattered projectile and ejected electron, and $\mu =1/2$ is the reduced mass of the two particles. $r_{fe}^{ave}$ is parallel to ${\mathbf{k}}_{fe}$ and is the average of the actual ejected electron-projectile distance; ${\mathbf{r}}_{fe}$. This may be expressed as

$$r_{fe}^{ave}={\displaystyle \frac{{\pi }^2}{16{ϵ}_t}}{\left(1+{\displaystyle \frac{0.627}{\pi }}\sqrt{{ϵ}_t}ln{ϵ}_t\right)}^2,$$

(21)

where ${ϵ}_t$ is the total energy of the scattered and ejected particles. The post-collision interaction is included in our calculations by multiplying the TDCS with the Coulomb distortion factor.

3. Results and Discussion

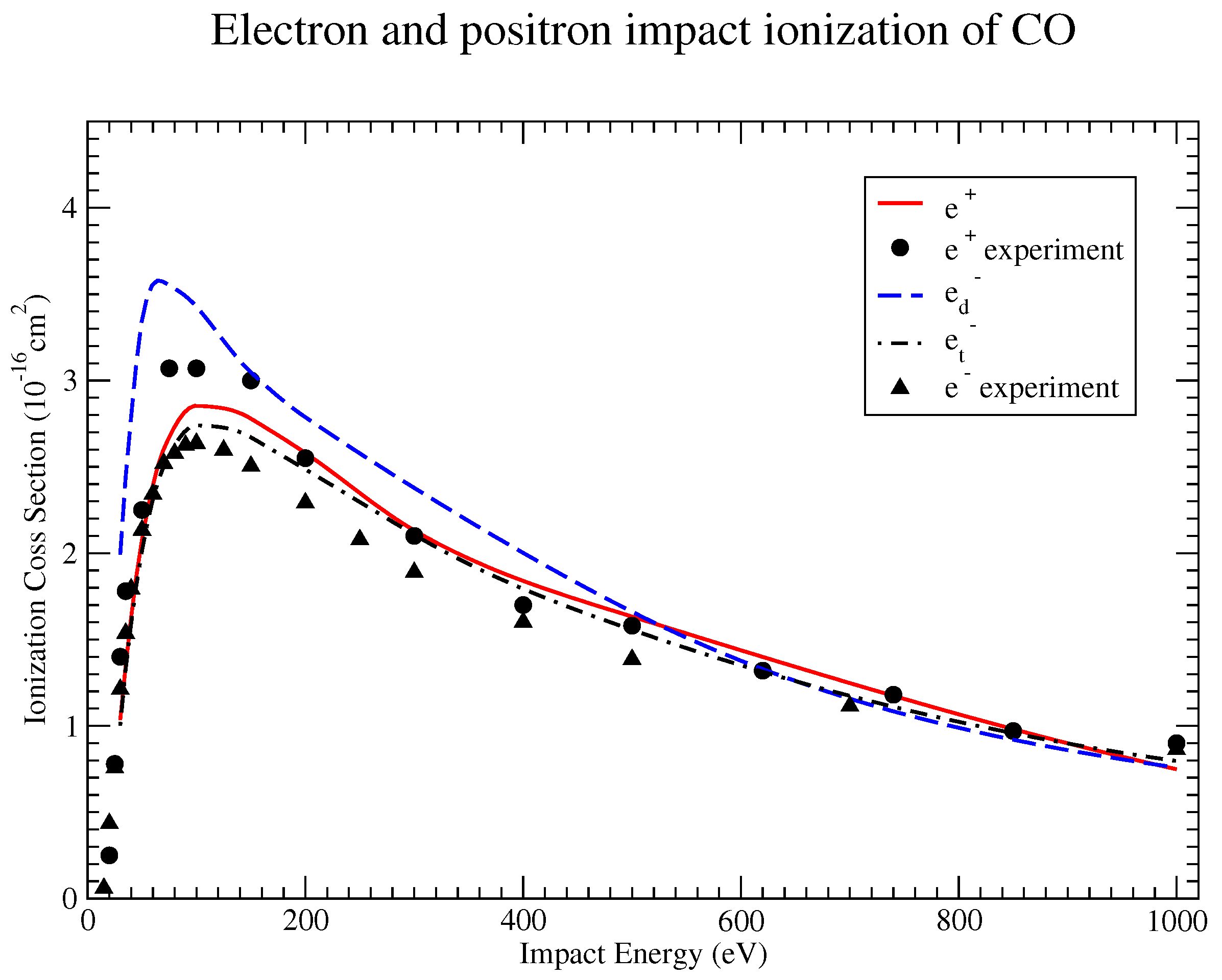
Our results obtained for the integrated total ionization cross-section of several molecules are presented in [11,12] for positron and electron projectiles. Here, we show only a few of these results, specifically the comparison of the cross-sections obtained for projectiles with opposite electric charges [12]. The best agreement with the measured cross sections was obtained by employing our ES model in the case of the N₂ and CO molecules. In both cases, the cross section is shown for a wide range of the projectile energy. In the case of electron projectiles, we calculated the TCS with and without the exchange interaction included. In the figures, $e_d^{-}$ is the cross section determined without using the exchange term in (3), while $e_t^{-}$ includes both the direct and exchange terms. $e^{+}$ is the TCS for the positron impact case.

Figure 1 and Figure 2 show a similar behavior for both the N₂ and CO molecules. For positron impact ionization, the calculated TCSs agree very well with the measurements. The direct TCS for electrons overestimates the experimental data below 500 eV. This shows that the inclusion of the exchange interaction is of crucial importance. When this interaction is included, the discrepancy between theory and measured data practically disappears as shown by the $e_t^{-}$ curve. Figure 1 and Figure 2 show that the effect of the projectile charge is more important at lower energies, especially around the peak, which is higher for positron TCSs. For fast projectiles, the positron and electron cross-sections seem to converge, suggesting a much-reduced dependence on the projectile charge.

We employed the models presented above in Section 2.3 to calculate TDCSs for both projectile types. Across several studies, we analyzed molecular targets like H₂ [13], N₂ [14], H₂O [15], ${\mathrm{CH}}_4$ [16,18], and ${\mathrm{NH}}_3$ [17,18]. TDCSs are an important part of the tool-set of theoretical and experimental studies. They give a complete description of the ionization process for a given orientation of the outgoing particles momenta and the electron energy. 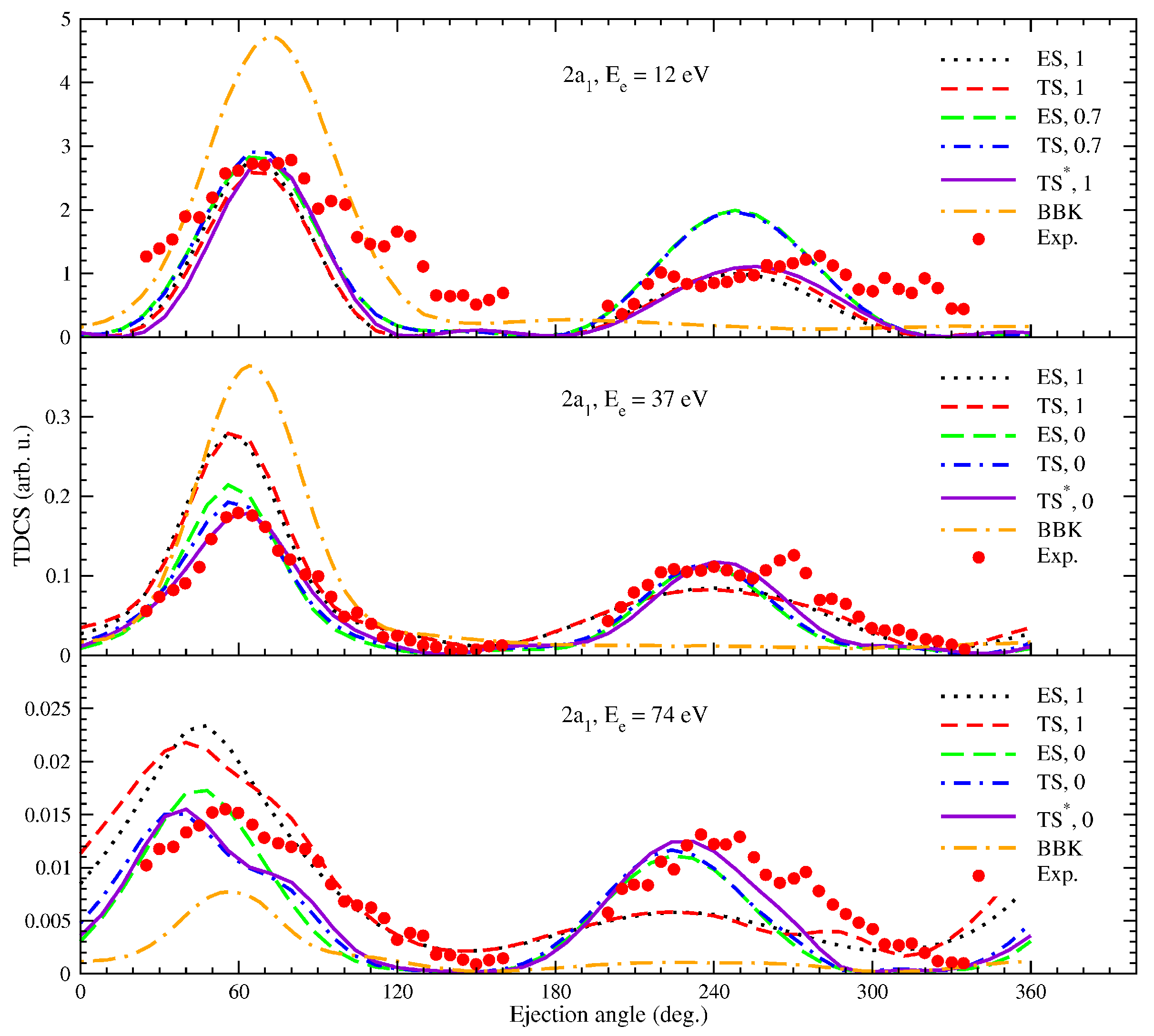In Figure 3 and Figure 4, we show a few results from [16], where we investigated the ionization of methane impacted by electrons. TDCSs were determined for the $2a_1$ and $1t_2$ molecular orbitals, respectively. Here, the energy of the scattered particle is $E_f=500$ eV, while the scattering angle was set to −$6^{\circ }$. We calculated the TDCS for $E_e=12$, 37, and 74 eV and compared our results with the measurements of [27] and the BBK (Brauner, Briggs, and Klar) model from the same study. As mentioned above in Section 2.2, the appearance of the backward peak is the result of a strong electron–nucleus interaction. However, our averaging method leads to a much weaker interaction. To overcome this deficiency of the model, we calculated the cross section also for an enhanced nuclear potential by systematically decreasing the radius of the sphere during the averaging process. In the figure legend, we show beside the name of the model the fraction of the initial radius for a particular case. We note that the experimental TDCS [27] was normalized to the forward peak of the ${\mathrm{TS}}^{*}$ model. Overall, the ${\mathrm{TS}}^{*}$ model shows the best agreement with the experimental measurements. For the $2a_1$ orbital in Figure 3, at the lowest ejected electron energy, this model provides the correct binary-to-recoil peak ratio for the original radius of the nuclear-charge sphere. At higher energies, all the nuclear charge need to be moved to the molecular center (${\mathrm{TS}}^{*},0$ model) to obtain the best ratio, although at $E_e=74$ eV, the peaks are observed at smaller angles than the experimental ones. Since the energy of the ejected electron is larger in this case, the post-collision interaction may play a more prominent role, causing the observed shift. We note that the PCI is not included in our calculations at this point. The BBK model shows a better positioning of the binary peak in this case but entirely lacks the backward peak.

Figure 4 shows a larger binary-to-recoil peak ratio for the $1t_2$ orbital. Our ${\mathrm{TS}}^{*}$ model, in general, describes well the behavior of the experimental data. Also, the position of the binary peak is much closer to the experimental one, even at high ejected electron energies.

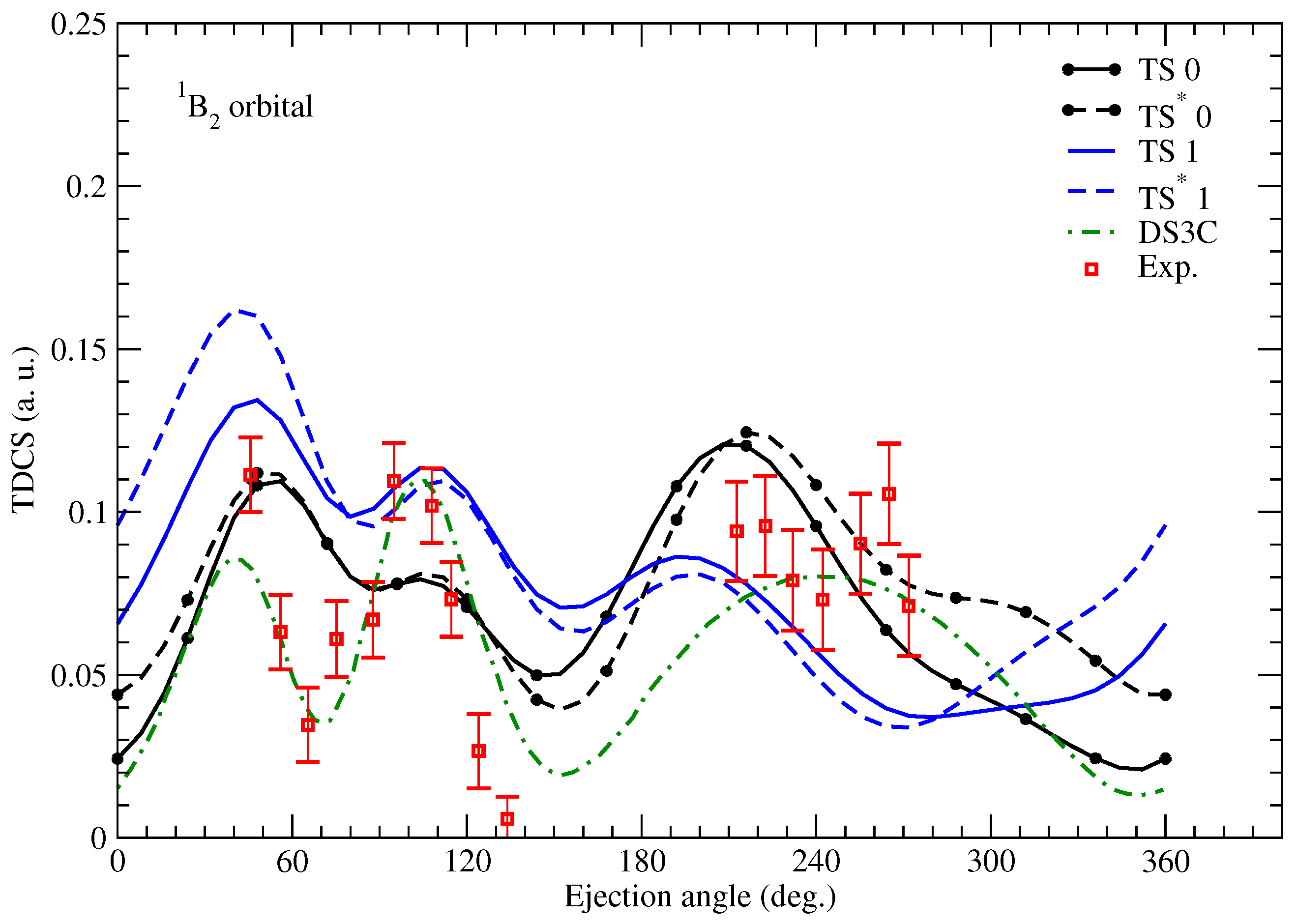
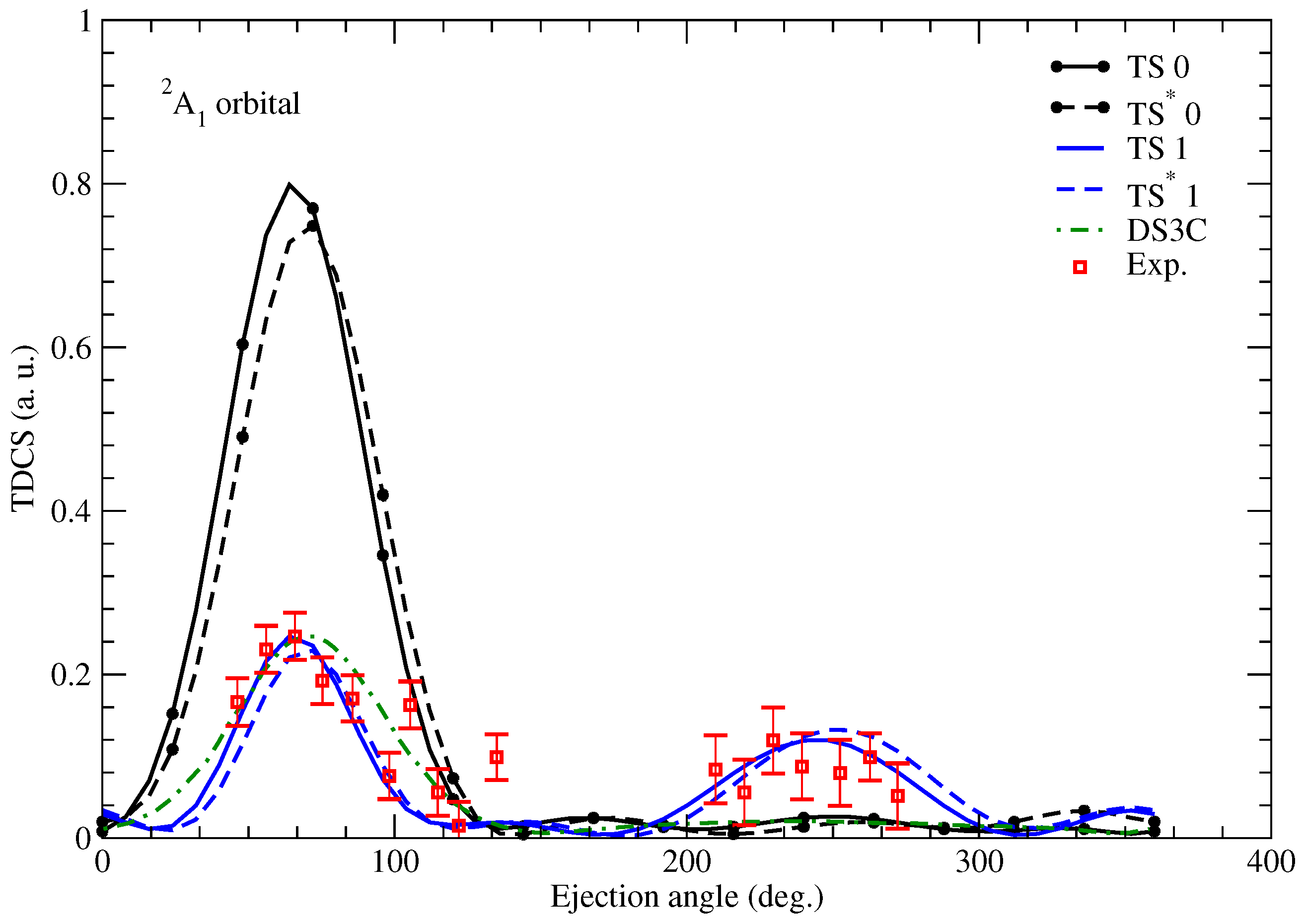
Since living tissues contain a large percentage of water, the ionization of this molecule is of great interest in radiology studies, for example. Below, we show a few results from [15] obtained for electron projectiles, since, in this case, experimental data were also available, unlike for positron projectiles. We calculated TDCSs employing the TS and ${\mathrm{TS}}^{*}$ models. The TDCSs were calculated for the $1B_1$, $3A_1$, $1B_2$, and $2A_1$ molecular orbitals shown in Figure 5, Figure 6, Figure 7 and Figure 8. The obtained results were compared to the measured data of [28] and the TDCSs determined with the DS3C model (dynamic screening of the three two-body Coulomb interaction) [29]. We used a projectile with an impact energy of $E_i=250$ eV, where $E_e=10$ eV, except for the $3A_1$ orbital, where $E_e=8$ eV. The projectile is observed at an angle of ${\theta }_f={15}^{\circ }$. It is worth mentioning that for water, we obtain a two-sphere structure as we rotate the molecule around the center of mass. The charge of the O nucleus is distributed on the smaller one, and the charge of the H nuclei are evenly distributed on the larger sphere.

In Figure 5, we obtain a qualitative agreement with the measured cross sections. At the forward peak, all our models show a double peak, characteristic of p-like orbitals. The binary-to-recoil peak ratio is closer to the ratio of the DS3C model for the TS model with the original radii of the spheres. No experimental recoil peak was measured for this orbital. However, our calculated cross section shows the recoil peak at lower angles compared to the DS3C cross section. The recoil peaks of the TS and ${\mathrm{TS}}^{*}$ models are much larger if all nuclear charges are concentrated at the center of mass. The position of this enhanced recoil peak is similar for the DS3C model, especially for the ${\mathrm{TS}}^{*}$ model. A similar behavior is observed for the $1B_2$ orbital in Figure 6. The recoil peaks calculated for the (TS, 0) and (${\mathrm{TS}}^{*}$, 0) cases show some agreement with the experimental one. In Figure 7, we show the results for the $3A_1$ orbital. Our models do not predict the double-peak structure of the experimental binary region. The DS3C shows, again, a double peak at the binary region for this orbital. We analyzed the source of the discrepancy in [15], where it was concluded that a dominant monopole term ($l_b=0$) is responsible for the single peak in our data. It was also shown that the cross section of the dipole term ($l_b=1$) shows a split forward region. For the almost spherical $2A_1$ orbital, we observe in Figure 8 a very good agreement of our calculated (TS, 1) and (${\mathrm{TS}}^{*}$, 1) cross sections with the experimental data. Our (TS, 0) and (${\mathrm{TS}}^{*}$, 0) models predict a flat curve at the recoil region, unlike for the other orbitals. A possible explanation may be that the electrons are localized around the nuclei with a high probability. This may lead to a stronger interaction with the nuclear core when we consider the nuclei at their original position, compared to the case when they are taken out from this high-electron-density region—see the (TS, 0) case.

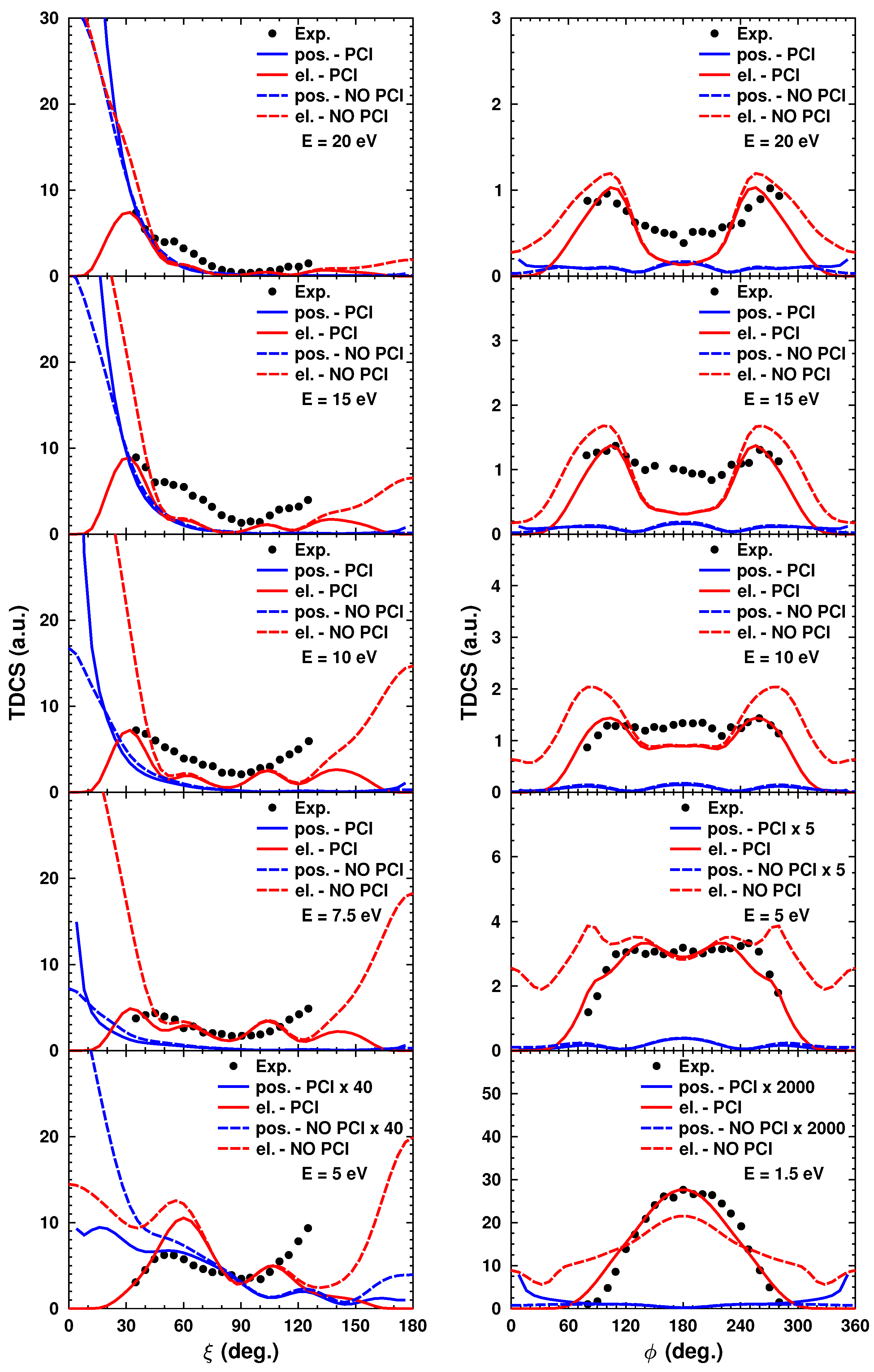
Finally, we show some of our results for the NH₃ molecule from [17]. We calculated TDCSs for both projectile types and for several molecular orbitals. Here, we show a few results for the $3a_1$ orbital. This study is somewhat different from the previous ones, since, here, we consider a coplanar geometry and a perpendicular geometry. In the latter case, the particles are ejected perpendicular to the incoming projectile’s direction. The scattered and the ejected particles emerge at the same angle (measured relative to the projectile trajectory) and with equal energy ($E_e=E_f<20$ eV). We calculated the TDCSs using the ${\mathrm{TS}}^{*}$ model. At such a low and symmetric energy, it is very important to include the PCI. We included this interaction through the Coulomb distortion factor as detailed above in Section 2.3. Figure 9 shows the calculated cross sections with the PCI included and without this interaction. Our results for electron projectiles are evaluated against the measurements of [30]. In Figure 9, we plot the TDCSs calculated in the scattering and perpendicular planes (left and right columns, respectively). The results show that in both planes, the inclusion of the PCI is essential. Without the PCI, the agreement with the measured data is considerably poorer for electron projectiles. No experimental data were available for positron impact ionization. Figure 9 shows that in the scattering plane, for positron TDCSs, there is noticeable intensity only at very low ejection angles, with a narrowing intensity width for lower energies. In contrast, the forward peak of the electron TDCS migrates toward larger ejection angles as the energy is decreased. The somewhat opposite behavior for the two projectile types is related to the enhanced PCI at very low energies. In the first case, the positron drags the electron toward the incident direction. For an electron projectile, we have a strong repulsion with the ejected electron, which causes the increase in the ejection angle at very low energies. In the perpendicular plane, we observe that the calculated electron and experimental cross sections evolve from a two-peak structure to a single-peak structure with decreasing electron energies. This effect is also attributed to the post-collision interaction. The electrons at low energies emerge at a larger mutual angle due to the strong repulsion between them. Except for the lowest energy, the positron cross section shows a central peak, which may be attributed to an enhanced positron–nucleus interaction. The appearance of the central peak may be the consequence of a complex collision process. As the positron is scattered by the nuclei, it may knock out an electron, which may undergo a backscattering by the nuclear core. The lack of the central peak at the lowest energy may be related to the overwhelming dominance of the PCI.

4. Conclusions

We have reviewed our group’s more important theoretical studies on the ionization of molecules by electron and positron impacts. The method used was the distorted-wave Born approximation, which is relatively simple and does not account properly for the few-body dynamics that occur in these processes. However, by a proper description of the wavefunction associated with the projectile and with the active electron, we could obtain in most of the studied cases results in good agreement with the experiments. We present the obtained total ionization cross sections for the N₂ and the CO molecules. The TCSs have the advantage that we can compare our results with experimental data for both projectiles, electrons and positrons. Our results calculated with the ES model (which considers plane waves to the incoming particle) are in good agreement with the experimental data for both projectiles. The results for electrons (considering the exchange effects) at low impact energies (below 200 eV) are lower than the cross sections for positrons. The differential cross sections are much more sensitive to the used model. A benchmark for these studies can be the TDCSs of methane by electron impact, where precise experimental data with good statistics are available [27]. The considered kinematics is an asymmetric one, with one of the emerging electrons being much faster than the other one, so the post-collision interaction may be neglected. We best reproduced the experimental data with our TS* model. Since the spherical averaging of the nuclear potential does not lead to a strong electric field, in order to also obtain a correct binary-to-recoil peak ratio for ejected electrons with a higher energy, we increased the nuclear potential by modifying the radius of the sphere, where the nuclear charge is distributed. For this target, the agreement of our calculations with the experimental data is remarkable. In the case of the water target, the experimental data for TDCS are much more sparse. In this case, we also investigated how the binary-to-recoil peak ratio depends on the nuclear potential, and the effect was huge. We could compare this to the experimental data only in the case of two orbitals, and it seemed that the original spherical averaging led to the best results. This can be explained by the low energy of the ejected electron. As a conclusion, increasing the nuclear potential relative to that obtained with the spherical averaging is necessary only for ejected electrons with a higher energy. Our study on the NH₃ molecule is very different because it considers doubly symmetric kinematics, particles leaving with the same velocity. In these conditions, the post-collision interaction of the emerging particles is essential, and we took it into account in our calculations. We compared the TDCSs obtained with electron and positron projectiles. Because of the different interactions of the two emerging particles in the two cases (repulsive and attractive), the obtained results are very different for both the scattering and the perpendicular planes. In the scattering plane for ejection angles close to zero, the positron cross section increases drastically, and the electron cross sections tend to zero. In the perpendicular plane, the cross sections for positron projectiles are very small relative to those for electrons. Our results are in good agreement with the experimental data for electron projectiles. Unfortunately, for positron projectiles, there are not yet experimental data published for the TDCSs for these kinematic conditions.