Many-Body Effects in a Composite Bosonic Josephson Junction
Abstract
1. Introduction
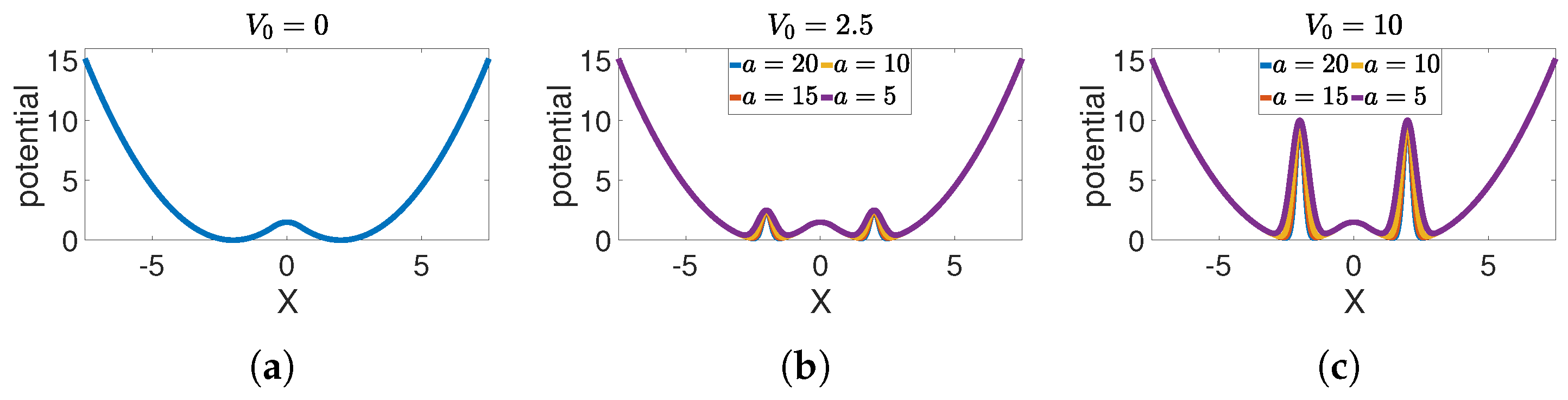
2. Formalism
3. Results and Discusson
3.1. Many-Body Dynamics
3.1.1. Survival Probability
3.1.2. Occupation Numbers
3.1.3. Many-Particle Variances
3.2. Universality of Fragmentation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Numerical Convergence of Dynamical Quantities
Appendix A.2. Convergence of Fragmentation and Depletion



Appendix A.3. Convergence of Many-Particle Position and Momentum Variances

References
- Cormick, C.; Ermann, L. Ground state of composite bosons in low-dimensional graphs. Phys. Rev. A 2023, 107, 043324. [Google Scholar] [CrossRef]
- Tao, Z.; Huang, W.; Niu, J.; Zhang, L.; Ke, Y.; Gu, X.; Lin, L.; Qiu, J.; Sun, X.; Yang, X.; et al. Interaction-induced topological pumping in a solid-state quantum system. arxiv 2023, arXiv:2303.04582. [Google Scholar]
- Benatti, F.; Carollo, F.; Floreanini, R.; Narnhofer, H.; Valiera, F. A quantum fluctuation description of charge qubits. arxiv 2023, arXiv:2304.13351. [Google Scholar] [CrossRef]
- Lewis, D.; Moutinho, J.P.; Costa, A.; Omar, Y.; Bose, S. Low-Dissipation Data Bus via Coherent Quantum Dynamics. arXiv 2023, arXiv:2304.02391. [Google Scholar] [CrossRef]
- Sakmann, K.; Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Exact Quantum Dynamics of a Bosonic Josephson Junction. Phys. Rev. Lett. 2009, 103, 220601. [Google Scholar] [CrossRef]
- Haldar, S.K.; Alon, O.E. Impact of the range of the interaction on the quantum dynamics of a bosonic Josephson junction. Chem. Phys. 2018, 509, 72–80. [Google Scholar] [CrossRef]
- Bhowmik, A.; Haldar, S.K.; Alon, O.E. Impact of the transverse direction on the many-body tunneling dynamics in a two-dimensional bosonic Josephson junction. Sci. Rep. 2020, 10, 21476. [Google Scholar] [CrossRef]
- Josephson, B. Possible new effects in superconductive tunnelling. Phys. Lett. 1962, 1, 251–253. [Google Scholar] [CrossRef]
- Smerzi, A.; Fantoni, S.; Giovanazzi, S.; Shenoy, S.R. Quantum Coherent Atomic Tunneling between Two Trapped Bose-Einstein Condensates. Phys. Rev. Lett. 1997, 79, 4950–4953. [Google Scholar] [CrossRef]
- Albiez, M.; Gati, R.; Fölling, J.; Hunsmann, S.; Cristiani, M.; Oberthaler, M.K. Direct Observation of Tunneling and Nonlinear Self-Trapping in a Single Bosonic Josephson Junction. Phys. Rev. Lett. 2005, 95, 010402. [Google Scholar] [CrossRef]
- Gati, R.; Oberthaler, M.K. A bosonic Josephson junction. J. Phys. B At. Mol. Opt. Phys. 2007, 40, R61. [Google Scholar] [CrossRef]
- LeBlanc, L.J.; Bardon, A.B.; McKeever, J.; Extavour, M.H.T.; Jervis, D.; Thywissen, J.H.; Piazza, F.; Smerzi, A. Dynamics of a Tunable Superfluid Junction. Phys. Rev. Lett. 2011, 106, 025302. [Google Scholar] [CrossRef] [PubMed]
- Gillet, J.; Garcia-March, M.A.; Busch, T.; Sols, F. Tunneling, self-trapping, and manipulation of higher modes of a Bose-Einstein condensate in a double well. Phys. Rev. A 2014, 89, 023614. [Google Scholar] [CrossRef]
- Burchianti, A.; Fort, C.; Modugno, M. Josephson plasma oscillations and the Gross-Pitaevskii equation: Bogoliubov approach versus two-mode model. Phys. Rev. A 2017, 95, 023627. [Google Scholar] [CrossRef]
- Hou, J.; Luo, X.W.; Sun, K.; Bersano, T.; Gokhroo, V.; Mossman, S.; Engels, P.; Zhang, C. Momentum-Space Josephson Effects. Phys. Rev. Lett. 2018, 120, 120401. [Google Scholar] [CrossRef] [PubMed]
- Milburn, G.J.; Corney, J.; Wright, E.M.; Walls, D.F. Quantum dynamics of an atomic Bose-Einstein condensate in a double-well potential. Phys. Rev. A 1997, 55, 4318–4324. [Google Scholar] [CrossRef]
- Sakmann, K.; Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Universality of fragmentation in the Schrödinger dynamics of bosonic Josephson junctions. Phys. Rev. A 2014, 89, 023602. [Google Scholar] [CrossRef]
- Theel, F.; Keiler, K.; Mistakidis, S.I.; Schmelcher, P. Entanglement-assisted tunneling dynamics of impurities in a double well immersed in a bath of lattice trapped bosons. New J. Phys. 2020, 22, 023027. [Google Scholar] [CrossRef]
- Vargas, J.; Nuske, M.; Eichberger, R.; Hippler, C.; Mathey, L.; Hemmerich, A. Orbital Many-Body Dynamics of Bosons in the Second Bloch Band of an Optical Lattice. Phys. Rev. Lett. 2021, 126, 200402. [Google Scholar] [CrossRef]
- Sakmann, K.; Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Quantum dynamics of attractive versus repulsive bosonic Josephson junctions: Bose-Hubbard and full-Hamiltonian results. Phys. Rev. A 2010, 82, 013620. [Google Scholar] [CrossRef]
- Khezri, M.; Dressel, J.; Korotkov, A.N. Qubit measurement error from coupling with a detuned neighbor in circuit QED. Phys. Rev. A 2015, 92, 052306. [Google Scholar] [CrossRef]
- Bhowmik, A.; Alon, O.E. Interference of longitudinal and transversal fragmentations in the Josephson dynamics of Bose-Einstein condensates. arXiv 2022, arXiv:2207.05513. [Google Scholar]
- Haldar, S.K.; Alon, O.E. Many-body quantum dynamics of an asymmetric bosonic Josephson junction. New J. Phys. 2019, 21, 103037. [Google Scholar] [CrossRef]
- Bhowmik, A.; Alon, O.E. Longitudinal and transversal resonant tunneling of interacting bosons in a two-dimensional Josephson junction. Sci. Rep. 2022, 12, 627. [Google Scholar] [CrossRef] [PubMed]
- Klaiman, S.; Streltsov, A.I.; Alon, O.E. Uncertainty product of an out-of-equilibrium many-particle system. Phys. Rev. A 2016, 93, 023605. [Google Scholar] [CrossRef]
- Mondal, D.; Sinha, S.; Ray, S.; Kroha, J.; Sinha, S. Classical route to ergodicity and scarring phenomena in a two-component Bose-Josephson junction. Phys. Rev. A 2022, 106, 043321. [Google Scholar] [CrossRef]
- Zibold, T.; Nicklas, E.; Gross, C.; Oberthaler, M.K. Classical Bifurcation at the Transition from Rabi to Josephson Dynamics. Phys. Rev. Lett. 2010, 105, 204101. [Google Scholar] [CrossRef]
- Abbarchi, M.; Amo, A.; Sala, V.G.; Solnyshkov, D.D.; Flayac, H.; Ferrier, L.; Sagnes, I.; Galopin, E.; Lemaître, A.; Malpuech, G.; et al. Macroscopic quantum self-trapping and Josephson oscillations of exciton polaritons. Nat. Phys. 2013, 9, 275–279. [Google Scholar] [CrossRef]
- Valtolina, G.; Burchianti, A.; Amico, A.; Neri, E.; Xhani, K.; Seman, J.A.; Trombettoni, A.; Smerzi, A.; Zaccanti, M.; Inguscio, M.; et al. Josephson effect in fermionic superfluids across the BEC-BCS crossover. Science 2015, 350, 1505–1508. Available online: https://www.science.org/doi/10.1126/science.aac9725 (accessed on 13 September 2024). [CrossRef]
- Strzys, M.P.; Anglin, J.R. Four-mode Bose-Hubbard model with two greatly differing tunneling rates as a model for the Josephson oscillation of heat. Phys. Rev. A 2010, 81, 043616. [Google Scholar] [CrossRef]
- Amico, L.; Birkl, G.; Boshier, M.; Kwek, L.C. Focus on atomtronics-enabled quantum technologies. New J. Phys. 2017, 19, 020201. [Google Scholar] [CrossRef]
- Amico, L.; Boshier, M.; Birkl, G.; Minguzzi, A.; Miniatura, C.; Kwek, L.C.; Aghamalyan, D.; Ahufinger, V.; Anderson, D.; Andrei, N.; et al. Roadmap on Atomtronics: State of the art and perspective. AVS Quantum Sci. 2021, 3, 039201. Available online: https://pubs.aip.org/avs/aqs/article/3/3/039201/570637/Roadmap-on-Atomtronics-State-of-the-art-and (accessed on 13 September 2024). [CrossRef]
- Amico, L.; Anderson, D.; Boshier, M.; Brantut, J.P.; Kwek, L.C.; Minguzzi, A.; von Klitzing, W. Colloquium: Atomtronic circuits: From many-body physics to quantum technologies. Rev. Mod. Phys. 2022, 94, 041001. [Google Scholar] [CrossRef]
- Franzosi, R.; Penna, V. Chaotic behavior, collective modes, and self-trapping in the dynamics of three coupled Bose-Einstein condensates. Phys. Rev. E 2003, 67, 046227. [Google Scholar] [CrossRef] [PubMed]
- Dey, A.; Cohen, D.; Vardi, A. Adiabatic Passage through Chaos. Phys. Rev. Lett. 2018, 121, 250405. [Google Scholar] [CrossRef]
- Wittmann W., K.; Castro, E.R.; Foerster, A.; Santos, L.F. Interacting bosons in a triple well: Preface of many-body quantum chaos. Phys. Rev. E 2022, 105, 034204. [Google Scholar] [CrossRef]
- Chianca, C.; Olsen, M. Quantum dynamics of a four-well Bose-Hubbard model with two different tunneling rates. Phys. Rev. A 2011, 83, 043607. [Google Scholar] [CrossRef]
- Khripkov, C.; Vardi, A. Coherence oscillations between weakly coupled Bose-Hubbard dimers. Phys. Rev. A 2014, 89, 053629. [Google Scholar] [CrossRef]
- Karmakar, S.; Keshavamurthy, S. Arnold web and dynamical tunneling in a four-site Bose–Hubbard model. Phys. D Nonlinear Phenom. 2021, 427, 133006. [Google Scholar] [CrossRef]
- Fölling, S.; Trotzky, S.; Cheinet, P.; Feld, M.; Saers, R.; Widera, A.; Müller, T.; Bloch, I. Direct observation of second-order atom tunnelling. Nature 2007, 448, 1029–1032. [Google Scholar] [CrossRef]
- Caliga, S.C.; Straatsma, C.J.E.; Anderson, D.Z. Transport dynamics of ultracold atoms in a triple-well transistor-like potential. New J. Phys. 2016, 18, 025010. [Google Scholar] [CrossRef]
- Bloch, I. Ultracold quantum gases in optical lattices. Nat. Phys. 2005, 1, 23–30. [Google Scholar] [CrossRef]
- Matthews, M.R.; Anderson, B.P.; Haljan, P.C.; Hall, D.S.; Holland, M.J.; Williams, J.E.; Wieman, C.E.; Cornell, E.A. Watching a Superfluid Untwist Itself: Recurrence of Rabi Oscillations in a Bose-Einstein Condensate. Phys. Rev. Lett. 1999, 83, 3358–3361. [Google Scholar] [CrossRef]
- Myatt, C.J.; Burt, E.A.; Ghrist, R.W.; Cornell, E.A.; Wieman, C.E. Production of Two Overlapping Bose-Einstein Condensates by Sympathetic Cooling. Phys. Rev. Lett. 1997, 78, 586–589. [Google Scholar] [CrossRef]
- Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Role of Excited States in the Splitting of a Trapped Interacting Bose-Einstein Condensate by a Time-Dependent Barrier. Phys. Rev. Lett. 2007, 99, 030402. [Google Scholar] [CrossRef]
- Alon, O.E.; Streltsov, A.I.; Cederbaum, L.S. Multiconfigurational time-dependent Hartree method for bosons: Many-body dynamics of bosonic systems. Phys. Rev. A 2008, 77, 033613. [Google Scholar] [CrossRef]
- Bernier, J.S.; Kollath, C.; Georges, A.; De Leo, L.; Gerbier, F.; Salomon, C.; Köhl, M. Cooling fermionic atoms in optical lattices by shaping the confinement. Phys. Rev. A 2009, 79, 061601. [Google Scholar] [CrossRef]
- Grond, J.; Betz, T.; Hohenester, U.; Mauser, N.J.; Schmiedmayer, J.; Schumm, T. The Shapiro effect in atomchip-based bosonic Josephson junctions. New J. Phys. 2011, 13, 065026. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Bruder, C. Dynamics of Hubbard Hamiltonians with the multiconfigurational time-dependent Hartree method for indistinguishable particles. Phys. Rev. A 2016, 94, 013616. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Bruder, C. Fragmented Superradiance of a Bose-Einstein Condensate in an Optical Cavity. Phys. Rev. Lett. 2017, 118, 013603. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Diorico, F.S.; Wu, R.; Molignini, P.; Papariello, L.; Lin, R.; Lévêque, C.; Exl, L.; Tsatsos, M.C.; Chitra, R.; et al. Many-body physics in two-component Bose–Einstein condensates in a cavity: Fragmented superradiance and polarization. New J. Phys. 2018, 20, 055006. [Google Scholar] [CrossRef]
- Chatterjee, B.; Tsatsos, M.C.; Lode, A.U.J. Correlations of strongly interacting one-dimensional ultracold dipolar few-boson systems in optical lattices. New J. Phys. 2019, 21, 033030. [Google Scholar] [CrossRef]
- Cosme, J.G.; Andersen, M.F.; Brand, J. Interaction blockade for bosons in an asymmetric double well. Phys. Rev. A 2017, 96, 013616. [Google Scholar] [CrossRef]
- Schurer, J.M.; Negretti, A.; Schmelcher, P. Capture dynamics of ultracold atoms in the presence of an impurity ion. New J. Phys. 2015, 17, 083024. [Google Scholar] [CrossRef]
- Lévêque, C.; Madsen, L.B. Time-dependent restricted-active-space self-consistent-field theory for bosonic many-body systems. New J. Phys. 2017, 19, 043007. [Google Scholar] [CrossRef]
- Katsimiga, G.C.; Mistakidis, S.I.; Koutentakis, G.M.; Kevrekidis, P.G.; Schmelcher, P. Many-body quantum dynamics in the decay of bent dark solitons of Bose–Einstein condensates. New J. Phys. 2017, 19, 123012. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Lévêque, C.; Madsen, L.B.; Streltsov, A.I.; Alon, O.E. Colloquium: Multiconfigurational time-dependent Hartree approaches for indistinguishable particles. Rev. Mod. Phys. 2020, 92, 011001. [Google Scholar] [CrossRef]
- Dutta, S.; Lode, A.U.J.; Alon, O.E. Fragmentation and correlations in a rotating Bose–Einstein condensate undergoing breakup. Sci. Rep. 2023, 13, 3343. [Google Scholar] [CrossRef]
- Löwdin, P.O. Quantum Theory of Many-Particle Systems. I. Physical Interpretations by Means of Density Matrices, Natural Spin-Orbitals, and Convergence Problems in the Method of Configurational Interaction. Phys. Rev. 1955, 97, 1474–1489. [Google Scholar] [CrossRef]
- Sakmann, K.; Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Reduced density matrices and coherence of trapped interacting bosons. Phys. Rev. A 2008, 78, 023615. [Google Scholar] [CrossRef]
- Penrose, O.; Onsager, L. Bose-Einstein Condensation and Liquid Helium. Phys. Rev. 1956, 104, 576–584. [Google Scholar] [CrossRef]
- Nozières, P.; Saint James, D. Particle vs. pair condensation in attractive Bose liquids. J. Phys. Fr. 1982, 43, 1133–1148. [Google Scholar] [CrossRef]
- Noziéres, P. Some Comments on Bose–Einstein Condensation. In Bose-Einstein Condensation; Griffin, A., Snoke, D.W., Stringari, S., Eds.; Cambridge University Press: Cambridge, UK, 1995; pp. 15–30. [Google Scholar] [CrossRef]
- Spekkens, R.W.; Sipe, J.E. Spatial fragmentation of a Bose-Einstein condensate in a double-well potential. Phys. Rev. A 1999, 59, 3868–3877. [Google Scholar] [CrossRef]
- Mueller, E.J.; Ho, T.L.; Ueda, M.; Baym, G. Fragmentation of Bose-Einstein condensates. Phys. Rev. A 2006, 74, 033612. [Google Scholar] [CrossRef]
- Grond, J.; Streltsov, A.I.; Cederbaum, L.S.; Alon, O.E. Excitation spectra of fragmented condensates by linear response: General theory and application to a condensate in a double-well potential. Phys. Rev. A 2012, 86, 063607. [Google Scholar] [CrossRef]
- Lieb, E.H.; Seiringer, R.; Yngvason, J. Bosons in a trap: A rigorous derivation of the Gross-Pitaevskii energy functional. Phys. Rev. A 2000, 61, 043602. [Google Scholar] [CrossRef]
- Lieb, E.H.; Seiringer, R. Proof of Bose-Einstein Condensation for Dilute Trapped Gases. Phys. Rev. Lett. 2002, 88, 170409. [Google Scholar] [CrossRef]
- Erdős, L.; Schlein, B.; Yau, H.T. Rigorous Derivation of the Gross-Pitaevskii Equation. Phys. Rev. Lett. 2007, 98, 040404. [Google Scholar] [CrossRef]
- Erdős, L.; Schlein, B.; Yau, H.T. Derivation of the cubic non-linear Schrödinger equation from quantum dynamics of many-body systems. Invent. Math. 2006, 167, 515–614. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haldar, S.K.; Bhowmik, A. Many-Body Effects in a Composite Bosonic Josephson Junction. Atoms 2024, 12, 66. https://doi.org/10.3390/atoms12120066
Haldar SK, Bhowmik A. Many-Body Effects in a Composite Bosonic Josephson Junction. Atoms. 2024; 12(12):66. https://doi.org/10.3390/atoms12120066
Chicago/Turabian StyleHaldar, Sudip Kumar, and Anal Bhowmik. 2024. "Many-Body Effects in a Composite Bosonic Josephson Junction" Atoms 12, no. 12: 66. https://doi.org/10.3390/atoms12120066
APA StyleHaldar, S. K., & Bhowmik, A. (2024). Many-Body Effects in a Composite Bosonic Josephson Junction. Atoms, 12(12), 66. https://doi.org/10.3390/atoms12120066




