Energy Shift of the Atomic Emission Lines of He-like Ions Subject to Outside Dense Plasma

Abstract

We present an extension of our study of the energy shift of the atomic emissions subject to charged-neutral outside dense plasma following the good agreement between the experimental measurements and our recent theoretical estimates for the $\alpha$ and $\beta$ emission lines of a number of H-like and He-like ions. In particular, we are able to further demonstrate that the plasma-induced transition energy shift could indeed be interpolated by the simple quasi-hydrogenic picture based on the application of the Debye–Hückel (DH) approximation for the $n=3$ to $n=2$ transitions of the He-like ions. Our theoretically estimated redshifts of those emissions may offer the impetus for additional experimental measurement to facilitate the diagnostic efforts in the determination of the temperature and density of the dense plasma.

1. Introduction

By carefully applying the spatial and temporal criteria of the Debye–Hückel (DH) approximation [1,2] to the atomic transitions subject to the charged-neutral outside dense plasma, we have shown recently that the ratio $R=\Delta \omega /{\omega }_0$ of the energy shifts $\Delta \omega$ from the plasma-free transition energy ${\omega }_0$ of the $\alpha$ and $\beta$ emission lines of a number of H-like and He-like ions could be expressed conveniently and approximately by a simple polynomial in terms of the reduced Debye length $\lambda$, i.e.,

$$\begin{array}{c}\hfill R(\lambda ;a,b,c)=a/{\lambda }^2+b/\lambda +c,\end{array}$$

(1)

where a, b, and c are three fitting coefficients which could be determined by the theoretical calculations [3,4,5]. The reduced Debye length $\lambda$ is given by

$$\begin{array}{c}\hfill \lambda =Z_{eff}D,\end{array}$$

(2)

where $Z_{eff}=Z-1$ is the effective nuclear charge for He-like ions and D is the Debye length in unit of the Bohr radius $a_0$ defined in terms of the ratio of the temperature $kT$ (in units of eV) and the plasma density N (in units of ${10}^{22}$ cm${}^{-3}$), i.e., [2,3,5]

$$\begin{array}{c}\hfill D=1.4048{\left(\frac{kT}{N}\right)}^{1/2}{a}_0.\end{array}$$

(3)

We should note that the outside plasma density $N=Z_{ion}{N}_{ion}=N_{electron}$ is the total charge density at a distance far away from the atom located at $r=0$, where $Z_{ion}=Z-1$ for the He-like ion and $N_{ion}$ is the ion density (i.e., number of ions per unit volume). More details of the Debye length D are given in Section 1.4 of [2]. We should point out that the DH approximation, based on the classical Maxwell–Boltzmann statistics, is known to work well for the gas-discharged plasma with relatively low density [2].

Our investigation, based on the DH approximation, and qualitatively, the quasi-hydrogenic picture, has led to theoretical estimation in agreement with the early measurement [6] from the laser-generated plasma at a temperature of around 300 eV with a density of $(5-10)\times {10}^{23}$ cm${}^{-3}$ (see Figure 3 of [4]). Subsequently, we have reported the agreement between our calculated $\Delta \omega$ and two more recent experimental measurements (see Figure 3 of [5]) from (i) the picosecond time-resolved experiment for the $\alpha$ emission line of the He-like Al ion [7] and (ii) the high-resolution satellite line-free experiment of the $\beta$ line of the He-like Cl ion [8]. Based on such agreements between theory and experiments, one will be able to offer a viable plasma diagnostics approach to characterize the density and temperature of the outside plasma, specified by Equation (3), in terms of the energy shifts, obtained from the experimental observation and/or the theoretical calculation given by Equation (1).

As we pointed out earlier [3,5], there are two critically important criteria for the application of the DH approximation to the atomic processes subject to outside charge-neutral plasma with a high density close to that of the solid (i.e., ${10}^{22}$ cm${}^{-3}$ or higher). Spatially, we expect that the atomic electron involved in the atomic processes will only interact indirectly with the outside plasma electrons to keep the atomic characteristic of the transition. In other words, the DH approximation should be applied to atomic transitions involving only the atomic electrons in the relatively low atomic states. More detailed discussions on the implication of the spatial criterion will be presented in Section 2 after the introduction of the radius of the Debye sphere A and its corresponding DH potential $V_{DH}$. Temporally, the time scale of the transition (e.g., the lifetime of the upper state) should be substantially different from the correlation time of the outside plasma, i.e., the inverse of the plasma frequency, or, $f_p=8.977\times {10}^3{N}^{1/2}$ Hz with the plasma density N. For the plasma with a density N of the order of ${10}^{22}$ cm${}^{-3}$, the correlation time is about ${10}^{-15}$ s. There are two important time scales for a given atomic process that one should consider in the application of the DH approximation, i.e., the lifetime of the atomic emission and the time for the electron moving around the nucleus. Following these two key criteria, one could assume that the outside plasma electrons are not directly involved in the atomic emission. In fact, the DH potential $V_{DH}$ experienced by the atomic electrons is only remotely affected by the freely moving outside plasma electrons and ions represented by the classical Maxwell–Boltzmann statistics. A detailed expression of $V_{DH}$, in the form of a screening Coulomb potential $-(Z/r)e^{-r/D}$ similar to the Yukawa potential in nuclear physics instead of the pure Coulomb potential $-Z/r$, will be given explicitly in our subsequent discussion.

We should point out that the DH approximation was extensively employed by others to study the atomic processes affected by the outside plasma [9,10,11,12,13,14,15,16,17,18,19,20]. However, most of these applications have included the Debye screening in the two-body interaction between the fast-moving atomic electrons, i.e., instead of $1/r_{12}$, a term in the form of $exp(-r_{12}/D)/r_{12}$ was applied. Since the Debye screening experienced by the atomic electrons subject to the infinitely heavy nucleus is due to the remote effects of the non-interacting outside plasma, there is no justification to include a similar Debye screening between the fast-moving atomic electrons due to the relatively low mobility of the outside plasma ions. The addition of the Debye screening between the atomic electrons not only would need substantially additional calculational efforts in the theoretical studies, it actually leads to the spurious result such as the only loosely two-electron bound state of the H${}^{-}$ ion would remain bound in the presence of the outside dense plasma [20]. In addition, we have also pointed out recently that by falsely including an extra factor of $(Z_{eff}+1)$ in the Debye length (i.e., assuming the effect of the Debye screening due to the slowly moving outside ions), the resulting estimation of the energy shifts from the DH approximation could be an order of magnitude larger than what it actually is [21,22].

Starting from the good agreements between our theoretical estimates and the experimentally observed redshifts for the $\alpha$ and $\beta$ emission lines of a few H-like and He-like ions [3,5], the main objective of this paper is to find out if the general qualitative feature given by Equation (1) still applies for the transitions involving other low atomic states, such as the one between the $n=3$ and $n=2$ states of the He-like ions. A theoretical estimate of such shifts also offers the possibilities for additional experimental measurements at energies substantially less than the $\alpha$ and $\beta$ emission lines studied earlier. It might therefore offer more plasma diagnostic possibilities based on atomic transitions.

2. Debye–Hückel Approximation and Theoretical Calculations

The Debye–Hückel (DH) approximation, based on the classical Maxwell–Boltzmann statistics for an electron–ion collisionless plasma, is known to work for the gas-discharged plasma at relatively low density [1,2]. The spatial and temporal criteria discussed earlier need to be met for the application of the DH approximation for atomic processes subject to outside dense plasma. The details of our theoretical procedures have been presented elsewhere [3,4,5] and we will limit our discussion to a few key aspects. In short, the atomic electron is subject to a DH potential $V_{DH}$ separated by a Debye sphere of radius A, with the nucleus charge Z and Debye length D given by Equation (3) [3,5,23,24], i.e.,

$$\begin{array}{c}\hfill V_{DH}\left(r\right)=\left\{\begin{array}{cc}{V}_i\left(r\right)=-Z{e}^2(\frac{1}{r}-\frac{1}{D+A}),\hfill & r\le A\hfill \\ & \\ V_o\left(r\right)=-Z{e}^2\left(\frac{D{e}^{A/D}}{(D+A)}\right)\frac{e^{-r/D}}{r},\hfill & r\ge A.\hfill \end{array}\right.\end{array}$$

(4)

For the plasma-free environment, the density N goes to zero and the potential $V_{DH}$ goes back to the Coulomb potential when the Debye length D approaches infinity. The radius of the Debye sphere A is an $ad$ $hoc$ parameter, which separates the plasma induced Debye potential $V_o$ outside the Debye sphere and the slightly modified $V_i$ inside the Debye sphere where the atomic characteristic dominates.

With a less attractive $V_{DH}$, all atomic levels will be uplifted in their orbital energies. For the inter-shell transition, the energy uplifting effect of the outside plasma is greater for the upper atomic level with the larger principal quantum number n. On the other hand, the relatively small plasma-free orbital energy of the upper level actually leads to an energy shift less than the one for the lower level of smaller n with a greater plasma-free energy. As a result, one should expect a redshift in the transition energy for such a process. For the intra-shell transitions, the energy uplifting is expected to be a bit more for the orbit with larger orbital angular momentum. An analytical formula for the leading order of general transitions between two hydrogenic orbitals was given as Equation (7) in [25]. However, additional effects, such as the relativistic effects [26] as well as the electron-electron correlation [25], may also affect the change in the respective energies due to the outside plasma. As a result, the resulting transition energy could either be redshifted or blueshifted. Judging from the fact that the contribution to the total energy shift $\Delta \omega$ for the transition is dominated by the uplifting of the energy level of the lower state, we need to ensure that the atomic characteristic of the lower state is kept to meet the spatial criterion for the application of the DH approximation discussed earlier. In other words, our approach would work adequately when the size of the lower atomic state of the transition is not too much greater than the radius of the Debye sphere. In the quasi-hydrogenic approach, the average size of the atom is approximately given by $n^2$ of the $n=1$ ground state. It is likely that the DH approximation may not apply as well as it could, should the lower state of the transition be higher than a state with $n=3$, when the size of the atomic orbit is one order of magnitude greater than the radius A of the Debye sphere.

The theoretical results presented in this paper are carried out both non-relativistically and relativistically with multi-configuration approaches. The non-relativistic results were calculated with the B-spline-based configuration interaction (BSCI) approach, based on the use of a complete two-electron basis, including both negative and positive one-electron orbitals. The calculational procedures were presented in detail earlier [3,5,27,28]. For the relativistic calculation, one starts with a set of atomic orbital wavefunctions (AOs) specified by the corresponding principal quantum number n, the orbital angular momentum l, and the total angular momentum j. It includes the spectroscopic AOs (with $n-l-1$ fixed nodes) and the pseudo AOs (without fixed nodes), which are to be included to represent the atomic state of interest. The energy of the atomic state function (ASF) $|\Gamma PJM\rangle$ of a state $\Gamma$ with parity P and its total angular momentum J, as well as the corresponding magnetic quantum number M, is obtained by diagonalizing the Hamiltonian $H_{DH}$ given by Equation (12) of [5], and the corresponding ASF is expressed in terms of the linear combination of a set of configuration state functions (CSFs) shown by Equation (15) of [5]. Individually, CSF is a linear combination of the Slater determinants of the atomic orbital functions corresponding to the electron configurations included in the calculation. Again, more details of the calculational procedure were presented in our earlier works [3,5,25,26,29].

3. Results and Discussions

As we already pointed out, the main purpose of this paper is to find out if the ratio R of the energy shifts $\Delta \omega$ from the plasma-free transition energy ${\omega }_0$, i.e., $R=\Delta \omega /{\omega }_0$, for a number of the $n=3$ to $n=2$ transitions of the He-like ions could still be expressed by the simple expression (1). We will first focus our discussion on the $1s3d$ ${}^1{D}_2$ to $1s2p$ ${}^1{P}_1$ transition, which has the largest oscillator strength among all $n=3$ to $n=2$ emissions for the He-like ions. Similar to our earlier works for the $\alpha$ and $\beta$ emission lines of He-like ions [3,4,5], the radius of the Debye sphere is given by $A=\eta r_g$, where $r_g$ is the average radius of the ground state of the He-like ion, or, $r_g=\langle 1s^2{}^1{S}_0\left|r\right|1s^2{}^1{S}_0\rangle$ and $\eta$ is a size parameter. 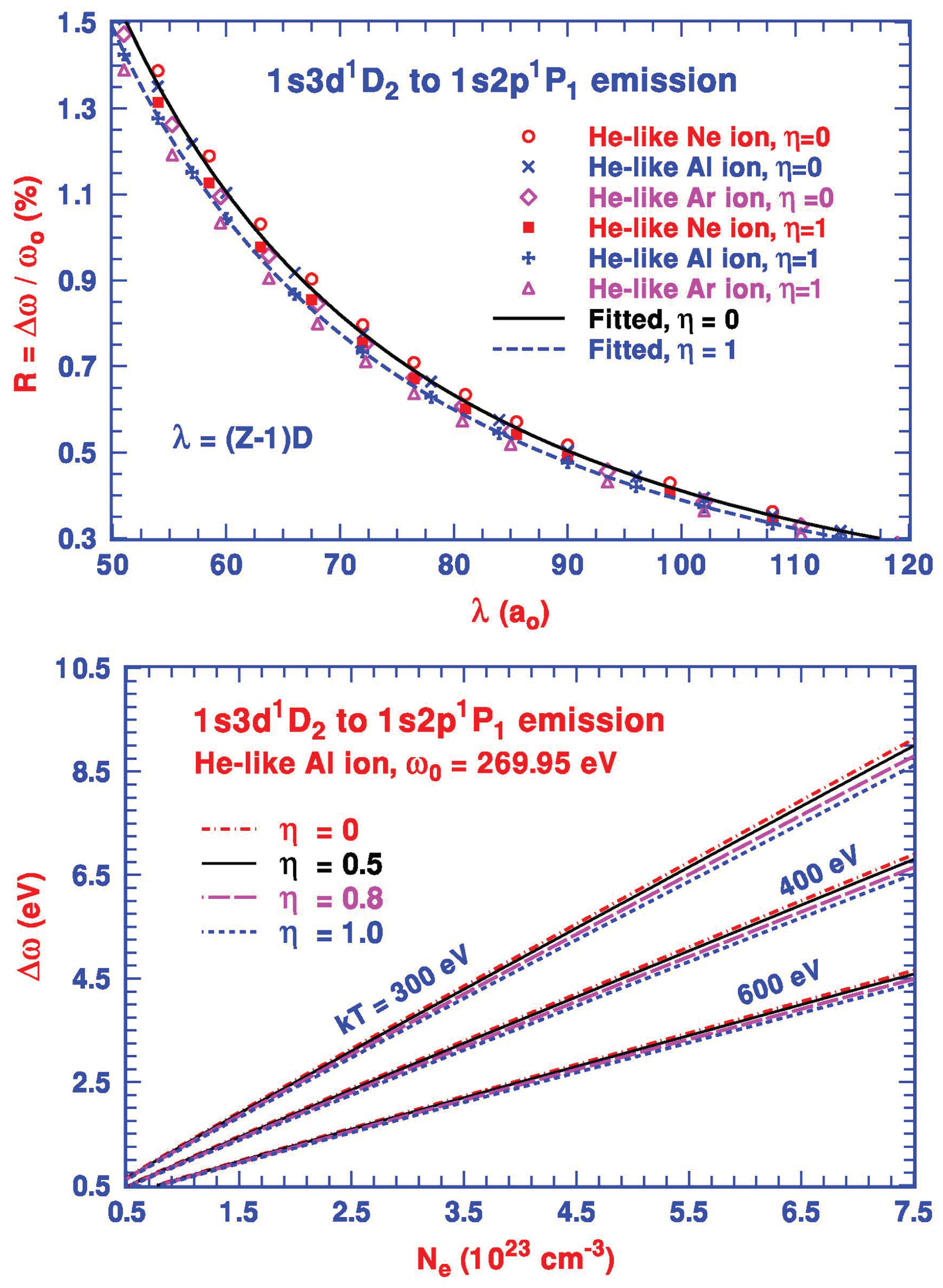Our calculated values of R as a function of $\lambda$ from the non-relativistic calculations for the He-like Ne, Al, and Ar ions for the $1s3d$ ${}^1{D}_2$ to $1s2p$ ${}^1{P}_1$ transition are shown in the top plot of Figure 1, with $\eta =0$ and $\eta =1$. Similar to the $\alpha$ and $\beta$ emission lines of He-like ions, the values R for different He-like ions are close to each other as $\lambda$ varies. For each ion, we first proceed to fit the calculated R for each $\eta$ to Equation (1) for a set of ($a_Z$, $b_Z$, $c_Z$) for all three ions. We then take the average from the individually fitted coefficients, i.e., $a_{\eta }=(a_{Ne-ion}+a_{Al-ion}+a_{Ar-ion})/3$. With a set of three average coefficients for each $\eta$, i.e., ($a_{\eta }$, $b_{\eta }$, $c_{\eta }$) listed in

Table 1. Fitted average coefficients $a_{\eta }$, $b_{\eta }$, and $c_{\eta }$ (in $A\left(e\right)=A\times {10}^e$) for the $n=3$ to $n=2$ transitions $1s3d$ ${}^1{D}_2$ to $1s2p$ ${}^1{P}_1$ (A), $1s3d$ ${}^3{D}_2$ to $1s2p$ ${}^3{P}_1$ (B), $1s3d$ ${}^3{D}_1$ to $1s2p$ ${}^3{P}_0$ (C), $1s3p$ ${}^1{P}_1$ to $1s2s$ ${}^1{S}_0$ (D), and $1s3p$ ${}^3{P}_0$ to $1s2s$ ${}^3{S}_1$ (E) of the He-like ions with the size parameters $\eta =0$, $0.5$, $0.8$ and 1 (R in percentage).

Transition	$\mathit{\eta }$	${\mathit{a}}_{\mathit{\eta }}$	${\mathit{b}}_{\mathit{\eta }}$	${\mathit{c}}_{\mathit{\eta }}$
A	0.0	3.6113(3)	7.8295(0)	−2.9215(−2)
	0.5	3.5557(3)	7.8493(0)	−2.9364(−2)
	0.8	3.4731(3)	7.8053(0)	−2.9149(−2)
	1.0	3.3983(3)	7.7693(0)	−2.9029(−2)
B	0.0	3.5495(3)	7.6024(0)	−2.8344(−2)
	0.5	3.4944(3)	7.6228(0)	−2.8495(−2)
	0.8	3.4113(3)	7.5938(0)	−2.8374(−2)
	1.0	3.3365(3)	7.5549(0)	−2.8254(−2)
C	0.0	3.5302(3)	8.6779(0)	−2.8059(−2)
	0.5	3.4916(3)	7.6217(0)	−2.2498(−2)
	0.8	3.4094(3)	7.5723(0)	−2.2260(−2)
	1.0	3.3333(3)	7.5645(0)	−2.2332(−2)
D	0.0	4.0145(3)	1.1414(1)	−4.2868(−2)
	0.5	3.9646(3)	1.1428(1)	−4.2975(−2)
	0.8	3.8995(3)	1.1406(1)	−4.2921(−2)
	1.0	3.8458(3)	1.1363(1)	−4.2703(−2)
E	0.0	3.8627(3)	1.0547(1)	−4.0564(−2)
	0.5	3.8028(3)	1.0810(1)	−4.2027(−2)
	0.8	3.7389(3)	1.0792(1)	−4.1972(−2)
	1.0	3.6868(3)	1.0745(1)	−4.1730(−2)

, we finally have the fitted R shown in the top plot for both $\eta =0$ and 1. We also note that the effect due to the different size factors appears to be smaller than the ones for the $\alpha$ and $\beta$ emission lines of He-like ions (see Figure 3 of [5]). This is likely due to the fact that for the $n=3$ to $n=2$ transition, the radii of the atomic orbits are greater than the ones for the $\alpha$ and $\beta$ emission lines. Qualitatively, since the leading coefficient $a_{\eta }$ is substantially greater than the other two coefficients $b_{\eta }$ and $c_{\eta }$, from Equations (1)–(3), the energy shifts $\Delta \omega$ are expected to vary approximately as a linear function of $(1/{\lambda }^2)$, or, plasma density $N_e$ for a fixed $kT$. Indeed, the bottom plot of Figure 1 shows the near-linear variation in $\Delta \omega$ of the He-like Al${}^{12+}$ ion from its plasma free transition energy ${\omega }_0=269.95$ eV [30] to a plasma electron density higher than ${10}^{23}$ cm${}^{-3}$.

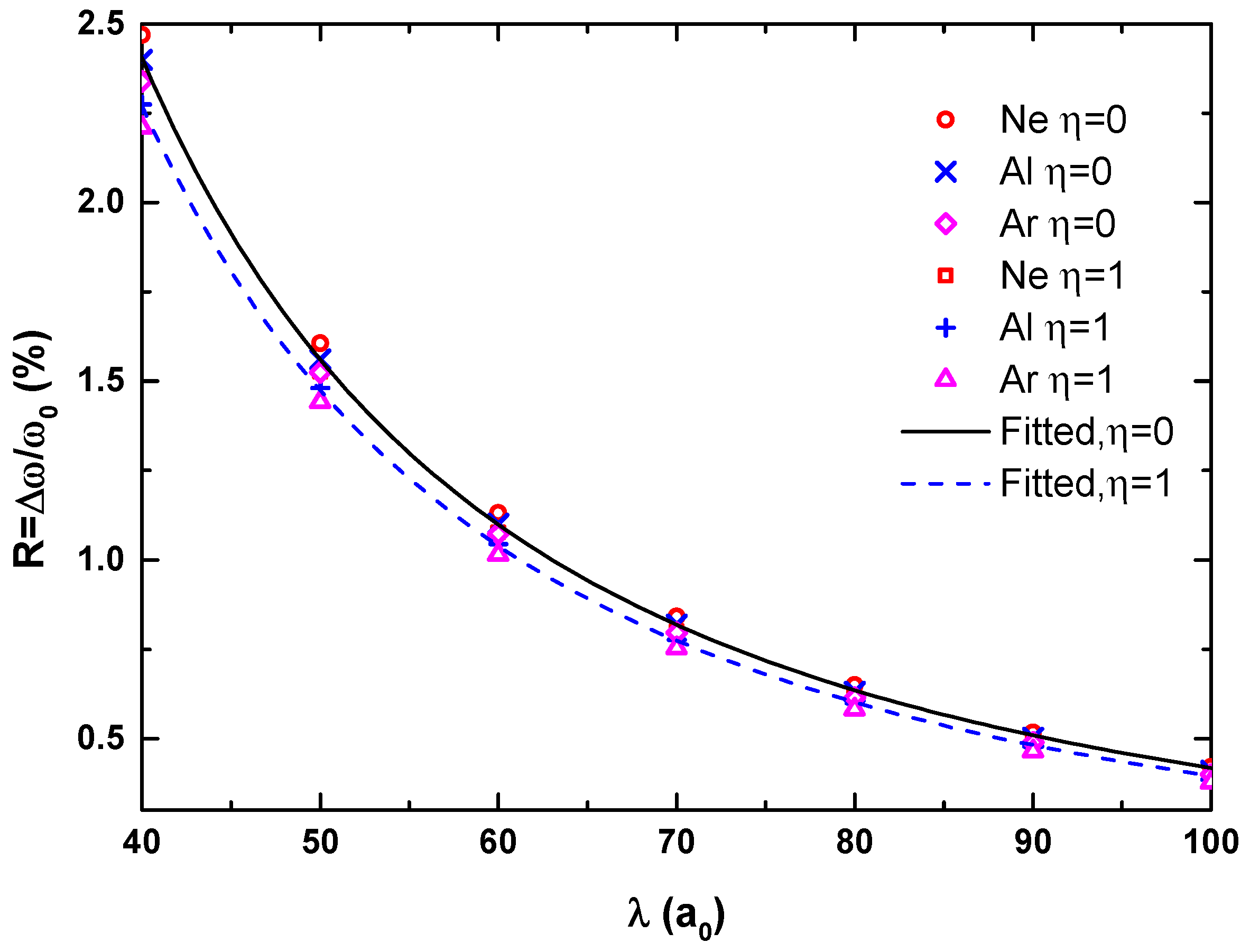
We have also carried out similar relativistic calculation with the approach outlined earlier. Figure 2 shows that the calculated relativistic values of R of the $1s3d$ ${}^1{D}_2$ to $1s2p$ ${}^1{P}_1$ transition with two different size factors $\eta =0$ and $\eta =1$ for the He-like Ne, Al, and Ar ions are nearly identical to our non-relativistic results shown by the top plot of Figure 1. Accordingly, our discussions below are based on our non-relativistic calculation.

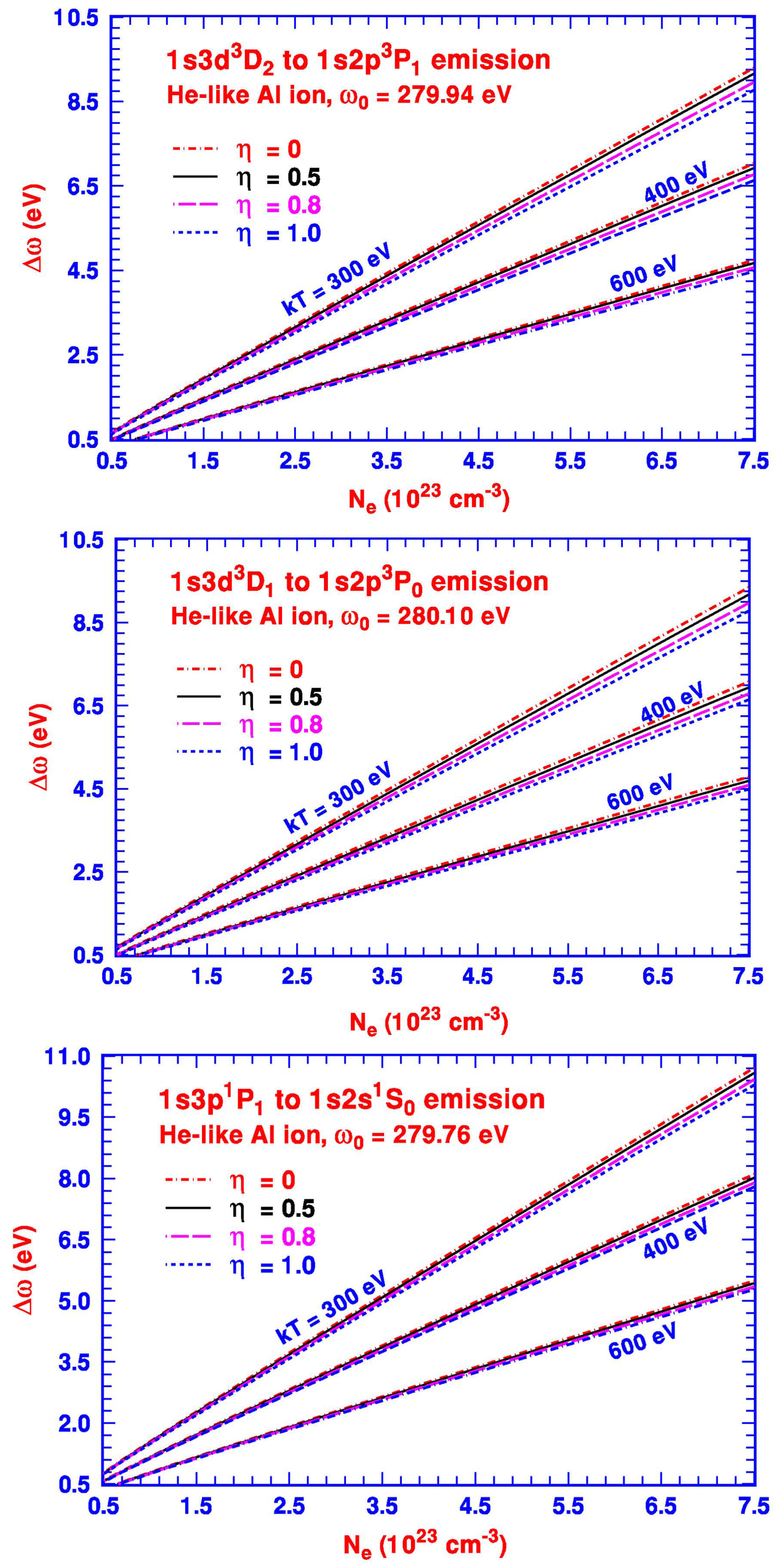
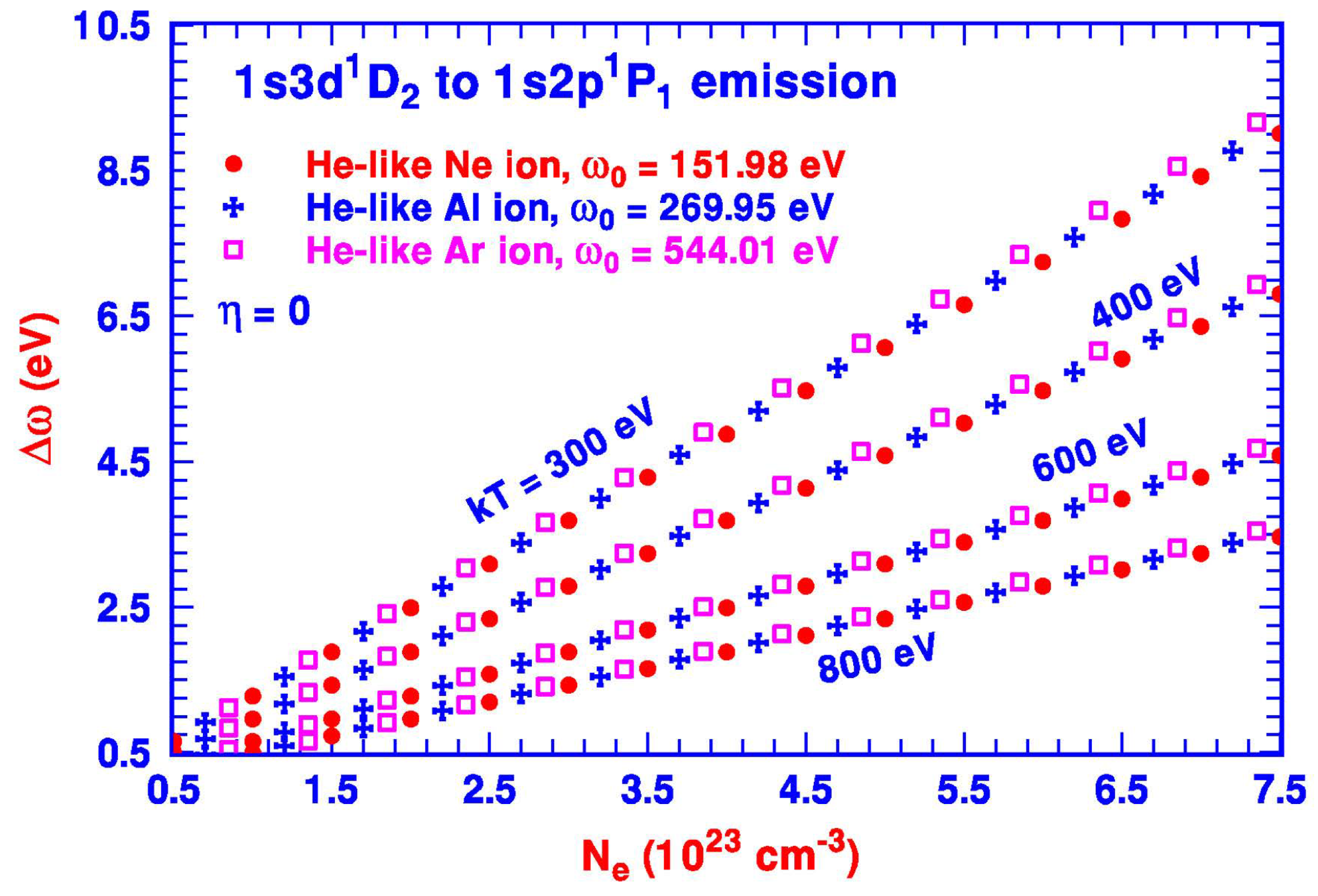
We have included in our study three additional $n=3$ to $n=2$ transitions, i.e., $1s3d$ ${}^3{D}_2$ to $1s2p$ ${}^3{P}_1$, $1s3d$ ${}^3{D}_1$ to $1s2p$ ${}^3{P}_0$, and $1s3p$ ${}^1{P}_1$ to $1s2s$ ${}^1{S}_0$, for the He-like ions to further examine if the quasi-hydrogenic feature of the energy shift of the atomic transition, due to the outside dense plasma based on the DH approximation, remains applicable. With the three fitted average coefficients $a_{\eta }$, $b_{\eta }$, and $c_{\eta }$ from our non-relativistic calculation also tabulated in Table 1 for these three transitions, our theoretically estimated redshifts $\Delta \omega$, as functions of the plasma density $N_e$ at a number of temperatures $kT$, are shown in Figure 3 for the He-like Al ion. We should point out that the plasma-free oscillator strengths for these three transitions are somewhat smaller than that of the $1s3d$ ${}^1{D}_2$ to $1s2p$ ${}^1{P}_1$ transition, and the plasma-free transition energies of these three transitions are close to each other and about 10 eV greater than the $1s3d$ ${}^1{D}_2$ to $1s2p$ ${}^1{P}_1$ transition for the He-like Al ion. From Figure 3, our calculations suggest that the shifts of the two ${}^{3}D$ to ${}^{3}P$ transitions are almost the same with $\Delta \omega$ slightly greater for the ${}^{1}P$ to ${}^{1}S$ transition at the same density $N_e$ and temperature $kT$. Should the experimental measurement be carried out, the implication of our calculation is that all three emissions will overlap and appear as one slightly broadened emission with a similar redshift $\Delta \omega$.

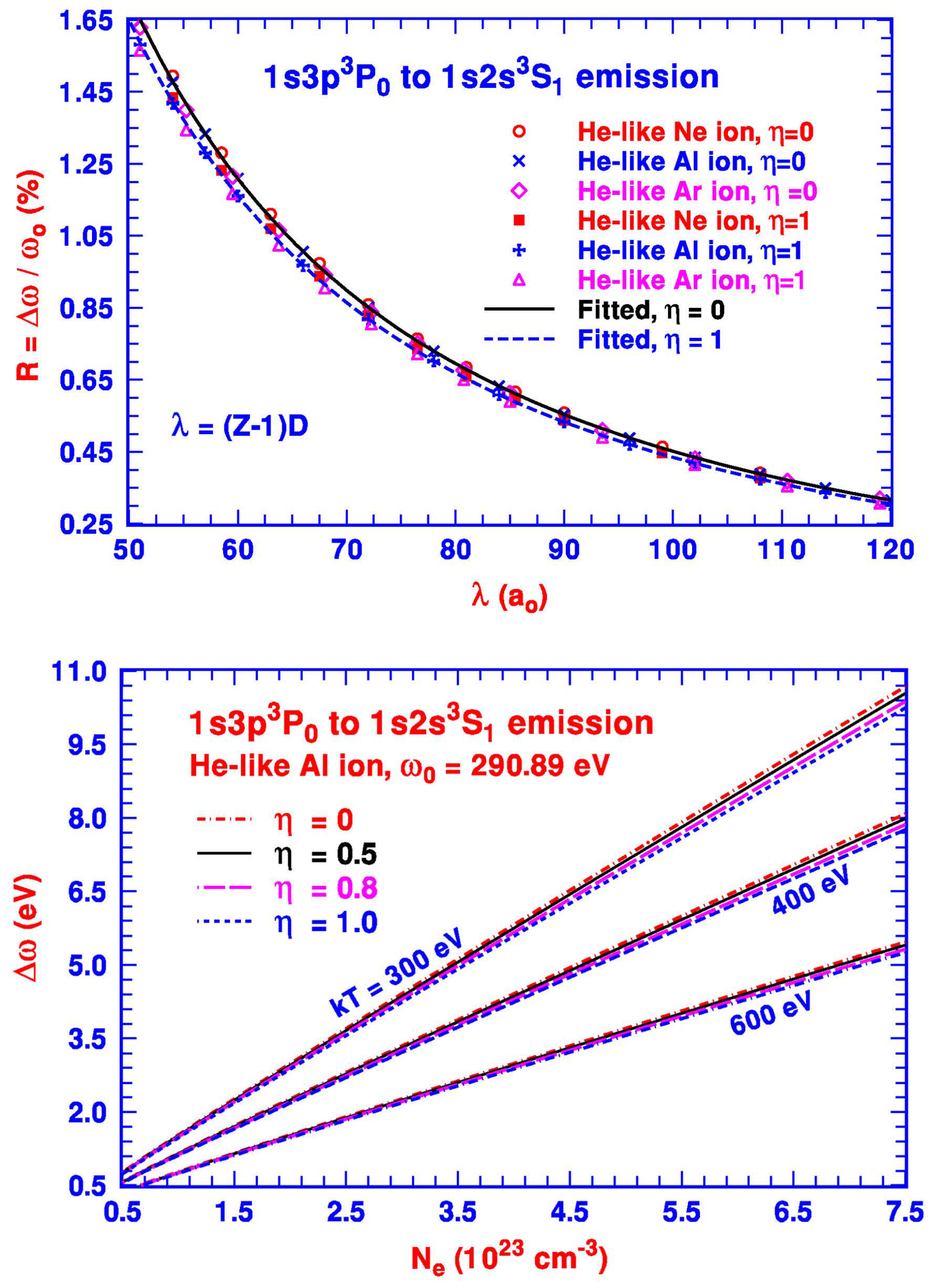
In addition to the four $n=3$ to $n=2$ emissions we discussed above, our study has also been extended to a somewhat weaker $1s3p$ ${}^3{P}_0$ to $1s2s$ ${}^3{S}_1$ transition with different plasma-free transition energy. Our calculated R, similar to the other transitions and shown in the top plot of Figure 4, follows the same expression in Equation (1) with the coefficients $a_{\eta }$, $b_{\eta }$, and $c_{\eta }$ listed in Table 1. We note again that the coefficients $a_{\eta }$ for all size parameters $\eta$ are substantially greater than the other two coefficients $b_{\eta }$, and $c_{\eta }$. As a result, similar to the other four emissions, we expect the same qualitative features of the energy shifts $\Delta \omega$ in terms of a nearly linear variation as a function of $N/kT$ shown by the bottom plot of Figure 4. Based on the results of our current theoretical calculation for the $n=3$ to $n=2$ transitions, we are able to conclude again that the transition energy shifts $\Delta \omega$ of the atomic emissions subject to outside dense plasma for the He-like ions indeed follow the quasi-hydrogenic qualitative feature given by Equation (1), based on the DH approximation as long as the spatial and temporal criteria are satisfied.

In this paper, we have focused on the transition energy for the reason that a few percents of the redshift are well within the experimental capability, which is more preferable than the measurement of the change in the oscillator strength involving the detailed and often difficult characterization of the line shapes of the transition. In fact, with the help of the theoretically fitted constants listed in Table 1, one could estimate the expected redshifts for all five $n=3$ to $n=2$ transitions of other He-like ions (beyond those presented in Figure 1, Figure 3 and Figure 4) for a given set of plasma density N and temperature $kT$ in an experimental measurement. For example, if the experimental measurement is more preferable at different transition energies for other He-like ions, Figure 5 presents the expected redshifts for the $1s3d$ ${}^1{D}_2$ to $1s2p$ ${}^1{P}_1$ transition for the He-like Ne and Ar ions, together with the one for the He-like Al ion shown in Figure 1.

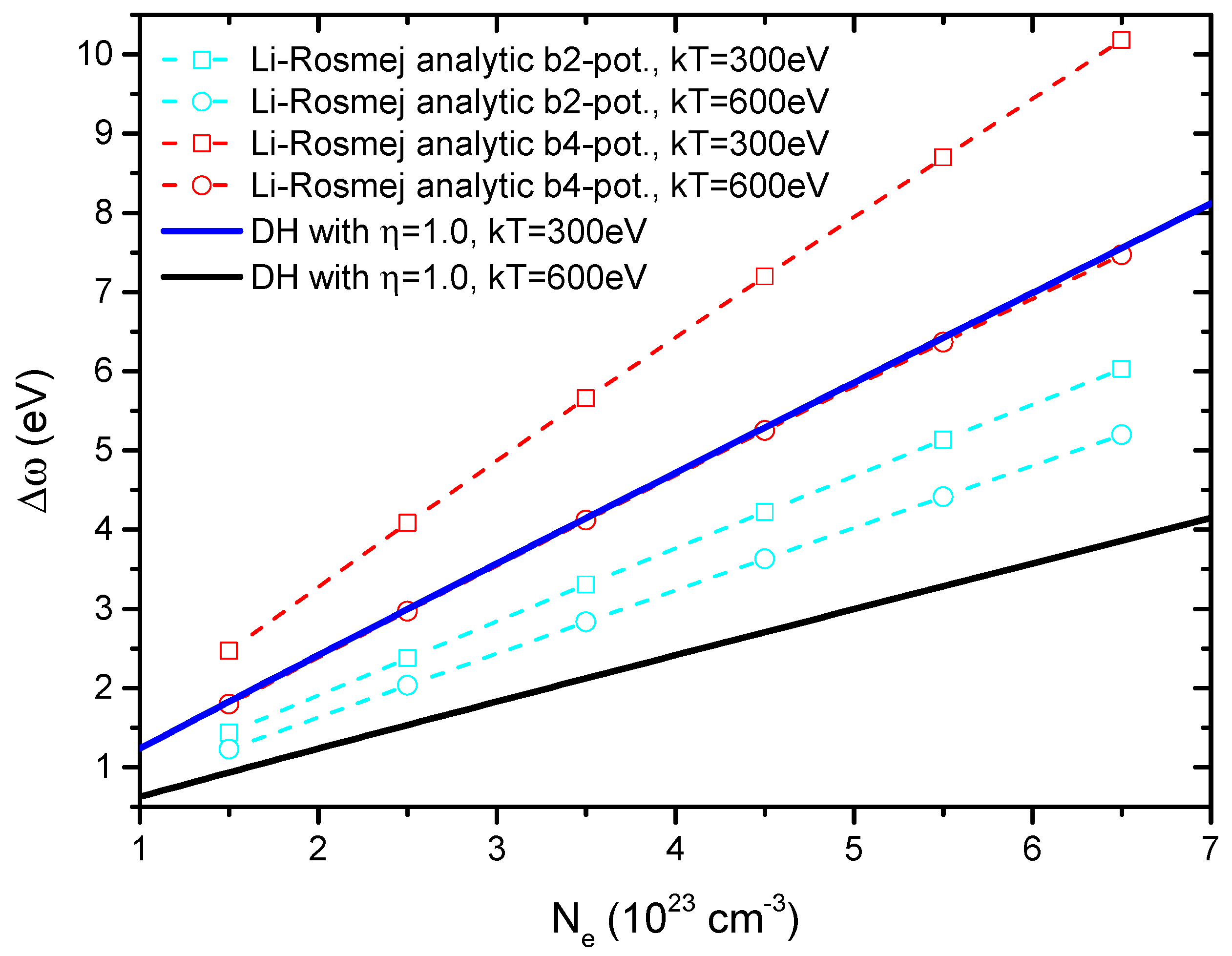
There are other recent theoretical estimates [31,32,33,34,35,36,37] including the ones based on the ion sphere (IS) model employing the Fermi–Dirac statistics for the outside plasma. The analytical IS approaches [32,33,34,35], with a number of different models, have offered some successes when compared with the measured data. For example, whereas some earlier versions of the generalized analytical IS approach have failed to account for the experimental data, its more advanced versions have generated estimates in agreement with the measured results (see, e.g., Figures 2 and 4 of [34]) similar to the agreements between the measured data and our DH estimates shown in Figure 3 of [5]. The other IS approach, i.e., the average-atom IS model with MCDF (Multi-configuration Dirac–Fock) approach [36,37] has led to estimated energy shifts in agreement with the experimental measurements by Beiersdorfer et al (see Figure 4 of [8] or Figure 1 of [36]), but fails to interpolate the measured results by Stillman et al (See Figure 2 of [37]). The key difference between the ion sphere approaches and the DH approximation employed in our theoretical calculation is our use of classical Maxwell–Boltzmann statistics, instead of the Fermi–Dirac statistics, to account for the outside non-interacting plasma electrons and ions. This difference in statistics had led to noticeable different temperature dependence of the resulting energy shifts between the IS and DH estimates (see, e.g., the relatively flat curve denoted as “IS from [1]” and the one with the larger slope as “DH with D from Equation (1)” shown in Figure 1 of [21]). This difference is also evident in the estimated redshifts $\Delta \omega$ for the $1s3d$ ${}^1{D}_2$ to $1s2p$ ${}^1{P}_1$ transition of the He-like Al ion between the two versions of the generalized analytic IS model and the DH calculations with $\eta =1$ shown in Figure 6. Hopefully, the results shown in this paper may provide the impetus for further experimental works to determine if the application of the classical Maxwell–Boltzmann statistics is indeed the more appropriate approach in treating the non-interacting electrons and ions in the outside dense plasma. The successful interplay between theoretical calculations and experimental measurements could further facilitate the plasma diagnostics to determine its density and temperature.