The Spin-Orbit Interaction: A Small Force with Large Implications
Abstract
1. Introduction
2. Spin-Orbit Splitting of Cooper Minima
3. Photoelectron Angular Distributions from s-States
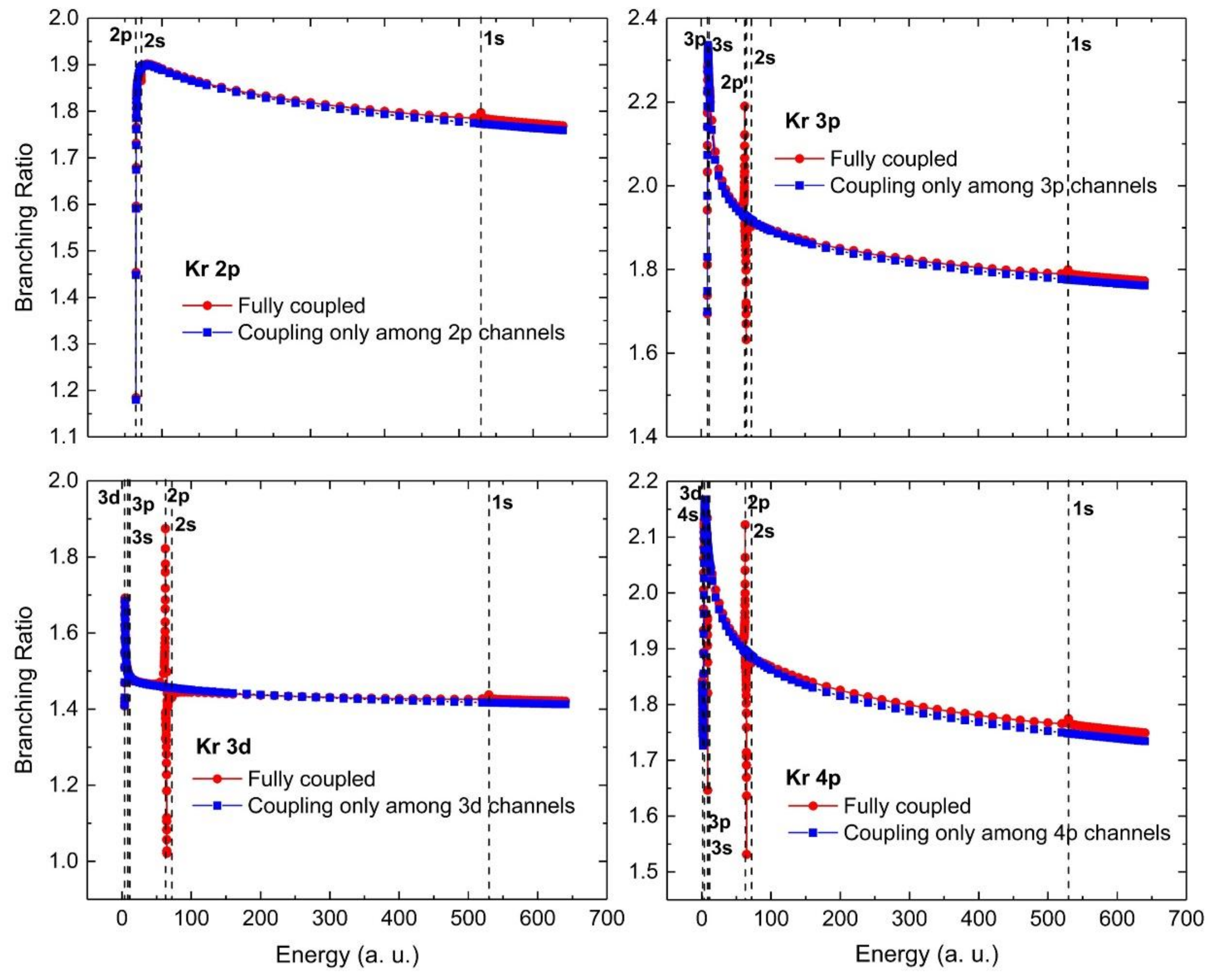
4. Branching Ratios at High Energy
5. Final Remarks
Funding
Conflicts of Interest
References
- Fano, U. Spin-Orbit Coupling: A Weak Force with Conspicuous Effects. Comments At. Molec. Phys. 1970, 2, 30–36. [Google Scholar]
- Cooper, J.W. Photoionization from Outer Atomic Subshells. A Model Study. Phys. Rev. 1962, 128, 681–693. [Google Scholar] [CrossRef]
- Manson, S.T. Systematics of zeros in dipole matrix elements for photoionizing transitions: Nonrelativistic calculations. Phys. Rev. A 1985, 31, 3698–3703. [Google Scholar] [CrossRef] [PubMed]
- Starace, A.F. Theory of Atomic Photoionization. In Handbuch der Physik; Mehlhorn, W., Ed.; Springer: Berlin/Heidelberg, Germany, 1882; Volume 32, pp. 1–121. [Google Scholar]
- Seaton, M.J. A comparison of theory and experiment for photo-ionization cross-sections II. Sodium and the alkali metals. Proc. Roy. Soc. Lond. Sect. A 1951, 208, 418–430. [Google Scholar]
- Kim, Y.S.; Ron, A.; Pratt, R.H.; Tambe, B.R.; Manson, S.T. Relativistic Effects in the Photoionization of High Z Elements: Splitting and Shifts in Minima. Phys. Rev. Lett. 1981, 46, 1326–1329. [Google Scholar] [CrossRef]
- Deshmukh, P.C.; Radojevic, V.; Manson, S.T. Relativistic Splitting of Cooper Minima in Radon: A Relativistic Random Phase Approximation Study. Phys. Lett. A 1986, 117, 293–296. [Google Scholar] [CrossRef]
- Deshmukh, P.C.; Tambe, B.; Manson, S.T. Relativistic Effects in the Photoionisation of Heavy Atoms: Cooper Minima. Aust. J. Phys. 1986, 39, 679–686. [Google Scholar] [CrossRef]
- Yin, R.Y.; Pratt, R.H. Survey of relativistic Cooper minima. Phys. Rev. A 1987, 35, 1149–1153. [Google Scholar] [CrossRef] [PubMed]
- Baral, S.; Saha, S.; Dubey, K.A.; Jose, J.; Deshmukh, P.C.; Razavi, A.K.; Manson, S.T. Unusual behavior of Cooper minima of ns subshells in high-Z atoms. Phys. Rev. A 2022, 105, 062819. [Google Scholar] [CrossRef]
- Manson, S.T.; Starace, A.F. Photoelectron Angular Distributions: Energy Dependence for s Subshells. Rev. Mod. Phys. 1982, 54, 389–406. [Google Scholar] [CrossRef]
- Fano, U.; Dill, D. Angular Momentum Transfer in the Theory of Angular Distributions. Phys. Rev. A 1972, 6, 185–192. [Google Scholar] [CrossRef]
- Huang, K.-N.; Johnson, W.; Cheng, K. Theoretical photoionization parameters for the noble gases argon, krypton, and xenon. At. Data Nucl. Data Tables 1981, 26, 33–45. [Google Scholar] [CrossRef]
- James, A.R.; Samson, J.; Gardner, L.; Starace, A.F. 2P3/2: 2P1/2 partial photoionization cross-section ratios in the rare gases. Phys. Rev. A 1975, 12, 1459–1463. [Google Scholar]
- Ron, A.; Kim, Y.S.; Pratt, R.H. Subshell branching ratios of partial photoionization cross sections. Phys. Rev. A 1981, 24, 1260–1263. [Google Scholar] [CrossRef]
- Kim, Y.S.; Pratt, R.H.; Ron, A. Nonstatistical behavior of photoeffect subshell branching ratios at high energies. Phys. Rev. A 1981, 24, 1889–1893. [Google Scholar] [CrossRef]
- Püttner, R.; Martins, J.B.; Marchenko, T.; Travnikova, O.; Guillemin, R.; Journel, L.; Ismail, I.; Goldsztejn, G.; Koulentianos, D.; Céolin, D.; et al. Nonstatistical Behavior of the Photoionization of Spin-Orbit Doublets. J. Phys. B 2021, 54, 085001. [Google Scholar] [CrossRef]
- Bethe, H.A.; Salpeter, E.E. Quantum Mechanics of One- and Two-Electron Atoms; Springer: Berlin/Heidelberg, Germany, 1957; p. 63ff. [Google Scholar]
- Munasinghe, C.R.; Deshmukh, P.C.; Manson, S.T. Photoionization branching ratios of spin-orbit doublets far above thresholds: Interchannel and relativistic effects in the noble gases. Phys. Rev. A 2022, 106, 013102. [Google Scholar] [CrossRef]
- Pazourek, R.; Nagele, S.; Burgdörfer, J. Attosecond chronoscopy of photoemission. Rev. Mod. Phys. 2015, 87, 765–802. [Google Scholar] [CrossRef]
- Deshmukh, P.C.; Banerjee, S.; Mandal, A.; Manson, S.T. Wigner-Eisenbud-Smith Time Delay in Atom-Laser Interactions. Eur. Phys. J. Spec. Top. 2021, 230, 4151–4164. [Google Scholar] [CrossRef]
- Kheifets, A.S. Wigner time delay in atomic photoionization. J. Phys. B 2023, 56, 022001. [Google Scholar] [CrossRef]

| Atom | 6s → p3/2 | 6s → p1/2 | Splitting |
|---|---|---|---|
| Hg (Z = 80) | 4.14 | 3.67 | 0.47 |
| Rn (Z = 86) | 5.93 | 4.43 | 1.5 |
| Ra (Z = 88) | 6.38 | 3.88 | 2.5 |
| No (Z = 102) | 11.7 | 6.7 | 5 |
| Cn (Z = 112) | 24.82 | 4.82 | 20 |
| Og (Z = 118) | 171.02 | 3.52 | 167.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manson, S.T. The Spin-Orbit Interaction: A Small Force with Large Implications. Atoms 2023, 11, 90. https://doi.org/10.3390/atoms11060090
Manson ST. The Spin-Orbit Interaction: A Small Force with Large Implications. Atoms. 2023; 11(6):90. https://doi.org/10.3390/atoms11060090
Chicago/Turabian StyleManson, Steven T. 2023. "The Spin-Orbit Interaction: A Small Force with Large Implications" Atoms 11, no. 6: 90. https://doi.org/10.3390/atoms11060090
APA StyleManson, S. T. (2023). The Spin-Orbit Interaction: A Small Force with Large Implications. Atoms, 11(6), 90. https://doi.org/10.3390/atoms11060090






