Fragmentation Dynamics of
Abstract
1. Introduction
2. Experimental Setup
3. Results and Discussions
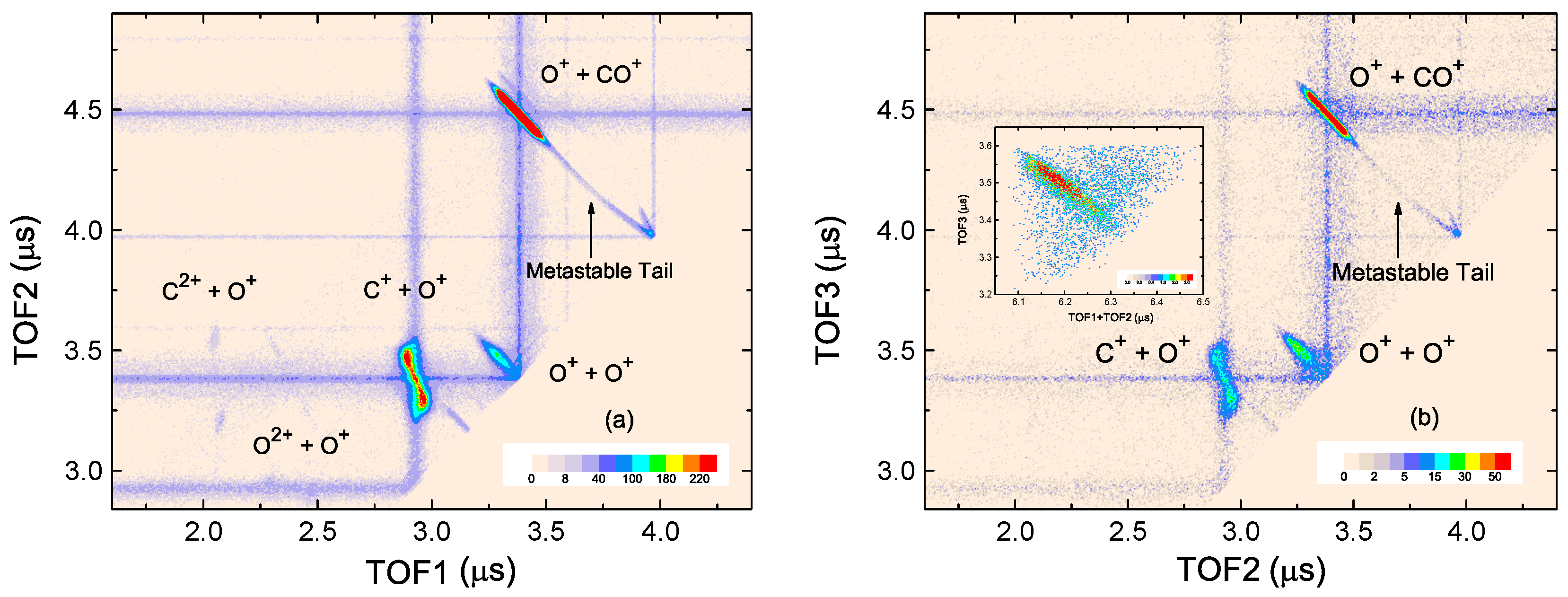
3.1. Two-Body Break-Up
3.2. Three-Body Break-Up
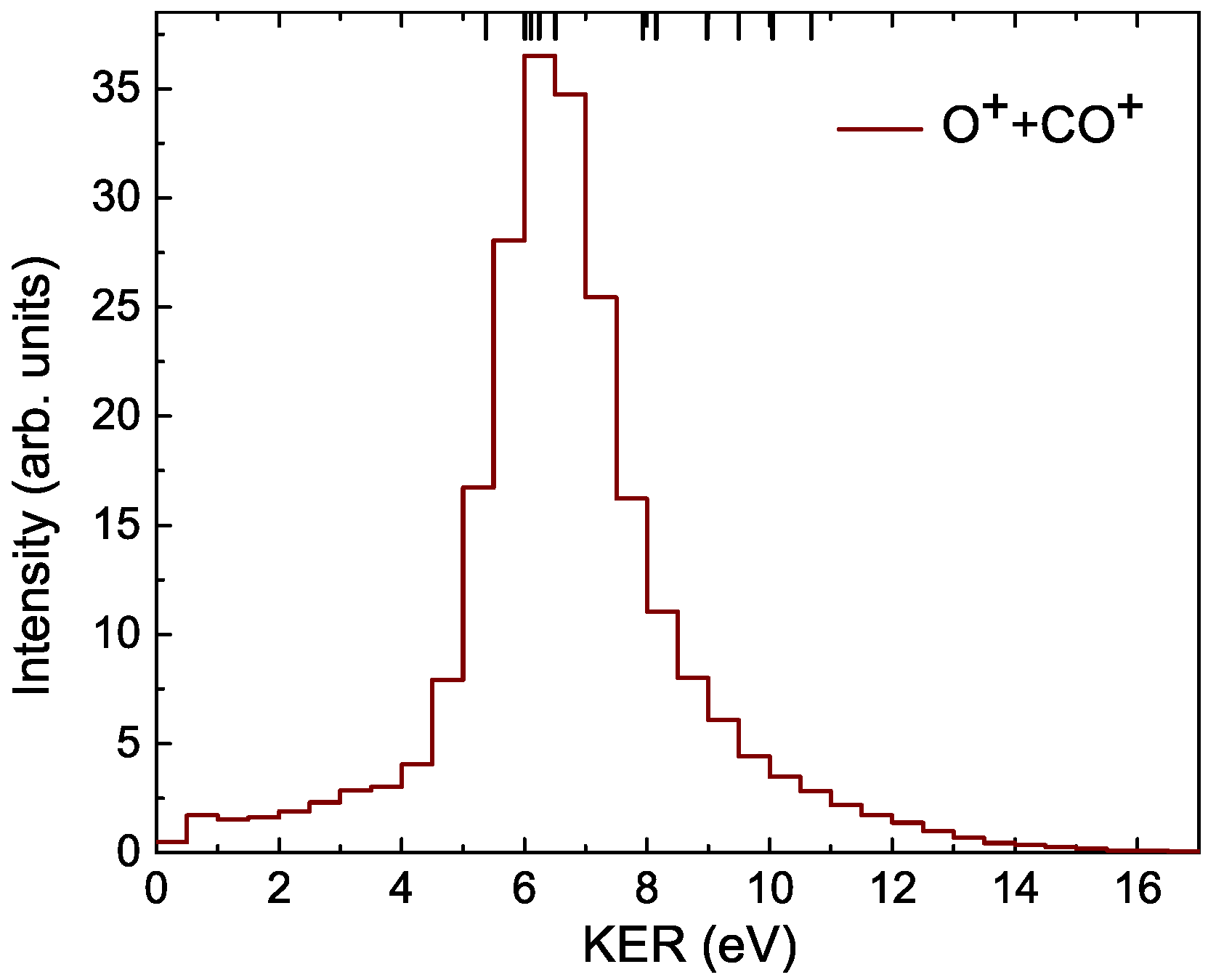
3.2.1. Fragmentationof CO
- 1.
- In the concerted decay, the two C=O bonds break simultaneously:
- 2.
- For a sequential or two-step decay, there can be two different situations:
- (a)
- In the initial charge separation (s(i)) process a charged fragment is released due to the break-up of the C=O bonds. Depending on which ion ( or ) is released first, s(i) is further categorized [19] as follows:
- (I)
- If the lighter ion is released in the first step:In this case, the slope of the coincidence trace should be:where m, m, and m are the masses of the lighter ion, the heavier ion, and the neutral atom, respectively.
- (II)
- Whereas, in the following casethe ion is released in the second step and the heavier ion is released in the first step, hence the slope of this coincidence trace should be:
- (b)
- For a deferred charge separation (s(d)) process, a neutral fragment is released due to the break-up of the C=O bonds.
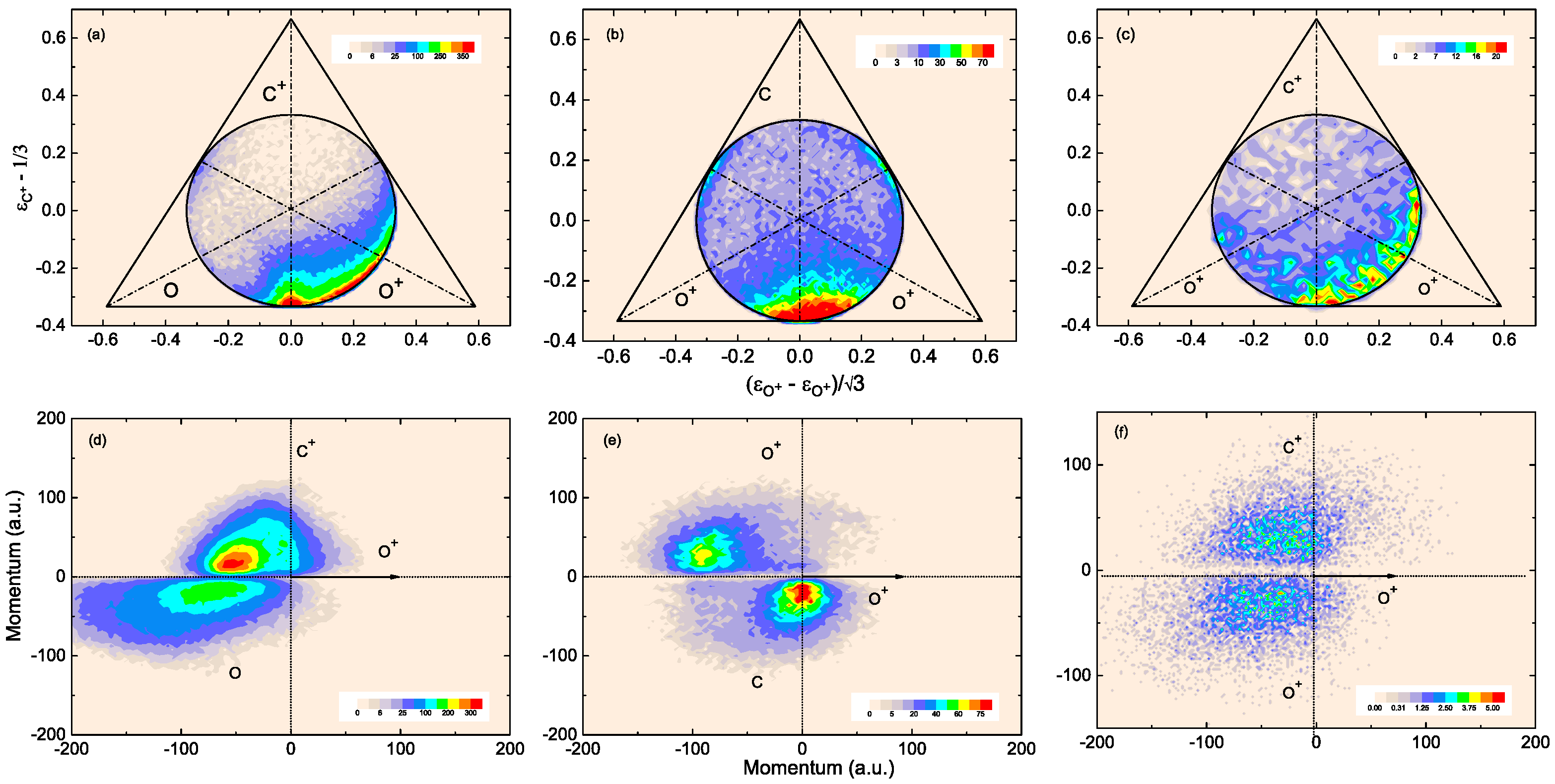
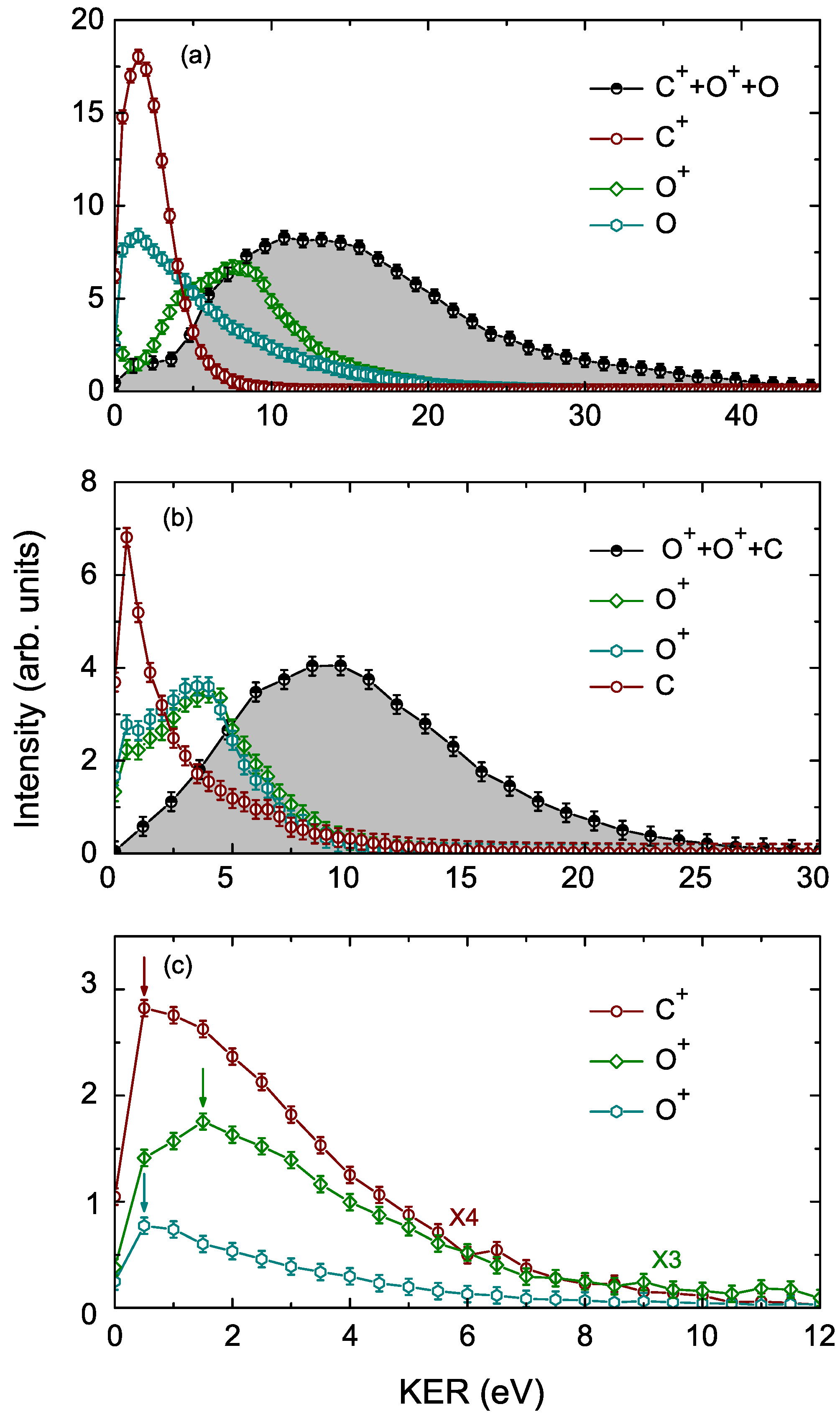
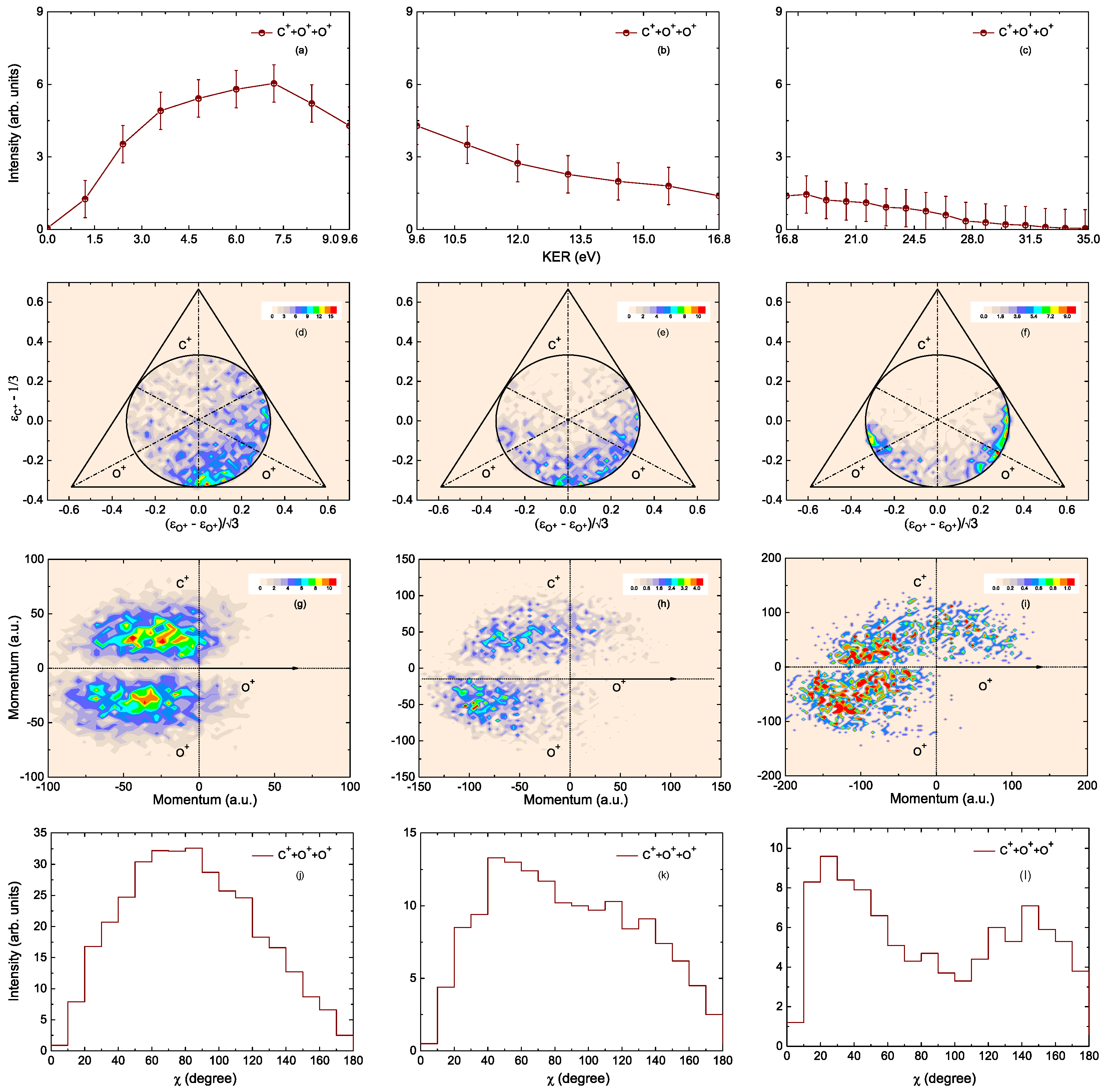
C + O + O Channel
O + O + C Channel
3.2.2. Fragmentationof CO
- (I.)
- Concerted fragmentation
- (II.)
- Two-step s(i)
- (III.)
- Two-step s(i)
- (IV.)
- Two-step s(d)
C + O + O Channel
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Janev, R.K. Atomic and Molecular Processes in Fusion Edge Plasmas; Springer: Berlin/Heidelberg, Germany, 2013; Available online: https://link.springer.com/book/10.1007/978-1-4757-9319-2 (accessed on 9 April 2023).
- Tielens, A.G.G.M. The molecular universe. Rev. Mod. Phys. 2013, 85, 1021. [Google Scholar] [CrossRef]
- De Vries, J.; Hoekstra, R.; Morgenstern, R.; Schlathölter, T. Charge driven fragmentation of nucleobases. Phys. Rev. Lett. 2003, 91, 053401. [Google Scholar] [CrossRef]
- López-Tarifa, P.; du Penhoat, M.-A.H.; Vuilleumier, R.; Gaigeot, M.-P.; Tavernelli, I.; Le Padellec, A.; Champeaux, J.-P.; Alcamí, M.; Moretto-Capelle, P.; Martín, F.; et al. Charge driven fragmentation of nucleobases. Phys. Rev. Lett. 2011, 107, 023202. [Google Scholar] [CrossRef]
- Neumann, N.; Hant, D.; Schmidt, L.P.H.; Titze, J.; Jahnke, T.; Czasch, A.; Schöffler, M.S.; Kreidi, K.; Jagutzki, O.; Schmidt-Böcking, H.; et al. Fragmentation Dynamics of CO23+ Investigated by Multiple Electron Capture in Collisions with Slow Highly Charged Ions. Phys. Rev. Lett. 2010, 104, 103201. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Tribedi, L.C.; Misra, D. Observation of a sequential process in charge-asymmetric dissociation of CO2q+(q=4,5) upon the impact of highly charged ions. Phys. Rev. A 2015, 92, 030701. [Google Scholar] [CrossRef]
- Adoui, L.; Tarisien, M.; Rangama, J.; Sobocinsky, P.; Cassimi, A.; Chesnel, J.Y.; Frémont, F.; Gervais, B.; Dubois, A.; Krishnamurthy, M.; et al. HCI-induced molecule fragmentation: Non-coulombic explosion and three-body effects. Phys. Scr. 2001, 2001, 89. [Google Scholar] [CrossRef]
- Siegmann, B.; Werner, U.; Lutz, H.O.; Mann, R. Complete Coulomb fragmentation of CO2 in collisions with 5.9 MeV u−1Xe18+ and Xe43+. J. Phys. B 2002, 35, 3755. [Google Scholar] [CrossRef]
- Jana, M.R.; Ghosh, P.N.; Bapat, B.; Kushawaha, R.K.; Saha, K.; Prajapati, I.A.; Safvan, C.P. Ion-induced triple fragmentation of CO23+ into C++O++O+. Phys. Rev. A 2011, 84, 062715. [Google Scholar] [CrossRef]
- Yan, S.; Zhu, X.L.; Zhang, P.; Ma, X.; Feng, W.T.; Gao, Y.; Xu, S.; Zhao, Q.S.; Zhang, S.F.; Guo, D.L.; et al. Observation of two sequential pathways of (CO2)3+ dissociation by heavy-ion impact. Phys. Rev. A 2016, 94, 032708. [Google Scholar] [CrossRef]
- Singh, R.K.; Lodha, G.S.; Sharma, V.; Prajapati, I.A.; Subramanian, K.P.; Bapat, B. Triply charged carbon dioxide molecular ion: Formation and fragmentation. Phys. Rev. A 2006, 74, 022708. [Google Scholar] [CrossRef]
- Kushawaha, R.K.; Kumar, S.S.; Prajapati, I.A.; Subramanian, K.P.; Bapat, B. Polarization dependence in non-resonant photo-triple-ionization of CO2. J. Phys. B 2009, 42, 105201. [Google Scholar] [CrossRef]
- Bryan, W.A.; Sanderson, J.H.; El-Zein, A.; Newell, W.R.; Taday, P.F.; Langley, A.J. Laser-induced Coulomb explosion, geometry modification and reorientation of carbon dioxide. J. Phys. B 2000, 33, 745. [Google Scholar] [CrossRef]
- Brichta, J.P.; Walker, S.J.; Helsten, R.; Sanderson, J.H. Ultrafast imaging of multielectronic dissociative ionization of CO2 in an intense laser field. J. Phys. B 2006, 40, 117. [Google Scholar] [CrossRef]
- Wu, C.; Wu, C.; Song, D.; Su, H.; Yang, Y.; Wu, Z.; Liu, X.; Liu, H.; Li, M.; Deng, Y.; et al. Nonsequential and sequential fragmentation of CO23+ in intense laser fields. Phys. Rev. Lett. 2013, 110, 103601. [Google Scholar] [CrossRef] [PubMed]
- Srivastav, S.; Bapat, B. Electron-impact-like feature in triple fragmentation of CO23+ under slow proton impact. Phys. Rev. A 2022, 105, 012801. [Google Scholar] [CrossRef]
- Sharma, V.; Bapat, B.; Mondal, J.; Hochlaf, M.; Giri, K.; Sathyamurthy, N. Dissociative double ionization of CO2: Dynamics, energy levels, and lifetime. J. Phys. Chem. A 2007, 111, 10205–10211. [Google Scholar] [CrossRef]
- Bhatt, P.; Singh, R.; Yadav, N.; Shanker, R. Formation, structure, and dissociation dynamics of CO2q+ (q≤3) ions due to impact of 12-keV electrons. Phys. Rev. A 2012, 85, 042707. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Lu, D.; Lu, G.C.; Wei, B.; Zhang, B.H.; Tang, Y.J.; Hutton, R.; Zou, Y. Fragmentation of CO22+ in collisions with low-energy electrons. Phys. Rev. A 2014, 61, 062705. [Google Scholar] [CrossRef]
- Hogreve, H. Stability properties of CO22+. J. Phys. B 1995, 28, L263. [Google Scholar] [CrossRef]
- Hochlaf, M.; Bennett, F.R.; Chambaud, G.; Rosmus, P. Theoretical study of the electronic states of CO2++. J. Phys. B 1998, 31, 2163–2175. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, B.Z.; Huang, M.B.; Meng, Q.; Tian, Z. Photodissociation mechanisms of the CO22+ dication studied using multi-state multiconfiguration second-order perturbation theory. J. Chem. Phys. 2013, 139, 174305. [Google Scholar] [CrossRef]
- Bise, R.T.; Choi, H.; Neumark, D.M. Photodissociation dynamics of the singlet and triplet states of the NCN radical. J. Chem. Phys. 1999, 111, 4923–4932. [Google Scholar] [CrossRef]
- Bise, R.T.; Hoops, A.A.; Choi, H.; Neumark, D.M. Photodissociation dynamics of the CNN free radical. J. Chem. Phys. 2000, 113, 4179–4189. [Google Scholar] [CrossRef]
- Bise, R.T.; Hoops, A.A.; Choi, H.; Neumark, D.M. Photoisomerization and Photodissociation Dynamics of the NCN, CNN, and HNCN Free Radicals. ACS Symp. Ser. 2001, 770, 296–311. [Google Scholar]
- Larimian, S.; Erattupuzha, S.; Mai, S.; Marquetand, P.; González, L.; Baltuška, A.; Kitzler, M.; Xie, X. Molecular oxygen observed by direct photoproduction from carbon dioxide. Phys. Rev. A 2017, 95, 011404. [Google Scholar] [CrossRef]
- Weltner, W., Jr.; Van Zee, R.J. Carbon molecules, ions, and clusters. Chem. Rev. 1989, 89, 1713–1747. [Google Scholar] [CrossRef]
- Van Orden, A.; Saykally, R.J.H. Small Carbon Clusters: Spectroscopy, Structure, and Energetics. Phys. Rep. 1998, 98, 2313–2358. [Google Scholar] [CrossRef] [PubMed]
- Maul, C.; Gericke, K.H. Photo induced three body decay. Int. Rev. Phys. Chem. 1997, 16, 1–79. [Google Scholar] [CrossRef]
- Strauss, C.E.M.; Houston, P.L. Correlations without coincidence measurements: Deciding between stepwise and concerted dissociation mechanisms for ABC → A + B + C. J. Phys. Chem. 1990, 94, 8751–8762. [Google Scholar] [CrossRef]
- Döner, R.; Mergel, V.; Jagutzki, O.; Spielberger, L.; Ullrich, J.; Moshammer, R.; Schmidt-Böcking, H. Cold Target Recoil Ion Momentum Spectroscopy: A ‘Momentum Microscope’ to View Atomic Collision Dynamic. Phys. Rep. 2000, 330, 95–192. [Google Scholar] [CrossRef]
- Ullrich, J.; Moshammer, R.; Dorn, A.; Dörner, R.; Schmidt, L.P.H.; Schmidt-Böcking, H. Recoil-ion and electron momentum spectroscopy: Reaction-microscopes. Rep. Prog. Phys. 2003, 66, 1463–1545. [Google Scholar] [CrossRef]
- Duley, A.; Tyagi, R.; Bari, S.B.; Kelkar, A.H. Design and characterization of a recoil ion momentum spectrometer for investigating molecular fragmentation dynamics upon MeV energy ion impact ionization. Rev. Sci. Instrum. 2022, 93, 113308. [Google Scholar] [CrossRef]
- Dujardin, G.; Winkoun, D. State to state study of the dissociation of doubly charged carbon dioxide cations. J. Chem. Phys. 1985, 83, 6222–6228. [Google Scholar] [CrossRef]
- Wang, E.; Shan, X.; Shi, Y.; Tang, Y.; Chen, X. Momentum imaging spectrometer for molecular fragmentation dynamics induced by pulsed electron beam. Rev. Sci. Instrum. 2013, 84, 123110. [Google Scholar] [CrossRef] [PubMed]
- Itikawa, Y. Cross Sections for Electron Collisions with Carbon Dioxide. J. Phys. Chem. Ref. Data 2002, 31, 749–767. [Google Scholar] [CrossRef]
- Field, T.A.; Eland, J.H.D. Lifetimes of metastable molecular doubly charged ions. Chem. Phys. Lett. 1993, 211, 436–442. [Google Scholar] [CrossRef]
- Slattery, A.E.; Field, T.A.; Ahmad, M.; Hall, R.I.; Lambourne, J.; Penent, F.; Lablanquie, P.; Eland, J.H.D. Spectroscopy and metastability of CO22+ molecular ions. J. Chem. Phys. 2005, 122, 084317. [Google Scholar] [CrossRef]
- Newton, A.S.; Sciamanna, A.F. Metastable Dissociation of the Doubly Charged Carbon Monoxide Ion. J. Chem. Phys. 1970, 53, 132–136. [Google Scholar] [CrossRef]
- Tsai, B.P.; Eland, J.H.D. Mass spectra and doubly charged ions in photoionization at 30.4 nm and 58.4 nm. Int. J. Mass Spectrom. Ion Phys. 1980, 36, 143–165. [Google Scholar] [CrossRef]
- Alagia, M.; Candori, P.; Falcinelli, S.; Lavollée, M.; Pirani, F.; Richter, R.; Stranges, S.; Vecchiocattivi, F. Double Photoionization of CO2 Molecules in the 34–50 eV Energy Range. J. Phys. Chem. A 2009, 113, 14755–14759. [Google Scholar] [CrossRef]
- Eland, J.H.D. Dynamics of fragmentation reactions from peak shapes in multiparticle coincidence experiments. Laser Chem. 1991, 11, 259–263. [Google Scholar] [CrossRef]
- Eland, J.H.D. The dynamics of three-body dissociations of dications studied by the triple coincidence technique PEPIPICO. Mol. Phys. 1987, 61, 725–745. [Google Scholar] [CrossRef]
- Tian, C.; Vidal, C.R. Single to quadruple ionization of CO2 due to electron impact. Phys. Rev. A 1998, 58, 3783. [Google Scholar] [CrossRef]
- Dalitz, R.H. On the analysis of -meson data and the nature of the -meson. Philos. Mag. J. Sci. 1953, 44, 1068–1080. [Google Scholar] [CrossRef]
- Laksman, J.; Månsson, E.P.; Grunewald, C.; Sankari, A.; Gisselbrecht, M.; Céolin, D.; Sorensen, S.L. Fragmentation of CO22+ in collisions with low-energy electrons. Phys. Rev. A 2012, 136, 104303. [Google Scholar]
- Guillemin, R.; Decleva, P.; Stener, M.; Bomme, C.; Marin, T.; Journel, L.; Marchenko, T.; Kushawaha, R.K.; Jänkälä, K.; Trcera, N.; et al. Selecting core-hole localization or delocalization in CS2 by photofragmentation dynamics. Nat. Comm. 2015, 6, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Wang, E.; Shan, X.; Shen, Z.; Gong, M.; Tang, Y.; Pan, Y.; Lau, K.C.; Chen, X. Pathways for nonsequential and sequential fragmentation of CO23+ investigated by electron collision. Phys. Rev. A 2015, 91, 052711. [Google Scholar] [CrossRef]
- Herzberg, G. Molecular Spectra and Molecular Structure II. Infrared and Raman Spectra of polyatomic molecules. Van Nostrand 1945, 200, 300–400. [Google Scholar]

| Molecular | Dissociation | KER |
|---|---|---|
| States | Limit | (eV) [22] |
| 6.01 | ||
| 6.11 | ||
| 6.24 | ||
| 6.51 | ||
| 5.37 | ||
| 7.93 | ||
| 8.15 | ||
| 8.98 | ||
| 9.50 | ||
| 10.05 | ||
| 10.68 |
| Fragmentation Channel | Experimental Results | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Theoretical Predictions [42,43] | Present Experiment | Electron Impact | |||||||
| s(i) | s(i) | s(d) | Concerted | Slope (Fitted) | R | 0.2 keV [19] | 0.6 keV [44] | 12 keV [18] | |
| O + CO | - | - | - | −1 | −1.09 ± 0.03 | 0.99 | −1.01 ± 0.01 | −1.00 ± 0.02 | −1.00 ± 0.02 |
| C + O + O | −0.5 | −2.33 | −1.0 | ∞ | −2.21 ± 0.01 | 0.99 | −1.75 ± 0.04 | −2.75 ± 0.04 | −2.75 ± 0.04 |
| O + O + C | −0.57 | - | −1.0 | −1 | −1.16 ± 0.02 | 0.97 | −1.03 ± 0.03 | −1.00 ± 0.02 | −1.00 ± 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duley, A.; Kelkar, A.H.
Fragmentation Dynamics of
Duley A, Kelkar AH.
Fragmentation Dynamics of
Duley, Avijit, and Aditya. H. Kelkar.
2023. "Fragmentation Dynamics of
Duley, A., & Kelkar, A. H.
(2023). Fragmentation Dynamics of







