Hypersatellite Kα Production in Trapped Ar Ions at KK Trielectronic Recombination Energies
Abstract
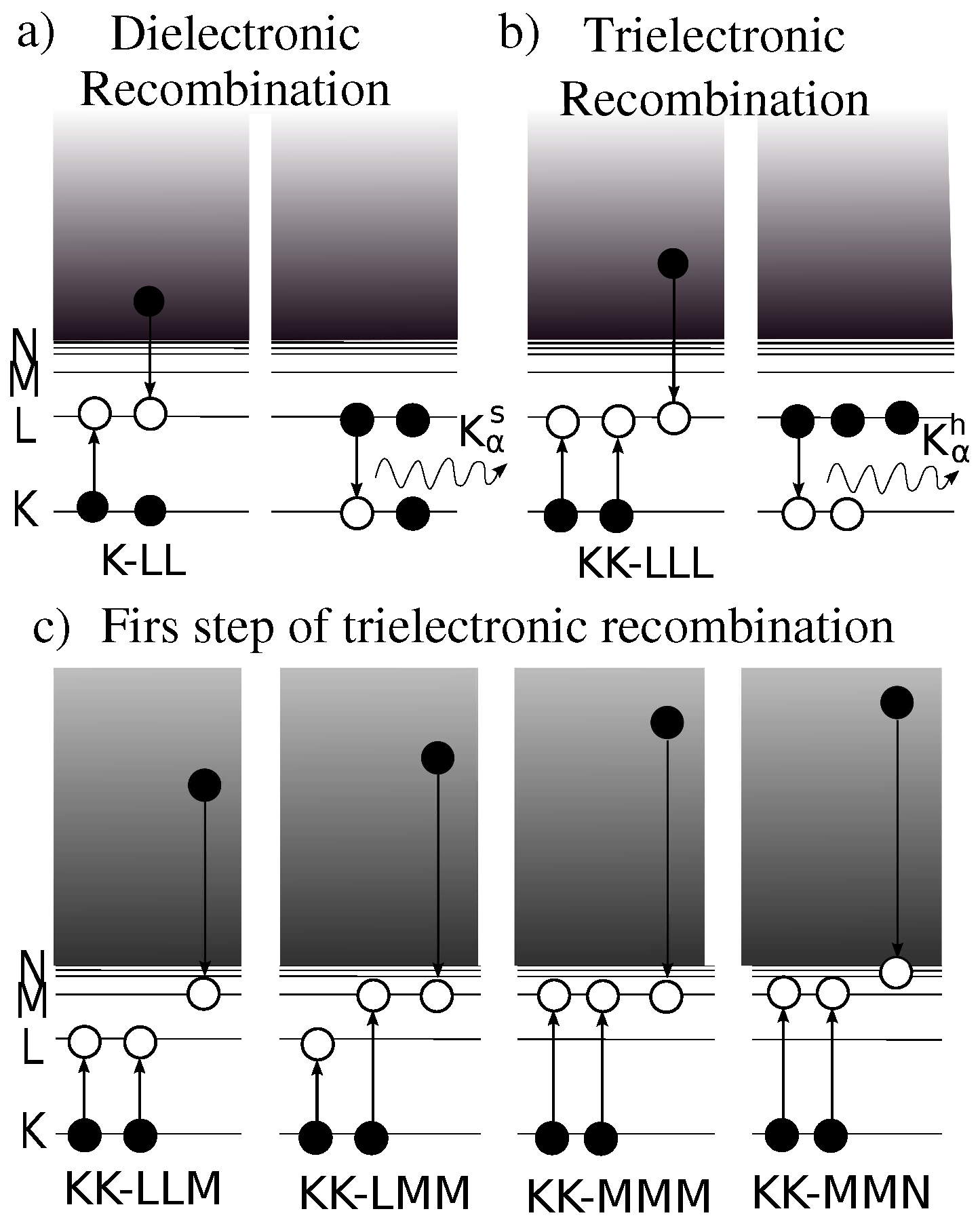
1. Introduction
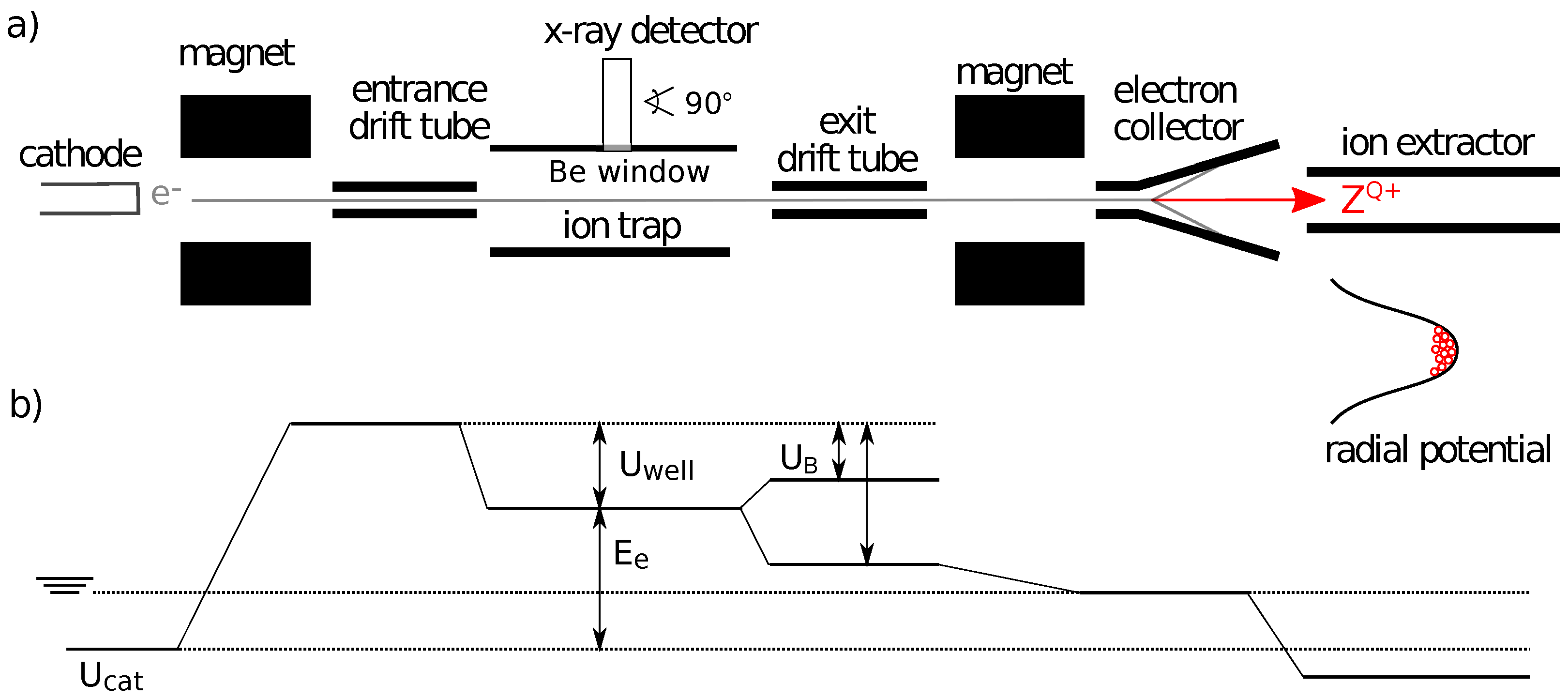
2. Experimental Setup
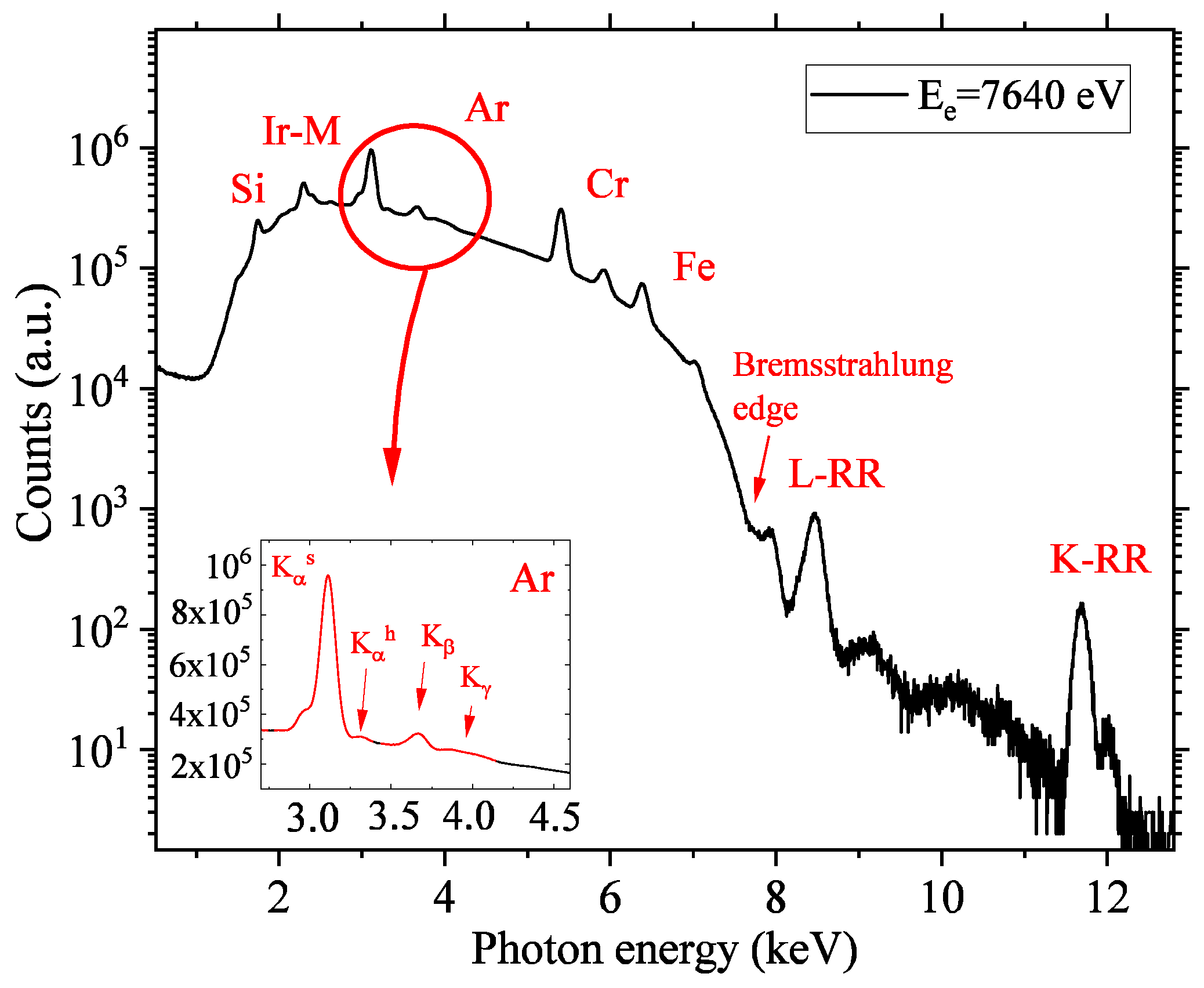
3. Results and Discussion
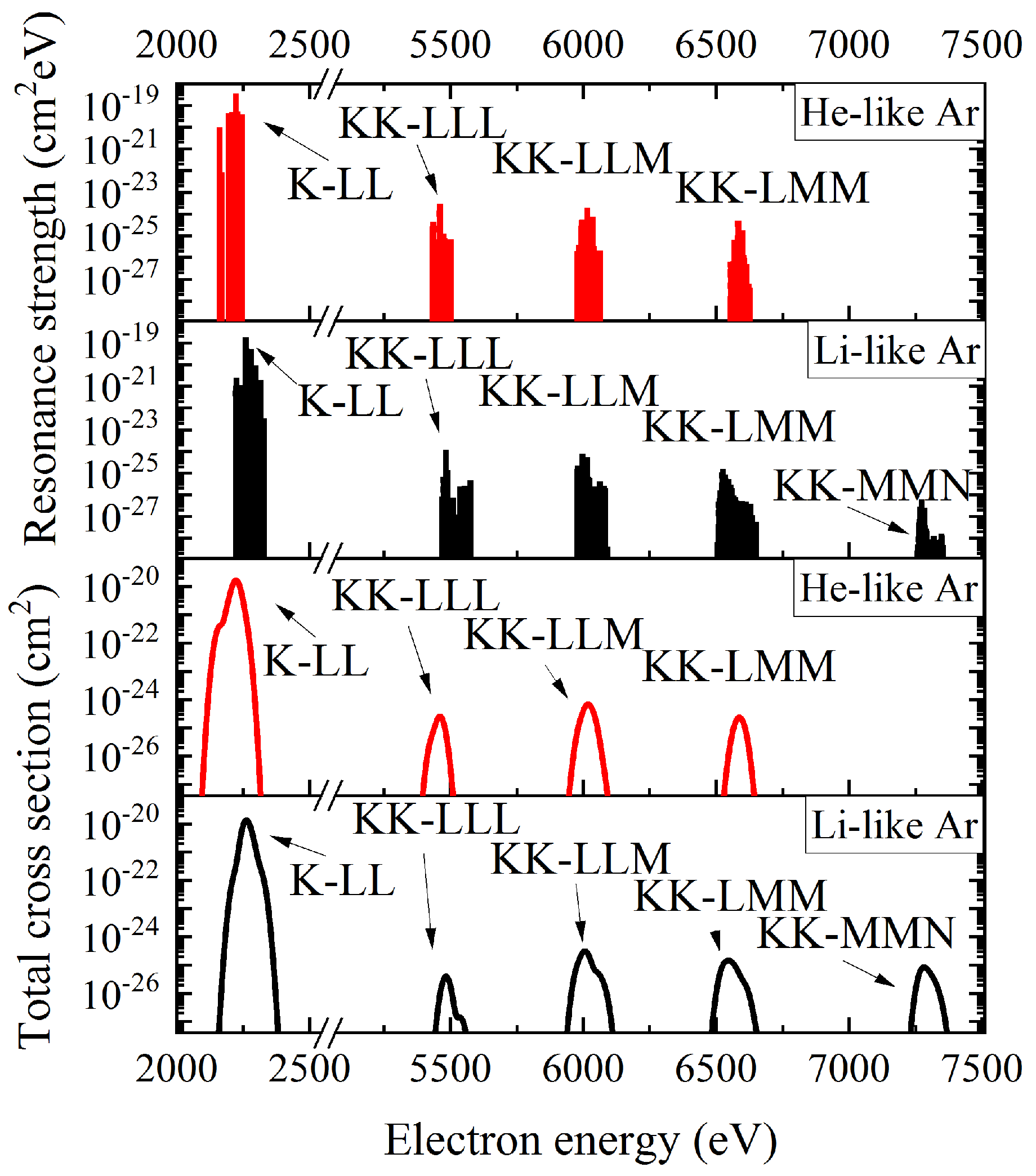
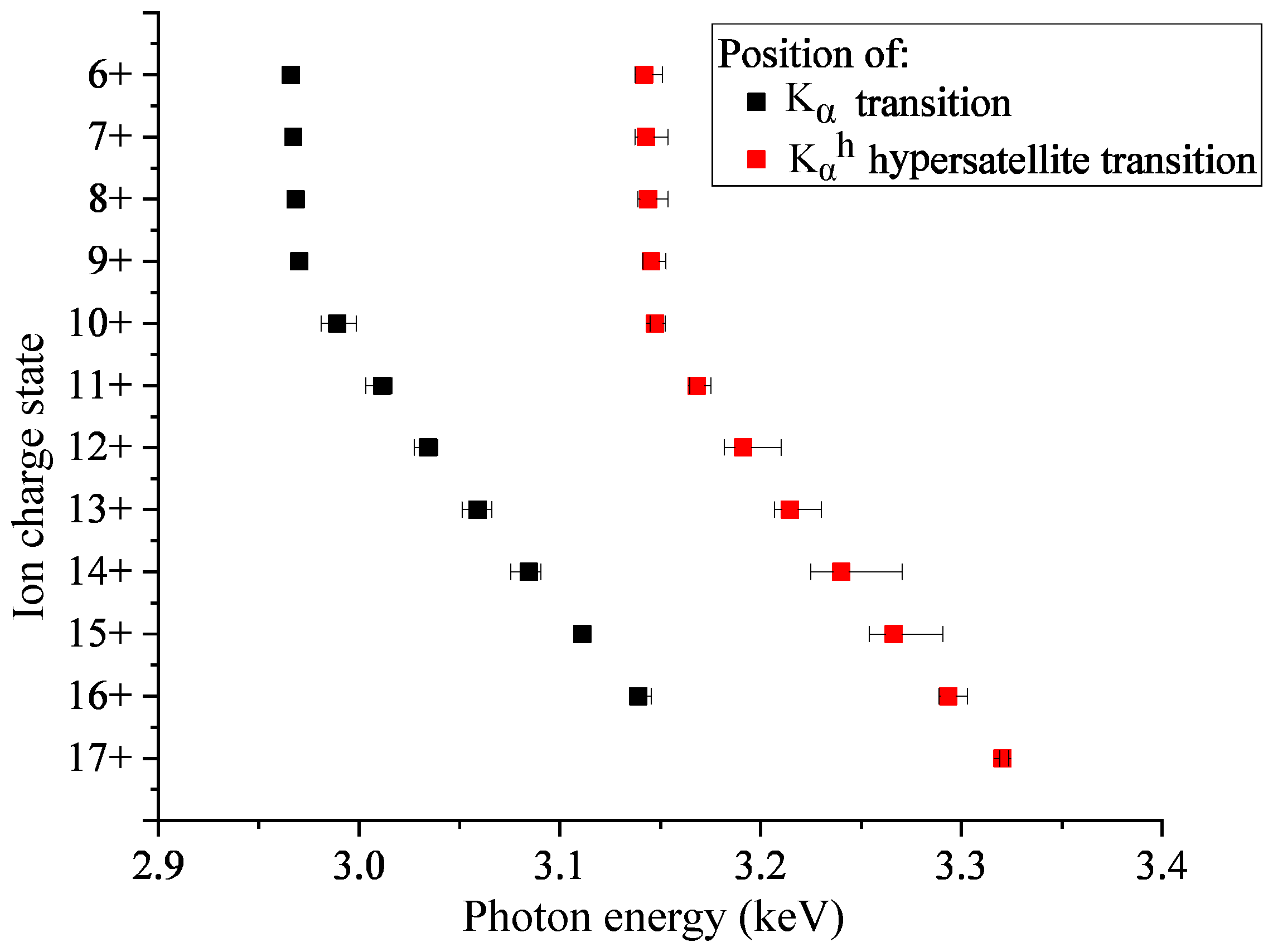
3.1. Selection of the Expected TR Energy Region
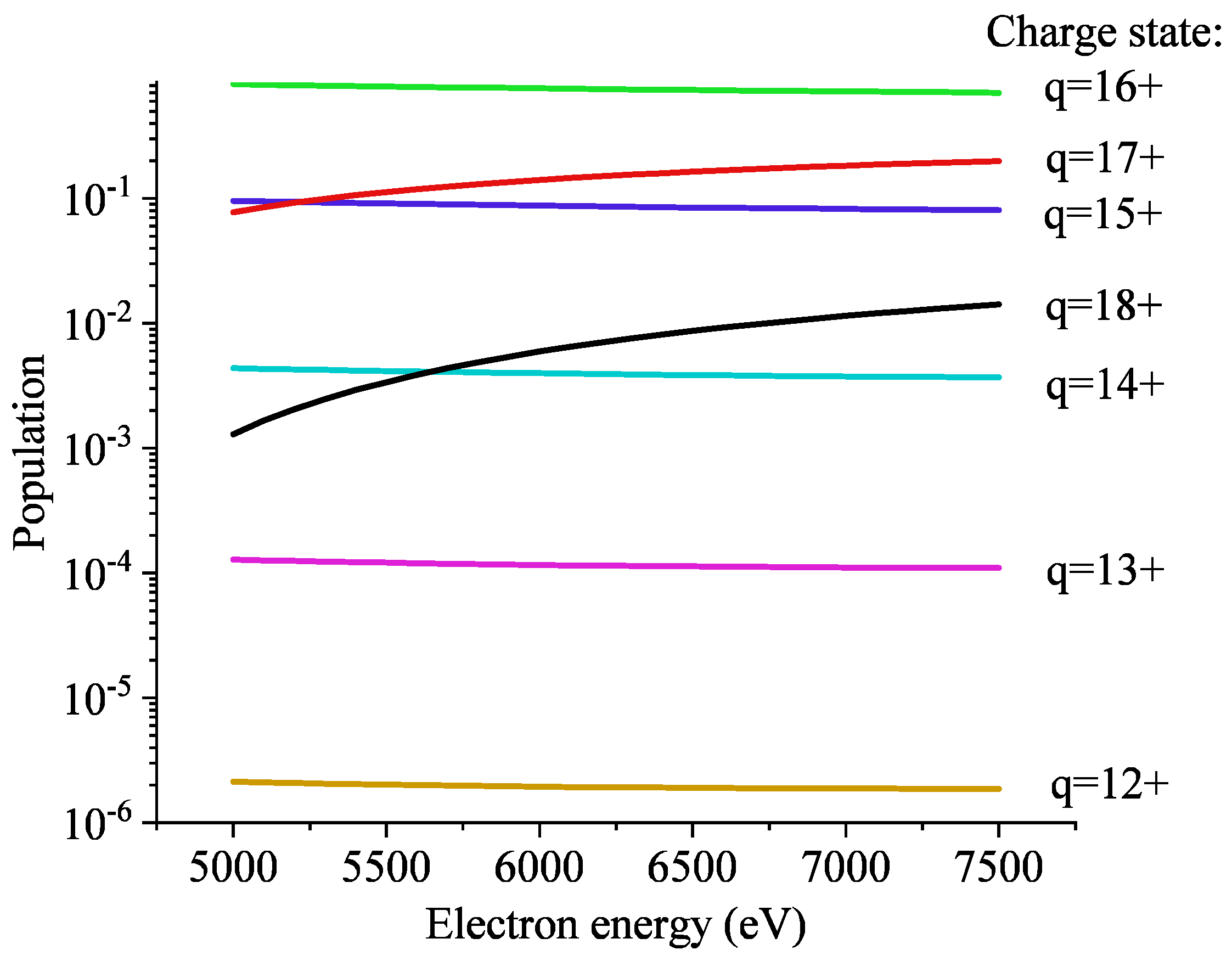
3.2. Ion Charge State Evolution in the Investigated Electron Energy Region
- Even if the TR process would take place for lower charge states, our measuring method would not be sensitive enough to this process. Thus, the collected hypersatellite K radiation would be only a very small fraction (≈) of a much stronger line.
- The observed K X-ray radiation is well separated from the K background for the highly charged ions.
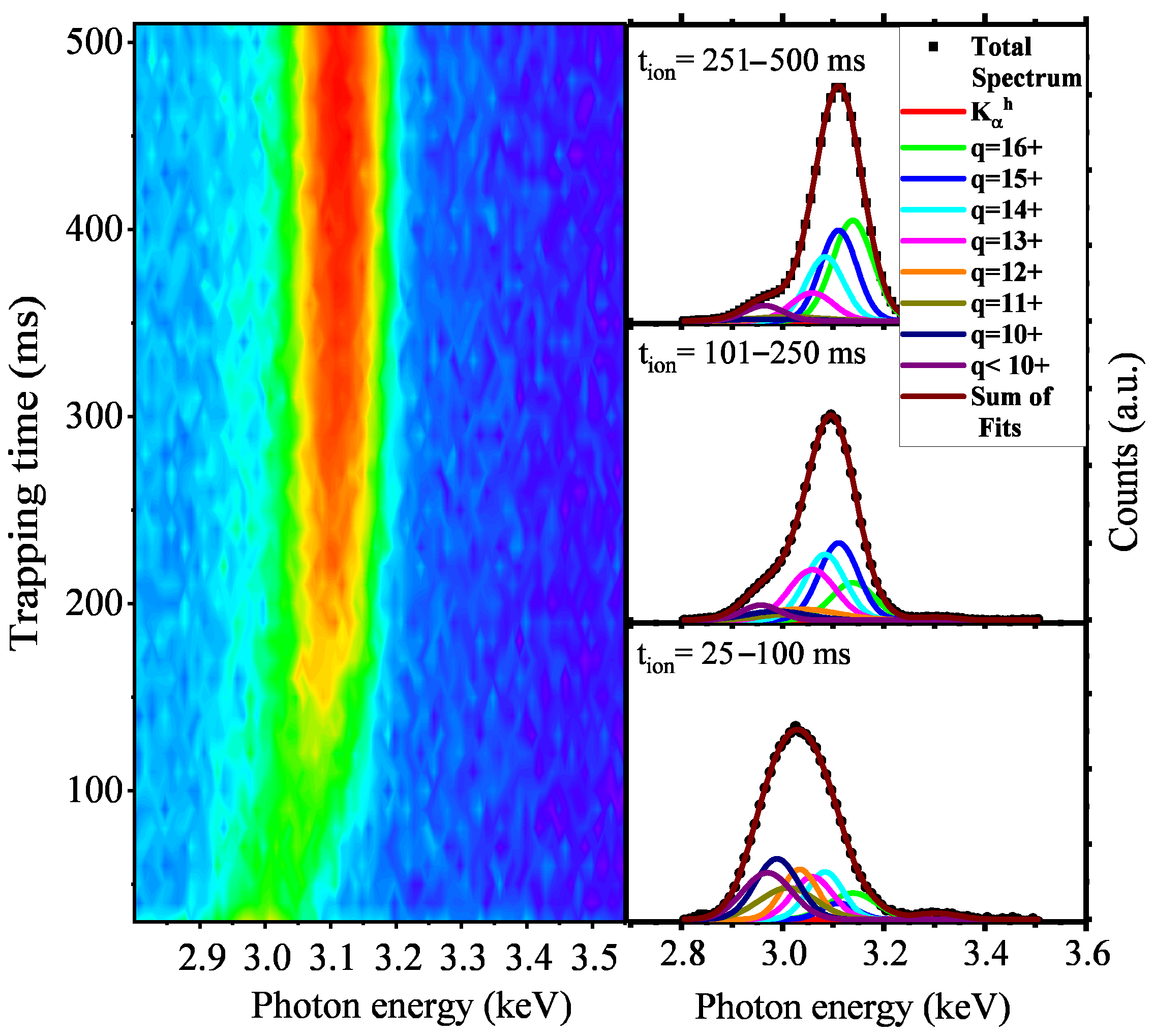
3.3. Simulations of the Time Evolution of the Ion Charge State
3.4. Data Analysis
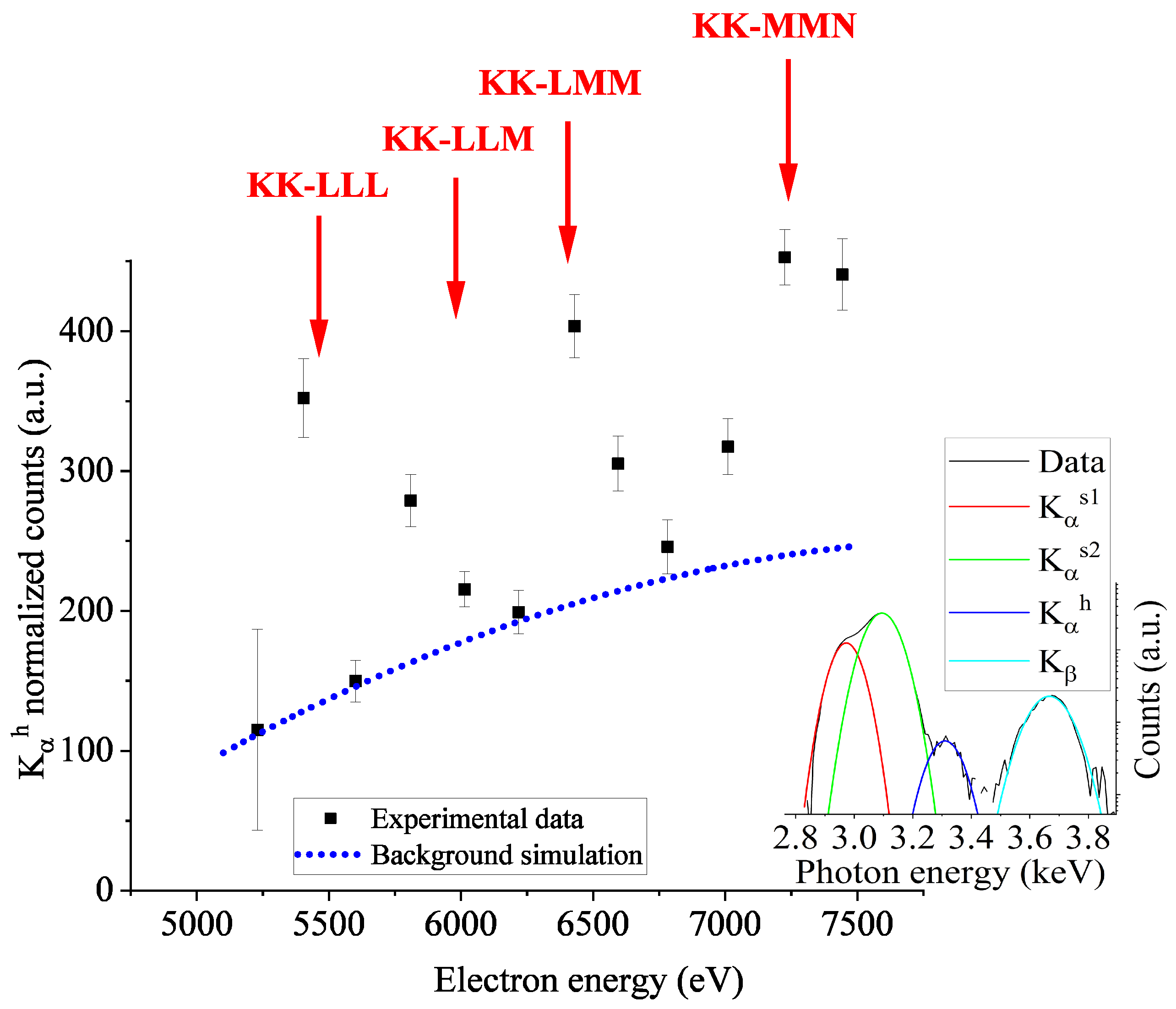
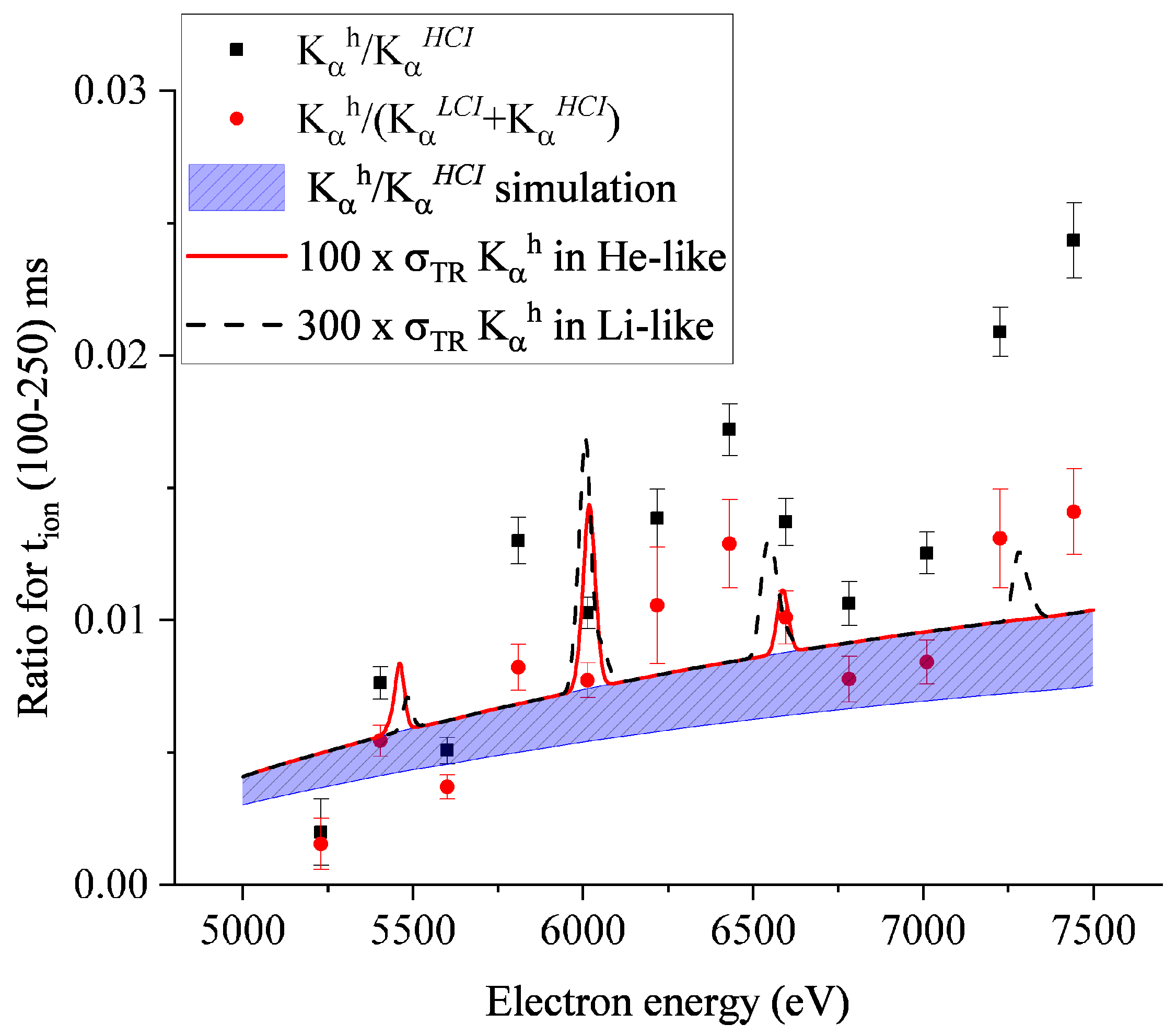
3.5. Observed Enhancement of the Hypersatellite Transition
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EBIT | Electron Beam Ion Trap |
| DR | Dielectronic recombination |
| TR | Intershell trielectronic recombination |
| QR | Intershell quadruelectronic recombination |
References
- Beiersdorfer, P.; Boyce, K.; Brown, G.; Chen, H.; Kahn, S.; Kelley, R.; May, M.; Olson, R.; Porter, F.; Stahle, C. Laboratory simulation of charge exchange-produced X-ray emission from comets. Science 2003, 300, 1558–1559. [Google Scholar] [CrossRef] [PubMed]
- Beiersdorfer, P.; Phillips, T.W.; Wong, K.L.; Marrs, R.E.; Vogel, D.A. Measurement of level-specific dielectronic-recombination cross sections of heliumlike Fe xxv. Phys. Rev. A 1992, 46, 3812–3820. [Google Scholar] [CrossRef] [PubMed]
- Gildart, L.; Ewald, A.W. Electron Mobility and Luminescence Efficiency in Cadmium Sulfide. Phys. Rev. 1951, 83, 359–363. [Google Scholar] [CrossRef]
- Auger, P. L’effet Photoélectrique Composé. Ph.D. Thesis, l’Université Paris-Sud, Paris, France, 1926; p. 183. [Google Scholar]
- Kilgus, G.; Habs, D.; Schwalm, D.; Wolf, A.; Badnell, N.R.; Müller, A. High-resolution measurement of dielectronic recombination of lithiumlike Cu26+. Phys. Rev. A 1992, 46, 5730–5740. [Google Scholar] [CrossRef]
- Lampert, A.; Wolf, A.; Habs, D.; Kenntner, J.; Kilgus, G.; Schwalm, D.; Pindzola, M.S.; Badnell, N.R. High-resolution measurement of the dielectronic recombination of fluorinelike selenium ions. Phys. Rev. A 1996, 53, 1413–1423. [Google Scholar] [CrossRef]
- Lestinsky, M.; Badnell, N.R.; Bernhardt, D.; Grieser, M.; Hoffmann, J.; Lukić, D.; Müller, A.; Orlov, D.A.; Repnow, R.; Savin, D.W.; et al. Electron-ion recombination of Fe X forming Fe IX and of Fe XI forming Fe X: Laboratory measurements and theoretical calculations. Astrophys. J. 2009, 698, 648–659. [Google Scholar] [CrossRef]
- Lestinsky, M.; Badnell, N.; Bernhardt, D.; Bing, D.; Grieser, M.; Hahn, M.; Hoffmann, J.; Jordon-Thaden, B.; Krantz, C.; Novotný, O.; et al. Electron-ion recombination of Mg6+ forming Mg5+ and of Mg7+ forming Mg6+: Laboratory measurements and theoretical calculations. Astrophys. J. 2012, 758, 40. [Google Scholar] [CrossRef]
- Schippers, S.; Bernhardt, D.; Müller, A.; Krantz, C.; Grieser, M.; Repnow, R.; Wolf, A.; Lestinsky, M.; Hahn, M.; Novotný, O.; et al. Dielectronic recombination of xenonlike tungsten ions. Phys. Rev. A 2011, 83, 012711. [Google Scholar] [CrossRef]
- Schippers, S.; Bernhardt, D.; Grieser, M.; Hahn, M.; Krantz, C.; Lestinsky, M.; Novotný, O.; Repnow, R.; Savin, D.; Wolf, A.; et al. Recombination of Au20+ at low electron–ion collision energies. Phys. Scr. 2011, 2011, 014039. [Google Scholar] [CrossRef]
- Brandau, C.; Kozhuharov, C.; Lestinsky, M.; Müller, A.; Schippers, A.; Stöhlker, T. Storage-ring experiments on dielectronic recombination at the interface of atomic and nuclear physics. Phys. Scr. 2015, 2015, T166. [Google Scholar] [CrossRef]
- Gall, A.C.; Foster, A.R.; Silwal, R.; Dreiling, J.M.; Borovik, A.; Kilgore, E.; Ajello, M.; Gillaspy, J.D.; Ralchenko, Y.; Takács, E. EBIT Observation of Ar Dielectronic Recombination Lines near the Unknown Faint X-ray Feature Found in the Stacked Spectrum of Galaxy Clusters. Astrophys. J. 2019, 872, 194. [Google Scholar] [CrossRef]
- Knapp, D.A.; Marrs, R.E.; Levine, M.A.; Bennett, C.L.; Chen, M.H.; Henderson, J.R.; Schneider, M.B.; Scofield, J.H. Dielectronic recombination of heliumlike nickel. Phys. Rev. Lett. 1989, 62, 2104–2107. [Google Scholar] [CrossRef]
- Knapp, D.A.; Marrs, R.E.; Schneider, M.B.; Chen, M.H.; Levine, M.A.; Lee, P. Dielectronic recombination of heliumlike ions. Phys. Rev. A 1993, 47, 2039–2046. [Google Scholar] [CrossRef]
- Fuchs, T.; Biedermann, C.; Radtke, R.; Behar, E.; Doron, R. Channel-specific dielectronic recombination of highly charged krypton. Phys. Rev. A 1998, 58, 4518–4525. [Google Scholar] [CrossRef]
- Radtke, R.; Biedermann, C.; Fuchs, T.; Fußmann, G.; Beiersdorfer, P. Measurement of the radiative cooling rates for high-ionization species of krypton using an electron beam ion trap. Phys. Rev. E 2000, 61, 1966–1974. [Google Scholar] [CrossRef] [PubMed]
- Beilmann, C.; Crespo López-Urrutia, J.R.; Mokler, P.H.; Ullrich, J. High resolution resonant recombination measurements using evaporative cooling technique. J. Instrum. 2010, 5, C09002. [Google Scholar] [CrossRef]
- Shah, C.; López-Urrutia, J.R.C.; Gu, M.F.; Pfeifer, T.; Marques, J.; Grilo, F.; Santos, J.P.; Amaro, P. Revisiting the Fe xvii Line Emission Problem: Laboratory Measurements of the 3s–2p and 3d–2p Line-formation Channels. Astrophys. J. 2019, 881, 100. [Google Scholar] [CrossRef]
- Schnell, M.; Gwinner, G.; Badnell, N.R.; Bannister, M.E.; Böhm, S.; Colgan, J.; Kieslich, S.; Loch, S.D.; Mitnik, D.; Müller, A.; et al. Observation of Trielectronic Recombination in Be-like Cl Ions. Phys. Rev. Lett. 2003, 91, 043001. [Google Scholar] [CrossRef] [PubMed]
- Orban, I.; Loch, S.D.; Böhm, S.; Schuch, R. Recombination rate coefficients of Be-like Si. Astrophys. J. 2010, 721, 1603–1607. [Google Scholar] [CrossRef]
- Beilmann, C.; Postavaru, O.; Arntzen, L.H.; Ginzel, R.; Keitel, C.H.; Mäckel, V.; Mokler, P.H.; Simon, M.C.; Tawara, H.; Tupitsyn, I.I.; et al. Intershell trielectronic recombination with K-shell excitation in Kr30+. Phys. Rev. A 2009, 80, 050702. [Google Scholar] [CrossRef]
- Beilmann, C.; Mokler, P.H.; Bernitt, S.; Keitel, C.H.; Ullrich, J.; Crespo López-Urrutia, J.R.; Harman, Z. Prominent Higher-Order Contributions to Electronic Recombination. Phys. Rev. Lett. 2011, 107, 143201. [Google Scholar] [CrossRef] [PubMed]
- Beilmann, C.; Harman, Z.; Mokler, P.H.; Bernitt, S.; Keitel, C.H.; Ullrich, J.; Crespo López-Urrutia, J.R. Major role of multielectronic K-L intershell resonant recombination processes in Li- to O-like ions of Ar, Fe, and Kr. Phys. Rev. A 2013, 88. [Google Scholar] [CrossRef]
- Shah, C.; Amaro, P.; Steinbrügge, R.; Beilmann, C.; Bernitt, S.; Fritzsche, S.; Surzhykov, A.; Crespo López-Urrutia, J.R.; Tashenov, S. Strong higher-order resonant contributions to X-ray line polarization in hot plasmas. Phys. Rev. E 2016, 93, 061201. [Google Scholar] [CrossRef] [PubMed]
- Shah, C.; Jörg, H.; Bernitt, S.; Dobrodey, S.; Steinbrügge, R.; Beilmann, C.; Amaro, P.; Hu, Z.; Weber, S.; Fritzsche, S.; et al. Erratum: Polarization measurement of dielectronic recombination transitions in highly charged krypton ions [Phys. Rev. A 92, 042702 (2015)]. Phys. Rev. A 2016, 94, 029905. [Google Scholar] [CrossRef]
- Biela-Nowaczyk, W.; Amaro, P.; Grilo, F.; Warczak, A. Higher-Order Recombination Processes in Argon Ions Observed via X-ray Emission in an EBIT. Atoms 2022, 11, 1. [Google Scholar] [CrossRef]
- Zaharakis, K.E.; Haar, R.R.; Woitke, O.; Zhu, M.; Tanis, J.A.; Badnell, N.R. Recombination in Kr34++H2 collisions. Phys. Rev. A 1995, 52, 2910–2914. [Google Scholar] [CrossRef]
- Chevallier, M.; Cohen, C.; Cue, N.; Dauvergne, D.; Dural, J.; Gangnan, P.; Kirsch, R.; L’Hoir, A.; Lelièvre, D.; Libin, J.F.; et al. Upper-limit determination of resonant trielectronic recombination cross-section for krypton using crystal channeling. Phys. Rev. A 2000, 61, 022724. [Google Scholar] [CrossRef]
- Biela, W.; Warczak, A.; Mucha, A.; Malarz, A. Enhanced Ar-K X-ray emission observed in EBIT at electron energies around 6500 eV. X-ray Spectrom. 2019, 48, 696–699. [Google Scholar] [CrossRef]
- Herrmann, G. Optical Theory of Thermal Velocity Effects in Cylindrical Electron Beams. J. Appl. Phys. 1958, 29, 127–136. [Google Scholar] [CrossRef]
- Currell, F.; Fussman, G. Physics of Electron Beam Ion Traps and Sources. IEEE Trans. Plasma Sci. 2005, 33, 1763–1777. [Google Scholar] [CrossRef]
- Penetrante, B.M.; Bardsley, J.N.; Levine, M.A.; Knapp, D.A.; Marrs, R.E. Evaporative cooling of highly charged dysprosium ions in an enhanced electron-beam ion trap. Phys. Rev. A 1991, 43, 4873–4882. [Google Scholar] [CrossRef] [PubMed]
- Schnopper, H.W.; Delvaille, J.P.; Kalata, K.; Sohval, A.R.; Abdulwahab, M.; Jones, K.W.; Wegner, H.E. X-ray measurements of bremsstrahlung and electron capture by fast positive ions. Phys. Lett. A 1974, 47, 61–62. [Google Scholar] [CrossRef]
- Beyer, H.; Kluge, H.J.; Shevelko, V. X-ray Radiation of Highly Charged Ions; Springer: Berlin/Heildelberg, Germany, 2010. [Google Scholar]
- Grilo, F.; Shah, C.; Kühn, S.; Steinbrügge, R.; Fujii, K.; Marques, J.; Feng Gu, M.; Paulo Santos, J.; Crespo López-Urrutia, J.R.; Amaro, P. Comprehensive Laboratory Measurements Resolving the LMM Dielectronic Recombination Satellite Lines in Ne-like Fe xvii Ions. Astrophys. J. 2021, 913, 140. [Google Scholar] [CrossRef]
- Gu, M.F. The flexible atomic code. Can. J. Phys. 2008, 86, 675–689. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Y.; Nakamura, N. Resonance strength for KLL dielectronic recombination of hydrogenlike krypton. Phys. Rev. A 2013, 87, 052706. [Google Scholar] [CrossRef]
- Stobbe, M. Zur Quantenmechanik photoelektrischer Prozesse. Ann. Der Phys. 1930, 399, 661–715. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biela-Nowaczyk, W.; Amaro, P.; Grilo, F.; La Mantia, D.S.; Tanis, J.; Warczak, A. Hypersatellite Kα Production in Trapped Ar Ions at KK Trielectronic Recombination Energies. Atoms 2023, 11, 58. https://doi.org/10.3390/atoms11030058
Biela-Nowaczyk W, Amaro P, Grilo F, La Mantia DS, Tanis J, Warczak A. Hypersatellite Kα Production in Trapped Ar Ions at KK Trielectronic Recombination Energies. Atoms. 2023; 11(3):58. https://doi.org/10.3390/atoms11030058
Chicago/Turabian StyleBiela-Nowaczyk, Weronika, Pedro Amaro, Filipe Grilo, David S. La Mantia, John Tanis, and Andrzej Warczak. 2023. "Hypersatellite Kα Production in Trapped Ar Ions at KK Trielectronic Recombination Energies" Atoms 11, no. 3: 58. https://doi.org/10.3390/atoms11030058
APA StyleBiela-Nowaczyk, W., Amaro, P., Grilo, F., La Mantia, D. S., Tanis, J., & Warczak, A. (2023). Hypersatellite Kα Production in Trapped Ar Ions at KK Trielectronic Recombination Energies. Atoms, 11(3), 58. https://doi.org/10.3390/atoms11030058






