Interaction of Electrons and Positrons with Protons Aligned in One-Dimension Line
Abstract
1. Introduction
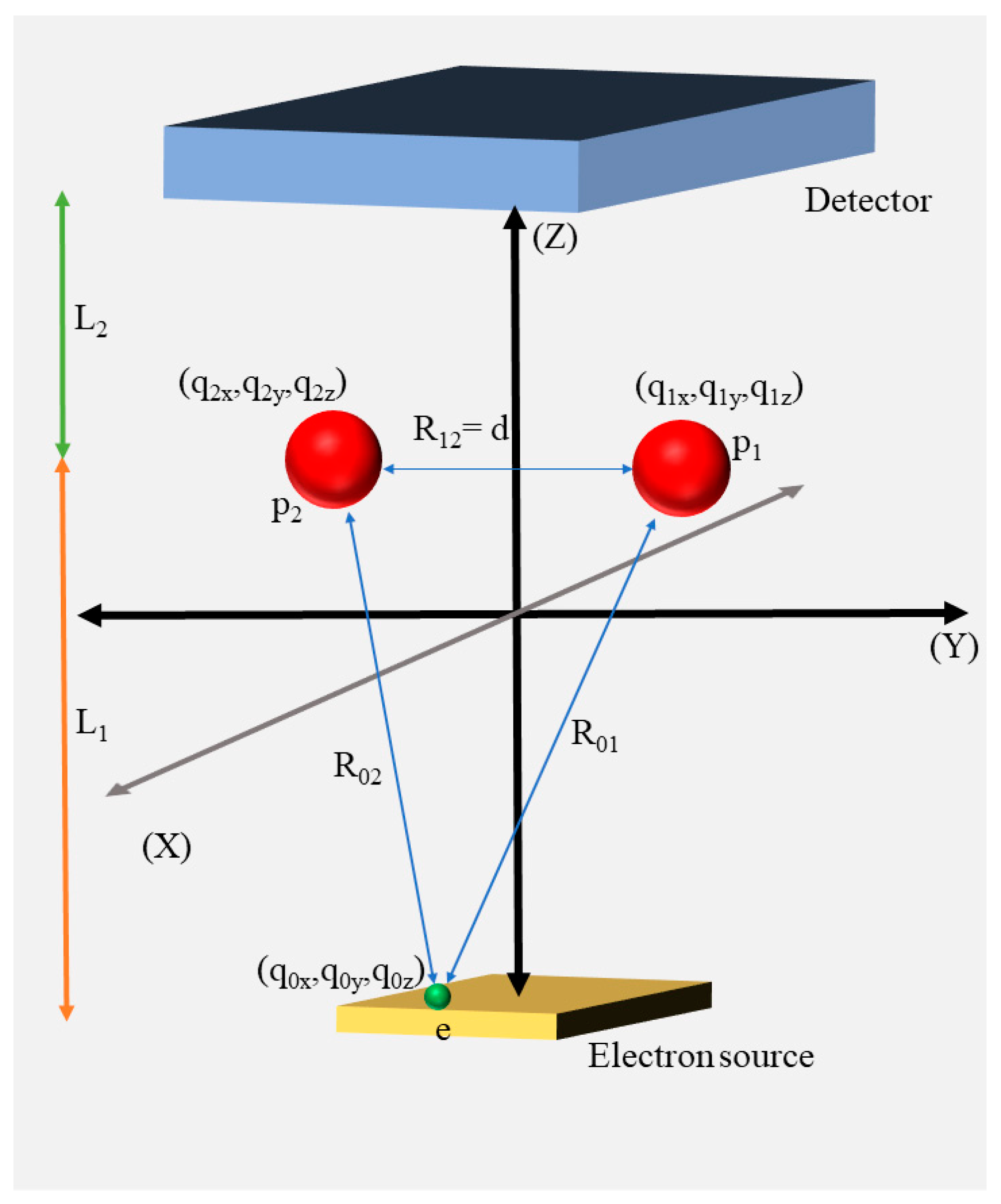
2. Theory
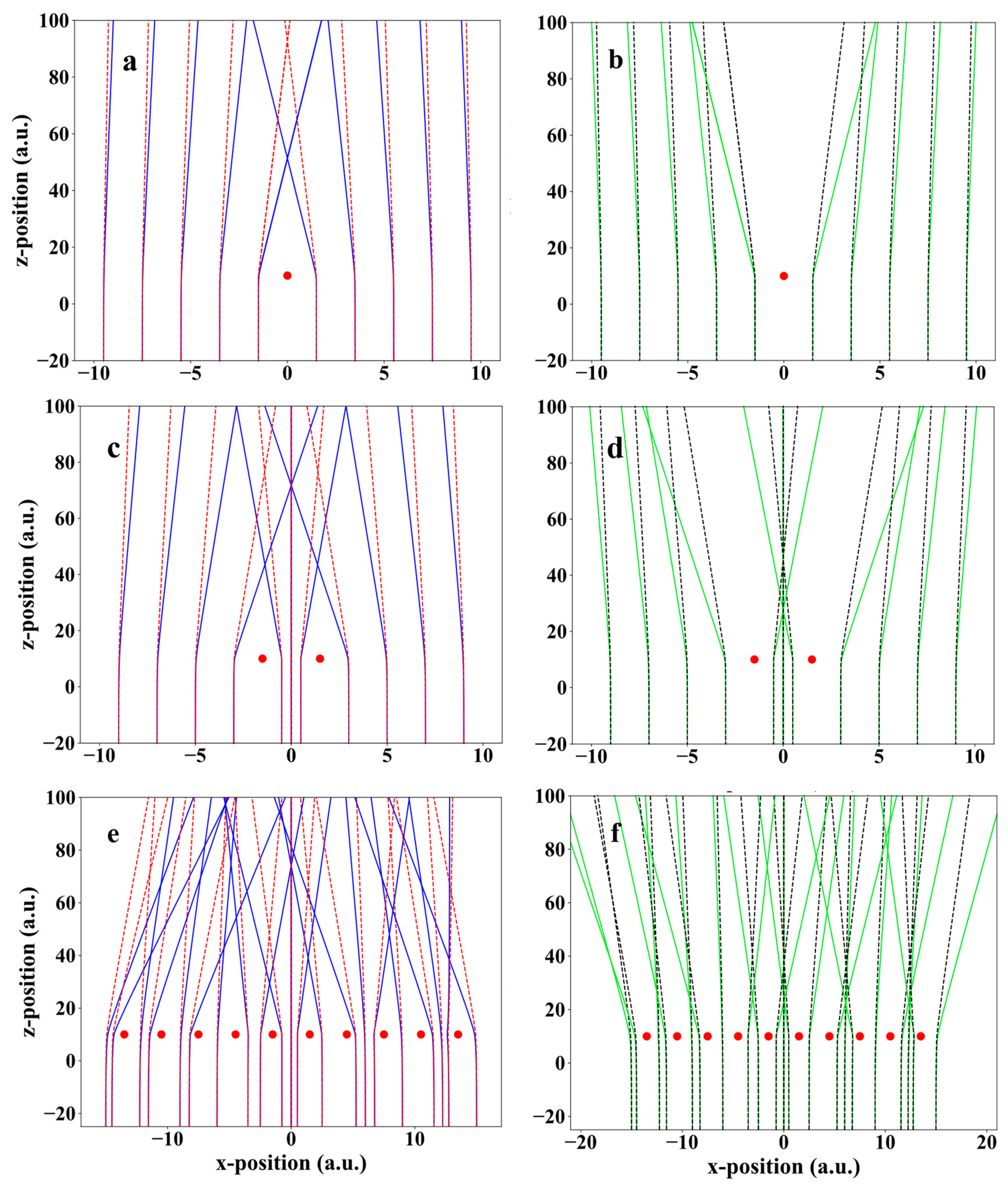
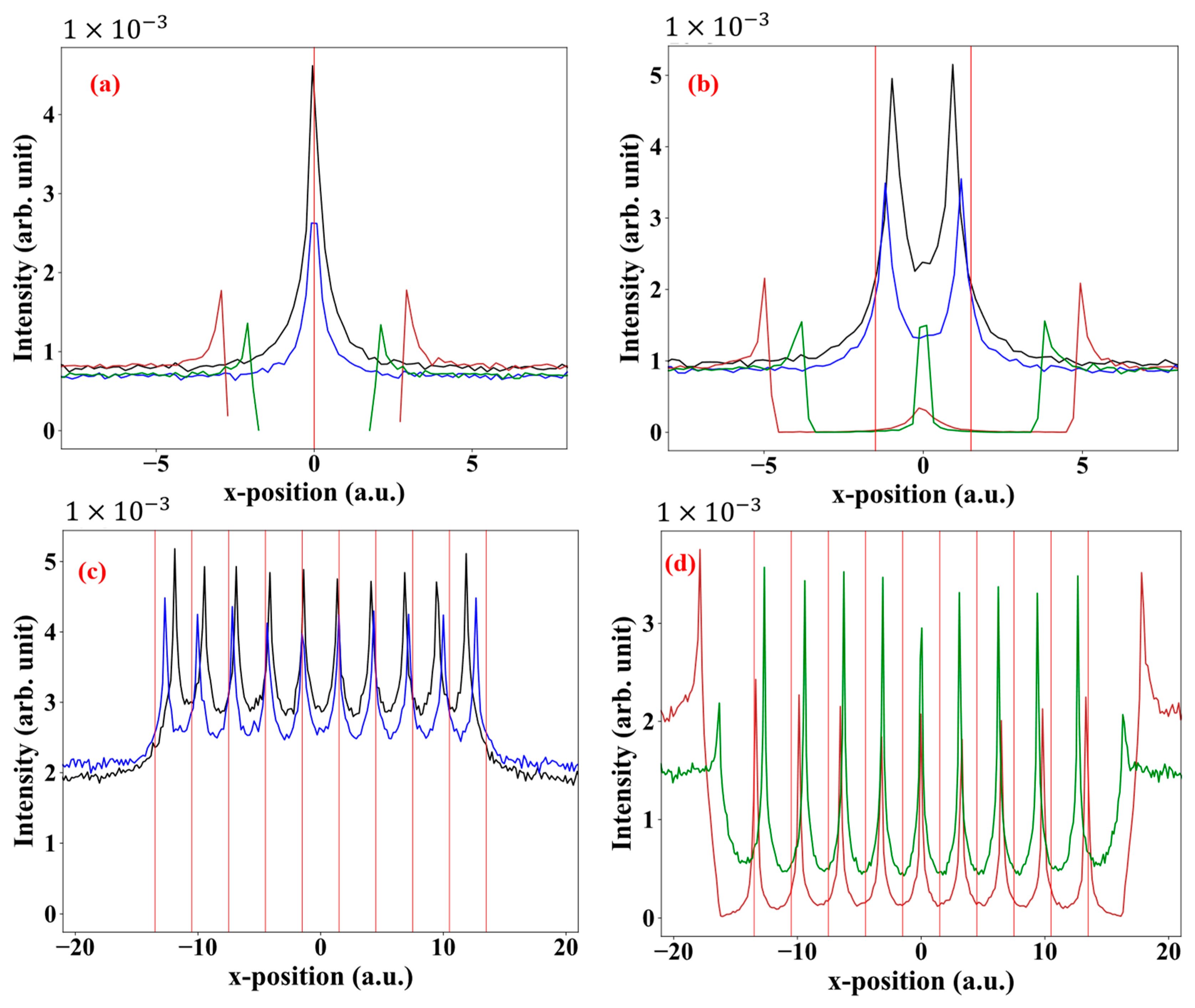
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tőkési, K. The role of projectile double scattering in positron–atom collisions. Radiat. Phys. Chem. 2007, 76, 624–626. [Google Scholar] [CrossRef]
- Afroz, S.; Haque, M.M.; Fazlul Haque, A.K.; Jakubassa-Amundsen, D.H.; Patoary, M.A.R.; Shorifuddoza, M.; Khandker, M.H.; Uddin, A.M. Elastic scattering of electrons and positrons from 115In atoms over the energy range 1 eV–0.5 GeV. Results Phys. 2020, 18, 103197. [Google Scholar] [CrossRef]
- Makochekanwa, C.; Kawate, H.; Sueoka, O.; Kimura, M.; Kitajima, M.; Hoshino, M.; Tanaka, H. Total and elastic cross-sections of electron and positron scattering from C3H4 molecules (allene and propyne). Chem. Phys. Lett. 2003, 368, 82–86. [Google Scholar] [CrossRef]
- Sueoka, O.; Makochekanwa, C.; Tanino, H.; Kimura, M. Total cross-section measurements for positrons and electrons colliding with alkane molecules: Normal hexane and cyclohexane. Phys. Rev. A 2005, 72, 042705. [Google Scholar] [CrossRef]
- Horowitz, C.J. Parity violation in astrophysics. Eur. Phys. J. A 2005, 24, 167–170. [Google Scholar] [CrossRef]
- Hossain, M.I.; Haque, A.; Patoary, M.A.R.; Uddin, M.A.; Basak, A.K. Elastic scattering of electrons and positrons by atomic magnesium. Eur. Phys. J. D 2016, 70, 41. [Google Scholar] [CrossRef]
- Crooks, G.B.; Rudd, M.E. Experimental Evidence for the Mechanism of Charge Transfer into Continuum States. Phys. Rev. Lett. 1970, 25, 1599. [Google Scholar] [CrossRef]
- Kövér, A.; Szabó, G.; Gulyás, L.; Tőkési, K.; Berényi, D.; Heil, O.; Groeneveld, K.O. Electron emission at backward angles from He2+, He+ (2 mev) → He, Ne, Ar collision systems. J. Phys. Colloq. 1987, 48, C9-289–C9-291. [Google Scholar] [CrossRef]
- Kövér, A.; Szabó, G.; Gulyás, L.; Tőkési, K.; Berényi, D.; Heil, O.; Groeneveld, K.O. The electron loss process at backward observation angles in collision systems He+ (2 MeV)-He, Ne, Ar. J. Phys. B At. Mol. Opt. Phys. 1988, 21, 3231. [Google Scholar] [CrossRef]
- Tőkési, K.; Mukoyama, T. Theoretical Investigation of the ECC Peak for Charged Particles with the CTMC Method. Bull. Inst. Chem. Res. Kyoto Univ. 1994, 72, 62–68. [Google Scholar]
- Gagyi-Pálffy, A.C.; Barna, I.F.; Gulyás, L.; Tőkési, K. Angular Differential Cross-Section for Ionization of Helium in C6+ Ion Collision. Chin. Phys. Lett. 2004, 21, 1258. [Google Scholar] [CrossRef]
- Tőkési, K.; Kövér, A. Existence of the electron capture to the continuum peak at positron impact. Nucl. Instrum. Methods Phys. Res. B Beam Interact. Mater. At. 1999, 154, 259–262. [Google Scholar] [CrossRef]
- Tőkési, K.; Kövér, A.J. Electron capture to the continuum at 54.4 eV positron-argon atom collisions. Phys. B At. Mol. Opt. Phys. 2000, 33, 3067. [Google Scholar] [CrossRef]
- Barna, I.F.; Tőkési, K.; Gulyás, L.; Burgdörfer, J. Total and angular differential cross sections of electrons emitted in collision between antiprotons and helium atoms. Radiat. Phys. Chem. 2007, 76, 495–498. [Google Scholar] [CrossRef]
- Tőkési, K.; Sarkadi, L.; Mukoyama, T.J. Model calculation of the electron capture to the continuum peak at neutral projectile impact. Phys. B At. Mol. Opt. Phys. 1997, 30, L123. [Google Scholar] [CrossRef]
- Hillenbrand, P.M.; Hagmann, S.; Groshev, M.E.; Banas, D.; Benis, P.E.; Brandau, C.; De Filippo, E.; Forstner, O.; Glorius, J.; Grisenti, R.E.; et al. Radiative electron capture to the continuum in U 89 + + N 2 collisions: Experiment and theory. Phys. Rev. A 2020, 101, 022708. [Google Scholar] [CrossRef]
- Nanos, S.; Quinto, M.A.; Madesis, I.; Laoutaris, A.; Zouros, T.J.M.; Rivarola, R.D.; Monti, J.M.; Benis, E.P. Subshell contributions to electron capture into the continuum in MeV/u collisions of deuterons with multielectron targets. Phys. Rev. A 2020, 105, 022806. [Google Scholar] [CrossRef]
- Olson, R.E.; Salop, A. Charge-transfer and impact-ionization cross sections for fully and partially stripped positive ions colliding with atomic hydrogen. Phys. Rev. A 1977, 16, 531–541. [Google Scholar] [CrossRef]
- Tőkési, K.; Hock, G. Double electron capture in collision up to 1500 keV/amu projectile impact. J. Phys. B 1996, 29, L119–L125. [Google Scholar] [CrossRef]
- Olson, R.E.; Reinhold, C.O.; Schultz, D.R. High-Energy Ion-Atom Collisions. In Proceedings of the IVth Workshop on High-Energy Ion-Atom Collision Processes, Debrecen, Hungary, 17–19 September 1990. [Google Scholar]
- Tőkési, K.; DuBois, R.D.; Mukoyama, T. Interaction of positronium with helium atoms—The classical treatment of the 5-body collision system. Eur. Phys. J. D 2014, 68, 255. [Google Scholar] [CrossRef]
- Tőkési, K.; Hock, G. Versatility of the exit channels in the three-body CTMC method. Nucl. Instrum. Meth. Phys. Res. B 1994, 86, 201–204. [Google Scholar] [CrossRef]
- Tőkési, K.; Barna, I.F.; Burgdörfer, J. Ionization of helium in positron impact. Nucl. Instrum. Methods Phys. Res. B 2005, 233, 307–311. [Google Scholar] [CrossRef]
- Kavčič, M.; Tőkési, K. Single and double K-shell ionization cross sections of silicon. Radiat. Phys. Chem. 2007, 76, 542–545. [Google Scholar] [CrossRef]
- Ziaeian, I.; Tőkési, K. Interaction of Be4+ and Ground State Hydrogen Atom—Classical Treatment of the Collision. Atoms 2020, 8, 27. [Google Scholar] [CrossRef]
- Atawneh, S.J.A.; Asztalos, Ö.; Szondy, B.; Pokol, G.I.; Tőkési, K. Ionization Cross Sections in the Collision between Two Ground State Hydrogen Atoms at Low Energies. Atoms 2020, 8, 31. [Google Scholar] [CrossRef]
- Acebal, E.; Otranto, S. Influence of the projectile charge sign in light particle single ionization of H2O. Eur. Phys. J. D 2019, 73, 91. [Google Scholar] [CrossRef]
- Tőkési, K. Double electron excitation of helium by charged particle impact. Nucl. Instrum. Methods Phys. Res. B 2019, 233, 266–269. [Google Scholar] [CrossRef]
- Oliveira, V.; Herbert, A.; Santos, A.; Tőkési, K. Electron capture and loss of O+ projectile in collision with water near the Bragg Peak Energies. Eur. Phys. J. D 2019, 73, 146. [Google Scholar] [CrossRef]
- Tőkési, K.; Varga, D. Energy distribution of elastically scattered electrons from double layer samples. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2016, 369, 109–121. [Google Scholar] [CrossRef]
- Sulik, B.; Tőkési, K. Accelerating Multiple Scattering of Electrons by Ion Impact: Contribution to Molecular Fragmentation and Radiation Damages. Adv. Quantum Chem. 2007, 52, 253–276. [Google Scholar]
- Young, T. The Bakerian lecture: Experiments and calculations relative to physical optics. Philos. Trans. R. Soc. 1804, 94, 1–16. [Google Scholar]
- Murray, A.J.; Hussey, M.J.; Kaiser, C.; Gao, J.; Madison, D.H. Electron impact ionization of molecules at low to intermediate energies—A search for Young’s double slit type interferences. J. Electron Spectrosc. Relat. Phenom. 2007, 161, 11–16. [Google Scholar] [CrossRef]
- Steiger, T.D.; Stehr, J.; Griffin, H.C.; Rogers, J.H.; Skalsey, M.; Van House, J. Development of intense, long-lived positron sources. Nucl. Instrum. Methods M Phys. Res. 1990, A299, 255–260. [Google Scholar] [CrossRef]
- Uesugi, Y.; Akagi, T.; Chehab, R.; Dadoun, O.; Furukawa, K.; Kamitani, T.; Kawada, S.; Omoric, T.; Takahashi, T.; Umemori, K.; et al. Development of an intense positron source using a crystal-amorphous hybrid target for linear colliders. Nucl. Instrum. Methods Phys. Res. B 2014, 319, 17–23. [Google Scholar] [CrossRef]
- Maekawa, M.; Wada, K.; Kawasuso, A. Development a new positron source for spin-polarized positron beam generation. Nucl. Inst. Methods Phys. Res. B 2020, 480, 49–55. [Google Scholar] [CrossRef]
- Gossman, D.; Perez-Garcia, B.; Hernandez-Aranda, R.I.; Forbes, A. Optical interference with digital holograms. Am. J. Phys. 2016, 84, 508. [Google Scholar] [CrossRef]
- Zhou, H.; Perreault, W.E.; Mukherjee, N.; Zare, R.N. Quantum mechanical double slit for molecular scattering. Science 2021, 374, 960–964. [Google Scholar] [CrossRef]
- Hecht, E. Interference. In Optics, 5th ed.; Borthakur, M., Tiwari, V., Eds.; Pearson Education Limited: Essex, UK, 2017; pp. 405–408. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Ajaleen, M.S.; Tőkési, K. Interaction of Electrons and Positrons with Protons Aligned in One-Dimension Line. Atoms 2023, 11, 46. https://doi.org/10.3390/atoms11030046
Al-Ajaleen MS, Tőkési K. Interaction of Electrons and Positrons with Protons Aligned in One-Dimension Line. Atoms. 2023; 11(3):46. https://doi.org/10.3390/atoms11030046
Chicago/Turabian StyleAl-Ajaleen, Musab S., and Károly Tőkési. 2023. "Interaction of Electrons and Positrons with Protons Aligned in One-Dimension Line" Atoms 11, no. 3: 46. https://doi.org/10.3390/atoms11030046
APA StyleAl-Ajaleen, M. S., & Tőkési, K. (2023). Interaction of Electrons and Positrons with Protons Aligned in One-Dimension Line. Atoms, 11(3), 46. https://doi.org/10.3390/atoms11030046




