Excitation of the 2P State of Atomic Hydrogen by Electron Impact

Abstract

The excitation cross sections of the 2P state of atomic hydrogen at low incident electron energies (from 0.755 to 3.5 Ry) were calculated using the variational polarized orbital method. Up to 13 partial waves (L = 1, 13) were used to obtain converged cross sections in the above energy range. The importance of the long-range forces is pointed out in the threshold region, and behavior of the cross section is indicated near the threshold. The polarization P of radiation emitted at right angle to the incident electron beam was calculated and the perpendicular cross section was also calculated.

1. Introduction

Cross sections for the excitation of the 2S state of atomic hydrogen at low incident electron energies were published [1] earlier using the variational polarized orbital method, also called a hybrid theory [2]. Now the same method is being applied to the excitation of the 2P state of atomic hydrogen. This method has been used in obtaining accurate phase shifts for electron–hydrogen elastic scattering [2], positron–hydrogen scattering [3], resonances in He and Li⁺ [4], cross sections for photoabsorption in two-electron systems, and radiative attachments [5]. Although this is a two-channel process, the variational polarized orbital method gave fairly accurate results [3,4,5] and the results compared well with those obtained using the close-coupling and R-matrix methods. Therefore, we expect to obtain accurate cross sections for the excitation of the 2P state as well. In the close-coupling method, the wave function has both 1S and 2P eigenstates and therefore, two coupled equations must be solved. Burke et al. [6], using the close-coupling approach, obtained cross section $\sigma ({\mathsf{a}}_0^2)$ = 3.039 at the incident energy of 4 Ry. Colhoun et al. [7] obtained the same value of the cross section at 4 Ry using a distorted-wave method. However, an experiment by William [8] found a cross section equal to 2.79 $\pm$ 0.24 ${\mathsf{a}}_0^2$ at an incident electron energy of 4 Ry. This gives a range between 2.55 and 3.03 ${\mathsf{a}}_0^2$. We calculated excitation cross sections in the range 0.755 to 3.5 Ry; they are shown in Table 1. Table 2 and Table 3 show the convergence with the partial waves L. At excitation, the incident electron loses an energy of 0.75 Ry and its angular momentum changes by one unit because ${\overrightarrow{L}}_i={\overrightarrow{L}}_t+{\overrightarrow{L}}_f$. Since $L_t=1$ for the P state, the final $L_f=L_i\pm 1$. Cross sections at higher energies were not calculated because many partial waves L are required to obtain converged results, this being a dipole-allowed transition. We use Rydberg units for energy and Bohr radius ${\mathsf{a}}_0$ for length, therefore cross sections are in ${\mathsf{a}}_0^2$ units.

Table 1. Present excitation cross sections $\sigma$(${\mathsf{a}}_0^2$) at various incident energies E(Ry).

E	$\mathit{\sigma }$	E	$\mathit{\sigma }$
0.755	5.808	1.05	11.366
0.76	7.623	1.2	7.062
0.78	12.457	1.5	3.418
0.80	14.947	2.0	2.230
0.83	16.830	2.5	1.959
0.85	17.522	3.0	1.700
0.90	16.878	3.5	1.543
0.95	15.474

Table 2. Cross sections (${\mathsf{a}}_0^2$) for 1S to 2P excitation for various incident energies E(Ry) in the variational polarized approximation.

Lm/E	0.755	0.76	0.78	0.80	0.83	0.85	0.90	0.95	1.05	1.2
1	5.646	7.187	10.564	11.604	11.602	11.133	9.943	7.708	5.017	2.658
2	5.807	7.622	12.433	14.936	16.718	17.102	16.515	14.850	10.934	6.325
3	5.808	7.623	12.437	14.946	16.829	17.515	16.768	15.420	11.230	6.745
4			12.457	14.947	16.830	17.522	16.878	15.465	11.335	6.949
5								15.474	11.366	7.031
6										7.062

Table 3. Cross sections (${\mathsf{a}}_0^2$) for 1S to 2P excitation for various incident energies E(Ry) in the variational polarized approximation.

Lm/E	1.50	2.00	2.50	3.0	3.5
1	0.947	0.289	0.127	0.069	0.046
2	2.218	0.611	0.270	0.155	0.104
3	2.704	0.998	0.628	0.339	0.231
4	3.044	1.376	0.950	0.593	0.427
5	3.235	1.661	1.240	0.853	0.648
6	3.334	1.851	1.467	1.078	0.856
7	3.383	1.972	1.631	1.258	1.034
8	3.407	2.077	1.747	1.395	1.178
9	3.418	2.148	1.826	1.498	1.292
10		2.196	1.881	1.573	1.381
11		2.229	1.918	1.628	1.449
12		2.239	1.941	1.670	1.502
13			1.959	1.700	1.543

2. Calculations

The present calculation was carried out using the variational polarized orbital method, which is a distorted-wave calculation because the two states 1S and 2P are treated separately. The total cross section from a state ‘i’ to a state ‘f’ is written as

$$\sigma =\frac{k_f}{k_i}{\displaystyle \int |T_{fi}{|}^{2}d\mathsf{\Omega }}.$$

(1)

In the above expression, $k_i$ and $k_f$ are the initial and final electron momenta and $T_{fi}$ is a matrix element for excitation from an initial state ${\mathrm{\Psi }}_i$ to the final state ${\psi }_f$ and is given by

$$T_{fi}=-(1/4\pi )⟨{\psi }_f\left|V\right|{\mathrm{\Psi }}_i⟩.$$

(2)

The potential is

$$V=-\frac{2Z}{r_1}+\frac{2}{r_{12}}$$

(3)

Z is the charge of the nucleus, $r_1$ and $r_2$ are the distances of the incident electron and the target electron, and $r_{12}=|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2|$. In calculating the incident wave function, we assume that the nucleus has an infinite mass and therefore the mass polarization term can be neglected in the derivation of the equation for the scattering function $u(\overrightarrow{r})$. The initial state wave function is given by

$$\mathrm{\Psi }({\overrightarrow{r}}_1,{\overrightarrow{r}}_2)=\frac{1}{\sqrt{2}}[u({\overrightarrow{r}}_1){\mathrm{\Phi }}^{pol}({\overrightarrow{r}}_1,{\overrightarrow{r}}_2)\pm (1\leftrightarrow 2)].$$

(4)

In the above equation, the plus sign refers to the singlet states and the minus sign refers to the triplet states. The perturbed ground state wave function of the target due to the incident electron [9] is

$${\mathrm{\Phi }}^{pol}({\overrightarrow{r}}_1,{\overrightarrow{r}}_2)={\varphi }_0({\overrightarrow{r}}_2)-\frac{{\chi }_{ST}(r_1)}{r_1^2}\frac{u_{1s\to 2p}(r_2)}{r_2}\frac{\cos ({\theta }_{12})}{\sqrt{Z\pi }}$$

(5)

The angle ${\theta }_{12}$ is the angle between ${\overrightarrow{r}}_1$ and ${\overrightarrow{r}}_2$. A smooth cutoff function, introduced by Shertzer and Temkin [10], is given by

$${\chi }_{ST}=1-e^{-2Z{r}_1}({(Z{r}_1)}^4/3+4{(Z{r}_1)}^3/3+2{(Z{r}_1)}^2+2Z{r}_1+1).$$

(6)

The function $u_{1s\to 2p}$ is given by

$$u_{1s\to 2p}(r_2)=e^{-Z{r}_2}(\frac{Z}{2}{r}_2^3+r_2^2).$$

(7)

The target function is given by

$${\varphi }_0(r_2)=\sqrt{\frac{Z^3}{\pi }}{e}^{-Z{r}_2}.$$

(8)

The scattering function $u({\overrightarrow{r}}_1)$ is given by

$$u({\overrightarrow{r}}_1)=\mathsf{a}(L)\frac{u(r_1)}{r_1}{Y}_{L\mathrm{o}}({\mathsf{\Omega }}_1).$$

(9)

The scattering function has a plane wave normalization given by

$$\mathsf{a}(L)=\sqrt{4\pi (2L+1)}.$$

(10)

The equation for $u(r_1)$ is obtained from

$$⟨Y_{L\mathrm{o}}({\mathsf{\Omega }}_1){\mathrm{\Phi }}^{pol}|H-E|{\mathrm{\Psi }}_i⟩=0$$

(11)

.

The initial state is assumed to be exact, and the final state has no exchange and polarization of the target; the outgoing electron is represented by a plane wave. The final state is given by

$${\psi }_f({\overrightarrow{r}}_1,{\overrightarrow{r}}_2)=e^{i{\overrightarrow{k}}_f·{\overrightarrow{r}}_1}{\varphi }_{2p}({\overrightarrow{r}}_2).$$

(12)

The excited state wave function is given by

$${\varphi }_{2p}({\overrightarrow{r}}_2)=e^{-z{r}_2/2}\frac{r_2}{\sqrt{24}}{Y}_{1\mu }({\mathsf{\Omega }}_2).$$

(13)

In the above, $\mu$ = −1, 0, 1. The cross section is given by

$$\sigma ({\mathsf{a}}_0^2)=\frac{k_f}{k_i}{\displaystyle \int }|T_{fi}{|}^{2}d{\mathsf{\Omega }}_{k_f}.$$

(14)

In Equations (12) and (14), $k_i$ and $k_f$ are the initial and the final momenta. This formulation was used for the two-electron systems earlier [11], giving reliable results for the excitation cross sections of the S and P states. Equation (14) can be simplified by using

$$e^{i{\overrightarrow{k}}_f·{\overrightarrow{r}}_1}={\displaystyle \sum _{lm}{(i)}^l{j}_l(k_f{r}_1)Y_{lm}({\mathsf{\Omega }}_1)Y_{lm}^{*}({\mathsf{\Omega }}_{k_f})}.$$

(15)

3. Results

Excitation cross sections from 1S to 2P are given in Table 1 at various incident energies. The cross section was maximum at E = 0.85 (Ry) where its value was 17.522 ${\mathsf{a}}_0^2$. Near the threshold, the cross section has a large value at L = 1 and then decreases rapidly, as can be seen from Table 2, where Lm is the maximum angular momentum of the incident electron.

Excitation cross section is given by

$$\begin{array}{l}\sigma ={\sigma }_{\mu =-1}+{\sigma }_{\mu =0}+{\sigma }_{\mu =1}\end{array}$$

(16)

Numerically, we find ${\sigma }_{\mu =1}={\sigma }_{\mu =-1}$, as expected because of invariance under parity because forces involved are electromagnetic forces. In Figure 1, we show the excitation cross sections. They go to zero as E goes to zero, as is obvious from Equation (14). There is a maximum at E = 0.85 Ry; after this energy, cross sections vary smoothly.

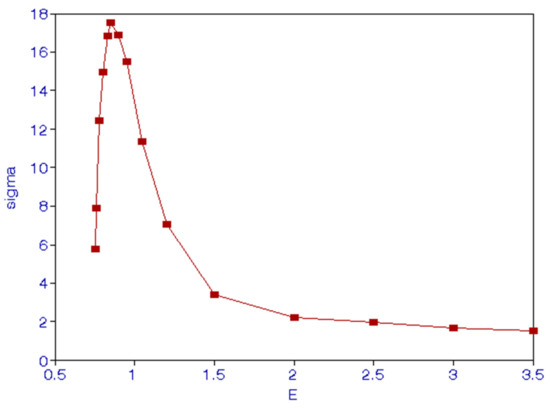
Figure 1. (Color online) Excitation cross sections (${\mathsf{a}}_0^2$) for incident energies E(Ry).

The long-range forces, Wigner [12] has emphasized the importance of such forces in a threshold region, have been included in the present calculations. Sadeghpour et al. [13] have shown that in the threshold region the cross sections are proportion to 1/${(\ln k_f)}^2$. The calculated cross sections can be fitted to $-3.324+\frac{359.329}{{(\ln k_f)}^2}+\frac{583.146}{{(\ln k_f)}^3}$. The fit shown in Figure 2 is quite good.

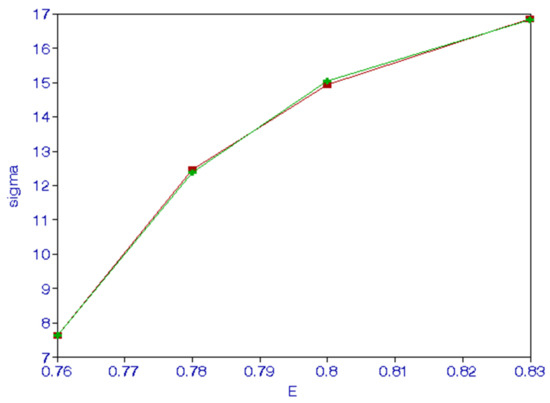
Figure 2. (Color online). Threshold behavior of 2P excitation cross sections (${\mathsf{a}}_0^2$) vs. the incident energy E(Ry).

4. Polarization and Perpendicular Cross Section

Percival and Seaton [14] have shown that the polarization of the radiation emitted at right angle to the incident electron beam is given by

$$P=\frac{3(1-x)}{7+11x}.$$

(17)

In the above express, $x=\frac{{\sigma }_{\mu =1}}{{\sigma }_{\mu =0}}$ and assuming an isotropic photon distribution, the perpendicular cross section [14] is given by

$${\sigma }_{\perp }=1.836{\sigma }_{m=1}+1.164{\sigma }_{m=0}$$

(18)

Burke et al. [6] calculated P and ${\sigma }_{\perp }$. We have calculated these quantities and they are given in Table 4 and Table 5. As energy of the incident electron comes close to the threshold, x tends to zero. This gives P = 3/7 = 4.286. This is confirmed from Table 4, which shows that P = 0.4218 at E = 0.755—just above the threshold. We indicate the behavior of polarization P in Figure 3 and of ${\sigma }_{\perp }$ in Figure 4. We see that ${\sigma }_{\perp }$ has a peak around E = 1 Ry. James et al. [15] show in their Figure 1 the theoretical and experimental variation of P with respect to the incident electron energy. They show that P approaches 0.35 at low energies. This is considerably lower than 3/7 inferred from Equation (17). Burke at al. [6] also show the variation in Figure 4 of their paper. Their Figure 4 appears very much like Figure 1 of [15]. We see from Figure 3 that there is a minimum of P around 2.5 Ry.

Table 4. Polarization of radiation.

E	P	E	P
0.755	0.4218	0.95	0.3040
0.76	0.4136	1.05	0.2647
0.78	0.3935	1.50	0.2031
0.80	0.3757	2.00	0.1741
0.83	0.3544	2.50	0.1521
0.85	0.3428	3.00	0.1566
0.90	0.3200	3.50	0.1547

Table 5. Perpendicular cross section.

E	${\mathit{\sigma }}_{\perp }$	E	${\mathit{\sigma }}_{\perp }$
0.755	6.339	0.95	17.020
0.76	8.286	1.05	10.033
0.78	14.285	1.50	3.524
0.80	17.055	2.00	2.348
0.83	18.949	2.50	1.993
0.85	19.342	3.00	1.793
0.90	18.660	3.50	1.576

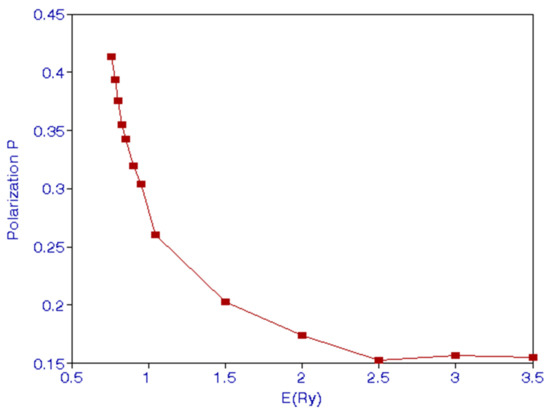
Figure 3. (Color online) Behavior of polarization P with E(Ry).

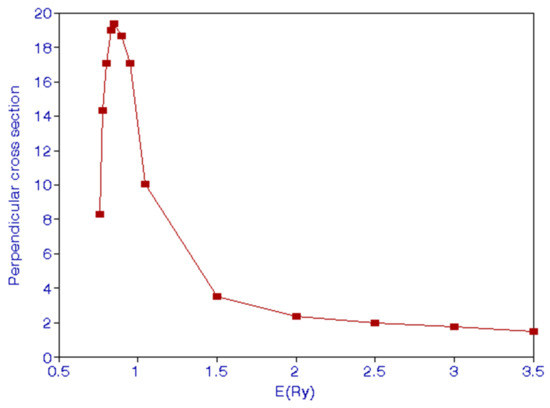
Figure 4. (Color online) Behavior of the perpendicular cross section, ${\sigma }_{\perp }$, with the incident energy E.

5. Conclusions

Calculations have been carried out for excitation of atomic hydrogen from 1S state to 2P state by electron impact, in a distorted-wave approximation using the variational polarized-orbital method. Cross sections have been calculated from the incident energy E = 0.755 to 3.5 Ry. Phase shifts and elastic cross sections in this energy range are given in [16]. Elastic cross sections are needed if total cross sections are measured. There are two calculations of excitation at 4.0 Ry and there are no results at low energies. It would be desirable to have calculations and experiments at low incident electron energies. It is also desirable to use a different version of Equation (12) in which exchange and target polarization in the final state are included. This would make the calculations very complicated. However, this would indicate the importance of exchange and target polarization in the final state.