Peculiar Physics of Heavy-Fermion Metals: Theory versus Experiment

Abstract

This review considers the topological fermion condensation quantum phase transition (FCQPT) that leads to flat bands and allows the elucidation of the special behavior of heavy-fermion (HF) metals that is not exhibited by common metals described within the framework of the Landau Fermi liquid (LFL) theory. We bring together theoretical consideration within the framework of the fermion condensation theory based on the FCQPT with experimental data collected on HF metals. We show that very different HF metals demonstrate universal behavior induced by the FCQPT and demonstrate that Fermi systems near the FCQPT are controlled by the Fermi quasiparticles with the effective mass $M^{*}$ strongly depending on temperature T, magnetic field B, pressure P, etc. Within the framework of our analysis, the experimental data regarding the thermodynamic, transport and relaxation properties of HF metal are naturally described. Based on the theory, we explain a number of experimental data and show that the considered HF metals exhibit peculiar properties such as: (1) the universal $T/B$ scaling behavior; (2) the linear dependence of the resistivity on T, $\rho \left(T\right)\propto A_{1}T$ (with $A_1$ is a temperature-independent coefficient), and the negative magnetoresistance; (3) asymmetrical dependence of the tunneling differential conductivity (resistivity) on the bias voltage; (4) in the case of a flat band, the superconducting critical temperature $T_c\propto g$ with g being the coupling constant, while the $M^{*}$ becomes finite; (5) we show that the so called Planckian limit exhibited by HF metals with $\rho \left(T\right)\propto T$ is defined by the presence of flat bands.

1. Introduction

Strongly correlated Fermi systems such as heavy-fermion metals, graphene, and high-$T_c$ superconductors exhibit the non-Fermi-liquid (NFL) behavior. Theoretical predictions [1,2,3,4] and experimental data collected on many of these systems show that at low temperatures a portion of their excitation spectrum becomes approximately dispersionless, giving rise to so-called flat bands and high-$T_c$ superconductivity, see, e.g., [1,5,6,7,8,9,10,11,12]. The emergence of flat bands at low T indicates that the system is close to a special quantum critical point, namely a topological fermion condensation quantum phase transition (FCQPT), leading to the formation of flat bands dubbed the fermion condensation (FC). The flat bands are formed by the Landau interaction between quasiparticles, while a frustration and van-Hove singularities can facilitate the process. Flat bands have notable features, e.g., raising temperatures, and the superconducting phase transition makes them upward tilted [3,4,13,14,15,16,17]. These observations have been predicted [3,4,14,15,17] and are in accordance with experimental data, see, e.g., [13,16,18]. Moreover, the FC theory allows one to qualitatively and quantitatively evaluate the NFL and Landau Fermi liquid (LFL) behaviors of strongly correlated Fermi systems, and explain the crossover from one another [1,2,4,15,19,20]. We note that in our review we analyze strongly correlated Fermi systems formed by and located near their topological FCQPT and consider experimental observations that are collected on such systems. Consideration of systems located relatively far from their topological FCQPT is possible within the framework of the FC theory as well, see, e.g., [15,19,20]. We review and explain recent prominent experimental results that to our best knowledge have not found alternative explanations and that strongly suggest that the topological FCQPT is a generic feature of many strongly correlated Fermi systems, being the universal cause of their non-Fermi-liquid behavior, and the fermion condensation theory is able to explain the extraordinary behavior of strongly correlated Fermi systems.

In our review we consider exciting experimental facts such as:

(1) Recent experimental findings of linear dependence on temperature T of the resistivity $\rho \left(T\right)\propto T$, collected on high $T_c$ superconductors (HTSC), graphene, heavy fermion (HF) and common metals reveal that the scattering rate 1$/\tau$ of charge carriers reaches the Planckian limit $1/\left(T\tau \right)=k_B/\hslash$, with $1/\tau$ being the scattering rate and $k_B$ and ℏ being the Boltzmann and Plank constants, respectively [21,22,23,24]. Within the framework of the FC theory, we show that the quasi-classical physics is still applicable for describing the linear T-dependence of resistivity of strongly correlated metals at their quantum criticality since flat bands, forming the quantum criticality, generate transverse zero-sound mode with the Debye temperature $T_D$ [25]. At $T\ge T_D$, the mechanism of the linear T-dependence is the same in both ordinary metals and strongly correlated ones and is represented by the electron–phonon scattering. Therefore, it is the electron–phonon scattering at $T\ge T_D$ that leads to the near material-independence of the lifetime $\tau$ that is expressed as $1/\left(\tau T\right)\sim k_B/\hslash$. As a result, we describe and explain recent exciting experimental observations of universal scattering rate related to the linear T-dependent resistivity of a large number of both strongly correlated Fermi systems and common metals [21,22,23,24]. We show that the observed scattering rate is explained by the emergence of flat bands formed by the topological FQCPT rather than by the so-called Planckian limit at which the assumed Planckian scattering rate occurs [25,26]. The Planckian limit then has to occur in common metals. Moreover, in magnetic fields, HF metals transit from the NFL to LFL behavior and $\rho \left(T\right)\propto T$ vanishes, being replaced by the LFL behavior $\rho \left(T\right)\propto A_2{T}^2$, with $A_2$ as the temperature-independent coefficient.

(2) Recent observations of the linear T-dependence, $\rho \left(T\right)\propto T$, at low temperatures, $T\to 0$, relate the slope of the linear T-dependent resistivity $\rho$ to the London penetration depth ${\lambda }_0$, indicating a universal scaling property

$$\frac{d\rho }{dT}\propto {\lambda }_0^2$$

(1)

for a large number of strongly correlated high-temperature superconductors [27]. This scaling relation spans several orders of magnitude in ${\lambda }_0$, attesting to the robustness of the empirical law (1) [28].

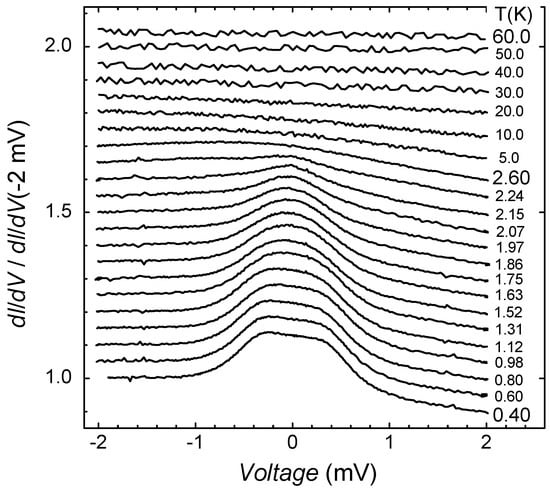
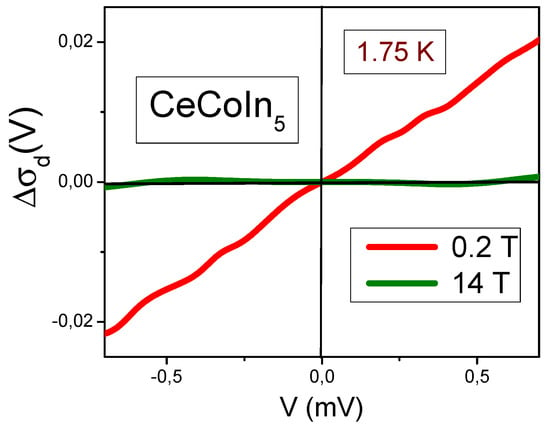
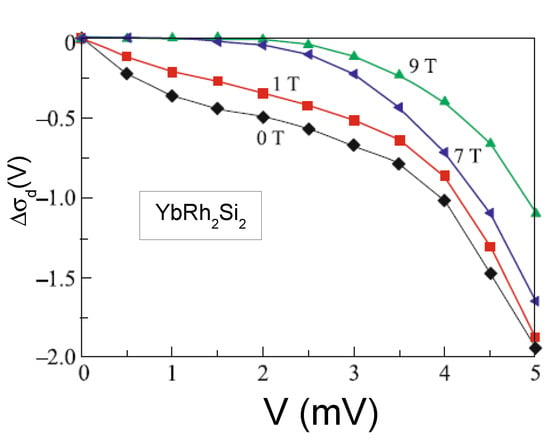
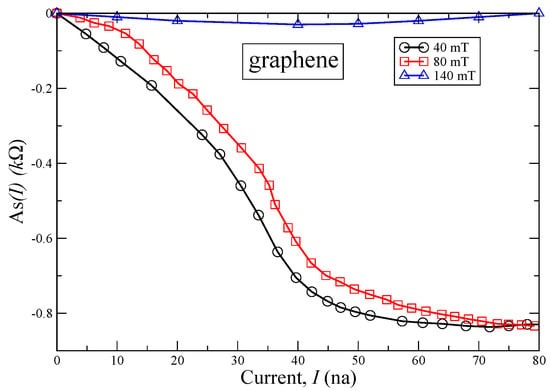
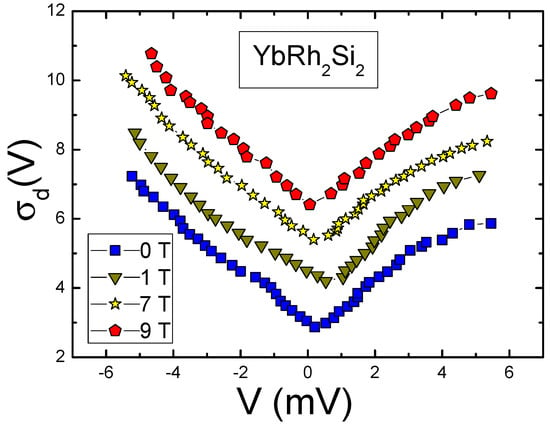
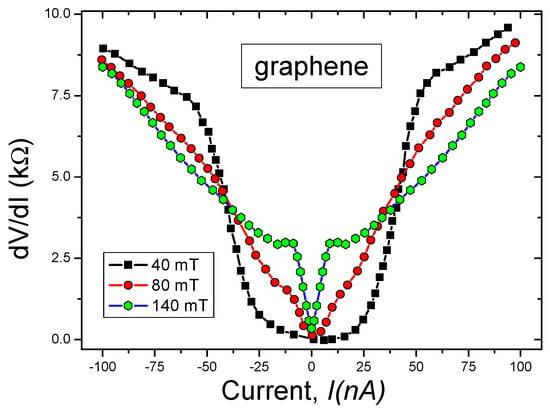
(3) We also analyze recent challenging experimental findings of tunneling differential conductivity $dI/dV={\sigma }_d\left(V\right)$ as a function of the applied bias voltage V, collected under the application of magnetic field B on the twisted graphene and the archetypical heavy-fermion metals ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$ and ${\mathrm{CeCoIn}}_5$ [5,29,30]. We explain the emergence of the asymmetrical part $\Delta {\sigma }_d={\sigma }_d\left(V\right)-{\sigma }_d(-V)$ and demonstrate that $\Delta {\sigma }_d$ vanishes in magnetic fields as predicted [31].

(4) We consider the recent outstanding experimental observation of the density $n_s$ of superconducting electrons that turns out to be much less than the total density $n_{\rho }$ of electrons at $T\to 0$ [32] as predicted [33].

(5) We show that the transition temperature $T_c$ is proportional to the superconducting coupling constant g,

$$T_c\propto g.$$

(2)

This fact, see Equation (2), leads to creating high-$T_c$ superconductors [1,5,6,7,8,9,10,11,12]. This observation is supported by special features of high-$T_c$ superconductivity based on flat bands, namely that $T_c$ is proportional to the Fermi velocity $V_F\propto 1/N_s\left(0\right)$ $V_F\propto T_c$, rather than $N_s\left(0\right)\propto 1/V_F\propto T_c$ as stated in standard BCS-like theories [13,16] as predicted [17].

Our results are in good agreement with experimental data and demonstrate that the topological FCQPT is an intrinsic feature of strongly correlated Fermi systems, and the FC theory can be viewed as the universal agent explaining the physics of strongly correlated Fermi systems.

2. Fermion Condensation

The theory of FC has been described several times, see, e.g., [4,15,19,20]; nonetheless, for the readers’ convenience, we briefly present this methodology. The usual approach to describe the ensembles of itinerant Fermi particles is the well-known Landau Fermi liquid theory [34,35]. This theory represents the real properties of a solid with itinerant electrons in terms of a Fermi gas of so-called quasiparticles with weak interaction. In this case, the quasiparticles represent the excited states of a solid or liquid states and are responsible for the low temperature thermodynamic, transport and relaxation properties of common metals. These quasiparticle excitations are characterized by the effective mass $M^{*}$, that is of the order of the bare mass of electron, M, and depends weakly on external parameters such as temperature T, magnetic field B, external pressure P, etc. [34,35]. However, the LFL theory cannot explain why the effective mass $M^{*}$ begins to depend strongly on the stimuli above and, for example, can even be a divergent function of magnetic field B or temperature T, see, e.g., [4,15,19,36]. Such a dependence is called the NFL behavior and is connected to the growth of the effective mass that occurs when the system approaches the topological fermion condensation quantum phase transition (FCQPT) leading to an FC state with flat bands [1,4,15,19]. Beyond the FCQPT, the system develops a flat band, formed by FC, and characterized by the topological charge that is different from both the topological charges of the Landau Fermi liquid (LFL) and marginal Fermi liquid, representing a new type of Fermi liquid [2,4,15,19,37]. Thus, the stability of FC is ensured by its topological charge, and it can be destroyed only by the first order phase transition, since the topological charge cannot acquire continuous values [2,15,19,37]. As a result of these unique properties of the FC state, a new state of matter is generated, represented by QSL, HF metals, quasicrystals, 2D liquids such as ${}^3\mathrm{He}$ and high-$T_c$ superconductors, so that 1D, 2D and 3D strongly correlated Fermi systems exhibit universal scaling behavior irrespective of their microscopic structure [15,19,20,38,39].

The main feature of FC theory is the existence of one more instability channel (additional to those of Pomeranchuk) that cannot be described within the framework of the Landau theory of Fermi liquid [35]. Indeed, under some conditions, the effective mass $M^{*}$ of LFL quasiparticle diverges, see, e.g., [15,19]. As a result, to keep the finite and positive effective mass at zero and finite temperatures, the Fermi surface changes its topology: the Fermi surface transforms into a Fermi layer, as seen in Figure 1. This topological phase transition generates the effective mass dependence on temperature, magnetic field, etc. We assume, without loss of generality [15,19], that the Fermi liquid is homogeneous. That is, in our model we account for the most important and common features only, neglecting marginal effects related to the crystalline anisotropy of solids [15,19,20]. The Landau equation for the quasiparticle effective mass $M^{*}$ reads [15,34,35]

$$\begin{array}{ccc}\hfill \frac{1}{M_{\sigma }^{*}(B,T)}& =& \frac{1}{M}+\sum _{{\sigma }_1}\int \frac{{\mathbf{p}}_F\mathbf{p}}{p_F^3}{F}_{\sigma ,{\sigma }_1}(p_F,p)\hfill \\ & \times & \frac{\partial n_{{\sigma }_1}(\mathbf{p},T,B)}{\partial p}\frac{dp}{{\left(2\pi \right)}^3},\hfill \end{array}$$

(3)

where $F_{\sigma ,{\sigma }_1}(p_F,p)$ is the interaction function, introduced by Landau. The function $F_{\sigma ,{\sigma }_1}(p_F,p)$, depending on momentum p, Fermi momentum $p_F$ and spin indices $\sigma$, ${\sigma }_1$, has the form of spherical harmonics with coefficients taken from the best fit to experiment. The fermion occupation number n in the Fermi–Dirac statistics reads

$$n_{\sigma }(p,T)={\left\{1+exp\left[\frac{({\epsilon }_{\sigma }(\mathbf{p},T)-{\mu }_{\sigma })}{T}\right]\right\}}^{-1},$$

(4)

where ${\epsilon }_{\sigma }(p,T)$ is the single-particle spectrum, and ${\mu }_{\sigma }$ is a spin-dependent chemical potential: ${\mu }_{\sigma }=\mu \pm {\mu }_{B}B$ where ${\mu }_B$ is the Bohr magneton. The magnetic field dependence occurs due to the Zeeman splitting shifting the system from its topological FCQPT [15].

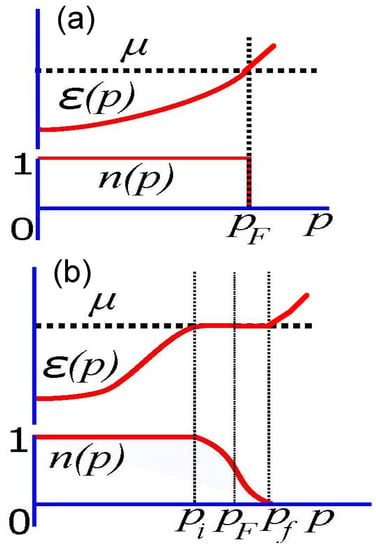
Figure 1. Diagram of flat bands near the FCQPT at zero temperature, $T=0$. Panel (a) shows normal Fermi sphere and corresponding quasiparticles spectrum $\epsilon \left(p\right)\simeq p^2/\left(2M\right)$ and occupation number $n\left(p\right)$ being a step function. Panel (b) displays the system in the FC state after the topological FCQPT. The Fermi sphere alters its topology, which is shown schematically as an emergence of a spherical layer of the thickness $p_f-p_i$. In this case, the Fermi momentum $p_F$ is hidden inside the flat band, defined by the condition $\epsilon \left(p\right)=\mu$ (7). This condition defines the flat band, shown as a dispersionless part of the spectrum $\epsilon \left(p\right)=\mu$, with $\mu$ being the chemical potential. The function $n\left(p\right)$ decreases gradually from $n\left(p_i\right)=1$ to $n\left(p_f\right)=0$ without violating the Pauli exclusion principle.

The standard procedure for obtaining the single-particle spectrum ${\epsilon }_{\sigma }(p,T)$ in the Landau theory is to vary the system energy $E\left[n_{\sigma }(p,T)\right]$ with regard to the occupation number n

$${\epsilon }_{\sigma }(p,T)=\frac{\delta E\left[n\right(p\left)\right]}{\delta n_{\sigma }\left(p\right)}.$$

(5)

We note that the Landau interaction entering Equation (3) is not of a special form since it is fixed by the simple condition that the system is in the FCQPT point [15,19]. The explicit form of the variational Equation (5) reads

$$\frac{\partial {\epsilon }_{\sigma }(p,T)}{\partial p}=\frac{p}{M}-\sum _{{\sigma }_1}\int \frac{\partial F_{\sigma ,{\sigma }_1}(p,p_1)}{\partial \mathbf{p}}{n}_{{\sigma }_1}(p_1,T)\frac{d^3{p}_1}{{\left(2\pi \right)}^3},$$

(6)

Later on for simplicity, we omit the spin indexes $\sigma$. In the FC phase (i.e., beyond the FCQPT) at $T=0$, Equation (5) takes the form [1]

$$\epsilon (p,T=0)=\mu ,p_i\le p\le p_f;0\le n\left(p\right)\le 1.$$

(7)

where $p_{i,f}$ stands for initial and final momenta (not to be confused with Fermi momentum $p_F$), where the flat band resides, see Figure 1. Condition (7) defines the flat band since in this case the quasiparticles have no dispersion. By this virtue, quasiparticles have the Fermi velocity $V_F=0$ and at $T=0$ are condensed with the same energy $\epsilon (p,T=0)=\mu$, representing the superconducting state with the finite order parameter $\kappa$, while the superconducting gap $\Delta =0$, see Section 7. As this resembles the case of Bose condensation, the corresponding phenomenon is called fermion condensation, being separated from LFL by the first order phase transition [1,2,37]. The system with FC acquires properties, being very different from those of ordinary Fermi liquids, since the Fermi liquid with FC forms a new, topologically-protected (and thus “extremely stable”) state of matter. This means that if FC is formed in a substance, it will define its properties at $T=0$ and at elevated temperatures as well. Figure 1 visualizes (at $T=0$) the consequences of the FCQPT on the Fermi surface, spectrum and occupation number of a Fermi liquid. The transformation from panel (a) (normal Fermi liquid) to panel (b) is represented by altering the Fermi surface topology so that in the normal Fermi liquid the layer of finite length $p_f-p_i$ appears instead of the Fermi surface located at Fermi momentum $p=p_F$. This immediately implies the emergence of the flat part of the spectrum defined by Equation (7), where all the condensed fermions are located. This, in turn, generates the gradual (instead of abrupt on the panel (a) decay of the occupation numbers $n\left(p\right)$ from $n=1$ at $p<p_i$ to $n=0$ at $p>p_f$.

Equations (3) and (7) allow one to determine the energy spectrum ${\epsilon }_{\sigma }(p,T)$ and occupation numbers $n_{\sigma }(p,T)$ in a self-consistent way. These quantities, in turn, permit the calculation of the effective mass, $p_F/M^{*}{=\partial \epsilon \left(p\right)/\partial p|}_{p=p_F}=V_F$. We emphasize that both magnetic field and temperature dependences of the effective mass $M^{*}(B,T)$ in the FC phase come from Equation (3) and from the T, B-dependence of ${\epsilon }_{\sigma }\left(p\right)$ and $n_{\sigma }\left(p\right)$. Calculated (by Equations (3) and (7)) spectrum and occupation numbers [15] in the FC phase are reported in Figure 2. At (almost) zero temperature, the flat portion of the spectrum is clearly seen at $p_i<p<p_f$. This shape of the spectrum defines $n\left(p\right)$ (Figure 2, panel (b)) in the form of “two steps”, gradually decaying from one to zero. Simultaneously, at relatively high temperatures (equal to $T/E_F=0.01$, which at $E_F\sim$ 1eV implies $T\simeq 100$ K) this part is rather strongly upward tilted. This shows that finite temperatures erode the FC state, making the effective mass $M^{*}$ finite, while the system acquires features similar to ordinary Fermi liquid [4,15].

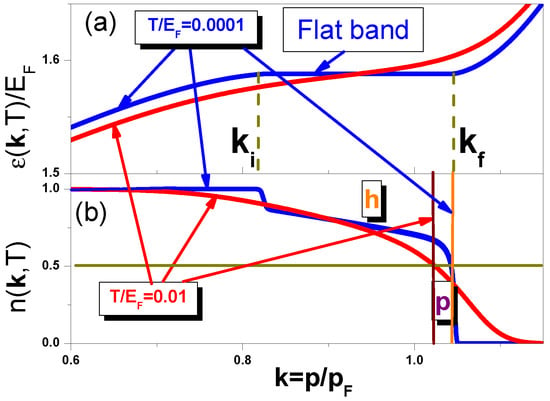
Figure 2. Flat band induced by FC. The calculated single-particle spectrum (a) and the quasiparticle occupation number (b) at small but finite temperatures versus the dimensionless momentum $k=p/p_F$, where $p_F$ is the Fermi momentum [15]. Temperature is measured in the units of $E_F$. At $T=0.01E_F$ and $T=0.0001E_F$, the vertical lines show the position of the Fermi level $E_F$ at which $n(k,T)=0.5$ (see the horizontal line in panel (b)). At $T=0.0001E_F$ (blue curve), the single-particle spectrum $\epsilon (k,T)$ is almost flat (marked “Flat band”) in the range $k_f-k_i$ (with $k_i=p_i/p_F$ and $k_f=k_f/p_F$ denoting, respectively, the initial and final momenta for FC realization, and $k=p/p_F$). Thus, in the range $k_f-k_i$ the density of states $N_0\to \infty$, and outside the range $N_0$ is finite. The distribution function $n(k,T)$ becomes more asymmetric with respect to the Fermi level $E_F$, generating the NFL behavior, and C invariance is broken. To illuminate the asymmetry, the area occupied by holes in panel (b) is labeled h (red) and that occupied by quasiparticles by p (maroon).

To gain more insights into the physical properties of the FC state, it is helpful to explore the system behavior at $T\to 0$. It was shown earlier [1,15,19] that the ground state of a system with FC is highly degenerate. In this case, the occupation numbers $n_0\left(p\right)$ of the FC state quasiparticles (i.e., having dispersionless spectrum or belonging to the flat band) change gradually from $n=1$ to $n=0$ at $T=0$. This variation occurs at $p_i\le p\le p_f$. It is clear that such a property of the occupation numbers drastically differs from the property of the usual Fermi–Dirac function property at $T=0$. Indeed, in that case, the Fermi–Dirac function is represented by the step function between $n=1$ and $n=0$ at $p=p_F$, where $p_F$ stands for Fermi momentum, see Figure 1.

At $T=0$, the infinite degeneracy of the ground state with FC leads to a T-independent entropy term [4,15], remaining finite at $T=0$ in violation of the Nernst theorem

$$S_0=-\sum _p[n_0\left(p\right)ln{n}_0\left(p\right)+(1-n_0\left(\mathbf{p}\right))ln(1-n_0\left(p\right))].$$

(8)

Thus, the infinite degeneracy of the FC ground state generated by flat bands, see Refs. [19,20] for a comprehensive discussion. We note that for systems where the Nernst theorem is violated due to the ground state degeneracy is a spin glass [40,41]. It is well known that in normal Fermi liquid the function $n\left(p\right)$ at finite temperatures loses its step-like feature at $p=p_F$, becoming continuous around this point. The same is valid for a Fermi liquid with flat bands; this conclusion follows from Equation (4). This means that at small but finite temperatures $T\ne 0$ the degeneracy of the above ground state is lifted, consequently the single-particle energy $\epsilon (p,T\ne 0)$ acquires a small dispersion [4]

$$\epsilon (p,T\to 0)=Tln\frac{1-n_0\left(p\right)}{n_0\left(\mathbf{p}\right)}.$$

(9)

From Equation (9), we see that the dispersion is proportional to T since the occupation numbers $n_0$ approximately remain the same as at $T=0$. This means that the entropy S in this case still remains $S\left(T\right)\ge S_0$. This situation also jeopardizes the Nernst theorem. To avoid this unphysical situation, the nearly flat bands representing the FC state should acquire dispersion in a way that the excess entropy $S_0$ should “dissolve” as $T\to 0$. This occurs by virtue of some additions to the FCQPT phase transition such as a ferromagnetic and/or a superconductive one, etc. [4,15,19]. Thus, at low temperatures the FC state has to be consumed by a number of phase transitions. This “consumption” can be viewed as a complicated phase diagram of an HF metal at its quantum critical point. In fact, at $T=0$ the FC state is represented by the superconducting state with the superconducting order parameter $\kappa =\sqrt{n\left(p\right)(1-n(p\left)\right)}$ that is finite in the region $(p_i-p_f)$ [15,33,42], for in the region $n\left(p\right)<1$, as shown in Figure 2. Nonetheless, the superconducting gap, $\Delta =0$, can be absent provided that the superconducting coupling constant $g=0$. In case of finite g, the gap exhibits very specific non-BCS behavior [43] $\Delta \propto g$, see, e.g., [1,4,44,45] and Section 7.

3. Scaling of Physical Properties

Experimental manifestations of the FC phenomenon correspond to the universal behavior of the physical properties of HF metals [15,19,20,46]. The physical properties of HF metals are formed due to flat bands and are widespread compounds [6]. To reveal the scaling, consider now the approximate solutions of Equation (3) [15,19,20]. At $B=0$, Equation (3) becomes strongly temperature dependent, which is a typical NFL feature and can be solved analytically [15,19,20,46]:

$$M^{*}\left(T\right)\simeq a_T{T}^{-2/3}.$$

(10)

At $T=0$, the analytical solution is

$$M^{*}\left(B\right)\simeq a_B{B}^{-2/3}.$$

(11)

Here, $a_T$ and $a_B$ are constants. Under the application of a magnetic field, the system transits to the LFL state with the effective mass becoming almost temperature independent and strongly dependent on B, as seen from Equation (11).

3.1. Internal Variables Revealing the Scaling Behavior

Equations (10) and (11) allow us to construct the approximate solution of Equation (3) in the form $M^{*}(B,T)=M^{*}(T/B)$. The introduction of “internal” scales simplifies the problem of constructing the universal scaling of the effective mass $M^{*}$, since in that case we eliminate the microscopic structure of the compound in question [15,19,20]. From the Figure 3a, we see that the effective mass $M^{*}(B,T)$ reaches a maximum $M_M^{*}$ at a certain temperature $T_M\propto B$ [15]. Accordingly, to measure the effective mass and temperature, it is convenient to introduce the scales $M_M^{*}$ and $T_M$. In this case, we have new variables $M_N^{*}=M^{*}/M_M^{*}$ that we call normalized effective mass and $T_N=T/T_M$ that we call normalized temperature. As a result, $M_N^{*}$ becomes a function of the only variable $T_N\propto T/B$, as seen from Figure 3b.

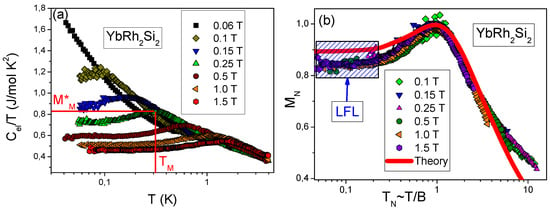
Figure 3. Electronic specific heat of ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$. Panel (a): Specific heat $C/T$, versus temperature T as a function of magnetic field B [36] shown in the legend. Panel (b): The normalized effective mass $M_N^{*}$ as a function of normalized temperature $T_N\propto T/B$. $M_N^{*}$ is extracted from the measurements of the specific heat $C/T$ on ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$ in magnetic field B [36], see panel (a), listed in the legend. Approximate constant effective mass $M^{*}$ at $T_N<1$ is typical for the normal Landau Fermi liquids, and is shown by the arrow.

In the vicinity of the FCQPT, the normalized effective mass $M_N^{*}\left(T_N\right)$ can be well approximated by a certain universal function [15,19], interpolating the solutions of Equation (3) between the LFL state, given by Equation (11), and the NFL one, given by Equation (10) [15]

$$M_N^{*}\left(T_N\right)\approx c_0\frac{1+c_1{T}_N^2}{1+c_2{T}_N^{8/3}}.$$

(12)

Here, $T_N=T/T_M$, $c_0=(1+c_2)/(1+c_1)$, where $c_1$ and $c_2$ are free parameters. Since the magnetic field B enters Equation (3) as ${\mu }_{B}B/T$, the maximum temperature $T_M\sim {\mu }_{B}B$. Consequently, from Equation (12),

$$T_M\simeq a_1{\mu }_{B}B;T_N=\frac{T}{T_M}=\frac{T}{a_1{\mu }_{B}B}\propto \frac{T}{B},$$

(13)

where $a_1$ is a dimensionless parameter, and ${\mu }_B$ is the Bohr magneton. Equation (13) shows that Equation (12) determines the effective mass as a function of the single variable $T_N\propto T/B$. That is, the curves $M_N^{*}(T,B)$ merge into a single one $M_N^{*}\left(T_N\right)$, $T_N=T/T_M$, as shown in Figure 4. Since $T_M\propto B$, from Equation (13) we conclude that the curves $M_N^{*}(T,B)$ coalesce into a single one $M_N^{*}(T_N=T/B)$, $T_N=T/T_M=T/B$, demonstrating the universal scaling in HF metals [15,19,20]. This universal scaling exhibited by $M_N$ is also shown in Figure 4. We note that Equations (12) and (13) allow one to describe the universal scaling behavior of HF metals, see, e.g., [15,19,20].

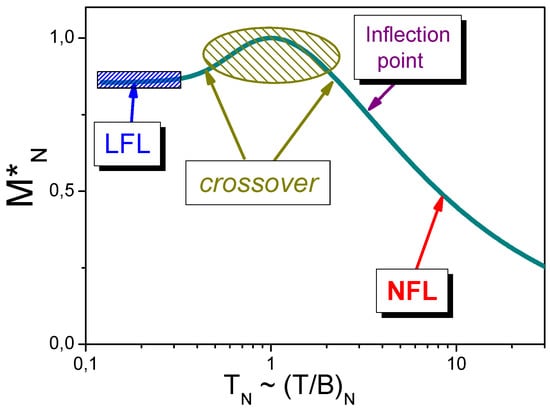
Figure 4. Scaling of the thermodynamic properties governed by the normalized effective mass $M_N^{*}$ in the case of the application of a magnetic field $T_N\propto T/B$, as follows from Equation (13). The solid curve depicts $M_N^{*}$ versus normalized temperature $T_N$. It is clearly seen that at finite $T_N<1$, the normal Fermi liquid properties take place. At $T_N\sim 1$, $M_N^{☆}$ enters the crossover state, and at growing temperatures it exhibits the NFL behavior.

One more important feature of the FC state is that apart from the fact that the Landau quasiparticle effective mass starts to depend strongly on external stimuli such as T and B, all relations, inherent in the LFL theory, formally remain the same. Namely, the famous LFL relation [35],

$$M^{*}(B,T)\propto \chi (B,T)\propto \frac{C(B,T)}{T}\propto {\gamma }_0.$$

(14)

still holds. Here, ${\gamma }_0$ is the Sommerfeld coefficient. Expression (14) has been related to the FC case, where the specific heat C, magnetic susceptibility $\chi$ and effective mass $M^{*}$ depend on T and B. Taking Equation (14) into account, we obtain that the normalized values of $C/T$ and $\chi$ are of the form [15,19]

$$M_N^{*}(B,T)={\chi }_N(B,T)={\left(\frac{C(B,T)}{T}\right)}_N.$$

(15)

From Equation (15) we see that the above thermodynamic properties have the same scaling displayed in Figure 4. As a result, we shall see that the observed scaling allows us to construct a general schematic phase diagram, see Section 3.3.

3.2. Magnetoresistance

In the LFL state, the resistivity $\rho (T,B)\propto A_2\left(B\right)T^2$. In the case of common metals, it is well known that $\rho (T,B)$ increases with the increasing applied magnetic field B and is described by the Kohler’s rule, see, e.g., [47]. In contrast, HF metals exhibit decreasing resistivity in magnetic fields when the metal in question transits from the NFL behavior to the LFL one, see, e.g., [48,49]. The $A\left(B\right)$ coefficient, being proportional to the quasiparticle —quasiparticle scattering cross section is found to be $A\propto {\left(M^{*}\left(B\right)\right)}^2$, as follows from Equation (11) [15,48]. Taking into account Equation (11), we obtain

$$A\left(B\right)\simeq A_0+\frac{D}{B-B_{c0}},$$

(16)

where $A_0$ and D are fitting parameters. Figure 5 displays experimental data for $A\left(B\right)$ collected on two HF metals: ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$ [48] and ${\mathrm{Tl}}_2{\mathrm{Ba}}_2{\mathrm{CuO}}_{6+\mathrm{x}}$ [49]. The solid curves represent our calculations, and the inset demonstrates that the well-known Kadowaki–Woods ratio [50] is conserved [48]. This experimental result is in good agreement with Equations (15) and (16).

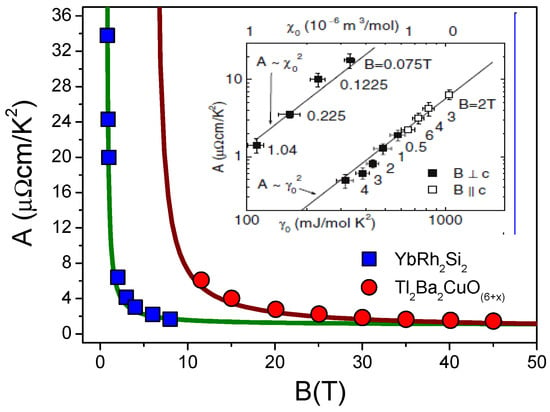
Figure 5. The charge transport coefficient $A\left(B\right)$ as a function of magnetic field B obtained in measurements on ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$ [48] and ${\mathrm{Tl}}_2{\mathrm{Ba}}_2{\mathrm{CuO}}_{6+\mathrm{x}}$ [49]. The different field scales are clearly indicated. The solid curves represent our calculations based on Equation (16) [15]. The inset (adapted from [51]) shows that $A\left(B\right)\propto \chi {\left(B\right)}^2\propto {\gamma }_0^2\propto {(C/T)}^2$.

To further elucidate the scaling of $A\left(B\right)$, we rewrite Equation (16) in the re-scaled variables $A/A_0$ and $B/B_{c0}$. Such a recasting immediately reveals the scaling nature of the behavior of these two substances. Both of them are driven to common QCP related to the FCQPT and induced by the application of a magnetic field. As a result, Equation (16) takes the form

$$\frac{A\left(B\right)}{A_0}\simeq 1+\frac{D_N}{B/B_{c0}-1},$$

(17)

where $D_N=D/\left(A_0{B}_{c0}\right)$ is a constant. From Equation (17), it is seen that upon applying the scaling to both coefficients $A\left(B\right)$ for ${\mathrm{Tl}}_2{\mathrm{Ba}}_2{\mathrm{CuO}}_{6+\mathrm{x}}$ and $A\left(B\right)$ for ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$, they are reduced to a function depending on the single variable $B/B_{c0}$, thus demonstrating the universal behavior. To support Equation (17), we plot both dependencies in the reduced variables $A/A_0$ and $B/B_{c0}$ in Figure 6; the universal scaling nature of the coefficients $A\left(B\right)$ of these two substances is immediately revealed. We note that the negative magnetoresistance of both ${\mathrm{Tl}}_2{\mathrm{Ba}}_2{\mathrm{CuO}}_{6+\mathrm{x}}$ and ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$ results from diminishing $A\left(B\right)$ under the application of a magnetic field as follows from Equation (11).

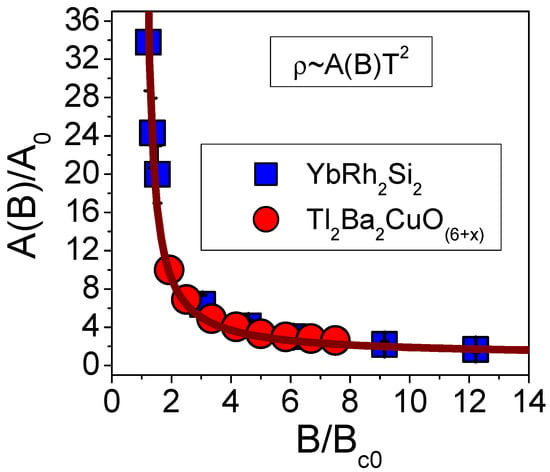
Figure 6. Normalized coefficient $A\left(B\right)/A_0\simeq 1+D_N/(y-1)$ given by Equation (17) as a function of a normalized magnetic field $y=B/B_{c0}$ shown by squares for ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$ and by circles for high-$T_c$ ${\mathrm{Tl}}_2{\mathrm{Ba}}_2{\mathrm{CuO}}_{6+\mathrm{x}}$. $D_N$ is the only fitting parameter.

The scaling behavior of the longitudinal magnetoresistance (LMR) collected on ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$ [48] confirms our above conclusions. This scaling behavior is displayed in Figure 7. Clearly, our calculations are in good agreement with the experimental data. Thus, the fermion condensation theory explains both the negative magnetoresistance and the crossover from the NFL behavior to the LFL one under the application of magnetic fields.

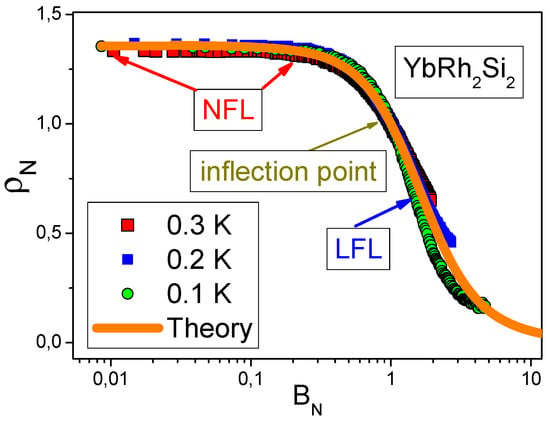
Figure 7. Magnetic field dependence of the longitudinal normalized magnetoresistance LMR versus a normalized magnetic field. The LMR ${\rho }_N$ was extracted from the LMR of ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$ at different temperatures [48] listed in the legend. The solid line represents our calculations [15]. The arrows show the NFL behavior at $B\ll T$, the inflection point and the LFL behavior at $B\gg T$.

3.3. Schematic Phase Diagram

Based on Equation (12) and Figure 3 and Figure 4, we can construct the schematic $T-B$ phase diagram of HF metals [52], reported in Figure 8. We assume here that at $T=0$ and $B=B_{c0}$ the system is approximately located at the FCQPT. In the case of $B_{c0}=0$, the system is located at the FCQPT without tuning. At fixed temperatures, the system is driven by the magnetic field B along the horizontal arrow (from the NFL to the LFL parts of the phase diagram). In turn, at fixed B and increasing T, the system moves from the LFL to the NFL regime along the vertical arrow. The hatched area indicating the crossover between the LFL and the NFL phases separates the NFL state from the slightly polarized paramagnetic LFL state. The crossover temperature $T_M\left(B\right)$ is given by Equation (13).

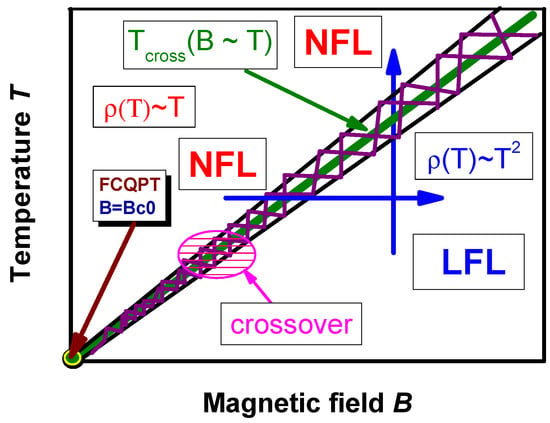
Figure 8. Schematic $T-B$ phase diagram of a strongly correlated Fermi system. The vertical and horizontal arrows crossing the transition region marked by the thick lines depict the LFL–NFL and NFL–LFL transitions at fixed B and T, respectively. At $B<B_{c0}$, the system is in its possible antiferromagnetic (AF) state, with $B_{c0}$ shown by the arrow as denoting a critical magnetic field destroying the AF state. Both the hatched areas shown by the arrow and by the solid curve $T_{\mathrm{cross}}(B\sim T)$ represent the crossover separating the domain of NFL behavior from the LFL domain. A part of the crossover is hidden in the possible AF state.

4. The Linear T-Dependent Resistivity and the Planckian Limit

For very different metals such as HF metals, high $T_c$ superconductors and common metals, $\rho \left(T\right)\propto T$, the linear dependence of resistivity on temperature and the universality of their fundamental physical properties have been explained within the framework of the FC theory [15,19,25]. On one hand, at low T, the linear T-resistivity

$$\rho \left(T\right)={\rho }_0+A_{1}T,$$

(18)

is experimentally observed in many strongly correlated compounds such as high-temperature superconductors and heavy-fermion metals located near their quantum critical points and therefore exhibiting quantum criticality and a new state of matter, see, e.g., [21,32]. Here, ${\rho }_0$ is the residual resistivity and A is a T-independent coefficient. Explanations based on quantum criticality for the T-linear resistivity have been given in the literature, see, e.g., [53,54,55,56,57,58,59] and Refs. therein. At room temperatures the T-linear resistivity is exhibited by conventional metals such as $\mathrm{Al}$, $\mathrm{Ag}$ or $\mathrm{Cu}$. In the case of a simple metal, the resistivity reads $e^{2}n\rho =p_F/\left(\tau v_F\right)$ [60], where e is the electronic charge, $\tau$ is the lifetime, n is the carrier concentration and $p_F$ and $v_F$ are the Fermi momentum and the Fermi velocity, respectively. Writing the lifetime $\tau$ (or inverse scattering rate) of quasiparticles in the form [58,61]

$$\frac{\hslash }{\tau }\simeq a_1+\frac{k_{B}T}{a_2},$$

(19)

we obtain [25]

$$a_2\frac{e^{2}n\hslash }{p_F{k}_B}\frac{\partial \rho }{\partial T}=\frac{1}{v_F},$$

(20)

where ℏ is Planck’s constant, $k_B$ is Boltzmanns constant, and $a_1$ and $a_2$ are T-independent parameters. Challenging problems for a theory dealing with strongly correlated Fermi systems are:

(1) Experimental data corroborate Equation (20) in the case of both strongly correlated metals and ordinary ones, provided that these demonstrate the linear T-dependence of their resistivity [21], see Figure 9;

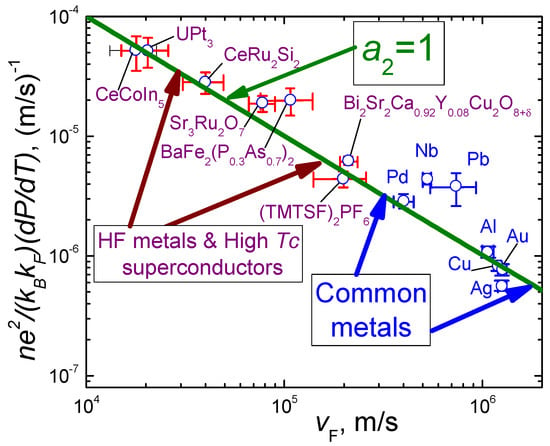
Figure 9. Scattering rates of different strongly correlated metals such as HF metals, high-$T_c$ superconductors, organic metals and conventional metals [21]. All these metals exhibit $\rho \left(T\right)\propto T$, and their Fermi velocities $V_F$ vary by two orders of magnitude. The parameter $a_2\simeq 1$ gives the best fit shown by the solid green line, see Equation (20). The region occupied by the common metals is displayed by the two blue arrows, and the two maroon arrows show the region of strongly correlated metals.

(2) Under the application of a magnetic field, HF metals and high-$T_c$ superconductors exhibit the LFL behavior, see Figure 8, and the Planckian limit dissolves in magnetic fields.

Moreover, the analysis of data in the literature for various compounds and ordinary metals with the linear dependence of $\rho \left(T\right)$ shows that the coefficient $a_2$ is always $0.7\le a_2\le 2.7$, notwithstanding the large differences in the absolute values of $\rho$, T and Fermi velocities $v_F$, varying by two orders of magnitude [21]. As a result, from Equation (19), the T-linear scattering rate is of the universal form, $1/\left(\tau T\right)\sim k_B/\hslash$, regardless of different systems displaying the T-linear dependence [19,21,25]. Indeed, this dependence is demonstrated by ordinary metals at temperatures higher than the Debye temperature, $T\ge T_D$, with an electron–phonon mechanism and by strongly correlated metals that are assumed to be fundamentally different from the ordinary ones since the linear T-dependence of their resistivity at temperatures of a few Kelvin is assumed to originate from excitations of electronic origin rather than from phonons [21]. We note that in some cuprates, the scattering rate has a momentum and doping $\mathrm{x}$ dependence omitted in Equation (20) [62,63,64]. Nonetheless, the fundamental picture outlined by Equation (20) is strongly supported by measurements of the resistivity on ${\mathrm{Sr}}_3{\mathrm{Ru}}_2{\mathrm{O}}_7$ for a wide range of temperatures: At $T\ge 100$ K, the resistivity again becomes linearly T-dependent at all applied magnetic fields, as it does at low temperatures and at the critical field $B_c\simeq 7.9$ T but with the coefficient A lower than that seen at low temperatures [21,25]. The same strongly correlated compound exhibits the similar behavior of the resistivity at both quantum critical regime and high temperatures. These facts allow us to expect that the same physics governs the Planckian limit in the case of strongly correlated and ordinary metals. As we will see, the physics here is explained within the fermion condensation theory, and is related to flat bands, the existence of which has been predicted many years ago [1,2,4,15,26,37].

As seen from Figure 9, the scaling relation spans two orders of magnitude in $V_F$, attesting to the robustness of the observed empirical law [21]. This behavior is explained within the framework of the FC theory since in both cases of common metals and strongly correlated ones, the scattering rate is defined by phonons [25]. In the case of common metals at $T>T_D$, it is well known fact that phonons make a main contribution to the linear dependence of the resistivity, see, e.g., [60]. It has been shown that quasi-classical physics describes the T-linear dependence of the resistivity of strongly correlated metals at $T>T_D$, since flat bands, forming the quantum criticality, generate transverse zero-sound mode with the Debye temperature $T_D$ located within the quantum criticality area [25,57,58]. Therefore, the linear T-dependence is formed by electron–phonon scattering in both ordinary metals and strongly correlated ones. As a result, it is electron–phonon scattering that leads to the near material independence of the lifetime $\tau$ that is expressed as

$$\frac{1}{\tau T}\sim \frac{k_B}{\hslash }.$$

(21)

We note that there can be another mechanism supporting the linear T-dependence even at $T<T_D$ that fails to warrant a constant $\tau$ regardless of the presence of the linear T-dependence of resistivity [25,58]. The mechanism comes from flat bands that are formed by the FC state and contribute to both the linear dependence of the resistivity and to the residual resistivity ${\rho }_0$, see Equation (18). Notably, these observations are in good agreement with the experimental data [25,58]. The important point here is that under the application of a magnetic field, the system in question transits from its NFL behavior to an LFL one, and both the flat bands and the FC state are destroyed [15,19], see the $T-B$ phase diagram depicted in Figure 8. Therefore, with resistivity $\rho \left(T\right)\propto T^2$, magnetoresistance becomes negative, while the residual resistivity ${\rho }_0$ jumps down by a step [19,24,25,58]. Such a behavior is in accordance with experimental data, see, e.g., the case of the HF metal ${\mathrm{CeCoIn}}_5$ [65] that also demonstrates the universal scattering rate at its NFL region, see Figure 9.

5. Asymmetrical Conductivity (Resistivity) of Strongly Correlated Conductors

Direct experimental studies of quantum phase transitions in HTSC and HF metals are of great importance for understanding the underlying physical mechanisms responsible for their anomalous properties. However, such studies of HF metals and HTSC are difficult because the corresponding critical points are usually concealed by their proximity to other phase transitions, commonly antiferromagnetic (AF) and/or superconducting (SC).

Furthermore, extraordinary properties of tunneling conductivity in the presence of a magnetic field were recently observed in a graphene preparation having a flat band [5], as well as in HTSCs and the HF metal ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$ [29,30]. Measuring and analyzing these properties will shed light on the nature of the quantum phase transitions occurring in these substances. Very recently, the scattering rate has been measured in graphene, and it is located near the universal value [23] given by Equation (21), being in accordance with data shown in Figure 9. All these experimental observations qualify graphene as a very interesting material for revealing the physics of strongly correlated Fermi systems.

Most of the experiments on HF metals and HTSCs explore their thermodynamic properties. However, it is equally important to determine other properties of these strongly correlated systems, notably quasiparticle occupation numbers $n(p,T)$ as a function of momentum p and temperature T. These quantities are not linked directly to the density of states (DOS) $N_s(\epsilon =0)$ determined by the quasiparticle energy $\epsilon$ or to the behavior of the effective mass $M^{*}$. Scanning tunneling microscopy [66,67,68] and point contact spectroscopy [28,69,70], being sensitive to both the density of states and quasiparticle occupation numbers, are ideal tools for exploring the effects of $\mathcal{C}$ and $\mathcal{T}$ symmetry violation. When $\mathcal{C}$ and $\mathcal{T}$ symmetries are not conserved, the differential tunneling conductivity and dynamic conductance are no longer symmetric functions of the applied voltage V.

Indeed, if under the application of bias voltage V, the current of electrons with the charge $-e$, traveling from HF to a common (i.e., “non-HF”) metal changes the sign of a charge carrier to $+e$, then current character and direction alter. Namely, now the carriers are holes with the charge $+e$ traveling from the common to the HF metal. Turning this around, one can obtain the same current of electrons provided that V is changed to $-V$. The resulting asymmetric differential conductivity $\Delta {\sigma }_d\left(V\right)={\sigma }_d\left(V\right)-{\sigma }_d(-V)$ becomes nonzero, as seen from Figure 10. On the other hand, if time t is changed to $-t$ (but charge is kept intact), the current changes its direction only. The same result can be achieved by $V\to -V$, and we conclude that $\mathcal{T}$ symmetry is broken, provided that $\Delta {\sigma }_d\left(V\right)\ne 0$. Thus, the presence of $\Delta {\sigma }_d\left(V\right)\ne 0$ signals violation of both $\mathcal{C}$ and $\mathcal{T}$ symmetries. Simultaneously, the change of both $e\to -e$ and $t\to -t$ returns the system to its initial state so that CT symmetry is conserved bearing in mind that the same consideration is true when analyzing ${\rho }_d\left(V\right)$. Note that the parity symmetry P is conserved, and the well-known CPT symmetry is not broken in the considered case. However, the time-reversal invariance and particle-hole symmetry remain intact in normal Fermi systems; the differential tunneling conductivity and dynamic conductance are symmetric functions of V. Therefore, conductivity asymmetry is not observed in conventional metals at low temperatures [28].

To determine the tunneling conductivity, we first calculate the tunneling current $I\left(V\right)$ through the contact point between the two metals. This is performed using the method of Harrison [66,67,68], based on the observation that $I\left(V\right)$ is proportional to the particle transition probability introduced by Bardeen [43]. Bardeen considered the probability $P_{12}$ of a particle (say an electron) making a transition from a State 1 on one side of the tunneling layer to a State 2 on the other side. Probability behaves as $P_{12}\sim {\left|t_{12}\right|}^2{N}_2\left(0\right)n_1(1-n_2)$ where $N_2\left(0\right)$ (at $\epsilon =0$) is the density of states in State 2, $n_{1,2}$ is the the electron occupation numbers in these states and $t_{12}$ is the transition matrix element. The total tunneling current I is then proportional to the difference between the currents from one to two and that from two to one, and is as follows.

$$\begin{array}{c}\hfill I\sim P_{12}-P_{21}\sim {\left|t_{12}\right|}^2{N}_1\left(0\right)N_2\left(0\right)\times \\ \hfill \left[n_1(1-n_2)-n_2(1-n_1)\right]=\\ \hfill |t_{12}{|}^2{N}_1\left(0\right)N_2\left(0\right)(n_1-n_2).\end{array}$$

(22)

Harrison applied the WKB approximation to calculate the matrix element [66,67,68], $t_{12}=t{\left(N_1\left(0\right)N_2\left(0\right)\right)}^{-1/2}$, where t denotes the resulting transition amplitude. Multiplication of expression (22) by two to account for the electron spin and integration over the energy $\epsilon$ leads to the expression for total (or net) tunneling current [66,67,68]:

$$I\left(V\right)={2\left|t\right|}^2\int \left[n_F(\epsilon -\mu -V)-n_F(\epsilon -\mu )\right]d\epsilon .$$

(23)

Here $n_F\left(\epsilon \right)$ is the electron occupation number for a metal in the absence of a FC, and we have adopted atomic units $e=m=\hslash =1$, where e and m are the electron charge and mass, respectively. Since temperature is low, $n_F\left(\epsilon \right)$ can be approximated by the step function $\theta (\epsilon -\mu )$, where $\mu$ is the chemical potential.

From Equation (23), it follows that quasiparticles with single-particle energies $\epsilon$ in the range $\mu \le \epsilon \le \mu +V$ contribute to the current, $I\left(V\right)=c_{1}V$ and ${\sigma }_d\left(V\right)\equiv dI/dV=c_1$, with $c_1=\mathrm{const}$. Thus, wthin the framework of LFL theory, the differential tunneling conductivity ${\sigma }_d\left(V\right)$, being a constant, is a symmetric function of the voltage V, i.e., ${\sigma }_d\left(V\right)={\sigma }_d(-V)$. In fact, the symmetry of ${\sigma }_d\left(V\right)$ holds provided $\mathcal{C}$ and $\mathcal{T}$ symmetries are observed, as is customary for LFL theory. Therefore, ${\sigma }_d\left(V\right)$ is symmetric, and this is common in the case of contact of two ordinary metals (without FC), regardless of whether they are in a normal or superconducting state. Note that a more rigorous consideration of the densities of states $N_1$ and $N_2$ entering Equation (22) for $\epsilon \simeq \mu$ requires their inclusion in the integrand of Equation (23) [71,72,73]. For example, see Equation (7) of Ref. [73], where this refinement has been carried out for the system of a magnetic adatom and scanning tunneling microscope tip. However, this complication does not break the $\mathcal{C}$ symmetry in the LFL case. Nonetheless, it will be seen below that if the system hosts FC, the presence of the density-of-states factors in the integrand of Equation (23) initiates the asymmetry of the tunneling spectra, since the density of states strongly depends on $\epsilon \simeq \mu$, see Figure 2. Indeed, the situation becomes quite different in the case of a strongly correlated Fermi system in the vicinity of the FCQPT that causes a flat band [1,2] and violates the $\mathcal{C}$ symmetry [15,19,74]. We note that as we have seen above, the violation of the $\mathcal{C}$ symmetry entails the violation of the $\mathcal{T}$ symmetry. Panel (a) of Figure 2 illustrates the resulting low-temperature single-particle energy spectrum $\epsilon (k,T)$. Panel (b), which displays the momentum dependence of the occupation numbers $n(k,T)$ in such a system, shows that the flat band induced by the FCQPT, as we have seen above, in fact, violates $\mathcal{T}$ symmetry as well. The broken $\mathcal{C}$ symmetry is reflected in the asymmetry of the regions occupied by particles (labeled p) and holes (labeled h) [15]. We note that the system in its superconducting state and located near the FCQPT exhibits asymmetrical tunneling conductivity, since the $\mathcal{C}$ symmetry remains broken in both the superconducting and the normal states. This observation conforms with the experimental facts [15,70], as seen from Figure 8.

We see from Figure 2 that at low temperatures the electronic liquid of the system has two components. One is an exotic component comprised of heavy electrons occupying momentum range $p_i<p<p_f$ surrounding the Fermi volume near the Fermi surface $p=p_F$. This component is characterized by the superconducting order parameter $\kappa \left(p\right)=\sqrt{n\left(p\right)(1-n(p\left)\right)}$. The other component is made up of normal electrons occupying the momentum range $0\le p\le p_i$ [15,33]. In particular, the density of paired charge carriers that form the superfluid density is no longer equal to the total particle density $n_{el}$ represented by paired and unpaired charge carriers. This violation of Leggett’s theorem is to be expected since both $\mathcal{C}$ and $\mathcal{T}$ invariants are violated in the NFL state of some HF metals and compounds [15,19,31,74].

We are proposing that for the strongly correlated many-fermion systems in question, the approximate equality $n_s\simeq n_{\mathit{el}}$ that would normally be expected for a real system approximating BCS behavior must be replaced by the inequality $n_s=n_{FC}\ll n_{\mathit{el}}$, where $n_{\mathrm{FC}}$ is the density of particles in the FC state [42]. This implies that the main contribution to $n_s$ comes from the FC state. Indeed, the wave function $\Xi$ describing the state of the Cooper pairs as a whole concentrates its associated probability density in the momentum domain of the flat band such that ${|\Xi |}^2\propto n_s$, with ${|\Xi |}^2\simeq 0$ outside this range. Being defined by the properties of FC, $n_s$ can be very small. Nor does it depend on $n_{el}$, so it can be expected that $n_s\ll n_{el}$ [33,42].

It is worth noting that the first studies of the overdoped copper oxides suggested that $n_s\ll n_{el}$, but this was attributed to pair-breaking and disorder [75,76,77], while recent studies with the measurements on ultra-clean samples of La${}_{2-x}$Sr${}_x$CuO${}_4$ authenticate the result that $n_s\ll n_{el}$ [32]. It is also relevant that the observed high values of $T_c$ together with the linear dependence of ${\rho }_{s0}\propto T_c$ [32] of the resistivity are not easily reconciled with the pair-breaking mechanism proposed for dirty superconductors, see, e.g., [53] and Section 7. One cannot expect that such a mechanism would be consistent with high values of $T_c$ and the increase of $T_c$ with doping x. It is worth noting that experimental observation shows that $A_1\left(x\right)/T_c\left(x\right)\simeq const$ [32,78]. This observation supports the theory of the FC condensation that demonstrates the same result $A_1(x_c-x)/T_c(x_c-x)=const$ [79,80]. Here, $x_c$ is the doping concentration at which the superconductivity sets in, and $(x_c-x)\propto n_s$ [42]. As a result, these evidences support the fermion condensation theory, suggesting the topological FCQPT as the underlying physical mechanism of both the unusual properties of overdoped copper oxides and the asymmetry of tunneling conductivity [1,2,15,19,81].

In case of a strongly correlated Fermi system with FC, the tunneling current becomes [15,31,82,83]

$$I\left(V\right)={2\left|t\right|}^2\int \left[n(\epsilon -\mu -V,T)-n_F(\epsilon -\mu ,T)\right]d\epsilon .$$

(24)

Here one of the distribution functions of ordinary metal $n_F$ on the right-hand side of Equation (23) is replaced by $n(\epsilon ,T)$, shown in Figure 2b. As a result, the asymmetric part of the differential conductivity $\Delta {\sigma }_d\left(V\right)={\sigma }_d\left(V\right)-{\sigma }_d(-V)$ becomes finite, and we obtain [15,19,31,70,82]

$$\Delta {\sigma }_d\left(V\right)\simeq c\left(\frac{V}{2T}\right)\frac{p_f-p_i}{p_F},$$

(25)

where $p_f$ and $p_i$ define the location of FC, see Figure 2, $p_F$ is the Fermi momentum and c is a constant of order unity.

Figure 10. Conductivity spectra ${\sigma }_d\left(V\right)=dI/dV$ measured on the HF metal ${\mathrm{CeCoIn}}_5$ with point contacts (Au/CeCoIn${}_5$) over a wide temperature range [84]. Curves ${\sigma }_d\left(V\right)$ are shifted vertically by 0.05 for clarity and normalized by the conductance at $-2$ mV. The asymmetry develops at $T\simeq 40$ K, becoming stronger at decreasing temperature and persisting below $T<T_c\simeq 2.3$ K in the superconducting state [84].

It is worth noting that Equation (25) is also valid even if the density of states $N_1$ and $N_2$ are taken into account, since all this does is change c. Note that the conductivity $\Delta {\sigma }_d\left(V\right)$ remains asymmetric in the superconducting phase of both HTSC and HF metals as well. In such cases, it is again the occupation number $n\left(p\right)$ that is responsible for the asymmetric part of $\Delta {\sigma }_d\left(V\right)$, since this function is not appreciably disturbed by the superconductive pairing. This is because usually, in forming the function $n\left(p\right)$, the Landau interaction contribution is stronger than that of the superconductive pairing [15]. As a result, $\Delta {\sigma }_d\left(V\right)$ remains approximately the same below the superconducting $T_c$ [15,31]. It is seen from Equation (25) and Figure 10 that with rising temperatures, the asymmetry diminishes and finally vanishes at $T\ge 40$ K. Such a behavior has been observed in measurements on the HF metal ${\mathrm{CeCoIn}}_5$ [84,85], displayed in Figure 10.

Under the application of a magnetic field B at sufficiently low temperatures $k_{B}T\lesssim {\mu }_{B}B$, where $k_B$ and ${\mu }_B$ are the Boltzmann constant and the Bohr magneton, the strongly correlated Fermi system transits from the NFL to the LFL regime [15,86]. As we have seen above, the asymmetry of the tunneling conductivity vanishes in the LFL state [15,31,70,82]. It is seen from Figure 11, that $\Delta {\sigma }_d\left(V\right)$, displayed in Figure 10 and extracted from experimental data [85], vanishes in the normal state at sufficiently high magnetic fields applied along the easy axis and low temperatures $k_{B}T<<{\mu }_B(B-B_c)$ with the critical field $B_c\simeq 5$ T in agreement with the prediction, see, e.g., [15,31,87]. Under this condition, the system transits from the NFL to the LFL behavior, with the resistance $\rho$ becoming a quadratic function of temperature, $\rho \left(T\right)\propto T^2$ [15]. The examples of suppression of the asymmetric parts of differential conductivity and resistance under the application of a magnetic field are shown in Figure 11, Figure 12 and Figure 13, respectively.

Figure 11. Asymmetric part $\Delta {\sigma }_d\left(V\right)$ of the tunneling differential conductivity measured on ${\mathrm{CeCoIn}}_5$ and extracted from the experimental data [85]. The asymmetric part vanishes at $B=14$ T and $T=1.75$ K, with $B_{c0}\simeq 5$ T.

Figure 12. Asymmetric parts $\Delta {\sigma }_d\left(V\right)$ of the tunneling differential conductivity measured on ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$ and extracted from the data shown in Figure 14.

Figure 13. Magnetic field (legend) dependence of the asymmetric part $As\left(I\right)=dV/dI\left(I\right)-dV/dI(-I)$ versus the current I, extracted from the data of Figure 15 for graphene.

Figure 14 shows the differential conductivity ${\sigma }_d$ observed in measurements on ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$ [29,30]. It is seen that asymmetry diminishes with increasing magnetic field B, as the minima of the curves shift to the point $V=0$, see also Figure 12 for details. The magnetic field is applied along the hard magnetization direction, $B\Vert c$, with $B_c\simeq 0.7$ T [30], where $B_c$ is the critical field suppressing the AF order [51]. The asymmetric part of the tunneling differential conductivity, $\Delta {\sigma }_d\left(V\right)$, extracted from the measurements shown in Figure 14, is displayed in Figure 12. It is seen that $\Delta {\sigma }_d\left(V\right)$ decreases as B increases. We predict that application of the magnetic field in the easy magnetization plane, $B\perp c$ with $B_c\simeq 0.06$ T, leads to a stronger suppression of the asymmetric part of the conductivity, observing that in this case the magnetic field effectively suppresses the antiferromagnetic order and the NFL behavior. Indeed, the experimental data show that low-temperature electrical resistivity $\rho \left(T\right)$ of the HF metal ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$, measured at $T\simeq 20$ mK, under the application of the magnetic field $B\ge 75$ mT along an easy magnetization plane, exhibits the LFL behavior $\rho \left(T\right)\propto T^2$, while at $B\simeq 60$ mT it demonstrates the NFL behavior, $\rho \left(T\right)\propto T$. At the same time, under the application of a magnetic field B along the hard magnetization direction, resistivity shows the LFL behavior at much higher $B\ge 0.8$ T [51]. The same transition from the NFL behavior to the LFL one is observed in measurements of the thermodynamic, transport and relaxation properties, see, e.g., [15,19,51]. We surmise that the asymmetric part $\Delta {\sigma }_d\left(V\right)$ vanishes as soon as ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$ enters its AF state, exhibiting the LFL behavior $\rho \left(T\right)\propto T^2$ at $B=0$ and $T<70$ mK.

Figure 14. Differential conductivity ${\sigma }_d\left(V\right)=dI/dV$ measured on ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$ under the application of a magnetic field (legend) along the hard magnetization direction [30].

Measuring the differential resistance ${\rho }_d\left(V\right)=dV/dI$ as a function of current I, one finds that the its symmetry properties are the same as those of ${\sigma }_d\left(V\right)$. Namely, under the application of a magnetic field, the asymmetry of the differential resistance vanishes as the system transits into the LFL state. The differential resistance ${\rho }_d\left(V\right)$ of graphene as a function of a direct current I for different magnetic fields B is reported in Figure 15 [5]. The asymmetric part of the differential resistance $As\left(I\right)={\rho }_d\left(V\right)-{\rho }_d(-V)$ diminishes with an increasing magnetic field, vanishing near $B\simeq 140$ mT. Such a behavior corroborates our conclusion, since the strongly correlated graphene sample has a perfect flat band, implying that the FC effects should be clearly manifested in this material [5].

Figure 15. Differential resistance $dV/dI$ of graphene versus current I at different magnetic fields B shown in the legend [5]. Weak asymmetry is observed at small magnetic fields.

Thus, in accordance with prediction [15,31,70,82], the asymmetric part tends to zero at tiny magnetic fields of 140 mT, as seen from Figure 13. Note that suppression of the asymmetric part under the application of a magnetic field has been observed in the HF metal ${\mathrm{YbCu}}_{5-\mathrm{x}}{\mathrm{Al}}_{\mathrm{x}}$ [81]. The asymmetry persists in the superconducting state of graphene [5] and is suppressed at $B\simeq 80$ mT. Disappearance of the asymmetric part of the differential conductivity in Figure 13 indicates that as the magnetic field increases, graphene transits from the NFL to the LFL state. We remark that the disappearance of the asymmetric part of the differential conductivity was predicted many years before the experimental observations [31,70,82]. It is worth noting that the decrease of the asymmetric part under the application of a magnetic field is an important feature, since the presence of the asymmetric part can be observed by a simple device, e.g., by a diode, since the asymmetric part does not vanish in a magnetic field. Moreover, at $B=0$, the asymmetric part observed in HF metals and HTSC can be explained in many ways, see, e.g., [88].

To support the statement that the NFL behavior of graphene vanishes in magnetic fields, we surmise that the resistance $\rho \left(T\right)$ should exhibit linear dependence $\rho \left(T\right)\propto A_{1}T$ in the normal state at zero magnetic field, as is generally the case in other strongly correlated Fermi systems. Indeed, at elevated magnetic fields and low temperatures $k_{B}T<<{\mu }_{B}B$, the system transits from the NFL behavior to the LFL behavior, causing the resistance to become a quadratic function of temperature $\rho \left(T\right)\propto T^2$ that confirms the LFL behavior [15,19,58].

6. Heavy-Fermion Metals and High-Temperature Superconductors: Scaling Relations

It has been shown that the behavior $\rho \left(T\right)\propto T$ as $T\to 0$ is an intrinsic property of cuprates associated with a universal scattering rate as well as the property of HF metals [21,22,24], see Section 4. It is stated that the behavior $\rho \left(T\right)\propto T$ is achieved when the scattering rate hits the Planckian limit, given by Equation (21), irrespective of the origin of the scattering process [22,24]. However, it is hardly possible that the linear T-dependence of resistivity of common metals is formed by the Planckian limit, as observed in Ref. [21], see Figure 9 and explanation in Ref. [25]. Moreover, HF metals and high-$T_c$ superconductors demonstrate scaling behavior under the application of a magnetic field, pressure, etc., see Figure 3a,b. In magnetic fields, these compounds are shifted from the NFL to the LFL behavior, see, e.g., [15,24]. All these extraordinary features are explained within the framework of the FC theory [1,15,19]. As a result, we can safely suggest that the main reason for the behavior given by Equation (21) is defined by phonons, taking place at $T\ge T_D$ in both strongly correlated Fermi systems and common metals [25].

Another experimental result [27] providing insight into the NFL behavior of strongly correlated Fermi systems is the universal scaling, which can also be explained using the flat band concept. The authors of Ref. [27] measured the temperature dependence $d\rho /dT$ of the resistivity $\rho$ for a large number of HTSC substances for $T>T_c$. Among these were LSCO and the well-known HF compound CeCoIn${}_5$; see Table I of Ref. [27]. They discovered quite remarkable behavior: for all substances considered, $d\rho /dT$ shows a linear dependence on the London penetration depth ${\lambda }_0^2$. All of the superconductors considered belong to the London type for which ${\lambda }_0>>{\xi }_0$, where ${\xi }_0$ is the zero-temperature coherence length, see, e.g., [42].

It has been shown that the scaling relation [27]

$$\frac{d\rho }{dT}\propto \frac{k_B}{\hslash }{\lambda }_0^2$$

(26)

remains valid over several orders of magnitude of ${\lambda }_0$, signifying its robustness. At the phase transition point $T=T_c$, the relation (26) yields the well-known Holmes law [27], see also [89] for its theoretical derivation:

$$\sigma T_c\propto {\lambda }_0^{-2},$$

(27)

in which $\sigma ={\rho }^{-1}$ is the normal state dc conductivity. It has been shown by Kogan [89] that Holms law applies even for the oversimplified model of an isotropic BCS superconductor. Within the same model of a simple metal, one can express the resistivity $\rho$ in terms of microscopic substance parameters [60]: $e^{2}n\rho \simeq p_F/\left(\tau v_F\right)$, where $\tau$ is the quasiparticle lifetime, n is the carrier density, and $v_F$ is the Fermi velocity. Taking into account that $p_F/v_F=M^{*}$, we arrive at the equation [28]

$$\rho =\frac{M^{*}}{n{e}^2\tau }.$$

(28)

Note that Equation (28) formally agrees with the well-known Drude formula. It has been shown in Ref. [42] that good agreement with experimental results [32] is achieved when the effective mass and the superfluid density are attributed to the carriers in the FC state only, i.e., $M^{*}\equiv M_{FC}$ and $n\equiv n_{FC}$. Keeping this in mind and utilizing the relation $1/\tau =k_{B}T/\hslash$ [19,25,87], we obtain

$$\rho =\frac{M_{FC}}{e^2{n}_{FC}}\frac{k_{B}T}{\hslash }\equiv 4\pi {\lambda }_0^2\frac{k_{B}T}{\hslash },$$

(29)

i.e., $d\rho /dT$ is indeed given by the expression (26). Equation (29) demonstrates that fermion condensation can explain all the above experimentally observed universal scaling relations. It is important to note that the FC approach presented here is not sensitive to and transcends the microscopic, non-universal features of the substances under study. This is attributed to the fact that the FC state is protected by its topological structure and therefore represents a new class of Fermi liquids [2,19]. In particular, consideration of the specific crystalline structure of a compound, its anisotropy, its defect composition, etc., do not change our predictions qualitatively. This strongly suggests that the FC approach provides a viable theoretical framework for explaining universal scaling relations similar to those discovered in experiments [27,32]. In other words, condensation of the charge carrier quasiparticles in the considered strongly correlated HTSCs, engendered by a quantum phase transition, is indeed the primary physical mechanism responsible for their observable universal scaling properties. This mechanism can be extended to a broad set of substances with very different microscopic characteristics, as discussed in detail in Refs. [15,19,20].

7. Influence of Superconducting State on Flat Bands

We continue to study Fermi systems with FC at $T=0$, employing weak BCS-like interaction with the coupling constant g [43]. We analyze the behavior of both the superconducting gap $\Delta$ and the superconducting order parameter $\kappa \left(p\right)$ as $g\to 0$. In case of BCS-like theories, one obtains the well-know result. Both $\kappa \to 0$ and $\Delta \to 0$, while the FC theory yields $\Delta \propto g$ [1,4,45,90,91]. To study the latter case, we start from the usual pair of equations for the Green’s functions $F^{+}(p,\omega )$ and $G(p,\omega )$ [60]

$$F^{+}=\frac{-g{\Xi }^{*}}{(\omega -E(p)+i0)(\omega +E(p)-i0)},$$

(30)

$$G=\frac{u^2\left(p\right)}{\omega -E\left(p\right)+i0}+\frac{v^2\left(\mathbf{p}\right)}{\omega +E\left(p\right)-i0},$$

(31)

where $E^2\left(p\right)={\xi }^2\left(p\right)+{\Delta }^2$, where $\xi \left(\mathbf{p}\right)=\epsilon \left(p\right)-\mu$. Here, $\epsilon \left(p\right)$ is the single particle energy, and $\mu$ is the chemical potential. The gap $\Delta$ and the function $\Xi$ are given by

$$\Delta =g|\Xi |,i\Xi =\int {\int }_{-\infty }^{\infty }{F}^{+}(\mathbf{p},\omega )\frac{d\omega dp}{{\left(2\pi \right)}^4}.$$

(32)

Denoting $v^2\left(p\right)=(1-\xi \left(p\right)/E\left(p\right))/2,v^2\left(\mathbf{p}\right)+u^2\left(p\right)=1$, simple algebra yields

$$\xi \left(p\right)=\Delta \frac{1-2v^2\left(p\right)}{2\kappa \left(p\right)}.$$

(33)

Here $\kappa \left(p\right)=u\left(p\right)v\left(p\right)$ is the superconducting order parameter. It follows from Equation (33) that $\xi \to 0$ when $\Delta \to 0$, provided that $\kappa \left(p\right)\ne 0$ in some region $p_i<p<p_f$; thus, the band becomes flat in the region, since $\epsilon \left(p\right)=\mu$ [15,17]. Note that in this case the BCS-like theory gives the standard result implying that both $\Delta =0$ and $\kappa =0$ since it is assumed that $\xi \left(p\right)$ is fixed. Then, we derive from Equations (32) and (33) that

$$i\Xi ={\int }_{-\infty }^{\infty }{F}^{+}(p,\omega )\frac{d\omega dp}{{\left(2\pi \right)}^4}=i\int \kappa \left(p\right)\frac{dp}{{\left(2\pi \right)}^3}.$$

(34)

From Equations (32)–(34), we readily see that as $g\to 0$ the superconducting gap $\Delta \to 0$, while the density $n_s$ of the superconducting electrons defined by $\Xi =n_s$ is finite, and the dispersion $\epsilon \left(p\right)$ becomes flat, $\xi =0$. While $\kappa \left(p\right)$ is finite in the region $p_i\le p\le p_f$, making $\Xi$ finite. As a result, in systems with FC, the gap $\Delta$ vanishes when $g\to 0$, but both the order parameter $\kappa \left(p\right)$ and $n_s$ are finite. When the coupling constant g increases, the gap $\Delta$ is given by Equation (2), and the superconducting temperature $T_c\propto g\Xi =g{n}_s$ [1,15]. As a result, one obtains the possibility to construct the room-$T_c$ superconductors [5,6,7,8,9,10,11,12]. At the same time $n_s\ll n_{\rho }$, where $n_{\rho }$ is the density of electrons [33,42]. Thus, in case of overdoped superconductors $n_s\ll n_{\rho }$ rather than $n_s=n_{\rho }$, as should be in BSC like theories [32,33,42]. Employing Equations (32) and (33), we deduce from Equations (30) and (31) that

$$F^{+}=-\frac{\kappa \left(p\right)}{\omega -E\left(\mathbf{p}\right)+i0}+\frac{\kappa \left(p\right)}{\omega +E\left(p\right)-i0}$$

(35)

$$G=\frac{u^2\left(p\right)}{\omega -E\left(p\right)+i0}+\frac{v^2\left(\mathbf{p}\right)}{\omega +E\left(p\right)-i0}.$$

(36)

In the region occupied by FC, the coefficients $v^2\left(p\right)$, $u^2\left(p\right)=1-v^2\left(p\right)$, $v\left(p\right)u\left(p\right)=\kappa \left(\mathbf{p}\right)\ne 0$ are given by $\epsilon \left(p\right)=\mu$, while $E\left(\mathbf{p}\right)\to 0$ [1,4,15]. From Equations (35) and (36), it is seen that when $g\to 0$, the equations for $F^{+}(p,\omega )$ and $G(p,\omega )$ are transformed in the FC region to [90]

$$F^{+}(p,\omega )=-\kappa \left(p\right)\left[\frac{1}{\omega +i0}-\frac{1}{\omega -i0}\right]$$

(37)

$$G(p,\omega )=\frac{u^2\left(p\right)}{\omega +i0}+\frac{v^2\left(\mathbf{p}\right)}{\omega -i0}.$$

(38)

Integrating $G(p,\omega )$ over $\omega$, one obtains $v^2\left(\mathbf{p}\right)=n\left(p\right)$. From Equation (32), it follows that $\Delta$ is a linear function of g [1,33,45,91]. Since the transition temperature $T_c\sim \Delta \propto g\to 0$, $\kappa \left(\mathbf{p}\right)$ vanishes at $T\to 0$ via the first order phase transition [2,15]. Thus, on one hand, the FC state with its flat band represents a special solution of the BSC equations. On the other hand, representing a contrast to BSC-like theories, Equation (33) gives the dependence of the spectrum $\xi$ on $\Delta \propto g$, thus, leading to $V_F\propto T_c$ [13,15,16,17].

Now we use Equation (33) to calculate the effective mass $M^{*}$ by differentiating both sides of this equation with respect to the momentum p at $p=p_F$ [15,17] and obtain

$$M^{*}\simeq p_F\frac{p_f-p_i}{2\Delta }.$$

(39)

From Equation (39), we obtain that $V_F\propto T_c\propto \Delta$ and conclude

$$V_F\simeq \frac{2\Delta }{p_f-p_i}\propto T_c.$$

(40)

From Equations (33) and (40), we see that as $T_c\propto \Delta \to 0$, the Fermi velocity $V_F\to 0$ and the band becomes exactly flat [13,17]. When $T_c\simeq g\Delta$ becomes finite at g increasing, the plateau starts to slightly tilt and is rounded at its end points, as seen from Figure 16. At increasing $\Delta \propto T_c$, both $M^{*}$ and the density of states $N_s\left(0\right)$ are diminished, causing increasing $V_F$. As seen from Figure 16, the plateau of the flat band of the superconducting system with FC is slightly upward tilted, and $M^{*}$ is diminished. It follows from Equation (9) that at $T>T_c$ the slope of the flat band is proportional to T, and this dependence can be measured by using ARPES. It is also seen from Figure 2 that both the particle - hole symmetry $\mathcal{C}$ and the time invariance $\mathcal{T}$ are violated generating the asymmetrical differential tunneling conductivity at the NFL behavior, and the NFL behavior is suppressed under the application of a magnetic field that drives the system to its Landau Fermi liquid state, see Section 5.

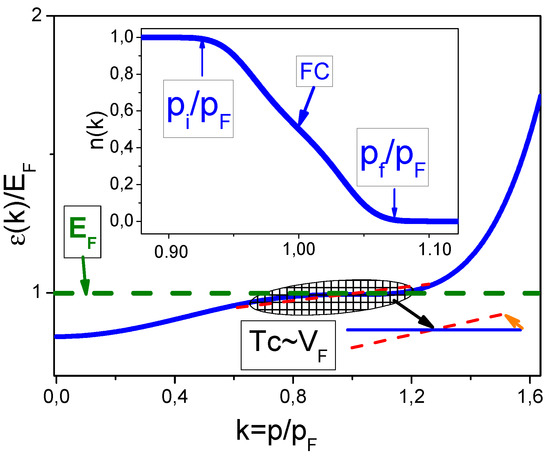
Figure 16. Flat band versus superconducting (SC) state. At $T=0$, the flat single particle spectrum with $V_F=0$ is depicted by the solid curve. The transformed flat band by SC with finite $V_F$ is displayed by the red dashed line, see Equation (40). This change is shown by the arrow and by the blue solid and red dashed lines. The dashed area shows the flat band deformation by the SC state. Inset: the occupation numbers $n\left(k\right)$ at $T=0$ as a function of the dimensionless momentum $k=p/p_F$. FC location is displayed by the arrow, with labels $p_i/p_F$ and $p_f/p_F$ revealing the area where $0<n\left(p\right)<1$, see Equation (7).

Measurements of $V_F$ as a function of $T_c$ [16] are depicted in Figure 17. The inset in Figure 17 shows experimental data collected on the high-$T_c$ superconductor ${\mathrm{Bi}}_2{\mathrm{Sr}}_2{\mathrm{CaCu}}_2{\mathrm{O}}_{8+\mathrm{x}}$ in measurements using scanning tunneling microscopy and spectroscopy; here, $\mathrm{x}$ is oxygen doping concentration [92]. The integrated local density of states is shown in arbitrary units (au). The straight line depicts the local density of states that is inversely proportional to $\Delta$. Note that the tunneling current is proportional to the integrated local density of states [92]. From the inset, it is clear that the data taken at the position with the highest integrated local density of states has the smallest gap value $\Delta$ [92]. These observations are in good agreement with Equations (39) and (40). Thus, our theoretical prediction [15,17] agrees very well with the experimental results [16,92,93]. We note that $V_F\to 0$ as $T_c\to 0$, as seen from Figure 17. This result shows that the flat band is disturbed by the finite value of $\Delta$, and possesses a finite slope that makes $V_F\propto T_c$, as seen from Figure 16. Indeed, from Figure 17, the experimental critical temperatures $T_c$ do not correspond to the minima of the Fermi velocity $V_F$ as they would in any theory wherein pairing is mediated by phonons (bosons) that are insensitive to $V_F$ as they would in any theory wherein pairing is mediated by phonons, or any other bosons, that are insensitive to $V_F$ [16].

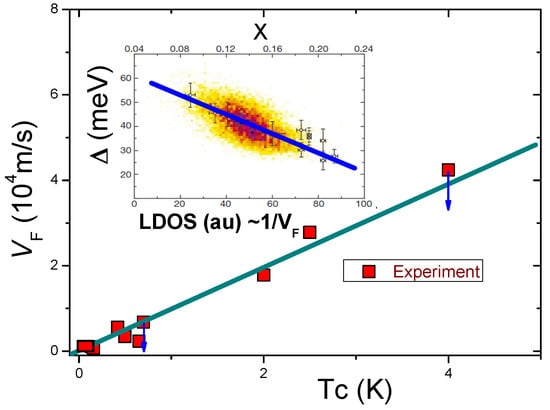
Figure 17. Experimental results (shown by the squares) for the average Fermi velocity $V_F$ versus the critical temperature $T_c$ for graphene (MATBG) [16]. The downward arrows depict that $V_F\le V_0$, with $V_0$ the maximal value shown by the red square. Theory is displayed by the solid straight line. Inset is adapted from [92] and shows experimental dependence of the superconducting gap $\Delta$ versus the integrated local density of states collected on the high-$T_c$ superconductor ${\mathrm{Bi}}_2{\mathrm{Sr}}_2{\mathrm{CaCu}}_2{\mathrm{O}}_{8+\mathrm{x}}$. Here $\mathrm{x}$ is oxygen doping concentration. The darker color represents more data points with the same integrated local density of states and the same size gap $\Delta$ [92]. The straight blue line shows average value $\Delta$ versus the integrated local density of states.

Thus, such a behavior is in stark contrast to that expected within the framework of the common BSC-like theories that do not assume that the single particle spectra strongly depends on $T_c$ [15,16,43]. This extraordinary behavior is explained within the framework of the FC theory based on the topological FCQPT, forming flat bands [15,17,19,20].

8. Discussion and Conclusions

The central message of the present review article is that if the electronic spectrum of a substance happens to feature a dispersionless part, or flat bands, it is invariably this aspect that is responsible for the measured properties that depart radically from those of the familiar condensed-matter systems described by the Landau Fermi liquid theory. This is the case regardless of the diverse microscopic details characterizing these substances, such as crystal symmetry and structure defects. The explanation of this finding rests on the fact that the fermion condensation most readily occurs in substances hosting flat bands, see, e.g., [1,5,6,7,8,9,10,11,12]. Experimental manifestations of the fermion condensation phenomena are varied, implying that different experimental techniques are most suitable for detecting and analyzing them.

To support the above statements, we have also considered recent challenging experimental observations within the framework of the fermion condensation theory. In summary, we have:

Explained the universal $T/B$ scaling behavior of the thermodynamic and transport properties, including the negative magnetoresistance of the HF metals;

Analyzed the recent challenging experimental facts regarding the tunneling differential conductivity $dI/dV={\sigma }_d\left(V\right)$ as a function of the applied bias voltage V collected under the application of a magnetic field B on the twisted graphene and the archetypical heavy-fermion metals ${\mathrm{YbRh}}_2{\mathrm{Si}}_2$ and ${\mathrm{CeCoIn}}_5$ [5,29,30];

Explained the emergence of the asymmetrical part $\Delta {\sigma }_d={\sigma }_d\left(V\right)-{\sigma }_d(-V)$ as well as that $\Delta {\sigma }_d$ vanishes in magnetic fields as was predicted [31];

We further examined the linear dependence on temperature of the resistivity $\rho \left(T\right)\propto A_{1}T$, demonstrated that $A_1(x_c-x)/T_c(x_c-x)=const$ and explained the data collected on high $T_c$ superconductors, graphene, heavy fermion (HF) and common metals, revealing that the scattering rate 1$/\tau$ of charge carriers reaches the Planckian limit;

Elucidated empirical observations of scaling properties [27] within the fermion condensation theory;

Investigated the recent extraordinary experimental observations of the density of superconducting electrons that turns out to be much less than the total density of electrons at $T\to 0$;

Shown that the transition temperature $T_c$ is proportional to the Fermi velocity $V_F$, $V_F\propto T_c$, rather than $N_s\left(0\right)\propto 1/V_F\propto T_c$;

Demonstrated that flat bands make $T_c\propto g$, with g being the coupling constant. It is of crucial importance to note that the flat band superconductivity has already been observed in twisted bilayer graphene, where due to the flat band, the transition temperature $T_c$ highly exceeds the limit dictated by the conventional BCS theory [5,6,7,8,9,10,11,12]. Thus, the basic task now is to attract more experimental groups to search for the room-$T_c$ superconductivity in graphite and other perspective materials.

Indeed, the physics here has been explained within the fermion condensation theory [33] and related to flat bands whose existence was predicted many years ago [1,2,4,15,26,33,37] and paved the way for high-$T_c$ superconductors [5,6,7,8,9,10,11,12]. In conclusion, this is a review of the recent outstanding experimental results that strongly suggest that the topological FCQPT is an intrinsic feature of many strongly correlated Fermi systems and can be viewed as the universal agent defining their non-Fermi liquid behavior. In addition, the fermion condensation theory is able to explain challenging features exhibited by strongly correlated Fermi systems.