Measurement of Photoionization Cross-Section for the Excited States of Atoms: A Review

Abstract

A review of experimental studies of the measurement of the photoionization cross-section for the excited states of the alkali atoms, alkaline earth atoms, and rare-gas atoms is presented, with emphasis on using multi-step laser excitation, ionization, and the saturation technique. The dependence of the photoionization cross-section from different intermediate states populated in the first step and ionized in the second step are discussed, including results on the photoionization cross-sections measured above the first ionization threshold. Results based on different polarizations of the exciting and the ionizing dye lasers are also discussed. Examples are provided, illustrating the photoionization cross-sections measured using thermionic diode ion detector, atomic beam apparatus in conjunction with a time-of-flight mass spectrometer and DC/RF glow discharge cell as an optogalvanic detection.

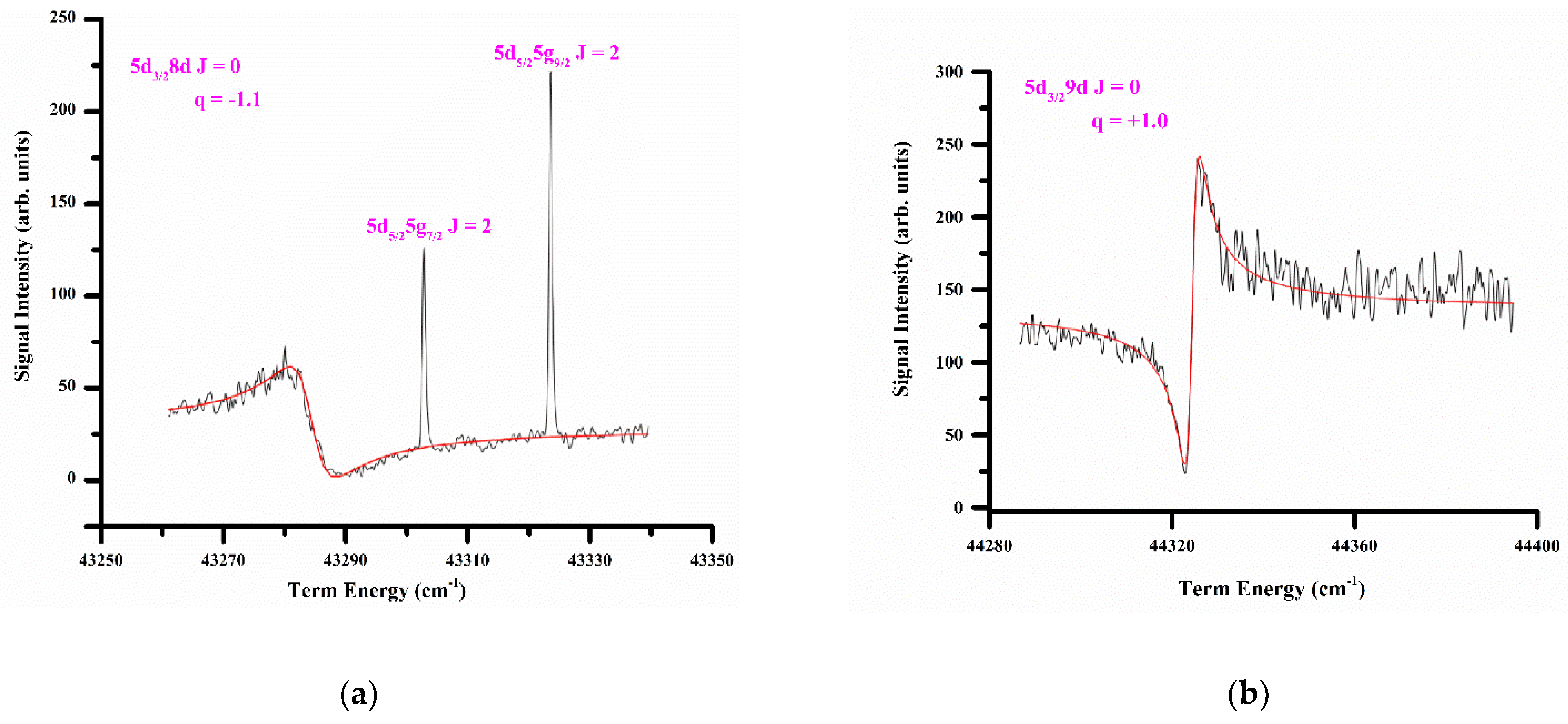
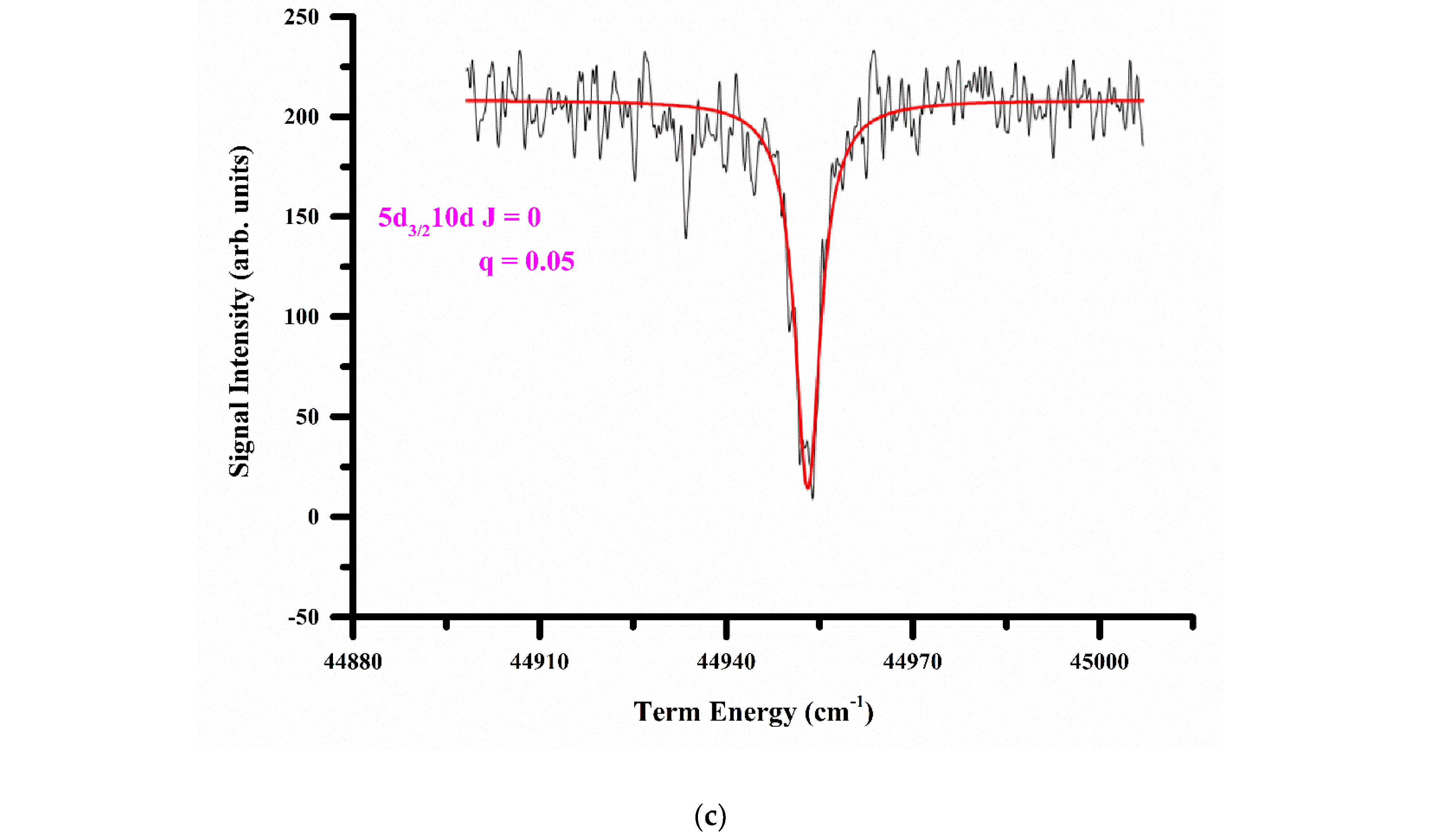
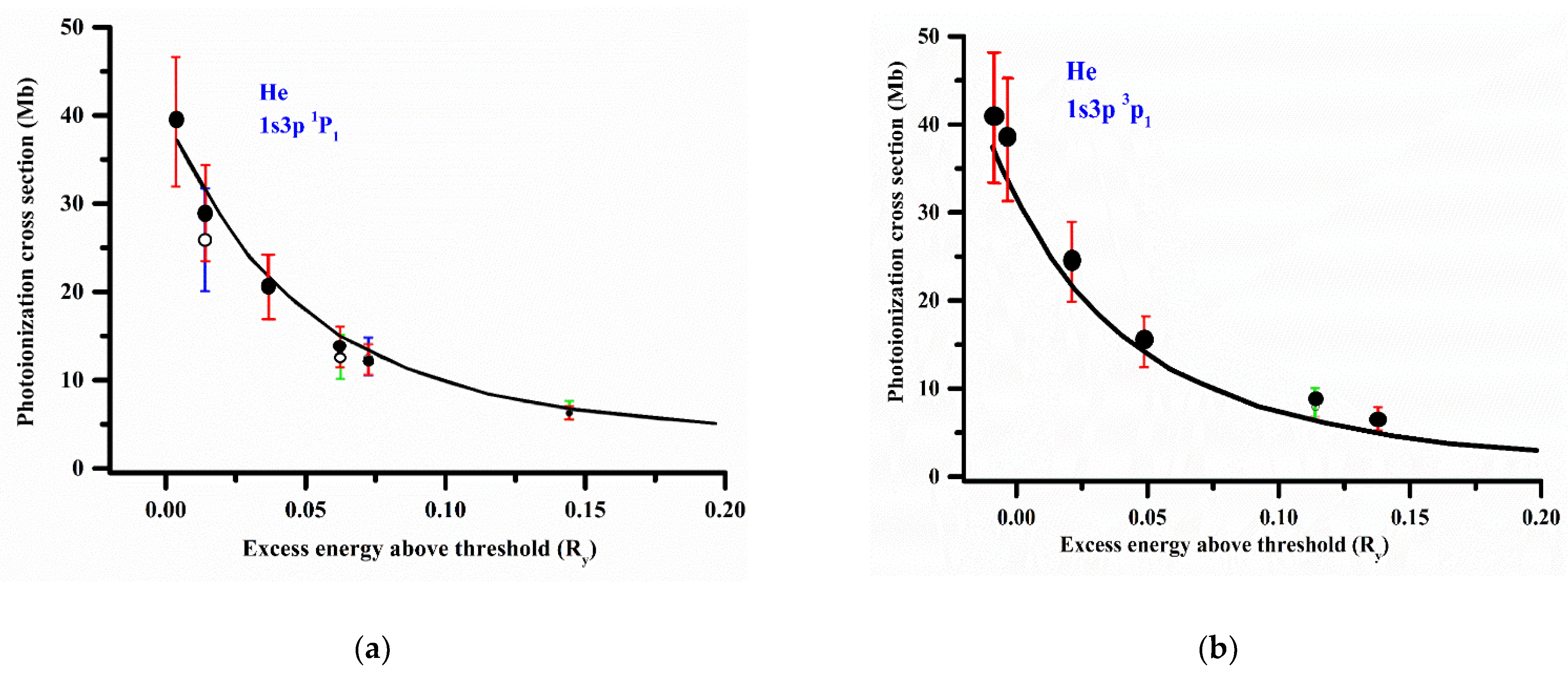
1. Introduction

Photoionization of atoms is one of the most fundamental processes in the interaction of radiation with matter that plays an important role in different fields of research. In particular, photoionization from the excited states has numerous applications in the stellar atmospheres, controlled thermonuclear research plasma, radiation protection, laser design, and radiative recombination. Therefore, accurate measurement of photoionization cross-sections from the excited states of atoms is a much more stimulating mission. Photo-excitation, photo-ionization, and recombination processes are occurring naturally all the time due to the radiation matter interaction, in the presence of the radiation emitted by the Sun. Since all the elements listed in the Periodic Table possess specific electronic configurations, electrons occupy different shells, and therefore the atoms in the ground state can be promoted to the excited states due to the photo-absorption process. However, if high energy radiation of (>10 eV) is available, then the outermost bound electron can be detached, resulting in a decomposition of atoms into ions and free electrons; a process termed photoionization.

$$Atom+h\nu \to ion+e^{-}.$$

Hydrogen is the simplest one-electron system, the electron from its ground state (1s ²S_1/2) can be promoted to the first excited state (2p ²P_1/2,3/2) via a dipole transition in the presence of 10.2 eV (121.57 nm) radiation. The interaction of radiation of energy 13.606 eV (911.36 nm) with the hydrogen atoms yields photoionization, depending on the energy density of the available radiation source, since one photon can only excite/ionize one atom. Since the dipole selection rules for excitation from the ground state limit the parity of the excited levels, therefore, only selected processes can be investigated. The advent of tune-able dye lasers has opened up vast possibilities to populate an excited state with a well-defined quantum number and then to excite or ionize atoms via multistep or multiphoton excitations. Thus, with monochromatic radiation of much higher intensity, ionization can be achieved through an intermediate state:

$$Atom \left(ground state\right)+h\nu \to atom \left(excited sate\right)+h\nu \to Ionization+e^{-}$$

Thus, hydrogen atoms from the ground state (1s ²S_1/2) can be promoted to the (2s ²S_1/2) state via a two-photon excitation in the presence of laser radiation at 243.14 nm. The situation is different in the case of the two-electron system. The helium atoms in the ground state (1s^{2 1}S₀) can be promoted to the first excited state (1s2p ¹P₁) in the presence of the 58.43 nm radiation and photo-ionized by the 24.212 eV (51.21 nm) radiation; He⁺ (1s ²S_1/2) plus a free electron in the εp continuum. The ground state of all the alkali atoms is the same as that of hydrogen, whereas that of alkaline earth is similar to helium. Therefore, the excited states as well the ionization fragments will be identical. As the atoms are excited to the higher principal quantum number levels, the successive energy difference between the Rydberg levels decreases (~2R/n³), where R is the Rydberg constant (13.606 eV) and n is the principal quantum number. The intensities of the Rydberg series also decrease as (1/n³) due to varying spatial overlap of the wave functions between the lower and the excited levels. Consequently, there is a natural limit up to which the highest member of a Rydberg series (n~740) can be experimentally measured, ($n~\sqrt[3]{\left(\frac{4\pi R \tau }{h}\right)}$), limitations due to the decreasing successive energy difference between the highly excited states and the lifetime or the widths of the spectral lines ($\mathsf{\Delta }E \mathsf{\Delta }t=\frac{h}{2\pi }$). Near the ionization threshold, numerous unresolved Rydberg levels exist that give rise to a sudden jump in the photo-absorption spectrum, which then monotonically decreases as the energies of the photons surpass the first ionization potential. Thus, one can measure the photoionization cross-section at the ionization threshold of any atom provided a suitable ultraviolet radiation continuum source is available. The intensity of an emission line due to an electric dipole transition from an upper level at energy E_u to a level at energy E_l is represented by Cowan [1], Axner et al. [2], Demtroeder [3], and Nahar and Paradhan [4]:

$$I^{em}=\left(\frac{h\nu }{4\pi }\right) A_{ul} N_{u },$$

where N_u is the total number of atoms in the upper level, hν is the energy of the emitted photon, and A_ul is the Einstein coefficient, which is related to the lifetime of the upper level. Thus, the higher the population of the upper level, the higher the intensity of the spectral line will be. The situation is slightly different in the case of absorption from a lower level to an upper level, as a source of radiation is required to induce the absorption process. The intensity I^abs transmitted through a vapor column of length L is represented as:

$$I^{abs}=I_0\left[1-\exp (-{\sigma }_{a }n L\right]\cong I_0 {\sigma }_{a }n L,$$

where I₀ is the intensity of the incident radiation beam, n is the number density in the lower level, L is the length of the uniformly distributed sample and ${\sigma }_{a }$ is the absorption cross-section. The difference between photo-excitation and photo-ionization is that in the former case the excitation is to a discrete state, whereas in the latter case the final state is a continuum channel. The transition probability is governed by the dipole transition moment. The probability of photoionization of atoms to ionic states is proportional to the photoionization cross-section, governed by a dipole transition between the initial and final state. The photo-ionization cross-section is proportional to the sum of the squares over all the available final states. In the dipole transitions, the angular momentum and parity selection rules are strictly followed; (${\ell }_f={\ell }_i\pm 1$), and even to odd or odd to even). Ionization from a specific subshell to various continuum channels are; $ns\to ϵp$, $np\to ϵs, \epsilon d$ and $nd\to ϵp, \epsilon f$. Furthermore, the transitions following the (${\ell }_f\to {\ell }_i+1$) selection rule are more probable, possessing higher intensities. The photoionization cross-section is usually much higher near the ionization threshold, and it decreases monotonically by increasing the photon energy above the first ionization threshold. The situation is even more interesting when the experiments are performed at photon energies much higher than the ionization potential. In hydrogen, the photoionization cross-section is maximum at the ionization threshold (13.606 nm) and it decreases monotonically at higher photon energies. A similar trend in photo-ionization prevails for all the alkali atoms, maximum at the ionization threshold and decreasing at higher photon energies. However, the situation gets complex in the case of alkaline earth elements or inert gases as numerous broad and asymmetric autoionizing resonances appear just above the first ionization threshold that is attributed either to the simultaneous excitation of both the valence electrons or to inner shell excitation.

Another characteristic of measuring the photo-ionization cross-section for the excited states of atoms is by populating the first excited state in the first step and then promoting the atoms from this excited state to the ionization threshold. The advantage of such experimental arrangements is that one needs much lower energy photons to photo-ionize atoms as compared with that from the ground state. In this review, we will present different experimental techniques to measure the photo-ionization cross-sections from the excited states of atoms concentrating on alkali atoms, alkaline earth atoms, and inert gases. Several groups have contributed to the photo-absorption measurement of atoms using conventional light sources, Beutler at Berlin, GV Marr at Reading University, WRS Garton at Imperial College, London, and ML Ginter at the Maryland University USA. The work was further extended in the VUV and XUV region using synchrotron radiation, Madden and Codling at NBS, JP Connerade at Bonn University, Sontag at Hamburg, Heinzmann at BESSY, and Ueda in Japan. Now, state-of-the-art storage rings coupled with insertion devices and free electron lasers are being extensively used to measure the photoionization cross-sections of atoms, molecules, and ions. There are several excellent books describing the basics of photoionization measuring techniques and data compilation: Samson [5], Berkowitz [6,7], and Schmidt [8]. The photoabsorption/photoionization cross-sections of atoms from the ground state of the alkali metal atoms have been widely studied by many researchers, such as Rothe [9,10], Marr and Creek [11], Weisheit [12], Ambartzumian et al. [13], and Duong et al. [14]. The spectra of alkaline earth atoms have also been extensively studied, Dichburn and Hudson [15], Garton and Codling [16,17,18], Hudson et al. [19], Carter et al. [20], Brown et al. [21,22,23], Wynne and Herman [24], Ueda et al. [25,26,27,28], Baig and Connerade [29], Griesmann et al. [30,31,32,33], Yie et al. [34], Chu et al. [35], and Maeda et al. [36,37] whereas the spectra of inert gases have been studied by Huffman et al. [38], Rundel [39], Ito et al. [40], Yoshino et al. [41,42,43], Bonin et al. [44], Baig and Connerade [45], and Ito et al. [46]. There are several reviews addressing the measurement of photoionization of atoms using synchrotron radiation, lasers, and a combination of synchrotron radiation with lasers for multistep excitation and ionization: The experimental data on the photoabsorption spectra of atoms due to inner-shell excitations using synchrotron radiation by Connerade and Baig in the “Handbook on Synchrotron Radiation” Marr [47], photoionization and collisional ionization of excited atoms using synchrotron radiation and laser radiation by Wuilleumier et al. [48], the XUV spectroscopy of metal atoms Sontag and Zimmermann [49], the pump-probe experiments in atoms involving laser and synchrotron radiation by Wuilleumier and Mayer [50], a combination of lasers and synchrotron radiation in studies of atomic photoionization by Mayer [51], photoionization cross sections of atomic ions from merged-beam experiments by Kjeldsen [52], the photo-dynamics of excited Ne, Ar, Kr and Xe atoms near the threshold by Sukhorukov et al. [53], experiments at FLASH by Bostedt et al. [54], photoionization of ion with synchrotron radiation: from ions in space to atoms in cages by Schippers et al. [55], roadmap of ultrafast X-ray atomic and molecular physics by Young et al. [56], roadmap on photonic, electronic, and atomic collision physics: light-matter interaction by Ueda et al. [57], and photoionization of astrophysically relevant atomic ions at PIPE by Schippers and Muller [58]. Numerous theoretical models have been developed for the calculation of the photoionization cross-sections. Cooper [59] used as a model the light absorption by a single electron moving in potential similar to the Hartree–Fock potential [H.F] appropriate to the outer subshell of each atom and reported for the rare gases He, Ne, Ar, and Kr, for Na, and the closed-shell ions Cu+ and Ag+. The sum rules were used to analyze the oscillator strength spectral distribution at higher energies. Manson and Cooper [60] used a one-electron model with Herman–Skillman central potential and calculated the photoionization in the soft x-ray range and explained the combined Z and energy dependence of the photoionization cross-sections for different subshells. Kennedy and Manson [61] calculated the photoionization in the noble gases using Hartree–Fock wave functions. Burke and Taylor [62] used the R-matrix method to calculate the electron-atom and ion collision cross-sections atomic polarizabilities to study the atomic photoionization processes in neon and argon. Aymar et al. [63] calculated the photoionization cross-sections for the s, p, and d Rydberg states of lithium, sodium, and potassium in the framework of the single-electron model (non-relativistic) using a parametric central potential. Jonson et al. [64] developed the relativistic random-phase approximation (RRPA) from the linearized time-dependent Hartree–Fock theory (H.F) and determined the excitation energies and oscillator strengths along with the helium, beryllium, magnesium, zinc, and neon isoelectronic sequences. Savukov [65] calculated the photoionization cross-section for the alkali-metal atoms in the framework of relativistic many-body perturbation theory (RMBPT) using quasi-continuum B-spline orbitals. It was inferred that the agreement with the experiment is improved compared to random phase approximation (RPA) and Dirac–Hartree–Fock approximation. The photoionization of potassium atoms from the ground and 4p, 5s–7s, and 3d–5d excited states have been calculated by Zatsarinny and Tayal [66] using the Dirac-based B-spline R-matrix method. The effect of the core polarization by the outer electron was included through the polarized pseudo-states. There was excellent agreement with the experiment for the cross-sections of the 4s photoionization and accurate description of the near-threshold Cooper–Seaton minimum. Kim and Tayal [67] used the non-iterative variational R-matrix method combined with multichannel quantum defect theory at the R-matrix surface to calculate the photoionization of the ground state of magnesium atom in the energy region between 3 s and 4p thresholds. Johnson et al. [68] analyzed the Beutler–Fano autoionizing resonances in the rare gas atoms using the relativistic multichannel quantum defect theory. The configuration interaction Pauli–Fock including the core polarization (CIPFCP) method has been applied by Petrov et al. [69,70] to calculate the total and partial cross-sections for the photoionization of excited noble gases. The photoionization cross-sections for the highly excited state and ions have been calculated for several atoms and ions by Nahar’s group [71,72,73] and references therein. Recently, the photoionization and electron-ion recombination of n = 1 to very high n-values of hydrogenic ions have been studied by Nahar [74] who also made available a FORTRAN program to compute photoionization cross-sections, recombination cross-sections, and rate coefficients for any principal quantum number and orbital angular momentum shell.

In the next section, the basics of the saturation technique to measure the photo-ionization for the excited states of atoms using multi-step laser excitation and ionization technique are presented.

2. Saturation Technique

Let us consider the simplest case of a two-step excitation and ionization process to measure the photoionization cross-section for the excited states of atoms. In the first step, the ground state atoms are resonantly excited to the first excited state by the excitation laser pulse and in the second step, the excited atoms are promoted to the continuum by the ionizing laser pulse. When both the laser beams are linearly polarized, the polarization vectors are parallel and only transitions between the magnetic sublevels Δm = 0 are allowed. The rate equations are used to develop a relationship between the produced photoions and the photoionization cross-section for that excited state. Assuming that collisions and spontaneous emission are discounted in a pure two-step photoionization process, the rate equations are written as Letokove [75], Burkhart et al. [76], He et al. [77], and Saleem et al. [78]:

$$\frac{d{N}_0}{dt}=-{\sigma }_a{\varphi }_{ex}\left(N_0-N_{ex}\right),$$

(1)

$$\frac{d{N}_{ex}}{dt}={\sigma }_a{\varphi }_{ex}\left(N_0-N_{ex}\right)-\sigma ({\lambda }_{io}){\varphi }_{io}{N}_{ex},$$

(2)

$$\frac{d{N}_I}{dt}=\sigma ({\lambda }_{io}){\varphi }_{io}{N}_{ex},$$

(3)

Here, ${\sigma }_a$ is the photoabsorption cross-section, ${\varphi }_{ex}$ is the photon flux of the exciting laser, $\sigma ({\lambda }_{io})$ is the photoionization cross-section of the excited state at the ionizer laser wavelength ${\lambda }_{io}$, ${\varphi }_{io}$ is the photon flux of the ionizing laser, $N_0$ is the population of the ground state, $N_{ex}$ is the population of the excited state, and $N_I$ is the number of ions produced as a result of two-step ionization. The first requirement for the saturation technique is that the intensity of the exciting laser pulse must be sufficiently high enough to saturate the excited state so that both the populations stay in equilibrium i.e., $N_0\cong N_{ex}$. The total number of atoms is, $N_T=N_0+N_{ex}=2N_{ex}$. Adding Equations (1) and (2):

$$\begin{array}{c}\frac{d(N_0+N_{ex})}{dt}=\frac{d(N_T)}{dt}=-\sigma ({\lambda }_{io}){\varphi }_{io}{N}_{ex}\hfill \\ \Rightarrow \frac{d{N}_{ex}}{dt}=-\frac{1}{2}\sigma ({\lambda }_{io}){\varphi }_{io}{N}_{ex}\hfill \\ \Rightarrow N_{ex}=\frac{N_0}{2}\exp \left(-\frac{1}{2}{\displaystyle \underset{-\infty }{\overset{t}{\int }}\sigma ({\lambda }_{io}){\varphi }_{io}(t^{\prime })d{t}^{\prime }}\right).\hfill \end{array}$$

(4)

Here, N₀ is the number density in the ground state before the arrival of the exciting laser pulse, and the exponential term containing t′ determines the decreasing number of the excited atoms at any time t after the arrival of the ionizer laser pulse. Integrating Equation (3) and inserting the value of N_ex from Equation (4);

$$N_I={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\sigma }({\lambda }_{io}){\varphi }_{io}(t)\hspace{0.33em}\frac{N_0}{2}\exp \left(-\frac{1}{2}{\displaystyle \underset{-\infty }{\overset{t}{\int }}\sigma ({\lambda }_{io}){\varphi }_{io}(t^{\prime })d{t}^{\prime }}\right)dt.$$

(5)

The solution of the equation yields:

$$N_I=N_0\left[1-\exp \left(-\frac{1}{2}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\sigma ({\lambda }_{io}){\varphi }_{io}(t)dt}\right)\right].$$

At saturation, $N_0\cong N_{ex}$, therefore;

$$N_I=N_{ex}\left[1-\exp \left(-\frac{1}{2}\sigma ({\lambda }_{io}){\mathsf{\Phi }}_{io}\right)\right].$$

(6)

Here ${\mathsf{\Phi }}_{io}$ is the fluence (energy/area) of the ionizing laser as seen by the atoms at the beam center: ${\mathsf{\Phi }}_{io}={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\varphi }_{io}(t)dt}$. However, the fluence is related to the energy E (J) of the ionizing laser pulse as: ${\mathsf{\Phi }}_{io}=\frac{{\lambda }_{io}E}{hcA}$. By substituting it in Equation (6):

$$N_I=N_{ex}\left[1-\exp \left(-\frac{1}{2}\sigma ({\lambda }_{io})\frac{{\lambda }_{io}E}{hcA}\right)\right].$$

(7)

However, the number of produced ions $N_I$ is related to the total charge Q that is produced by the ions in the ionizing volume V(cm³) as: N_I = Q/eV. While performing experiments, photoions produced as a result of two-step photoionization are registered as a voltage signal, which is related to the charge as $Q=\left(\frac{Voltagesignal}{R}\right)\times \mathsf{\Delta }t$, where R is the terminating resistance (ohm) at the oscilloscope and $\mathsf{\Delta }t$ (seconds) is the pulse width (FWHM) of the photoion signal peak. A final equation turns out to be:

$$N_I=N_{ex}V\left[1-\exp \left(-\frac{1}{2}\sigma ({\lambda }_{io})\frac{{\lambda }_{io}E}{hcA}\right)\right].$$

(8)

The absolute value of the photoionization cross-section σ(λ_io) for a particular excited state at a specific ionizing laser wavelength λ_io is extracted from a least-squares fit to the experimentally measured ionization data (N_I) as a function of the energy (J) of the ionizing laser beam (E). This relation shows that the photoionization signal approaches saturation as the energy of the ionizing laser is increased to a much higher value. However, every detection system encounters certain limitations. This equation is applicable under the following assumptions:

• The first step transition remains saturated (i.e., N₀ ≈ N_ex), during the exciting laser pulse duration (10 ns);
• The laser intensity of the exciting laser is kept much higher than that required to saturate the transition. Consequently, the Rabi frequency is high, and the spontaneous emission may be ignored during the laser pulse;
• The intensity of the ionizing laser is sufficiently higher than that required to completely ionize atoms in the excited state.

The photoionization cross-section σ is then extracted from a least-squares fit to the experimental photoion data registered as a function of the energy density (Energy/area) of the ionizing laser. The error associated with this method is (i) in determining the cross-sectional area in the interaction region, (ii) in measuring the pulse energy with an energy meter, (iii) in the transmission of the optical windows, and (iv) in the fitting process. Thus, to extract an accurate absolute value of the photoionization cross-section, it is important to accurately measure the correctional area (A) of the laser beam and the Energy per pulse (E) of the ionizing laser. The energy density/intensity of a laser beam in the interaction region depends on its spot size, which can be calculated under the assumption of a Gaussian laser beam:

$$diameter of the focused beam=\left(\frac{4}{\pi }\right)\lambda \left(\frac{f}{D}\right).$$

(9)

Here, d is the diameter of the focused laser beam, $\lambda$ is the laser wavelength, f is the focal length of the focusing lens, and D is the diameter of the laser beam falling on the focusing lens. However, the depth of focus for the laser beam can be calculated as:

$$depth of focus=\left(\frac{8}{\pi }\right)\lambda {\left(\frac{f}{D}\right)}^2.$$

(10)

The cross-sectional area is also calculated under the diffraction limitations: Demtröder [3].

$$Cross sectional area=\pi {\omega }_0^2\left[1+{\left(\frac{z {\lambda }_{io }}{\pi {\omega }_0^2}\right)}^2\right].$$

(11)

Here, ${\omega }_0=\left(\frac{\lambda f}{\pi {\omega }_s}\right)$ is a diffraction-limited radius at Z = 0, ω_s is the radius of the spot size of the ionizing laser beam on the focusing lens, λ_io is the wavelength of the ionizing laser, and z is the distance on the beam propagation axis from the focus. Thus, an accurate value of the cross-sectional area depends on the accuracy of Z and ω_s. A rough estimation of the cross-sectional area can also be determined either by using a photographic method by measuring the burn spot or using a thermopile in combination with a moveable knife-edge intersecting the laser beam. Based on the experimental uncertainties, the cross-section can be determined with ±15% accuracy. Photoionization cross-section is conventionally reported in Mb units, where 1 Mb = 10⁻¹⁸ cm².

The two-step excitation and ionization experiments are normally conducted using narrow-bandwidth tunable dye lasers, pumped by a high-power laser such as Ruby, Nitrogen, Excimer, or Nd:YAG laser. A 600 nm dye laser beam with a 5 mm diameter, and focused with a lens of 100 mm focal length, the diameter of the focused dye laser beam will be about 15 µ and the depth of the focused beam will be about 610 µ. Once the diameter of the ionizing laser beam is measured, the laser beam’s cross-sectional area and the energy density of the dye laser can be determined. Thus, one measures the ion signal as a function of the intensity of the ionizing laser beam. Initially, the ionization signal keeps on increasing as the energy of the ionizing laser is increased. This is because one photon can only ionize one atom. As the intensity of the ionizing laser is increased, the number of ions also increases up to a point where the ionization signal stops increasing even with any further increase in the intensity of the ionizing laser beam. At this point, saturation in the ionization signal sets in, which is why this technique is termed “saturation technique”. The experimental data points are used to fit Equation (8), which yields the absolute value of the photoionization cross-section of the excited state and the ground state density of the atom. The determination of N_ex is independent of the photoionization cross-section, which is determined from the asymptotic value, while σ is associated with the shape of the experimental data of ionization signal curve against the ionizing laser intensity. The accurate determination of N_ex requires that both the transitions must be saturated, and that the ionizing volume is measured accurately. The ionizing volume is defined as the interaction volume of the overlap region of the exciting and the ionizing laser beams in the effective collection region.

At the Atomic and Molecular Physics Laboratory, Quaid-i-Azam University, Islamabad, Pakistan, we have developed different experimental arrangements to measure the photoionization cross-section for the excited states of atoms: a thermionic diode ionic detector based on the heat pipe design by Niemax [79], Baig et al. [80,81], and Yaseen et al. [82], an optogalvanic effect-based detection system by Barbieri et al. [83] and Babin et al. [84], using a DC discharge system, as in Piracha et al. [85], Stockhausen et al. [86], and Hanif et al. [87], a RF discharge system, as in Zia et al. [88,89], and an atomic beam apparatus coupled with a time-of-flight mass spectrometer based on a linear TOF design as in Wiley and McLaren [90] and Saleem et al. [91]. Several other techniques for the measurement of photoionization cross-sections are also being used such as the modulated fluorescence technique by Gilbert et al. [92], a magneto-optical trap (MOT) system by Wippel et al. [93], Madsen and Thomsen [94], and Dinneen et al. [95], the isotope-selective photoionization for calcium ion trapping by Lucas et al. [96], and finally by Marago et al. [97], who measured the photoionization cross-section for the 6p ²P_3/2 excited laser-cooled cesium atoms. The photoionization cross-sections of the excited states of titanium, cobalt, and nickel were reported by Yang et al. [98]. Cong et al. [99] used resonance-enhanced multiphoton ionization coupled with a time-of-flight mass spectrometer. Zheng et al. [100] reported the measurements of photoionization cross-sections of the excited states of cobalt using a two-color, two-step resonance ionization technique in conjunction with a molecular beam time-of-flight (TOF) mass spectrometer at the threshold and near-threshold regions (0–1.2 eV). A comparison and working principles of different experimental techniques being used for the measurements of the photoionization cross-section from the ground state or excited states of atoms were presented by Saleem et al. [101]. In the next sections, we present details about the measurements of the photoionization cross-sections for the excited states of alkali atoms.

3. Alkali Atoms

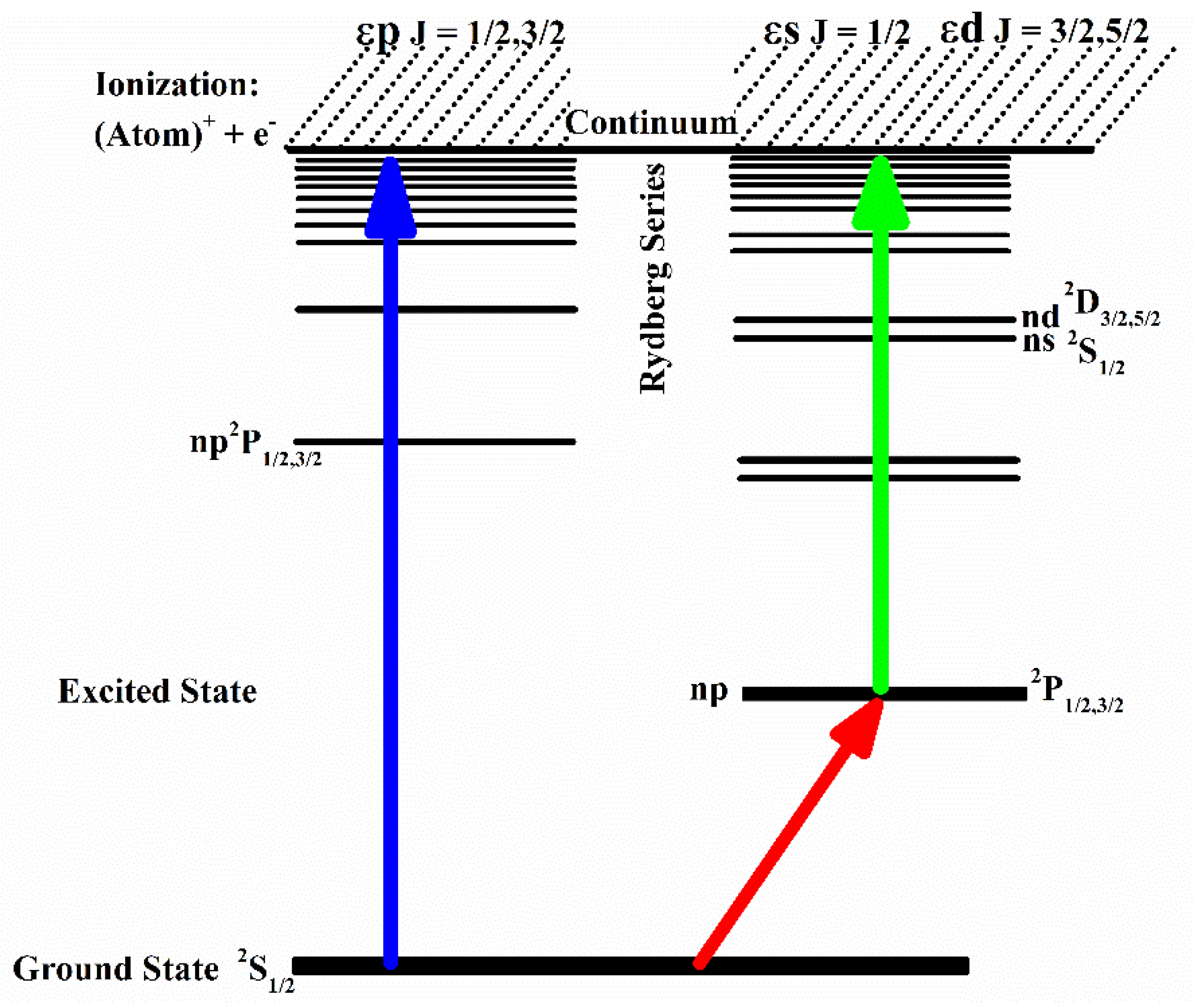
The ground state configurations for the alkali atoms are similar to that of hydrogen, having a single electron in the ground state, ms ²S_1/2 (m = 2, 3, 4, 5, and 6 for Li, Na K, Rb, and Cs, respectively). The atoms from the ground state are excited by the Rydberg states: np ²P_1/2,3/2, and photoionization activates as the energies of the interacting photons approach the value of the first ionization potential of an atom. The process of photoionization from the ground state yields an ion plus a free electron and the continuum above the first ionization threshold is represented as εp (ℓ = 1; J = 1/2, 3/2) channels.

ms ²S_1/2 (excitation) → np ²P_1/2,3/2 (ionization) → εp continuum (J = 1/2, 3/2).

All the alkali atoms show monotonically decreasing photoionization cross-sections above the first ionization threshold, just like the photoionization cross-section in the hydrogen atom. The pioneering work on the measurement of the photoionization cross-section from the excited states of lithium and sodium was reported by Rothe [9,10] using the recombination radiation method. The photoionization cross-section for the 2p excited state at the threshold is 19.7 ± 3.0 Mb, assuming the oscillator strength of the 5s ²S_1/2 → 2p ²P_1/2 transition as 0.00417. The photoionization of the alkali metals atoms, sodium, potassium rubidium, and cesium was measured by Marr [11] and Weisheit [12]. The advent of lasers and dye lasers enabled the measurement of photoionization cross-sections for the excited state of atoms at and above the first ionization threshold. The first excited state mp ²P_1/2,3/2 in alkali atoms is populated in the first step by tuning a dye laser at an appropriate wavelength, a second dye laser is scanned up to the first ionization threshold, and the ns ²S_1/2 and nd ²D_3/2,5/2 Rydberg series are observed. Above the first ionization threshold, the continuum is represented as εs (ℓ = 0; J = 1/2), εd (ℓ = 2; J = 3/2, 5/2). Thus, by selecting excited levels of different ℓ-values in the first step, different εℓ (ℓ = 0, 1, 2, 3…) channels in the continuum can be explored. The total photoionization cross-section is the sum of the partial cross-sections:

$${\sigma }_{j0}(\mathsf{\Delta }E)(Mb)=\frac{4}{3}{\pi }^2\alpha a_0^2\mathsf{\Delta }E\frac{1}{2J_0+1}{\displaystyle \sum _{\ell j}|<n_0{\ell }_0{J}_0||D(r)||\epsilon \ell J>{|}^2},$$

(12)

where εℓ are the continuum channels; εs (J = 1/2) or εd (J = 3/2, 5/2), J₀ is the J-value of the intermediate level (J = 1/2, 3/2), ℓ₀ = 1 for p, ∆E is the energy difference between the ionizing photon energy and the ionization potential, a₀ is the Bohr radius, and α is the fine structure constant.

In

Table 1. Two-step excitation and ionization laser wavelengths for the alkali atoms.

Atom	First Step (Excitation) ms 2S1/2 → mp 2P1/2,3/2	Second Step (Excitation) mp 2P1/2,3/2 → ns 2S1/2        → nd 2D3/2,5/2	Ionization Threshold εs, (J = 1/2) εd, (J = 3/2, 5/2)
Li I	2p 2P1/2 670.793 nm   2P3/2 670.778 nm	349.8 nm 349.8 nm	43,487.150 cm−1
Na I	3p 2P1/2 589.592 nm   2P3/2 588.995 nm	408.2 nm 408.5 nm	41,449.451 cm−1
K I	4p 2P1/2 769.896 nm   2P3/2 766.489 nm	454.0 nm 455.2 nm	35,009.814 cm −1
Rb I	5p 2P1/2 794.760 nm   2P3/2 780.027 nm	473.6 nm 479.0 nm	33,690.810 cm−1
Cs I	6p 2P1/2 894.347 nm   2P3/2 852.113 nm	494.3 nm 508.2 nm	31,406.467 cm−1

, the laser wavelength to access the resonance levels in the first step and the ionizing laser wavelengths in the second step for all the alkali atoms are enlisted. The first step laser wavelengths are mostly in the red region, whereas the ionizing laser wavelength is in the green region, which can easily be achieved by a dye laser pumped by a Nd: YAG laser (2nd or 3rd harmonics), excimer laser, or nitrogen laser.

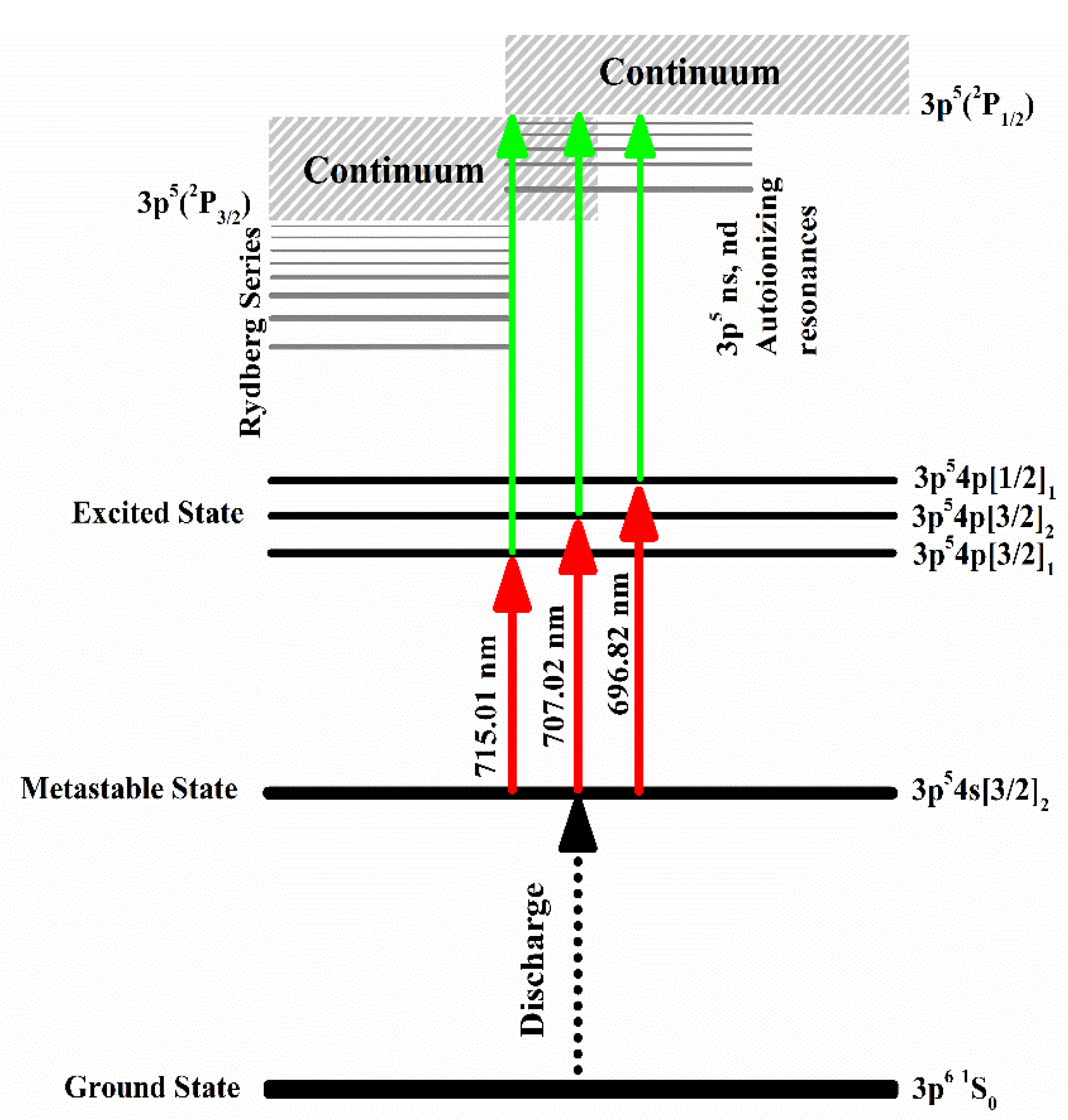
A schematic diagram for the two-step laser excitation and ionization for the alkali atoms is presented in Figure 1.

The pioneering work to measure the photoionization cross-section for the excited state of the rubidium atoms using the saturation technique was performed by Ambartzumian et al. [13], who used a Ruby laser pumped dye laser system coupled with a heat pipe containing rubidium vapor and measured the photoionization cross-section for the 6p ²P_1/2 and 6p ²P_3/2 excited states. The exciting laser was focused by a lens onto a glass cell containing rubidium vapor and the laser radiation was tuned in resonance to the 5s ²S_1/2 → 6p ²P_1/2, _3/2 transitions for selective excitation at 421.56 nm and 420.18 nm, respectively. For producing ionization, a part of the fundamental (694.30 nm) or its second harmonic (347.15 nm) was directed into the cell from the opposite side. The irradiated volume was limited by inserting diaphragms on both ends of the cell and the dependence of the ionization signal on the intensity of the ionizing radiation at constant cell temperature was recorded. The intensity of the ionizing laser was varied, and the corresponding ionization signal was measured. At the low intensity of the ionizing laser, the dependence of the ionization was linear, and with an increase in the ionizing laser intensity, it deviated from linearity and tended to saturation, which means that at high-intensity, the total ionization of the excited transpires. The values of the cross-sections are (1.7 ± 0.4) × 10⁻¹⁷ cm² for the 6p ²P_3/2 state and (1.5 ± 0.4) × 10⁻¹⁷ cm² for the 6p ²P_1/2 at the 694.3 nm ionizing laser wavelength. The value of the photoionization cross-section for the 6p ²P_3/2 state was determined as (1.9 ± 0.5) × 10⁻¹⁷ cm² at the 347.15 nm ionizing laser wavelength. Subsequently, Heinzmann et al. [102] measured the photoionization cross-section for the 7p ²P_1/2 excited state of cesium at 459.3 nm ionizing laser wavelength as (6.2 ± 0.5) × 10⁻¹⁸ cm²_, and for the 7p ²P_3/2 excited states at 455.5 nm ionizing laser wavelength as (8.8 ± 1.6) × 10⁻¹⁸ cm². The photoionization of the 6p ²P_{1/2, 3/2} fine-structure levels of cesium was measured by Nygaard et al. [103] using a triple-crossed beam experiment covering the wavelength region from 500 nm to 250 nm. The photoionization cross-section for the 6p ²P_3/2 and ²P_1/2 excited states was measured at 508.3 nm and 494.4 nm ionizing wavelengths at the first ionization threshold. The absolute photoionization cross-sections for the 5s and 4d excited states of sodium were measured by Smith et al. [104] using two stabilized single-mode CW dye lasers intersecting with the sodium atomic beam to stepwise excite atoms to the desired excited state, and the fundamental wavelength of the Nd:YAG laser at 1064 nm was used as an ionizing laser. The cross-section for the 5s state was determined as (1.49 ± 0.13) × 10⁻¹⁸ cm² and that for the 4d state as (15.2 ± 1.70) × 10⁻¹⁸ cm². The photoionization cross-section for the 7p ²P_3/2 and 6d ²D_3/2 excited states of cesium was reported by Gerwert and Kollath [105] and that for the 7 s state of cesium at 540 nm ionizing laser wavelength was measured by Gilbert et al. [92] as 1.14 (10) × 10⁻¹⁹ cm² using the modulated fluorescence technique. Bonin et al. [106] measured the absolute photoionization cross-section of the 7d ²D_3/2 excited state of cesium at different ionizing laser wavelengths using the fluorescence reduction technique.

The absolute value of the photoionization cross-section of the excited 7p state of potassium was measured by Baohua and Zuren [107] at two ionizing laser wavelengths, 321.8 nm, and 643.6 nm, as (0.9 ± 0.6) Mb and (1.9 ± 0.9) Mb, respectively. Maeda and Ambe [108] measured the photoionization cross-sections for the 7d and 8d states of cesium using the technique of measuring the fluorescence signal from the excited states of atoms due to photoionization. The photoionization cross-sections were reported as (3.5 ±1.4) × 10⁻¹⁸ cm² and (3.1±1.2) × 10⁻¹⁸ cm² for the 7d ²D_3/2 and 7d ²D_5/2 states and (2.4 ± 1.0) × 10⁻¹⁸ cm² and (1.6 ± 0.6) × 10⁻¹⁸ cm² for the 8d ²D_3/2 and 8d ²D_5/2 states, respectively. The photoionization cross-section for the 6p ²P_3/2 excited laser-cooled cesium atoms was measured by Marago et al. [97]. Subsequently, Patterson et al. [109] measured the photoionization cross-section of the 6p ²P_3/2 excited state of cesium confined in a magneto-optical trap. The photoionization rate was measured by monitoring the decay of the trap fluorescence during exposure to ionizing laser radiation, using several lines of Ar-ion laser in the wavelength range 457.9 to 501.7 nm and the photoionization cross-section at 496.5 nm ionizing laser wavelength was reported as (1.86 ± 0.15) × 10⁻¹⁷ cm². Petrov et al. [110] presented the effect of the polarization of the atomic core by the outer electron on the near-threshold photoionization of excited alkali atoms (Na–Cs). Partial and total cross-sections for photo-ionization of the np-electron were computed utilizing the configuration interaction technique with Pauli–Fock atomic orbitals (CIPF) and including the long-range core polarization potential (CP). The variational principle was applied to calculate the core polarization potential. Comparison with previous theoretical results and with available experimental data was presented for the total cross-section σ, for the electron angular distribution parameter β, for the ratio ν = |Dd/Ds| of the reduced electric dipole matrix elements, and the phase shift difference ∆ = δd − δs, associated with the d-wave and s-wave continua, respectively. A magneto-optical trap (MOT) system was used by Wippel et al. [93] to measure the photoionization cross-sections of the first excited states of sodium and lithium. A two-element magneto-optical trap (MOT) for Na and Li⁷ or Li⁶ was used to cool and trap each atom separately. A fraction of the cold atoms was maintained in the first ²P_3/2 excited state by the cooling laser and the excited state atoms were ionized by the laser light in the near ultra-violet region. Duncan et al. [111] also used the magneto-optical trap (MOT) system to measure the photoionization cross-section of the 5 d ²D_5/2 excited state of rubidium at the ionizing laser wavelengths ranging from 1064 to 532 nm. The lifetimes and photoionization cross-sections at 10.6 m of the nd Rydberg states of Rb measured in a magneto-optical trap were assessed by Gabinini [112].

The work on the measurement of photoionization cross-sections for the excited states of atoms was initiated by our group in 2002 and we measured the photoionization cross-section for the 3p ²P_1/2 and ²P_3/2 excited levels of sodium as 2.16 (43) Mb and 3.74 (74) Mb, respectively, using two-step laser excitation in conjunction with a thermionic diode working in the space charge limited mode and employing the saturation technique (Amin et al. [113]. The photoionization cross-section for the 4d ²D_5/2 level was measured as 12.2 (2.4) Mb by populating this level via two-photon excitation from the ground (Amin et al. [114]. The cross-section for the 4d ²D_3/2 level via the 3p ²P_1/2 level intermediate level and for the 4d ²D_3/2,5/2 levels via the 3p ²P_3/2 level was reported as (9.6 ± 1.9) Mb, and (12.8 ± 2.5) Mb, respectively. This work was extended to measure the cross-section for the excited levels of lithium for the 2p ²P_1/2,3/2, 3d ²D_3/2,5/2, and 3s ²S_1/2 excited states at different ionizing laser wavelengths, above the first ionization threshold, as stated by Amin et al. [115]. By changing the ionization photon energy, the smooth frequency dependence of the cross-sections was observed for the 2p and 3d excited states of lithium. The photoionization cross-section for the 4p ²P_3/2 and ²P_1/2 states at 355 nm was measured as (7.2 ± 1.1) Mb and (5.6 ± 0.8) Mb and for the 5d ²D_5/2,3/2 state as (28.9 ± 4.3) Mb (Amin et al. [116]. The cross-section for the 5d ²D_3/2 state was populated via the 4p ²P_1/2 intermediate state and for the 5d ²D_5/2,3/2 states via the 4p ²P_3/2 intermediate state as (25.1 ± 3.8) Mb and (30.2 ± 4.5) Mb. The photoionization cross-sections for the 3p level of sodium at the first ionization threshold were reported as 7.63 (90) Mb by Rothe [10], and Aymar et al. [63] calculated its value as 7.38 Mb. Preses et al. [117] determined the photoionization cross-section from the 3p ²P_3/2 state of Na up to the first ionization threshold, with the help of two antiparallel, interpenetrating pulsed laser beams pumped by the frequency-doubled (532 nm) and tripled (355 nm) outputs of a Nd:YAG laser. They determined the value of the cross-section as 8.5 Mb with an estimated uncertainty of about 25%. Petrov et al. [110] calculated the photoionization cross-section of the 3p ²P_3/2 state at about ≈ 8 Mb. Wippel et al. [93], using the trapping technique, trapped a fraction of Na atoms in the 3p ²P_3/2 excited state and then ionized them with a laser adjusted at ∼407.8 nm. They determined the value of the cross-section at the threshold as 6.9(1) Mb. Miculis and Meyer [118] calculated the photoionization cross-section from 3p ²P_3/2 at and above the threshold as 6.9 (1) Mb, which is in excellent agreement with the recently reported values 3p ²P_1/2 as 7.9 (1.3) Mb and 3p ²P_3/2 as 6.7 (1.1) Mb by Baig et al. [119]. The photoionization cross-section for the 4s ²S_1/2 state of sodium at the first ionization threshold was measured by Rafiq et al. [120] as (0.65 ± 0.10) Mb using a thermionic diode ion detector. The photoionization cross-sections from the 6p ²P_3/2 and 7p ²P_3/2 excited states of potassium have been measured at different ionizing laser wavelengths using an atomic beam apparatus coupled with a time-of-flight mass spectrometer by Yar et al. [121,122]. Haq and Nadeem [123] measured the photoionization cross-section for the 6p ²P_3/2 state of cesium at the ionization threshold, which was measured at 25 ± 4 Mb as well as at different ionizing lasers wavelengths. The cross-section for the 5p ²P_3/2 state of rubidium was reported as 18.8 ± 3 Mb by Nadeem and Haq [124], whereas Shahzada et al. [125] reported the photoionization cross-section for the 3p ²P_1/2,3/2 levels of lithium at the first ionization threshold as (30.0 ± 4.8) Mb, and also determined the oscillator strengths of the 3p ²P → nd ²D Rydberg transitions. Saleem et al. 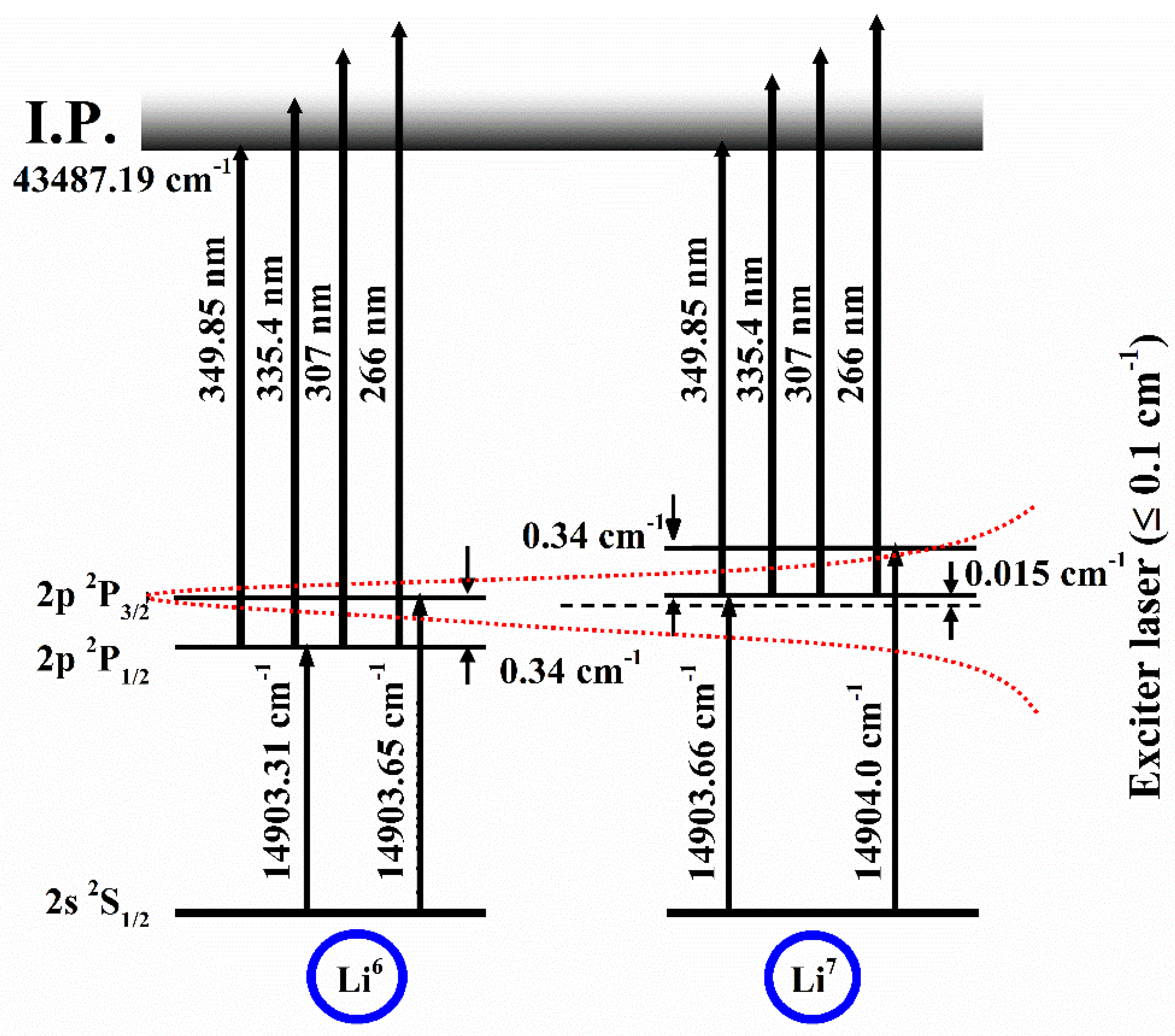[126] used a two-step selective excitation and ionization technique coupled with an atomic beam apparatus and a time-of-flight (TOF) mass spectrometer and measured the photoionization cross-sections of the lithium isotopes Li⁶ and Li⁷ for the 2p excited state as (15 ± 2.5) Mb and (18 ± 2.5) Mb, respectively. The excitation scheme is shown in Figure 2.

A technique for the isotopic enrichment of lithium isotope was demonstrated by Saleem et al. [127], who employed the two-step photoionization technique along with a narrow-band dye laser in conjunction with a time-of-flight mass spectrometer, which yielded a high degree of selectivity by tuning the dye laser at the resonance levels of Li⁶ and Li⁷. It was inferred that the concentration of the natural abundance of the Li⁶ isotope becomes enhanced up to over 47% as the exciter dye laser was tuned to 2p ²P_1/2 of Li⁶, even if the linewidth of the exciter laser was not sufficiently narrow to excite the isotopic level. Although the linewidth of the exciting dye laser was not narrow enough to selectively excite the 2p ²P_{1/2, 3/2} levels of Li⁷, TOF-MS separated both the lithium isotopes on the time axis. Consequently, the photoionization signals of the resolved fine structure components as a function of the intensity of the ionizing laser were measured simultaneously. The exciting laser was tuned at 670.8 nm to populate the 2p-excited state via a single-photon excitation. The exciting laser was tuned to the ²P_1/2 excited state of Li⁶, between the ²P_3/2 of Li⁶ and ²P_1/2 of Li⁷ and ²P_3/2 of Li⁷ while the ionizing laser wavelength was fixed for the measurement of the photoionization cross-section for both the lithium isotopes. The photoionization cross-section from the 2p ²P_1/2 excited state of Li⁶ and for the 2p ²P_3/2 excited states of Li⁷ was also measured by tuning the exciter laser to the corresponding excited state. The energy of the exciter laser at any frequency was kept fixed and the energy of the ionizer laser was varied using neutral density filters to achieve the complete ionization of the excited isotopic atoms. 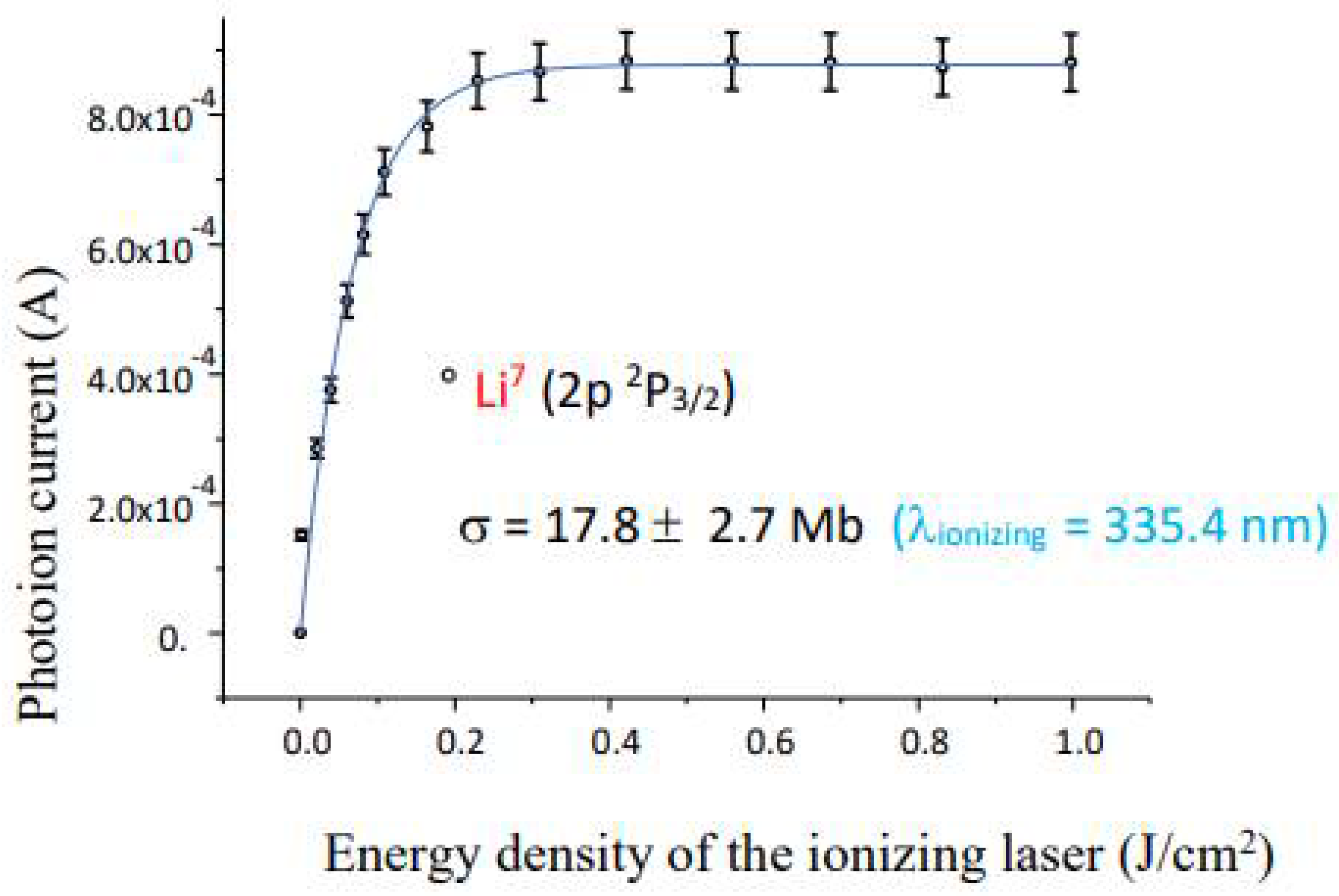The resulting photoion signals from the 2p ²P_1/2 excited state of Li⁷ versus the ionizing laser energy density at 335.4 nm are shown in Figure 3.

The photoion signal increases with an increase in the energy density of the ionizer laser up to a certain value, then stops increasing further, and finally saturation sets in. The solid line that passes through the experimental data points is the least square fit to Equation (7), which yields the absolute photoionization cross-section of the 2p fine structure excited states at 335.4 nm ionizer laser wavelength. The measurements of the photoionization cross-section from the 2p ²P_{1/2, 3/2} excited states of lithium using different ionizing laser wavelengths at and above the first ionization threshold are listed in

Table 2. Experimentally determined photoionization cross-sections from the 2p ²P_{1/2, 3/2} excited states of both isotopes of lithium at different ionizing laser wavelengths.

Lithium Isotope	Excited-State	Ionizing Laser Wavelength	Cross-Section σ (Mb)	Reference
Li6	2p 2P1/2, 3/2	334.4 nm	15 ± 15	Wipple et al. [93]
		335.8 nm	6 (−5, +20)	Wipple et al. [93]
		335.4 nm	15.0 ± 2.3	Saleem et al. [126]
	2p 2P3/2	349.85 nm	15.4 ± 2.3	Saleem et. al. [126]
		335.4 nm	14.8 ± 2.2
		307 nm	10.5 ± 1.6
		266 nm	6.8 ± 1.0
	2p 2P1/2	349.85 nm	13.8 ± 2.0
		335.4 nm	13.2 ± 1.9
		307 nm	9.5 ± 1.4
		266 nm	5.9 ± 0.9
Li7	2p 2P1/2, 3/2	334.4 nm	16.2 ± 2.5	Wipple et al. [93]
		335.8 nm	18.3 ± 2.8	Wipple et al. [93]
		335.4 nm	18.0 ± 2.7	Saleem et al. [126]
	2p 2P3/2	349.85 nm	19.2 ± 2.9	Saleem et al. [126]
		335.4 nm	17.8 ± 2.7
		307 nm	12.5 ± 1.9
		266 nm	8.0 ± 1.2
	2p 2P1/2	349.85 nm	16.5 ± 2.5
		335.4 nm	15.5 ± 2.3
		307 nm	10.8 ± 1.6
		266 nm	6.8 ± 1.0

. The reason for using different ionizing lasers is that by varying the frequency of the ionizing laser, the electrons of different kinetic energies are produced and the behavior of the photoionization in different regions of the continuum can be investigated. The value of the photoionization cross-section decreases as the ionizing laser wavelength is decreased.

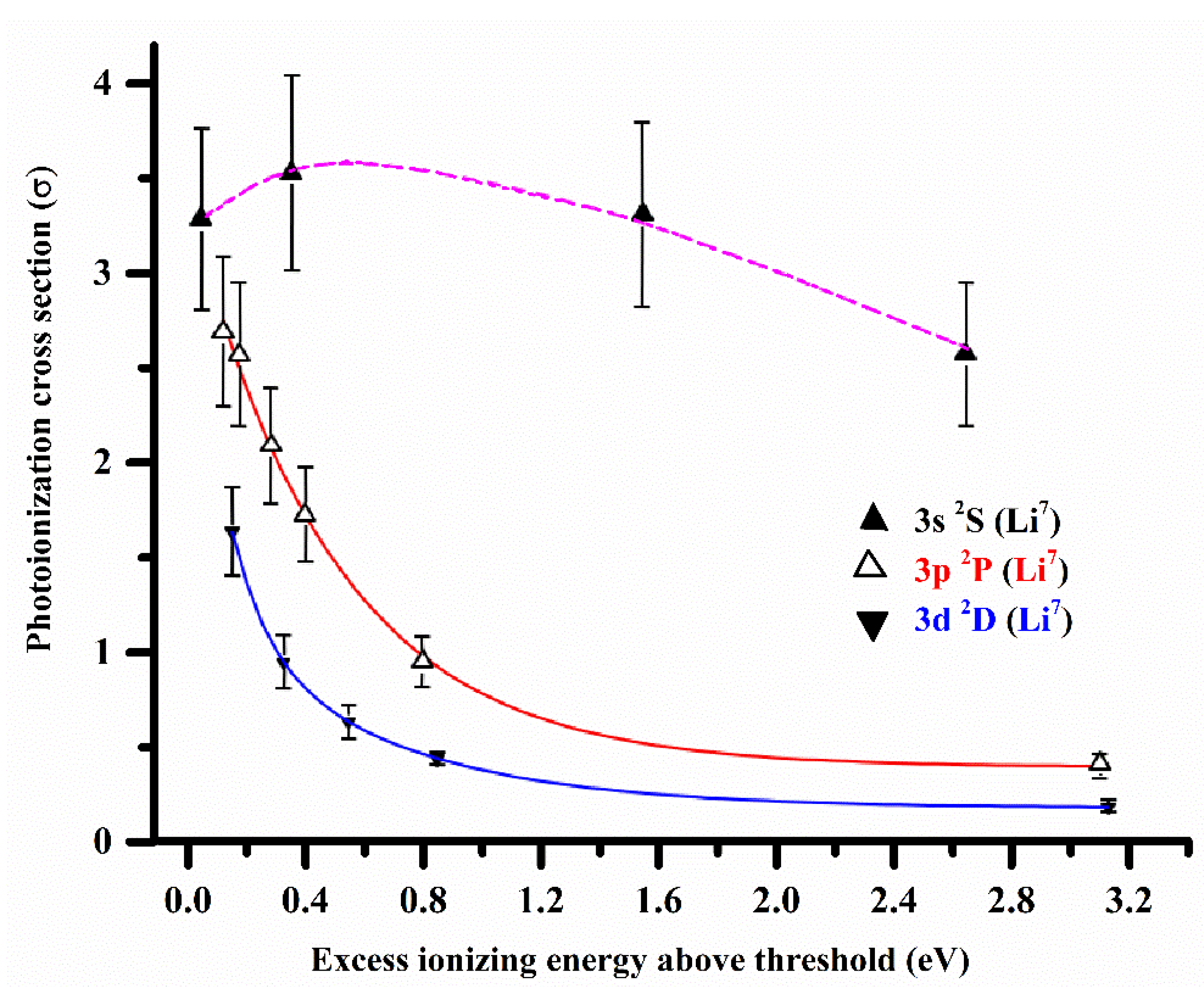
The photoionization cross-sections for the 2p, 3s, 3p, 3d, and 4s. The 4p and 4d excited states of both isotopes of lithium using two-step laser excitation and ionization coupled with a time-of-flight mass spectrometer (TOF-MS) have been extensively studied by Hussain et al. [128] and Saleem et al. [129]. The measured values of the photoionization cross-sections, above the first ionization threshold, for the same principal quantum number n = 3 but at different orbital angular momentum states ℓ = 0, 1, 2 (3s, 3p, 3d), are collectively shown in Figure 4.

The values of the cross-section from the 3s and 4s excited states were multiplied by a factor of 25 just to compare the trends of photoionization cross-sections with other states. The dotted lines passing through the values of the cross-section of 3s excited states at different ionizing wavelengths are not the fitted curves but are simply drawn for the comparison with the 3p, and 3d excited states. The solid lines are the exponential decay fit to the experimental data points for the photoionization cross-section from the 3p and 3d excited states. The behavior of the photoionization cross-section for the excited states is correlated with the difference between the initial state quantum defect and the final continuum threshold phase shift. The quantum defects of s and p states of lithium are 0.40 and 0.05, respectively, and effectively zero for ℓ ≥ 2. Thus, only transitions involving s or p states are non-hydrogenic. The oscillator strength distribution in the discrete and continuum regions of the spectrum of lithium was explored by Hussain et al. [130], who determined the photoionization cross-section for the 3s ²S_1/2 level at the first ionization threshold and then extracted the f-values of the 3s ²S–np ²P Rydberg series. Felfli and Manson [131] remarked that a difference of about 0.5 is necessary to have a Cooper minimum in the continuum. There is only one channel εp through which the electrons from the ns excited states can be promoted to the ionization continuum. The difference between the ns quantum defect and the threshold εp phase shift is 0.37, which is less than 0.5, and therefore a minimum is expected in the discrete region near the threshold. The presence of these minima causes the ns cross-section to be anomalously small at the threshold (Lahiri and Manson [132,133] and the references therein). The measured values of the cross-section for the 3s and 4s excited states at the threshold by Saleem et al. [129] are in good agreement with the calculations by Lahiri and Manson [132] in comparison with Aymar et al. [63]. Saha et al. [134] performed the multi-configuration Hartree–Fock calculation of the photoionization of the excited Na 4d state. Recently, Qi et al. [135] calculated the photo-ionization cross-sections for several excited states of lithium and their calculations are in excellent agreement with that reported by our group.

Interestingly, the photoionization cross-sections for the 3s ²S and 4s ²S excited states of lithium first increase to a maximum value and then decreases with the increase in the ionizing laser photon energy, also deviating from the hydrogenic behavior. A smooth decrease in the photoionization cross-section above the ionization threshold is attributed to the fact that when the ionizing electron gains high kinetic energy, its electron wave becomes more oscillatory and, as a result, the vacated orbital and the photoelectron wave are no more in the same spatial region and consequently the photoionization cross-section for that ionizing photon decreases (Green and Decleva [136]). The behavior of the photoionization cross-section from the np-excited states also differs from that of the ns or nd excited states. The excited electrons from the p-states can be promoted to the ionization continuum through two different channels np → εs and np → εd. The cross-sections decrease monotonically with the increase in the ionizing laser wavelength above the first ionization threshold, but this falloff of the cross-section is not hydrogenic due to the smaller quantum defects for the p-states. Furthermore, near the threshold, the cross-section increases with n and then falls off more rapidly with the excess photon energy. The rapid decay of the cross-section near the threshold with an increase in the principal quantum number n indicates the decreasing contribution of the non-hydrogenic region of the potential. For the photoionization of the atoms from the nd-excited states, there are two possible ionization channels, εp and εf, through which the excited electrons from these states can be uplifted to the ionization region. The nd → εp cross-section is slightly different from hydrogenic, owing to the small p-wave phase shift, but the nd → εf is completely hydrogenic because for ℓ ≥ 2, the quantum defects or phase shifts are effectively zero. The fitted curves through the measured data points for the 3d ²D excited state decrease more sharply with the increase in the ionizing laser photon energy. This decreasing behavior of the cross-section from the nd excited states is hydrogenic as compared to that of the ns or np excited states.

The ionization from the ground state of alkali atoms possesses two partial waves, εp, J = 1/2 and J = 3/2, due to the spin-orbit effect. They have slightly different phases, and their amplitudes pass through zero at different energies. Thus, photoionization from the ground state passes through a minimum in the region of maximum overlap of the εp wave functions with the ground state wave function as a function of the photon energy. Sandner et al. [137] measured the photoionization of potassium in the vicinity of the minimum in the cross-section using a time-of-flight technique. The photoionization cross-sections for the alkali metal atoms were calculated in the framework of the relativistic many-body perturbation theory (RMBPT) using B-spline orbitals by Savukov [65]. Zatsarinny and Tayal [66] used the Dirac-based B-spline R-matrix method to investigate the photoionization of atomic potassium from the 4s ground and 4p, 5s-7s, 3d-5d excited states. The effect of the core polarization by the outer electron was included through the polarized pseudo-states. Besides the dipole core polarization, they found a noticeable influence of the quadrupole core polarization. Excellent agreement with the experiment for cross-sections of the 4s photoionization, including an accurate description of the near-threshold Cooper–Seaton minimum was observed. A close agreement with the experiment for the 4p photoionization was also noticed, but there were unexpectedly large discrepancies with the available experimental data for photoionization of the 5d and 7s excited states. The existence of a Cooper minimum in the experimentally measured photoionization cross-sections for the 7s ²S_1/2 excited state of potassium using a two-step laser excitation technique in conjunction with a time-of-flight mass spectrometer was reported by Yar et al. [138]. The photoionization cross-sections for the 7s ²S_1/2 state were determined as (9.78 ± 0.01) × 10⁻², (3.30 ± 0.49) × 10⁻⁴, (5.47 ± 0.82) × 10⁻³, and (2.06 ± 0.30) × 10⁻² Mb at the ionizing laser wavelengths 1064, 700, 532, and 355 nm, respectively. 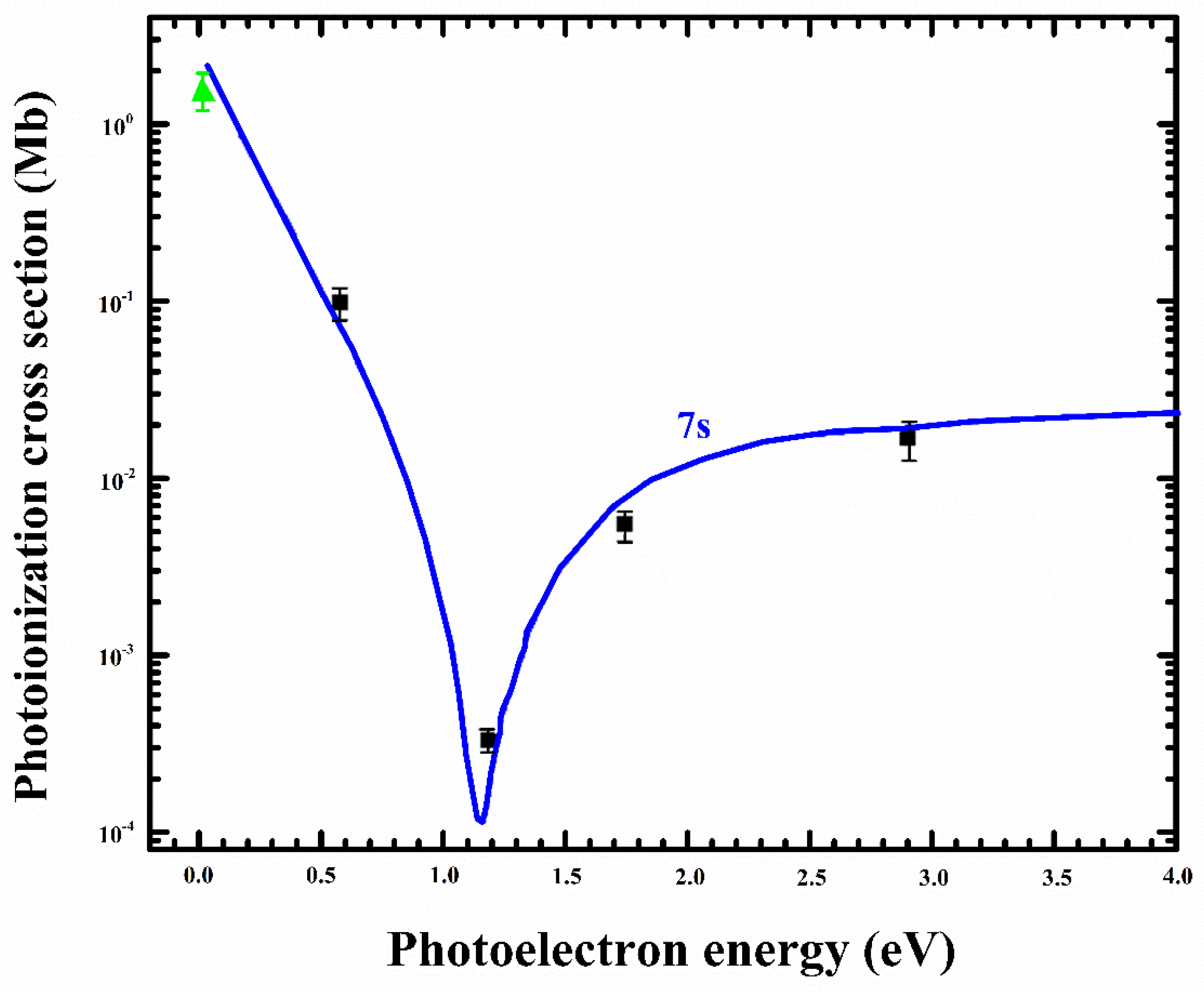In Figure 5, the measured photoionization cross-section for the 7s excited state of potassium at and above the first ionization threshold is presented along with the theoretical calculations of the cross-section by Zatsarinny and Tayal [66]. A minimum in the cross-section, termed the Cooper minimum, is evident at ∼1.25 eV above the first ionization threshold, which is in agreement with the theoretical prediction.

Once the photoionization cross-section for the excited state at the first ionization threshold is determined, the f-values of the Rydberg transitions attached to the intermediate state can be calculated using a simple relation (Mende et al. [139]).

$$f_n=\frac{mc}{\pi }\left(\frac{4\pi {\epsilon }_0}{e^2}\right)\left(\frac{S^n}{S^{+}}\right)\left(\frac{{\lambda }^{+}}{{\lambda }_n}\right){\sigma }^{+}.$$

(13)

Here, $f_n$ is the oscillator strength for the nth transition of a Rydberg series, ${\sigma }^{+}$ is the photoionization cross-section measured at the ionization threshold wavelength ${\lambda }^{+}$, $S^{+}$ is the ion signal at the ionization threshold, and $S^n$ is the integrated ion signal intensity for the nth transition. Using the absolute value of the cross-section at the ionization threshold, the oscillator strengths of all the discrete Rydberg transitions for which the ionization probability is unity ($p_n\cong 1$) were determined. However, the experimental conditions have to be optimized, such as the oven temperature and the buffer gas pressure, so that the ionization probability for the Rydberg states approaches one. Moreover, the energy difference between the first ionization threshold and n = 20 for potassium is ≈0.035 eV, whereas the value of K_BT (thermal energy) is ≈0.046 eV at T = 540 K. As the energy gap between n = 20 and the first ionization threshold is less than the thermal energy, it therefore enhances the ionization efficiency of the Rydberg states for n ≥ 20. Kalyar et al. [140] measured the absolute values of the cross-sections from the 4p ²P_3/2 and ²P_1/2 excited levels at the ionization threshold as (6.3 ± 0.9) Mb and (5.4 ± 0.8) Mb, respectively, and the oscillator strengths for the 4p ²P_1/2 → nd ²D_3/2 and 4p ²P_3/2→nd ²D_{3/2, 5/2} Rydberg transitions were also deduced by using the measured cross-sections of the 4p ²P_1/2 and ²P_3/2 levels at the ionization threshold.

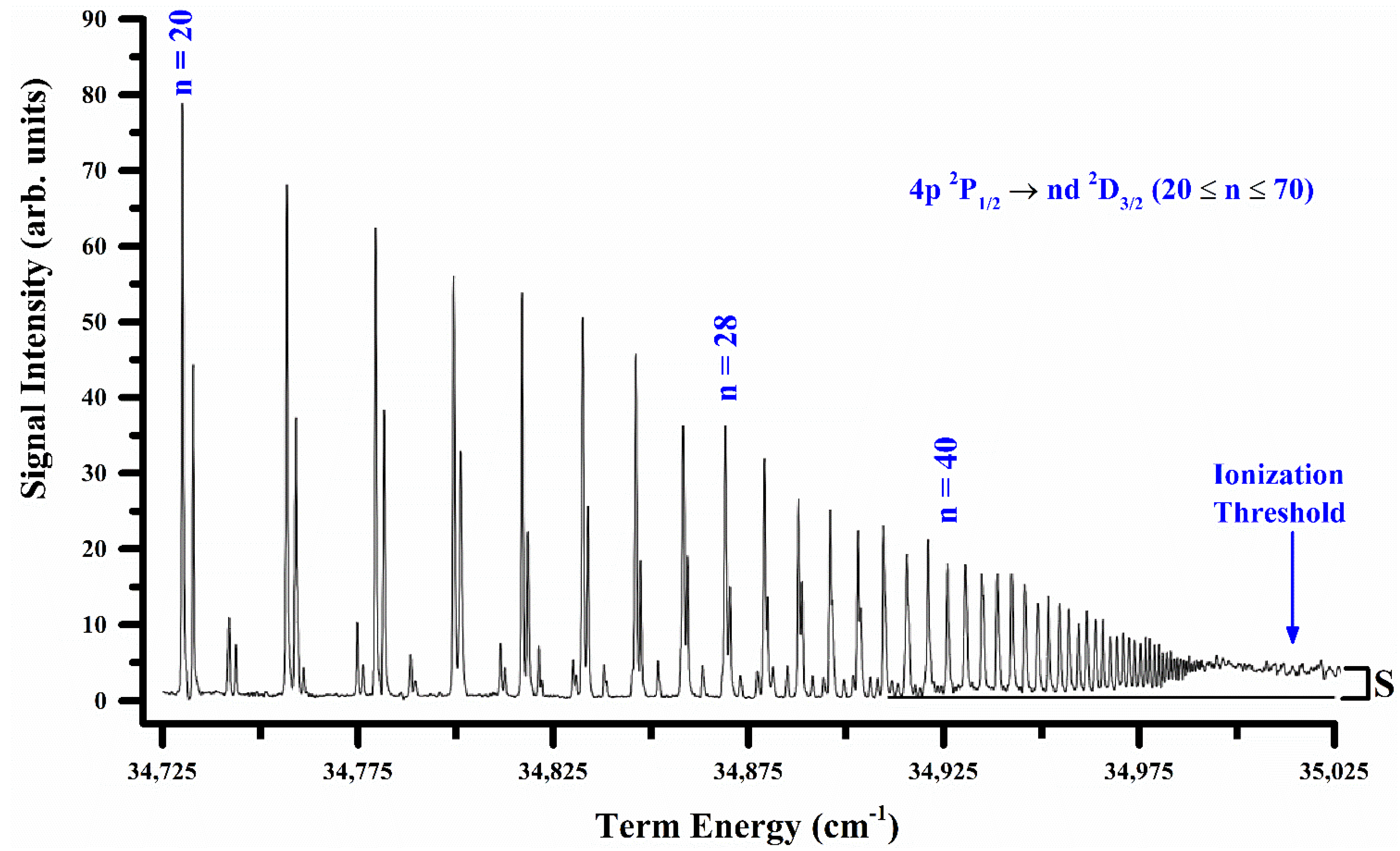
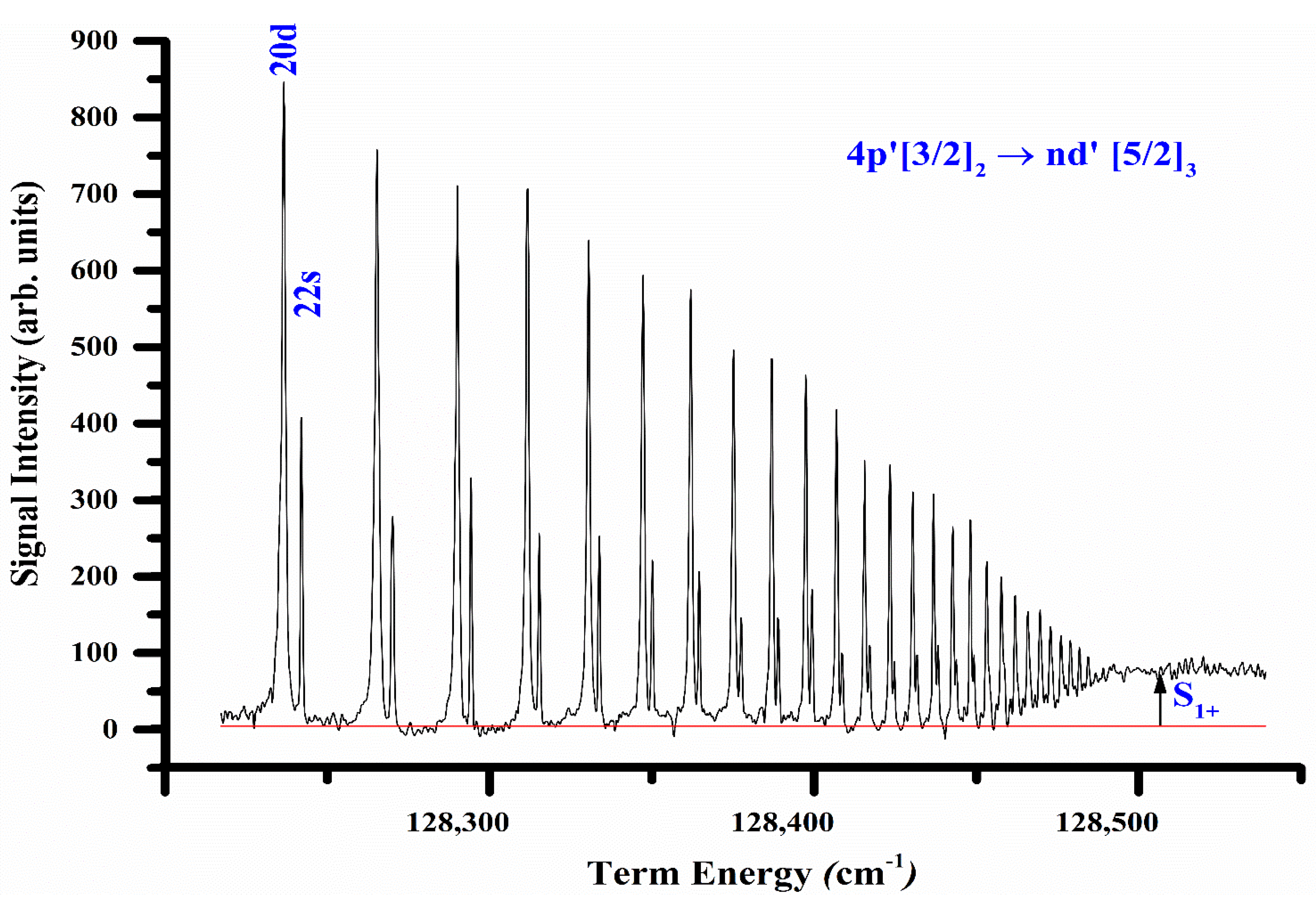
The Rydberg series excited from the 4p ²P_1/2 excited state of potassium up to the first ionization threshold is presented in Figure 6. The optical oscillator strengths for the 4p ²P_3/2 → nd ²D_3/2,5/2 (20 ≤ n ≤ 70) Rydberg transitions were calibrated using the measured absolute value of the photoionization cross-section (6.3 ± 0.9) Mb for the 4p ²P_3/2 level at the ionization threshold, whereas the values of $S^n$, ${\lambda }^n$ and $S^{+}$ were extracted from the recorded spectrum, as marked in Figure 6. The photoionization cross-sections for the 7p ²P_3/2 excited state of potassium near the first ionization threshold using a two-step laser excitation/ionization technique in conjunction with a time-of-flight (TOF) mass spectrometer were reported as (3.52 ± 0.52) Mb, (2.21 ± 0.33) Mb, (1.35 ± 0.22) Mb, and (0.54 ± 0.08) Mb at four ionizing laser wavelengths; 1064 nm, 643.61 nm, 532 nm, and 355 nm, respectively, by Yar et al. [138]. Recently, Collister et al. [141] measured the non-resonant photoionization cross-section of the 7P ²P_3/2 state of francium for 442 nm light as (20.8 ± 7.1) Mb using a magneto-optical trap system. The photoionization rate was deduced from the change in the trap lifetime. The results are consistent with a simple extrapolation of known cross-sections for other alkali atoms. In

Table 3. Experimentally measured values of the photoionization cross-section for the resonance transitions of alkali atoms.

Atom	First Step (Excitation) ms 2S1/2 → mp 2P1/2,3/2	Second Step (Ionization) mp 2P1/2,3/2 → εs J = 1/2        → εd J = 3/2, 5/2	Photoionization Cross-Section at Threshold Mb (1 Mb = 10−18 cm2)
Li I	2p 2P1/2  670.793 nm       2P3/2  670.778 nm	349.8 nm 349.8 nm	16.5 ± 2.5 19.2 ± 2.9
Na I	3p 2P1/2  589.592 nm       2P3/2  588.995 nm	408.2 nm 408.5 nm	7.9 ± 1.3 6.7 ± 1.1
K I	4p 2P1/2  769.896 nm       2P3/2  766.489 nm	454.0 nm 455.2 nm	5.4 ± 0.8 6.3 ± 0.9
Rb I	5p 2P1/2  794.760 nm       2P3/2  780.027 nm	473.6 nm 479.0 nm	18.8 ± 3.0
Cs I	6p 2P1/2  894.347 nm       2P3/2  852.113 nm	494.3 nm 508.2 nm	25 ± 4

, we enlist the laser wavelengths for the first-step excitation, laser wavelengths of the ionizing laser, and measured photoionization cross-sections for the resonance lines of lithium, potassium, sodium, rubidium, and cesium at the first ionization threshold.

In the next section, the photoionization cross-section for the excited states of the alkaline earth atoms is presented.

4. Alkaline Earth Atoms

The ground state configurations for the alkaline earth atoms possess a filled s-subshell, ms^{2 1}S₀ (m = 3, 4, 5, and 6 for Mg, Ca, Sr, and Ba, respectively). The atoms from the ground state are excited to the Rydberg states forming singlet or triplet states; msnp ¹P_1, ³P_0,1,2. Photoionization sets in as the energy of the interacting photons is equal to the first ionization potential of the atom. Photoionization from the ground state is represented as ms (²S_1/2) εp (ℓ = 1; J = 0, 1, 2) continuum channels. The alkaline earth atoms show some broad and asymmetric line profiles above the first ionization threshold due to the simultaneous excitation of both the valence electrons. The absorption spectra of alkaline earth atoms from the ground state to the ionization threshold and above the threshold have been extensively studied by several groups around the globe.

A multistep-laser excitation technique has also been employed to measure the photoionization cross-section for the excited states of these atoms. The data on the highly excited states of atoms and particularly alkaline earth atoms have been studied by many researchers around the world, and has been compiled by Gallagher [142] and Connerade [143]. In

Table 4. Two-step excitation and ionization laser wavelengths for the Alkaline Earth Atoms.

Atom	First Step (Excitation) ms2 1S0 → msnp 1P1, 3P1	Second Step (Excitation) msmp 1P1 → ms np 1S0, 3S1    3P1 → ms nd 1D2, 3D1,2,3	Ionization Potential εs (J = 0, 1) εd (J = 0,1,2,3)
Mg I	3s3p 1P1  285.213 nm           3P1  457.109 nm	375.6 nm 251.5 nm	61,671.05 cm−1
Ca I	4s4p 1P1  422.544 nm           3P1  657.278 nm	389.8 nm 293.3 nm	49,305.95 cm−1
Sr I	5s5p 1P1  460.733 nm           3P1  689.259 nm	412.6 nm 318.2 nm	45,932.09 cm−1
Ba I	6s6p 1P1  553.548 nm           3P1  791.133 nm	340.1 nm 417.1 nm	42,034.91 cm−1

, we summarize the laser wavelengths for the first step excitation and the second step excitation/ionization to measure the photoionization cross-sections experimentally. Except for Mg, where the first step laser is in the UV region, all the other required laser wavelengths are in the visible region, and the experiments can be performed with ease.

The first absolute measurement of the cross-section for photoionization from the selectively excited 3s3p ¹P₁ atomic state of magnesium at the 3p^{2 1}S₀ autoionizing resonance was reported by Bradley et al. [144] using two tunable pulsed lasers. The peak of the cross-section was reported as (8 ± 4) × 10⁻¹⁶ cm² at 300.0 nm and the half-width of resonance was measured as 2.5 nm. Besides, the ratio of the cross-sections to the 3p^{2 1}S₀ and ¹D₂ states was measured as 14:1. The effect of polarization of the lasers was exploited to identify the angular momentum states of the autoionizing levels. Madsen and Thomsen [94] measured the resonant photo-ionization of the 3s3p ¹P₁ level of magnesium at the near-resonant light at 285 nm using a magneto-optical trap. The extracted absolute photo-ionization cross-section was (8.1 ± 2.3) × 10⁻¹⁷ cm², which is in good agreement with the theoretical calculations. Rafiq et al. [145] measured the photoionization cross-section from the 3s3p ¹P₁ excited state of magnesium in the energy region from the first ionization threshold up to 1.4 eV excess energy using two-step photoionization and the saturation ionization technique in conjunction with an atomic beam source and a time-of-flight mass spectrometer. The absolute value of the photoionization cross-sections from the 3s3p ¹P₁ excited state near the 3s ionization threshold was measured as (90 ± 16) Mb (at 354.5 nm ionizing wavelength) for the dominating isotope (²⁴Mg), whereas the value at the peak of the 3p^{2 1}S₀ auto-ionizing resonance was determined as (785 ± 141) Mb. This measured value is in close agreement with that reported by Bradley [144].

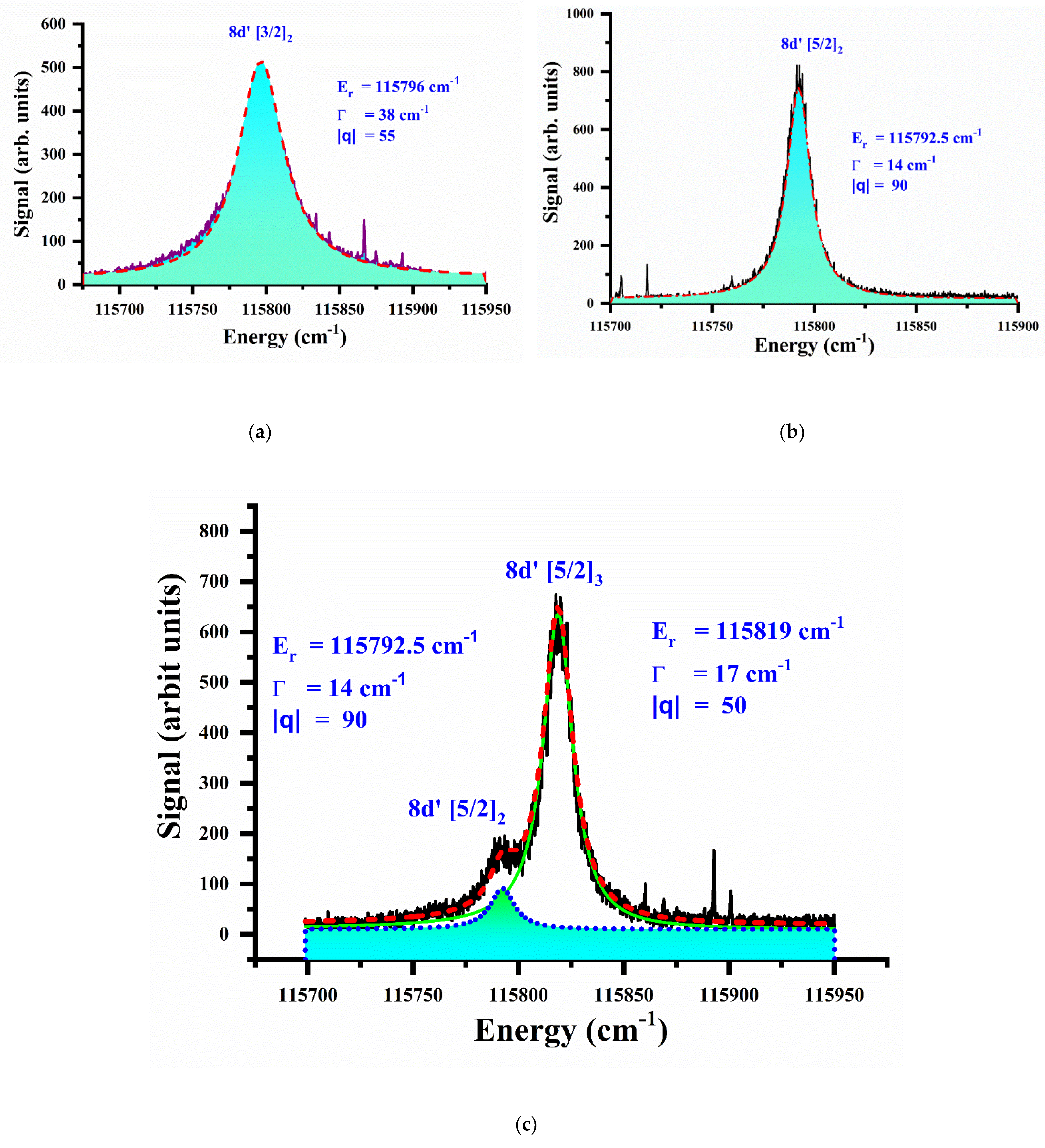
In

Table 5. Comparison of experimental and theoretical excitation energies E_r, width Γ, and line profile index q for the doubly excited 3p^{2 1}S₀ auto-ionization state of magnesium. The experimental uncertainty is predicted by the values in the parentheses.

Energy Er (cm−1)	Width Γ (cm−1)	Line Profile Index, q	References
Theoretical
68,600	137		Thompson et al. [146]
68,130	271		Chang [147]
67,936	331		Moccia and Spizzo [148]
68,700	316		Fang and Chang [149]
68,231			Kim [150]
Experimental
68,275 (11)	276 (11)		Bradley et al. [144]
68,268 (4)	278 (8)	24.4 (1)	Bonanno et al. [151]
68,275 (11)			Okasaka and Fukuda [152]
68,273	280		Shao et al. [153]
68,270 (5)	280 (5)	24.5 (5)	Rafiq et al. [145]

, a comparison of different experimental and theoretical results is presented for the resonance energy, width, and q-parameter of this autoionizing resonance in magnesium. The agreement is reasonably good, which shows the maturity of the experimental evidence and the theoretical models.

Kim [150] calculated the photoionization cross-sections for the Mg⁺ (3s, 3p, 4s, and 3d) states from the 3s3p ^1,3P excited states of atomic magnesium from the first ionization threshold up to the Mg⁺ 4p threshold limit using the enhanced non-iterative variational R-matrix approach combined with multichannel quantum defect theory at the R-matrix surface. Recently, Wang et al. [154] theoretically studied the photoionization cross-sections of the excited levels (3s3p ³P_0,1,2) of atomic Mg using both the nonrelativistic and fully relativistic R-matrix method. The calculations show significant differences (a factor of 3) from the former experimental values. More experimental measurements of the photoionization cross-sections from the (3s3p ³P_0,1,2) excited states of Mg are desirable. The gf-values of the lower members of the principal series of calcium and photoionization cross-section at the first ionization threshold were determined by Parkinson et al. [155] using the hook method. Geiger [156] calculated the bound oscillator strength distribution and density of oscillator strength in the continuum using multichannel quantum defect theory and reported the oscillator strengths of the 4s^{2 1}S₀ → 4snp ¹P₁ and 4s^{2 1}S₀ → 3d4p ¹P₁ transitions. Barrientos and Martin [157] computed the oscillator strengths of the principal series of alkaline earth atoms and determined the photoionization cross-section of magnesium and calcium. The relative oscillator strengths from the 4s4p ¹P₁ excited state to the 4sns ¹S₀ (n = 6, 7), the 4snd ¹D₂ (n = 6, 7), the 4p^{2 1}D₂, and the 4p^{2 1}S₀ states were measured by Smith [158]. The autoionization of the Rydberg series 3dnp ¹P₁ in calcium was studied by Karamatskos et al. [159] using an atomic beam apparatus and the synchrotron radiation facility at BESSY. Subsequently, Griessmann et al. [30] measured the cross-sections of the doubly excited resonances in calcium using a hot-wire diode detector and the synchrotron radiation facility at Hamburg. Lucas et al. [96] used resonance photoionization for the isotope-selective loading of Ca ions into a Paul trap. The 4s^{2 1}S₀ → 4s4p ¹P₁ transition was driven by a 423 nm laser and the atoms were photoionized by a second laser at 389 nm. The lower limit for the absolute photoionization cross-section was reported as 170 Mb. Daily et al. [160] used two-photon photoionization of the Ca 4s3d ¹D₂ level in an optical dipole trap and reported the 4s4f ¹F₃ photoionization cross-section as 230 Mb. Sato et al. [161] studied the single and double photoionization of Ca atoms between 35 and 42 nm. The absolute values of the photoionization cross-sections for the 4s4p ¹P₁ and 4s4p ³P₁ excited states of calcium at the 4s ionization threshold were measured by Haq et al. [162] as 140 ± 20 Mb and 117 ± 20 Mb, respectively. This value of the photoionization cross-section is in good agreement with that reported by Daily et al. [160].

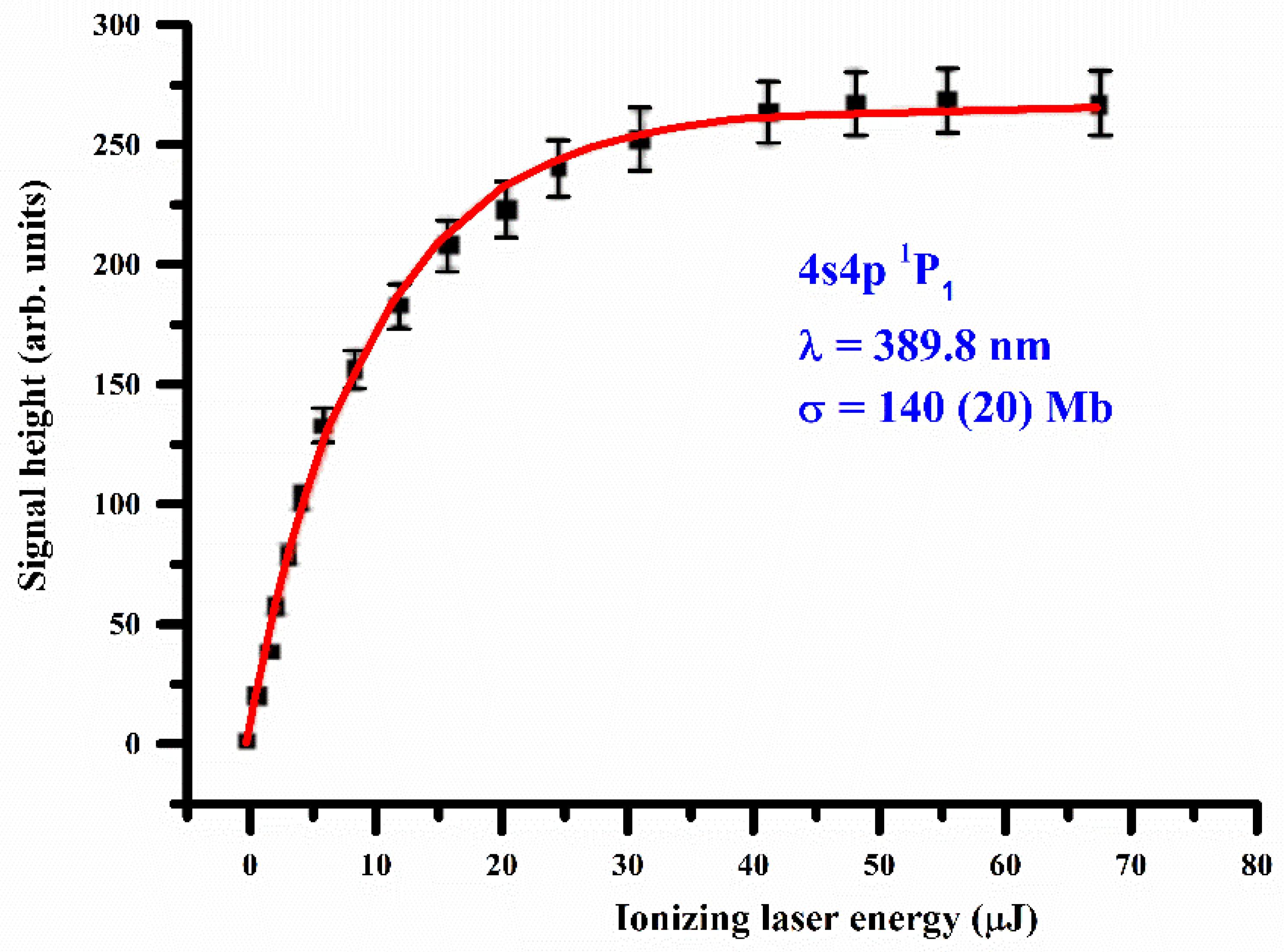
Figure 7 shows a typical ion-signal plot, keeping the 4s4p ¹P₁ level saturated while the ionizing laser wavelength was adjusted at 389.8 nm, which corresponds to the first ionization threshold. The continuous line that passes through the experimental data points is a fit of Equation (8), which yields the value of the photoionization cross-section. Subsequently, the measured values of the photoionization cross-sections for the 4s4p ¹P₁ and ³P₁ levels at the threshold were used to calibrate the f-values of the transitions excited from the 4s4p ^1,3P₁ intermediate, terminating at the first ionization threshold. The Rydberg transitions are identified as 4s4p ¹P₁ → 4snd ¹D₂ and 4s4p ³P₁ → 4snd ³D_2, respectively.

Ewart and Purdie [163] studied the two-photon excitation of the even parity 5sns ¹S₀ and 5snd ¹D₂ Rydberg states and an autoionization level 4d^{2 1}D₂ just above the first ionization threshold of strontium. The 5p_1/2ns_1/2 and 5p_3/2 ns J = 1 autoionizing states were reported by Xu et al. [164], whereas the even parity J = 0 autoionizing spectrum below the 4d_5/2 threshold was reported by Kompitsas [165]. The absolute photoabsorption cross-sections of strontium from the 5s ionization threshold to the 5p threshold were measured by Chu et al. [35] who reported the absolute value of the cross-section for the 5s ionization threshold as 7.2 ± 0.9 Mb. Luc-Koenig et al. [166] studied the two-photon ionization processes from the ground state of strontium using the jj-coupled Eigen-channel R-matrix approach combined with the multichannel quantum defect theory. Mende and Kock [167] applied the saturation technique and determined the photoionization cross-section at the first ionization threshold as 12 ± 2.5 Mb, which was used to calibrate the f-values of the 5s^{2 1}S₀ → 5snp ¹P₁ Rydberg series. The photoionization cross-sections from the 5s5p ¹P₁ excited state of strontium just above the first ionization threshold show a giant resonance, with a peak cross-section as 56 (10) Mb, as stated by Mende et al. [139]. The spatial distribution of the photons in the laser pulse was measured with a CCD camera and applied in the evaluation procedure as a Gauss profile. Based on a 12-state non-relativistic close coupling R-matrix calculation, the giant resonance was assigned as predominantly (5p²) ¹D₂ with a strong admixture of (4d²) ¹D₂. Baig et al. [81] presented a comparison between the line shape of an even parity isolated autoionization resonance (4d² + 5p²) ¹D₂ in strontium excited from the ground state either via two-photon non-resonant excitation or by the two-step resonant excitation processes. It was reported that the line shape q-parameter is different for the two processes, while the width of the resonance is independent of the excitation mechanism. Subsequently, Haq et al. [168] measured the photoionization cross-section from the 5s5p ¹P₁ and 5s6s ¹S₀ levels of strontium at the first ionization threshold as well as at six different wavelengths between 355 nm and 410 nm.

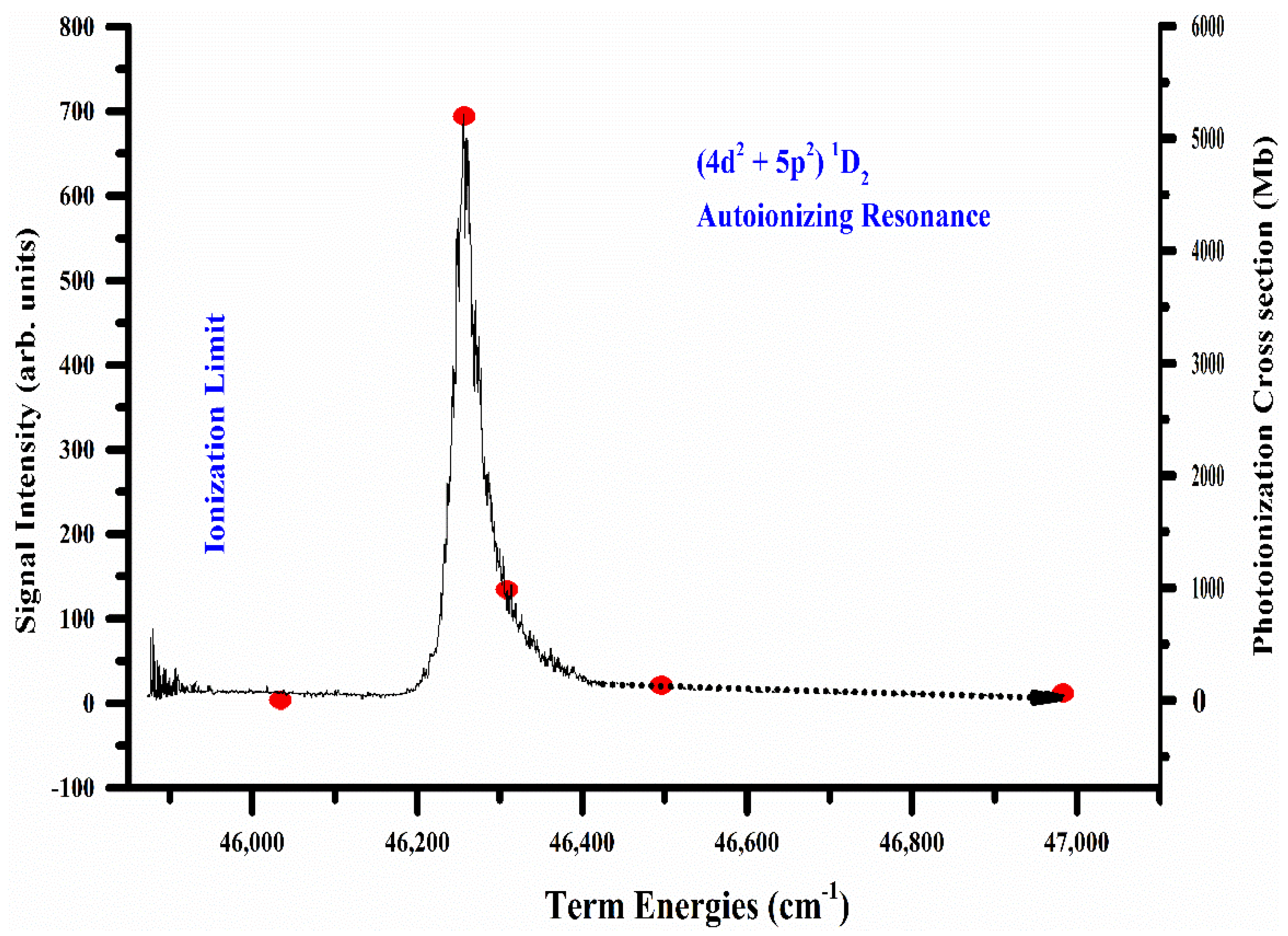
The dominant autoionizing resonance (4d² + 5p²) ¹D₂ excited from the 5s5p ¹P₁ intermediate level is reproduced in Figure 8. The absolute value of the cross-section at the peak of the (4d² + 5p²) ¹D₂ autoionizing resonance was determined as 5450 (18%) Mb. The photoionization cross-section was also measured at different ionizing laser wavelengths; 410 nm, 405 nm, 404 nm, 400 nm, and 390 nm. Interestingly, the measured values of the photoionization cross-sections completely retrace the line profile of the autoionizing resonance. The normalization was found to be very consistent, and by selecting any one of the measured points as a reference, the value of the cross-section at any other point is reproducible. Using Fano’s relation for an isolated autoionizing resonance, the resonance energy (E_r = 46,379 (1) cm⁻¹), width (Γ = 45 (5) cm⁻¹) and line profile index (q = 6.8 (2)) were extracted.

In

Table 6. Comparison of the resonance energy and width of the (4d² + 5p²) ¹D₂ autoionizing resonance.

Experimental		Calculated		References
Energy (cm−1)	Width (cm−1)	Energy (cm−1)	Width (cm−1)
46,380	60	-	-	Esherick [169]
46,376.8	56.2	-	-	Mende et al. [139]
46,380.1	59.6			Dai et al. [170]
-	-	46,433	71	Luc-Koenig et al. [166]
46,380	56 (1)	-	-	Baig et al. [81]
46,379 (1)	45 (5)	-	-	Haq et al. [168]

, a comparison of the resonance energy and width of this domination autoionizing resonance is presented, showing a good agreement.

The absolute values of the photoionization cross-sections for the 5s5p ¹P₁ and 5s5p ³P₁ excited states of strontium at the first ionization threshold were measured by Haq et al. [171] as 11.4 ± 1.8 Mb and 10.7 ± 1.7 Mb, respectively, using a thermionic diode ion detector. These threshold photoionization cross-sections values were then used to determine the oscillator strengths of the 5s5p ¹P₁ → 5snd ¹D₂ and 5s5p ³P₁ → 5snd ³D₂ Rydberg transitions. The oscillator strength densities in the continuum corresponding to the 5s5p ³P₁ excited state were determined by measuring the photoionization cross-sections at five ionizing wavelengths above the first ionization threshold. Haq et al. [172] measured the photoionization cross-section from the 5s6s ¹S₀ excited state of strontium using a linearly polarized dye laser with the polarization vector along the direction of propagation. The total angular momentum of the excited state is J = 0, therefore the M_j = 0 sublevel is populated. The polarization vector of the ionizing laser was set parallel to that of the exciting laser, which accessed the M_j = 0 out of the M_j = 0, ±1 sublevels of the 5s εp, J = 1 continuum. By adjusting the polarization vector of the ionizing laser perpendicular to that of the exciting laser, the accessible channels were 5s εp J = 1 and M_j = ±1, and the corresponding cross-section at the threshold was determined as 1.1 ± 0.2 Mb. However, by adjusting the polarization vector of the ionizing laser at the magic angle of 54.7°, the photoionization cross-section was measured as 1.0 ± 0.2 Mb. The measured absolute value of the photoionization cross-section for the 5s6s ¹S₀ excited state of strontium at the 5s threshold was also used to extract the f values of the 5s6s ¹S₀ → 5snp ¹P₁ Rydberg transitions.

Burkhardt et al. [76] employed multi-step laser excitation and ionization to measure the photoionization cross-sections of the resonance levels of sodium (3p ²P_3/2), potassium (4p ²P_3/2), and barium (6s6p ¹P₁), and their atomic densities in the ground states. In this experiment, a beam of the atoms was generated, which intersected at the center of an electrically shielded cell by two collinear laser beams. One laser beam was used to excite the atoms to the resonance level and the other to photo-ionize the atoms out of that level. The diameter of the excitation laser beam was 3 mm, and the energy of the laser was 75 μJ. The ionization laser beam was the frequency tripled (353.3 nm) output of the same Nd:YAG laser (1064 nm) used to pump the dye lasers. The diameter of the ionization laser beam was much smaller than that of the exciting laser beam by a long focal length lens to make the ionizing volume as nearly cylindrical as possible over the ion collection length. The values of the photoionization cross-sections were reported as (3.7 ± 0.7) × 10⁻¹⁸ cm², for the 3p ²P_3/2 level of sodium, as (7.6 ± 1.1) × 10⁻¹⁸ cm² for the 4p ²P_3/2 level of potassium, and as (17.6 ± 2.3) × 10⁻¹⁸ cm² for the 6s6p ¹P₁ level of barium. Kallenbach et al. [173] measured the photoionization cross-section for the 6s6p ¹P₁ level of barium using a thermionic diode ion detector in combination with a two-step pulsed laser excitation and ionization technique. The barium atoms were excited to the resonance level by a nitrogen laser (1MW, 4ns) pumped dye laser (energy 4 μJ and width 0.3 nm) tuned to the 6s^{2 1}S₀ → 6s6p ¹P₁ transition at 553.5 nm. The second dye laser (energy 4 μJ and width 0.08 nm) was tuned at high lying Rydberg states and across the photoionization threshold for the 6s6p ¹P₁ level of Ba at 416 nm. The absorption oscillator strengths of the 6s6p ¹P₁ → 6snd ³D₂ transitions were measured along with the photoionization cross-section at the threshold as (5 ± 2) × 10⁻²⁰ m². Willke and Kock [174] improved the experimental arrangements to measure the cross-sections for photoionization for the excited states of barium by using a Nd:YAG pumped dye laser system and a very narrow bandwidth dye laser (0.2 cm⁻¹) in conjunction with the thermionic diode technique. The revised value of the photoionization cross-section for the 6s6p ¹P₁ level of barium at the threshold was reported as 80 Mb, which is in good agreement with the theoretical values, 120 × 10⁻¹⁸ cm² (Bartschat and MacLaughlin [175]) and 100 × 10⁻¹⁸ cm² (Greene and Theodosiou [176]). The barium ion signal of the high-lying Rydberg transitions up to and above the ionization threshold of the 6s continuum was also measured and the observed Rydberg series were designated as 6s6p ¹P₁ → 6snd ¹D₂ transitions. The photoionization cross-section for the 6s6p ¹P₁ level was also measured above the ionization threshold up to 381 nm, showing numerous autoionizing resonances. The polarization of the exciting and the ionizing lasers also plays an important role in the measurement of the photoionization cross-section. Therefore, if the exciting and the ionizing lasers pulses are linearly polarized, the photoionization cross-section will depend on the angle θ between the two laser polarization directions (He et al. [77]):

$$\mathsf{\sigma }\left(\mathsf{\theta }\right)={\cos }^2\mathsf{\theta }{\mathsf{\sigma }}^{‖}+{\cos }^2\mathsf{\theta }{\mathsf{\sigma }}^{\perp },$$

(14)

where ${\mathsf{\sigma }}^{‖}$ and ${\mathsf{\sigma }}^{\perp }$ are the cross-sections for the parallel and perpendicular polarizations of the exciting and the ionizing laser beams, respectively. When both the lasers are linearly polarized and the polarization vectors are parallel, then only the term ${\cos }^2\mathsf{\theta }{\mathsf{\sigma }}^{‖}$ contributes to the measured cross-section. He et al. [77] measured the absolute photoionization cross-sections for the 6s6p ¹P₁ excited state of Ba in the threshold region and found a good agreement with the theoretically calculated value. The “magic” angle was used for the relative orientation of the linear polarization of the exciting and ionizing lasers, as, at this orientation angle, the measured cross-section is the same as if the excited state is populated isotropically. Keller et al. [177] measured the photoion spectra and angular distribution of photoelectrons using a two-color, two-photon resonant ionization of barium and probed the effect of the photoionization pathway on the autoionization processes. Using 6s6p ¹P₁ and 5d6p ¹P₁ as intermediate states, the 5dnd autoionizing states were studied, showing a dramatic difference in the profiles of the autoionizing resonances. Wilke and Kock [174] measured the absolute photoionization cross-sections from an excited state of Ba I using an improved thermionic diode technique with an excellent signal-to-noise ratio from the threshold of the 6s continuum at 417 nm down to 370 nm. The prominent resonances were fitted Beutler–Fano profiles, extracting the parameters that show good agreement with the experimental as well as theoretical studies. He et al. [178] reported the absolute cross-sections for photoionization of isotropically populated Ba (6s6p ¹P₁) to each accessible final state (0, 1, and 2) from the threshold to 370 nm, using spectra obtained with four different combinations of linear and circular polarization of the exciting and ionizing radiation. The effects of de-alignment due to the hyperfine interaction of the nuclear spin I = 2 isotopes of barium were also taken into account. The results were in good agreement with R-matrix predictions of shapes and positions of autoionizing resonances as well as the magnitudes of the background (non-resonance) cross-sections, but some discrepancies with oscillator strengths of the autoionizing states were remarked. It was inferred that to obtain the correct magnitude of the background cross-section theoretically, it is important to include the electron correlation effects in the wave functions of both initial and final states. Data were also presented that verify the equivalence of obtaining the total photoionization cross-section by properly combining two sets of data, each acquired with a different angle between linear polarization vectors, e.g., parallel and perpendicular, or by making a single measurement at the magic angle, 54.74⁰. Langadec et al. [179] reported the experimental and theoretical studies of the photoionization for the 6p² multiplet in barium, in the range 350–402 nm, by considering the 6p^{2 3}P₀, 6p^{2 1}D_2, and 6p^{2 3}P₂ states, after the 6p^{2 3}P₁ state, which was studied by Carre et al. [180]. The differential cross-sections from below to above the 6p_1/2 threshold, where several 6p_1/2nl; J and 6p_3/2nl resonances were excited using different cases of laser polarizations, and the experimental results were compared with eigen-channel R-matrix calculations. Kalyar et al. [181] measured the photoionization cross-section measurements for the 6s6p ¹P₁ and ³P₁ excited states of barium at the first ionization threshold as 90 ± 14 Mb and 102 ± 15 Mb, respectively. Li and Budker [182] measured the photoionization cross-sections of two even parity excited states of barium, 5d6d ³D₁ and 6s7d ³D₂, at the 556.6 nm ionization laser wavelength, and reported that the total cross-section depends on the relative polarization of the atoms and the ionization laser light. Kalyar et al. [183] extended these studies and investigated the line shapes of the 6s7p configuration based on ¹P₁, ³D_1, and ³P₁ autoionizing resonances using the 6snp (n = 6, 7, 8) and 5d6p ¹P₁ as intermediate states. It was inferred, based on the extracted Fano parameters of the resonance line profiles, that the width of an autoionizing resonance is independent of the excitation path while the line profile parameter changes with the selection of different states. The even-parity autoionizing resonances in barium using two-step laser excitation via the 5d6p ¹P₁ intermediate level covering the energy region from the first ionization threshold to the 5d ²D _5/2 limit using an atomic beam apparatus in conjunction with a time-of-flight mass spectrometer were studied by Kalyar et al. [184].

In Figure 9, the photoionization spectra of barium excited from the 5d6p ¹P₁ intermediate level are presented at two polarization vector orientations of the ionizing laser; parallel or perpendicular to the exciting laser polarization. The selection of the combinations of polarization vectors of the two laser beams permits access to the final states with different total angular momentum. The probability of absorption of a photon is proportional to the square of the modulus of the dipole matrix element, as stated by Elizarov and Cherepkov [185]:

$$W_{n_0{l}_0{J}_0{m}_0\to n_1{l}_1{J}_1{m}_1}\propto {\left|\left.〈n_1{l}_1{J}_1{M}_1\right|D_q\left|n_0{l}_0{J}_0{M}_0\right.〉\right|}^2.$$

(15)

Here J and M_j are the total angular momentum and its projection, respectively, and D_q are the spherical components; q = 0 applies to the linearly polarized light and ±1 to the circularly polarized light. The Wigner–Eckart theorem leads to the separation of the matrix element into a geometrical and physical part, as the angles are incorporated in the coefficients and the physical part is expressed in terms of a reduced matrix element:

$$\left.〈n_1{l}_1{J}_1{M}_1\right|D_q\left|n_0{l}_0{J}_0{M}_0\right.〉={\left(-1\right)}^{J_1-M_1}\left(\begin{array}{lll}{J}_1& 1& J_0\\ -M_1& q& M_0\end{array}\right)〈n_1{l}_1{J}_1‖D‖n_0{l}_0{J}_0〉.$$

(16)

The dipole matrix element describing the absorption of a second photon in the second step can be described as:

$$\left.〈n_2{l}_2{J}_2{M}_2\right|D_q\left|n_1{l}_1{J}_1{M}_1\right.〉={\left(-1\right)}^{J_2-M_2}\left(\begin{array}{lll}{J}_2& 1& J_1\\ -M_2& q& M_1\end{array}\right)〈n_2{l}_2{J}_2‖D‖n_1{l}_1{J}_1〉.$$

(17)

Only those values of the total angular momentum via the single-photon absorption are allowed, for which the two 3j-symbols in the above two equations are non-vanishing. In the first-step excitation from the ground state 6s^{2 1}S₀ (J = 0 and M_j = 0) with the linearly polarized light, the 5d6p ¹P₁ (J = 1 and M_j = 0) level is populated. When the polarization vector of the second-step laser beam is set parallel to that of the first-step laser, the final states possessing M_j = 0, J = 0, and 2 are allowed while J = 1 is forbidden. However, when the polarization vector of the second step laser is set perpendicular to that of the first laser, the excited states possessing M_j = ±1, J = 1, and 2 are allowed but J = 0 is forbidden.

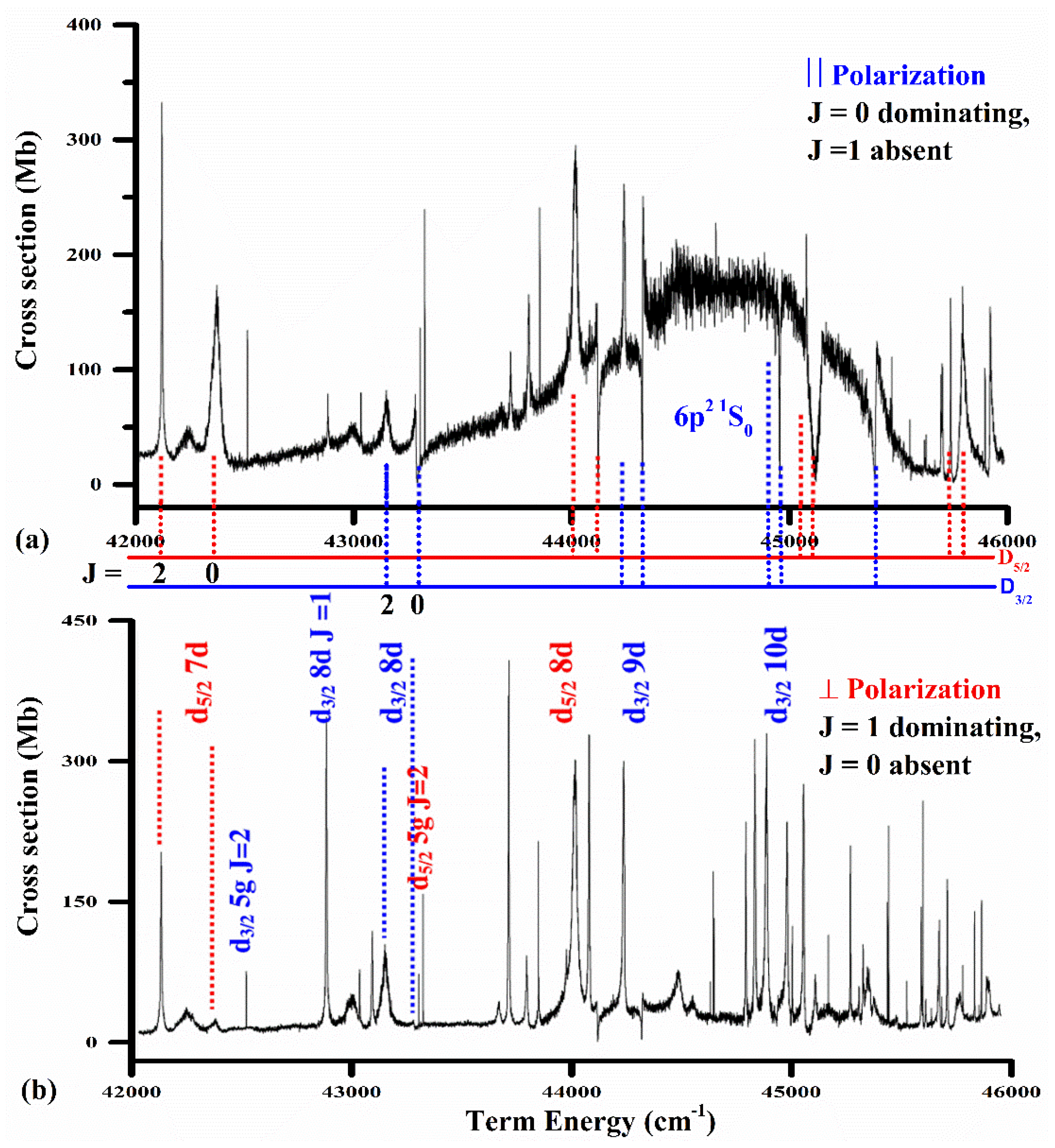
Thus, the 6p^{2 1}S₀ excited state is only accessible from the 5d6p ¹P₁ intermediate state when the polarization vectors of the exciting as well as that of the ionizing dye lasers are parallel to each other (Figure 9a), and this J = 0 transition will be forbidden in the case of the polarization vector perpendicular to that of the exciting dye laser (Figure 9b). The transitions possessing J = 0 are allowed but J = 1 are forbidden in the first arrangement. In the second arrangement, transitions with J = 0 are forbidden and J = 1 are allowed. Indeed, the broad autoionizing resonance 6p^{2 1}S₀ possessing J = 0 is absent in the spectrum recorded with the polarization vectors set perpendicular to each other. Some forbidden lines also appear in the spectra, which may emerge either due to the admixture of the elliptically polarized light as the light is not 100% linearly polarized or due to the hyperfine depolarization, as reported by Wood et al. [186]. The J = 2 lines are present in both the spectra, and thus the assignment of the J values to the resonances is unambiguously assigned. As in the upper trace, the dominating lines possess J = 0; therefore, the superimposed broad feature is identified as the 6p^{2 1}S₀ autoionizing resonance, which disappears in the lower trace, in conformity with the spectra for the parallel polarization of the two lasers in the work of Lange et al. [187] and Wood et al. [186] for the photoionization from the 6s6p ¹P₁ excited state.

The line shape of the 6p^{2 1}S₀ autoionizing resonance was fitted with Fano’s relation (Fano [188]), describing the interaction of a discrete state with one continuum. The photoionization cross-section of an isolated autoionizing state is represented as:

$$\sigma (\epsilon )={\sigma }_a\frac{{(q+\epsilon )}^2}{1+{\epsilon }^2}+{\sigma }_b,$$

(18)

where $\epsilon =\frac{(E-E_r)}{\mathsf{\Gamma }/2}$ measures the departure of the incident photon energy E from the resonance energy E_r, Γ is the width of the autoionizing resonance, $\sigma (\epsilon )$ represents the absorption cross-section for photons of energy E, whereas ${\sigma }_a$ and ${\sigma }_b$ are the portions of the cross-section of the continuum that interact and do not interact with the discrete level, respectively, and q is the line profile index parameter. The fitting yields the parameters: resonance energy = 44,850.50 cm⁻¹, width 980 ± 50 cm⁻¹, q = −5.4 ± 2, and absolute value of photoionization cross-section = 185 ± 35 Mb. The interactions between the 6p^{2 1}S₀ broad feature and the 5d_5/2nd J = 0 Rydberg series were simulated using the phase-shifted multichannel quantum defect theory (MQDT), as shown by Gallagher [142], showing very interesting line shapes of the autoionizing resonances. There is clear evidence of a change in the q-values of the Rydberg series of the autoionizing resonances in the vicinity of the broad 6p^{2 1}S₀ resonance. The q-parameter describes the ratio of the transition dipole moment connecting the ground state to the discrete level and the continuum channel. The line profile is a Lorentzian shape when q is very large, and it will be asymmetric when q is small, with a minimum either below or above the resonance energy when q is either positive or negative. A window resonance appears when the value of q is very small or nearly zero.

In Figure 10a, the line profile of the 5d_3/2 8d (J = 0) autoionizing resonance is reproduced along with the Fano profile fitting of Equation (16). Due to its interaction with the 6p^{2 1}S₀ broad resonance, the line profile is asymmetric, with a minimum above the resonance energy and the q-value is −1.1. The experimentally observed and the simulated line profile of the 5d_3/2 9d (J = 0) autoionizing resonance is shown in Figure 10b. The interaction with the 6p^{2 1}S₀ broad resonance reveals an asymmetric line profile, with a minimum below the resonance energy and the extracted q-value is +1.0.

In Figure 10c, the line profile of the 5d_3/2 10d (J = 0) autoionizing resonance is reproduced. The interaction with the 6p^{2 1}S₀ broad resonance results in a window-type line profile. The Fano line profile fitting yields the value of q = 0.05.

Tolsma et al. [189] calculated the one and two-photon ionization cross-sections of the aligned 6s6p ¹P₁ state of barium in the energy range between the 5_d3/2 and 5_d5/2 states of Ba+. These photoionization spectra were also measured in the same energy region, driving the one- or two-photon processes with the second or first harmonic of a tunable dye laser, respectively. The calculations were performed using the Eigen-channel R-matrix method and multichannel quantum defect theory and calculated the autoionizing resonances in this energy range. The calculations provided an absolute normalization for the experiment, reproduced the resonance structures in both the one- and two-photon cross-sections, and confirmed other aspects of the experimental observations. Afrousheh et al. [190] investigated the spectroscopic behavior of the 5d_3/2nd (J = 0 and 2) autoionizing Rydberg series of barium under collision with rare gases using two-photon excitation of the two valence electrons in the 6s^{2 1}S₀ ground state of barium. The barium vapor was produced in a heat-pipe-like oven, and a tunable dye laser pumped by an excimer laser was used as the excitation source. The spectral behavior of the autoionizing resonances was investigated in the presence of inert gases Ar, Kr, and Xe at different pressures. The collision-induced line shifts were measured and the shift parameters for the even-parity 5d_3/2 nd (J = 0) and 5d_3/2 nd (J = 2) autoionizing states were extracted from the data.

In

Table 7. Measured values of photoionization cross-sections for the resonance and inter-combination transitions in alkaline earth atoms.

Atom	First Step (Excitation) ms2 1S0 → msnp 1P1, 3P1	Second Step (Ionization) msmp 1P1 → ms εs, εd    3P1 → ms εs, εd	Photoionization Cross-Section
Mg I	3s3p 1P1  285.213 nm           3P1  457.109 nm	375.6 nm 251.5 nm	90 ± 16 Mb
Ca I	4s4p 1P1  422.544 nm           3P1  657.278 nm	389.8 nm 293.3 nm	140 ± 20 Mb 117 ± 20 Mb
Sr I	5s5p 1P1  460.733 nm           3P1  689.259 nm	412.6 nm 318.2 nm	11.4 ± 1.8 Mb 10.7 ± 1.7 Mb
Ba I	6s6p 1P1  553.548 nm           3P1  791.133 nm	340.1 nm 417.1 nm	90 ± 14 Mb 102 ± 15 Mb

, we enlist the values of the photoionization cross-sections for the resonance lines of alkaline earth atoms.

In the next section, the autoionizing resonances in the spectra of inert gases are presented.

5. Inert Gases

Helium is the simplest atomic system, and therefore the photoionization of helium atoms is of considerable importance as it provides a prospect to evaluate different atomic models and comparison with the experimental observation. Stebbings et al. [191] determined the absolute cross-section for the photoionization of helium 1s2s ¹S and 1s2s ³S metastable atoms from the threshold to 240 nm and compared the results with the theoretical calculations. The ultraviolet radiation was generated by frequency, doubling the output of a nitrogen pumped dye laser. Subsequently, Dunning and Stebbings [192] used a molecular beam in conjunction with a tunable laser and measured the absolute cross-sections for the photoionization of helium 3p ^1,3P, 4p ^1,3P, and 5p ^1,3P atoms excited optically from the 1s2s ^1,3S metastable levels at the wavelength used for its excitation from the metastable states. Marr [193] reported the cross-section data for the photoionization of the ground-state helium atoms from threshold to 200 eV and compared it with the RPAE calculations. Domke et al. [194] (and references therein) reported an extensive study on the double-excitation resonances of helium using a synchrotron radian facility (BESSY) and measured the resonance energies, linewidths, Fano q-parameters, and quantum defects of the various Rydberg series that were compared with the theoretical calculations. Schulz et al. [195] measured the double-excitation resonance of helium at a much improved spectral resolution in the soft x-ray range. The resonance parameters of the photo doubly excited helium were determined by Rost et al. [196], who systematically analyzed the doubly excited Rydberg series in helium, taking into account the theoretical results and experimental data on photoionization cross-sections, the quantum defects, the width, the oscillator strengths, and the shape parameters of the ¹P Rydberg series. Chan et al. [197] described an alternative method for the measurement of absolute optical oscillator strengths (cross-sections) for electronic excitation of free atoms and molecules throughout the discrete region of the valence-shell spectrum at high energy resolution. The absolute scale was obtained from the Thomas–Reich–Kuhn sum-rule normalization of the Bethe–Born transformed electron-energy-loss spectrum without involving the difficult determinations of photon flux or target density. The measured dipole oscillator strengths for helium excitation 1s^{2 1}S → np ¹P (n = 2–7) were in excellent quantitative agreement with the earlier calculations. The absolute measurements were also compared with other experimental and theoretical oscillator strength determinations for photoexcitation and photoionization processes in helium up to 180 eV, including the 2snp and 3snp autoionizing resonances in the 59–72-eV energy region. Gisselbrecht et al. [198] reported the absolute photoionization cross-sections of the excited, short-lived He^* 1s2p ¹P and 1s3p ¹P states in the region close to the He⁺ 1s ²S threshold (from 0 to 2 eV). The intermediate He^{* 1,3}p states were populated by photoabsorption of a high-order harmonic of an intense picosecond tunable laser and subsequently ionized by absorption of photons of several fixed frequencies ranging from the near-infrared to the ultraviolet (752 nm, 532 nm, 355 nm, 266 nm). The results confirmed the earlier experimental theoretical work. Sahoo and Ho [199] reported the theoretical photoionization cross-sections for He 1s2s ¹S and He 1s2p ¹P states in a Debye plasma environment by the complex coordinate rotation method, using a finite L2 basis set constructed from one electron Laguerre orbitals. The plasma environment was found to appreciably influence the photoionization cross-sections near the ionization threshold. The photoionization cross-sections of helium were compared with other theoretical and experimental results, showing good agreement. A new minimum in the photoionization cross-section curve for the metastable 1s2s ¹S state was also predicted.

An alternate experimental technique to access the highly excited states of helium and autoionizing resonances in inert gases is to use a mild discharge, either a DC or RF, that populates the metastable states. One laser is used to excite the atoms from the metastable state to an intermediate upper level and a second tunable dye laser is employed to access the autoionizing states. The advantage of such an experimental arrangement is that the dye lasers working in the visible region can be used for excitation and ionization studies. The photoionization cross-sections for the excited states can also be measured using the saturation technique, as described for the case of alkali atoms and alkaline earth atoms. Figure 11a,b shows the photoionization cross-sections for the 1s3p ¹P and 1s3p ³P excited states of helium, at and near-ionization threshold region (0–0.2 Ry) measured by Hussain et al. [200]. The 1s2s ¹S metastable level was populated by running a DC glow discharge, the 1s3p ¹P level was populated by tuning the dye laser at 310.7 nm, and the 1s3p ³P level by the dye laser tuned at 388.97 nm, whereas the photoionization cross-sections were measured at different ionizing laser wavelengths: 826.4, 752, 630, 532, 501, and 355 nm for the 1s3p ¹P level and at 784.6, 752, 630, 532, 389, and 355 nm for the 1s3p ³P level. Smooth frequency dependence of the cross-section was observed for both the excited states following the theoretical calculations. The measured values of the photoionization cross-sections are in close agreement with the reported theoretical values by Jacobs [201] and experimental values by Gisselbrecht et al. [198] and Dunning and Stebbings [192].

The oscillator strength distribution in the discrete and continuous regions of the spectrum of helium from the 2s ¹S₀ metastable using a low-pressure RF glow discharge was measured by Hussain et al. [130]. The measured value of the photoionization cross-section for the 2s ¹S₀ excited state at the first ionization threshold was used to determine the f values for the 2s ¹S₀ → np ¹P₁ Rydberg series from n = 10 to n = 52. The f values of the Rydberg series decrease smoothly with an increase of the principal quantum number. In the continuum region, the oscillator strength densities were determined by measuring the photoionization cross-sections from the 2s ¹S₀ excited state at five ionizing laser wavelengths above the first ionization threshold. The discrete f values smoothly merge into the continuous oscillator strength densities across the ionization threshold.

The ionization potentials of inert gases are much higher than that of the alkali atoms or alkaline earth atoms, and therefore one needs a vacuum-ultraviolet radiation source to observe the Rydberg series and the ionization continuum. The ground state configuration of the inert gases is a filled p-subshell and the ionization of an outer p-electron from the ground state yields two ionic levels; p⁵ (²P_3/2 and ²P_1/2). The p⁵(²P_1/2) ns, nd Rydberg levels lying above the first ionization threshold (²P_3/2) are degenerated with the p⁵ εℓ continuum above the (²P_3/2) ionization threshold, and consequently the line shapes are broad and asymmetric due to autoionization, due to the interaction of the discrete levels with the adjacent continuum, as shown by Fano [188]. The autoionizing resonance in Ar, Kr, and Xe from the ground state has been studied by Yoshino [41,42,43], who used conventional light sources, and by synchrotron radiation (Maden and Codling [202], Baig and Connerade [45], and Ueda [203,204]).

The photoionization cross-sections and photoelectron angular distribution parameters across the 4p⁵(²P_1/2) ns’, and nd’ autoionization resonances in Ar, Kr, and Xe were reported by Wu et al. [205], and subsequently, Maeda et al. [206] measured their photoabsorption cross-sections in the autoionization regions. Using the ionization of inert gases from the ground state, only the J = 1 upper levels are accessible via single-photon excitation. The higher angular momentum states can be approached either via multi-photon excitation, as shown by Pratt et al. [207], Koeckhoven et al. [208,209], and Blazewicz et al. [210], or by multi-step excitation from the ground state (Rundel et al. [39], Grandin and Husson [211], Wada et al. [212], Wang and Knight [213], King and Latimer [214], Harth et al. [215], and Klar et al. [216]). Alternatively, the mp⁵(m+1)s [1/2]₀ and [3/2]₂ metastable states can be populated by running a discharge enabling one to approach the ℓ = 0, 2 excited states via two-photon excitation (Knight and Wang [217], L’Huillier et al. [218], Piracha et al. [85,219], and Ahmed et al. [220,221]).

A schematic diagram for the two-step excitation and ionization for the argon atom is shown in Figure 12.

The excited states are represented in the j_cK-coupling scheme (Racah [222], Cowan [1]) as nℓ [K]_J, where ℓ is the orbital angular momentum of the excited electron and K is the vector sum of the orbital angular momentum of the excited electron and the angular momentum of the core electrons. The total angular momentum J is the vector sum of K and the spin quantum number of the excited electron. The prime refers to the terms associated with the 4p⁵(²P_1/2) ionic state. According to the electric dipole selection rules in the jK-coupling scheme: Δj = 0, ΔK = 0, ±1 and ΔJ = 0, ±1, the Rydberg series can be studied. Since the first excited states of all the inert gages lie more than 10 eV above the ground state, a radiation source emitting in the VUV region is therefore required to access these states. However, the metastable state can be populated by running a mild discharge, either in a DC or RF environment. The excitation of an electron from the 3p sub-shell yields four levels: 3p⁵4s [3/2]_2, 3p⁵4s [3/2]₁, 3p⁵4s’ [1/2]₀, 3p⁵4s’ [1/2]₁. The 4s [3/2]₂, and 4s’ [1/2]₀ are the metastable states while the 4s [3/2]₁ and 4s’ [l/2]₁ states are short-lived and combine instantly with the ground state. The 3p⁵(²P_3/2) and 3p⁵(²P_1/2) are the parent ion levels that combine with the added electron and yield the Rydberg series converging to two ionization limits. Dunning and Stebbings [192] used a molecular beam apparatus in conjunction with a pulsed tunable UV laser to study the photoionization of argon and krypton in the wavelength range 325–269 nm and reported the p⁵(²P_1/2) nf and np levels, which autotomize into the underlying ²P_3/2 continuum. Gornik et al. [223] reported the 5p⁵ 5d [K = 5/2]_{J = 3} and 5p⁵ 5d [K = 1/2]_{J = 3} atomic states of xenon excited by two-photon absorption from the ground state. Wu et al. [205] reported the photoionization cross-sections and photoelectron angular distribution parameters across the autoionizing resonances for Ar, Kr, and Xe using the synchrotron radiation-based photoelectron spectroscopy. Samson and Stolte [224] reported the absolute photoionization cross-sections for neon, argon, krypton, and xenon from threshold to 125 eV with an accuracy of 61 to 3% in both tabular and graphical form. These data were compared with the optical oscillator strength measurements of Bonin et al. [44], who used the Dipole (e, e) collision technique. The autoionizing resonances in Ar, Kr, and Xe were also studied via three-photon excitation from the ground state by Prat et al. [207] and Koechhoven et al. [208], who reported the p⁵(²P_3/2) ns [1/2]₁, nd [3/2]₁, nd [5/2]₃, and ng [7/2]₃ levels. Subsequently, Koechhoven et al. [209] reported the p⁵(²P_3/2) np [1/2]₀, np [3/2]₂, nf [5/2]₂, and nf [7/2]₄ autoionizing resonances in inert gases using four-photon excitation from the ground state. The spectra of argon, krypton, and xenon in the autoionization region using a two-step resonant laser excitation and Optogalvanic detection technique were reported by Baig et al. [225]. By selecting (m)p⁵ (m + 1)p [3/2]₂ as an intermediate state (m = 4, 5, and 6 for Ar, Kr, and Xe, respectively), the (m)p⁵ nd [5/2]₃ autoionizing resonances were studied. The Multichannel Quantum Defect Theory (MQDT) parameters were derived from the analysis of the series perturbations among the (m)p⁵ nd [5/2]₃, (m)p⁵ nd [7/2]_3, and (m)p⁵ nd [5/2]₃ series in the discrete region using the phase-shifted formulation of the three-channel quantum defect theory Gallagher [142] and from the line profile analysis of the autoionizing resonances above the first ionization threshold. The predicted reduced widths for the autoionizing resonances based on the series perturbation analysis showed good agreement with those of the experimentally observed profiles.

The 2p⁵(²P_1/2) np [J = 0, 1, 2] and 2p⁵(²P_1/2) nf [J = 2] autoionizing Rydberg states of Ne by two-step two-color photoionization of ground-state neon atoms via the intermediate states 2p⁵ (²P_3/2)3s J = 1 and 2p⁵(²P_1/2)3s J = 1, followed by time-of-flight ion detection and strong interference between the direct and virtual intershell photoexcitation channels in autoionizing resonances production, especially for the np J = 0 series, were reported by Petrov et al. [226]. The reduced width Γr = 6431 cm⁻¹ and the quantum defect µ_p = 0.7634 of the 2p⁵ _1/2 13p J = 0 resonance were found to be in good agreement with the experimental results Γ = 5334 cm⁻¹ and µp = 0.7662 determined with a Fano-type line shape analysis. The even parity mp⁵(²P_1/2) np’ and mp⁵ (²P_1/2) nf’ autoionizing resonances of Ar, Kr, and Xe (m = 3, 4, 5) were studied experimentally and theoretically by Petrov et al. [227] by one-photon excitation from the lower-lying intermediate levels. The high-resolution measurements for the Ar(nf), Kr(12p, 8f), and Xe(8p) resonances were reported and the line shape parameters for these resonances were derived by a Fano-type analysis. The experimental spectra and the resonance parameters were compared with theoretical calculations, which were based on the configuration interaction Pauli–Fock approach, including core polarization.

The oscillator strengths of the 2p⁵ (²P_1/2) nd’ J = 2, 3 autoionizing resonances in neon were studied by Mahmood et al. [228] using a DC discharge, multistep laser excitation/ionization, and Optogalvanic detection technique. The excited states were approached using two-step laser excitation via 2p⁵ 3p’ [1/2]₁, 2p⁵ 3p’ [3/2]₁, and 2p⁵ 3p’ [3/2]₂ intermediate levels, which were accessed from the 2p⁵ 3s [1/2]₂ metastable level. The f-values were determined for the nd’ [3/2]₂, nd’ [5/2]_2, and nd’ [5/2]₃ series following the K = J = +1 selection rules. The photoionization cross-section at the 2p^{5 2}P_1/2 ionization threshold was determined as 5.5(6) Mb. Claessens et al. [229] reported the photoionization-cross-section for the 2p⁵3p ³D₃ state of neon at the wavelengths of 351 and 364 nm by monitoring the decay of the fluorescence of atoms trapped in a magneto-optical atom trap under the presence of a photo-ionizing laser. The absolute photoionization cross-sections were obtained as (2.05 ± 0.25) × 10⁻¹⁸ cm² at 351 nm and (2.15 ± 0.25) × 10⁻¹⁸ cm² at 364 nm ionizing laser wavelength. The photoionization of excited (2p⁵ 3p, J = 3) atoms over the photoelectron energy range 0–2.5 eV was calculated by Petrov et al. [69] using the configuration interaction Pauli–Fock with a core polarization method. Subsequently, Petrov et al. [230] calculated the photoionization cross-sections for Ne atoms in the excited 2p⁵3p [K]J (J = 0 − 3) levels at near-threshold energies within the configuration interaction Pauli–Fock approach, including core polarization. The computed spectra and the line shape parameters of the odd parity 2P⁵ (²P_1/2) ns and nd autoionizing resonances were in good agreement with high-resolution laser spectroscopic results. In addition, the absolute partial photoionization cross-sections for the ²P_3/2 and ²P_1/2 channels at photoelectron energies up to 7 eV were determined. Except for the highest lying 2p1(¹S₀) level, these cross-sections monotonically decrease with energy (as reported earlier in single-electron calculations for the Ne(2p⁵3p) configuration) with branching ratios that essentially reflect the core compositions of the 2px levels. For the 2p1 level, the resonance structure and the partial cross-sections were reported to be strongly influenced by a Cooper–Seaton minimum in the d_3/2 channel, located just above the ²P_1/2 ionization limit. Mahmood et al. [231] reported the photoionization cross-section from three intermediate levels 2p⁵ 3p’ [1/2]₁, 2p⁵ 3p’ [3/2]₂ and 2p⁵ 3p’ [5/2]₃ of neon up to the 2p^{5 2}P_1/2 ionization threshold using the optogalvanic technique. Baig et al. [232] measured the excitation spectra from the 2p⁵3p [5/2]_3,2 levels in neon using two-step laser excitation and ionization in conjunction with an optogalvanic detection in DC and RF discharge cells. The 2p⁵3p [5/2]_3,2 intermediate levels were approached via the collisionally populated 2p⁵3s [3/2]₂ metastable levels. The Rydberg series 2p⁵(²P_3/2)nd [7/2]₄, 2p⁵(²P_3/2)ns and the parity forbidden transitions 2p⁵(²P_3/2)np [5/2]₃ were observed from the 2p⁵3p [5/2]₃ level, whereas the 2p⁵(²P_3/2)nd [7/2]₃, 2p⁵(²P_3/2)ns [3/2]₂, and 2p⁵(²P_1/2)nd [5/2]₃ series were observed from the 2p⁵3p [5/2]₂ level in accordance with the J = K = ± 1 selection rules. The photoionization cross-sections from the 2p⁵3p’ [5/2]₃ intermediate levels were measured at eight ionizing laser wavelengths (399, 395, 390, 385, 380, 370, 364, and 355 nm), which is in good agreement with that reported by Petrov et al. (2008) and that from the 2p⁵3p’ [5/2]₂ level at 401.8 nm

In a high-resolution study of odd argon (²P_3/2 ns, nd, J = 2, 3), Rydberg states using transverse resonant two-photon CW laser excitation of metastable (4s ³P₂) atoms in a collimated beam via the (4p ³D₃) level was performed by Weber et al. [233]. The perturbations in the spectra associated with the (²P_1/2 8d₀, 9d₀, J = 2, 3) levels and widths of the low-lying (nd₀, J = 2, 3) autoionization resonances were determined. The multichannel quantum defect theory (MQDT) analysis of the measured bound Rydberg levels yielded reliable Eigen-channel quantum defect parameters to describe the odd J = 2 and 3 spectra of Ar in the bound as well as in the autoionization region. Using a mild DC discharge system coupled with a multistep laser excitation and ionization scheme and optogalvanic detection, Aslam et al. [234] studied the 3p⁵nd [3/2]₂ and nd [5/2]_2,3 Rydberg series, converging to the 3p⁵(²P_3/2) and (²P_1/2) limits, excited from the 3p⁵4p’ [l/2]₁, 3p^s4p’ [3/2]₁, and 3p⁵4p’ [3/2]₂, and the intermediate levels that were populated from the 3p^s4s [3/2]₂ metastable levels of argon. Three perturbers, 3p⁵(²P_1/2)8d’ [3/2]₂, 3p⁵(²P_1/2)8d’ [5/2]_2, and 3p⁵(²P_1/2)8d’ [5/2]₃, were identified, as reported earlier by Weber et al. [233], and their interaction with the 3p⁵(²P_3/2) nd J = 2, 3 Rydberg series were studied using the multichannel quantum defect theory (MQDT). The parameters obtained by fitting the lines shapes of the corresponding autoionizing resonances adjacent to the first ionization threshold 3p⁵(²P_1/2)9d [3/2]₂, 3p(²P_1/2) 9d [5/2]_2, and 3p(²P_1/2) 9d [5/2]₃ show good correlation with those determined from the MQDT analysis in the discrete region. Qian et al. [235] studied the ionization spectrum of Ar in the energy region between the ionization thresholds for Ar⁺ (²P_3/2) and Ar⁺ (²P_1/2) using VUV synchrotron radiation and high-repetition-rate IR optical parametric oscillator (OPO) laser source.

The photoionization cross-section for the 3p⁵4p’ [3/2]₁, 3p⁵4p’ [3/2]₂, and [1/2]₁ intermediate levels were measured by Baig et al. [236] at the 3p^{5 2}P_1/2 ionization threshold as 34 ± 5, 31 ± 5, and 28 ± 4 Mb, respectively. The absolute values of the cross-section at the 3p^{5 2}P_1/2 threshold were used to determine the f-values for the 4p’ [3/2]₁ → nd [5/2], 4p’ [3/2]₂ → nd [5/2]₃, and 4p’ [1/2]₁ → nd [3/2]₂ Rydberg transitions. In Figure 13, we reproduce the 3p⁵(²P_1/2)nd [5/2]₃ Rydberg series due to excitation from the 3p⁵4p’ [3/2]₂ intermediate level showing the linear behavior of the optogalvanic detector, as the intensities of the higher members of the series decreases nearly to (1/n³) and the calibration of the f-values was straight forward. In

Table 8. Line profile analysis of the autoionizing resonances in Ar, Kr, and Xe.

Atom	Resonance	Er (cm−1)	Γ (cm−1)	q	ν1/2	${\mathsf{\Gamma }}_{\mathit{r}}=\left(\mathsf{\Gamma }{\mathit{\nu }}_{1/2}^3\right)$
Ar	9d′ [5/2]2	127 075 (1)	8 (1)	−30 (5)	8.651 (2)	5180
	9d′ [5/2]3	127 090 (1)	9 (2)	−30 (5)	8.695 (2)	5915
Kr	6d′ [5/2]2	113 205 (3)	45 (5)	−35 (5)	4.648 (2)	4520
	6d′ [5/2]3	113 285 (3)	50 (5)	−30 (5)	4.685 (2)	5140
Xe	7d′ [5/2]2	103 008 (3)	40 (8)	−20 (5)	4.524 (2)	3700
	7d′ [5/2]3	103 110 (3)	55 (8)	−20 (5)	4.567 (2)	5240

, we enlist the results of the line profile analysis of the leading autoionizing resonances in Ar, Kr, and Xe, revealing the resonance energies, widths, line profile parameters, effective quantum number, and reduced widths.

Wright et al. [237] reported an experimental and theoretical study of the photoionization of even parity autoionizing Rydberg series of argon. The 4s’ [1/2]₀ and 4s [3/2]₂ metastable states were used to access the even-parity autoionizing resonances between the first and second ionization limits and the widths and energies of the overlapping resonances data were determined by fitting to a sum of Fano-type or Shore-type profiles. A combination of synchrotron radiation and lasers was exploited by Lee et al. [238], who used synchrotron radiation to excite the 3p⁵(²P_1/2) {3d’ [3/2]₁, 5d’ [3/2]₁, 5s’ [3/2]₁, 5s’ [1/2]₁, 7s’ [1/2]₁}, and 3p⁵(²P_3/2) {6d [1/2]₁, 6d [3/2]₁, and 8s [3/2]₁} intermediate levels and then the autoionizing Rydberg series 3p⁵(²P_1/2)np’{ [1/2]₀,₁, [3/2]_1,2, and nf’ [5/2]₂}) were excited using lasers. The spectral line shapes of the autoionizing resonances were analyzed with Beuler–Fano profiles. Petrov et al. [70] (reported the 3p⁵_1/2 np J = 0, 1, 2 and 3p⁵_1/2nf J = 2 autoionizing Rydberg states of Ar by two-step two-color photoionization of ground-state argon atoms via the intermediate levels 3p⁵_1/24s [1/2]₁, 3p⁵_3/25s [3/2]₁, and 3p⁵_3/23d [1/2]₁, followed by time-of-flight ion detection. Accurate energy positions and widths were determined for the 15p [1/2]₀, 15p [3/2]_2, and 13f [5/2]₂ resonances. The measured spectra and earlier results obtained for the intermediate levels 5s [1/2]₁,7s [1/2]₁, and 8s [3/2]₁ were compared with absolute cross-sections and calculated with the configuration interaction Pauli–Fock core-polarization method.

The pioneering work on the absorption spectrum of krypton was reported by Beutler [239] in which the 4p⁵ ns and 4p⁵ nd odd-parity J = 1 states were observed. Yoshino and Tanaka [42] extended these studies by observing the 4p⁵ nd series up to a much higher principal quantum number and extracting the value of the first ionization potential of krypton. Klar et al. [240] used two-step laser excitation of metastable Kr (4p⁵5s ³P_0,2) atoms via selected Kr (4p⁵5s J = 1, 2) levels, and recorded the low-lying autoionizing resonances Kr(²P_1/2 nd, J = 2, 3) (n = 6, 7) at high resolution in two different experiments (atomic beam spectroscopy and opt-galvanic spectroscopy in a discharge). Accurate values for the resonance positions (quantum defects) and the (reduced) widths were determined, and the profile indices were reported. For comparison, multichannel quantum defect theory (MQDT) analyses, using energy-dependent MQDT parameters, were carried out for the odd Kr (J = 1, 2, 3) levels, yielding good agreement in the quantum defects and partial agreement in the predicted reduced widths for the nd resonances with the experimental values. Moreover, the simplified phase-shifted quantum defect theory analyses of the measured bound odd Kr (J = 2 and 3) Rydberg levels were carried out to provide improved insight into the dominant decay mechanism of the resonances. A summary and comparative discussion of the reduced widths for the nd [K]J resonances of all the rare-gas atoms Ne, Ar, Kr, and Xe was also presented. The odd-parity autoionizing resonances in krypton 4p⁵ns [1/2]_0,1, 4p⁵nd [3/2]₂, and 4p⁵nd [5/2]_2,3 excited from three intermediate levels 4p⁵ 5p’ [1/2]₁, 4p⁵ 5p’ [3/2]₁, and 4p⁵ 5p’ [3/2]₂ were studied by Baig et al. [241] using resonant two-photon excitation from the 4p⁵ 5s [3/2]₂ metastable level in a mild DC discharge and an optogalvanic detection technique.

To demonstrate the utility of the selected polarization vectors of the first and second laser, the autoionizing resonance for n = 8 in krypton, 4p⁵8d’ [3/2]₂, 4p⁵8d’ [5/2]₂, and 4p⁵8d’ [5/2]₃ excited from the 4p⁵5p’ [1/2]_1, 4p⁵5p’ [3/2]_1, and 4p⁵5p’ [3/2]₂ intermediate levels using both the lasers linearly polarized were studied. Within the framework of the transitions selection rules, only the 5p⁵8d’ [3/2]₂ transitions are allowed from the 4p⁵5p’ [1/2]₁ intermediate level and the line profile is shown in Figure 14a. The 5p⁵8d’ [5/2]₂ is only accessible from the 4p⁵5p’ [3/2]₁ intermediate level and, indeed, an isolated resonance was observed, as shown in Figure 14b. However, both the 4p⁵8d’ [5/2]₂ and 4p⁵8d’ [5/2]₃ states are allowed from the 4p⁵5p’ [3/2]₂ intermediate level, but 4p⁵8d’ [5/2]₃ dominates in intensity. The line profiles are shown in Figure 14c. Since both the resonances possess different J-values, they are non-interacting, and therefore the individual profiles were fitted and the sum of the two profiles yields the full curve. The fitted Fano profile for the 4p⁵8d’ [5/2]₂ resonance is with q-parameter = −90, Γ = 14 cm⁻¹ and E_r = 115,792.5 cm⁻¹ and that of 4p⁵8d’ [5/2]₃ is q-parameter = −50, Γ = 17 cm⁻¹ and E_r = 115,819 cm⁻¹. The even parity autoionizing resonances in krypton were studied by Li et al. [242] from the metastable states 4p⁵5s [3/2]₂ and 4p⁵5s’ [1/2]₀ using a pulsed DC discharge and subsequent single-photon excitations to the 4p⁵np’ [3/2]_1,2, [1/2]₁ and 4p⁵nf’ [5/2]₃ Rydberg states.

The work on the Rydberg states in Xe below the 5p^{5 2}P_3/2 or 5p^{5 2}P_1/2 thresholds accessed from the Xe 5p^{6 1}S₀ ground state includes one-photon excitation of the odd parity ns J = 1 and nd J = 1 states and multiphoton excitation of odd or even Rydberg states by non-resonant or resonant multiphoton excitation. In addition, single-photon or resonant or non-resonant two-photon excitation from the metastable levels of Xe has been exploited to study even and odd Rydberg states. Using two different experimental set-ups involving optogalvanic spectroscopy and atomic beam spectroscopy with mass spectrometric ion detection, respectively, Hanif et al. [243] reported the 5p^{5 2}P_1/2 nd [K = 3/2]J = 2 and [K = 5/2]J = 2,3 autoionizing resonances of xenon by means of two-step resonant laser excitation from the metastable Xe (J = 2, 0) levels. By selecting a particular intermediate level, 6p [1/2]₁ and 6p [3/2]_1,2, autoionizing resonances with specified K and J values were addressed. Level energies and resonance widths were derived by a Beutler–Fano-type line shape analysis. Extended calculations for the Xe (ns J = 0, 1), Xe (nd J = 1, 2, 3), and Xe (ng J = 3) autoionizing resonances were also performed based on the Pauli–Fock approach and include core polarization and electron correlation effects at a high level. Alois et al. [244] studied the photoionization of short-lived Rydberg states in Xe using resonant atomic excitation by synchrotron radiation and subsequent ionization by a tunable dye laser. By combining circular and linear polarization of the synchrotron as well as of the laser photons, the partial photoionization cross-sections were separated in the region of overlapping autoionizing resonances of different symmetry and the parameters of the resonances were extracted. Hanif et al. [243] observed the even parity autoionizing resonances built on the 5p⁵ 7p and 5p⁵ 4f configurations in xenon using the laser optogalvanic detection technique in conjunction with a DC discharge cell. The autoionizing resonances 5p⁵ 7p [1/2]₁ and 5p⁵ 7p [3/2]₁ excited from the 5p⁵ 6s [1/2]₀ metastable level and the 5p⁵ 7p [3/2]₂ resonance excited from the 5p⁵ 6s [1/2]₁ level were studied. In addition, the 5p⁵(²P_1/2)nf (n = 4 and 5) autoionizing resonances excited from the collisionally populated levels of the 5p⁵5d configuration were investigated. The resonance energies, quantum defects, line-shape parameters, and resonance widths were determined by fitting the observed resonance profiles to Fano’s formula for the photoionization cross-section. Petrov et al. [245] studied the near-threshold photoionization from the excited states of p⁵p (J = 0–3) levels of Ar, Kr, and Xe. The absolute total and partial cross-sections for photoionization of excited mp⁵(m+1)p J = 0–3 levels in Ar, Kr, and Xe (m = 3–5) near the threshold was calculated using the configuration interaction Pauli–Fock, including the core polarization (CIPFCP) approach. The line shapes of the mp⁵ (²P_1/2) ns and nd autoionizing resonances and their variation with the character of the intermediate excited J = 0–3 state were also studied. Sukhorokov et al. [53] presented a review of the experimental and theoretical studies of the threshold photoionization of the heavier rare-gas atoms with particular emphasis on the autoionizing resonances in the spectral region between the lowest two ionization thresholds ²P_3/2 and ²P_1/2, accessed from the ground or excited states. The observed trends in the positions, widths, and shapes of the autoionizing resonances depending on the atomic number, the principal quantum number n, the orbital angular momentum quantum number, and further quantum numbers specifying the fine- and hyperfine-structure levels were summarized and supplemented with the ab initio and multichannel quantum defect theory calculations. Besides, the effects of various approximations in the theoretical treatment of photoionization in these systems were analyzed. The studies on the measurements of the photoionization cross sections for the excited states of atoms, molecules, and ions are still very actively being carried out at different synchrotron radiation facilities, and new data are being provided to compare with the theoretical models.

The ionization dynamic of atoms exposed to high power lasers, (intensities of 10²⁰ W/cm², short pulse duration of 10 fs, and high repetition rates) has been extensively studied, as the presence of strong laser fields that drastically alters the nature of atomic systems. The interaction of laser field with atoms in the regime from multiphoton to tunneling ionization has been comprehensively studied by several groups that are summarized in a review by DiMauro et al. [246]. Yamakawa et al. [247] exposed Xe atoms to an IR laser (800 nm laser wavelength, 20 fs pulse duration) having an intensity range of 10¹³–10¹⁸ W/cm² and observed the ion yields of Xe⁺–Xe²⁰⁺ as a function of laser intensity. The experimental data were compared with the results from a single active electron-based Ammosov–Delone–Krainov model. A double laser-plasma technique was used by Lu et al. [248] to measure the photoabsorption spectrum of Bi⁺ covering the wavelength range from 37 and 60 nm. One laser was used to produce the vacuum ultraviolet continuum radiation and the second laser-produced plasma was used as the sample of atoms to be probed. The observed structure was identified due to 5d–6p transitions with the help of the Cowan suit to the atomic codes. The synchrotron radiation (SR) facilities have been extensively used to study the photoionization from the ground state of the atoms. A combination of synchrotron radiation with a tunable laser further enhanced the capabilities to study the photoionization from the excited states. Aloise et al. [244] used the resonant atomic excitation by synchrotron radiation and subsequent ionization by a tunable dye laser to study the photoionization of short-lived Rydberg states. The 5d (J = 1) level of xenon at 10.401 eV and 7s (J = 1) at 10.562 eV were excited from the ground state with SR. The 4f’ (J = 2) autoionizing resonance from the 5d J = 1 and the 8p’ J = 0, 1, 2 autoionizing resonances from the 7s J = 1 level were investigated. By combining the circular and linear polarization of the synchrotron radiation as well as the laser photons, the partial photoionization cross-sections were measured.

The advent of powerful soft X-ray sources based on storage rings with insertion devices, free-electron laser (FEL), and high-harmonic generation techniques, has opened up new avenues for the photoionization studies of small quantum systems. The first FEL facility (FLASH) was developed at DESY, Germany, in 2005, which provides ultra-short pulses at high fundamental photon energies (13–48 nm) with high peak and average power. For the pump-probe experiments, an optical laser facility was also set up, which provides femtosecond infrared (110 fs, 800 nm) and picosecond visible (12 ps, 532 nm) pulses, electronically synchronized with the FEL (pulse duration 19–50 fs) pulses. Mayer et al. [249] measured the two-photon ionization of atomic helium by combining the femtosecond extreme ultraviolet pulses from the free-electron laser (FLASH) with the intense light pulses from a synchronized neodymium-doped yttrium lithium fluoride laser. The two-photon ionization measurements were in good agreement with the theoretical predictions. Sorokin et al. [250] studied the multiphoton ionization of neon and helium by the ion mass-to-charge spectroscopy using a focused beam at 42.8 nm, 38.4 eV photon energy, and irradiance of up to 10¹⁴ W/cm² and observed direct, sequential, and resonant two-, three-, and four-photon excitations as a function of absolute photon intensity. It was inferred that the atomic and ionic photoionization cross-sections are dominantly due to sequential excitation as compared to direct multiphoton processes. Martins et al. [251] studied the multiphoton ionization of neon atoms using the PG0 branch of the FLASH monochromator beamline to observe the Ne⁺ 2p → nℓ resonances in the energy region 41 and 42 eV. Richter et al. [252] studied the photoionization of different rare gases acquired at FLASH by applying ion spectroscopy at the wavelength of 13.7 nm and irradiance levels of thousands of terawatts per square centimeter. The degree of nonlinear photoionization was found to be significantly higher than for neon, argon, and krypton. The collective giant 4d resonance of Xe may be responsible for this effect, which arises in this spectral range. Schippers et al. [55] presented the use of X-rays from a synchrotron radiation source and the photo-ion merged-beams technique to study the photoionization of mass/charge selected ionized atoms, molecules, and clusters. Examples for photoionization of atomic ions were discussed by going from the outer shell ionization of simple few-electron systems to the inner-shell ionization of complex electron ions. The unique capabilities of the photon-ion merged-beams technique for the study of photoabsorption by nanoparticles were demonstrated by the examples of endohedral fullerene ion. Young et al. [56] reported a roadmap of ultrafast X-ray atomic and molecular physics, highlighting the contributions into four categories: ultrafast molecular dynamics, multidimensional x-ray spectroscopies, high-intensity x-ray phenomena, and attosecond x-ray science. The development of X-ray free-electron lasers (XFELs) and table-top sources of x-rays based upon high harmonic generation (HHG) have revolutionized the field of ultrafast x-ray atomic and molecular physics. XFELs provide very intensity (10²⁰ W cm⁻²) of X-rays at wavelengths down to ∼10 nm, and HHG provides high time resolution (∼10⁻¹⁸ s) and a large coherent bandwidth at longer wavelengths. Thus, one can focus on individual atoms and view electronic and nuclear motion on their intrinsic scales using these X-ray sources. The XFEL (European XFEL, Swiss-FEL, and PAL-FEL in Korea) has opened new fields of multiphoton and nonlinear X-ray physics, where the behavior of matter under extreme conditions can be explored. The time resolution and pulse synchronization provided by HHG sources are used to study the time delays in photoionization, and charge migration in molecules. At the 60th anniversary of the ICPEAC conference celebrations, three roadmaps on photonic, electronic, and atomic collision physics were published. Ueda et al. [57] presented Roadmap I, in which the focus was on light-matter interaction. With the advent of new light sources, such as X-ray free-electron lasers and attosecond lasers, studies of ultrafast electronic and molecular dynamics are rapidly growing. Besides, experiments with the established synchrotron radiation sources and femtosecond lasers using state-of-the-art detection systems are enlightening new scientific areas that have never before been explored. The photon-target experiments are growing from atoms and small molecules to complex systems such as biomolecules, fullerene, clusters, and solids. This roadmap contains several exciting contributions by experts in the fields, such as photoionization of ions, photo-double ionization of atoms and molecules, molecular-frame photoelectron angular distributions from static to time-resolved, and photo-induced reaction dynamics probed by COLTRIMS.

A review of the recent work on the photoionization of atomic ions of astrophysical interest was presented by Schippers and Muller [58] based on the experimental work performed at the photon-ion merged-beam setup PIPE, installed at the XUV beamline of PETRA III synchrotron radiation source operated by DESY, Hamburg, Germany. Results on single and multiple L-shell photoionizations of Fe⁺, Fe²⁺, and Fe³⁺ ions, and single and multiple K-shell photoionizations of C⁻, C⁺, C⁴⁺, Ne^+, and Si²⁺ ions were discussed in an astrophysical context. Interestingly, it was inferred that the results of the photon-ion merged-beams method at the world’s brightest synchrotron radiation light source has led to a breakthrough in the experimental study of atomic inner-shell photoionization processes with ions. Katravulapally et al. [253] studied the photoionization of lithium-ion via its double-excited states 2s2p ¹P using a free-electron laser (FEL) radiation and also calculated the ionization yield using the perturbative statistical description of the atomic dynamics. It was inferred that the FEL temporal fluctuations affect the line shape, and is strongly dependent on intensity and pulse’s coherence time. A further increase in intensity enhances the Li²⁺ ionization, causing further distortion in the line shape of Li⁺. The two-photon ionization cross sections and asymmetry parameters within the independent-particle approximation and relativistic second-order perturbation theory were calculated by Hofbrucker et al. [254]. The dependence of the asymmetry parameters on the polarization and energy of the incident radiation as well as on the angular momentum properties of the ionized electrons were studied. These studies have also been expanded for measuring the photoionization cross-section of the simplest enol and vinyl alcohol, as shown by Rosch [255], who employed multiplexed photoionization mass spectrometry at 308 nm and reported the cross-sections 7.5 ± 1.9 Mb and 10.005 eV and 8.1 ± 1.9 Mb at 10.205 eV. There are several papers addressing the photoionization cross sections for the excited states of atoms published every year, and this field of research is still very active.

6. Conclusions

The photoionization cross-sections for the excited states of alkali atoms, alkaline earth atoms, and inert gases have been presented as studied by several researchers. It is observed that, by in large, the measured photoionization cross-sections by different groups are in reasonable agreement and also agree with the theoretical calculations. The situation in the alkali atoms is very satisfactory, as the issue of normalization that was persistent in the early measurements has been overcome by employing many advanced experimental techniques such as multi-step laser excitation, the saturation technique, and the technique of ion trapping and cooling to monitor the intensity variations. Three experimental techniques are commonly used; thermionic diode-ion detector, the optogalvanic detection-based system, and atomic beam apparatus coupled with a time-of-flight mass spectrometer. The measurement using a thermionic diode ion detector has to be done very carefully as it is prone to suffer from the linearity of the detection system and accurate determination of the interaction area. However, with careful alignment and proper adjustment of the exciting and ionizing laser beams, reliable measurements can be performed. The situation in the optogalvanic-based detection system is relatively better, as the interaction area is very small and can easily be determined at the crossing point of the exciting and the ionizing laser beams in a discharge. The preferable experimental setup is an atomic beam apparatus coupled with a time-of-flight mass spectrometer, as the interaction area is well defined at the intersection of the atomic beam and the exciting and ionizing laser beams. The TOF mass spectrometer has the advantage over the thermionic diode and the atomic beam apparatus, as it enables simultaneous measurement of different spectroscopic properties of the selected isotopic masses. It also ensures that the emergence of the photoion signal is purely due to the isotope of interest. Further, it is possible to study the singly, doubly, triply, etc., photoionization states of atoms. The measurements of the photoionization cross-sections for different excited states of the two isotopes of lithium and three isotopes of magnesium have demonstrated the advantage of this experimental setup. There have been extensive calculations on the highly ionized atomic systems, whereas experimental data are available on the photoionization from the excited states of atoms and molecules. With the availability of intense VUV/soft X-ray radiation sources such as storage rings along with insertion devices and free-electron lasers, the field of measuring the photoionization cross-section from the excited states of atoms, molecules, and ions using improved experimental techniques and supplemented by the more advanced theoretical calculations will remain an active area of research in the coming years.