Influence of Alfvén Ion–Cyclotron Waves on the Anisotropy of Solar Wind Turbulence at Ion Kinetic Scales
Abstract
1. Introduction
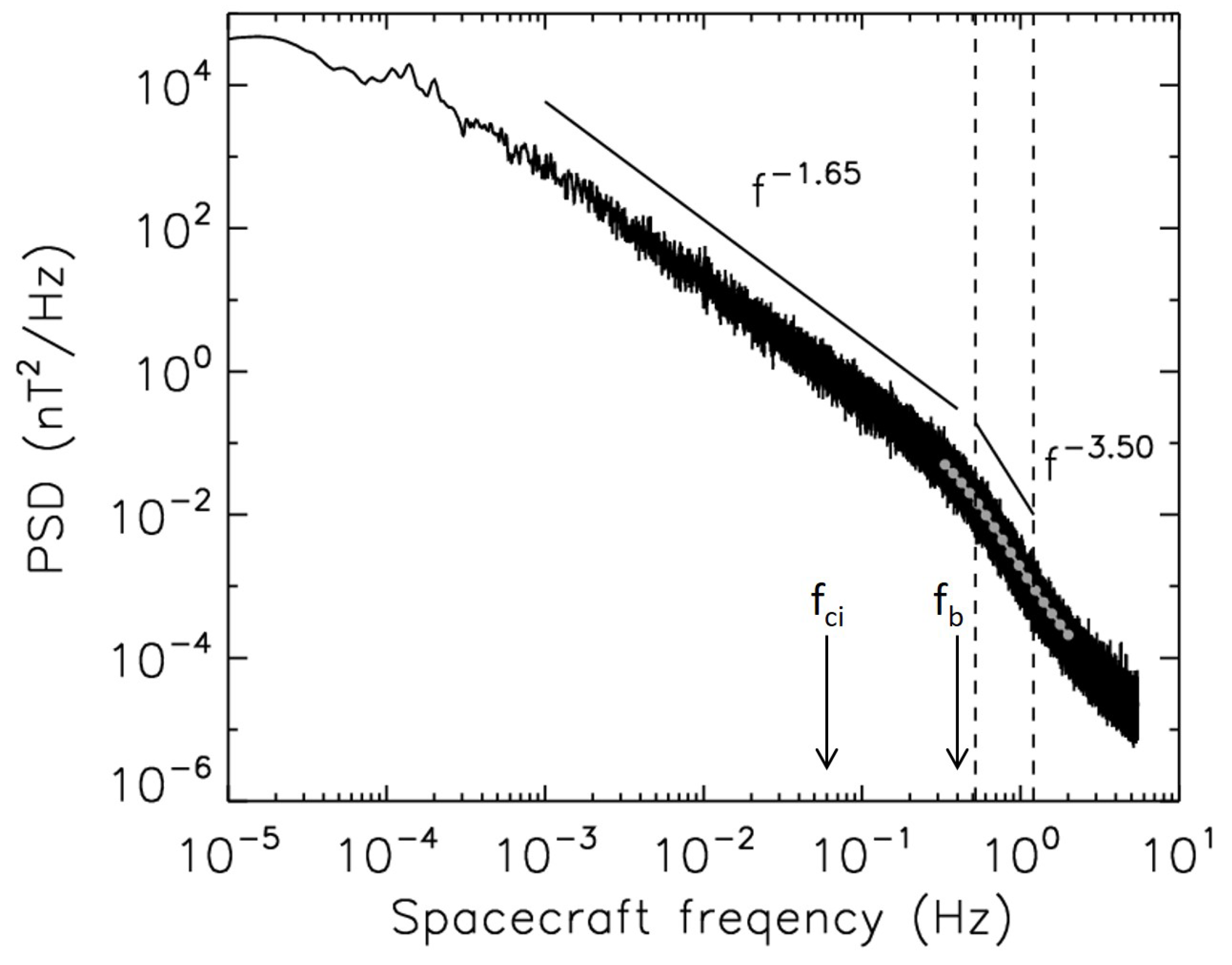
2. Data and Methods
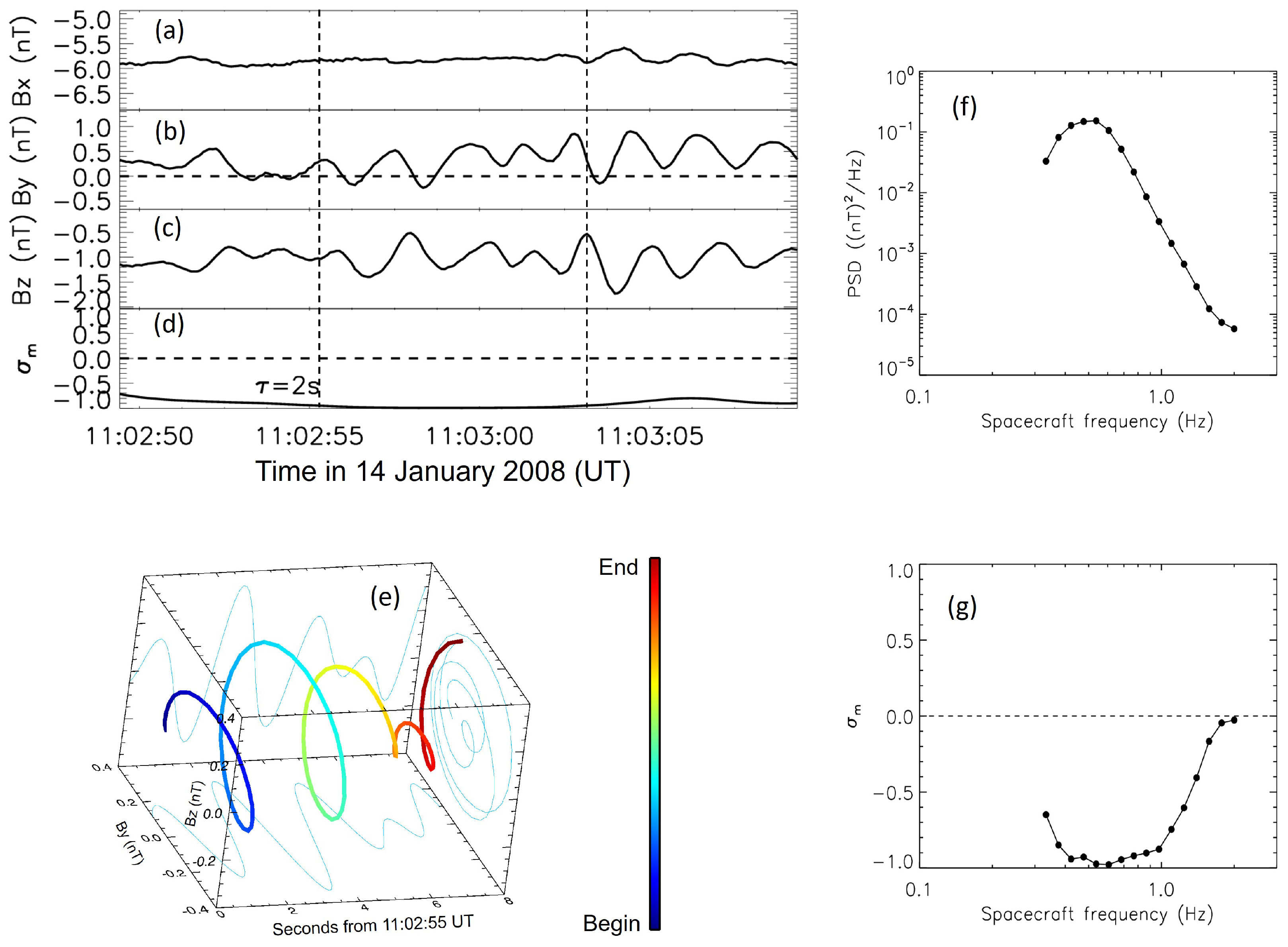
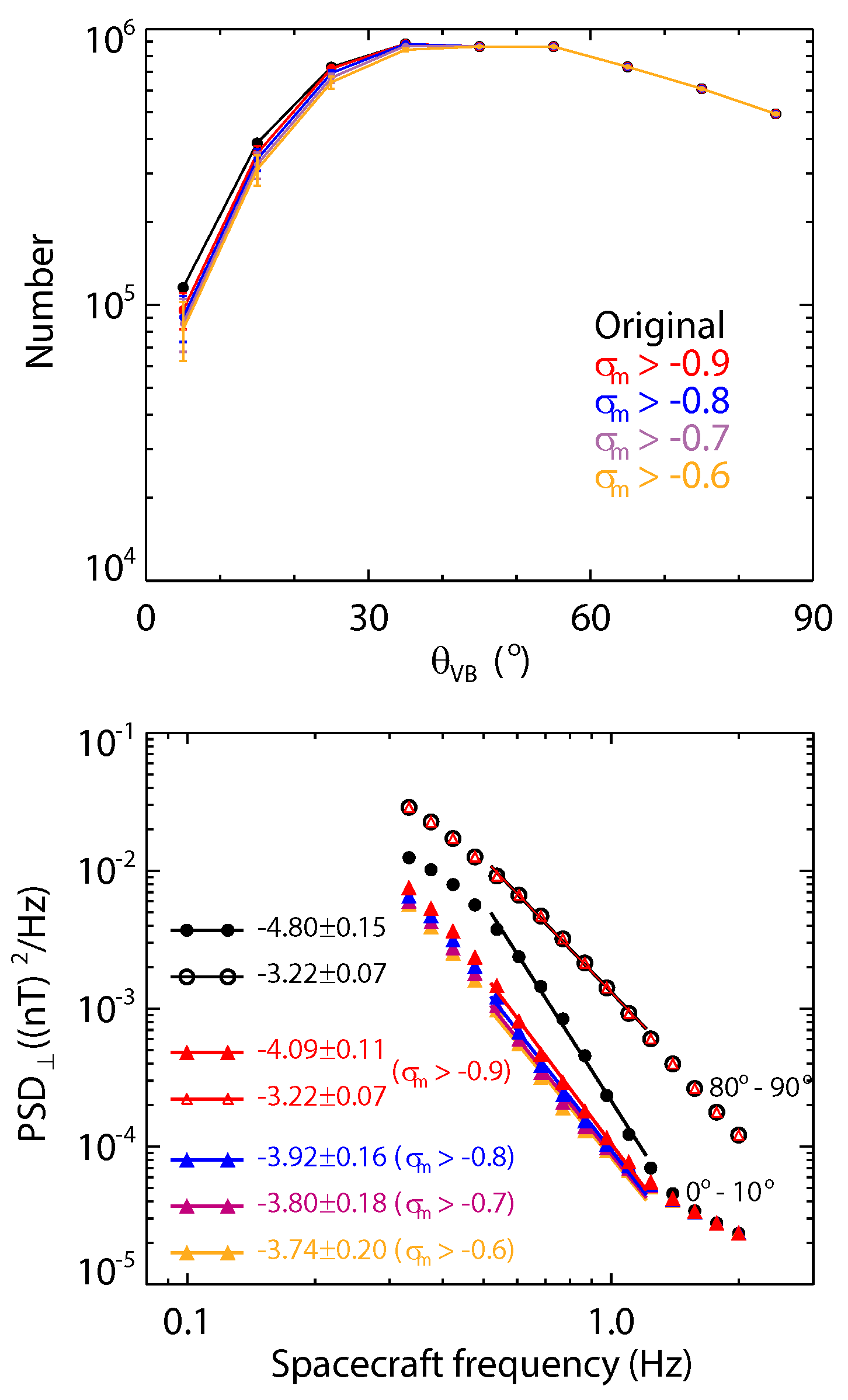
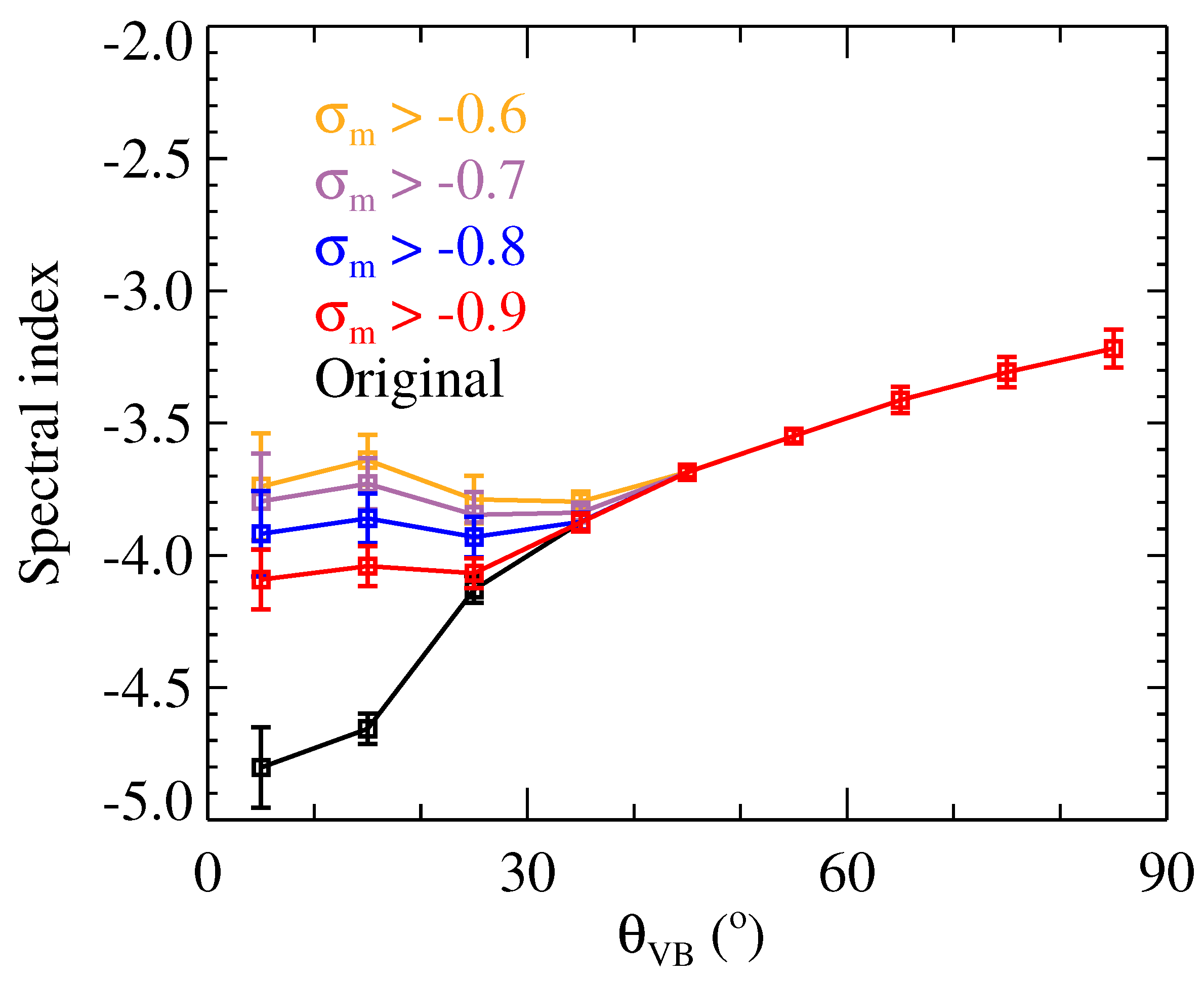
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tu, C.Y.; Marsch, E. MHD structures, waves and turbulence in the solar wind: Observations and theories. Space Sci. Rev. 1995, 73, 1–210. [Google Scholar] [CrossRef]
- Goldstein, M.L.; Roberts, D.A.; Matthaeus, W.H. Magnetohydrodynamic Turbulence in the Solar Wind. ARA&A 1995, 33, 283–326. [Google Scholar] [CrossRef]
- Bruno, R.; Carbone, V. The Solar Wind as a Turbulence Laboratory. Living Rev. Sol. Phys. 2013, 10, 2. [Google Scholar] [CrossRef]
- Kolmogorov, A. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Akademiia Nauk SSSR Doklady 1941, 30, 301–305. [Google Scholar]
- Podesta, J.J.; Roberts, D.A.; Goldstein, M.L. Power spectrum of small-scale turbulent velocity fluctuations in the solar wind. J. Geophys. Res. (Space Phys.) 2006, 111, A10109. [Google Scholar] [CrossRef]
- Podesta, J.J.; Roberts, D.A.; Goldstein, M.L. Spectral Exponents of Kinetic and Magnetic Energy Spectra in Solar Wind Turbulence. Astrophys. J. 2007, 664, 543–548. [Google Scholar] [CrossRef]
- Salem, C.; Mangeney, A.; Bale, S.D.; Veltri, P. Solar Wind Magnetohydrodynamics Turbulence: Anomalous Scaling and Role of Intermittency. Astrophys. J. 2009, 702, 537–553. [Google Scholar] [CrossRef]
- Alexandrova, O.; Chen, C.H.K.; Sorriso-Valvo, L.; Horbury, T.S.; Bale, S.D. Solar Wind Turbulence and the Role of Ion Instabilities. Space Sci. Rev. 2013, 178, 101–139. [Google Scholar] [CrossRef]
- Kiyani, K.H.; Osman, K.T.; Chapman, S.C. Dissipation and heating in solar wind turbulence: From the macro to the micro and back again. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2015, 373, 20140155. [Google Scholar] [CrossRef]
- Roberts, O.W.; Li, X. Evidence of the Ion Cyclotron Resonance at Proton Kinetic Scales in the Solar Wind. Astrophys. J. 2015, 802, 1. [Google Scholar] [CrossRef]
- Leamon, R.J.; Smith, C.W.; Ness, N.F.; Matthaeus, W.H.; Wong, H.K. Observational constraints on the dynamics of the interplanetary magnetic field dissipation range. J. Geophys. Res. 1998, 103, 4775. [Google Scholar] [CrossRef]
- Smith, C.W.; Hamilton, K.; Vasquez, B.J.; Leamon, R.J. Dependence of the Dissipation Range Spectrum of Interplanetary Magnetic Fluctuationson the Rate of Energy Cascade. Astrophys. J. Lett. 2006, 645, L85–L88. [Google Scholar] [CrossRef]
- Bruno, R.; Telloni, D. Spectral Analysis of Magnetic Fluctuations at Proton Scales from Fast to Slow Solar Wind. Astrophys. J. Lett. 2015, 811, L17. [Google Scholar] [CrossRef]
- Wang, T.; Cao, J.B.; Fu, H.; Liu, W.; Dunlop, M. Turbulence in the Earth’s cusp region: The k-filtering analysis. J. Geophys. Res. (Space Phys.) 2014, 119, 9527–9542. [Google Scholar] [CrossRef]
- Wang, T.; Cao, J.; Fu, H.; Meng, X.; Dunlop, M. Compressible turbulence with slow-mode waves observed in the bursty bulk flow of plasma sheet. Geophys. Res. Lett. 2016, 43, 1854–1861. [Google Scholar] [CrossRef]
- Huang, S.Y.; Zhou, M.; Sahraoui, F.; Vaivads, A.; Deng, X.H.; André, M.; He, J.S.; Fu, H.S.; Li, H.M.; Yuan, Z.G.; et al. Observations of turbulence within reconnection jet in the presence of guide field. Geophys. Res. Lett. 2012, 39, L11104. [Google Scholar] [CrossRef]
- Huang, S.Y.; Sahraoui, F.; Deng, X.H.; He, J.S.; Yuan, Z.G.; Zhou, M.; Pang, Y.; Fu, H.S. Kinetic Turbulence in the Terrestrial Magnetosheath: Cluster Observations. Astrophys. J. Lett. 2014, 789, L28. [Google Scholar] [CrossRef]
- Chen, C.H.K.; Boldyrev, S. Nature of Kinetic Scale Turbulence in the Earth’s Magnetosheath. Astrophys. J. 2017, 842, 122. [Google Scholar] [CrossRef]
- Sahraoui, F.; Hadid, L.; Huang, S. Magnetohydrodynamic and kinetic scale turbulence in the near-Earth space plasmas: A (short) biased review. Rev. Mod. Plasma Phys. 2020, 4, 4. [Google Scholar] [CrossRef]
- Li, H.; Jiang, W.; Wang, C.; Verscharen, D.; Zeng, C.; Russell, C.T.; Giles, B.; Burch, J.L. Evolution of the Earth’s Magnetosheath Turbulence: A Statistical Study Based on MMS Observations. Astrophys. J. Lett. 2020, 898, L43. [Google Scholar] [CrossRef]
- Zhu, X.; He, J.; Verscharen, D.; Zhao, J. Composition of Wave Modes in Magnetosheath Turbulence from Sub-ion to Sub-electron Scales. Astrophys. J. 2019, 878, 48. [Google Scholar] [CrossRef]
- Chen, C.H.K.; Horbury, T.S.; Schekochihin, A.A.; Wicks, R.T.; Alexandrova, O.; Mitchell, J. Anisotropy of Solar Wind Turbulence between Ion and Electron Scales. Phys. Rev. Lett. 2010, 104, 255002. [Google Scholar] [CrossRef] [PubMed]
- Cho, J.; Lazarian, A. The Anisotropy of Electron Magnetohydrodynamic Turbulence. Astrophys. J. Lett. 2004, 615, L41–L44. [Google Scholar] [CrossRef]
- Schekochihin, A.A.; Cowley, S.C.; Dorland, W.; Hammett, G.W.; Howes, G.G.; Quataert, E.; Tatsuno, T. Astrophysical Gyrokinetics: Kinetic and Fluid Turbulent Cascades in Magnetized Weakly Collisional Plasmas. Astrophys. J. Suppl. Ser. 2009, 182, 310–377. [Google Scholar] [CrossRef]
- Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics: Mechanics of Turbulence; Courier Corporation: North Chelmsford, MA, USA, 1975; Volume 2. [Google Scholar]
- Cho, J.; Lazarian, A. Simulations of Electron Magnetohydrodynamic Turbulence. Astrophys. J. 2009, 701, 236–252. [Google Scholar] [CrossRef]
- Behannon, K.W. Observations of the Interplanetary Magnetic Field between 0.46 and 1 A.U. by the Mariner 10 Spacecraft. Ph.D. Thesis, National Aeronautics and Space Administration Goddard Space Flight Center, Greenbelt, MD, USA, 1976. [Google Scholar]
- Tsurutani, B.T.; Arballo, J.K.; Mok, J.; Smith, E.J.; Mason, G.M.; Tan, L.C. Electromagnetic waves with frequencies near the local proton gyrofrequency: ISEE-3 1 AU observations. Geophys. Res. Lett. 1994, 21, 633–636. [Google Scholar] [CrossRef]
- Jian, L.K.; Russell, C.T.; Luhmann, J.G.; Strangeway, R.J.; Leisner, J.S.; Galvin, A.B. Ion Cyclotron Waves in the Solar Wind Observed by STEREO Near 1 AU. Astrophys. J. Lett. 2009, 701, L105–L109. [Google Scholar] [CrossRef]
- Jian, L.K.; Wei, H.Y.; Russell, C.T.; Luhmann, J.G.; Klecker, B.; Omidi, N.; Isenberg, P.A.; Goldstein, M.L.; Figueroa-Viñas, A.; Blanco-Cano, X. Electromagnetic Waves near the Proton Cyclotron Frequency: STEREO Observations. Astrophys. J. 2014, 786, 123. [Google Scholar] [CrossRef]
- Wicks, R.T.; Alexander, R.L.; Stevens, M.; Wilson, L.B., III; Moya, P.S.; Viñas, A.; Jian, L.K.; Roberts, D.A.; O’Modhrain, S.; Gilbert, J.A.; et al. A Proton-cyclotron Wave Storm Generated by Unstable Proton Distribution Functions in the Solar Wind. Astrophys. J. 2016, 819, 6. [Google Scholar] [CrossRef]
- He, J.; Marsch, E.; Tu, C.; Yao, S.; Tian, H. Possible Evidence of Alfvén-cyclotron Waves in the Angle Distribution of Magnetic Helicity of Solar Wind Turbulence. Astrophys. J. 2011, 731, 85. [Google Scholar] [CrossRef]
- He, J.; Tu, C.; Marsch, E.; Yao, S. Do Oblique Alfvén/Ion-cyclotron or Fast-mode/Whistler Waves Dominate the Dissipation of Solar Wind Turbulence near the Proton Inertial Length? Astrophys. J. Lett. 2012, 745, L8. [Google Scholar] [CrossRef]
- He, J.; Tu, C.; Marsch, E.; Yao, S. Reproduction of the Observed Two-component Magnetic Helicity in Solar Wind Turbulence by a Superposition of Parallel and Oblique Alfvén Waves. Astrophys. J. 2012, 749, 86. [Google Scholar] [CrossRef][Green Version]
- Podesta, J.J.; Gary, S.P. Magnetic Helicity Spectrum of Solar Wind Fluctuations as a Function of the Angle with Respect to the Local Mean Magnetic Field. Astrophys. J. 2011, 734, 15. [Google Scholar] [CrossRef]
- Podesta, J.J. Observations of Electromagnetic Fluctuations at Ion Kinetic Scales in the Solar Wind. Astrophys. Space Sci. Proc. 2012, 33, 177. [Google Scholar] [CrossRef]
- Lion, S.; Alexandrova, O.; Zaslavsky, A. Coherent Events and Spectral Shape at Ion Kinetic Scales in the Fast Solar Wind Turbulence. Astrophys. J. 2016, 824, 47. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Zhao, G.Q.; Lin, Y.; Wang, X.Y.; Feng, H.Q.; Wu, D.J.; Kasper, J.C. Two Correlations with Enhancement Near the Proton Gyroradius Scale in Solar Wind Turbulence: Parker Solar Probe (PSP) and Wind Observations. Astrophys. J. 2022, 924, 92. [Google Scholar] [CrossRef]
- Lepping, R.P.; Acũna, M.H.; Burlaga, L.F.; Farrell, W.M.; Slavin, J.A.; Schatten, K.H.; Mariani, F.; Ness, N.F.; Neubauer, F.M.; Whang, Y.C.; et al. The Wind Magnetic Field Investigation. Space Sci. Rev. 1995, 71, 207–229. [Google Scholar] [CrossRef]
- Wicks, R.T.; Horbury, T.S.; Chen, C.H.K.; Schekochihin, A.A. Anisotropy of Imbalanced Alfvénic Turbulence in Fast Solar Wind. Phys. Rev. Lett. 2011, 106, 045001. [Google Scholar] [CrossRef]
- Wang, X.; Tu, C.; He, J.; Marsch, E.; Wang, L. The Influence of Intermittency on the Spectral Anisotropy of Solar Wind Turbulence. Astrophys. J. Lett. 2014, 783, L9. [Google Scholar] [CrossRef]
- Bruno, R.; Trenchi, L. Radial Dependence of the Frequency Break between Fluid and Kinetic Scales in the Solar Wind Fluctuations. Astrophys. J. Lett. 2014, 787, L24. [Google Scholar] [CrossRef]
- Chen, C.H.K.; Leung, L.; Boldyrev, S.; Maruca, B.A.; Bale, S.D. Ion-scale spectral break of solar wind turbulence at high and low beta. Geophys. Res. Lett. 2014, 41, 8081–8088. [Google Scholar] [CrossRef]
- Wang, X.; Tu, C.Y.; He, J.S.; Wang, L.H. Ion-Scale Spectral Break in the Normal Plasma Beta Range in the Solar Wind Turbulence. J. Geophys. Res. Space Phys. 2018, 123, 68–75. [Google Scholar] [CrossRef]
- Wang, X.; Tu, C.; He, J.; Wang, L. On the Full-range β Dependence of Ion-scale Spectral Break in the Solar Wind Turbulence. Astrophys. J. 2018, 857, 136. [Google Scholar] [CrossRef]
- Sahraoui, F.; Goldstein, M.L.; Belmont, G.; Canu, P.; Rezeau, L. Three Dimensional Anisotropic k Spectra of Turbulence at Subproton Scales in the Solar Wind. Phys. Rev. Lett. 2010, 105, 131101. [Google Scholar] [CrossRef] [PubMed]
- Roberts, O.W.; Li, X.; Li, B. Kinetic Plasma Turbulence in the Fast Solar Wind Measured by Cluster. Astrophys. J. 2013, 769, 58. [Google Scholar] [CrossRef]
- Horbury, T.S.; Forman, M.; Oughton, S. Anisotropic Scaling of Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 2008, 101, 175005. [Google Scholar] [CrossRef] [PubMed]
- Podesta, J.J. Dependence of Solar-Wind Power Spectra on the Direction of the Local Mean Magnetic Field. Astrophys. J. 2009, 698, 986–999. [Google Scholar] [CrossRef]
- Wei, H.Y.; Jian, L.K.; Russell, C.T.; Omidi, N. Ion Cyclotron Waves in the Solar Wind. Wash. DC Am. Geophys. Union Geophys. Monogr. Ser. 2016, 216, 253–267. [Google Scholar] [CrossRef]
- Telloni, D.; Carbone, F.; Bruno, R.; Zank, G.P.; Sorriso-Valvo, L.; Mancuso, S. Ion Cyclotron Waves in Field-aligned Solar Wind Turbulence. Astrophys. J. Lett. 2019, 885, L5. [Google Scholar] [CrossRef]
- Hamilton, K.; Smith, C.W.; Vasquez, B.J.; Leamon, R.J. Anisotropies and helicities in the solar wind inertial and dissipation ranges at 1 AU. J. Geophys. Res. (Space Phys.) 2008, 113, A01106. [Google Scholar] [CrossRef]
- Gary, S.P.; Smith, C.W. Short-wavelength turbulence in the solar wind: Linear theory of whistler and kinetic Alfvén fluctuations. J. Geophys. Res. (Space Phys.) 2009, 114, A12105. [Google Scholar] [CrossRef]
- Telloni, D.; Bruno, R.; Trenchi, L. Radial Evolution of Spectral Characteristics of Magnetic Field Fluctuations at Proton Scales. Astrophys. J. 2015, 805, 46. [Google Scholar] [CrossRef]
- Bowen, T.A.; Mallet, A.; Huang, J.; Klein, K.G.; Malaspina, D.M.; Stevens, M.; Bale, S.D.; Bonnell, J.W.; Case, A.W.; Chandran, B.D.G.; et al. Ion-scale Electromagnetic Waves in the Inner Heliosphere. Astrophys. J. Suppl. Ser. 2020, 246, 66. [Google Scholar] [CrossRef]
- Alexandrova, O.; Carbone, V.; Veltri, P.; Sorriso-Valvo, L. Solar wind Cluster observations: Turbulent spectrum and role of Hall effect. Planet. Space Sci. 2007, 55, 2224–2227. [Google Scholar] [CrossRef]
- Alexandrova, O.; Carbone, V.; Veltri, P.; Sorriso-Valvo, L. Small-Scale Energy Cascade of the Solar Wind Turbulence. Astrophys. J. 2008, 674, 1153–1157. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Huang, L.; Wang, Y.; Yuan, H. Influence of Alfvén Ion–Cyclotron Waves on the Anisotropy of Solar Wind Turbulence at Ion Kinetic Scales. Universe 2023, 9, 399. https://doi.org/10.3390/universe9090399
Wang X, Huang L, Wang Y, Yuan H. Influence of Alfvén Ion–Cyclotron Waves on the Anisotropy of Solar Wind Turbulence at Ion Kinetic Scales. Universe. 2023; 9(9):399. https://doi.org/10.3390/universe9090399
Chicago/Turabian StyleWang, Xin, Linzhi Huang, Yuxin Wang, and Haochen Yuan. 2023. "Influence of Alfvén Ion–Cyclotron Waves on the Anisotropy of Solar Wind Turbulence at Ion Kinetic Scales" Universe 9, no. 9: 399. https://doi.org/10.3390/universe9090399
APA StyleWang, X., Huang, L., Wang, Y., & Yuan, H. (2023). Influence of Alfvén Ion–Cyclotron Waves on the Anisotropy of Solar Wind Turbulence at Ion Kinetic Scales. Universe, 9(9), 399. https://doi.org/10.3390/universe9090399





