Hartree–Fock Calculations in Semi-Infinite Matter with Gogny Interactions
Abstract
1. Introduction
2. Materials and Methods
2.1. Infinite Nuclear Matter
2.2. Semi Infinite Nuclear Matter
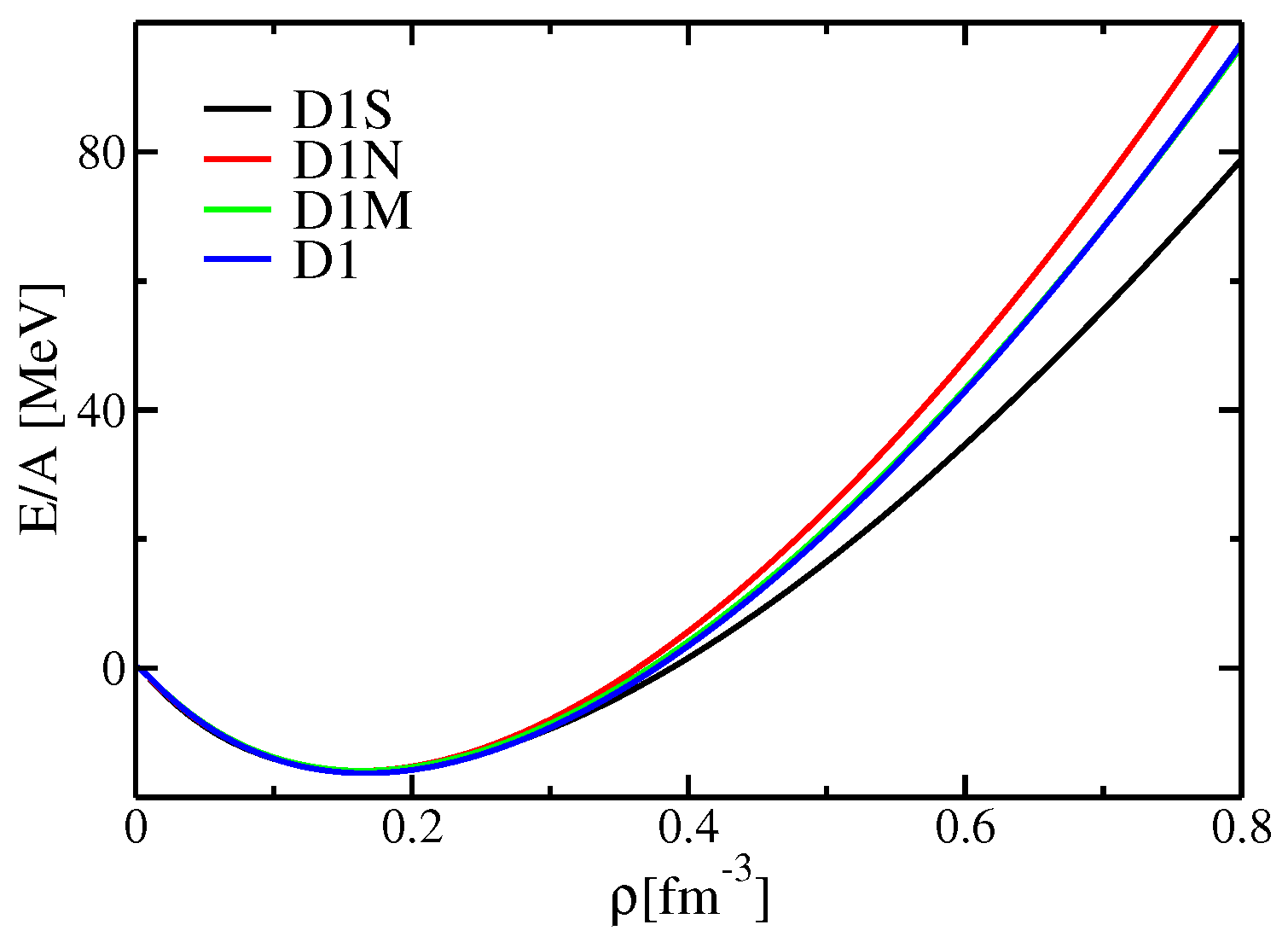
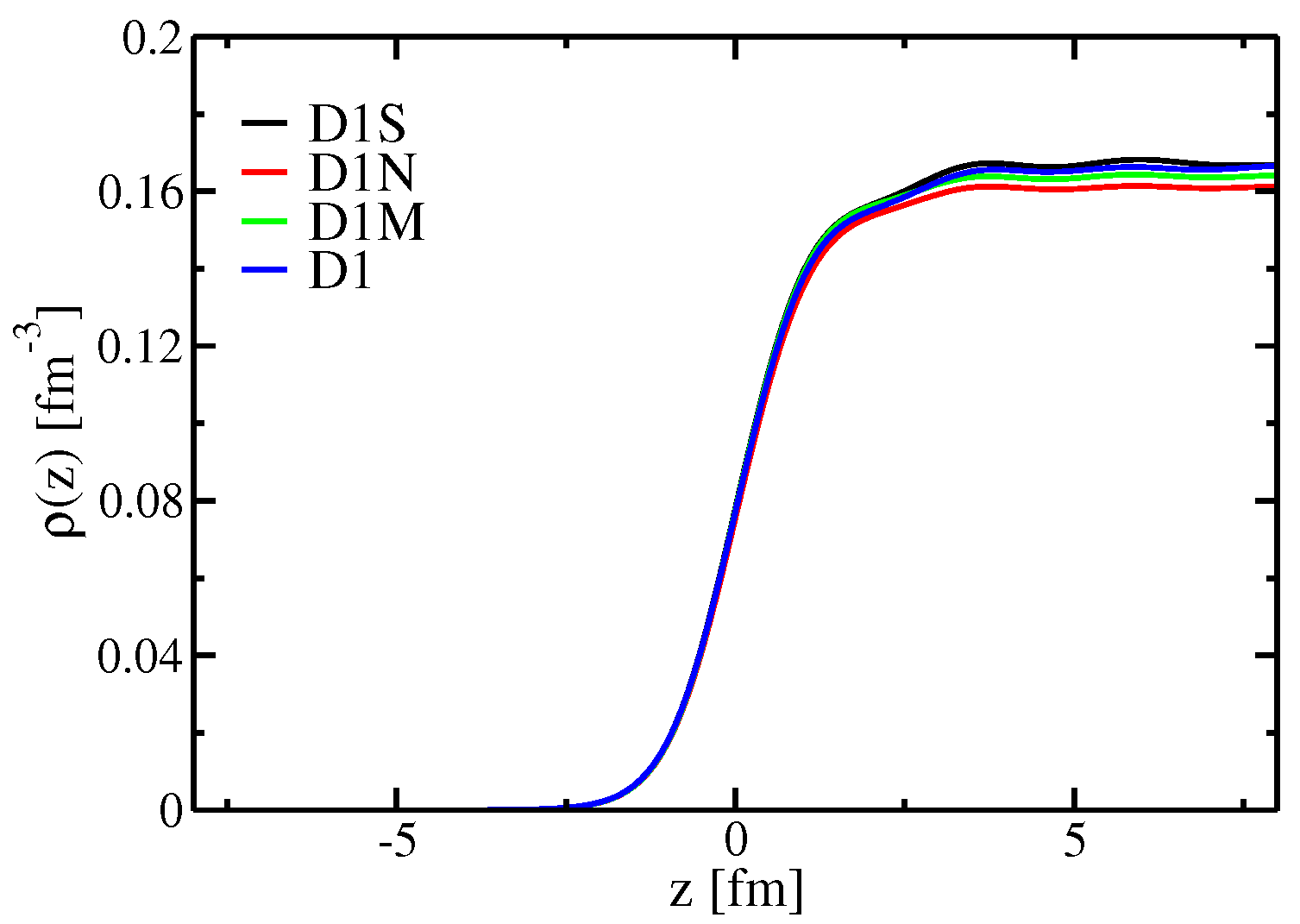
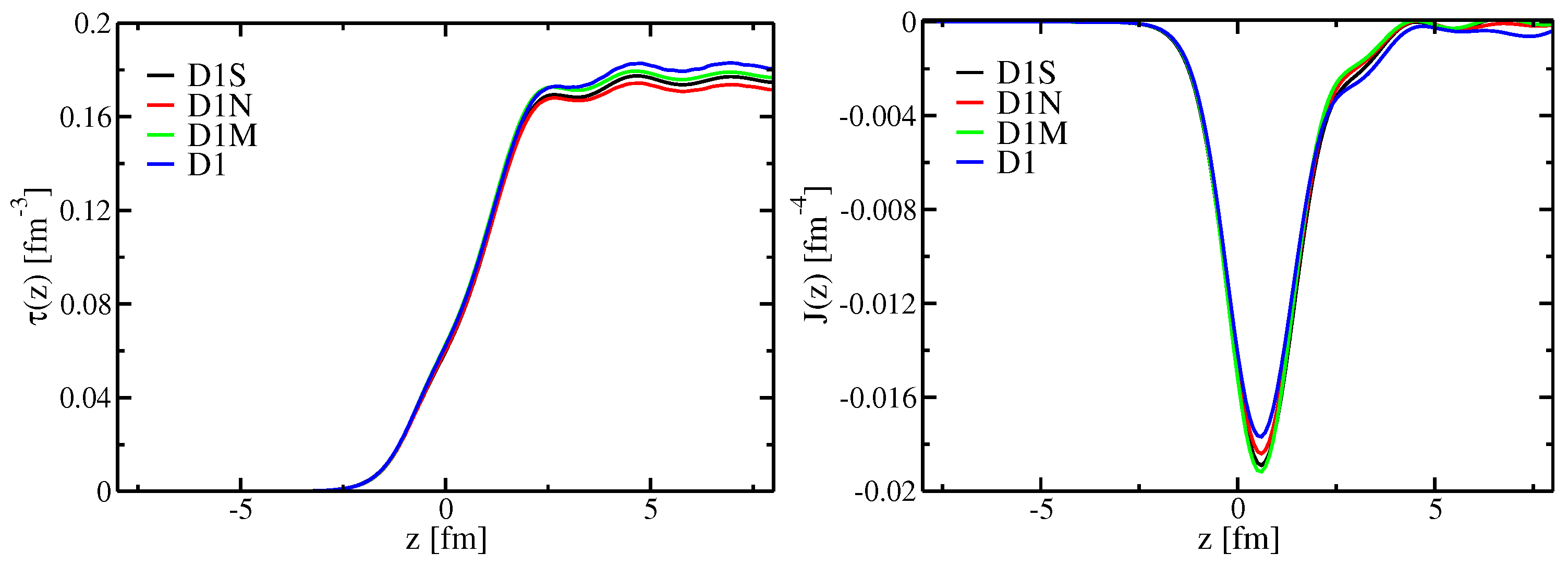
3. Results
3.1. Numerical Procedure
3.2. Surface Energy
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Gogny Potential in INM
| 1 | |
| 2 | In order to apply the Numerov method, we use a step of fm along the z direction |
References
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Pastore, A. An introduction to bootstrap for nuclear physics. J. Phys. G Nucl. Part. Phys. 2019, 46, 052001. [Google Scholar] [CrossRef]
- Brink, D.M.; Broglia, R.A. Nuclear Superfluidity: Pairing in Finite Systems; Cambridge University Press: Cambridge, UK, 2005; Volume 24. [Google Scholar]
- Bender, M.; Heenen, P.H.; Reinhard, P.G. Self-consistent mean-field models for nuclear structure. Rev. Mod. Phys. 2003, 75, 121–180. [Google Scholar] [CrossRef]
- Vautherin, D.; Brink, D.M. Hartree-Fock calculations with Skyrme’s interaction. I. Spherical nuclei. Phys. Rev. C 1972, 5, 626. [Google Scholar] [CrossRef]
- Goriely, S.; Tondeur, F.; Pearson, J. A Hartree–Fock nuclear mass table. At. Data Nucl. Data Tables 2001, 77, 311–381. [Google Scholar] [CrossRef]
- Skyrme, T. The effective nuclear potential. Nucl. Phys. 1958, 9, 615–634. [Google Scholar] [CrossRef]
- Dechargé, J.; Gogny, D. Hartree-Fock-Bogolyubov calculations with the D1 effective interaction on spherical nuclei. Phys. Rev. C 1980, 21, 1568. [Google Scholar] [CrossRef]
- Nakada, H. Hartree-Fock approach to nuclear matter and finite nuclei with M3Y-type nucleon-nucleon interactions. Phys. Rev. C 2003, 68, 014316. [Google Scholar] [CrossRef]
- Davesne, D.; Becker, P.; Pastore, A.; Navarro, J. Infinite matter properties and zero-range limit of non-relativistic finite-range interactions. Ann. Phys. 2016, 375, 288–312. [Google Scholar] [CrossRef]
- Kortelainen, M.; Lesinski, T.; Moré, J.; Nazarewicz, W.; Sarich, J.; Schunck, N.; Stoitsov, M.; Wild, S. Nuclear energy density optimization. Phys. Rev. C 2010, 82, 024313. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities Part II. Nuclei far from stabilities. Nucl. Phys. A 1998, 635, 231–256. [Google Scholar] [CrossRef]
- Erler, J.; Klüpfel, P.; Reinhard, P. Misfits in Skyrme–Hartree–Fock. J. Phys. G Nucl. Part. Phys. 2010, 37, 064001. [Google Scholar] [CrossRef]
- Jodon, R.; Bender, M.; Bennaceur, K.; Meyer, J. Constraining the surface properties of effective Skyrme interactions. Phys. Rev. C 2016, 94, 024335. [Google Scholar] [CrossRef]
- Ryssens, W.; Bender, M.; Bennaceur, K.; Heenen, P.H.; Meyer, J. Impact of the surface energy coefficient on the deformation properties of atomic nuclei as predicted by Skyrme energy density functionals. Phys. Rev. C 2019, 99, 044315. [Google Scholar] [CrossRef]
- Proust, P.; Lallouet, Y.; Davesne, D.; Meyer, J. Surface energy coefficient of an N2LO Skyrme energy functional: A semiclassical extended Thomas-Fermi approach. Phys. Rev. C 2022, 106, 054321. [Google Scholar] [CrossRef]
- Côté, J.; Pearson, J. Hartree-fock calculations of semi-infinite nuclear matter with complete forces (finite-range and spin-orbit term). Nucl. Phys. A 1978, 304, 104–126. [Google Scholar] [CrossRef]
- Chamel, N.; Haensel, P. Physics of neutron star crusts. Living Rev. Relativ. 2008, 11, 10. [Google Scholar] [CrossRef]
- Davesne, D.; Pastore, A.; Navarro, J. Linear response theory with finite-range interactions. Prog. Part. Nucl. Phys. 2021, 120, 103870. [Google Scholar] [CrossRef]
- Farine, M.; Von-Eiff, D.; Schuck, P.; Berger, J.; Dechargé, J.; Girod, M. Towards a new effective interaction of the Gogny type. J. Phys. G Nucl. Part. Phys. 1999, 25, 863. [Google Scholar] [CrossRef]
- Grasso, M.; Anguiano, M. Tensor parameters in Skyrme and Gogny effective interactions: Trends from a ground-state-focused study. Phys. Rev. C 2013, 88, 054328. [Google Scholar] [CrossRef]
- Otsuka, T.; Matsuo, T.; Abe, D. Mean field with tensor force and shell structure of exotic nuclei. Phys. Rev. Lett. 2006, 97, 162501. [Google Scholar] [CrossRef]
- Chappert, F.; Pillet, N.; Girod, M.; Berger, J.F. Gogny force with a finite-range density dependence. Phys. Rev. C 2015, 91, 034312. [Google Scholar] [CrossRef]
- Berger, J.; Girod, M.; Gogny, D. Microscopic analysis of collective dynamics in low energy fission. Nucl. Phys. A 1984, 428, 23–36. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Martins, J.S.; Delfino, A.; Stone, J.R.; Stevenson, P. Skyrme interaction and nuclear matter constraints. Phys. Rev. C 2012, 85, 035201. [Google Scholar] [CrossRef]
- Centelles, M.; Roca-Maza, X.; Vinas, X.; Warda, M. Nuclear symmetry energy probed by neutron skin thickness of nuclei. Phys. Rev. Lett. 2009, 102, 122502. [Google Scholar] [CrossRef] [PubMed]
- Roca-Maza, X.; Centelles, M.; Vinas, X.; Warda, M. Neutron skin of Pb 208, nuclear symmetry energy, and the parity radius experiment. Phys. Rev. Lett. 2011, 106, 252501. [Google Scholar] [CrossRef] [PubMed]
- Fattoyev, F.; Piekarewicz, J.; Horowitz, C.J. Neutron skins and neutron stars in the multimessenger era. Phys. Rev. Lett. 2018, 120, 172702. [Google Scholar] [CrossRef] [PubMed]
- Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Implications of PREX-2 on the equation of state of neutron-rich matter. Phys. Rev. Lett. 2021, 126, 172503. [Google Scholar] [CrossRef]
- Chappert, F.; Girod, M.; Hilaire, S. Towards a new Gogny force parameterization: Impact of the neutron matter equation of state. Phys. Lett. B 2008, 668, 420–424. [Google Scholar] [CrossRef]
- Goriely, S.; Hilaire, S.; Girod, M.; Péru, S. First Gogny-Hartree-Fock-Bogoliubov nuclear mass model. Phys. Rev. Lett. 2009, 102, 242501. [Google Scholar] [CrossRef]
- Libert, J.; Girod, M.; Delaroche, J.P. Microscopic descriptions of superdeformed bands with the Gogny force: Configuration mixing calculations in the A 190 mass region. Phys. Rev. C 1999, 60, 054301. [Google Scholar] [CrossRef]
- Sobiczewski, A.; Litvinov, Y.A. Predictive power of nuclear-mass models. Phys. Rev. C 2014, 90, 017302. [Google Scholar] [CrossRef]
- Swiatecki, W. The nuclear surface energy. Proc. Phys. Soc. Sect. A 1951, 64, 226. [Google Scholar] [CrossRef]
- Friedel, J. Metallic alloys. Nuovo Cim. (1955–1965) 1958, 7, 287–311. [Google Scholar] [CrossRef]
- Stocker, W. Spin-orbit coupling and properties of the nuclear surface. Nucl. Phys. A 1970, 140, 305–318. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A.; Romer, R.H. Handbook of mathematical functions with formulas, graphs, and mathematical tables. Am. J. Phys. 1988, 56, 958. [Google Scholar] [CrossRef]
- Rohoziński, S.; Dobaczewski, J.; Nazarewicz, W. Self-consistent symmetries in the proton-neutron Hartree-Fock-Bogoliubov approach. Phys. Rev. C 2010, 81, 014313. [Google Scholar] [CrossRef]
- Baldo, M.; Lombardo, U.; Saperstein, E.; Zverev, M. Microscopic study of the effective pairing interaction in semi-infinite nuclear matter with the separable NN-interaction. Nucl. Phys. A 1998, 628, 503–536. [Google Scholar] [CrossRef]
- Baldo, M.; Lombardo, U.; Saperstein, E.; Zverev, M. Solving the Bogolyubov equations for semi-infinite nuclear matter in the case of a nonlocal gap. Phys. At. Nucl. 1999, 62, 66–85. [Google Scholar]
- Noumerov, B. A method of extrapolation of perturbations. MNRAS 1924, 84, 592. [Google Scholar] [CrossRef]
- Bennaceur, K.; Dobaczewski, J. Coordinate-space solution of the Skyrme–Hartree–Fock–Bogolyubov equations within spherical symmetry. The program HFBRAD (v1. 00). Comput. Phys. Commun. 2005, 168, 96–122. [Google Scholar] [CrossRef]
- Bonche, P.; Koonin, S.; Negele, J. One-dimensional nuclear dynamics in the time-dependent Hartree-Fock approximation. Phys. Rev. C 1976, 13, 1226. [Google Scholar] [CrossRef]
- Vautherin, D.; Vénéroni, M. Solution of the nuclear Hartree-Fock equations in coordinate space. Phys. Lett. B 1967, 25, 175–178. [Google Scholar] [CrossRef]
- Michel, N. A simple and efficient numerical scheme to integrate non-local potentials. Eur. Phys. J. A 2009, 42, 523–527. [Google Scholar] [CrossRef]
- Grasso, M.; Van Giai, N.; Sandulescu, N. Continuum HFB calculations with finite range pairing interactions. Phys. Lett. B 2002, 535, 103–108. [Google Scholar] [CrossRef][Green Version]
- Blanchon, G.; Dupuis, M.; Arellano, H.F.; Bernard, R.; Morillon, B. SIDES: Nucleon–nucleus elastic scattering code for nonlocal potential. Comput. Phys. Commun. 2020, 254, 107340. [Google Scholar] [CrossRef]
- Atkinson, K.E. An Introduction to Numerical Analysis; John Wiley and Sons: New York, NY, USA, 1989. [Google Scholar]
- Sellahewa, R.; Rios, A. Isovector properties of the Gogny interaction. Phys. Rev. C 2014, 90, 054327. [Google Scholar] [CrossRef]
| [MeV] | |
|---|---|
| D1 | 20.3 |
| D1S | 18.4 |
| D1N | 18.2 |
| D1M | 18.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davesne, D.; Pastore, A.; Navarro, J. Hartree–Fock Calculations in Semi-Infinite Matter with Gogny Interactions. Universe 2023, 9, 398. https://doi.org/10.3390/universe9090398
Davesne D, Pastore A, Navarro J. Hartree–Fock Calculations in Semi-Infinite Matter with Gogny Interactions. Universe. 2023; 9(9):398. https://doi.org/10.3390/universe9090398
Chicago/Turabian StyleDavesne, Dany, Alessandro Pastore, and Jesus Navarro. 2023. "Hartree–Fock Calculations in Semi-Infinite Matter with Gogny Interactions" Universe 9, no. 9: 398. https://doi.org/10.3390/universe9090398
APA StyleDavesne, D., Pastore, A., & Navarro, J. (2023). Hartree–Fock Calculations in Semi-Infinite Matter with Gogny Interactions. Universe, 9(9), 398. https://doi.org/10.3390/universe9090398






