Constraining Dark Boson Decay Using Neutron Stars
Abstract
1. Introduction
2. Neutron Stars
2.1. Quark Meson Coupling Model
2.2. Formalism including Neutron Decay
2.3. Tolman–Oppenheimer–Volkoff Equations
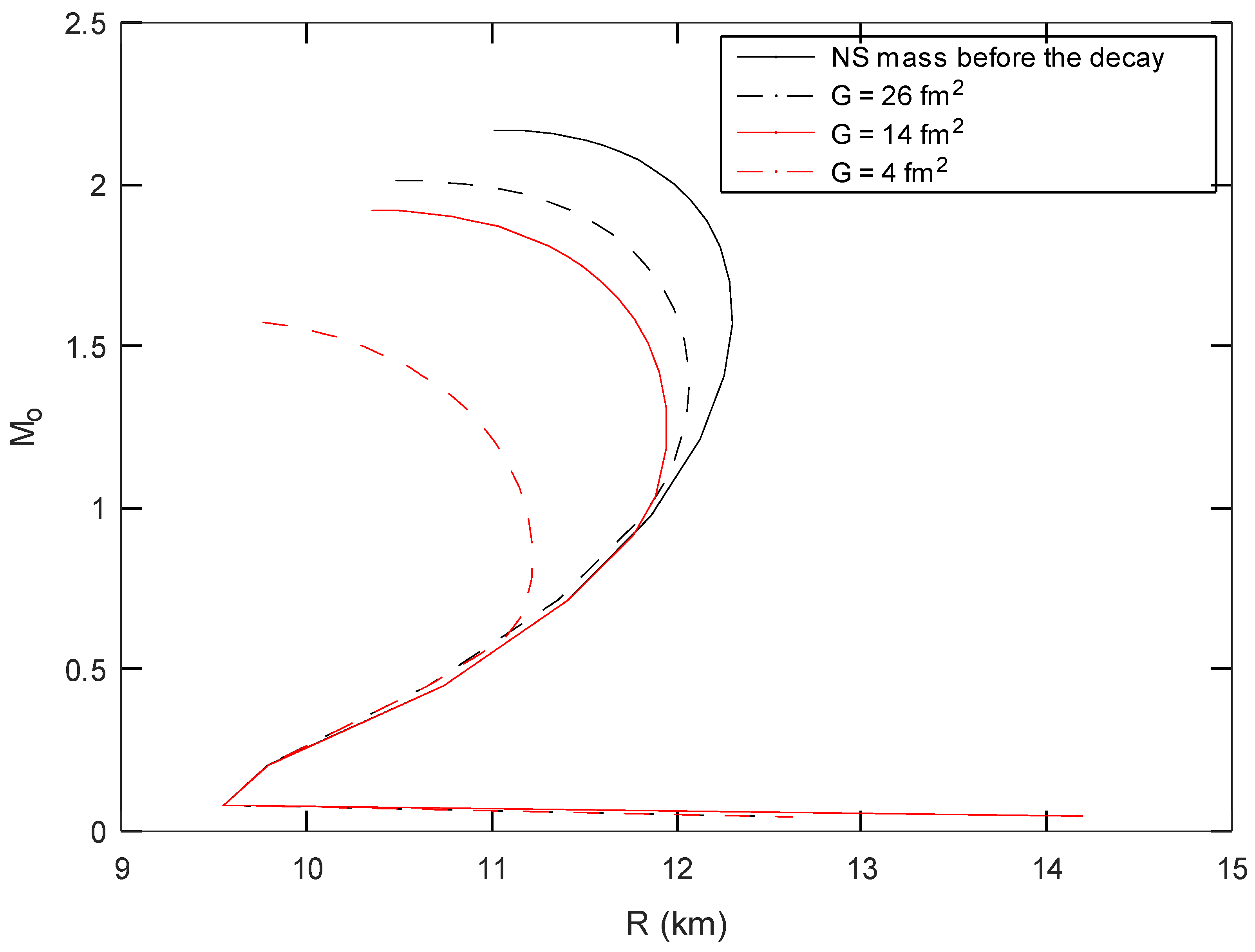
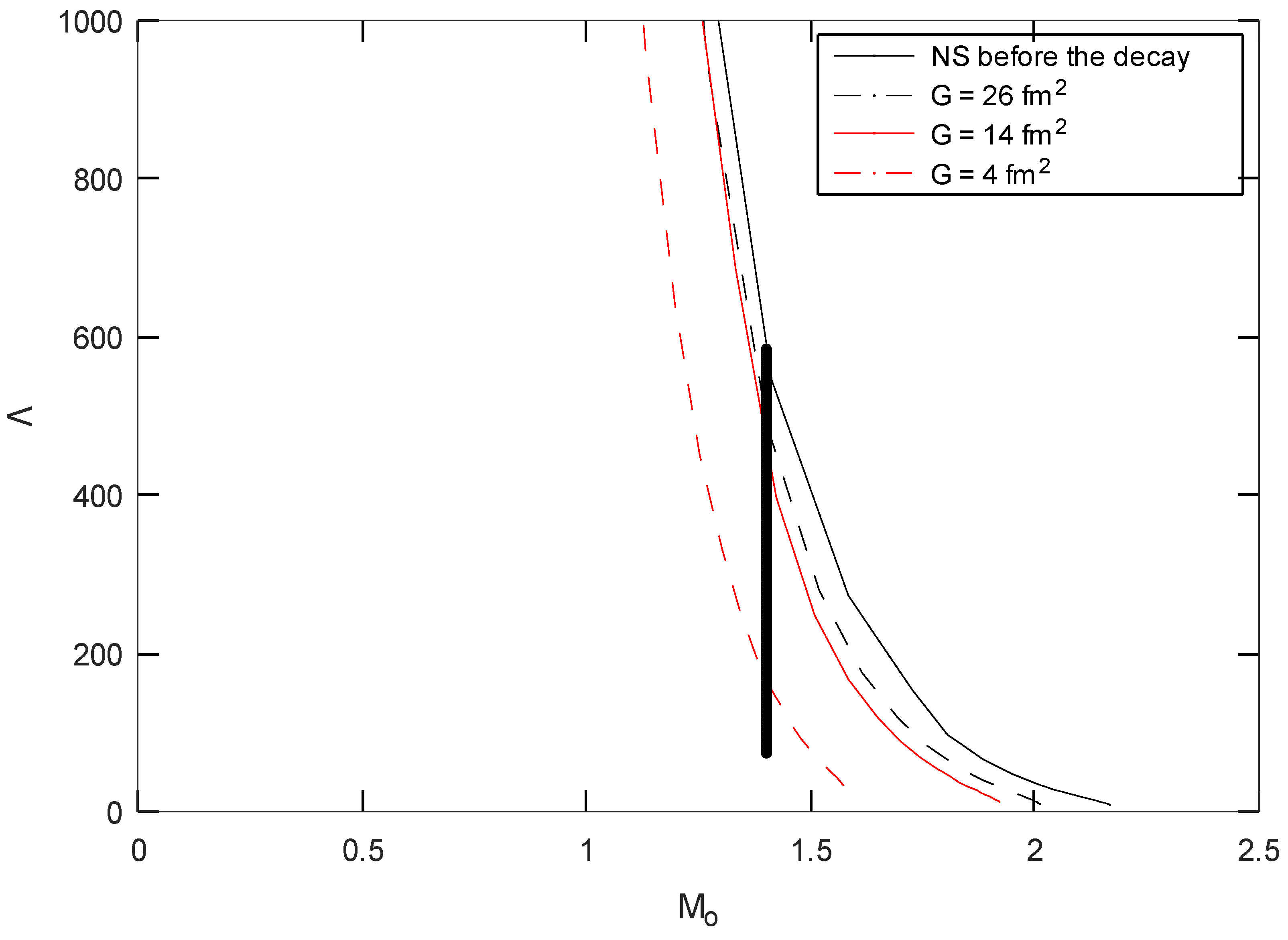
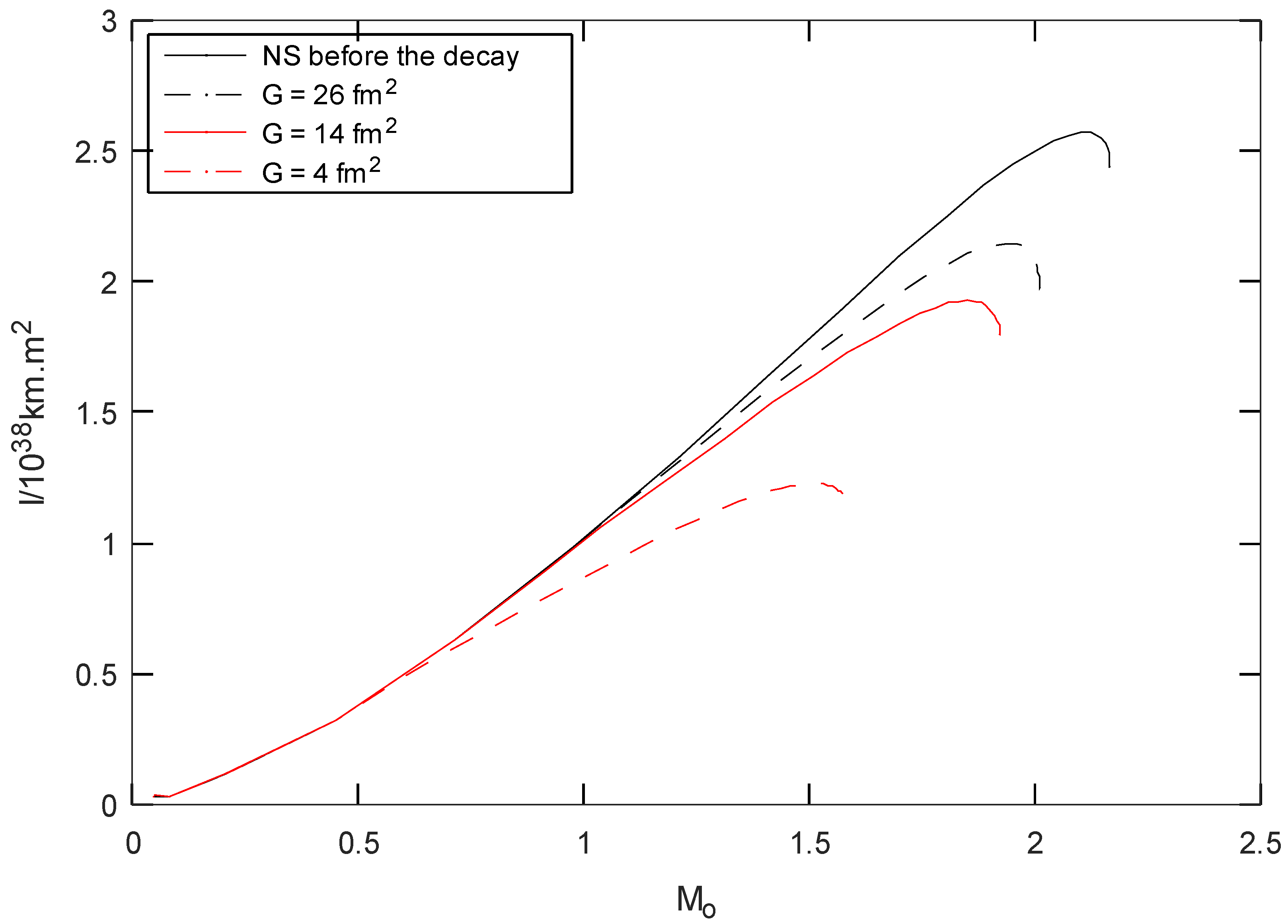
3. Results
4. Decay Modes of Bosons
4.1. Scalars and Pseudoscalars
4.2. Spin-1
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
| 1 |
References
- Wietfeldt, F.E.; Greene, G.L. Colloquium: The neutron lifetime. Rev. Mod. Phys. 2011, 83, 1173–1192. [Google Scholar] [CrossRef]
- Serebrov, A.P.; Kolomensky, E.A.; Fomin, A.K.; Krasnoshchekova, I.A.; Vassiljev, A.V.; Prudnikov, D.M.; Shoka, I.V.; Chechkin, A.V.; Chaikovskiy, M.E.; Varlamov, V.E.; et al. Neutron lifetime measurements with a large gravitational trap for ultracold neutrons. Phys. Rev. C 2018, 97, 055503. [Google Scholar] [CrossRef]
- Pattie, R.W., Jr.; Callahan, N.B.; Cude-Woods, C.; Adamek, E.R.; Broussard, L.J.; Clayton, S.M.; Currie, S.A.; Dees, E.B.; Ding, X.; Engel, E.M.; et al. Measurement of the neutron lifetime using a magneto-gravitational trap and in situ detection. Science 2018, 360, 627–632. [Google Scholar] [CrossRef] [PubMed]
- Tan, W. Neutron oscillations for solving neutron lifetime and dark matter puzzles. Phys. Lett. B 2019, 797, 134921. [Google Scholar] [CrossRef]
- Steyerl, A.; Pendlebury, J.M.; Kaufman, C.; Malik, S.S.; Desai, A.M. Quasielastic scattering in the interaction of ultracold neutrons with a liquid wall and application in a reanalysis of the Mambo I neutron-lifetime experiment. Phys. Rev. C 2012, 85, 065503. [Google Scholar] [CrossRef]
- Yue, A.T.; Dewey, M.S.; Gilliam, D.M.; Greene, G.L.; Laptev, A.B.; Nico, J.S.; Snow, W.M.; Wietfeldt, F.E. Improved Determination of the Neutron Lifetime. Phys. Rev. Lett. 2013, 111, 222501. [Google Scholar] [CrossRef]
- Otono, H. LiNA—Lifetime of neutron apparatus with time projection chamber and solenoid coil. Nucl. Instrum. Meth. A 2017, 845, 278–280. [Google Scholar] [CrossRef]
- Olive, K. Review of Particle Physics. Chin. Phys. C 2016, 40, 100001. [Google Scholar] [CrossRef]
- Gonzalez, F.M.; Fries, E.M.; Cude-Woods, C.; Bailey, T.; Blatnik, M.; Broussard, L.J.; Callahan, N.B.; Choi, J.H.; Clayton, S.M.; Currie, S.A.; et al. Improved Neutron Lifetime Measurement with UCNτ. Phys. Rev. Lett. 2021, 127, 162501. [Google Scholar] [CrossRef]
- Fornal, B.; Grinstein, B. Dark Matter Interpretation of the Neutron Decay Anomaly. Phys. Rev. Lett. 2018, 120, 191801, Erratum in Phys. Rev. Lett. 2020, 124, 219901. [Google Scholar] [CrossRef]
- Grinstein, B.; Kouvaris, C.; Nielsen, N.G. Neutron Star Stability in Light of the Neutron Decay Anomaly. Phys. Rev. Lett. 2019, 123, 091601. [Google Scholar] [CrossRef] [PubMed]
- Fornal, B.; Grinstein, B. Neutron’s dark secret. Mod. Phys. Lett. A 2020, 35, 2030019. [Google Scholar] [CrossRef]
- Tang, Z.; Blatnik, M.; Broussard, L.; Choi, J.; Clayton, S.; Cude-Woods, C.; Currie, S.; Fellers, D.; Fries, E.; Geltenbort, P.; et al. Search for the Neutron Decay n→ X+γ where X is a dark matter particle. Phys. Rev. Lett. 2018, 121, 022505. [Google Scholar] [CrossRef] [PubMed]
- Serebrov, A.P.; Aleksandrov, E.B.; Dovator, N.A.; Dmitriev, S.P.; Fomin, A.K.; Geltenbort, P.; Kharitonov, A.G.; Krasnoschekova, I.A.; Lasakov, M.S.; Murashkin, A.N.; et al. Experimental search for neutron: Mirror neutron oscillations using storage of ultracold neutrons. Phys. Lett. B 2008, 663, 181–185. [Google Scholar] [CrossRef]
- Motta, T.F.; Guichon, P.A.M.; Thomas, A.W. Implications of Neutron Star Properties for the Existence of Light Dark Matter. J. Phys. G 2018, 45, 05LT01. [Google Scholar] [CrossRef]
- Motta, T.F.; Guichon, P.A.M.; Thomas, A.W. Neutron to Dark Matter Decay in Neutron Stars. Int. J. Mod. Phys. A 2018, 33, 1844020. [Google Scholar] [CrossRef]
- Baym, G.; Beck, D.H.; Geltenbort, P.; Shelton, J. Testing Dark Decays of Baryons in Neutron Stars. Phys. Rev. Lett. 2018, 121, 061801. [Google Scholar] [CrossRef]
- McKeen, D.; Nelson, A.E.; Reddy, S.; Zhou, D. Neutron Stars Exclude Light Dark Baryons. Phys. Rev. Lett. 2018, 121, 061802. [Google Scholar] [CrossRef]
- Husain, W.; Motta, T.F.; Thomas, A.W. Consequences of neutron decay inside neutron stars. J. Cosmol. Astropart. Phys. 2022, 10, 028. [Google Scholar] [CrossRef]
- Ivanov, A.N.; Höllwieser, R.; Troitskaya, N.I.; Wellenzohn, M.; Berdnikov, Y.A. Neutron Dark Matter Decays. arXiv 2018, arXiv:1806.10107. [Google Scholar] [CrossRef]
- Strumia, A. Dark Matter interpretation of the neutron decay anomaly. J. High Energy Phys. 2022, 2022, 67. [Google Scholar] [CrossRef]
- Husain, W.; Thomas, A.W. Novel neutron decay mode inside neutron stars. J. Phys. Nucl. Part. Phys. 2022, 50, 015202. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Atta, D.; Imam, K.; Basu, D.N.; Samanta, C. Compact bifluid hybrid stars: Hadronic matter mixed with self-interacting fermionic asymmetric dark matter. Eur. Phys. J. 2017, 77, 440. [Google Scholar] [CrossRef]
- Bertone, G.; Fairbairn, M. Compact stars as dark matter probes. Phys. Rev. D 2008, 77, 043515. [Google Scholar] [CrossRef]
- Kouvaris, C. WIMP annihilation and cooling of neutron stars. Phys. Rev. D 2008, 77, 023006. [Google Scholar] [CrossRef]
- Ciarcelluti, P.; Sandin, F. Have neutron stars a dark matter core? Phys. Lett. B 2011, 695, 19–21. [Google Scholar] [CrossRef]
- Sandin, F.; Ciarcelluti, P. Effects of mirror dark matter on neutron stars. Astropart. Phys. 2009, 32, 278–284. [Google Scholar] [CrossRef]
- Leung, S.C.; Chu, M.C.; Lin, L.M. Dark-matter admixed neutron stars. Phys. Rev. D 2011, 84, 107301. [Google Scholar] [CrossRef]
- Ellis, J.; Hütsi, G.; Kannike, K.; Marzola, L.; Raidal, M.; Vaskonen, V. Dark matter effects on neutron star properties. Phys. Rev. D 2018, 97, 123007. [Google Scholar] [CrossRef]
- Bell, N.F.; Busoni, G.; Motta, T.F.; Robles, S.; Thomas, A.W.; Virgato, M. Nucleon Structure and Strong Interactions in Dark Matter Capture in Neutron Stars. Phys. Rev. Lett. 2020, 127, 111803. [Google Scholar] [CrossRef]
- Husain, W.; Thomas, A.W. Possible nature of dark matter. J. Cosmol. Astropart. Phys. 2021, 2021, 086. [Google Scholar] [CrossRef]
- Mielke, E.W.; Schunck, F.E. Boson stars: Alternatives to primordial black holes? Nucl. Phys. B 2000, 1, 185–203. [Google Scholar] [CrossRef]
- Blinnikov, S.I.; Khlopov, M. Possible astronomical effects of mirror particles. Sov. Astron. 1983, 27, 371–375. [Google Scholar]
- Horowitz, C.; Reddy, S. Gravitational Waves from Compact Dark Objects in Neutron Stars. Phys. Rev. Lett. 2019, 122, 071102. [Google Scholar] [CrossRef] [PubMed]
- Bertoni, B.; Nelson, A.E.; Reddy, S. Dark matter thermalization in neutron stars. Phys. Rev. D 2013, 88, 123505. [Google Scholar] [CrossRef]
- Berryman, J.M.; Gardner, S.; Zakeri, M. Neutron Stars with Baryon Number Violation, Probing Dark Sectors. Symmetry 2022, 14, 518. [Google Scholar] [CrossRef]
- McKeen, D.; Pospelov, M.; Raj, N. Neutron Star Internal Heating Constraints on Mirror Matter. Phys. Rev. Lett. 2021, 127, 061805. [Google Scholar] [CrossRef]
- de Lavallaz, A.; Fairbairn, M. Neutron Stars as Dark Matter Probes. Phys. Rev. D 2010, 81, 123521. [Google Scholar] [CrossRef]
- Busoni, G. Capture of Dark Matter in Neutron Stars. Moscow Univ. Phys. 2022, 77, 301–305. [Google Scholar] [CrossRef]
- Sen, D.; Guha, A. Implications of feebly interacting dark sector on neutron star properties and constraints from GW170817. Mon. Not. Roy. Astron. Soc. 2021, 504, 3. [Google Scholar] [CrossRef]
- Guha, A.; Sen, D. Feeble DM-SM interaction via new scalar and vector mediators in rotating neutron stars. J. Cosmol. Astropart. Phys. 2021, 09, 027. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 448. [Google Scholar] [CrossRef] [PubMed]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C.; et al. GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar] [CrossRef]
- Lawley, S.; Bentz, W.; Thomas, A.W. Nucleons, nuclear matter and quark matter: A Unified NJL approach. J. Phys. G 2006, 32, 667–680. [Google Scholar] [CrossRef]
- Whittenbury, D.L.; Carroll, J.D.; Thomas, A.W.; Tsushima, K.; Stone, J.R. Quark-Meson Coupling Model, Nuclear Matter Constraints and Neutron Star Properties. Phys. Rev. C 2014, 89, 065801. [Google Scholar] [CrossRef]
- Whittenbury, D.L.; Matevosyan, H.H.; Thomas, A.W. Hybrid stars using the quark-meson coupling and proper-time Nambu–Jona-Lasinio models. Phys. Rev. C 2016, 93, 035807. [Google Scholar] [CrossRef]
- Bodmer, A.R. Collapsed Nuclei. Phys. Rev. D 1971, 4, 1601–1606. [Google Scholar] [CrossRef]
- Witten, E. Cosmic separation of phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Bombaci, I.; Parenti, I.; Vidana, I. Quark Deconfinement and Implications for the Radius and the Limiting Mass of Compact Stars. Astrophys. J. 2004, 614, 314–325. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, C. Quantum nucleation of up-down quark matter and astrophysical implications. Phys. Rev. D 2020, 102, 083003. [Google Scholar] [CrossRef]
- Terazawa, H. Super-Hypernuclei in the Quark-Shell Model. J. Phys. Soc. Jpn. 1989, 58, 3555–3563. [Google Scholar] [CrossRef]
- Bednarek, I.; Haensel, P.; Zdunik, J.L.; Bejger, M.; Mańka, R. Hyperons in neutron-star cores and a 2M pulsar. Astron. Astrophys. 2012, 543, A157. [Google Scholar] [CrossRef]
- Vidaña, I. Hyperons and neutron stars. AIP Conf. Proc. 2015, 1645, 79–85. [Google Scholar] [CrossRef]
- Oertel, M.; Gulminelli, F.; Providência, C.; Raduta, A.R. Hyperons in neutron stars and supernova cores. Eur. Phys. J. A 2016, 52, 1–22. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef]
- Balberg, S.; Gal, A. An effective equation of state for dense matter with strangeness. Nucl. Phys. A 1997, 625, 435–472. [Google Scholar] [CrossRef]
- Glendenning, N.K. Neutron stars are giant hypernuclei? Astrophys. J. 1985, 293, 470–493. [Google Scholar] [CrossRef]
- Kaplan, D.; Nelson, A. Strange goings on in dense nucleonic matter. Phys. Lett. B 1986, 175, 57–63. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Pei, S.; Weber, F. Signal of Quark Deconfinement in the Timing Structure of Pulsar Spin-Down. Phys. Rev. Lett. 1997, 79, 1603–1606. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Moszkowski, S.A. Reconciliation of neutron-star masses and binding of the Λ in hypernuclei. Phys. Rev. Lett. 1991, 67, 2414–2417. [Google Scholar] [CrossRef]
- Glendenning, N.K. Quark Stars. In Compact Stars: Nuclear Physics, Particle Physics and General Relativity; Springer: New York, NY, USA, 1997; pp. 289–302. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L. Nuclear Matter in Neutron Stars. In Handbook of Supernovae; Alsabti, A.W., Murdin, P., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 1331–1351. [Google Scholar] [CrossRef]
- Shuryak, E.V. Quantum chromodynamics and the theory of superdense matter. Physrep 1980, 61, 71–158. [Google Scholar] [CrossRef]
- Weber, F.; Negreiros, R.; Rosenfield, P. Neutron Star Interiors and the Equation of State of Superdense Matter. In Neutron Stars and Pulsars; Springer: Berlin/Heidelberg, Germany, 2009; Volume 357. [Google Scholar]
- Spinella, W.M.; Weber, F. Hyperonic neutron star matter in light of GW170817. Astron. Nachrichten 2019, 340, 145–150. [Google Scholar] [CrossRef]
- Weber, F. Strange Quark Matter Inside Neutron Stars. In Handbook of Supernovae; Alsabti, A.W., Murdin, P., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–24. [Google Scholar] [CrossRef]
- Terazawa, H. A new trend in high-energy physics: Current topics in nuclear and particle physics. In Proceedings of the International Conference on New Trends in High-Energy Physics: Experiment, Phenomenology, Theory, Yalta, Ukraine, 22–29 September 2001; pp. 246–255. [Google Scholar]
- Husain, W.; Thomas, A.W. Hybrid stars with hyperons and strange quark matter. AIP Conf. Proc. 2021, 2319, 080001. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. Neutron Star Structure and the Equation of State. Astrophys. J. 2001, 550, 426–442. [Google Scholar] [CrossRef]
- Zhao, T.; Lattimer, J.M. Quarkyonic matter equation of state in beta-equilibrium. Phys. Rev. D 2020, 102, 023021. [Google Scholar] [CrossRef]
- Drischler, C.; Han, S.; Lattimer, J.M.; Prakash, M.; Reddy, S.; Zhao, T. Limiting masses and radii of neutron stars and their implications. Phys. Rev. C 2021, 103, 045808. [Google Scholar] [CrossRef]
- Cierniak, M.; Blaschke, D. Hybrid neutron stars in the mass-radius diagram. Astron. Nachr. 2021, 342, 819–825. [Google Scholar] [CrossRef]
- Shahrbaf, M.; Blaschke, D.; Typel, S.; Farrar, G.R.; Alvarez-Castillo, D.E. Sexaquark dilemma in neutron stars and its solution by quark deconfinement. Phys. Rev. D 2022, 105, 103005. [Google Scholar] [CrossRef]
- Nishizaki, S.; Yamamoto, Y.; Takatsuka, T. Hyperon-Mixed Neutron Star Matter and Neutron Stars. Prog. Theor. Phys. 2002, 108, 703–718. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Togashi, H.; Tamagawa, T.; Furumoto, T.; Yasutake, N.; Rijken, T.A. Neutron-star radii based on realistic nuclear interactions. Phys. Rev. C 2017, 96, 065804. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Yasutake, N.; Rijken, T.A. Quark-quark interaction and quark matter in neutron stars. Phys. Rev. C 2022, 105, 015804. [Google Scholar] [CrossRef]
- Motta, T.F.; Thomas, A.W. The role of baryon structure in neutron stars. Mod. Phys. Lett. A 2022, 37, 2230001. [Google Scholar] [CrossRef]
- Guichon, P.A.M. A Possible Quark Mechanism for the Saturation of Nuclear Matter. Phys. Lett. B 1988, 200, 235–240. [Google Scholar] [CrossRef]
- Guichon, P.A.M.; Saito, K.; Rodionov, E.N.; Thomas, A.W. The Role of nucleon structure in finite nuclei. Nucl. Phys. A 1996, 601, 349–379. [Google Scholar] [CrossRef]
- Stone, J.R.; Guichon, P.A.M.; Reinhard, P.G.; Thomas, A.W. Finite Nuclei in the Quark-Meson Coupling Model. Phys. Rev. Lett. 2016, 116, 092501. [Google Scholar] [CrossRef]
- Rikovska Stone, J.; Guichon, P.; Matevosyan, H.; Thomas, A. Cold uniform matter and neutron stars in the quark–meson-coupling model. Nucl. Phys. A 2007, 792, 341–369. [Google Scholar] [CrossRef]
- Saito, K.; Tsushima, K.; Thomas, A.W. Nucleon and hadron structure changes in the nuclear medium and impact on observables. Prog. Part. Nucl. Phys. 2007, 58, 1–167. [Google Scholar] [CrossRef]
- DeGrand, T.A.; Jaffe, R.L.; Johnson, K.; Kiskis, J.E. Masses and Other Parameters of the Light Hadrons. Phys. Rev. D 1975, 12, 2060. [Google Scholar] [CrossRef]
- Guichon, P.A.M.; Stone, J.R.; Thomas, A.W. Quark–Meson-Coupling (QMC) model for finite nuclei, nuclear matter and beyond. Prog. Part. Nucl. Phys. 2018, 100, 262–297. [Google Scholar] [CrossRef]
- Motta, T.F.; Kalaitzis, A.M.; Antić, S.; Guichon, P.A.M.; Stone, J.R.; Thomas, A.W. Isovector Effects in Neutron Stars, Radii and the GW170817 Constraint. Astrophys. J. 2019, 878, 159. [Google Scholar] [CrossRef]
- Krein, G.; Thomas, A.W.; Tsushima, K. Fock terms in the quark meson coupling model. Nucl. Phys. A 1999, 650, 313–325. [Google Scholar] [CrossRef]
- Tolman, R.C. Effect of Inhomogeneity on Cosmological Models. Proc. Natl. Acad. Sci. USA 1934, 20, 169–176. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love Numbers of Neutron Stars. Astrophys. J. 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D 2010, 81, 123016. [Google Scholar] [CrossRef]
- Cline, J.M.; Cornell, J.M. Dark decay of the neutron. J. High Energy Phys. 2018, 7, 81. [Google Scholar] [CrossRef]
- Rajendran, S.; Ramani, H. Composite solution to the neutron lifetime anomaly. Phys. Rev. D 2021, 103, 035014. [Google Scholar] [CrossRef]
- Berezhiani, Z.; Biondi, R.; Mannarelli, M.; Tonelli, F. Neutron-mirror neutron mixing and neutron stars. Eur. Phys. J. C 2021, 81, 1–23. [Google Scholar] [CrossRef]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Ann. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Bramante, J.; Linden, T.; Tsai, Y.D. Searching for dark matter with neutron star mergers and quiet kilonovae. Phys. Rev. D 2018, 97, 055016. [Google Scholar] [CrossRef]
- Antypas, D.; Banerjee, A.; Bartram, C.; Baryakhtar, M.; Betz, J.; Bollinger, J.J.; Boutan, C.; Bowring, D.; Budker, D.; Carney, D.; et al. New Horizons: Scalar and Vector Ultralight Dark Matter. arXiv 2022, arXiv:2203.14915. [Google Scholar] [CrossRef]
- Cadamuro, D.; Redondo, J. Cosmological bounds on pseudo Nambu-Goldstone bosons. J. Cosmol. Astropart. Phys. 2012, 2, 032. [Google Scholar] [CrossRef]
- Caputo, A.; O’Hare, C.A.J.; Millar, A.J.; Vitagliano, E. Dark photon limits: A cookbook. Phys. Rev. D 2021, 104, 095029. [Google Scholar] [CrossRef]
- Aprile, E.; Abe, K.; Agostini, F.; Ahmed Maouloud, S.; Alfonsi, M.; Althueser, L.; Angelino, E.; Angevaare, J.R.; Antochi, V.C.; Antón Martin, D.; et al. Emission of single and few electrons in XENON1T and limits on light dark matter. Phys. Rev. D 2022, 106, 022001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Husain, W.; Sengupta, D.; Thomas, A.W. Constraining Dark Boson Decay Using Neutron Stars. Universe 2023, 9, 307. https://doi.org/10.3390/universe9070307
Husain W, Sengupta D, Thomas AW. Constraining Dark Boson Decay Using Neutron Stars. Universe. 2023; 9(7):307. https://doi.org/10.3390/universe9070307
Chicago/Turabian StyleHusain, Wasif, Dipan Sengupta, and A. W. Thomas. 2023. "Constraining Dark Boson Decay Using Neutron Stars" Universe 9, no. 7: 307. https://doi.org/10.3390/universe9070307
APA StyleHusain, W., Sengupta, D., & Thomas, A. W. (2023). Constraining Dark Boson Decay Using Neutron Stars. Universe, 9(7), 307. https://doi.org/10.3390/universe9070307







