Abstract
Upcoming LIGO–Virgo–KAGRA (LVK) observational runs offer new opportunities to probe the central engines of extreme transient events. Cosmological gamma-ray bursts (GRBs) and core-collapse supernovae (CC-SNe), in particular, are believed to be powered by compact objects, i.e., a neutron star (NS) or black hole (BH). A principal distinction between an NS and BH is the energy reservoir in the angular momentum . Per unit mass, this reaches a few percent in a rapidly rotating NS and tens of percent in a Kerr BH, respectively. Calorimetry by on a descending chirp may break the degeneracy between the two. We review this approach, anticipating new observational opportunities for planned LVK runs. GRB170817A is the first event revealing its central engine by a descending chirp in gravitational radiation. An accompanying energy output is observed during GRB170817A in the aftermath of the double neutron star merger GW170817. The progenitors of normal long GRBs, on the other hand, are the rare offspring of CC-SNe of type Ib/c. Yet, the extended emission to SGRBs (SGRBEEs) shares similar durations and the same Amati-relation of the prompt GRB emission of LGRBs, pointing to a common central engine. The central engine of these extreme transient events has, hitherto, eluded EM observations alone, even when including neutrino observations, as in SN1987A. The trigger signaling the birth of the compact object and the evolution powering these events is expected to be revealed by an accompanying GW signal, perhaps similar to that of GRB170817A. For GRB170817A, exceeds in the initial hyper-massive neutron star (HMNS) produced in the immediate aftermath of GW170817. It identifies the spin-down of a Kerr BH of mass ∼ defined by the total mass of GW170817. This observation is realized in spectrograms generated by Butterfly matched filtering, a time-symmetric analysis with equal sensitivity to ascending and descending chirps, calibrated by signal injection experiments. It is implemented on a heterogeneous computing platform with synaptic parallel processing in F90/C++/C99 under bash. A statistical significance of is derived from multi-messenger event timing, based on a probability of false alarm (PFA) factored over a probability by causality and a p-value of consistency between H1 and L1 observations. For upcoming observations, this approach may be applied to similar emissions from SNIb/c and GRBs in the Local Universe, upon the mass-scaling of present results by the mass of their putative black hole-central engines.
1. Introduction
With the detection of compact binary coalescence, which is well-established by LIGO–Virgo–KAGRA (LVK) [1,2,3], advancing search methods promise astronomical observations in a radically new window to unmodeled gravitational-wave (GW) transient sources. The evolving Universe is rife with extreme transient sources associated with the endpoints of massive stars and their compact stellar mass remnants, i.e., neutron stars (NS) and black holes (BH). Stellar mass BHs are believed to form in the core collapse of massive stars at the tail of the Salpeter stellar initial mass function [4]. Those observed with LIGO–Virgo–KAGRA (LVK) are in binaries sufficiently compact to merge within the Hubble time and appear to originate in the late-time Universe, no earlier than around the peak of the cosmic star formation rate [5]. LVK observations include a few mergers of double neutron star (DNS) and NS-BH systems. The DNS merger GW170817 stands out for its associated kilonova AT2017gfo and GRB170817A [6,7,8,9], providing the first member of the upcoming joint EM-GW surveys expected from upcoming LVK observational runs. With improved detector sensitivity, upcoming runs offer new opportunities to probe the formation and evolution of the central engines of core-collapse supernovae (CC-SNe) and gamma-ray bursts (GRBs).
Gamma-ray bursts were discovered serendipitously [10] as non-thermal high-energy transient events with a bimodal distribution in duration, isotropically distributed over the sky [11,12,13,14]. They appear as short (s) and long GRBs (s), mirrored in relatively hard and soft extended spectra, respectively, with the latter satisfying the Amati-relation [15] between the peak energy () and isotropic equivalent energy output (), and related correlations [16,17,18,19,20,21]. While the prompt GRB emission has been attributed to dissipation in shocks derived from ultra-relativistic baryon-poor jets (BPJs) (e.g., [22,23,24]) and references therein), our description is mostly phenomenological and a detailed theoretical modeling is still lacking. Nevertheless, a BH appears favored over an NS in powering their central engines [25,26,27,28]. BPJs may be produced in a black hole–torus system [29,30,31,32] by virtue of baryon purity along open magnetic flux tubes subtended over the black hole event horizon [33,34].
GW170817 demonstrates a DNS origin of the short GRB GRB170817A [6,35], while normal long GRBs are known to be associated with the envelope-stripped CC-SNe of type Ib/c (e.g., [36]). The latter follows the identification of their cosmological origin [37,38,39,40,41] in the endpoint of massive stars [42,43,44,45,46,47,48]. Some short GRBs come with long-duration extended emissions (SGRBEEs), which satisfy the aforementioned Amati-relation of long GRBs [49,50]. GRB060614 stands out with a duration of s (15–350 keV) [51,52,53,54,55]. With no evidence of an associated supernova [51], its initial hard spike, characteristic of short GRBs, points to a common progenitor, believed to be a merger similar to GW170817, as opposed to a failed supernova. Attributing its initial short hard spike to the formation of its central engine, this would be obscured in a failed supernova by the opaque remnant stellar envelope. By similarity in duration and spectra of EE to SGRBs and the prompt GRB emission of LGRBs derived from mergers and, respectively, CC-SNe, these high-energy emissions appear to derive from a common central engine. Their long durations point to a secular time scale for the lifetime of their central engines, i.e., a dissipative rather than a dynamical time scale, such as the fall-back of matter from debris or, respectively, a remnant stellar envelope. This timescale possibly represents the lifetime of the spin of a rapidly spinning Kerr BH interacting with the surrounding high-density matter [56].
Corrected for beaming, the prompt GRB emission of LGRBs has true energy in gamma rays narrowly distributed about [57,58,59].
LGRBs show a positive correlation of luminosity with variability [60], the latter down to time scales (ms) [25]. The extreme luminosity of GRBs and their possible counterparts in sources of ultra-high energy cosmic rays (UHECRs) may, in fact, originate from the intermittent behaviors of their central engines (e.g., [61,62,63,64,65]). The dimensionless measure of energetic time-variability [66,67]
far exceeds the same of Eddington-limited sources, such as the micro-quasar GRS1915+105 [68], showing their central engines to be extremely compact. Here, denotes the unit of luminosity in general relativity, given by the velocity of light c and Newton’s constant G. Combined, ms variability and (2) point to a central engine powered by an NS or stellar mass BH [33,69,70,71,72,73].
The energetic time-variability (2) ties in well with a stellar mass compact object produced in the core collapse of massive stars, when the nuclear burning phase ceases. Notably, pulsars in supernova remnants are neutron stars, e.g., Vela and the Crab [74], and some may be found in NS binaries, such as the Hulse–Taylor system PSR 1913+16 [75] and the relativistic binary PSR J0737-3039 [76].
While the identification of pulsars with rotating neutron stars is unambiguous, the electromagnetic spectrum offers compelling but inconclusive evidence of the nature of the central engine of GRBs despite their common origin in (the remnants of) massive stars. From the first principles, a BH cannot act similar to a pulsar by the inherent alignment of the magnetic moment and spin [77,78]. On account of the Kerr metric [79], however, the energy reservoir per unit mass in the angular momentum of a rotating BH can vastly “outsize” that of a rapidly spinning NS by an order of magnitude. This offers the potential to break the degeneracy between the two, provided a suitable fraction of is channeled into radiation “unseen”—beyond the electromagnetic spectrum—given the existing constraint (1).
LVK observations offer, for the first time, a means to extend our probe of central engines to all current radiation channels, including gravitational radiation.
Searches for unmodeled GW emissions may be approached in spectrograms, covering the bandwidth of sensitivity of the LVK detectors. Candidate GW transient emissions may, herein, appear as chirps, ascending from mergers or descending in the spin-down of a compact object, notably a neutron star or a black hole.
This appears opportune for extreme transient events powered by a BH interacting with surrounding high-density matter, when gravitational radiation may be the dominant channel of emission with the accompanying output in MeV neutrinos and electromagnetic radiation [34]. Starting from the progenitor, we look for the trigger signaling the birth of the central engine. Of particular interest is the DNS merger GW170817 [6] and, perhaps, the more numerous energetic SNIb/c associated with LGRBs [80,81].
At the relative proximity of Mpc [82,83], GW170817 produces a compact object triggering the onset of GRB170817A [6,7,8,9]. Extended emissions in gravitational radiation may tell us about the nature of the central engine of GRB170817A—NS or BH—in addition to the physical properties of the progenitor GW170817 [84,85,86,87], realizing a key objective of multi-messenger observations [88,89].
GW170817 reveals the extended evolution in complex multi-messenger emission, which includes the kilonova AT2017gfo and GRB170817A of duration s [90], following this DNS merger at time [91],
where dots refer to emissions in MeV neutrinos and gravitational radiation. AT2017gfo has been attributed to a powerful MeV neutrino-driven wind from the initial hypermassive NS (HMNS) produced in the immediate aftermath of GW170817, although additional contributions following delayed gravitational collapse cannot be excluded by (neutrino-driven) neutron-rich winds from a relatively lower temperature torus [33,34] around a BH [92,93,94,95,96].
A LIGO gravitational-wave observation of (3) requires a sensitivity close to the limit defined by the strain-noise amplitude of the detectors conforming to the theory of matched filtering [97]. In particular, the ascending chirp GW170817 may be followed by an unmodeled descending chirp characteristic for the spin-down of the HMNS [98,99,100] and/or the compact object powering GRB170817A. A suitable starting point to probe for unmodeled signals in (3) is provided by the Butterfly matched filtering over a bank of time-symmetric templates of intermediate duration, originally developed to identify a broadband Kolmogorov spectrum in bright GRBs of the BeppoSAX catalog at high frequencies [101]. This approach realizes equal sensitivity to ascending and descending chirps at a sensitivity on par with CBC when this bank is sufficiently dense in : the frequency f and its time rate-of-change , suitably accelerated by heterogeneous computing [102].
We quantify the above-mentioned trigger by event timing. Given the uniform prior on timing in astrophysics on time scales less than a Hubble time and in instrumentation, event timing produces estimates of significance expressed in terms of the probability of false alarm (PFA): a type I error, given the null hypothesis of the background, assuming no event. Accurate event-timing parameterization is derived from probability density functions (PDFs), particularly for the start times of burst events. Combining statistically independent PFAs requires distinguishing between continuous and discrete stochastic variables (e.g., [70,103,104,105,106]). This is opportune when event timing extends over the mean and the difference of observations across two detectors, notably LIGO H1 and L1. Equivalent to a unitary transformation given by the rotation over , this generates statistically independent PFAs. A leading-order interpretation of results derives from energy and frequency in the gravitational-wave emission at hand, subject to priors, such as the total mass-energy of the system and limits on the mathematical–physical properties of HMNS and Kerr BHs.
In this review, we revisit a recent direct detection of a descending chirp in gravitational waves during GRB170817A and the observational consequences for its central engine. Given the upcoming LVK observations, we emphasize the methods of analysis by anticipating new opportunities to probe the central engines of GRBs and associated SNIb/c in the Local Universe, given the significant improvement in sensitivity in upcoming LVK runs. Accordingly, this review is organized as follows:
- The spin energy in the gravitational collapse of the initial HMNS (e.g., [100,107,108]), to a Kerr black hole (Section 2);
- Event timing in multi-messenger observations (Section 3);
- Observing GW transient sources in time-symmetric spectrograms (Section 4);
- What triggered GRB170817A following GW170817? (Section 5);
Section 7 and Section 8 are included for completeness, closely following the original work in [109].
In Section 9, we conclude with a discussion on observational consequences and an outlook on possibly similar approaches to study the central engine of GRBs and SNIb/c in the Local Universe with upcoming LVK observations in joint EM-GW observations.
2. Gravitational Collapse of an HMNS to a Kerr Black Hole
The multi-messenger events SN1987A and GRB170817A both have known progenitors: the blue supergiant (Sanduleak-69 202) in the LMC at a distance of 50 kpc [110,111] with an associated MeV neutrino burst [112,113] and, respectively, from the merger event GW170817 of a double neutron star (DNS). They have the initial formation of a (hyper)massive NS in common, whose fate is inconclusive based on these progenitor data alone. For a complete interpretation, it is essential, however, to determine its continuing evolution. (This includes its potential prior evolution in the case of SN1987A, below). A continued (delayed) gravitational collapse to a BH may have dramatic implications for the central engine powering the supernova explosion and, respectively, GRB170817A, given the principal distinction in the energy reservoir in the angular momentum of an HMNS [114] and a Kerr BH (e.g., [115]). After all, classical mechanics teaches us that the prompt gravitational collapse increases , preserving mass M and angular momentum J.
In (3), gradually decreases during the merger phase GW170817, reaching the first minimum at coalescence to an HMNS. If long-lived, may continue a decline upon radiating baryon-rich winds and, perhaps, gravitational radiation when sufficiently non-axisymmetric deformations are present. Any loss of stability, however, by spin-down, cooling, and internal re-distribution of J, may result in the delayed gravitational collapse to a BH. If so, this enhances as the following estimate shows. Conserving M and J in the prompt gravitational collapse preserves the specific angular momentum of the newly formed black hole and, hence, the dimensionless Kerr parameter . The spin energy of the HMNS increases to [56,79]. Specialized to GW170817, we estimate [109]
where for the moment of inertia of the HMNS with the gravitational radius , radius R, and angular velocity . Here, G is Newton’s constant and c is the velocity of light, and we ignore further enhancement from, e.g., hyperaccretion (e.g., [116,117]). This enhancement sets the stage for potentially significant extended emissions by coupling to non-axisymmetric high-density matter surrounding the black hole at relatively moderate gravitational-wave frequencies [34], distinct from what might derive directly from the progenitor HMNS.
Previously, we reported on the direct detection of a descending chirp in gravitational radiation during GRB170817A [118]. Starting between the time of merger and the onset of GRB170817A, its total energy output [81]
is emitted at gravitational-wave frequencies Hz. For quadrupole gravitational-wave emissions, (5) is to be seen against the estimated bound on in the spin energy of the initial HMNS,
With (5) exceeding (6) by a factor of about 4, even at a maximal radius R, Equation (5) breaks the degeneracy between the HMNS and a BH. This holds true especially given the start time s of (5), the post-merger to GW170817, when neutrino cooling and internal dissipation are expected to produce a uniform rotator [119]. In contrast, Equation (5) is consistent with radiated off in the spin-down of a Kerr BH against a non-axisymmetric high-density torus [81].
The above shows the power of calorimetry in gravitational radiation, breaking the degeneracy between an (HM)NS and BH formed in continuing gravitational collapse. Indeed, EM calorimetry falls woefully short; the combined output of GRB170817A and AT2017gfo [120,121,122,123,124] is limited to
Even so, EM observations provide us with crucial information on event timing.
3. Event Timing in Multi-Messenger Observations
SN1987A is instructive once again, for its similar arrival times of the MeV neutrino burst in Kamiokande II and IMB [112,125,126], signaling the core collapse of its massive stellar progenitor, well before the optical light of this type II supernova explosion in the LMC at a distance of about 50 kpc. Likewise, GW170817 is picked up by LIGO H1 and L1 detectors, essentially simultaneously (L1 slightly before H1) to the progenitor of GRB170817A in NGC4993 at a distance of 40 Mpc. (Accompanying the MeV neutrino emission is a posteriori undetectable). These two delay times represent causality between the progenitor star, trigger, and the ensuing events: SN 1987A and, respectively, the binary progenitor of the ensuing high-energy transient GRB170817A.
While consistent, the two multi-messenger datasets in SN1987A and GRB170817A do not necessarily cover the complete evolution from the progenitor to the final remnant. Moreover, Equation (3) shows an additional kilonova AT2017gfo, derived from neutron-rich winds in evolution after the merger, which may include the delayed gravitational collapse to and evolution of a rotating black hole. SN1987A might have had two precursor triggers in the MeV emission (see [113]). A low-count but potentially significant MeV neutrino burst was picked up by the Liquid Scintillation Detector (LSD) and KII a few hours prior to the main KII-IMB MeV neutrino burst (reviewed in [127,128]). It may suggest a possible two-stage process, starting with the formation of a DNS to radiate off the excess angular momentum in the gravitational radiation before coalescence into a (proto)-NS producing the primary MeV neutrino burst [126].
3.1. The Gap Time between GRB170817A and Its Progenitor GW170817
A complete observation covering the entire evolution from the progenitor to the final remnant in (3), therefore, may involve additional precursor GW signals. In particular, the true trigger of GRB170817A may be defined by a gravitational-wave signal that starts in the gap between the merger GW170817 at and the time-of-onset of GRB170817A at ,
This gap time may be accounted for by the sum of the lifetime of the HMNS on the basis of the duration of the MeV neutrino wind powering AT2017gfo [129] and a delay time between the observed time-of-onset of GRB170817A,
Following the gravitational collapse of the HMNS, we identify with the relativistic delay time between GRB170817A and the start time of the gravitational-wave emission signaling the birth of its engine. Attributing GRB170817A to a dissipative front at a distance r from the central engine, propagating at an angle relative to the line-of-sight to the observer, ; thus,
assuming the same velocity of propagation for both gravitational waves and electromagnetic radiation (e.g., [130,131]) (also see [22]).
Assuming for a Lorentz factor of the ultra-relativistic jet powering the GRB, (cf. [23,132]). However, GRB170817A is likely seen off-axis at [133]. Estimating r, this approximation may not apply, and the more conservative second term on the right of (10) must be used instead.
Assuming AT2017gfo to be mostly powered by the MeV neutrino-driven neutron-rich wind from the initial HMNS, its “blue” component [134,135] implies a finite lifetime of this HMNS of about s [129,136,137,138]. (see [139,140,141,142] for a possibly long-lived supermassive NS remnant). This still leaves a positive delay time between the gravitational collapse of the HMNS and GRB170817A, here identified with the relativistic time delay (10). We proceed with the time of formation of the central engine of GRB170817A, i.e., at a preceding trigger time ,
where denotes the interval of (8) (Figure 1) with an observable descending chirp (Figure 2, Section 5) starting at
based on the mean of , inferred from an independent analysis of H1 and L1 data (Section 8). This delay time of the gravitational collapse (12) is indeed consistent with s [129] of the HMNS inferred from AT2017gfo [24,81,129,143,144,145,146,147,148] (reviewed in [9]).
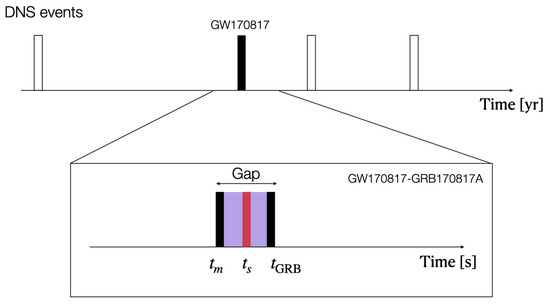
Figure 1.
Schematic of event timing in GW170817-GRB170817A, where denotes the merger time and is the time-of-onset of the accompanying GRB170817A following a gap s (bottom). By causality, the central engine of GRB170817A forms in this gap: , with a potentially accompanying output , provided is resolved at a sufficiently high resolution ). The initial HMNS formed in the immediate aftermath of GW170817 experiences gravitational collapse to a black hole disk or torus system if exceeds the canonical bounds on the maximal spin energy of the HMNS, given the observed frequency in gravitational radiation (4). (Reprinted from [109]).
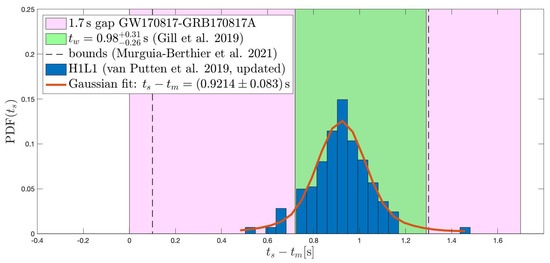
Figure 2.
PDF() (blue) of the start time in a descending chirp in gravitational radiation with duration ∼s contemporaneous with GRB170817A (s [90]). The delay time s (updated from [118]) satisfies causality (11) with , carrying PFA (14). This delay is consistent with the lifetime of the HMNS (green, [129]). By energy and frequency , it reveals black hole spin-down in the central engine of GRB170817A, following rejuvenation in gravitational collapse of the initial HMNS. Estimates of the lifetime of the HMNS are included (as reviewed in [9]). (Reprinted from [109]).
Combined with [133], s, we arrive at (cf. [149])
for , where AU cm. For the first time, EM-GW observations hereby constrain (10), which is central to the process of prompt GRB emissions.
3.2. Event Timing by the Trigger Time of GRB170817A
In searches for gravitational-wave emissions triggered by gravitational collapse, Equation (11) defines the aforementioned gap condition, providing a causality constraint on with a uniform prior. These priors are considered canonical for timing in astrophysics, (specifically over time scales less than a Hubble time) and are also widely adopted in instrumentation. Over an observational time T, Equation (11) hereby carries PFA—a type I error—for it to be satisfied by mere chance under the null hypothesis () of the stationary detector noise,
A specific implementation involves an indicator function that marks an event time , here, the start time of a candidate’s emission feature, according to a global maximum of over the observation time T. is a continuous stochastic observable, where is well-defined and unique. Under the null hypothesis, is uniformly distributed over , and (11) is satisfied by mere chance with probability , following a partitioning of over bins. This produces PFA (14).
In contrast, gravitational-wave emissions from a putative central engine of GRB170817A () change our expectation to , with a bias to (11), provided that is suitably devised to pick up its emission. Accordingly,
for , depending on the signal-to-noise ratio (SNR). A Monte Carlo simulation of Pr illustrates a function of the SNR, where is the location of the maximum of in data over n bins given by the sum of noise plus a signal from a source at G in a selected bin [109]. In the absence of a signal, this probability reduces to the PFA, which, here, is equal to the chance of winning a single bet in European roulette (e.g., [150]).
Event timing by (11) produces a PFA (14) fixed by context; here, it is GW170817-GRB170817A. This is quite different from PFAs inferred from a statistic in a continuous observable, such as SNR. In particular, (14) does not involve numerical or observational parameters, such as trial factors, provided that (11) applies. The latter requires that the measurement uncertainty in be small relative to , i.e.,
where is derived from the PDF() defined by the measurement at hand (Section 7). In this sense, (11) represents a discrete event-timing condition. The minimum of Pr, PFA (14) is an ordinary probability that can be easily combined with other PFAs [151,152,153]. Box 1 highlights some key elements of this section.
Box 1. The delayed trigger time of GRB170817A.
- GW170817 initially produced an HMNS, evidenced by the kilonova AT2017gfo, followed by GRB170817A across a duration gap of s, containing the time of the gravitational collapse of the HMNS to a BH, .
- The black hole is initially rapidly spinning, as evidenced by an output in Hz, exceeding the spin energy of the HMNS.
- The EM-GW event timing shows tight consistency in the lifetime s of the HMNS [129] and the start time s of the extended emission (Figure 2).
4. Observations of GW Transient Emission in Time-Symmetric Spectrograms
The prototypical spectrograms are produced by time-sliced fast Fourier transforms (FFTs). High-resolution spectrograms are obtained by applying a filtering process that covers the effectively dense cover of the desired bandwidth by discrete frequencies, subject to the Nyquist sample rate criterion. When applied to searches for transient signals in noisy data [97,154], a further restriction is derived from the choice of the time slice : a finite bandwidth associated with each frequency is derived from the time–frequency uncertainty relation,
This sensitivity allows for the detection of transient signals characterized by time-varying frequencies with a finite slope up to . Time-sliced FFT hereby realizes a time-symmetric sensitivity, improved by a factor with , according to the theory of matched filtering. When is large, the condition limits . According to the theory of matched filtering, the signal-to-noise improvement is hereby limited to
Figure 3 shows the spectrograms by the time-sliced FFT to H1- and L1-data of GW170817.
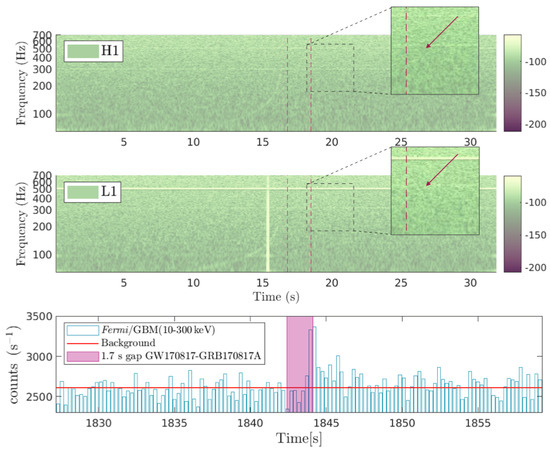
Figure 3.
(Upper and middle panels) Spectrograms (32 s) of about GW170817 for H1 and L1 were generated by conventional time-sliced FFT (using GWXplore [149]). The ascending chirp produced by the merger in the run-up to coalescence is clearly expressed. Following the coalescence event, a descending chirp can be distinguished during GRB170817A. (lower panel) This outcome serves as an illustration of a time-symmetric, unmodeled observation of a transient GW event. (Reprinted from [149]).
For instance, a chirp-changing frequency by a few hundred Hz over the course of a few seconds has a slew rate of s and, hence, . For frequencies below 1 kHz, (18) leaves an improvement of no more than a factor of a few.
4.1. Butterfly Matched Filtering
To go beyond (18), we circumvent (17) by considering an alternative filter bank of chirp-like templates of frequencies with finite , with compact support over a choice of . Chirp-like templates enable the capture of signals with finite over some intermediate time scale of the phase coherence. (In searches for unknown signals, is a search parameter). To this end, we consider a two-dimensional bank of templates densely covering a region in . Time symmetry can be preserved by construction, i.e., by taking the differences between such chirp-like templates and their time-reversed counterparts. This approach has been successfully applied in the identification of the broadband Kolmogorov turbulence in the Poisson noise-dominated light curves of bright GRBs in the BeppoSAX catalog [101]. Figure 4 shows the resulting spectrum, which can be resolved with an order of magnitude beyond what is achieved with the conventional Fourier analysis. An early porting to the gravitational-wave data analysis to SN2010br is reported in [155].
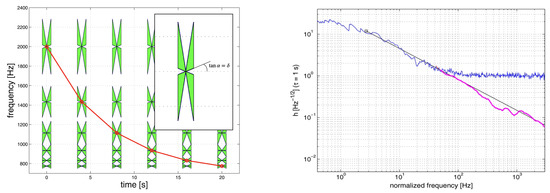
Figure 4.
(Left panel) Butterfly matched filtering schematically indicated by patterns (“green”) with a minimum slew rate at each point in the time–frequency domain. It is realized by a dense bank of chirp-like time-symmetric templates of intermediate duration. (Reprinted from [155]). Signal tracks pass through the green butterfly patterns and are suppressed otherwise. In particular, horizontal tracks of constant frequency signals are suppressed, whereby butterfly matched filtering is complementary to conventional Fourier–based filtering methods. (Right panel) Broadband Kolmogorov spectrum in an ensemble-averaged spectrum, extending to the Nyquest frequency of 1 kHz of 42 bright long GRBs in the BeppoSAX catalog, by filtering over a dense bank of 8.64 million templates (purple line). By displaying the extension of the Kolmogorov spectrum into high frequencies, this result demonstrates a sensitivity to turbulence that is more than an order of magnitude superior to the conventional Fourier analysis (blue). (Reprinted from [101]).
In searches for unknown signals, a key parameter is the intermediate time scale of the phase coherence , which may be present in the signal with a minimum in the time ratio-of-change of frequency (Figure 4). The core idea of Butterfly matched filtering involves using a filter composed of a bank of time-symmetric templates with a duration ; these templates are dense in both f and . should be restricted to the values intermediate to the total duration of the candidate signal and the total search period. Additionally, the change of frequency in time satisfies
Figure 4 provides a schematic representation using butterflies, indicating a finite range of slew rates (19) at each point in the time–frequency domain.
Time-symmetric templates are created by linearly superposing a segment from a master template with its time-reversed counterpart. The resulting time-symmetric templates ensure equal sensitivity to ascending and descending chirps [101],
where refers to a chirp-like template with compact support over a duration .
Generally, the performance gain in picking up signals with time-varying frequencies via matched filtering is expected to depend on the type of noise. The Poisson noise-dominated analysis of Figure 4 shows an improvement in sensitivity by (20), up to an order of magnitude over the conventional Fourier analysis. The gravitational strain-noise data can be effectively modeled as colored Gaussian noise, and further, with numerous lines, notably the violin modes of suspension wires. While Poisson noise is tightly correlated with the signal strength, the gravitational-wave detector noise is completely decoupled from signals passing by. The sensitivity gain of Butterfly matched filtering over the Fourier analysis may, therefore, be similar but not identical to the result shown in Figure 4. An explicit calculation is obtained by appealing to the theoretical gain in the signal-to-noise ratio by in the matched filtering, where N denotes the number of periods captured phase-coherently over the intermediate time scale set by the duration of a template.
4.1.1. Sensitivity Gain over the Time-Sliced Fourier Analysis
Regarding signals with time-varying frequencies, the gain in sensitivity of Butterfly matched filtering over the time-sliced Fourier analysis can be seen as follows. Consider a quasi-monochromatic signal admitting a Taylor series expansion , where refers to the n-th derivative at of its frequency as a function of time t. The matched filtering over a duration attempts to track the associated change in phase, . The Fourier analysis captures over a duration until this is out of phase by , relative to the true total phase , causing destructive interference. That is, , i.e., , is commensurate with the above-mentioned derivation based on the time–frequency uncertainty relation. Extending this argument to Butterfly matched filtering, which captures , we insist that , i.e., with . The improvement in is given by the ratio of these bounds, , implying a sensitivity improved by
of Butterfly matched filtering over the time-sliced Fourier analysis.
4.1.2. Application to Gravitational-Wave Data
By in (19) being sufficiently large, constant frequency signals hereby tend to be relatively suppressed, distinguishing Butterfly matched filtering from conventional Fourier analysis. This effective suppression of constant frequency is demonstrated in the line suppression of unwhitened LIGO data [155], and is further improved by pre-whitening [109,118].
An illustrative example is a signal featuring a change in frequency with the characteristic time scale of decay . In this case, and and, hence,
where . By applying (22) to a descending chirp in gravitational radiation below 700 kHz down to 200 Hz over s, we have Hz and . This leads to a gain of 2.2. In the application to gravitational-wave observations, this gain effectively brings the source closer by a factor of 2. This factor of 2 represents a significant improvement in search sensitivity roughly equivalent to one decade improvement in LIGO sensitivity.
The results of the individual H1 and L1 spectrograms may further be considered in (H1,L1)-spectrograms merged by frequency coincidences (Figure 5), providing further improvement, in contrast, by a factor of . The total gain over the time-sliced Fourier analysis of a single detector output is, hereby, 3.12.
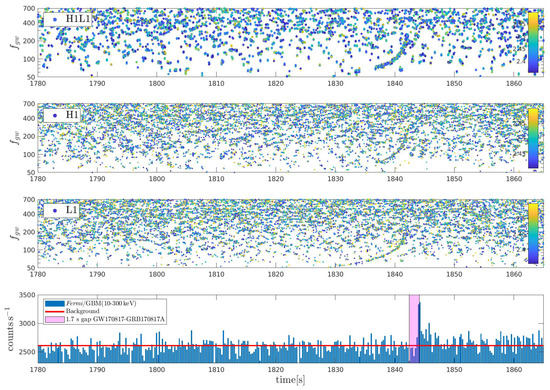
Figure 5.
The ascending–descending emission during GW170817-GRB170817A in merged (top panel) and individual (middle panels) H1,L1 spectrograms, where merging is by frequency coincidences Hz (top panel). Included is GRB170817A (lower panel). (Reprinted from [109]).
By extending (21) and (22) to include dense filtering up to , we expect a gain over the time-sliced FFT:
For instance, when using and dense filtering in , an additional gain of 1.54 over Butterfly matched filtering () is achieved, as well as a gain of 4.80 over time-sliced FFT () in the merged (H1,L1) spectrograms. Indeed, Figure 5 shows improved visual contrast consistent with the gain (23) for the ascending–descending chirp in Figure 3. Box 2 highlights some key findings of this section.
Box 2. High-resolution spectrograms: Fourier versus Butterfly matched filtering.
- GW transients may be ascending or descending chirps in gravitational radiation of mergers and, respectively, the spin-down of a compact object.
- GW transients can be searched for in high-resolution spectrograms covering the bandwidth of sensitivity of LVK over a time scale of time-slicing.
- A gain in sensitivity (23) obtains in Butterfly matched filtering over a bank of time-symmetric chirp-like templates densely covering a region of spaces.
5. Ascending–Descending GW Transient Emission during GW170817-GRB170817A
Quite generally, CBC and remnant compact objects shedding angular momentum in gravitational radiation are manifested in ascending and, respectively, descending chirps. Butterfly matched filtering [155] aims to capture ascending and descending chirps alike, selectively amplifying signals whose frequencies are slowly wandering in time and suppressing signals whose frequencies are essentially constant.
5.1. Observation in H1L1 Data
The result (5) is seen in (H1,L1)-spectrograms generated by Butterfly matched filtering. It has equal sensitivity to ascending and descending chirps by construction (20), all else being equal. Previous LIGO searches by power-excess methods, as discussed in [6,156,157], have been found to fall short of a detection threshold of [158]. This search threshold is within the excluded zone [109], beyond the total mass-energy of GW170817, with a sensitivity to signals post-merger being 0.3% compared to in GW170817 [6].
Figure 5 shows a probe of H1L1 data covering GW170817-GRB170817A by Butterfly matched filtering. The extended ascending–descending emission suggests gravitational radiation contemporaneous with GRB170817A. Produced by its central engine, this would represent emissions from compact remnant(s) of GW170817.
For a detailed consideration of the extended emission feature in Figure 5, we calibrate the sensitivity of our spectrograms to estimate the energy output in the descending branch as a potential constraint on the nature of the central engine of GRB170817A, followed by the parameter estimation and estimates of statistical significance.
5.2. Calibrated Response Curves
Sensitivity can be calibrated using response curves generated through signal injection experiments. Here, we focus on signal characteristics for the spin-down of a compact object: a descending chirp in gravitational radiation (5).
For descending chirps resulting from the spin-down of a compact object due to gravitational radiation, the following “1 + 3” parameterization is used:
appended as a delayed descending chirp to a model ascending chirp of GW170817. These curves comprise a start time —the trigger time—and three nuisance parameters, the time scale of descent , the start frequency , and the late-time frequency . Alternatively, (24) is “2 + 2” when estimating with nuisance parameters .
Figure 6 shows the results of the descending chirp models following a model merger signal GW170817 at its distance Mpc. These injections are performed before GW170817A, ensuring a sufficient distance to avoid interference with GW170817, yet remaining close enough to essentially share the same data quality.
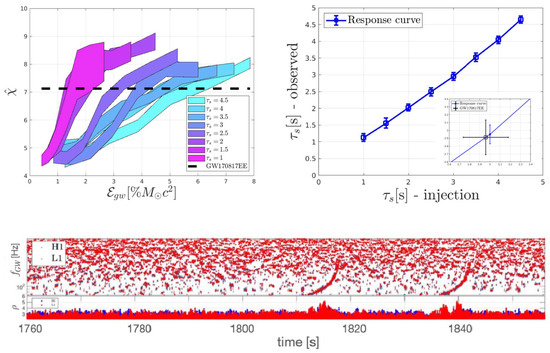
Figure 6.
(Top left panel) Response curves from modeled merger plus (delayed) post-merger signals by injection experiments on H1L1 data containing GW170817 with parameter recovery (top right panel) by image analysis of (H1,L1)-spectrograms merged by frequency coincidences (lower panel). Response curves cover descending chirps with of a few and time scales of descent covering the post-merger emission feature in GW170817. The dashed line indicates the mean peaks, averaged over time slices that are within the 10 ms light-travel time between the H1 and L1 detectors (Reprinted from [109]). (A movie showcasing the injection experiments can be found at https://zenodo.org/record/4390382, accessed on 25 May 2023).
Thus, Figure 6 shows two ascending–descending signals: the first corresponds to the injected signals, and the second represents GW170817 along with its accompanying delayed extended emission feature. Figure 6 includes results of the two-parameter injection experiments over energies and time scales
given the source distance Mpc of GW170817 [83], keeping Hz, and Hz.
A descending chirp of the form (24) is captured by scanning over all the parameters , by image analysis over the H1L1 data of s, containing GW170817. This process is realized in steps in () at 33 Hz in for a total of values [109]. The response curves of Figure 6 are averaged over 41 tiny (surrogate) time slides between H1 and L1, which corresponds to their light crossing travel time of 10 ms. Box 3 some key conclusions on the central engine of GRB170817A.
Box 3. What is the central engine of GRB170817A?
- The ascending–descending chirp in GW170817 represents a merger followed by delayed spin-down of a Kerr black hole during GRB170817A.
- This observation is seen in spectrograms generated by Butterfly matched filtering calibrated by signal injection experiments.
- EM-GW event timing shows consistency between s of GRB170817A [90], s and time scale of descent s.
6. Exascale Computing by Synaptic Parallel Processing
Observations of unknown signals require two (or more) detectors with comparable nominal behaviors to cross-correlate independent candidate signals. Over large datasets, such as full observational runs, the generation of spectrograms through matched filtering presents a novel computational challenge in generating spectrograms produced by matched filtering, covering a sufficiently broad range and density in . For a candidate feature in a spectrogram, the next step is to quantify its properties by parameter estimation. This notably includes the extraction of the probability density function (PDF) of a choice of parameters, such as those encountered in event timing. Matched filtering is a computer-intense task involving cross-correlation between the data and templates, which scales bilinearly with the data length and size of the template bank. Substantial additional computational costs are, therefore, incurred, particularly in the process of parameter estimation.
6.1. Acceleration by High-Performance Computing
To meet this challenge, we appeal to modern computational approaches in hardware and software. Specific methods to accelerate matched filtering by a few orders of magnitude derive from efficient algorithms, modern computing hardware, and network computing:
- Efficient evaluation in the Fourier domain using the fast Fourier transform (FFT);
- Heterogeneous computing by offloading inverse FFTs to graphics processor units (GPUs);
- Distributed computing on a platform, load-balanced by synaptic parallel processing.
The requirement for these computational components is more evident by illustrating the scale of computation in obtaining a single spectrogram, using cross-correlation, for instance, for H1L1 data around GW170817-GRB170817A. Consider data with durations of s in H1 and L1 containing this event, partitioned in 32 s segments. With a template bank of templates, a single spectrogram of the entire T duration of data requires cross-correlations for . This is equivalent to 373 tera-floating point operations (teraFLOPs) in single precision (SP, f32), assuming that FFT is used and the data are sampled at 4096 Hz. This will be increased to 60 petaFLOPs when extending over time slides (below). Calibration over 56 injections requires some 3.3 exaFLOPs to produce response curves in Figure 6.
The gain in evaluating correlations in the Fourier domain when array sizes are sufficiently large is well-known. A further gain is obtained by heterogeneous computing by offloading inverse FFTs to GPUs, realizing the speed-up of at least an order of magnitude (Figure 7). For matched filtering, this requires care in circumventing bandwidth limitations of the peripheral computer interface express (PCIe) between GPU(s) and the host CPU. The key involves the use of pre- and post-callback functions, with the latter limiting the GPU output to the tail of the matched filtering output, which may contain a candidate signal, discarding the bulk of the output [102].
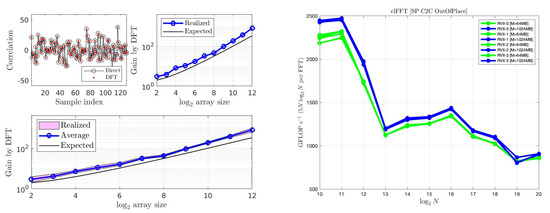
Figure 7.
(Left panel) Emulation of gain increase with the array size in matched filtering, evaluated by FFT versus direct evaluation. (Right panel) Benchmark of the OpenCL routine clFFT in CSP/OutOfPLace as a function of the array size N for two batch sizes measured by allocation M in global memory. Array sizes exceeding require calls to global memory due to the limited size of the local memory in the matrix transpose, causing a drop in performance limited by 1 TB/s of bandwidth in HBM. clButterfly [102] uses a default segment of samples (32 s at a 4096 Hz sampling rate with a batch size over per 4096 s frame). (Reprinted from [109], https://zenodo.org/record/6475673, https://zenodo.org/record/1242679, accessed on 25 May 2023).
Invariably, this approach involves some mixed-language programming, e.g., F90/C++ for the host and C99 for the GPU kernels. Open compute language (OpenCL) is a commonly used interfacing between the host and GPU [159,160]. Quite generally, the gain in the compute performance when offloading tasks to GPUs depends on the arithmetic intensity (e.g., [161]), expressing a ratio of demand on the compute versus memory resources. In practice, the latter includes limitations in the PCIe bandwidth between the GPU and host. The computed performance of the FFT exhibits a typical break as a function of the array size due to a loss in arithmetic intensity when the array size exceeds the limit of the local memory of the GPU’s compute units. Across the board, the performance drops well below the theoretical peak-compute performance, limited by memory bandwidth to global memory; access is relatively slow when a large number of clock cycles are involved.
Figure 7 shows variations in the arithmetic intensity of the OpenCL implementation clFFT on GPUs obtained in a benchmark. When array sizes are large, the results are about 7% of the theoretical peak-compute performance, showing the need for high-bandwidth memory (HBM) and, to scale acceleration, multiple GPU nodes. Circumventing the aforementioned PCIe bandwidth limitations is essential in the application of matched filtering.
6.2. Dynamical Load Balancing by Synaptic Parallel Processing
When analyzing a large number of data frames, high throughput can be realized by distributed computing on a platform of multi-GPU nodes organized over one or more local area networks (LANs). In the face of a heterogeneous platform consisting of nodes with varying compute performances, further optimization is obtained with dynamical load balancing by use of synaptic parallel processing [162]. This approach takes advantage of the embarrassingly parallel processing of a collection of independent tasks. Independent tasks can be specified in a list of instructions given by line items for dissemination on a platform of heterogeneous compute nodes organized in one or more local area networks (LANs).
Dynamical load-balanced processing is realized through synaptic computing, where individual nodes independently request line items from a shared task list with atomic access [162]. Access may be passive or through a traditional handshake protocol. This approach does not involve a central server, apart from a network-attached storage (NAS) device to collect output from all tasks onto a central location. In fact, this approach is the reverse of traditional approaches, where a server assigns tasks to clients.
7. Parameter Estimation in an Extended Foreground of (H1,L1)-Spectrograms
An event-timing analysis requires high-resolution parameter estimation by extracting probability density functions (PDFs) of observables, such as the start time and related parameters in (24). The expectation value and uncertainty can be inferred by calculating the mean and standard deviations from the data, which are needed for inferring the statistical significance of a candidate feature based on (11) and, independently, the consistency of observations in the independent detector channels (H1 and L1). Below, we discuss the PDFs obtained from H1 and L1, specifically the mean values from the merged (H1,L1) spectrograms. The independent H1 and L1 analysis is deferred to the following section.
For the descending chirp in gravitational radiation, a PDF() is extracted, based on the parameter estimation (24) applied to the merged (H1,L1) spectrograms, using an indicator function . Our indicator function measures the correlation strength between H1 and L1 [81,109] as a function of all four parameters in (24). The evaluation involves heterogeneous computing and, to save memory, the output is limited to at maxima over (.
7.1. PDFs from the Extended Foreground Analysis over Small Time Slides
A traditional foreground analysis with zero time slides between H1 and L1 data defines . A PDF( is obtained by repeating this estimate over a large number () of small time slides between H1 and L1 over the extended foreground
Time slides are selected from a distribution of small and large time slides distributed symmetrically around zero, including a neighborhood of 0 (by 41 tiny time slides within the light travel time of 10 ms between H1 and L1).
The PDF( and PFF() are derived from PDF( by tracing out , respectively, , i.e., the projection of a cluster defined by in the plane of the parameter space over (26).
A candidate signal is identified by the cluster centered about ), defined by the maximum of over (26), as shown in Figure 8. (When estimating ), are the nuisance parameters projected out by taking maxima, as image analysis runs over all four parameters for each time slide ). The degree of clustering in the space is quantified by the number of elements in a box
normalized to the total number of time slides (26). A 100% result defines an extremal cluster in the parameter space (.
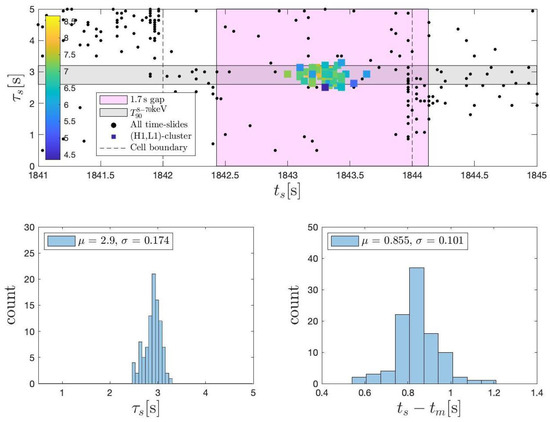
Figure 8.
PDF in (24) from the image analysis of (H1,L1)-spectrograms over time slides. Extremal clustering (100%) of the global maximum appears in the extended foreground over small time slides (26). PDF() shows a time delay s ( s) of a descending chirp, satisfying , signaling the gravitational collapse to a Kerr black hole that triggers GRB170817A in (3). The PDF() is consistent with s of GRB170817A [90], identified with the lifetime of black hole spins interacting with surrounding high-density matter. (Reprinted from [109]).
For background, ensembles of peaks (and their degrees of clustering) are identified in each of the 1024 cells with a duration of s, covering an analysis over a total duration of s using the aforementioned snippets of H1L1 data. Each cell has a total of time slides over s, including (26). According to (26) and (27), up to can be clustered.
7.2. Clustering in Parameter Space
Absent of a gravitational-wave signal, and are uncorrelated and fail to cluster with a uniform statistic in . In response to a gravitational-wave signal passing by, however, and cluster about a central value, which is representative of a correlation between H1 and L1 (Figure 8). The degree of clustering arising from such correlation strength is representative of the signal strength that, if present, will be persistent over the extended foreground (26). Crucially, extremal clustering provides a robust guard against false positives: weak signals or glitches occurring independently in H1 or L1 inevitably generate local maxima in , but fail to produce extremal clustering.
Figure 9 evidences the uniqueness of extremal clustering in the extended emission feature, identifying
and satisfying the aforementioned causality condition (11). In particular, (11) is satisfied by PDF( (upon projecting out ) with
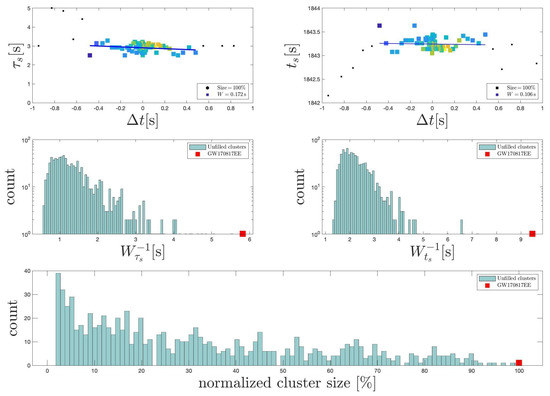
Figure 9.
The extremal clustering in and of the descending chirp in (H1,L1)-spectrograms, merged by frequency coincidences Hz, is unique in clustering considered among all 1024) cells of s covering . (Reprinted from [109]).
The start time of the descending chirp in Figure 2 defines a trigger of GRB170817A, establishing the descending chirp as the emission from the central engine of GRB170817A in (3) [81]. In fact, Ref. (29) satisfies the more stringent causality condition in Butterfly matched filtering,
where s refers to the duration of the templates in our Butterfly matched filtering.
The first PFA derives from , satisfying by mere chance under the null hypothesis of a background of noise only with no gravitational wave passing by. According to (14), we have [118]
It follows that carries a PFA with an equivalent two-sided Gaussian-equivalent significance of and a false alarm rate (FAR) of about 1 per month. ( (e.g., [163])). Box 4 summarizes the high-resolution observations on event timing in GRB170817-GRB170817A.
Box 4. High-resolution event timing in the extended foreground by the exascale HPC.
- Exascale HPC is achieved by synaptic parallel processing on a heterogeneous compute platform [162] in the mixed F90/C++/C99 using OpenCL and bash.
8. Consistent Event Timing in Independent H1 and L1 Analyses
A further criterion for observation is the consistency in event timing in independent H1 and L1 analyses:
is zero within the resolution of our observation. This is evaluated by their respective PDFs. The event timing analysis between H1 and L1 yields a PFA that is statistically independent of the previous PFA (14). Recall that the mean and differences of two estimates represent a rotation of the two-channel data over which corresponds to a unitary transformation of H1 and L1 data. The total PFA is obtained by factoring over these two PFAs.
We note that the joint PDF over has an equivalent expression over , where is the mean and square brackets refer to the differences: , . In the previous section, the mean is effective in the merged (H1,L1)-spectrograms.
With no gravitational wave passing by, H1 and L1 detectors are uncorrelated. In this case, the mean and difference in are statistically independent. The aforementioned PDF then factorizes as . We are at liberty to project out differences, leaving and (31), further projecting out based on (30). Projecting out reduces the same to independent of the context; that is, blind to GW170817-GRB170817 under the null hypothesis in (3).
Consistency is measured by cross-correlating the PDF() obtained for H1 and L1. This gives rise to a PFA in the consistency of the time difference with zero, taking into account finite resolution in the two PDFs of .
PDF()s are obtained from H1 and L1 at high resolution, about an order of magnitude below , by sampling over a large number of trials. (In the case at hand, the resolution remains above the light travel time between the two LIGO detectors). For this purpose, PDF()s are generated by trials: template seeds in Butterfly matched filtering with output branched into H1 and L1 spectrograms over the offsets , up to stride m.
Butterfly matched filtering uses a dense rather than orthogonal bank of templates, with each possibly providing an approximate match over the intermediate time scale of the phase coherence [101,102]. The output of data samples are typically covered by a multiplicity of neighboring templates. On average, time-stepping
in is hereby below the sample time of s of the H1L1 data, giving , which is typically 0 or s, with STD ≃ s. Therefore, on average, there are 7 samples in a stride of , with a small STD of the order of Hz [109]. The high resolution is derived from offsets , effectively, by subsampling.
Figure 10 and Figure 11 show the results of independent H1 and L1 analyses by PDF() for each one. For the total duration s of H1L1 data, the local maximum of shows a correlation of , where and . This is expected in independent H1 and L1 analyses [109]. PDFs() of H1 and L1 are maximally correlated at a time slide that is consistent with zero within the resolution s of our binning. This maximum is global; it is maximal among all the maxima identified in each of the 64 segments of 32 s, covering the entire analysis over s. By (32),
is the -value of consistency with two-sided Gaussian-equivalent significance of and the FAR of ∼1 per 1.4 years. The factor of 4 in (34) is a combination of 2 coefficients. The first is a factor of 2, which originates from taking the absolute value in at the peak of the cross-correlation between PDF and PDF. Additionally, the uniform prior in astrophysical timing and leads to a top-hat distribution in , giving another factor of 2.
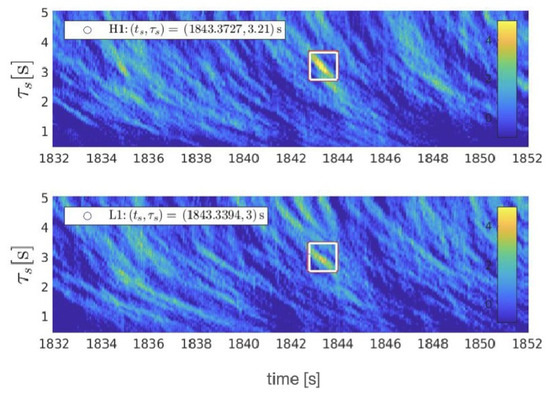
Figure 10.
One sample of PDF comprising elements from individual H1 and L1 analyses, shown around the merger time s. Over s of data, time differences and are at local maxima of over 64 segments of 32 s. These two trials are uncorrelated, evidenced by a correlation . (Reprinted from [109]).
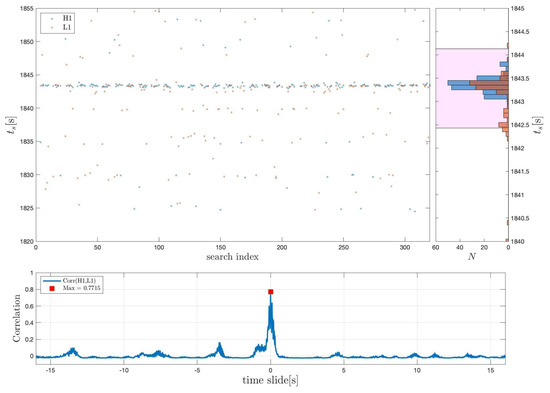
Figure 11.
PDFs( of H1 and L1 centered around and . Binned over s, the cross-correlation (over each segment covering the snippet of H1L1 data of s) uniquely identifies a global maximum in segment 58 corresponding GW170817, consistent with a zero time difference in the bin . (Reprinted from [109]).
In the mean of the PDF()s of H1 and L1, the delay time in the gravitational collapse to a black hole satisfies
consistent with (29), in the mean from the merged (H1,L1)-spectrograms. The delay times (35) and (29) identify the trigger of GRB170817A by the associated descending chirp in gravitational radiation. It is notably consistent with the lifetime s of the progenitor HMNS derived from (neutron-rich) outflow propagation times and the mass of blue ejecta [129]; its survival time is based on neutrino cooling and internal dissipation of rotational energy (e.g., [119]). Maximal clustering (35) comes with PDF. Mean values of in H1 and L1 are, respectively, s and s. s (H1) and s (L1) associated with the cluster (35) satisfy the mean
The result (36) is consistent with , derived from (29) in the merged (H1,L1)-spectrograms; (29) and (36) are representative of the lifetime of the black hole spin and provide constraints on of GRB170817A [90,109]. Box 5 summarizes the two independent analyses.
Box 5. Statistically independent PFAs of the trigger time of GRB170817A.
- Independent event timings derive from the mean and difference in , equivalent to a unitary transformation of H1 and L1 data, here obtained from merged and individual H1 and L1 spectrograms.
9. Conclusions and Outlook
The EM observations of SN1987A demonstrate the power of multi-messenger observations in identifying the formation of an NS that would otherwise be hidden by the opaque stellar envelope. In the absence of a rigorous identification of the nature of the remnant [164], however, the true trigger of the explosion eludes this neutrino observation. It is unknown whether the NS underwent further collapse to become a BH.
9.1. Principal Results
The EM-GW observations of GRB170817A provide evidence for the progenitor system of a short GRB: the DNS system GW170817. In this case, there is an additional observation of a trigger in the gap of 1.7 s between GW170817 and GRB170817A. It signals the start time of a descending chirp in gravitational radiation characteristics of the spin-down of a compact object powering the central engine of GRB170817A, with extended emissions covering the entire duration of this burst (Box 1). This is the first detection of a non-merger gravitational wave signal, discovered in high-resolution spectrograms (Box 2). Note that the finite delay time (35) in gravitational collapse to a Kerr black hole (Box 3), in agreement with independent estimates of the lifetime of the HMNS (Figure 2), rules out a BH-NS merger progenitor to GRB170817A [165].
PFA (31) and PFA (34) pertain to the mean and difference in based on the merged (H1,L1) spectrograms and, respectively, individual H1 and L1 spectrograms obtained from event timing constraints , evaluated by statistically independent PDFs( therein. The PDFs( of are extracted by means of HPC, accelerated by software, hardware, and distributed computing (Box 4). A Z-score of 5.49 is derived from the joint PFA , and is on par with the GW170817-GRB170817A association [6] (Box 5). Table 1 summarizes these PFAs.

The first direct observation of the spin-down of a Kerr BH is of principal significance to extreme transient events, by the universality of black holes in modern astronomy and the unique power of Kerr black holes compared to neutron stars. The high confidence level of this observation (Table 1) and the agreement in event timing in EM-GW (Box 1 and Box 3) suggest that this process may be observed in upcoming LVK observational runs.
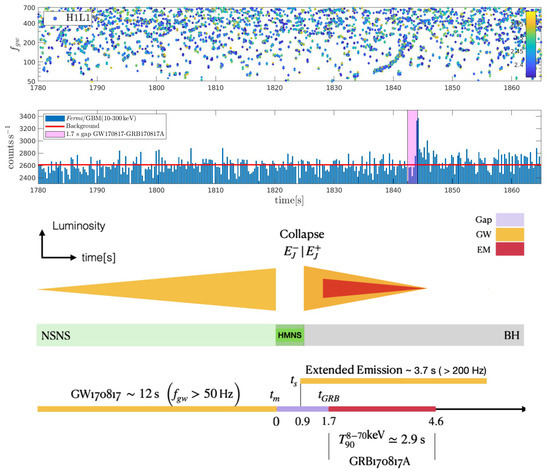
Figure 12.
Chronicle of GW170817 with merger time and start time of a descending branch signaling the birth of the central engine of GRB170817A with delayed time-of-onset (10). The energy reservoir in the angular momentum is rejuvenated in the (delayed) gravitational collapse of the initial HMNS at , producing of the black hole, exceeding the physical limits of the HMNS. (Reprinted and revised from [109]).
9.2. Outlook on Upcoming LVK Observations
The present results have potentially significant implications for upcoming observations of NS-NS mergers. These mergers inevitably have masses that are different from GW170817, resulting in commensurably different lifetimes of the initial HMNS produced in the coalescence. Observing multiple DNS mergers (sufficiently nearby) offers the opportunity to measure the correlation between the total system mass and the lifetime of the initial HMNS (reviewed for O4 in [149]), providing a potentially powerful constraint of the equation of state of neutron star matter.
In [81], the descending chirp is observed to agree remarkably well with quadrupole gravitational radiation emitted at a radius of times the ISCO around the Kerr BH formed in the gravitational collapse of the initial HMNS at the time (35). Since black holes do not retain the memory of their progenitors, except for the total mass and angular momentum, these findings are particularly interesting in the context of type Ib/c supernovae that give rise to black holes. This is also relevant in relation to their connection (albeit with a small branching ratio) to normal long GRBs [67] and superluminous supernovae [166,167].
LVK O4-5 observations are more favorable for detecting joint EM-GW signals from SN Ib/c, considering their relatively larger mass compared to the remnants of DNS mergers. A high black hole mass provides an advantage in terms of the potential for enhanced energy emissions at relatively low frequencies. These low frequencies align with or may overlap with the bandwidth of maximal sensitivity of LVK detectors. While rare, a failed GRB-SNe may, nevertheless, be luminous in gravitational radiation, and more frequent than DNS mergers, which may be tested with upcoming LVK probes in SN Ib/c events within the Local Universe.
Funding
This research is supported, in part, by the NRF of the Republic of Korea, no. 2018044640.
Data Availability Statement
The data underlying this article were accessed from the LIGO Open Science Center (accessed on 25 May 2023) https://www.gwosc.org, specifically the 2048 s dataset 10.7935/K5B8566F, containing the merger GW170817. The data generated in this research will be shared upon reasonable request to the corresponding author.
Acknowledgments
The author thanks the anonymous reviewers for a constructive comments on this manuscript. The author gratefully acknowledges LIGO-Caltech and INC, UCSD, for hospitality over a sabbatical visit, where some of this work was performed. LIGO O2 data are from the LIGO Open Science Center of the LIGO Laboratory and LIGO Scientific Collaboration (LSC), M. Vallisneri et al., 2014, Proc. 10th LISA Symp., University of Florida, Gainesville (18–23 May), arxiv:1410.4839, funded by the U.S. National Science Foundation. The original GW170817 2048 s dataset is available at 10.7935/K5B8566F from the LIGO Laboratory and the LSC. Virgo is funded by the French Centre National de Recherche Scientifique (CNRS), the Italian Instituto Nazionale della Fisica Nucleare (INFN), and the Dutch Nikhef, with contributions from Polish and Hungarian institutes. Additional support is acknowledged from MEXT, the JSPS Leading-edge Research Infrastructure Program, the JSPS Grant-in-Aid for Specially Promoted Research 26000005, the MEXT Grant-in-Aid for Scientific Research on Innovative Areas 24103005, the JSPS Core-to-Core Program, Advanced Research Networks, and the joint research program of the Institute for Cosmic Ray Research. Computations have been performed on a dedicated platform with dynamical load balancing via synaptic parallel processing.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| OpenCL | open compute language |
| GPU | graphics processor unit |
| PCIe | peripheral computer interface express |
References
- Abbott, R. et al. [The LIGO Scientific Collaboration and the Virgo Collaboration] GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo during the First Half of the Third Observing Run. Phys. Rev. X 2021, 11, 021053. [Google Scholar]
- Abbott, R. et al. [The LIGO Scientific Collaboration and the Virgo Collaboration] Population Properties of Compact Objects from the Second LIGO—Virgo Gravitational-Wave Transient Catalog. Astrophys. J. Lett. 2021, 913, L7. [Google Scholar] [CrossRef]
- Abbott, R. et al. [The LIGO Scientific Collaboration and the Virgo Collaboration] GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run. arXiv 2021, arXiv:2111.03606. [Google Scholar]
- Salpeter, E.E. The Luminosity Function and Stellar Evolution. Astrophys. J. 1955, 121, 161. [Google Scholar] [CrossRef]
- Park, H.J.; Kim, S.J.; Kim, S.; van Putten, M.H.P.M. On the Mass Function of GWTC-2 Binary Black Hole Systems and Their Progenitors. Astrophys. J. 2022, 938, 69. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [The LIGO Scientific Collaboration and the Virgo Collaboration] Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. 2017, 848, L12. [Google Scholar] [CrossRef]
- Dai, Z.G. Gravitational waves from post-merger radially oscillating millisecond pulsars. Astron. Astrophys. 2019, 662, 194. [Google Scholar] [CrossRef]
- De Pietri, R.; Feo, A.; Font, J.A.; Löffler, F.; Pasquali, M.; Stergioulas, N. Numerical-relativity simulations of long-lived remnants of binary neutron star mergers. Phys. Rev. D 2020, 101, 064052. [Google Scholar] [CrossRef]
- Murguia-Berthier, A.; Ramirez-Ruiz, E.; De Colle, F.; Janiuk, A.; Rosswog, S.; Lee, W.H. The Fate of the Merger Remnant in GW170817 and Its Imprint on the Jet Structure. Astrophys. J. 2021, 908, 152. [Google Scholar] [CrossRef]
- Klebesadel, R.W.; Strong, I.B.; Olson, R.A. Observations of Gamma-Ray Bursts of Cosmic Origin. Astrophys. J. 1973, 182, L85. [Google Scholar] [CrossRef]
- Band, D.; Matteson, J.; Ford, L.; Schaefer, B.; Palmer, D.; Teegarden, B.; Cline, T.; Briggs, M.; Paciesas, W.; Pendleton, G.; et al. BATSE Observations of Gamma-Ray Burst Spectra. I. Spectral Diversity. Astrophys. J. 1993, 413, 281. [Google Scholar] [CrossRef]
- Paciesas, W.S.; Meegan, C.A.; Pendleton, G.N.; Briggs, M.S.; Kouveliotou, C.; Koshut, T.M.; Lestrade, J.P.; McCollough, M.L.; Brainerd, J.J.; Hakkila, J.; et al. The Fourth BATSE Gamma-Ray Burst Catalog (Revised). Astrophys. J. Suppl. Ser. 1999, 122, 465. [Google Scholar] [CrossRef]
- Nakar, E. Short-Hard Gamma-Ray Bursts. Phys. Rep. 2007, 442, 166. [Google Scholar] [CrossRef]
- Berger, E. Short-Duration Gamma-Ray Bursts. Annu. Rev. Astron. Astrophys. 2015, 52, 43–105. [Google Scholar] [CrossRef]
- Amati, L.; Frontera, F.; Tavani, M.; in ’t Zand, J.J.M.; Antonelli, A.; Costa, E.; Feroci, M.; Guidorzi, C.; Heise, J.; Masetti, N.; et al. Intrinsic spectra and energetics of BeppoSAX Gamma-Ray Bursts with known redshifts. Astron. Astrophys. 2002, 390, 81. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Ghisillini, G.; Lazzati, D. The Collimation-corrected Gamma-Ray Burst Energies Correlate with the Peak Energy of Their νFν Spectrum. Astrophys. J. 2004, 616, 331. [Google Scholar] [CrossRef]
- Nava, L.; Ghisellini, G.; Ghirlanda, G.; Tavecchio, F.; Firmani, C. On the interpretation of spectral-energy correlations in long gamma-ray bursts. Astron. Astrophys. 2006, 450, 471. [Google Scholar] [CrossRef]
- Campana, S.; Guidorzi, C.; Tagliaferri, G.; Chincarini, G.; Moretti, A.; Rizzuto, D.; Romano, P. Are Swift gamma-ray bursts consistent with the Ghirlanda relation? Astron. Astrophys. 2007, 472, 395–401. [Google Scholar] [CrossRef]
- Ghisellini, G.; Celotti, A.; Ghirlanda, G.; Firmani, C.; Nava, L. Re-born fireballs in gamma-ray bursts. Mon. Not. R. Astron. Soc. 2007, 382, L72. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M. Nonthermal High-Energy Emissions from Black Holes by a Relativistic Capillary Effect. Astrophys. J. 2008, 685, L63. [Google Scholar] [CrossRef]
- Shahmoradi, A.; Nemiroff, R.J. Short versus long gamma-ray bursts: A comprehensive study of energetics and prompt gamma-ray correlations. Mon. Not. R. Astron. Soc. 2015, 451, 126. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M.; Levinson, A. Relativistic Astrophysics of the Transient Universe; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Zhang, B. The delay time of gravitational wave—Gamma-ray burst associations. Front. Phys. 2019, 14, 64402. [Google Scholar] [CrossRef]
- Lazzati, D.; Ciolfi, R.; Perna, R. Intrinsic Properties of the Engine and Jet that Powered the Short Gamma-Ray Burst Associated with GW170817. Astrophys. J. 2020, 898, 59. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T. Variability in Gamma-Ray Bursts: A Clue. Astrophys. J. 1997, 485, 270. [Google Scholar] [CrossRef]
- Piran, T.; Sari, R. Implications of Temporal Structure in GRBs. In Proceedings of the 18th Texas Symposium on Relativistic Astrophysics and Cosmology, Chicago, IL, USA, 15–20 December 1996; Olinto, A.V., Frieman, J.A., Schramm, D.N., Eds.; p. 494. [Google Scholar]
- Kobayashi, S.; Piran, T.; Sari, R. Can Internal Shocks Produce the Variability in Gamma-Ray Bursts? Astrophys. J. 1997, 490, 92. [Google Scholar] [CrossRef]
- Nakar, E.; Piran, T. Temporal properties of short gamma-ray bursts. Mon. Not. R. Astron. Soc. 2002, 330, 920. [Google Scholar] [CrossRef]
- Eichler, D.; Livio, M.; Piran, T.; Schramm, D.N. Nucleosynthesis, neutrino bursts and γ-rays from coalescing neutron stars. Nature 1989, 340, 126. [Google Scholar] [CrossRef]
- Woosley, S.E. Gamma-ray bursts from stellar mass accretion disks around black holes. Astrophys. J. 1993, 405, 273. [Google Scholar] [CrossRef]
- Paczynski, B. Are Gamma-Ray Bursts in Star-Forming Regions? Astrophys. J. 1998, 494, L45. [Google Scholar] [CrossRef]
- Paczynski, B. Cosmological gamma-ray bursts. Acta Astron. 1991, 41, 257. [Google Scholar]
- Levinson, A.; Eichler, D. Baryon Purity in Cosmological Gamma-Ray Bursts as a Manifestation of Event Horizons. Astrophys. J. 1993, 418, 386. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M.; Levinson, A. Theory and Astrophysical Consequences of a Magnetized Torus around a Rapidly Rotating Black Hole. Astrophys. J. 2003, 584, 937. [Google Scholar] [CrossRef]
- Paczynski, B. Gamma-ray bursters at cosmological distances. Astrophys. J. 1986, 308, L43. [Google Scholar] [CrossRef]
- Gal-Yam, A.; Bruch, R.; Schulze, S.; Yang, Y.; Perley, D.A.; Irani, I.; Sollerman, J.; Kool, E.C.; Soumagnac, M.T.; Yaron, O.; et al. A WC/WO star exploding within an expanding carbon-oxygen-neon nebula. Nature 2022, 601, 201. [Google Scholar] [CrossRef]
- Costa, E.; Frontera, F.; Heise, J.; Feroci, M.; in’t Zand, J.; Fiore, F.; Cinti, M.N.; Dal Fiume, D.; Nicastro, L.; Orlandini, M.; et al. Discovery of an X-ray afterglow associated with the γ-ray burst of 28 February 1997. Nature 1997, 387, 783. [Google Scholar] [CrossRef]
- van Paradijs, J.; Groot, P.J.; Galama, T.; Kouveliotou, C.; Strom, R.G.; Telting, J.; Rutten, R.G.M.; Fishman, G.J.; Meegan, C.A.; Pettini, M.; et al. Transient optical emission from the error box of the γ-ray burst of 28 February 1997. Nature 1997, 386, 686–689. [Google Scholar] [CrossRef]
- Metzger, M.R.; Djorgovski, S.G.; Kulkarni, S.R.; Steidel, C.C.; Adelberger, K.L.; Frail, D.A.; Costa, E.; Frontera, F. Spectral constraints on the redshift of the optical counterpart to the γ-ray burst of 8 May 1997. Nature 1997, 387, 879. [Google Scholar] [CrossRef]
- Amati, L.; Piro, L.; Antonelli, A.; Butler, R.C.; Costa, E.; Cusumano, G.; Feroci, M.; Frontera, F.; Heise, J.; in’t Zand, J.; et al. BeppoSAX observations of GRB970508: First evidence of bursting activity continuing on very long time scale. Nucl. Phys.-Proc. Suppl. 1998, 69, 656–659. [Google Scholar] [CrossRef]
- Bloom, J.S.; Djorgovski, S.G.; Kulkarni, S.R. The redshift and the ordinary host galaxy of GRB 970228. Astrophys. J. 2001, 554, 678. [Google Scholar] [CrossRef]
- Galama, T.J.; Vreeswijk, P.M.; van Paradijs, J.; Kouveliotou, C.; Augusteijn, T.; Patat, F.; Heise, J.; in’t Zand, J.; Groot, P.J.; Wijers, R.A.M.J.; et al. On the possible association of SN 1998bw and GRB 980425. Nature 1998, 395, 670. [Google Scholar] [CrossRef]
- Hjorth, J.; Sollerman, J.; Møller, P.; Fynbo, J.P.U.; Woosley, S.E.; Kouveliotou, C.; Tanvir, N.R.; Greiner, J.; Andersen, M.I.; Castro-Tirado, A.J.; et al. A very energetic supernova associated with the γ-ray burst of 29 March 2003. Nature 2003, 423, 847. [Google Scholar] [CrossRef] [PubMed]
- Stanek, K.Z.; Matheson, T.; Garnavich, P.M.; Martini, P.; Berlind, P.; Caldwell, N.; Challis, P.; Brown, W.R.; Schild, R.; Krisciunas, K.; et al. Spectroscopic Discovery of the Supernova 2003dh Associated with GRB 030329. Astrophys. J. 2003, 591, L17. [Google Scholar] [CrossRef]
- Matheson, T.; Garnavich, P.M.; Stanek, K.Z.; Bersier, D.; Holland, S.T.; Krisciunas, K.; Caldwell, N.; Berlind, P.; Bloom, J.S.; Bolte, M.; et al. Photometry and Spectroscopy of GRB 030329 and Its Associated Supernova 2003dh: The First Two Months. Astrophys. J. 2003, 599, 394. [Google Scholar] [CrossRef]
- Modjaz, M.; Stanek, K.Z.; Garnavich, P.M.; Berlind, P.; Blondin, S.; Brown, W.; Calkins, M.; Challis, P.; Diamond-Stanic, A.M.; Hao, H.; et al. Early-Time Photometry and Spectroscopy of the Fast Evolving SN 2006aj Associated with GRB 060218. Astrophys. J. 2006, 645, L21. [Google Scholar] [CrossRef]
- Guetta, D.; Della Valle, M. On the Rates of Gamma-Ray Bursts and Type Ib/c Supernovae. Astrophys. J. 2007, 657, L73. [Google Scholar] [CrossRef]
- Kelly, P.L.; Kirshner, R.P.; Kahre, M. Long γ-Ray Bursts and Type Ic Core-Collapse Supernovae Have Similar Locations in Hosts. Astrophys. J. 2008, 687, 1201. [Google Scholar] [CrossRef]
- Amati, L.; Della Valle, M.; Frontera, F.; Malesani, D.; Guidorzi, C.; Montanari, E.; Pian, E. On the consistency of peculiar GRBs 060218 and 060614. with the Ep,i − Eiso correlation. Astron. Astrophys. 2007, 463, 913. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M.; Lee, G.M.; Della Valle, M.; Amati, L.; Levinson, A. On the origin of short GRBs with extended emission and long GRBs without associated SN. Mon. Not. R. Astron. Soc. 2014, 444, L58. [Google Scholar] [CrossRef]
- Della Valle, M.; Chincarini, G.; Panagia, N.; Tagliaferri, G.; Malesani, D.; Testa, V.; Fugazza, D.; Campana, S.; Covino, S.; Mangano, V.; et al. An enigmatic long-lasting gamma-ray burst not accompanied by a bright supernova. Nature 2006, 444, 1050. [Google Scholar] [CrossRef]
- Fynbo, J.P.U.; Watson, D.; Thoene, C.C.; Sollerman, J.; Bloom, J.S.; Davis, T.M.; Hjorth, J.; Jakobsson, P.; Joergensen, U.G.; Graham, J.F.; et al. No supernovae associated with two long-duration γ-ray bursts. Nature 2006, 444, 1047. [Google Scholar] [CrossRef]
- Gehrels, N.; Norris, J.P.; Barthelmy, S.D.; Granot, J.; Kaneko, Y.; Kouveliotou, C.; Markwardt, C.B.; Mészáros, P.; Nakar, E.; Nousek, J.A.; et al. A new γ-ray burst classification scheme from GRB060614. Nature 2006, 444, 1044. [Google Scholar] [CrossRef]
- Gal-Yam, A.; Ofek, E.O.; Poznanski, D.; Levinson, A.; Waxman, E.; Frail, D.A.; Soderberg, A.M.; Nakar, E.; Li, W.D.; Filippenko, A.V. Radio and Optical Follow-up Observations of a Uniform Radio Transient Search: Implications for Gamma-Ray Bursts and Supernovae. Astrophys. J. 2006, 639, 331. [Google Scholar] [CrossRef]
- Gal-Yam, A.; Fox, D.B.; Price, P.A.; Ofek, E.O.; Davis, M.R.; Leonard, D.C.; Soderberg, A.M.; Schmidt, B.P.; Lewis, K.M.; Peterson, B.A.; et al. A novel explosive process is required for the γ-ray burst GRB 060614. Nature 2006, 444, 1053. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M. Superradiance in a torus magnetosphere around a black hole. Science 1999, 284, 115. [Google Scholar] [CrossRef]
- Frail, D.A.; Kulkarni, S.R.; Sari, R.; Djorgovski, S.G.; Bloom, J.S.; Galama, T.J.; Reichart, D.E.; Berger, E.; Harrison, F.A.; Price, P.A.; et al. Beaming in Gamma-Ray Bursts: Evidence for a Standard Energy Reservoir. Astrophys. J. 2001, 567, L41. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Ghisillini, G.; Firmani, C. Gamma-ray bursts as standard candles to constrain the cosmological parameters. New J. Phys. 2006, 8, 123. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Ghisellini, G.; Salvaterra, R.; Nava, L.; Burlon, D.; Tagliaferri, G.; Campana, S.; D’Avanzo, P.; Melandri, A. The faster the narrower: Characteristic bulk velocities and jet opening angles of gamma-ray bursts. Mon. Not. R. Astron. Soc. 2013, 428, 123. [Google Scholar] [CrossRef]
- Reichart, D.E.; Lamb, D.Q.; Fenimore, E.E.; Ramirez-Ruiz, E.; Cline, T.L.; Hurley, K. A Possible Cepheid-like Luminosity Estimator for the Long Gamma-Ray Bursts. Astrophys. J. 2001, 552, 57. [Google Scholar] [CrossRef]
- Levinson, A.; Boldt, E. UHECR production by a compact black hole dynamo: Application to Sgr A*. Astrop. Phys. 2002, 16, 265. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M.; Gupta, A.C. Non-thermal transient sources from rotating black holes. Mon. Not. R. Astron. Soc. 2009, 394, 2238. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M. Extreme luminosities in ejecta produced by intermittent outflows around rotating black holes. Mon. Not. R. Astron. Soc. 2015, 447, L11. [Google Scholar] [CrossRef]
- Moncada, R.J.; Colon, R.A.; Guerra, J.J.; O’Dowd, M.J.; Anchordoqui, L.A. Ultrahigh energy cosmic ray nuclei from remnants of dead quasars. J. High Energy Astrophys. 2017, 13, 32. [Google Scholar] [CrossRef]
- Gottlieb, O.; Bromberg, O.; Levinson, A. Intermittent mildly magnetized jets as the source of GRBs. Mon. Not. R. Astron. Soc. 2021, 504, 3947. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M. Electron-Positron Outflow from Black Holes. Phys. Rev. Lett. 2000, 84, 3752. [Google Scholar] [CrossRef] [PubMed]
- van Putten, M.H.P.M.; Levinson, A.; Frontera, F.; Guidorzi, C.; Amati, L.; Della Valle, M. Prospects for multi-messenger extended emission from core-collapse supernovae in the Local Universe. EPJ Plus 2019, 134, 547. [Google Scholar] [CrossRef]
- Mirabel, I.F.; Rodriguez, L.F. A superluminal source in the Galaxy. Nature 1994, 371, 46. [Google Scholar] [CrossRef]
- Piran, T. The physics of gamma-ray bursts. Rev. Mod. Phys. 2004, 76, 1143. [Google Scholar] [CrossRef]
- Thompson, C. A model of gamma-ray bursts. Mon. Not. R. Astron. Soc. 1994, 270, 480. [Google Scholar] [CrossRef]
- Metzger, B.D.; Giannios, D.; Thompson, T.A.; Bucciantini, N.; Quataert, E. The protomagnetar model for gamma-ray bursts. Mon. Not. R. Astron. Soc. 2011, 413, 2031. [Google Scholar] [CrossRef]
- Piran, T.; Nakar, E.; Mazzali, P.; Pian, E. Relativistic Jets in Core-collapse Supernovae. Astrophys. J. 2019, 871, L25. [Google Scholar] [CrossRef]
- Nakar, E. The electromagnetic counterparts of compact binary mergers. Phys. Rep. 2020, 886, 1–84. [Google Scholar] [CrossRef]
- Hewish, A. Pulsars. Annu. Rev. Astron. Astrophys. 1970, 8, 265. [Google Scholar] [CrossRef]
- Hulse, R.A.; Taylor, J.H. Discovery of a pulsar in a binary system. Astrophys. J. 1975, 195, L51. [Google Scholar] [CrossRef]
- Burgay, M.; D’Amico, N.; Possenti, A.; Manchester, R.N.; Lyne, A.G.; Joshi, B.C.; McLaughlin, M.A.; Kramer, M.; Sarkissian, J.M.; Camilo, F.; et al. An increased estimate of the merger rate of double neutron stars from observations of a highly relativistic system. Nature 2003, 426, 531–533. [Google Scholar] [CrossRef]
- Carter, B. Global Structure of the Kerr Family of Gravitational Fields. Phys. Rev. 1968, 174, 1559. [Google Scholar] [CrossRef]
- Wald, R.M. Black hole in a uniform magnetic field. Phys. Rev. D 1974, 10, 1680. [Google Scholar] [CrossRef]
- Kerr, R.P. Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics. Phys. Rev. Lett. 1963, 11, 237. [Google Scholar] [CrossRef]
- LSC. LSC-Virgo White Paper on GW Data Analysis and Astrophysics, LIGO T1800058-v2. 2018. Available online: https://dcc.ligo.org/LIGO-T1800058/public (accessed on 25 May 2023).
- van Putten, M.H.P.M.; Della Valle, M.; Levinson, A. Multi-messenger Extended Emission from the Compact Remnant in GW170817. Astrophys. J. 2019, 876, L2. [Google Scholar] [CrossRef]
- Coulter, D.A.; Foley, R.J.; Kilpatrick, C.D.; Drout, M.R.; Piro, A.L.; Shappee, B.J.; Siebert, M.R.; Simon, J.D.; Ulloa, N.; Kasen, D.; et al. Swope Supernova Survey 2017a (SSS17a), the optical counterpart to a gravitational wave source. Science 2017, 358, 1556. [Google Scholar] [CrossRef]
- Cantiello, M.; Jensen, J.B.; Blakeslee, J.P.; Berger, E.; Levan, A.J.; Tanvir, N.R.; Raimondo, G.; Brocato, E.; Alexander, K.D.; Blanchard, P.K.; et al. A Precise Distance to the Host Galaxy of the Binary Neutron Star Merger GW170817 Using Surface Brightness Fluctuations. Astrophys. J. 2018, 854, L31. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [The LIGO Scientific Collaboration and the Virgo Collaboration] GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed]
- Drago, A.; Pagliara, G. Merger of Two Neutron Stars: Predictions from the Two-families Scenario. Astrophys. J. 2018, 852, L32. [Google Scholar] [CrossRef]
- De Pietri, R.; Drago, A.; Feo, A.; Pagliara, G.; Pasquali, M.; Traversi, S.; Wiktorowicz, G. Merger of compact stars in the two-families scenario. Astrophys. J. 2019, 881, 122. [Google Scholar] [CrossRef]
- Bauswein, A. Equation of state constraints from multi-messenger observations of neutron star mergers. Ann. Phys. 2019, 411, 167958. [Google Scholar] [CrossRef]
- Acernese, F.; Amico, P.; Alshourbagy, M.; Antonucci, F.; Aoudia, S.; Astone, P.; Avino, S.; Babusci, B.; Ballardin, G.; Barone, F.; et al. Gravitational waves by gamma-ray bursts and the Virgo detector: The case of GRB 050915a. Class. Quantum Grav. 2007, 24, S671. [Google Scholar] [CrossRef]
- Cutler, C.; Thorne, K.S. An Overview of Gravitational-Wave Sources. In Proceedings of the 16th International Conference, Durban, South Africa, 15–21 July 2001; Bishop, N.T., Maharaj, S.D., Eds.; [Google Scholar]
- Pozanenko, A.S.; Barkov, M.V.; Minaev, P.Y.; Volnova, A.A.; Mazaeva, E.D.; Moskvitin, A.S.; Krugov, M.A.; Samodurov, V.A.; Loznikov, V.M.; Lyutikov, M. GRB 170817A Associated with GW170817: Multi-frequency Observations and Modeling of Prompt Gamma-Ray Emission. Astrophys. J. 2018, 852, L30. [Google Scholar] [CrossRef]
- Akutsu, M. et al. [KAGRA Collaboration] Overview of KAGRA: KAGRA science. Prog. Theor. Exp. Phys. 2021, 05A103. [Google Scholar] [CrossRef]
- Fernández, R.; Metzger, B.D. Delayed outflows from black hole accretion tori following neutron star binary coalescence. Mon. Not. R. Astron. Soc. 2013, 435, 502. [Google Scholar] [CrossRef]
- Just, O.; Bauswein, A.; Ardevol Pulpillo, R.; Goriely, S.; Thomas Janka, H. Comprehensive nucleosynthesis analysis for ejecta of compact binary mergers. Mon. Not. R. Astron. Soc. 2015, 448, 541. [Google Scholar] [CrossRef]
- Siegel, D.M.; Metzger, B.D. Three-Dimensional General-Relativistic Magnetohydrodynamic Simulations of Remnant Accretion Disks from Neutron Star Mergers: Outflows and r-Process Nucleosynthesis. Phys. Rev. Lett. 2017, 119, 231102. [Google Scholar] [CrossRef]
- Zhu, J.-P.; Yang, Y.-P.; Liu, L.-D.; Huang, Y.; Zhang, B.; Li, Z.; Yu, Y.-W.; Gao, H. Kilonova Emission from Black Hole–Neutron Star Mergers. I. Viewing-angle-dependent Lightcurves. Astrophys. J. 2020, 897, 20. [Google Scholar] [CrossRef]
- Fujibayashi, S.; Shibata, M.; Wanajo, S.; Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y. Mass ejection from disks surrounding a low-mass black hole: Viscous neutrino-radiation hydrodynamics simulation in full general relativity. Phys. Rev. D 2020, 101, 083029. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [The LIGO Scientific Collaboration and the Virgo Collaboration] A guide to LIGO-Virgo detector noise and extraction of transient gravitational-wave signals. Class. Quantum Grav. 2020, 37, 055002. [Google Scholar] [CrossRef]
- Baiotti, L.; Giacomazzo, B.; Rezolla, L. Accurate evolutions of inspiralling neutron-star binaries: Prompt and delayed gravitational collapse to a black hole. Phys. Rev. D 2008, 78, 084033. [Google Scholar] [CrossRef]
- Dall’Osso, S.; Giacomazzo, B.; Perna, R.; Stella, L. Gravitational waves from massive magnetars formed in binary neutron star mergers. Astrophys. J. 2015, 798, 25. [Google Scholar] [CrossRef]
- Baiotti, L.; Rezzolla, L. Binary neutron-star mergers: A review of Einstein’s richest laboratory. Rep. Prog. Phys. 2017, 80, 096901. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M.; Frontera, F.; Guidorzi, C. Broadband Turbulent Spectra in Gamma-Ray Burst Light Curves. Astrophys. J. 2014, 286, 146. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M. Deep searches for broadband extended gravitational-wave emission bursts by heterogeneous computing. Prog. Theor. Exp. Phys. 2017, 093F01. [Google Scholar] [CrossRef]
- Blocker, C.; Conway, J.; Demortier, L.; Heinrich, J.; Junk, T.; Lyons, L.; Punzi, G. (CDF Statistics Committee). 2006. Available online: http://physics.rockefeller.edu/~luc/technical_reports/cdf8023_facts_about_p_values.pdf (accessed on 25 May 2023).
- Fisher, R.A. Statistical Methods for Research Workers; Oliver and Boyd: Edinburgh, UK, 1932. [Google Scholar]
- Fisher, R.A. Questions and answers #14. Am. Stat. 1948, 2, 30. [Google Scholar]
- Simonson, K.M.; West, R.D.; Hansen, R.L.; LaBruyere, T.E., III; Van Benthem, M.H. A statistical approach to combining multisource information in one-class classifiers. Stat. Anal. Data Min. 2017, 10, 199. [Google Scholar] [CrossRef]
- Rosswog, S.; Liebendörfer, M.; Thielemann, F.-K.; Davies, M.B.; Benz, W.; Piran, T. Mass ejection in neutron star mergers. Astron. Astrophys. 1999, 341, 499–526. [Google Scholar]
- Ciolfi, R. The key role of magnetic fields in binary neutron star mergers. Gen. Rel. Grav. 2020, 52, 59. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M.; Della Valle, M. Central engine of GRB170817A: Neutron star versus Kerr black hole based on multimessenger calorimetry and event timing. Astron. Astrophys. 2023, 669, A36. [Google Scholar] [CrossRef]
- West, R.M.; Lauberts, A.; Jorgensen, H.E.; Schuster, H.E. Astrometry of SN 1987A and Sanduleak-69 202. Astron. Astrophys. 1987, 177, L1. [Google Scholar]
- Pietrzynski, G.; Graczyk, D.; Gallenne, A.; Gieren, W.; Thompson, I.B.; Pilecki, B.; Karczmarek, P.; Gorski, M.; Suchomska, K.; Taormina, M.; et al. A distance to the Large Magellanic Cloud that is precise to one per cent. Nature 2019, 567, 200. [Google Scholar] [CrossRef]
- Hirata, K.; Kajita, T.; Koshiba, M.; Nakahata, M.; Oyama, Y.; Sato, N.; Suzuki, A.; Takita, M.; Totsuka, Y.; Kifune, T.; et al. Observation of a neutrino burst from the supernova SN1987A. Phys. Rev. Lett. 1987, 58, 1490. [Google Scholar] [CrossRef]
- Arnett, W.D.; Bahcall, J.N.; Kirshner, R.P.; Woosley, S.E. Supernova 1987A. Annu. Rev. Astron. Astrophys. 1989, 27, 629. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L.; Bejger, M.; Lattimer, J.M. Keplerian frequency of uniformly rotating neutron stars and strange stars. Astron. Astrophys. 2009, 502, 605. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M. Near-extremal black holes as initial conditions of long GRB supernovae and probes of their gravitational-wave emission. Astrophys. J. 2015, 810, 7. [Google Scholar] [CrossRef]
- Bardeen, J.M. Kerr Metric Black Holes. Nature 1970, 226, 64–65. [Google Scholar] [CrossRef]
- Levinson, A.; Globus, N. Ultra-relativistic, neutrino driven flows in GRBs: A double transonic flow solution in Schwarzschild spacetime. Astrophys. J. 2013, 770, 159. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M.; Della Valle, M. Observational evidence for extended emission to GW170817. Mon. Not. R. Astron. Soc. 2019, 482, L46. [Google Scholar] [CrossRef]
- Beniamini, P.; Lu, B. Survival Times of Supramassive Neutron Stars Resulting from Binary Neutron Star Mergers. Astrophys. J. 2021, 920, 109. [Google Scholar] [CrossRef]
- Connaughton, V. >LIGO/Virgo G298048: Fermi GBM Trigger 170817.529 and LIGO Single IFO Trigge. GRB Coordinates Network: 2017; No. 21506. Available online: https://gcn.gsfc.nasa.gov/gcn3/21506.gcn3 (accessed on 25 May 2023).
- Savchenko, V.; Ferrigno, C.; Kuulkers, E.; Bazzano, A.; Bozzo, E.; Brandt, S.; Chenevez, J.; Courvoisier, T.J.-L.; Diehl, R.; Domingo, A.; et al. INTEGRAL Detection of the First Prompt Gamma-Ray Signal Coincident with the Gravitational-wave Event GW170817. Astrophys. J. 2017, 848, L15. [Google Scholar] [CrossRef]
- Mooley, K.P.; Deller, A.T.; Gottlieb, O.; Nakar, E.; Hallinan, G.; Bourke, S.; Frail, D.A.; Horesh, A.; Corsi, A.; Hotokezaka, K. A mildly relativistic wide-angle outflow in the neutron-star merger event GW170817. Nature 2018, 554, 207. [Google Scholar] [CrossRef]
- Mooley, K.P.; Deller, A.T.; Gottlieb, O.; Nakar, E.; Hallinan, G.; Bourke, S.; Frail, D.A.; Horesh, A.; Corsi, A.; Hotokezaka, K. Superluminal motion of a relativistic jet in the neutron-star merger GW170817. Nature 2018, 561, 355. [Google Scholar] [CrossRef]
- Ascenzi, S.; Oganesyan, G.; Branchesi, M.; Ciolfi, R. Electromagnetic Counterparts of Compact Binary Mergers. J. Plasma Phys. 2021, 71, 845870102. [Google Scholar] [CrossRef]
- Bionta, R.M. Observation of a neutrino burst in coincidence with supernova 1987A in the Large Magellanic Cloud. Phys. Rev. Lett. 1987, 58, 1494. [Google Scholar] [CrossRef]
- Imshennik, V.S.; Ryazkshaya, O.G. A Rotating Collapsar and Possible Interpretation of the LSD Neutrino Signal from SN 1987 A. Astron. Lett. 2004, 30, 14. [Google Scholar] [CrossRef]
- Ryazhskaya, O.G. Problems of Neutrino Radiation from SN 1987A: 30 years later. Phys. Atomic Nucl. 2018, 81, 113. [Google Scholar] [CrossRef]
- Galeotti, P.; Pizella, G. Supernova 1987A, 30 Years Later. Phys. At. Nucl. 2018, 81, 105. [Google Scholar]
- Gill, R.; Nathanail, A.; Rezzolla, L. When Did the Remnant of GW170817 Collapse to a Black Hole? Astrophys. J. 2019, 876, 139. [Google Scholar] [CrossRef]
- Goldstein, A.; Veres, P.; Burns, E.; Briggs, M.S.; Hamburg, R.; Kocevski, D.; Wilson-Hodge, C.A.; Preece, R.D.; Poolakkil, S.; Roberts, O.J.; et al. An ordinary short gamma-ray burst with extraordinary implications: Fermi-GBM detection of GRB170817A. Astrophys. J. 2017, 848, L14. [Google Scholar] [CrossRef]
- Ioka, K.; Nakamura, T. Can an off-axis gamma-ray burst jet in GW170817 explain all the electromagnetic counterparts? Prog. Theor. Exp. Phys. 2018, 043E02. [Google Scholar] [CrossRef]
- Lazzati, D. Short Duration Gamma-Ray Bursts and Their Outflows in Light of GW170817. Front. Astron. Space Sci. 2020, 7, 78. [Google Scholar] [CrossRef]
- Mooley, K.P.; Anderson, J.; Lu, W.B. Optical measurement of superluminal motion in the neutron-star merger GW170817. Nature 2022, 610, 273. [Google Scholar] [CrossRef]
- Smartt, S.J.; Chen, T.-W.; Jerkstrand, A.; Coughlin, M.; Kankare, E.; Sim, S.A.; Fraser, M.; Inserra, C.; Maguire, K.; Chambers, K.C.; et al. A kilonova as the electromagnetic counterpart to a gravitational-wave source. Nature 2017, 551, 75. [Google Scholar] [CrossRef]
- Pian, E.; D’Avanzo, P.; Benetti, S.; Branchesi, M.; Brocato, E.; Campana, S.; Cappellaro, E.; Covino, S.; D’Elia, V.; Fynbo, J.P.U.; et al. Spectroscopic identification of r-process nucleosynthesis in a double neutron-star merger. Nature 2017, 551, 67. [Google Scholar] [CrossRef]
- Pooley, D.; Kumar, P.; Wheeler, J.C.; Grossan, B. GW170817 Most Likely Made a Black Hole. Astrophys. J. 2018, 859, L23. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Hotokezaka, K.; Fromm, S.A.; Bernuzzi, S.; Roberts, L.F. Binary Neutron Star Mergers: Mass Ejection, Electromagnetic Counterparts and Nucleosynthesis. Astrophys. J. 2018, 869, 130. [Google Scholar] [CrossRef]
- Lucca, M.; Sagunski, L. The lifetime of binary neutron star merger remnants. J. High Energy Astrophys. 2020, 27, 33–37. [Google Scholar] [CrossRef]
- Ren, J.; Lin, D.B.; Zhang, L.L.; Li, X.Y.; Liu, T.; Lu, R.J.; Wang, X.G.; Liang, E.W. A Pulsar Wind Nebula Embedded in the Kilonova AT 2017gfo Associated with GW170817/GRB 170817A. Astrophys. J. 2019, 885, 60. [Google Scholar] [CrossRef]
- Ravi, V.; Lasky, P.D. The birth of black holes: Neutron star collapse times, gamma-ray bursts and fast radio bursts. Mon. Not. R. Astron. Soc. 2014, 441, 2433. [Google Scholar]
- Lü, H.-J.; Shen, J.; Lan, L.; Rice, J.; Lei, W.-H.; Liang, E.-W. Diagnosing the remnants of binary neutron star merger from GW170817/GRB170817A event. Mon. Not. R. Astron. Soc. 2019, 486, 4479–4484. [Google Scholar] [CrossRef]
- Piro, L.; Troja, E.; Zhang, B.; Ryan, G.; van Eerten, H.; Ricci, R.; Wieringa, M.H.; Tiengo, A.; Butler, N.R.; Cenko, S.B.; et al. A long-lived neutron star merger remnant in GW170817: Constraints and clues from X-ray observations. Mon. Not. R. Astron. Soc. 2019, 483, 1912. [Google Scholar] [CrossRef]
- Granot, J.; Guetta, D.; Gill, R. Lessons from the Short GRB 170817A: The First Gravitational-wave Detection of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 850, L24. [Google Scholar] [CrossRef]
- Gottlieb, O.; Nakar, E.; Piran, T.; Hotokezaka, K. A cocoon shock breakout as the origin of the γ-ray emission in GW170817. Mon. Not. R. Astron. Soc. 2018, 479, 588. [Google Scholar] [CrossRef]
- Nakar, E.; Gottlieb, O.; Piran, T.; Kasliwal, M.M.; Hallinan, G. From γ to Radio: The Electromagnetic Counterpart of GW170817. Astrophys. J. 2018, 867, 18. [Google Scholar] [CrossRef]
- Metzger, B.D.; Thompson, T.A.; Quataert, E.A. A Magnetar Origin for the Kilonova Ejecta in GW170817. Astrophys. J. 2018, 856, 101. [Google Scholar] [CrossRef]
- Xie, X.; Zrake, J.; MacFadyen, A. Numerical Simulations of the Jet Dynamics and Synchrotron Radiation of Binary Neutron Star Merger Event GW170817/GRB 170817A. Astrophys. J. 2018, 863, 58. [Google Scholar] [CrossRef]
- Hamidani, H.; Kiuchi, K.; Ioka, K. Jet propagation in neutron star mergers and GW170817. Mon. Not. R. Astron. Soc. 2020, 491, 3192. [Google Scholar] [CrossRef]
- Abchouyey, M.A.; van Putten, M.H.P.M.; Amati, L. Observational prospects of double neutrons star mergers and their multi-messenger afterglows: LIGO discovery power, event rates and diversity. Astrophys. J. 2023; to appear. [Google Scholar]
- van Putten, M.H.P.M.; van Putten, P.F.A.M. Roulette Registration System. US Patent 5785321, 27 July 1998. Available online: https://portal.unifiedpatents.com/patents/patent/US-5785321-A (accessed on 25 May 2023).
- Theiler, J. Combining Statistical Tests by Multiplying p-Values. Astrophysics and Radiation Measurements Group: NIS-2, 2004; Available online: https://citeseerx.ist.psu.edu (accessed on 25 May 2023).
- Heard, N.; Rubin-Delancy, P. Choosing between Methods of Combining p-values. Biometrika 2018, 105, 239. [Google Scholar] [CrossRef]
- Whitlock, M.C. Combining probability from independent tests: The weighted Z-method is superior to Fisher’s approach. J. Evol. Biol. 2005, 18, 1368. [Google Scholar]
- Accadia, T.; Acernese, F.; Antonucci, F.; Astone, P.; Ballardin, G.; Barone, F.; Barsuglia, M.; Bauer, T.S.; Beker, M.G.; Belletoile, A.; et al. Noise from scattered light in Virgo’s second science run data. Class. Quantum Grav. 2010, 27, 194011. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M. Directed searches for broadband extended emission in gravitational-wave emission from nearby energetic core-collapse supsernovae. Astrophys. J. 2016, 810, 7. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [The LIGO Scientific Collaboration and the Virgo Collaboration] Search for Gravitational Waves from a Long-lived Remnant of the Binary Neutron Star Merger GW170817. Astrophys. J. 2019, 875, 160. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [The LIGO Scientific Collaboration and the Virgo Collaboration] [The LIGO Scientific Collaboration and the Virgo Collaboration]. Model comparison from LIGO-Virgo data on GW170817’s binary components and consequences for the merger remnant. Class. Quantum Grav. 2020, 37, 045006. [Google Scholar] [CrossRef]
- Sun, L.; Melatos, A. Application of hidden Markov model tracking to the search for long-duration transient gravitational waves from the remnant of the binary neutron star merger GW170817. Phys. Rev. D 2019, 99, 123003. [Google Scholar] [CrossRef]
- AMD Inc. 2022. Available online: https://sep5.readthedocs.io/en/latest/Programming_Guides/Opencl-programming-guide.html (accessed on 25 May 2023).
- Khronos Group. 2022. Available online: https://www.khronos.org/opencl (accessed on 25 May 2023).
- Rocki, K.; Van Essendelft, D.; Sharapov, I.; Schreiber, R.; Morrison, M.; Kibardin, V.; Portnoy, A.; Dietiker, J.F.; Syamlal, M.; James, M. Fast Stencil-Code Computation on a Wafer-Scale Processor. In Proceedings of the SC20: International Conference for High Performance Computing, Networking, Storage and Analysis, Atlanta, GA, USA, 9–19 November 2020. [Google Scholar]
- van Putten, M.H.P.M. Method for High-Throughput Data-Processing by Distributed Heterogeneous Computing. US Patent Appl. 18/182,338, 12 March 2023. [Google Scholar]
- Huntington, A.S.; Williams, G.M.; Lee, A.O. Modeling false alarm rate and related characteristics of laser ranging and LIDAR avalanche photodiode photoreceivers. Opt. Eng. 2018, 57, 073106. [Google Scholar] [CrossRef]
- Alp, D.; Larsson, J.; Fransson, C.; Indebetouw, R.; Jerkstrand, A.; Ahola, A.; Burrows, D.; Challis, P.; Cigan, P.; Cikota, A. The 30 Year Search for the Compact Object in SN 1987A. Astrophys. J. 2018, 864, 174. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Dietrich, T. Can a black hole–neutron star merger explain GW170817, AT2017gfo, and GRB170817A? Phys. Rev. D 2019, 100, 043011. [Google Scholar] [CrossRef]
- Dong, S.; Shappee, B.J.; Prieto, J.L.; Jha, S.W.; Stanek, K.Z.; Holoien, T.W.-S.; Kochanek, C.S.; Thompson, T.A.; Morrell, N.; Thompson, I.B.; et al. ASASSN-15lh: A highly super-luminous supernova. Science 2015, 351, 6270. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M.; Della Valle, M. On extreme transient events from rotating black holes and their gravitational wave emission. Mon. Not. R. Astron. Soc. 2017, 464, 3219. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).