Abstract
Fast Radio Bursts (FRBs) are millisecond-duration transient events that are typically observed at radio wavelengths and cosmological distances but their origin remains unclear. Furthermore, most FRB origin models are related to the processes at stellar scales, involving neutron stars, blackholes, supernovae, etc. In this paper, our purpose is to determine whether multi-structural one-off FRBs and repeaters share similarities. To achieve this, we focus on analyzing the relationship between the FRB event rate and the star formation rate, complemented by statistical testing methods. Based on the CHIME/FRB Catalog 1, we calculate the energy functions for four subsamples, including apparent non-repeating FRBs (one-offs), repeaters, multi-structural one-offs, and the joint repeaters and multi-structural events, respectively. We then derive the FRB event rates at different redshifts for all four subsamples, all of which were found to share a similar cosmological evolution trend. However, we find that the multi-structural one-offs and repeaters are distinguishable from the KS and MWW tests.
1. Introduction
The field of FRB research has undergone a rapid development in terms of observational analysis, leading to significant progress in understanding this enigmatic astronomical event [1,2,3,4,5]. Since the first fast radio burst (FRB) was published in 2007 [6], more than 600 FRBs have been detected [7,8]. The Canadian Hydrogen Intensity Mapping Experiment (CHIME) largely enhanced the detected FRB samples, which made it possible to study FRB populations more precisely [8,9]. Meanwhile, numerous studies have investigated the potential connections between FRBs and GRBs, as well as the cosmological aspects related to FRBs (e.g., [10,11,12,13]). Despite the increasing number of detected FRBs, their origins and radiation mechanisms remain uncertain. To explain the possible origins of FRBs, numerous models have been proposed [14,15,16]. Platts et al. [17] provided a detailed summary of FRB radiation mechanisms and potential progenitors. Zhang et al. [5] also summarized a catalog of possible models to explain the origins of FRBs. Among these models, Li et al. [18] confirmed that some FRBs likely originate from magnetars but it is still unclear if magnetars are the origins of all FRBs [19,20,21].
Hashimoto et al. [22] analyzed the event rates of non-repeating FRBs and repeaters and found that they trace different cosmological histories. Locatelli et al. [23] and James et al. [24] discovered that FRBs exhibit redshift evolution behavior. Arcus et al. [25] used a method similar to that of James et al. [24] to find that both the star formation rate density and stellar mass density evolutionary histories can describe the FRB evolutionary history. Zhang et al. [26], using Parkes and ASKAP FRB samples, also found that they could not distinguish between the two evolutionary histories.
Generally, FRBs are usually divided into two categories: repeating and non-repeating FRBs based on whether repeating bursts have been observed. Most of the current FRB samples are non-repeating FRBs. Although repeating FRBs and non-repeating FRBs have different widths, bandwidths [27], rotation measures [28], and variation time-scales of the circular polarization [29], whether all FRB sources repeat is still in debate [30,31]. To determine if an FRB is a repeater, one must spend plenty of time consistently monitoring an FRB source [3,32]. Monitoring all FRBs requires a significant time investment, yet expanding the sample size of repeating bursts is crucial for understanding their origins. As the number of observations grows, some non-repeating FRBs display multi-component frequency-time patterns reminiscent of those observed in repeating FRBs [27,33]. Consequently, we attempt to identify that some non-repeating FRBs with these multi-structures could potentially be candidates for repeating FRBs [33]. Energy functions are essential to calculate the FRB number density and allow one to investigate the redshift evolution of volumetric occurrence rates of FRBs [22,24,34]. Our purpose is to enhance our comprehension of FRB origins by examining the relations of multi-structural one-offs, repeaters, and non-repeating FRBs. To achieve this, we investigate their event rate evolution and statistical properties.
The structure of this paper is as follows: Section 2 elaborates on the data selection criteria, FRB samples utilized in this study, and the categorization of FRBs. In Section 3, we provide an in-depth explanation of the research methodologies implemented in this paper. Section 4 presents the findings derived from energy functions, event rates, and statistical tests. By comparing the results from both event rate analyses and statistical tests, we draw our conclusions in Section 5.
2. Data Selection
2.1. Selection Function
To avoid a sample bias in the FRB population analysis, it is essential to consider the sample bias caused by the instrument selection effect to obtain a relatively accurate sample distribution. CHIME collaboration [8] developed a method for calculating the selection function of CHIME through simulated FRBs. Based on the real FRBs detected in CHIME/FRB Catalog 1, Hashimoto et al. [34] provided the selection function for FRBs with a signal-to-noise(SNR) greater than 10. In this study, we use the selection functions (5)–(8) from Hashimoto et al. [34]. By implementing the selection functions, we can rectify the FRB number density, thereby circumventing the influence of instrument effects on the computation of event rates.
2.2. Samples
This paper utilizes data from the CHIME/FRB Catalog 1. As the first FRB survey catalog released by CHIME/FRB, it encompasses 536 bursts detected between 25 July 2018 and 1 July 2019. The survey spans 214.8 days and includes 474 non-repeating FRBs and 18 repeaters [8]. The availability of the CHIME/FRB Catalog 1 facilitates more precise statistical analysis in FRB population studies. While composing this paper, CHIME identified 25 new repeating FRBs [35]. To maximize the sample size without introducing new biases, we cross-referenced these 25 newly discovered repeating bursts with the CHIME/FRB Catalog 1. We found that some one-off FRBs in the CHIME/FRB Catalog 1 exhibited repeating characteristics. Thus, we updated the information for these newly added repeating bursts in the CHIME/FRB Catalog 1, which increased the number of repeaters and slightly reduced the number of non-repeating FRBs accordingly. In order to ensure the data used reflects the intrinsic energy distribution of FRBs as accurately as possible, we first filtered the CHIME sample using the following selection criteria:
- bonsai_snr > 10;
- ;
- Not detected in far side-lobes;
- (ms);
- excluded_flag = 0;
- The first detected burst if the FRB source is a repeater;
- (Jy ms).
After applying the above selection function, we retained 202 FRBs, including 17 repeating FRBs and 185 one-offs. Within these 185 one-offs, we found that some FRBs have multiple pulse components (multi-structures). After manual examination, we identified 18 multi-structural one-offs in the current sample. To conduct a statistical analysis and event rate analysis of this subset, we analyzed them as a distinct category. The detailed sample classification can be found in Section 2.3.
2.3. Classification
In order to study the relationship between the event rates and redshifts of different types of FRBs, we divided the FRB samples into four groups:
- One-offs without multi-structures (167 cases);
- Repeaters (20 cases);
- Multi-structural one-offs (18 cases);
- Repeaters + multi-structural one-offs (38 cases).
In the process of identifying multi-structural one-offs, we employed the criteria of being able to distinguish two or more pulse profiles in the time domain. Ultimately, we selected 18 FRBs from one-offs in CHIME/FRB Catalog 1 which satisfied the selection functions as the sample of multi-structural one-offs.
The purpose of dividing the data into the above four categories was to explore whether different classes of FRBs share similar evolution with redshifts and to investigate the possibility that multi-structural one-offs could be candidates for repeaters. In the group of one-offs, to avoid contamination of the non-repeating FRBs sample by multi-structural one-offs, we removed FRBs with multi-structures from the one-offs.
3. Method
3.1. Redshift Calculation
In the sample we used, only a portion of the FRBs had redshifts derived from optical localization. Moreover, Michilli et al. [36] reported 13 FRBs with baseband localization and we cross-referenced these 13 FRBs with redshift measurements with those in the CHIME/FRB Catalog 1, updating the redshifts for our sample accordingly. For FRBs with optical redshifts, we used the redshifts obtained from optical instead of redshifts calculated from the DM-z relation for subsequent calculations. For other FRBs without optical redshifts, we employed dispersion measures (DMs) to determine their corresponding redshifts.
The observed DM of FRBs is composed of the following components:
where represents the Galactic dispersion contribution, for which we employed the model for estimation. To account for the redshift variation caused by , we adopted a log-normal distribution for . In our work, we adopted the mean value and the variance in the log-normal distribution, reported by Macquart et al. [37]. Afterwards, we divided the obtained from the log-normal distribution by a factor of , yielding the final contribution of . Following Hashimoto et al. [34], we utilized . The calculation of refers to Equation (2), (4) in Maquart et al. [37], and the cosmological parameters used in this paper are from the Planck15 cosmological model. Deriving the redshift through usually relies on and its fluctuation. The fluctuation of causes a large error in the estimated redshift. In this work, we used Equations (B1) and (B2) derived by Hashimoto et al. [22] as the fluctuation function. Based on Equation (1), we can directly calculate the redshift using the Markov Chain Monte Carlo (MCMC) method through DM.
3.2. Calculation of Energy Functions
After obtaining the redshifts of FRBs, we can estimate the luminosity distances of the FRBs based on their redshifts and convert the observed energy to the energy in the rest frame, enabling us to examine the energy distributions of FRBs.
To study the event rate as a function of redshift, we need to calculate the energy function in different redshift intervals. Therefore, for the four groups of FRBs mentioned in Section 2.3, we first divided the redshift intervals as follows: the redshift intervals of one-offs are 0.05, 0.30, 0.68, 1.38, 3.60; due to the relatively small redshifts of repeaters and multi-structural one-offs, we decided to use the redshift intervals of 0.05, 0.31, 0.72, and 1.50. Subsequently, following Equations (10)–(23) from Hashimoto et al. [34], we use the Vmax method to calculate the number density of the FRBs [38], and based on the calculated results of the number density, we obtained data points for the energy functions in different redshift intervals, ultimately deriving the energy equations in different redshift intervals. In the calculation of the number density, we used the CHIME selection functions for correction, where our sample yielded .
3.3. Statistical Tests
In order to analyze whether the three groups of FRBs in Section 2.3 have similar distributions from another perspective, we conducted the Kolmogorov–Smirnov (K–S) test [39] on the observed parameters of the three groups of FRBs to determine if the parameter distributions of each group exhibit significant differences. To avoid test biases caused by insufficient sample sizes from repeaters and multi-structural one-offs as much as possible, we also took the Mann–Whitney–Wilcoxon test (M–W–W) and the Wilcoxon rank sum test [40] on the observed parameters of the FRB groups.
The K–S test, M–W–W test, and Wilcoxon rank-sum test are all non-parametric tests. Compared to the K–S test, the M–W–W test and Wilcoxon rank-sum test are more suitable for statistical tests with small samples [40]. Each statistical test provides two parameters: statistical correlations and p-values. Generally, when the p-value is below 0.05, the two test samples are considered to come from different distributions. In this work, the test threshold (significance level) we employed is . Table 1, Table 2 and Table 3 are the results of K–S test, M-W-W test, and Wilcoxon rank-sum test, respectively.

Table 1.
p-values from K–S test.

Table 2.
p-values from M–W–W test.

Table 3.
p-values from Wilcoxon rank-sum test.
4. Results and Discussion
4.1. Energy Functions
We found that, in the lower redshift interval, the energy function of one-offs exhibits a steeper slope at higher energies and a relatively flatter slope at lower energies, resembling the Schechter energy function shape. Consequently, we took the Schechter energy function (Luo et al. [41]) to fit the energy function for the four subsamples of FRBs. The Schechter energy function is characterized by:
where is the normalization factor, is the slope in the linear scale, and is the cut-off energy. When fitting the energy functions, since there are relatively more data in the first redshift interval, we used the first redshift interval to fit the slope of the energy functions. The slope of the remaining redshift intervals was determined using the fitting results of the first redshift interval and the remaining parameters were fitted. Finally, the best-fitting values are shown in Table 4. The best-fitted Schechter energy functions are demonstrated in Figure 1.

Table 4.
Best-fitted parameters of FRB energy functions.
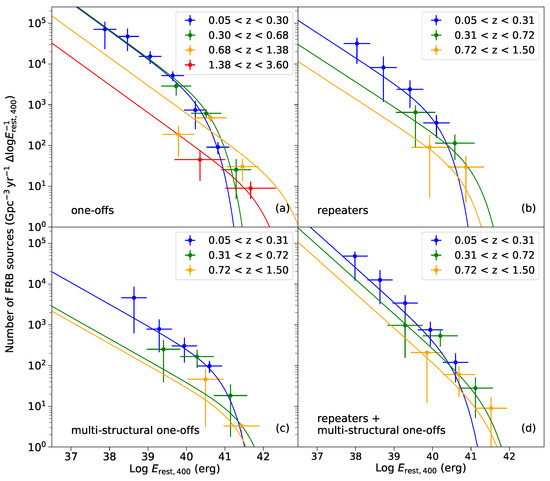
Figure 1.
Energy functions of four FRB groups; (a–d) demonstrate the energy functions of one-offs, repeaters, multi-structural one-offs, and the merged group, repeaters, and multi-structural one-offs as a whole, respectively. The vertical errors are given by MCMC. The lines are the best-fitted result.
We discovered that, within the error range, the slope of the energy equation for one-offs in our result is basically consistent with the results of James et al. [24]. Due to the limitation of the sample size of repeaters and multi-structural one-offs, we can only provide a rough constraint on the slope of energy functions, respectively. We estimate that a larger sample size would allow us to obtain more accurate constraints.
4.2. History of Redshift Evolution
The calculation of FRB event rates is an effective approach to understand the nature of FRBs [34]. To investigate whether different types of FRBs have similar evolutions and to explain whether multi-structural one-offs may have similarities to repeaters, we calculate the relationship between event rates and redshift for each group of FRBs.
By integrating the energy functions corresponding to the four groups of FRBs in Section 4.1 at different redshift intervals, we can obtain the event rates of each FRB group at different redshifts. The uncertainties in the event rates are directly calculated using the MCMC method during the energy function fitting process. The energy integration range we selected is , consistent with the ranges used in Shin et al. [42] and Hashimoto et al. [22,34]. Figure 2 demonstrates the relationships between event rates and redshifts for one-offs, repeaters, and multi-structural one-offs, respectively.
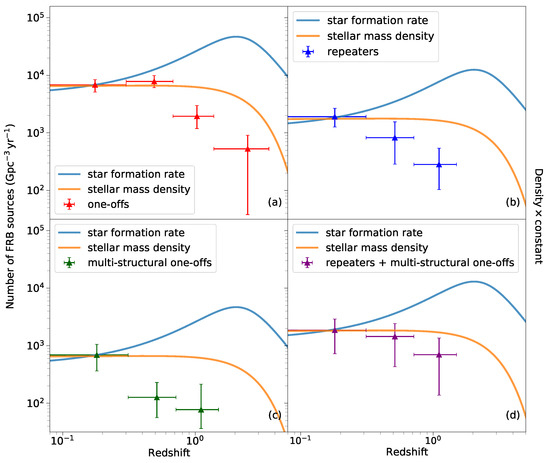
Figure 2.
Event rate relation with redshift; (a–d) demonstrate the event rate of one-offs, repeaters, multi-structural one-off, and the merged group, repeaters, and multi-structural one-offs as a whole, respectively. The blue and yellow lines stand for cosmic star-formation rate and cosmic stellar-mass density evolution history, respectively. The vertical errors in the volumetric event rates are given by MCMC from energy function fitting. To compare the event rate trend of different groups of FRBs with redshift, we adjusted the star formation rate and stellar mass density to be same as the number of sources at the first redshift value in each group by a multiple of the constant to the density.
To compare the volumetric event rate of FRBs with both cosmic star formation rate density and cosmic stellar mass density, we used the following two equations. First is the star formation rate density given by Madau et al. [43] denoted as follows:
and second is the cosmic stellar mass density from Hashimoto et al. [22]. This function is the fitting result of the observed data in López Fernández et al. [44]:
The relationship between event rates and redshifts indicates that, within the uncertainty, the cosmological history of non-repeating FRBs is inconsistent with the evolutionary history of the star formation rate. This conclusion aligns with Hashimoto et al. [34]. Based on the current sample size, we believe that the relationship between event rates and redshift for the four groups of FRBs tends to align more with the evolutionary history of stellar mass density.
4.3. Statistical Analysis
The results of the K–S test from Table 1 demonstrate that there are noteworthy disparities in the distributions of dispersion, pulse width, and bandwidth between repeaters and non-repeating FRBs, indicating that they may have different distributions. Under the same parameters, the distribution of repeaters and multi-structural one-offs is different.
In the aspect of non-repeating FRBs and repeaters, the cumulative distribution plot demonstrated in Figure A1b illustrates the differences in pulse width distributions between repeaters and non-repeating FRBs. It is evident that, after normalizing the two distributions, there are differences in the CDF distributions. The mean value of pulse widths in the non-repeating FRBs are narrower than those of repeaters, implying that the radiation mechanisms of repeating and non-repeating FRBs may be different.
While in the aspect of multi-structural one-offs and repeaters, the results of the statistical analysis show different distributions. Table 2 and Table 3 present the results of the M–W–W and Wilcoxon rank-sum tests, respectively. Although some parameters show differences in their test results compared to the K–S test, the overall conclusions implied by the results remain consistent: the origins of repeaters and multi-structural one-offs may be different. It is also found that the mean values of the pulse width and scattering time of multi-structural one-offs are lower than repeaters, indicating that multi-structural one-offs may have unique characteristics compared to repeaters. Additionally, multi-structural one-offs do not show significant differences from non-repeating FRBs. It is important to note that the statistical results may be biased due to the small sample size. Therefore, with a larger sample size for both groups, the conclusions may differ from those currently obtained.
5. Conclusions
“Multi-structural” is believed to indicate the presence of repeating FRBs [33]. In this paper, we calculated the energy functions of four subsamples, apparent non-repeating FRBs, repeaters, multi-structural one-offs, and the joint sample of repeaters and multi-structural one-offs using the Vmax method in CHIME/FRB Catalog 1. After analyzing the event rate evolution history and conducting the K–S and M–W–W tests, we drew the following conclusions:
- The trend of the event rate of non-repeating FRBs is consistent with what was found by Hashimoto et al. [22]. The redshift evolution of the event rate of repeaters, however, shows no similarity with that of the star formation rate, which was suggested by Hashimoto et al. [22] and James et al. [24]. We calculated the energy functions for 167 one-offs, 20 repeaters, 18 multi-structural one-offs, and 38 repeaters and multi-structural one-offs combined. The redshift evolution of all four subsamples was found to be distinct from that of the star formation rate.
- We carried out statistical testing to quantify the similarities between multi-structural one-offs and repeaters. We found that, based on the current sample size, the difference between repeaters and multi-structural one-offs can be distinguished from statistical analysis and the differences between multi-structural one-offs and usual one-offs are not significant. Through K–S and M–W–W test, we can conclude that multi-structural one-offs may have differences to repeaters. Whether morphological multi-structural one-offs are candidates of repeaters still needs to be determined when a larger sample size is available.
Funding
This work was funded by the National Natural Science Foundation of China (No. 11988101, 12203069) and the National SKA Program of China/2022SKA0130100. This work was also supported by the Office the Leading Group for Cyberspace Affairs, CAS (No. CAS-WX2023PY-0102). Z.Z. is supported by NSFC grant No. 12041302, and U1931110. Z.Z. is also supported by the science research grant from the China Manned Space Project with grant no. CMS-CSST-2021-A08.
Data Availability Statement
The dataset we used in the work is available in the CHIME/FRB Catalog 1 accessed on 10 March 2023, https://www.chime-frb.ca/catalog.
Acknowledgments
The authors gratefully acknowledge valuable discussions with T. Hashimoto, and Y.C. Li. And, we greatly acknowledge two anonymous referees for their valuable comments and suggestions, which have significantly improved the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A shows the observed parameter distributions of one-offs, repeating FRBs, and multi-structural one-offs, where the upper (lower) panels correspond to the cumulative (differential) distribution of the observed parameters, respectively.
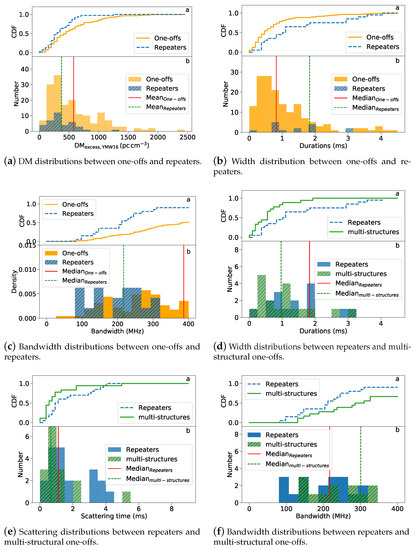
Figure A1.
Parameter distributions of one-offs, repeaters, and multi-structural one-offs. Here, multi-structures in (d–f) stand for groups of multi-structural one-offs. The upper pannel, (a), gives the cumulative distributions of the observed parameters, as the lower pannel, (b), demonstrates the differential distributions of the observed parameters of different groups of FRBs.
References
- Chatterjee, S.; Law, C.J.; Wharton, R.S.; Burke-Spolaor, S.; Hessels, J.W.T.; Bower, G.C.; Cordes, J.M.; Tendulkar, S.P.; Bassa, C.G.; Demorest, P.; et al. A Direct Localization of a Fast Radio Burst and Its Host. Nature 2017, 541, 58–61. [Google Scholar] [CrossRef] [PubMed]
- The CHIME/FRB Collaboration. A Second Source of Repeating Fast Radio Bursts. Nature 2019, 566, 235–238. [Google Scholar] [CrossRef] [PubMed]
- Caleb, M.; Keane, E. A Decade and a Half of Fast Radio Burst Observations. Universe 2021, 7, 453. [Google Scholar] [CrossRef]
- Petroff, E.; Hessels, J.W.T.; Lorimer, D.R. Fast Radio Bursts. Astron. Astrophys. Rev. 2019, 27, 4. [Google Scholar] [CrossRef]
- Zhang, B. The Physical Mechanisms of Fast Radio Bursts. Nature 2020, 587, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Lorimer, D.R.; Bailes, M.; McLaughlin, M.A.; Narkevic, D.J.; Crawford, F. A Bright Millisecond Radio Burst of Extragalactic Origin. Science 2007, 318, 777–780. [Google Scholar] [CrossRef]
- Petroff, E.; Barr, E.D.; Jameson, A.; Keane, E.F.; Bailes, M.; Kramer, M.; Morello, V.; Tabbara, D.; Van Straten, W. FRBCAT: The Fast Radio Burst Catalogue. Publ. Astron. Soc. Aust. 2016, 33, e045. [Google Scholar] [CrossRef]
- Amiri, M.; Andersen, B.C.; Bandura, K.; Berger, S.; Bhardwaj, M.; Boyce, M.M.; Boyle, P.J.; Brar, C.; Breitman, D.; Cassanelli, T.; et al. The First CHIME/FRB Fast Radio Burst Catalog. ApJS 2021, 257, 59. [Google Scholar] [CrossRef]
- Chen, B.H.; Hashimoto, T.; Goto, T.; Kim, S.J.; Santos, D.J.D.; On, A.Y.L.; Lu, T.-Y. Uncloaking Hidden Repeating Fast Radio Bursts with Unsupervised Machine Learning. Mon. Not. R. Astron. Soc. 2022, 509, 1227–1236. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, B. Cosmological implications of fast radio burst/gamma-ray burst associations. ApJ 2014, 783, L35. [Google Scholar] [CrossRef]
- Gao, H.; Li, Z.; Zhang, B. Fast radio burst/gamma-ray burst cosmography. ApJ 2014, 788, 189. [Google Scholar] [CrossRef]
- Zhou, B.; Li, X.; Wang, T.; Fan, Y.-Z.; Wei, D.-M. Fast Radio Bursts as a Cosmic Probe? Phys. Rev. D 2014, 89, 107303. [Google Scholar] [CrossRef]
- Madhavacheril, M.S.; Battaglia, N.; Smith, K.M.; Sievers, J.L. Cosmology with KSZ: Breaking the Optical Depth Degeneracy with Fast Radio Bursts. Phys. Rev. D 2019, 100, 103532. [Google Scholar] [CrossRef]
- Cordes, J.M.; Chatterjee, S. Fast Radio Bursts: An Extragalactic Enigma. Annu. Rev. Astron. Astrophys. 2019, 57, 417–465. [Google Scholar] [CrossRef]
- Petroff, E.; Hessels, J.W.T.; Lorimer, D.R. Fast Radio Bursts at the Dawn of the 2020s. Astron. Astrophys. Rev. 2022, 30, 2. [Google Scholar] [CrossRef]
- Lyubarsky, Y. Emission Mechanisms of Fast Radio Bursts. Universe 2021, 7, 56. [Google Scholar] [CrossRef]
- Platts, E.; Weltman, A.; Walters, A.; Tendulkar, S.P.; Gordin, J.E.B.; Kandhai, S. A Living Theory Catalogue for Fast Radio Bursts. Phys. Rep. 2019, 821, 1–27. [Google Scholar] [CrossRef]
- Li, C.K.; Lin, L.; Xiong, S.L.; Ge, M.Y.; Li, X.B.; Li, T.P.; Lu, F.J.; Zhang, S.N.; Tuo, Y.L.; Nang, Y.; et al. HXMT Identification of a Non-Thermal X-Ray Burst from SGR J1935+2154 and with FRB 200428. Nat. Astron. 2021, 5, 378–384. [Google Scholar] [CrossRef]
- Lin, L.; Zhang, C.F.; Wang, P.; Gao, H.; Guan, X.; Han, J.L.; Jiang, J.C.; Jiang, P.; Lee, K.J.; Li, D.; et al. No Pulsed Radio Emission during a Bursting Phase of a Galactic Magnetar. Nature 2020, 587, 63–65. [Google Scholar] [CrossRef]
- The CHIME/FRB Collaboration. A Bright Millisecond-Duration Radio Burst from a Galactic Magnetar. Nature 2020, 587, 54–58. [Google Scholar] [CrossRef]
- Bochenek, C.D.; Ravi, V.; Belov, K.V.; Hallinan, G.; Kocz, J.; Kulkarni, S.R.; McKenna, D.L. A Fast Radio Burst Associated with a Galactic Magnetar. Nature 2020, 587, 59–62. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, T.; Goto, T.; On, A.Y.L.; Lu, T.-Y.; Santos, D.J.D.; Ho, S.C.-C.; Kim, S.J.; Wang, T.-W.; Hsiao, T.Y.-Y. No Redshift Evolution of Non-Repeating Fast Radio Burst Rates. Mon. Not. R. Astron. Soc. 2020, 498, 3927–3945. [Google Scholar] [CrossRef]
- Locatelli, N.; Ronchi, M.; Ghirlanda, G.; Ghisellini, G. The Luminosity–Volume Test for Cosmological Fast Radio Bursts. A&A 2019, 625, A109. [Google Scholar]
- James, C.W.; Prochaska, J.X.; Macquart, J.-P.; North-Hickey, F.O.; Bannister, K.W.; Dunning, A. The Fast Radio Burst Population Evolves, Consistent with the Star Formation Rate. Mon. Not. R. Astron. Soc. Lett. 2021, 510, L18–L23. [Google Scholar] [CrossRef]
- Arcus, W.R.; Macquart, J.-P.; Sammons, M.W.; James, C.W.; Ekers, R.D. The Fast Radio Burst Dispersion Measure Distribution. Mon. Not. R. Astron. Soc. 2021, 501, 5319–5329. [Google Scholar] [CrossRef]
- Zhang, R.C.; Zhang, B.; Li, Y.; Lorimer, D.R. On the Energy and Redshift Distributions of Fast Radio Bursts. Mon. Not. R. Astron. Soc. 2020, 501, 157–167. [Google Scholar] [CrossRef]
- Pleunis, Z.; Good, D.C.; Kaspi, V.M.; Mckinven, R.; Ransom, S.M.; Scholz, P.; Bandura, K.; Bhardwaj, M.; Boyle, P.J.; Brar, C.; et al. Fast Radio Burst Morphology in the First CHIME/FRB Catalog. ApJ 2021, 923, 1. [Google Scholar] [CrossRef]
- Feng, Y.; Li, D.; Yang, Y.-P.; Zhang, Y.; Zhu, W.; Zhang, B.; Lu, W.; Wang, P.; Dai, S.; Lynch, R.S.; et al. Frequency-Dependent Polarization of Repeating Fast Radio Bursts—Implications for Their Origin. Science 2022, 375, 1266–1270. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, Y.-K.; Li, D.; Yang, Y.-P.; Wang, P.; Niu, C.-H.; Dai, S.; Yao, J.-M. Circular Polarization in Two Active Repeating Fast Radio Bursts. Sci. Bull. 2022, 67, 2398–2401. [Google Scholar] [CrossRef]
- Caleb, M.; Stappers, B.W.; Rajwade, K.; Flynn, C. Are All Fast Radio Bursts Repeating Sources? Mon. Not. R. Astron. Soc. 2019, 484, 5500–5508. [Google Scholar] [CrossRef]
- Cui, X.-H.; Zhang, C.-M.; Wang, S.-Q.; Zhang, J.-W.; Li, D.; Peng, B.; Zhu, W.-W.; Wang, N.; Strom, R.; Ye, C.-Q.; et al. Fast Radio Bursts: Do Repeaters and Non-Repeaters Originate in Statistically Similar Ensembles? Mon. Not. R. Astron. Soc. 2020, 500, 3275–3280. [Google Scholar] [CrossRef]
- Connor, L.; Petroff, E. On Detecting Repetition from Fast Radio Bursts. ApJL 2018, 861, L1. [Google Scholar] [CrossRef]
- Hessels, J.W.T.; Spitler, L.G.; Seymour, A.D.; Cordes, J.M.; Michilli, D.; Lynch, R.S.; Gourdji, K.; Archibald, A.M.; Bassa, C.G.; Bower, G.C.; et al. FRB 121102 Bursts Show Complex Time–Frequency Structure. ApJ 2019, 876, L23. [Google Scholar] [CrossRef]
- Hashimoto, T.; Goto, T.; Chen, B.H.; Ho, S.C.-C.; Hsiao, T.Y.-Y.; Wong, Y.H.V.; On, A.Y.L.; Kim, S.J.; Kilerci-Eser, E.; Huang, K.-C.; et al. Energy Functions of Fast Radio Bursts Derived from the First CHIME/FRB Catalogue. Mon. Not. R. Astron. Soc. 2022, 511, 1961–1976. [Google Scholar] [CrossRef]
- Collaboration, T.C.; Andersen, B.C.; Bandura, K.; Bhardwaj, M.; Boyle, P.J.; Brar, C.; Cassanelli, T.; Chatterjee, S.; Chawla, P.; Cook, A.M.; et al. CHIME/FRB Discovery of 25 Repeating Fast Radio Burst Sources 2023. ApJ 2023, 947, 83. [Google Scholar]
- Michilli, D.; Bhardwaj, M.; Brar, C.; Patel, C.; Gaensler, B.M.; Kaspi, V.M.; Kirichenko, A.; Masui, K.W.; Sand, K.R.; Scholz, P.; et al. Sub-Arcminute Localization of 13 Repeating Fast Radio Bursts Detected by CHIME/FRB 2022. arXiv 2022, arXiv:2212.11941. [Google Scholar]
- Macquart, J.-P.; Prochaska, J.X.; McQuinn, M.; Bannister, K.W.; Bhandari, S.; Day, C.K.; Deller, A.T.; Ekers, R.D.; James, C.W.; Marnoch, L.; et al. A Census of Baryons in the Universe from Localized Fast Radio Bursts. Nature 2020, 581, 391–395. [Google Scholar] [CrossRef]
- Schmidt, M. Space Distribution and Luminosity Functions of Quasi-Stellar Radio Sources. ApJ 1968, 151, 393. [Google Scholar] [CrossRef]
- Smirnov, N. Table for Estimating the Goodness of Fit of Empirical Distributions. Ann. Math. Stat. 1948, 19, 279–281. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Luo, R.; Lee, K.; Lorimer, D.R.; Zhang, B. On the Normalized FRB Luminosity Function. Mon. Not. R. Astron. Soc. 2018, 481, 2320–2337. [Google Scholar] [CrossRef]
- Shin, K.; Masui, K.W.; Bhardwaj, M.; Cassanelli, T.; Chawla, P.; Dobbs, M.; Dong, F.A.; Fonseca, E.; Gaensler, B.M.; Herrera-Martín, A.; et al. Inferring the Energy and Distance Distributions of Fast Radio Bursts Using the First CHIME/FRB Catalog. ApJ 2023, 944, 105. [Google Scholar] [CrossRef]
- Madau, P.; Fragos, T. Radiation Backgrounds at Cosmic Dawn: X-Rays from Compact Binaries. ApJ 2017, 840, 39. [Google Scholar] [CrossRef]
- López Fernández, R.; González Delgado, R.M.; Pérez, E.; García-Benito, R.; Cid Fernandes, R.; Schoenell, W.; Sánchez, S.F.; Gallazzi, A.; Sánchez-Blázquez, P.; Vale Asari, N.; et al. Cosmic Evolution of the Spatially Resolved Star Formation Rate and Stellar Mass of the CALIFA Survey. A&A 2018, 615, A27. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).