The Elasticity of the Neutron Star Mantle: The Improved Compressible Liquid Drop Model for Cylindrical Phases
Abstract
1. Introduction
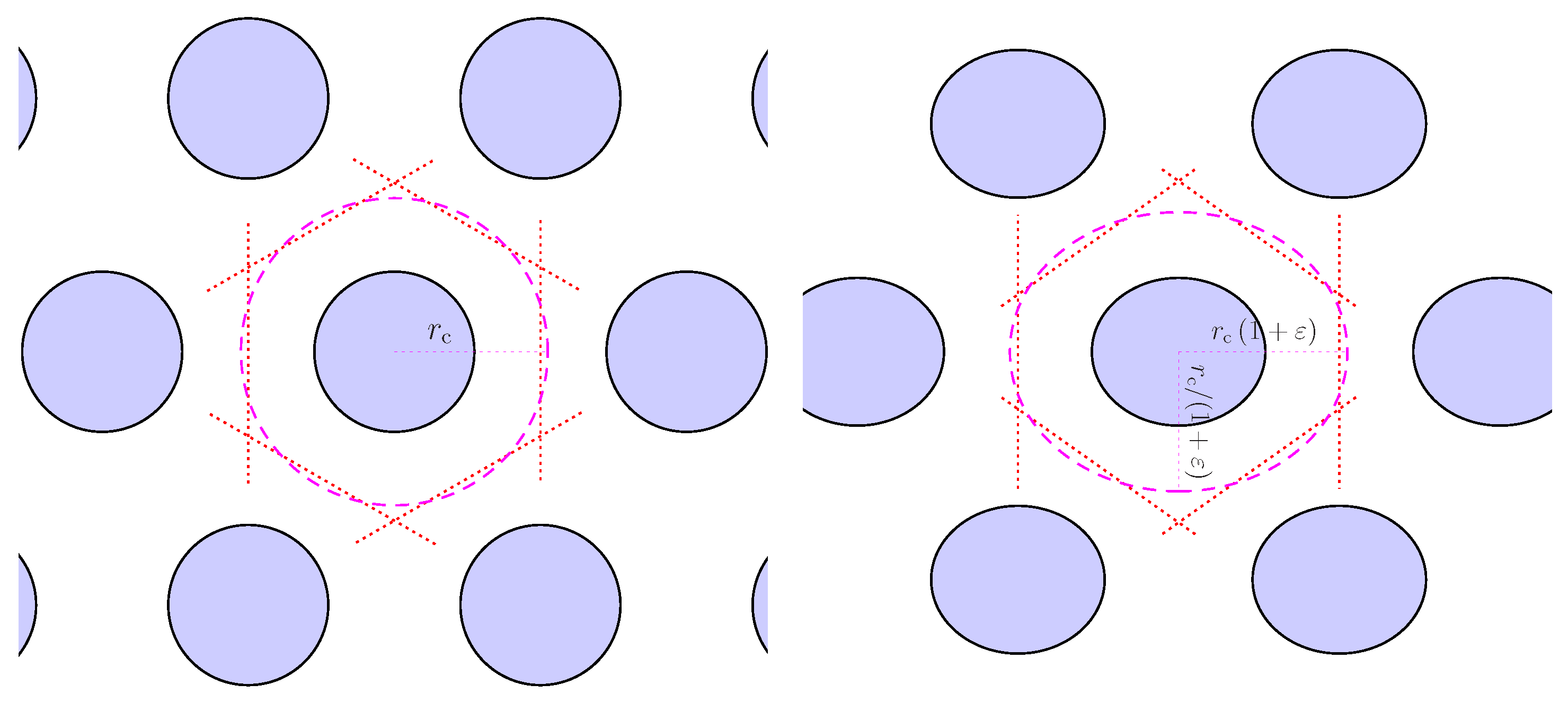
2. Formalism
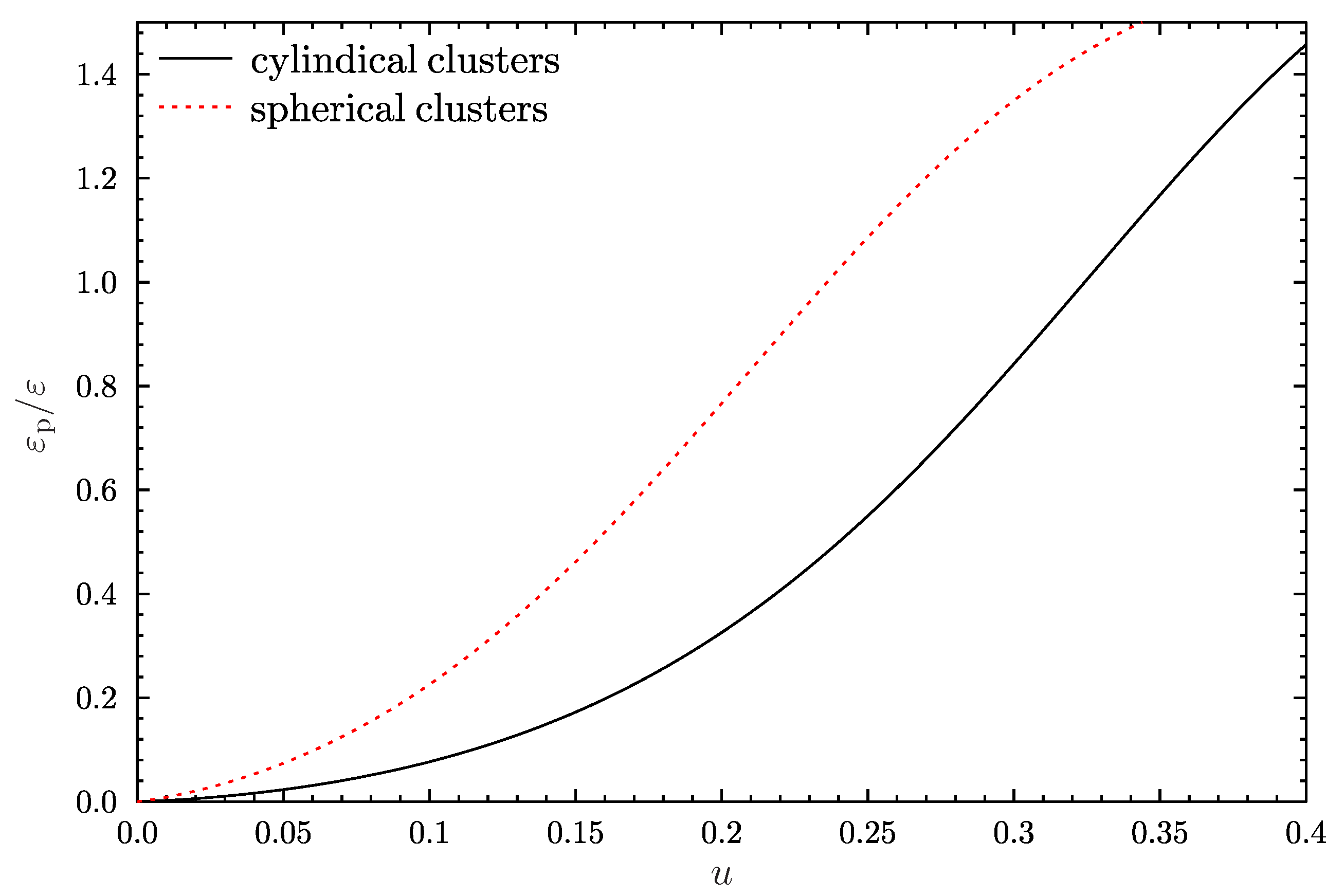
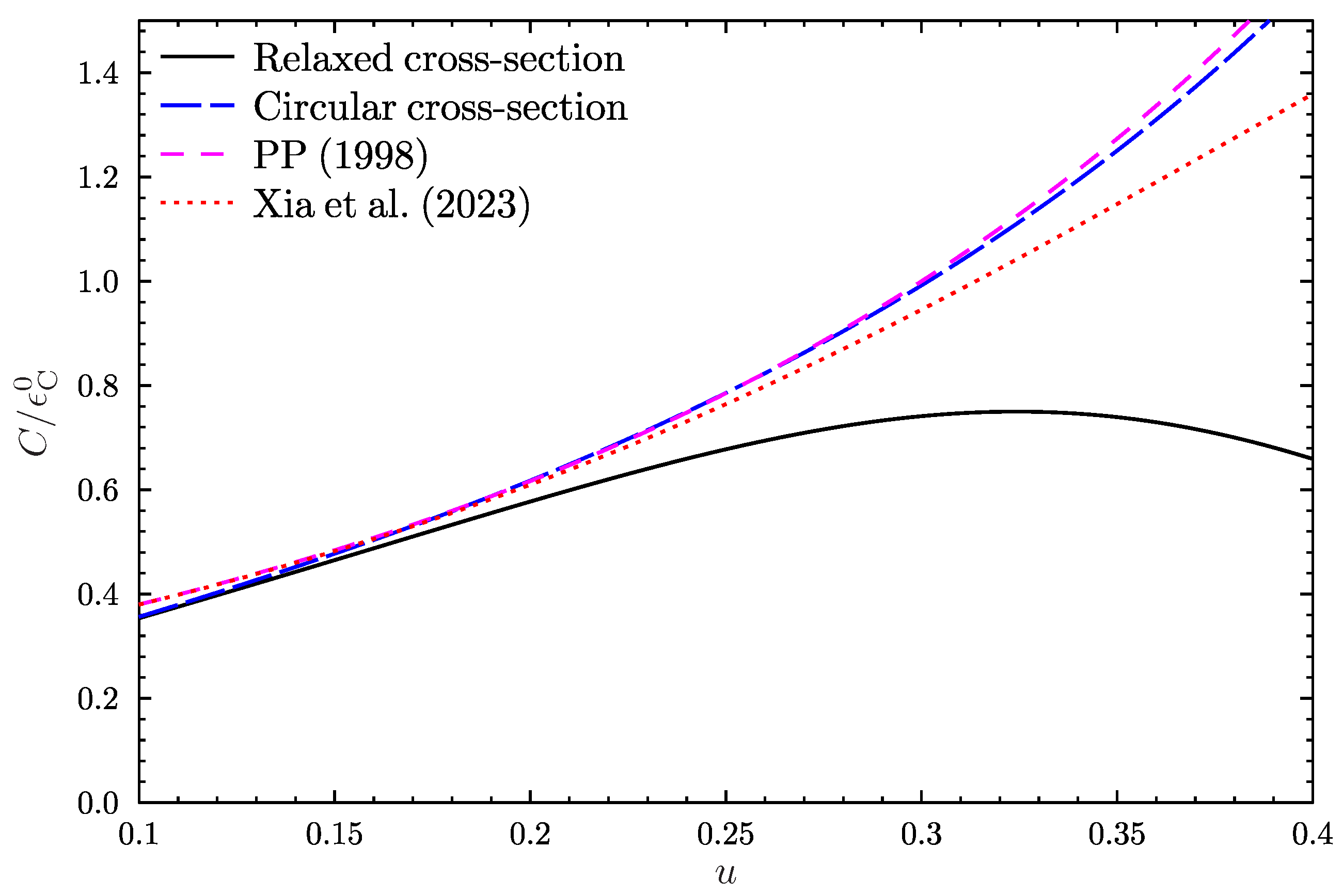
3. Results
4. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CLDM | Compressible liquid drop model |
| ETF | Extended Thomas–Fermi |
| 1 | Derivations for the inverted phase can be performed straightforwardly by substituting , and treating as the linear radius of the neutron phase, located in the center. |
| 2 | Note that terms up to should be included to obtain this expression. |
| 3 | Thanks to the minimization procedure over internal variables, corrections in the order of contribute to the energy at the order of , and thus can be neglected |
References
- Ravenhall, D.G.; Pethick, C.J.; Wilson, J.R. Structure of Matter below Nuclear Saturation Density. Phys. Rev. Lett. 1983, 50, 2066–2069. [Google Scholar] [CrossRef]
- Hashimoto, M.; Seki, H.; Yamada, M. Shape of nuclei in the crust of a neutron star. Prog. Theor. Phys. 1984, 71, 320–326. [Google Scholar] [CrossRef]
- Lorenz, C.P.; Ravenhall, D.G.; Pethick, C.J. Neutron star crusts. Phys. Rev. Lett. 1993, 70, 379–382. [Google Scholar] [CrossRef] [PubMed]
- Oyamatsu, K. Nuclear shapes in the inner crust of a neutron star. Nucl. Phys. A 1993, 561, 431–452. [Google Scholar] [CrossRef]
- Douchin, F.; Haensel, P.; Meyer, J. Nuclear surface and curvature properties for SLy Skyrme forces and nuclei in the inner neutron-star crust. Nucl. Phys. A 2000, 665, 419–446. [Google Scholar] [CrossRef]
- Iida, K.; Watanabe, G.; Sato, K. Formation of Nuclear “Pasta” in Cold Neutron Star Matter. Prog. Theor. Phys. 2001, 106, 551–559. [Google Scholar] [CrossRef]
- Nakazato, K.; Iida, K.; Oyamatsu, K. Curvature effect on nuclear “pasta”: Is it helpful for gyroid appearance? Phys. Rev. C 2011, 83, 065811. [Google Scholar] [CrossRef]
- Newton, W.G.; Gearheart, M.; Li, B.A. A Survey of the Parameter Space of the Compressible Liquid Drop Model as Applied to the Neutron Star Inner Crust. Astrophys. J. Suppl. Ser. 2013, 204, 9. [Google Scholar] [CrossRef]
- Sharma, B.K.; Centelles, M.; Viñas, X.; Baldo, M.; Burgio, G.F. Unified equation of state for neutron stars on a microscopic basis. Astron. Astrophys. 2015, 584, A103. [Google Scholar] [CrossRef]
- Schuetrumpf, B.; Nazarewicz, W. Twist-averaged boundary conditions for nuclear pasta Hartree-Fock calculations. Phys. Rev. C 2015, 92, 045806. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Horowitz, C.J.; Schuetrumpf, B. Quantum nuclear pasta and nuclear symmetry energy. Phys. Rev. C 2017, 95, 055804. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. II. Pasta phases in semiclassical approximation. Phys. Rev. C 2020, 101, 015802. [Google Scholar] [CrossRef]
- Oyamatsu, K.; Iida, K.; Sotani, H. Systematic study of pasta nuclei in neutron stars with families of the empirical nuclear equations of state. J. Phys. Conf. Ser. 2020, 1643, 012059. [Google Scholar] [CrossRef]
- Xia, C.J.; Maruyama, T.; Yasutake, N.; Tatsumi, T.; Zhang, Y.X. Nuclear pasta structures and symmetry energy. Phys. Rev. C 2021, 103, 055812. [Google Scholar] [CrossRef]
- Ji, F.; Hu, J.; Shen, H. Nuclear pasta and symmetry energy in the relativistic point-coupling model. Phys. Rev. C 2021, 103, 055802. [Google Scholar] [CrossRef]
- Dinh Thi, H.; Carreau, T.; Fantina, A.F.; Gulminelli, F. Uncertainties in the pasta-phase properties of catalysed neutron stars. Astron. Astrophys. 2021, 654, A114. [Google Scholar] [CrossRef]
- Dinh Thi, H.; Fantina, A.F.; Gulminelli, F. The effect of the energy functional on the pasta-phase properties of catalysed neutron stars. Eur. Phys. J. A 2021, 57, 296. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. III. Inclusion of microscopic corrections to pasta phases. Phys. Rev. C 2022, 105, 015803. [Google Scholar] [CrossRef]
- Shchechilin, N.N.; Zemlyakov, N.A.; Chugunov, A.I.; Gusakov, M.E. Pasta Phases in Neutron Star Mantle: Extended Thomas–Fermi vs. Compressible Liquid Drop Approaches. Universe 2022, 8, 582. [Google Scholar] [CrossRef]
- Parmar, V.; Das, H.C.; Kumar, A.; Kumar, A.; Sharma, M.K.; Arumugam, P.; Patra, S.K. Pasta properties of the neutron star within effective relativistic mean-field model. Phys. Rev. D 2022, 106, 023031. [Google Scholar] [CrossRef]
- Chamel, N.; Pearson, J.M.; Shchechilin, N. Is there pasta in neutron stars? Eur. Phys. J. Web Conf. 2022, 274, 07013. [Google Scholar] [CrossRef]
- Dinh Thi, H.; Fantina, A.F.; Gulminelli, F. Properties of pasta phases in catalyzed neutron stars. arXiv 2022, arXiv:2206.07969. [Google Scholar]
- Pelicer, M.R.; Menezes, D.P.; Dutra, M.; Lourenço, O. Do short range correlations inhibit the appearance of the nuclear pasta? arXiv 2022, arXiv:2211.14002. [Google Scholar]
- Berry, D.K.; Caplan, M.E.; Horowitz, C.J.; Huber, G.; Schneider, A.S. “Parking-garage” structures in nuclear astrophysics and cellular biophysics. Phys. Rev. C 2016, 94, 055801. [Google Scholar] [CrossRef]
- Schneider, A.S.; Berry, D.K.; Briggs, C.M.; Caplan, M.E.; Horowitz, C.J. Nuclear “waffles”. Phys. Rev. C 2014, 90, 055805. [Google Scholar] [CrossRef]
- Newton, W.G.; Cantu, S.; Wang, S.; Stinson, A.; Kaltenborn, M.A.; Stone, J.R. Glassy quantum nuclear pasta in neutron star crusts. Phys. Rev. C 2022, 105, 025806. [Google Scholar] [CrossRef]
- Caplan, M.E.; Horowitz, C.J. Colloquium: Astromaterial science and nuclear pasta. Rev. Mod. Phys. 2017, 89, 041002. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Berry, D.K. Shear viscosity and thermal conductivity of nuclear “pasta”. Phys. Rev. C 2008, 78, 035806. [Google Scholar] [CrossRef]
- Yakovlev, D.G. Electron transport through nuclear pasta in magnetized neutron stars. Mon. Not. R. Astron. Soc. 2015, 453, 581–590. [Google Scholar] [CrossRef]
- Schmitt, A.; Shternin, P. Reaction Rates and Transport in Neutron Stars. In The Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 455–574. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Gusakov, M.E.; Haensel, P. Bulk viscosity in a neutron star mantle. Mon. Not. R. Astron. Soc. 2018, 481, 4924–4930. [Google Scholar] [CrossRef]
- Nandi, R.; Schramm, S. Transport Properties of the Nuclear Pasta Phase with Quantum Molecular Dynamics. Astrophys. J. 2018, 852, 135. [Google Scholar] [CrossRef]
- Pelicer, M.R.; Antonelli, M.; Menezes, D.P.; Gulminelli, F. Anisotropic electron transport in the nuclear pasta phase. Mon. Not. R. Astron. Soc. 2023, 521, 743–759. [Google Scholar] [CrossRef]
- Gusakov, M.E.; Yakovlev, D.G.; Haensel, P.; Gnedin, O.Y. Direct Urca process in a neutron star mantle. Astron. Astrophys. 2004, 421, 1143–1148. [Google Scholar] [CrossRef]
- Alloy, M.D.; Menezes, D.P. Nuclear “pasta phase” and its consequences on neutrino opacities. Phys. Rev. C 2011, 83, 035803. [Google Scholar] [CrossRef]
- Schuetrumpf, B.; Martínez-Pinedo, G.; Reinhard, P.G. Survey of nuclear pasta in the intermediate-density regime: Structure functions for neutrino scattering. Phys. Rev. C 2020, 101, 055804. [Google Scholar] [CrossRef]
- Lin, Z.; Caplan, M.E.; Horowitz, C.J.; Lunardini, C. Fast neutrino cooling of nuclear pasta in neutron stars: Molecular dynamics simulations. Phys. Rev. C 2020, 102, 045801. [Google Scholar] [CrossRef]
- Pethick, C.; Potekhin, A. Liquid crystals in the mantles of neutron stars. Phys. Lett. B 1998, 427, 7–12. [Google Scholar] [CrossRef]
- Sotani, H. Constraints on pasta structure of neutron stars from oscillations in giant flares. Mon. Not. R. Astron. Soc. 2011, 417, L70–L73. [Google Scholar] [CrossRef]
- Gearheart, M.; Newton, W.G.; Hooker, J.; Li, B.A. Upper limits on the observational effects of nuclear pasta in neutron stars. Mon. Not. R. Astron. Soc. 2011, 418, 2343–2349. [Google Scholar] [CrossRef]
- Sotani, H. Crustal torsional oscillations inside the deeper pasta structures. Astron. Nachrichten 2019, 340, 920–923. [Google Scholar] [CrossRef]
- Biswas, B.; Nandi, R.; Char, P.; Bose, S. Role of crustal physics in the tidal deformation of a neutron star. Phys. Rev. D 2019, 100, 044056. [Google Scholar] [CrossRef]
- Gittins, F.; Andersson, N.; Pereira, J.P. Tidal deformations of neutron stars with elastic crusts. Phys. Rev. D 2020, 101, 103025. [Google Scholar] [CrossRef]
- Caplan, M.E.; Schneider, A.S.; Horowitz, C.J. Elasticity of Nuclear Pasta. Phys. Rev. Lett. 2018, 121, 132701. [Google Scholar] [CrossRef]
- Xia, C.J.; Maruyama, T.; Yasutake, N.; Tatsumi, T.; Zhang, Y.X. Elastic properties of nuclear pasta in a fully three-dimensional geometry. Phys. Lett. B 2023, 839, 137769. [Google Scholar] [CrossRef]
- Pethick, C.J.; Zhang, Z.W.; Kobyakov, D.N. Elastic properties of phases with nonspherical nuclei in dense matter. Phys. Rev. C 2020, 101, 055802. [Google Scholar] [CrossRef]
- Zemlyakov, N.A.; Chugunov, A.I. Neutron star inner crust: Reduction of shear modulus by nuclei finite size effect. Mon. Not. R. Astron. Soc. 2023, 518, 3813–3819. [Google Scholar] [CrossRef]
- Gusakov, M.E.; Chugunov, A.I. Thermodynamically Consistent Equation of State for an Accreted Neutron Star Crust. Phys. Rev. Lett. 2020, 124, 191101. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Pethick, C.J.; Ravenhall, D.G.; Lamb, D.Q. Physical properties of hot, dense matter: The general case. Nucl. Phys. A 1985, 432, 646–742. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1: Equation of State and Structure; Springer: New York, NY, USA, 2007; Volume 326. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; U.S. Government Printing Office: Washington, DC, USA, 1972.
- Ramanukan, S. Modular Equations and Approximations to π. Quart. J. Pure App. Math. 1914, 45, 350–372. [Google Scholar]
- Kondratyev, B.P. Potential Theory. New Methods and Problems with Solutions; Mir: Moscow, Russia, 2007. (In Russian) [Google Scholar]
- Zemlyakov, N.A.; Chugunov, A.I. Stability of Spherical Nuclei in the Inner Crust of Neutron Stars. Particles 2022, 5, 225–234. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities. Nucl. Phys. A 1997, 627, 710–746. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zemlyakov, N.A.; Chugunov, A.I. The Elasticity of the Neutron Star Mantle: The Improved Compressible Liquid Drop Model for Cylindrical Phases. Universe 2023, 9, 220. https://doi.org/10.3390/universe9050220
Zemlyakov NA, Chugunov AI. The Elasticity of the Neutron Star Mantle: The Improved Compressible Liquid Drop Model for Cylindrical Phases. Universe. 2023; 9(5):220. https://doi.org/10.3390/universe9050220
Chicago/Turabian StyleZemlyakov, Nikita A., and Andrey I. Chugunov. 2023. "The Elasticity of the Neutron Star Mantle: The Improved Compressible Liquid Drop Model for Cylindrical Phases" Universe 9, no. 5: 220. https://doi.org/10.3390/universe9050220
APA StyleZemlyakov, N. A., & Chugunov, A. I. (2023). The Elasticity of the Neutron Star Mantle: The Improved Compressible Liquid Drop Model for Cylindrical Phases. Universe, 9(5), 220. https://doi.org/10.3390/universe9050220




