Phases of Rotating Black Objects in d = 5 Einstein–Gauss–Bonnet Theory
Abstract
1. Introduction
2. The Model and the Static Limit
2.1. Action, Equations and Scaled Quantities
2.2. The Schwarzschild–Tangherlini Solution in EGB Theory
3. Rotating Black Holes: The Case of Equal Angular Momenta
3.1. The Ansatz and Particular Cases
3.2. The Domain of Existence and Attractors
4. Black Objects Rotating in a Single Plane: Holes and Rings
4.1. The Ansatz and Quantities of Interest
4.2. The Solutions
5. Further Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | Various numerical factors in Equation (7) have been chosen such that in the static limit with , while the maximal value for Einstein gravity BH solutions is . |
| 2 | Static EGB solutions with a horizon topology (i.e., BRs) are also known to exist [23], although not in closed form. However, these solutions (still) possess a conical singularity, and thus are physically less interesting. |
| 3 | |
| 4 | The limit corresponds to the extremal MP solution in Einstein gravity. |
| 5 | Note, that a part of the boundary of the -domain consists of a configurations with maximal entropy, which do not coincide with the other sets of limiting solutions. |
| 6 | Note that the line element (21) can be employed as well in the study of solitonic compact objects, in which case the range of the radial coordinate is . Such configurations possess no horizon () and satisfy a specific set of boundary conditions at the origin, (with and ), while the boundary conditions at and at are similar to those employed for BHs with spherical horizon topology. Additionally, one remarks that the static limit of the line-element (21) results in the Schwarzschild–Tangherlini-EGB solution in isotropic coordinates, i.e., with a different radial coordinates than in (9). |
| 7 | |
| 8 | The MP solution with rotation in a single plane has . For the corresponding BRs one finds instead , and , with . |
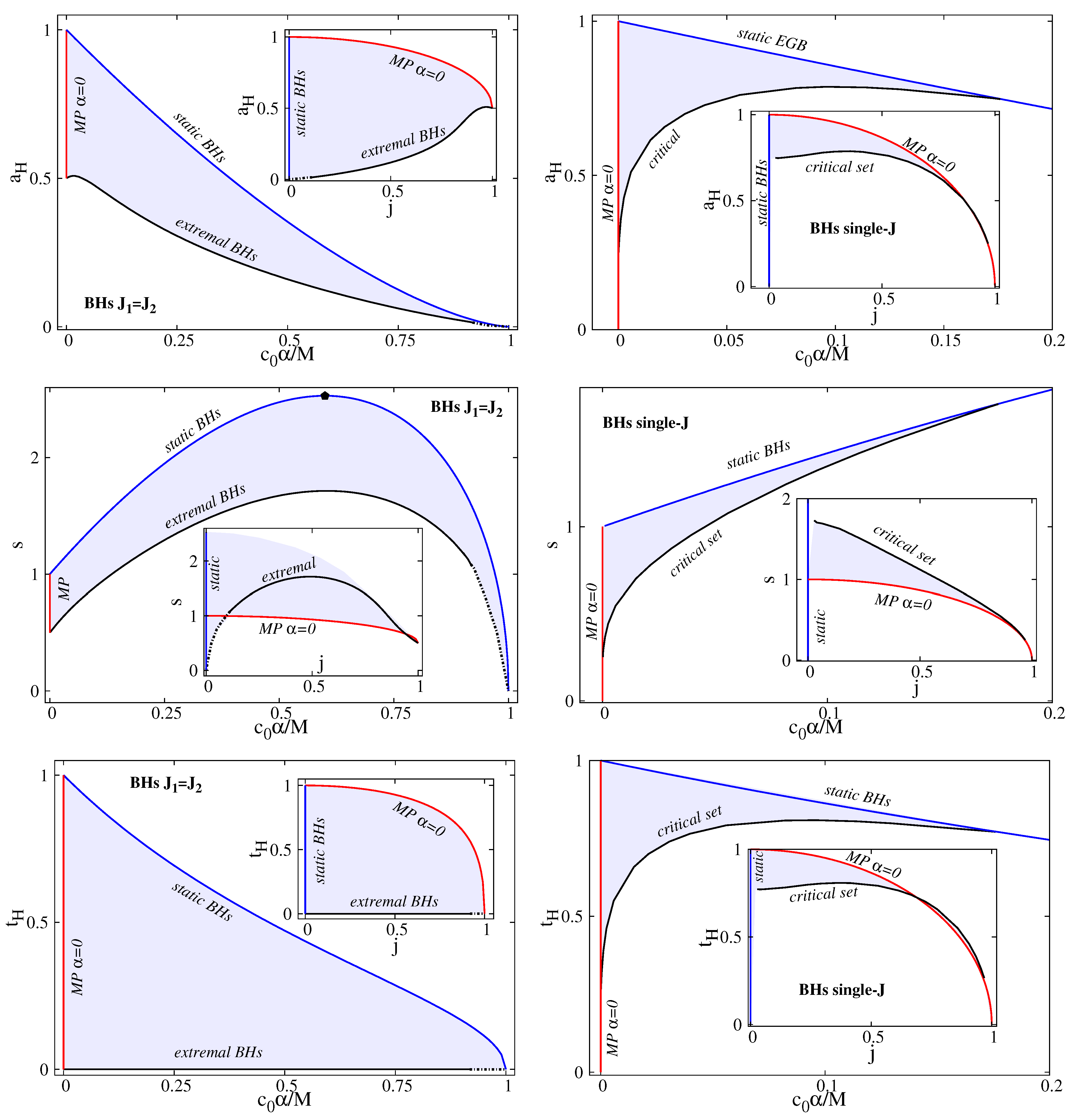
| 9 | One remarks that the horizon area of BRs, when considered as a function of angular momentum (at fixed mass), exhibits a "loop" in the vicinity of (instead of a spike, as for ), see the inset in Figure 2. The existence of such loops in the phase diagram of spinning solutions has also been noticed in some models with non-Abelian matter fields [27,28]. |
| 10 |
References
- Lovelock, D. The Einstein tensor and its generalizations. J. Math. Phys. 1971, 12, 498. [Google Scholar] [CrossRef]
- Antoniadis, I.; Ferrara, S.; Minasian, R.; Narain, K.S. R**4 couplings in M- and type II theories on Calabi–Yau spaces. Nucl. Phys. B 1997, 507, 571. [Google Scholar] [CrossRef]
- Ferrara, S.; Khuri, R.R.; Minasian, R. M-Theory on a Calabi–Yau Manifold. Phys. Lett. B 1996, 375, 81. [Google Scholar] [CrossRef]
- Gross, D.J.; Witten, E. Superstring Modifications Of Einstein’s Equations. Nucl. Phys. B 1986, 277, 1. [Google Scholar] [CrossRef]
- Metsaev, R.R.; Tseytlin, A.A. Two loop beta function for the generalized bosonic sigma model. Phys. Lett. B 1987, 191, 354. [Google Scholar] [CrossRef]
- Callan, C.G.; Myers, R.C.; Perry, M.J. Black holes in string theory. Nucl. Phys. B 1988, 311, 673. [Google Scholar]
- Myers, R.C. Higher-derivative gravity, surface terms and string theory. Phys. Rev. D 1987, 36, 392. [Google Scholar] [CrossRef]
- Boulware, D.G.; Deser, S. String Generated Gravity Models. Phys. Rev. Lett. 1985, 55, 2656. [Google Scholar] [CrossRef]
- Wheeler, J.T. Symmetric Solutions To The Gauss–Bonnet Extended Einstein Equations. Nucl. Phys. B 1986, 268, 737. [Google Scholar] [CrossRef]
- Tangherlini, F.R. Schwarzschild field in n dimensions and the dimensionality of space problem. Nuovo Cim. 1963, 27, 636. [Google Scholar] [CrossRef]
- Jacobson, T.; Myers, R.C. Black Hole Entropy And Higher Curvature Interactions. Phys. Rev. Lett. 1993, 70, 3684. [Google Scholar] [CrossRef]
- Wald, R.M. Black hole entropy is the Noether charge. Phys. Rev. D 1993, 48, 3427. [Google Scholar] [CrossRef] [PubMed]
- Garraffo, C.; Giribet, G. The Lovelock Black Holes. Mod. Phys. Lett. A 2008, 23, 1801. [Google Scholar] [CrossRef]
- Charmousis, C. Higher order gravity theories and their black hole solutions. Lect. Notes Phys. 2009, 769, 299. [Google Scholar]
- Anabalon, A.; Deruelle, N.; Morisawa, Y.; Oliva, J.; Sasaki, M.; Tempo, D.; Troncoso, R. Kerr–Schild ansatz in Einstein–Gauss–Bonnet gravity: An exact vacuum solution in five dimensions. Class. Quant. Grav. 2009, 26, 065002. [Google Scholar] [CrossRef]
- Kim, H.C.; Cai, R.G. Slowly Rotating Charged Gauss–Bonnet Black holes in AdS Spaces. Phys. Rev. D 2008, 77, 024045. [Google Scholar] [CrossRef]
- Alexeyev, S.; Popov, N.; Startseva, M.; Barrau, A.; Grain, J. Kerr-Gauss–Bonnet Black Holes: Exact Analytical Solution. J. Exp. Theor. Phys. 2008, 106, 709. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Simply rotating higher dimensional black holes in Einstein–Gauss–Bonnet theory. Phys. Rev. D 2020, 102, 084030. [Google Scholar] [CrossRef]
- Brihaye, Y.; Radu, E. Five-dimensional rotating black holes in Einstein–Gauss–Bonnet theory. Phys. Lett. B 2008, 661, 167. [Google Scholar] [CrossRef][Green Version]
- Brihaye, Y.; Kleihaus, B.; Kunz, J.; Radu, E. Rotating black holes with equal-magnitude angular momenta in d=5 Einstein–Gauss–Bonnet theory. J. High Energy Phys. 2010, 11, 098. [Google Scholar] [CrossRef]
- Emparan, R.; Reall, H.S. A rotating black ring in five dimensions. Phys. Rev. Lett. 2002, 88, 101101. [Google Scholar] [CrossRef]
- Myers, R.C.; Perry, M.J. Black Holes In Higher Dimensional Space-Times. Annals Phys. 1986, 172, 304. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Radu, E. Generalized Weyl solutions in d=5 Einstein–Gauss–Bonnet theory: The Static black ring. J. High Energy Phys. 2010, 2, 092. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Radu, E. d ≥ 5 static black holes with S2×Sd-4 event horizon topology. Phys. Lett. B 2009, 678, 301. [Google Scholar] [CrossRef][Green Version]
- Kleihaus, B.; Kunz, J.; Radu, E. Black ringoids: Spinning balanced black objects in d≥5 dimensions – the codimension-two case. J. High Energy Phys. 2015, 1, 117. [Google Scholar] [CrossRef]
- Emparan, R.; Reall, H.S. Black Rings. Class. Quant. Grav. 2006, 23, R169. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Neemann, U. Gravitating stationary dyons and rotating vortex rings. Phys. Lett. B 2005, 623, 171–178. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Navarro-Lerida, F.; Neemann, U. Stationary Dyonic Regular and Black Hole Solutions. Gen. Rel. Grav. 2008, 40, 1279–1310. [Google Scholar] [CrossRef]
- Kobayashi, T.; Tanaka, T. Five-dimensional black strings in Einstein–Gauss–Bonnet gravity. Phys. Rev. D 2005, 71, 084005. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Radu, E. Rotating Black Holes in Dilatonic Einstein–Gauss–Bonnet Theory. Phys. Rev. Lett. 2011, 106, 151104. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Mojica, S.; Radu, E. Spinning black holes in Einstein–Gauss–Bonnet–dilaton theory: Nonperturbative solutions. Phys. Rev. D 2016, 93, 044047. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kleihaus, B.; Kunz, J.; Radu, E. Phases of Rotating Black Objects in d = 5 Einstein–Gauss–Bonnet Theory. Universe 2023, 9, 156. https://doi.org/10.3390/universe9040156
Kleihaus B, Kunz J, Radu E. Phases of Rotating Black Objects in d = 5 Einstein–Gauss–Bonnet Theory. Universe. 2023; 9(4):156. https://doi.org/10.3390/universe9040156
Chicago/Turabian StyleKleihaus, Burkhard, Jutta Kunz, and Eugen Radu. 2023. "Phases of Rotating Black Objects in d = 5 Einstein–Gauss–Bonnet Theory" Universe 9, no. 4: 156. https://doi.org/10.3390/universe9040156
APA StyleKleihaus, B., Kunz, J., & Radu, E. (2023). Phases of Rotating Black Objects in d = 5 Einstein–Gauss–Bonnet Theory. Universe, 9(4), 156. https://doi.org/10.3390/universe9040156





