Leptogenesis and Dark Matter–Nucleon Scattering Cross Section in the SE6SSM
Abstract
1. Introduction
2. The Extension of the MSSM with Exact Custodial Symmetry
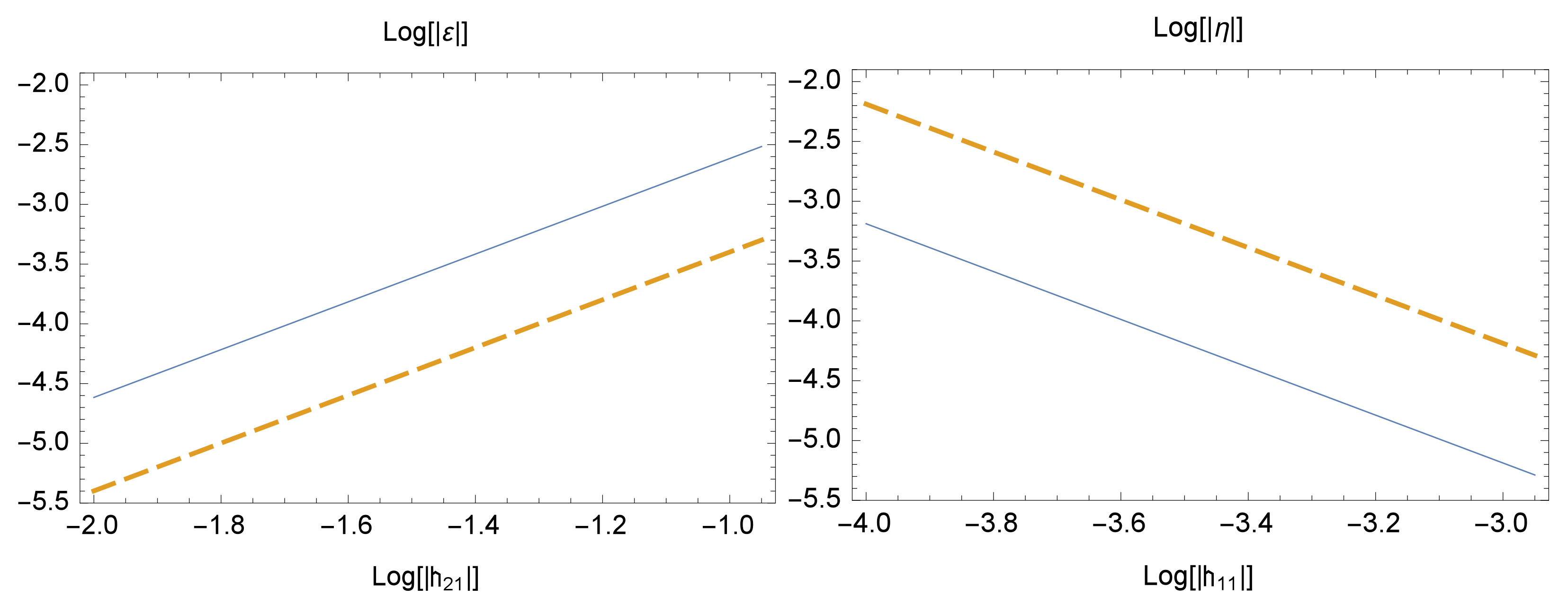
3. Generation of Lepton and Baryon Asymmetries
4. Dark Matter-Nucleon Scattering Cross Section
5. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sakharov, A.D. Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe. JETP Lett. 1967, 5, 24. [Google Scholar]
- Ignatiev, A.Y.; Krasnikov, N.V.; Kuzmin, V.A.; Tavkhelidze, A.N. Universal CP noninvariant superweak interaction and baryon asymmetry of the universe. Phys. Lett. B 1978, 76, 436–438. [Google Scholar] [CrossRef]
- Yoshimura, M. Unified gauge theories and the baryon number of the Universe. Phys. Rev. Lett. 1978, 41, 281. [Google Scholar] [CrossRef]
- Toussaint, D.; Treiman, S.B.; Wilczek, F.; Zee, A. Matter—Antimatter accounting, thermodynamics, and black hole radiation. Phys. Rev. D 1979, 19, 1036. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmological production of baryons. Phys. Rev. Lett. 1979, 42, 850. [Google Scholar] [CrossRef]
- Yoshimura, M. Origin of cosmological baryon asymmetry. Phys. Lett. B 1979, 88, 294–298. [Google Scholar] [CrossRef]
- Barr, S.M.; Segre, G.; Weldon, H.A. The magnitude of the cosmological baryon asymmetry. Phys. Rev. D 1979, 20, 2494. [Google Scholar] [CrossRef]
- Nanopoulos, D.V.; Weinberg, S. Mechanisms for cosmological baryon production. Phys. Rev. D 1979, 20, 2484. [Google Scholar] [CrossRef]
- Affleck, I.; Dine, M. A new mechanism for baryogenesis. Nucl. Phys. B 1985, 249, 361–380. [Google Scholar] [CrossRef]
- Dine, M.; Randall, L.; Thomas, S.D. Baryogenesis from flat directions of the supersymmetric standard model. Nucl. Phys. B 1996, 458, 291–323. [Google Scholar] [CrossRef]
- Fukugita, M.; Yanagida, T. Baryogenesis Without Grand Unification. Phys. Lett. B 1986, 174, 45–47. [Google Scholar] [CrossRef]
- Riotto, A.; Trodden, M. Recent progress in baryogenesis. Ann. Rev. Nucl. Part. Sci. 1999, 49, 35–75. [Google Scholar] [CrossRef]
- Huber, S.J.; Schmidt, M.G. Electroweak baryogenesis: Concrete in a SUSY model with a gauge singlet. Nucl. Phys. B 2001, 606, 183–230. [Google Scholar] [CrossRef]
- Minkowski, P. μ→eγ at a Rate of One Out of 109 Muon Decays? Phys. Lett. B 1977, 67, 421–428. [Google Scholar] [CrossRef]
- Kuzmin, V.A.; Rubakov, V.A.; Shaposhnikov, M.E. On The Anomalous Electroweak Baryon Number Nonconservation in the Early universe. Phys. Lett. B 1985, 155, 36–42. [Google Scholar] [CrossRef]
- Rubakov, V.A.; Shaposhnikov, M.E. Electroweak baryon number non-conservation in the Early Universe and in high-energy collisions. Usp. Fiz. Nauk 1996, 166, 493. [Google Scholar] [CrossRef]
- Davidson, S; Ibarra, A. A lower bound on the right-handed neutrino mass from leptogenesis. Phys. Lett. B 2002, 535, 25–32. [Google Scholar] [CrossRef]
- Hamaguchi, K.; Murayama, H.; Yanagida, T. Leptogenesis from sneutrino-dominated early universe. Phys. Rev. D 2002, 65, 043512. [Google Scholar] [CrossRef]
- Khlopov, M.Y.; Linde, A.D. Is it easy to save the gravitino? Phys. Lett. B 1984, 138, 265–268. [Google Scholar] [CrossRef]
- Ellis, J.R.; Kim, J.E.; Nanopoulos, D.V. Cosmological gravitino regeneration and decay. Phys. Lett. B 1984, 145, 181–186. [Google Scholar] [CrossRef]
- Khlopov, M.Y.; Levitan, Y.L.; Sedelnikov, E.V.; Sobol, I.M. Nonequilibrium cosmological nucleosynthesis of light elements: Calculations by the Monte Carlo method. Phys. Atom. Nucl. 1994, 57, 1393–1397. [Google Scholar]
- Kawasaki, M.; Kohri, K.; Moroi, T. Big-bang nucleosynthesis and hadronic decay of long-lived massive particles. Phys. Rev. D 2005, 71, 083502. [Google Scholar] [CrossRef]
- Kohri, K.; Moroi, T.; Yotsuyanagi, A. Big-bang nucleosynthesis with unstable gravitino and upper bound on the reheating temperature. Phys. Rev. D 2006, 73, 123511. [Google Scholar] [CrossRef]
- Nevzorov, R.; Thomas, A.W. E6 inspired composite Higgs model. Phys. Rev. D 2015, 92, 075007. [Google Scholar] [CrossRef]
- Nevzorov, R.; Thomas, A.W. LHC signatures of neutral pseudo-Goldstone boson in the E6CHM. J. Phys. G 2017, 44, 075003. [Google Scholar] [CrossRef]
- Nevzorov, R.; Thomas, A.W. Baryon asymmetry generation in the E6CHM. Phys. Lett. B 2017, 774, 123–129. [Google Scholar] [CrossRef]
- Nevzorov, R. E6 GUT and Baryon Asymmetry Generation in the E6CHM. Universe 2022, 8, 33. [Google Scholar] [CrossRef]
- Hewett, J.L.; Rizzo, T.G. Low-Energy Phenomenology of Superstring Inspired E(6) Models. Phys. Rept. 1989, 183, 193–381. [Google Scholar] [CrossRef]
- Langacker, P. The Physics of Heavy Z′ Gauge Bosons. Rev. Mod. Phys. 2009, 81, 1199. [Google Scholar] [CrossRef]
- Khlopov, M.Y.; Shibaev, K.I. New physics from superstring phenomenology. Grav. Cosmol. Suppl. 2002, 8, 45. [Google Scholar]
- Khlopov, M.Y. What comes after the Standard model? Prog. Part. Nucl. Phys. 2021, 116, 103824. [Google Scholar] [CrossRef]
- King, S.F.; Moretti, S.; Nevzorov, R. Theory and phenomenology of an exceptional supersymmetric standard model. Phys. Rev. D 2006, 73, 035009. [Google Scholar] [CrossRef]
- King, S.F.; Moretti, S.; Nevzorov, R. Exceptional supersymmetric standard model. Phys. Lett. B 2006, 634, 278–284. [Google Scholar] [CrossRef]
- King, S.F.; Moretti, S.; Nevzorov, R. A Review of the Exceptional Supersymmetric Standard Model. Symmetry 2020, 12, 557. [Google Scholar] [CrossRef]
- Hambye, T.; Ma, E.; Raidal, M.; Sarkar, U. Allowable low-energy E(6) subgroups from leptogenesis. Phys. Lett. B 2001, 512, 373–378. [Google Scholar] [CrossRef]
- Nevzorov, R. Leptogenesis as an origin of hot dark matter and baryon asymmetry in the E6 inspired SUSY models. Phys. Lett. B 2018, 779, 223–229. [Google Scholar] [CrossRef]
- Nevzorov, R. E6 inspired SUSY models with custodial symmetry. Int. J. Mod. Phys. A 2018, 33, 1844007. [Google Scholar] [CrossRef]
- Nevzorov, R. E6 inspired supersymmetric models with exact custodial symmetry. Phys. Rev. D 2013, 87, 015029. [Google Scholar] [CrossRef]
- Athron, P.; Mühlleitner, M.; Nevzorov, R.; Williams, A.G. Non-Standard Higgs Decays in U(1) Extensions of the MSSM. JHEP 2015, 1501, 153. [Google Scholar] [CrossRef]
- Howl, R.; King, S.F. Planck Scale Unification in a Supersymmetric Standard Model. Phys. Lett. B 2007, 652, 331–337. [Google Scholar] [CrossRef]
- Howl, R.; King, S.F. Minimal E6 Supersymmetric Standard Model. JHEP 2008, 0801, 030. [Google Scholar] [CrossRef]
- Howl, R.; King, S.F. Exceptional Supersymmetric Standard Models with non-Abelian Discrete Family Symmetry. JHEP 2008, 0805, 008. [Google Scholar] [CrossRef]
- Howl, R.; King, S.F. Solving the Flavour Problem in Supersymmetric Standard Models with Three Higgs Families. Phys. Lett. B 2010, 687, 355–362. [Google Scholar] [CrossRef]
- Athron, P.; Hall, J.P.; Howl, R.; King, S.F.; Miller, D.J.; Moretti, S.; Nevzorov, R. Aspects of the Exceptional Supersymmetric Standard Model. Nucl. Phys. Proc. Suppl. 2010, 200–202, 120–129. [Google Scholar] [CrossRef]
- Hall, J.P.; King, S.F. Bino Dark Matter and Big Bang Nucleosynthesis in the Constrained E6SSM with Massless Inert Singlinos. JHEP 2011, 1106, 006. [Google Scholar] [CrossRef]
- Callaghan, J.C.; King, S.F. E6 Models from F-theory. JHEP 2013, 1304, 034. [Google Scholar] [CrossRef]
- Callaghan, J.C.; King, S.F.; Leontaris, G.K. Gauge coupling unification in E6 F-theory GUTs with matter and bulk exotics from flux breaking. JHEP 2013, 1312, 037. [Google Scholar] [CrossRef]
- Khalil, S.; Moretti, S.; Rojas-Ciofalo, D.; Waltari, H. Multicomponent dark matter in a simplified E6SSM. Phys. Rev. D 2020, 102, 075039. [Google Scholar] [CrossRef]
- Nevzorov, R. On the Suppression of the Dark Matter-Nucleon Scattering Cross Section in the SE6SSM. Symmetry 2022, 14, 2090. [Google Scholar] [CrossRef]
- Suematsu, D. Neutralino decay in the mu problem solvable extra U(1) models. Phys. Rev. D 1998, 57, 1738. [Google Scholar] [CrossRef]
- Keith, E.; Ma, E. Generic consequences of a supersymmetric U(1) gauge factor at the TeV scale. Phys. Rev. D 1997, 56, 7155. [Google Scholar] [CrossRef]
- Keith, E.; Ma, E. Efficacious Extra U(1) Factor for the Supersymmetric Standard Model. Phys. Rev. D 1996, 54, 3587. [Google Scholar] [CrossRef] [PubMed]
- Suematsu, D.; Yamagishi, Y. Radiative symmetry breaking in a supersymmetric model with an extra U(1). Int. J. Mod. Phys. A 1995, 10, 4521–4536. [Google Scholar] [CrossRef]
- Daikoku, Y.; Suematsu, D. Mass bound of the lightest neutral Higgs scalar in the extra U(1) models. Phys. Rev. D 2000, 62, 095006. [Google Scholar] [CrossRef]
- King, S.F.; Moretti, S.; Nevzorov, R. Gauge coupling unification in the exceptional supersymmetric standard model. Phys. Lett. B 2007, 650, 57–64. [Google Scholar] [CrossRef]
- Sperling, M.; Stöckinger, D.; Voigt, A. Renormalization of vacuum expectation values in spontaneously broken gauge theories. JHEP 2013, 1307, 132. [Google Scholar] [CrossRef]
- Sperling, M.; Stöckinger, D.; Voigt, A. Renormalization of vacuum expectation values in spontaneously broken gauge theories: Two-loop results. JHEP 2014, 1401, 068. [Google Scholar] [CrossRef]
- Ma, E. Neutrino masses in an extended gauge model with E(6) particle content. Phys. Lett. B 1996, 380, 286–290. [Google Scholar] [CrossRef]
- Hall, J.P.; King, S.F. Neutralino Dark Matter with Inert Higgsinos and Singlinos. JHEP 2009, 0908, 088. [Google Scholar] [CrossRef]
- Hall, J.P.; King, S.F.; Nevzorov, R.; Pakvasa, S.; Sher, M. Novel Higgs Decays and Dark Matter in the E6SSM. Phys. Rev. D 2011, 83, 075013. [Google Scholar] [CrossRef]
- Athron, P.; Thomas, A.W.; Underwood, S.J.; White, M.J. Dark matter candidates in the constrained Exceptional Supersymmetric Standard Model. Phys. Rev. D 2017, 95, 035023. [Google Scholar] [CrossRef]
- Nevzorov, R. Quasifixed point scenarios and the Higgs mass in the E6 inspired supersymmetric models. Phys. Rev. D 2014, 89, 055010. [Google Scholar] [CrossRef]
- Nevzorov, R.; Trusov, M.A. Infrared quasifixed solutions in the NMSSM. Phys. Atom. Nucl. 2001, 64, 1299–1314. [Google Scholar] [CrossRef]
- Nevzorov, R.; Trusov, M.A. Quasifixed point scenario in the modified NMSSM. Phys. Atom. Nucl. 2002, 65, 335. [Google Scholar] [CrossRef]
- Athron, P.; Harries, D.; Nevzorov, R.; Williams, A.G. E6 Inspired SUSY benchmarks, dark matter relic density and a 125 GeV Higgs. Phys. Lett. B 2016, 760, 19–25. [Google Scholar] [CrossRef]
- Athron, P.; Harries, D.; Nevzorov, R.; Williams, A.G. Dark matter in a constrained E6 inspired SUSY model. JHEP 2016, 1612, 128. [Google Scholar] [CrossRef]
- Athron, P.; King, S.F.; Miller, D.J.; Moretti, S.; Nevzorov, R. The Constrained E6SSM. arXiv 2008, arXiv:0810.0617. [Google Scholar]
- Athron, P.; King, S.F.; Miller, D.J.; Moretti, S.; Nevzorov, R. Constrained Exceptional Supersymmetric Standard Model with a Higgs Near 125 GeV. Phys. Rev. D 2012, 86, 095003. [Google Scholar] [CrossRef]
- Athron, P.; Binjonaid, M.; King, S.F. Fine Tuning in the Constrained Exceptional Supersymmetric Standard Model. Phys. Rev. D 2013, 87, 115023. [Google Scholar] [CrossRef]
- Athron, P.; Harries, D.; Williams, A.G. Z′ mass limits and the naturalness of supersymmetry. Phys. Rev. D 2015, 91, 115024. [Google Scholar] [CrossRef]
- Athron, P.; Stöckinger, D.; Voigt, A. Threshold Corrections in the Exceptional Supersymmetric Standard Model. Phys. Rev. D 2012, 86, 095012. [Google Scholar] [CrossRef]
- King, S.F.; Moretti, S.; Nevzorov, R. Spectrum of Higgs particles in the ESSM. arXiv 2006, arXiv:hep-ph/0601269. [Google Scholar]
- King, S.F.; Moretti, S.; Nevzorov, R. E6SSM. AIP Conf. Proc. 2007, 881, 138. [Google Scholar]
- Belyaev, A.; Hall, J.P.; King, S.F.; Svantesson, P. Novel gluino cascade decays in E6 inspired models. Phys. Rev. D 2012, 86, 031702. [Google Scholar] [CrossRef]
- Belyaev, A.; Hall, J.P.; King, S.F.; Svantesson, P. Discovering E6 supersymmetric models in gluino cascade decays at the LHC. Phys. Rev. D 2013, 87, 035019. [Google Scholar] [CrossRef]
- Nevzorov, R.; Pakvasa, S. Exotic Higgs decays in the E6 inspired SUSY models. Phys. Lett. B 2014, 728, 210–215. [Google Scholar] [CrossRef]
- Hall, J.P.; King, S.F.; Nevzorov, R.; Pakvasa, S.; Sher, M. Nonstandard Higgs decays in the E6SSM. PoS 2010, QFTHEP2010, 069. [Google Scholar]
- Nevzorov, R.; Pakvasa, S. Nonstandard Higgs decays in the E6 inspired SUSY models. Nucl. Part. Phys. Proc. 2016, 273–275, 690–695. [Google Scholar] [CrossRef]
- Nevzorov, R. Higgs Boson with Mass around 125 GeV in SUSY Extensions of the SM. Phys. Atom. Nucl. 2020, 83, 338–350. [Google Scholar] [CrossRef]
- Hesselbach, S.; Miller, D.J.; Moortgat-Pick, G.; Nevzorov, R.; Trusov, M. Theoretical upper bound on the mass of the LSP in the MNSSM. Phys. Lett. B 2008, 662, 199–207. [Google Scholar] [CrossRef]
- Hesselbach, S.; Miller, D.J.; Moortgat-Pick, G.; Nevzorov, R.; Trusov, M. The Lightest neutralino in the MNSSM. arXiv 2007, arXiv:0710.2550. [Google Scholar]
- Hesselbach, S.; Miller, D.J.; Moortgat-Pick, G.; Nevzorov, R.; Trusov, M. Lightest Neutralino Mass in the MNSSM. arXiv 2008, arXiv:0810.0511. [Google Scholar]
- Frere, J.M.; Nevzorov, R.B.; Vysotsky, M.I. Stimulated neutrino conversion and bounds on neutrino magnetic moments. Phys. Lett. B 1997, 394, 127–131. [Google Scholar] [CrossRef]
- Gu, Y.; Khlopov, M.; Wu, L.; Yang, J.M.; Zhu, B. Light gravitino dark matter: LHC searches and the Hubble tension. Phys. Rev. D 2020, 102, 115005. [Google Scholar] [CrossRef]
- Feng, J.L.; Su, S.; Takayama, F. Supergravity with a gravitino LSP. Phys. Rev. D 2004, 70, 075019. [Google Scholar] [CrossRef]
- Bolz, M.; Brandenburg, A.; Buchmuller, W. Thermal production of gravitinos. Nucl. Phys. B 2001, 606, 518–544. [Google Scholar] [CrossRef]
- Eberl, H.; Gialamas, I.D.; Spanos, V.C. Gravitino thermal production revisited. Phys. Rev. D 2021, 103, 075025. [Google Scholar] [CrossRef]
- The Planck collaboration. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Hook, A.; McGehee, R.; Murayama, H. Cosmologically Viable Low-energy Supersymmetry Breaking. Phys. Rev. D 2018, 98, 115036. [Google Scholar] [CrossRef]
- Luty, M.A. Baryogenesis Via Leptogenesis. Phys. Rev. D 1992, 45, 455. [Google Scholar] [CrossRef]
- Flanz, M.; Paschos, E.A.; Sarkar, U. Baryogenesis from a lepton asymmetric universe. Phys. Lett. B 1995, 345, 248–252. [Google Scholar] [CrossRef]
- Plumacher, M. Baryogenesis and lepton number violation. Z. Phys. C 1997, 74, 549–559. [Google Scholar] [CrossRef]
- Buchmuller, W.; Plumacher, M. CP asymmetry in Majorana neutrino decays. Phys. Lett. B 1998, 431, 354–362. [Google Scholar] [CrossRef]
- Campbell, B.A.; Davidson, S.; Olive, K.A. Inflation, neutrino baryogenesis, and (S)neutrino induced baryogenesis. Nucl. Phys. B 1993, 399, 111–136. [Google Scholar] [CrossRef]
- Covi, L.; Roulet, E.; Vissani, F. CP violating decays in leptogenesis scenarios. Phys. Lett. B 1996, 384, 169–174. [Google Scholar] [CrossRef]
- Plumacher, M. Baryon asymmetry, neutrino mixing and supersymmetric SO(10) unification. Nucl. Phys. B 1998, 530, 207–246. [Google Scholar] [CrossRef]
- Buchmuller, W.; Di Bari, P.; Plumacher, M. Leptogenesis for pedestrians. Ann. Phys. 2005, 315, 305–351. [Google Scholar] [CrossRef]
- Barbieri, R.; Creminelli, P.; Strumia, A.; Tetradis, N. Baryogenesis through leptogenesis. Nucl. Phys. B 2000, 575, 61–77. [Google Scholar] [CrossRef]
- Endoh, T.; Morozumi, T.; Xiong, Z.H. Primordial lepton family asymmetries in seesaw model. Prog. Theor. Phys. 2004, 111, 123–149. [Google Scholar] [CrossRef]
- Vives, O. Flavoured leptogenesis: A successful thermal leptogenesis with N1 mass below 108 GeV. Phys. Rev. D 2006, 73, 073006. [Google Scholar] [CrossRef]
- Abada, A.; Davidson, S.; Josse-Michaux, F.X.; Losada, M.; Riotto, A. Flavour issues in leptogenesis. JCAP 2006, 0604, 004. [Google Scholar] [CrossRef]
- Nardi, E.; Nir, Y.; Roulet, E.; Racker, J. The importance of flavor in leptogenesis. JHEP 2006, 0601, 164. [Google Scholar] [CrossRef]
- Abada, A.; Davidson, S.; Ibarra, A.; Josse-Michaux, F.X.; Losada, M.; Riotto, A. Flavour matters in leptogenesis. JHEP 2006, 0609, 010. [Google Scholar] [CrossRef]
- Antusch, S.; King, S.F.; Riotto, A. Flavour-dependent leptogenesis with sequential dominance. JCAP 2006, 0611, 011. [Google Scholar] [CrossRef]
- Davidson, S.; Nardi, E.; Nir, Y. Leptogenesis. Phys. Rept. 2008, 466, 105. [Google Scholar] [CrossRef]
- Khalil, S.; Moretti, S.; Rojas-Ciofalo, D.; Waltari, H. Monophoton signals at e+e− colliders in a simplified E6SSM. Phys. Rev. D 2021, 104, 035008. [Google Scholar] [CrossRef]
- Khalil, S.; Kowalska, K.; Moretti, S.; Rojas-Ciofalo, D.; Waltari, H. A combined approach to the analysis of space and ground experimental data within a simplified E6SSM. Eur. Phys. J. C 2022, 82, 1058. [Google Scholar] [CrossRef]
- Kovalenko, P.A.; Nevzorov, R.B.; Ter-Martirosian, K.A. Masses of Higgs bosons in supersymmetric theories. Phys. Atom. Nucl. 1998, 61, 812–824. [Google Scholar]
- Nevzorov, R.B.; Trusov, M.A. Particle spectrum in the modified NMSSM in the strong Yukawa coupling limit. J. Exp. Theor. Phys. 2000, 91, 1079. [Google Scholar] [CrossRef]
- Nevzorov, R.B.; Ter-Martirosyan, K.A.; Trusov, M.A. Higgs bosons in the simplest SUSY models. Phys. Atom. Nucl. 2002, 65, 285. [Google Scholar] [CrossRef]
- Nevzorov, R.; Miller, D.J. Approximate solutions for the Higgs masses and couplings in the NMSSM. arXiv 2004, arXiv:hep-ph/0411275. [Google Scholar]
- Arkani-Hamed, N.; Delgado, A.; Giudice, G.F. The Well-tempered neutralino. Nucl. Phys. B 2006, 741, 108–130. [Google Scholar] [CrossRef]
- Chalons, G.; Dolan, M.J.; McCabe, C. Neutralino dark matter and the Fermi gamma-ray lines. JCAP 2013, 02, 016. [Google Scholar] [CrossRef]
- Ellis, J.R.; Olive, K.A.; Savage, C. Hadronic Uncertainties in the Elastic Scattering of Supersymmetric Dark Matter. Phys. Rev. D 2008, 77, 065026. [Google Scholar] [CrossRef]
- Kalinowski, J.; King, S.F.; Roberts, J.P. Neutralino Dark Matter in the USSM. JHEP 2009, 0901, 066. [Google Scholar] [CrossRef]
- Bélanger, G.; Boudjema, F.; Pukhov, A.; Semenov, A. micrOMEGAs3: A program for calculating dark matter observables. Comput. Phys. Commun. 2014, 185, 960–985. [Google Scholar] [CrossRef]
- Alarcon, J.M.; Martin Camalich, J.; Oller, J.A. The chiral representation of the πN scattering amplitude and the pion-nucleon sigma term. Phys. Rev. D 2012, 85, 051503. [Google Scholar] [CrossRef]
- Thomas, A.W.; Shanahan, P.E.; Young, R.D. Strangeness in the nucleon: What have we learned? Nuovo Cim. C 2012, 035N04, 3. [Google Scholar]
- Cheng, H.Y.; Chiang, C.W. Revisiting Scalar and Pseudoscalar Couplings with Nucleons. JHEP 2012, 1207, 009. [Google Scholar] [CrossRef]
- Alarcon, J.M.; Geng, L.S.; Martin Camalich, J.; Oller, J.A. The strangeness content of the nucleon from effective field theory and phenomenology. Phys. Lett. B 2014, 730, 342–346. [Google Scholar] [CrossRef]
- Maniatis, M. The Next-to-Minimal Supersymmetric extension of the Standard Model reviewed. Int. J. Mod. Phys. A 2010, 25, 3505–3602. [Google Scholar] [CrossRef]
- Sirunyan, A.M. et al. [CMS Collaboration]. Search for resonant and nonresonant new phenomena in high-mass dilepton final states at = 13 TeV. JHEP 2021, 07, 208. [Google Scholar]
- Aad, G. et al. [ATLAS Collaboration]. Search for high-mass dilepton resonances using 139 fb−1 of pp collision data collected at = 13 TeV with the ATLAS detector. Phys. Lett. B 2019, 796, 68–87. [Google Scholar] [CrossRef]
- Hisano, J.; Ishiwata, K.; Nagata, N.; Takesako, T. Direct Detection of Electroweak-Interacting Dark Matter. JHEP 2011, 07, 005. [Google Scholar] [CrossRef]
- Hisano, J.; Ishiwata, K.; Nagata, N. Direct Search of Dark Matter in High-Scale Supersymmetry. Phys. Rev. D 2013, 87, 035020. [Google Scholar] [CrossRef]
- Nagata, N.; Shirai, S. Higgsino Dark Matter in High-Scale Supersymmetry. JHEP 2015, 01, 029. [Google Scholar] [CrossRef]
- Aalbers, J. et al. [LZ Collaboration]. First Dark Matter Search Results from the LUX-ZEPLIN (LZ) Experiment. arXiv 2022, arXiv:2207.03764. [Google Scholar]
- Amole, C. et al. [PICO Collaboration]. Dark Matter Search Results from the Complete Exposure of the PICO-60 C3F8 Bubble Chamber. Phys. Rev. D 2019, 100, 022001. [Google Scholar] [CrossRef]
- Akerib, D.S. et al. [LUX-ZEPLIN Collaboration]. Projected WIMP sensitivity of the LUX-ZEPLIN dark matter experiment. Phys. Rev. D 2020, 101, 052002. [Google Scholar] [CrossRef]
- Aprile, E. et al. [XENON Collaboration]. Projected WIMP sensitivity of the XENONnT dark matter experiment. JCAP 2020, 11, 031. [Google Scholar] [CrossRef]
- Aalbers, J. et al. [DARWIN Collaboration]. DARWIN: Towards the ultimate dark matter detector. JCAP 2016, 11, 017. [Google Scholar] [CrossRef]
- Aalseth, C.E. et al. [DarkSide-20k Collaboration]. DarkSide-20k: A 20 tonne two-phase LAr TPC for direct dark matter detection at LNGS. Eur. Phys. J. Plus 2018, 133, 131. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Huang, P.; Mustafayev, A.; Tata, X. Radiative natural SUSY with a 125 GeV Higgs boson. Phys. Rev. Lett. 2012, 109, 161802. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Huang, P.; Tata, X. Natural Supersymmetry: LHC, dark matter and ILC searches. JHEP 2012, 05, 109. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Huang, P.; Mickelson, D.; Mustafayev, A.; Tata, X. Radiative natural supersymmetry: Reconciling electroweak fine-tuning and the Higgs boson mass. Phys. Rev. D 2013, 87, 115028. [Google Scholar] [CrossRef]
- Cirelli, M.; Fornengo, N.; Strumia, A. Minimal dark matter. Nucl. Phys. B 2006, 753, 178–194. [Google Scholar] [CrossRef]
- Aad, G. et al. [ATLAS Collaboration]. Searches for electroweak production of supersymmetric particles with compressed mass spectra in = 13 TeV pp collisions with the ATLAS detector. Phys. Rev. D 2020, 101, 052005. [Google Scholar] [CrossRef]
- Sirunyan, A.M. et al. [CMS Collaboration]. Search for supersymmetry with a compressed mass spectrum in the vector boson fusion topology with 1-lepton and 0-lepton final states in proton-proton collisions at = 13 TeV. JHEP 2019, 08, 150. [Google Scholar]
- Baer, H. et al. [ILC Collaboration]. The International Linear Collider Technical Design Report—Volume 2: Physics. arXiv 2013, arXiv:1306.6352. [Google Scholar]
- Aad, G. et al. [ATLAS Collaboration]. Search for pairs of scalar leptoquarks decaying into quarks and electrons or muons in = 13 TeV pp collisions with the ATLAS detector. JHEP 2020, 10, 112. [Google Scholar]
- Aad, G. et al. [ATLAS Collaboration]. Search for pair production of third-generation scalar leptoquarks decaying into a top quark and a τ-lepton in pp collisions at = 13 TeV with the ATLAS detector. JHEP 2021, 06, 179. [Google Scholar]
- Sirunyan, A.M. et al. [CMS Collaboration]. Searches for physics beyond the standard model with the MT2 variable in hadronic final states with and without disappearing tracks in proton-proton collisions at = 13 TeV. Eur. Phys. J. C 2020, 80, 3. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.; Langacker, P.; Nelson, B.D. Theory and Phenomenology of Exotic Isosinglet Quarks and Squarks. Phys. Rev. D 2008, 77, 035003. [Google Scholar] [CrossRef]


| 1 | 0 | 0 | ||||||||||
| 1 | 1 | 2 | 2 | 1 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nevzorov, R. Leptogenesis and Dark Matter–Nucleon Scattering Cross Section in the SE6SSM. Universe 2023, 9, 137. https://doi.org/10.3390/universe9030137
Nevzorov R. Leptogenesis and Dark Matter–Nucleon Scattering Cross Section in the SE6SSM. Universe. 2023; 9(3):137. https://doi.org/10.3390/universe9030137
Chicago/Turabian StyleNevzorov, Roman. 2023. "Leptogenesis and Dark Matter–Nucleon Scattering Cross Section in the SE6SSM" Universe 9, no. 3: 137. https://doi.org/10.3390/universe9030137
APA StyleNevzorov, R. (2023). Leptogenesis and Dark Matter–Nucleon Scattering Cross Section in the SE6SSM. Universe, 9(3), 137. https://doi.org/10.3390/universe9030137








