Approximate Analytical Solutions of the Schrödinger Equation with Hulthén Potential in the Global Monopole Spacetime
Abstract
1. Introduction
2. Nonrelativistic Quantum Mechanics in the Global Monopole Spacetime
3. Scattering Phase Shift
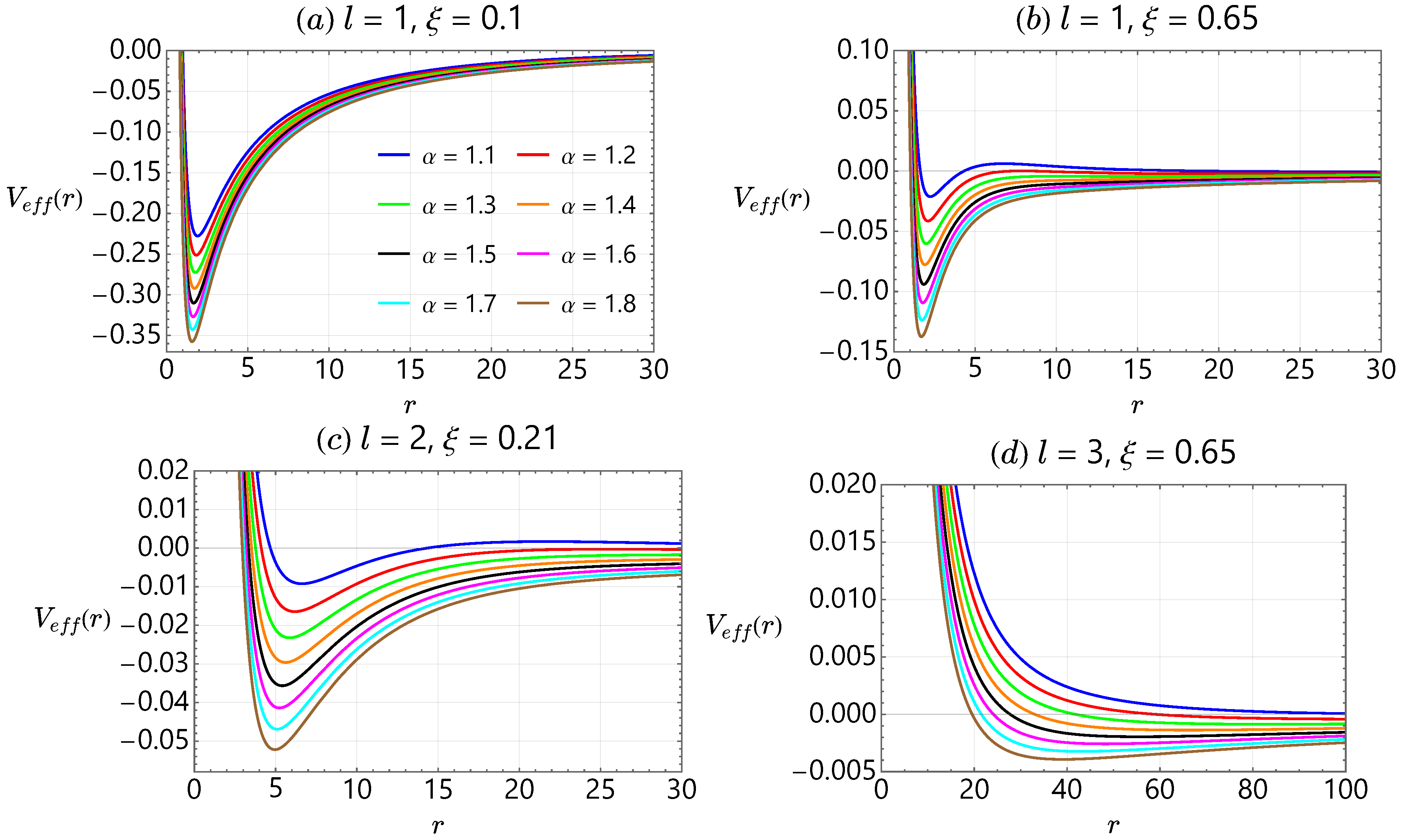
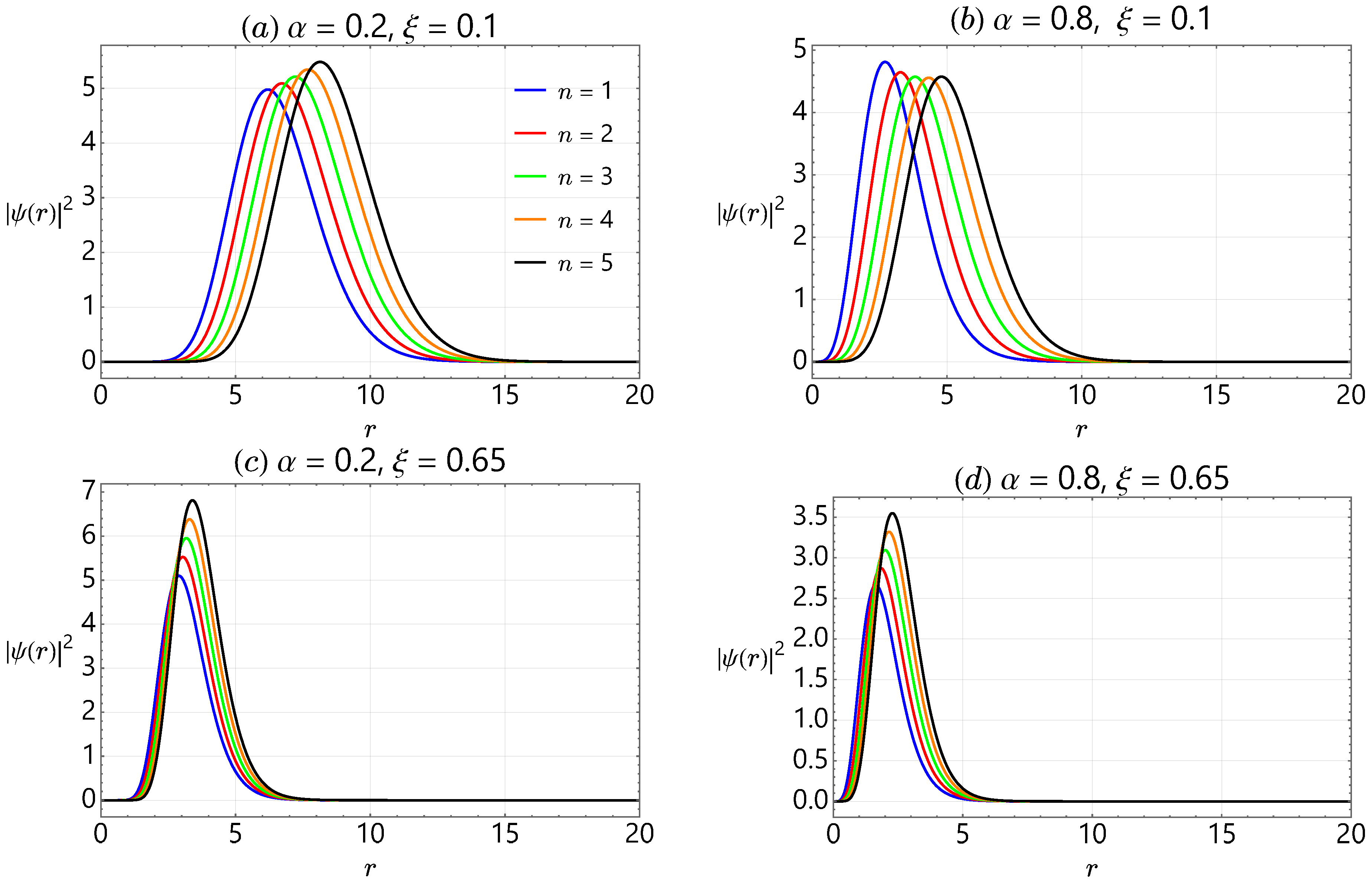
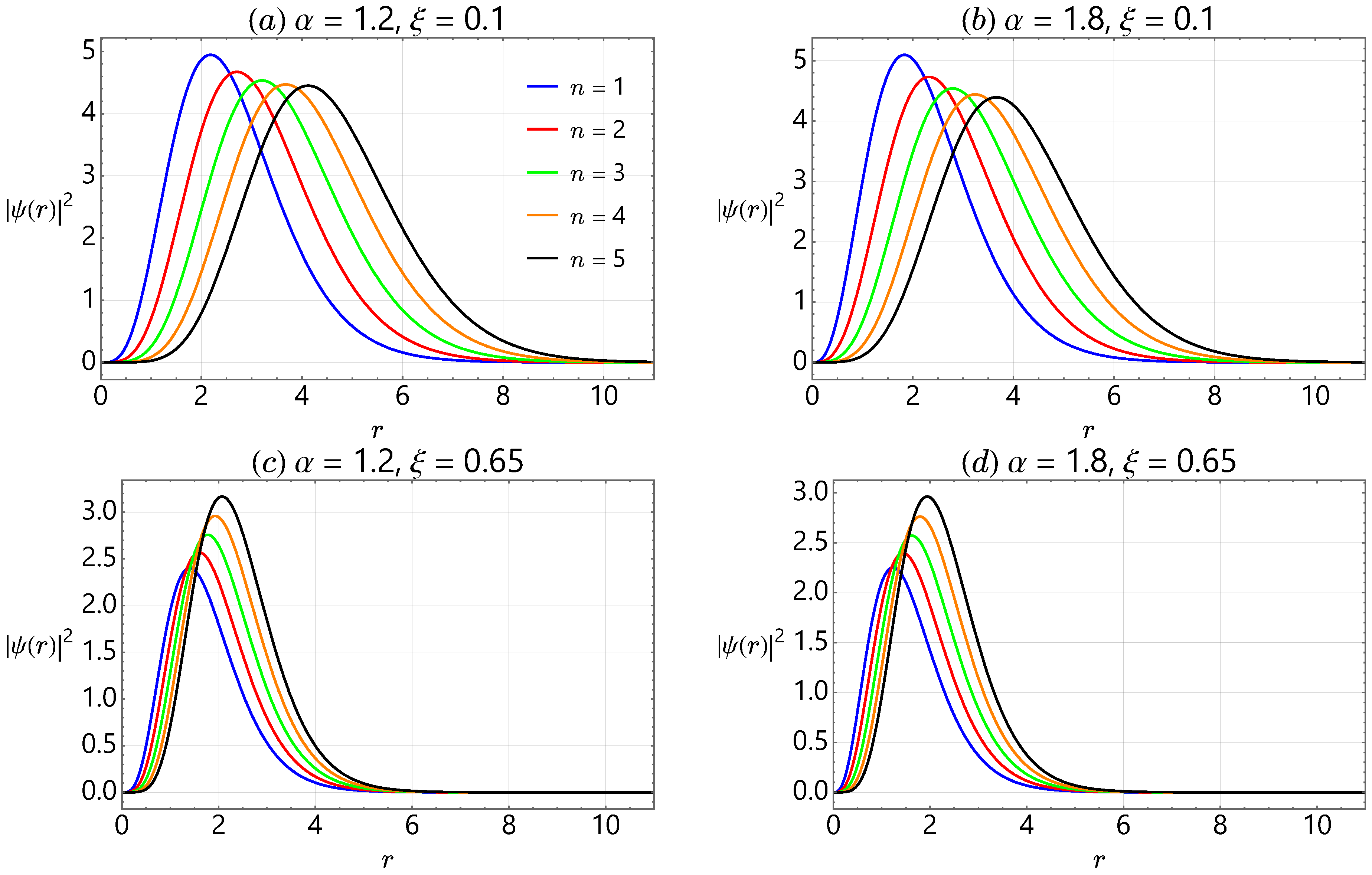
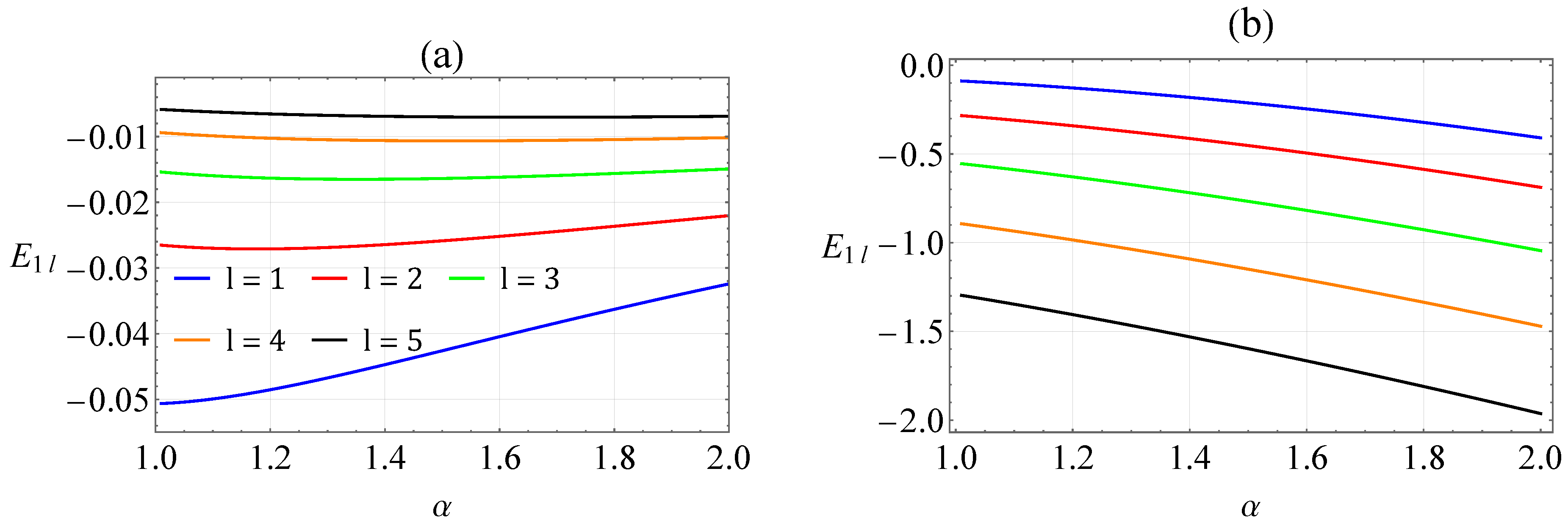
4. Analysis of Bound States
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Suzko, A.; Velicheva, E. Exactly Solvable Models for the Generalized Schrödinger Equation. In Mathematical Modeling and Computational Science; Adam, G., Buša, J., Hnatič, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 182–188. [Google Scholar]
- Griffiths, D.J. Introduction to Quantum Mechanics, 2nd ed.; Addison-Wesley: Boston, MA, USA, 2005. [Google Scholar]
- Davies, B.; Delves, L.M. An Exactly Soluble Two-body Problem with Non-central Forces. Aust. J. Phys. 1963, 16, 311–313. [Google Scholar] [CrossRef]
- Karayer, H.; Demirhan, D. Exact analytical solution of Schrödinger equation for a generalized noncentral potential. Eur. Phys. J. Plus 2022, 137, 527. [Google Scholar] [CrossRef]
- Wang, X.H.; Chen, C.Y.; You, Y.; Lu, F.L.; Sun, D.S.; Dong, S.H. Exact solutions of the Schrödinger equation for a class of hyperbolic potential well. Chin. Phys. B 2022, 31, 040301. [Google Scholar] [CrossRef]
- López-Villanueva, J.A.; Melchor, I.; Cartujo, P.; Carceller, J.E. Modified Schrödinger equation including nonparabolicity for the study of a two-dimensional electron gas. Phys. Rev. B 1993, 48, 1626–1631. [Google Scholar] [CrossRef] [PubMed]
- El-Nabulsi, R.A. Quantum dynamics in low-dimensional systems with position-dependent mass and product-like fractal geometry. Phys. E Low-Dimens. Syst. Nanostruct. 2021, 134, 114827. [Google Scholar] [CrossRef]
- Biswas, D.; Ghosh, S. Quantum mechanics of a particle on a torus knot: Curvature and torsion effects. Europhys. Lett. 2020, 132, 10004. [Google Scholar] [CrossRef]
- Vilenkin, A.; Shellard, E.P.S. Cosmic Strings and Other Topological Defects; Cambridge University Press: Canbridge, UK, 2000. [Google Scholar]
- Durrer, R.; Kunz, M.; Melchiorri, A. Cosmic structure formation with topological defects. Phys. Rep. 2002, 364, 1–81. [Google Scholar] [CrossRef]
- Ma, L.; Zeng, X.C. Unravelling the Role of Topological Defects on Catalytic Unzipping of Single-Walled Carbon Nanotubes by Single Transition Metal Atom. J. Phys. Chem. Lett. 2018, 9, 6801–6807. [Google Scholar] [CrossRef] [PubMed]
- Jagodzinski, H. Points, lines and walls in liquid crystals, magnetic systems and various ordered media by M. Kléman. Acta Crystallogr. Sect. A 1984, 40, 309–310. [Google Scholar] [CrossRef]
- Vilenkin, A. Gravitational field of vacuum domain walls and strings. Phys. Rev. D 1981, 23, 852–857. [Google Scholar] [CrossRef]
- De A Marques, G.; Bezerra, V.B. Non-relativistic quantum systems on topological defects spacetimes. Class. Quantum Gravity 2002, 19, 985–995. [Google Scholar] [CrossRef]
- Katanaev, K.O. Geometric theory of defects. Physics-Uspekhi 2005, 48, 675. [Google Scholar] [CrossRef]
- Katanaev, M.O.; Volovich, I.V. Theory of defects in solids and three-dimensional gravity. Ann. Phys. 1992, 216, 1–28. [Google Scholar] [CrossRef]
- Ahmed, F. Effects of rotating frames of reference and Cornell-type potential on modified quantum oscillator field in magnetic cosmic string space–time. Int. J. Mod. Phys. A 2022, 37, 2250122. [Google Scholar] [CrossRef]
- Yang, Y.; Jing, J.; Tian, Z. Probing cosmic string spacetime through parameter estimation. Eur. Phys. J. C 2022, 82, 688. [Google Scholar] [CrossRef]
- Edet, C.; Nwbabuzor, P.; Ettah, E.; Duque, C.; Ali, N.; Ikot, A.; Mahmoud, S.; Asjad, M. Magneto-transport and thermal properties of the Yukawa potential in cosmic string space-time. Results Phys. 2022, 39, 105749. [Google Scholar] [CrossRef]
- Chen, H.; Long, Z.W.; Long, C.Y.; Zare, S.; Hassanabadi, H. The influence of Aharonov–Casher effect on the generalized Dirac oscillator in the cosmic string space-time. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250133. [Google Scholar] [CrossRef]
- Zhou, R.; Bian, L. Gravitational waves from cosmic strings after a first-order phase transition. Chin. Phys. C 2022, 46, 043104. [Google Scholar] [CrossRef]
- Mustafa, O. PDM Klein–Gordon oscillators in cosmic string spacetime in magnetic and Aharonov–Bohm flux fields within the Kaluza–Klein theory. Ann. Phys. 2022, 440, 168857. [Google Scholar] [CrossRef]
- Cuzinatto, R.R.; de Montigny, M.; Pompeia, P.J. Non-commutativity and non-inertial effects on a scalar field in a cosmic string space-time: I. Klein–Gordon oscillator. Class. Quantum Gravity 2022, 39, 075006. [Google Scholar] [CrossRef]
- Cuzinatto, R.R.; de Montigny, M.; Pompeia, P.J. Non-commutativity and non-inertial effects on a scalar field in a cosmic string space-time: II. Spin-zero Duffin–Kemmer–Petiau-like oscillator. Class. Quantum Gravity 2022, 39, 075007. [Google Scholar] [CrossRef]
- Ahmed, F. Generalized Klein–Gordon oscillator with a uniform magnetic field under the influence of Coulomb-type potentials in cosmic string space–time and Aharonov–Bohm effect. Can. J. Phys. 2021, 99, 496–500. [Google Scholar] [CrossRef]
- Ahmed, F. Effects of uniform rotation and electromagnetic potential on the modified Klein–Gordon oscillator in a cosmic string space-time. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150187. [Google Scholar] [CrossRef]
- Silva, M.; Mohammadi, A. Scattering cross-section in gravitating cosmic string spacetimes. Class. Quantum Gravity 2021, 38, 205006. [Google Scholar] [CrossRef]
- Guvendi, A.; Hassanabadi, H. Relativistic Vector Bosons with Non-minimal Coupling in the Spinning Cosmic String Spacetime. Few-Body Syst. 2021, 62, 57. [Google Scholar] [CrossRef]
- Yang, Y.; Hassanabadi, H.; Chen, H.; Long, Z.W. DKP oscillator in the presence of a spinning cosmic string. Int. J. Mod. Phys. E 2021, 30, 2150050. [Google Scholar] [CrossRef]
- Ahmed, F. Spin-0 scalar particle interacts with scalar potential in the presence of magnetic field and quantum flux under the effects of KKT in 5D cosmic string spacetime. Mod. Phys. Lett. A 2021, 36, 2150004. [Google Scholar] [CrossRef]
- Cunha, M.M.; Silva, E.O. Self-Adjoint Extension Approach to Motion of Spin-1/2 Particle in the Presence of External Magnetic Fields in the Spinning Cosmic String Spacetime. Universe 2020, 6, 203. [Google Scholar] [CrossRef]
- Cunha, M.M.; Dias, H.S.; Silva, E.O. Dirac oscillator in a spinning cosmic string spacetime in external magnetic fields: Investigation of the energy spectrum and the connection with condensed matter physics. Phys. Rev. D 2020, 102, 105020. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Hassanabadi, H. Scattering states of Dirac equation in the presence of cosmic string for Coulomb interaction. Int. J. Mod. Phys. A 2015, 30, 1550124. [Google Scholar] [CrossRef]
- Sun, X.Q.; Zhu, P.; Hughes, T.L. Geometric Response and Disclination-Induced Skin Effects in Non-Hermitian Systems. Phys. Rev. Lett. 2021, 127, 066401. [Google Scholar] [CrossRef]
- Oliveira, J.; Garcia, G.; Porfírio, P.; Furtado, C. Graphene-based topological insulator in the presence of a disclination submitted to a uniform magnetic field. Ann. Phys. 2021, 425, 168384. [Google Scholar] [CrossRef]
- Zare, S.; Hassanabadi, H.; de Montigny, M. Nonrelativistic particles in the presence of a Cariñena–Perelomov–Rañada–Santander oscillator and a disclination. Int. J. Mod. Phys. A 2020, 35, 2050071. [Google Scholar] [CrossRef]
- Belouad, A.; Jellal, A.; Bahlouli, H. Electronic properties of graphene quantum ring with wedge disclination. Eur. Phys. J. B 2021, 94, 75. [Google Scholar] [CrossRef]
- Jiang, J.; Ranabhat, K.; Wang, X.; Rich, H.; Zhang, R.; Peng, C. Active transformations of topological structures in light-driven nematic disclination networks. Proc. Natl. Acad. Sci. USA 2022, 119, e2122226119. [Google Scholar] [CrossRef] [PubMed]
- Monderkamp, P.A.; Wittmann, R.; te Vrugt, M.; Voigt, A.; Wittkowski, R.; Löwen, H. Topological fine structure of smectic grain boundaries and tetratic disclination lines within three-dimensional smectic liquid crystals. Phys. Chem. Chem. Phys. 2022, 24, 15691–15704. [Google Scholar] [CrossRef] [PubMed]
- Bakke, K. Topological effects of a disclination on quantum revivals. Int. J. Mod. Phys. A 2022, 37, 2250046. [Google Scholar] [CrossRef]
- Pandey, A.; Singh, M.; Gupta, A. Positive disclination in a thin elastic sheet with boundary. Phys. Rev. E 2021, 104, 065002. [Google Scholar] [CrossRef]
- Kleinert, H. Gauge Fields in Condensed Matter; World Scientific: Singapore, 1989. [Google Scholar] [CrossRef]
- Su, W.P.; Schrieffer, J.R.; Heeger, A.J. Soliton excitations in polyacetylene. Phys. Rev. B 1980, 22, 2099–2111. [Google Scholar] [CrossRef]
- Kleman, M.; Friedel, J. Disclinations, dislocations, and continuous defects: A reappraisal. Rev. Mod. Phys. 2008, 80, 61–115. [Google Scholar] [CrossRef]
- Barriola, M.; Vilenkin, A. Gravitational field of a global monopole. Phys. Rev. Lett. 1989, 63, 341–343. [Google Scholar] [CrossRef] [PubMed]
- Kaur, L.; Wazwaz, A.M. Einstein’s vacuum field equation: Painlevé analysis and Lie symmetries. Waves Random Complex Media 2021, 31, 199–206. [Google Scholar] [CrossRef]
- Kaur, L.; Gupta, R.K. On certain new exact solutions of the Einstein equations for axisymmetric rotating fields. Chin. Phys. B 2013, 22, 100203. [Google Scholar] [CrossRef]
- Kaur, L.; Gupta, R.K. On symmetries and exact solutions of the Einstein–Maxwell field equations via the symmetry approach. Phys. Scr. 2013, 87, 035003. [Google Scholar] [CrossRef]
- Ali, M.S.; Bhattacharya, S. Vacuum polarization of Dirac fermions in the cosmological de Sitter global monopole spacetime. Phys. Rev. D 2022, 105, 085006. [Google Scholar] [CrossRef]
- Grats, Y.V.; Spirin, P.A. Vacuum polarization in the field of a multidimensional global monopole. J. Exp. Theor. Phys. 2016, 123, 807–813. [Google Scholar] [CrossRef]
- Barroso, V.S.; Pitelli, J.P.M. Vacuum fluctuations and boundary conditions in a global monopole. Phys. Rev. D 2018, 98, 065009. [Google Scholar] [CrossRef]
- Ahmed, F. Relativistic motions of spin-zero quantum oscillator field in a global monopole space-time with external potential and AB-effect. Sci. Rep. 2022, 12, 8794. [Google Scholar] [CrossRef]
- De Montigny, M.; Pinfold, J.; Zare, S.; Hassanabadi, H. Klein–Gordon oscillator in a global monopole space–time with rainbow gravity. Eur. Phys. J. Plus 2021, 137, 54. [Google Scholar] [CrossRef]
- Bragança, E.A.F.; Vitória, R.L.L.; Belich, H.; de Mello, E.R.B. Relativistic quantum oscillators in the global monopole spacetime. Eur. Phys. J. C 2020, 80, 206. [Google Scholar] [CrossRef]
- Anacleto, M.; Brito, F.; Ferreira, S.; Passos, E. Absorption and scattering of a black hole with a global monopole in f(R) gravity. Phys. Lett. B 2019, 788, 231–237. [Google Scholar] [CrossRef]
- Pu, J.; Han, Y. On Hawking Radiation via Tunneling from the Reissner-Nordström-de Sitter Black Hole with a Global Monopole. Int. J. Theor. Phys. 2017, 56, 2061–2070. [Google Scholar] [CrossRef]
- Shao, J.Z.; Wang, Y.J. Scattering and absorption of particles by a black hole involving a global monopole. Chin. Phys. B 2012, 21, 040404. [Google Scholar] [CrossRef]
- Ita, B.I.; Louis, H.; Ubana, E.I.; Ekuri, P.E.; Leonard, C.U.; Nzeata, N.I. Evaluation of the bound state energies of some diatomic molecules from the approximate solutions of the Schrodinger equation with Eckart plus inversely quadratic Yukawa potential. J. Mol. Model. 2020, 26, 349. [Google Scholar] [CrossRef]
- Onyenegecha, C.P.; Ukewuihe, U.M.; Opara, A.I.; Agbakwuru, C.B.; Okereke, C.J.; Ugochukwu, N.R.; Okolie, S.A.; Njoku, I.J. Approximate solutions of Schrödinger equation for the Hua plus modified Eckart potential with the centrifugal term. Eur. Phys. J. Plus 2020, 135, 571. [Google Scholar] [CrossRef]
- Louis, H.; Ita, B.I.; Nzeata, N.I. Approximate solution of the Schrödinger equation with Manning-Rosen plus Hellmann potential and its thermodynamic properties using the proper quantization rule. Eur. Phys. J. Plus 2019, 134, 315. [Google Scholar] [CrossRef]
- Oyewumi, K.; Falaye, B.; Onate, C.; Oluwadare, O.; Yahya, W. Thermodynamic properties and the approximate solutions of the Schrödinger equation with the shifted Deng–Fan potential model. Mol. Phys. 2014, 112, 127–141. [Google Scholar] [CrossRef]
- Bayrak, O.; Boztosun, I. Bound state solutions of the Hulthén potential by using the asymptotic iteration method. Phys. Scr. 2007, 76, 92–96. [Google Scholar] [CrossRef]
- Agboola, D. The Hulthén potential in D-dimensions. Phys. Scr. 2009, 80, 065304. [Google Scholar] [CrossRef]
- Saad, N. The Klein–Gordon equation with a generalized Hulthén potential in D-dimensions. Phys. Scr. 2007, 76, 623–627. [Google Scholar] [CrossRef]
- Peng, X.L.; Liu, J.Y.; Jia, C.S. Approximation solution of the Dirac equation with position-dependent mass for the generalized Hulthén potential. Phys. Lett. A 2006, 352, 478–483. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Andrade, F.M.; Silva, E.O.; Hassanabadi, H. Scattering and bound states for the Hulthén potential in a cosmic string background. Eur. Phys. J. C 2017, 77, 270. [Google Scholar] [CrossRef]
- Jusufi, K.; Werner, M.C.; Banerjee, A.; Övgün, A. Light deflection by a rotating global monopole spacetime. Phys. Rev. D 2017, 95, 104012. [Google Scholar] [CrossRef]
- Bezerra de Mello, E.R.; Furtado, C. Nonrelativistic scattering problem by a global monopole. Phys. Rev. D 1997, 56, 1345–1348. [Google Scholar] [CrossRef]
- Hulthén, L. On the characteristic solutions of the Schrödinger deuteron equation. Ark. Mat. Astron. Fys. A 1942, 28, 5. [Google Scholar]
- Qiang, W.C.; Dong, S.H. Analytical approximations to the solutions of the Manning–Rosen potential with centrifugal term. Phys. Lett. A 2007, 368, 13–17. [Google Scholar] [CrossRef]
- Chen, C.Y.; Lu, F.L.; Sun, D.S. Approximate analytical solutions of scattering states for Klein-Gordon equation with Hulthén potentials for nonzero angular momentum. Cent. Eur. J. Phys. 2008, 6, 884–890. [Google Scholar] [CrossRef]
- Jia, C.S.; Liu, J.Y.; Wang, P.Q. A new approximation scheme for the centrifugal term and the Hulthén potential. Phys. Lett. A 2008, 372, 4779–4782. [Google Scholar] [CrossRef]
- Sakurai, J.J. Modern Quantum Mechanics, revised ed.; Addison-Wesley: Boston, MA, USA, 1994. [Google Scholar]
- Wei, G.-F.; Chen, W.-L.; Wang, H.-Y.; Li, Y.-Y. The scattering states of the generalized Hulthén potential with an improved new approximate scheme for the centrifugal term. Chin. Phys. B 2009, 18, 3663–3669. [Google Scholar] [CrossRef]
- Hassanabadi, H.; Yazarloo, B.H.; Hassanabadi, S.; Zarrinkamar, S. The Semi-Relativistic Scattering States of the Hulthén and Hyperbolic-Type Potentials. Acta Phys. Pol. A 2013, 124, 20–22. [Google Scholar] [CrossRef]
- Landau, L.; Lifshitz, E. Quantum Mechanics: Non-Relativistic Theory; Course of Theoretical Physics; Elsevier Science: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Greene, R.L.; Aldrich, C. Variational wave functions for a screened Coulomb potential. Phys. Rev. A 1976, 14, 2363–2366. [Google Scholar] [CrossRef]
- Adebimpe, O.; Onate, C.; Salawu, S.; Abolanriwa, A.; Lukman, A. Eigensolutions, scattering phase shift and thermodynamic properties of Hulthén-Yukawa potential. Results Phys. 2019, 14, 102409. [Google Scholar] [CrossRef]
- Ahmadov, A.; Aslanova, S.; Orujova, M.; Badalov, S.; Dong, S.H. Approximate bound state solutions of the Klein-Gordon equation with the linear combination of Hulthén and Yukawa potentials. Phys. Lett. A 2019, 383, 3010–3017. [Google Scholar] [CrossRef]
- Edet, C.O.; Ikot, A.N. Effects of Topological Defect on the Energy Spectra and Thermo-magnetic Properties of CO Diatomic Molecule. J. Low Temp. Phys. 2021, 203, 84–111. [Google Scholar] [CrossRef]
- Eshghi, M.; Sever, R.; Ikhdair, S.M. Energy states of the Hulthen plus Coulomb-like potential with position-dependent mass function in external magnetic fields. Chin. Phys. B 2018, 27, 020301. [Google Scholar] [CrossRef]
- Aomoto, K.; Kita, M.; Kohno, T.; Iohara, K. Theory of Hypergeometric Functions; Springer Monographs in Mathematics; Springer: Tokyo, Japan, 2011. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover Publications: New York, NY, USA, 1972. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. (Eds.) NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Bayrak, O.; Kocak, G.; Boztosun, I. Any l-state solutions of the Hulthén potential by the asymptotic iteration method. J. Phys. Math. Gen. 2006, 39, 11521–11529. [Google Scholar] [CrossRef]



| Values | |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alves, S.S.; Cunha, M.M.; Hassanabadi, H.; Silva, E.O. Approximate Analytical Solutions of the Schrödinger Equation with Hulthén Potential in the Global Monopole Spacetime. Universe 2023, 9, 132. https://doi.org/10.3390/universe9030132
Alves SS, Cunha MM, Hassanabadi H, Silva EO. Approximate Analytical Solutions of the Schrödinger Equation with Hulthén Potential in the Global Monopole Spacetime. Universe. 2023; 9(3):132. https://doi.org/10.3390/universe9030132
Chicago/Turabian StyleAlves, Saulo S., Márcio M. Cunha, Hassan Hassanabadi, and Edilberto O. Silva. 2023. "Approximate Analytical Solutions of the Schrödinger Equation with Hulthén Potential in the Global Monopole Spacetime" Universe 9, no. 3: 132. https://doi.org/10.3390/universe9030132
APA StyleAlves, S. S., Cunha, M. M., Hassanabadi, H., & Silva, E. O. (2023). Approximate Analytical Solutions of the Schrödinger Equation with Hulthén Potential in the Global Monopole Spacetime. Universe, 9(3), 132. https://doi.org/10.3390/universe9030132






