Damping Scenarios of Kink Oscillations of Solar Coronal Loops
Abstract
1. Introduction
2. The Model
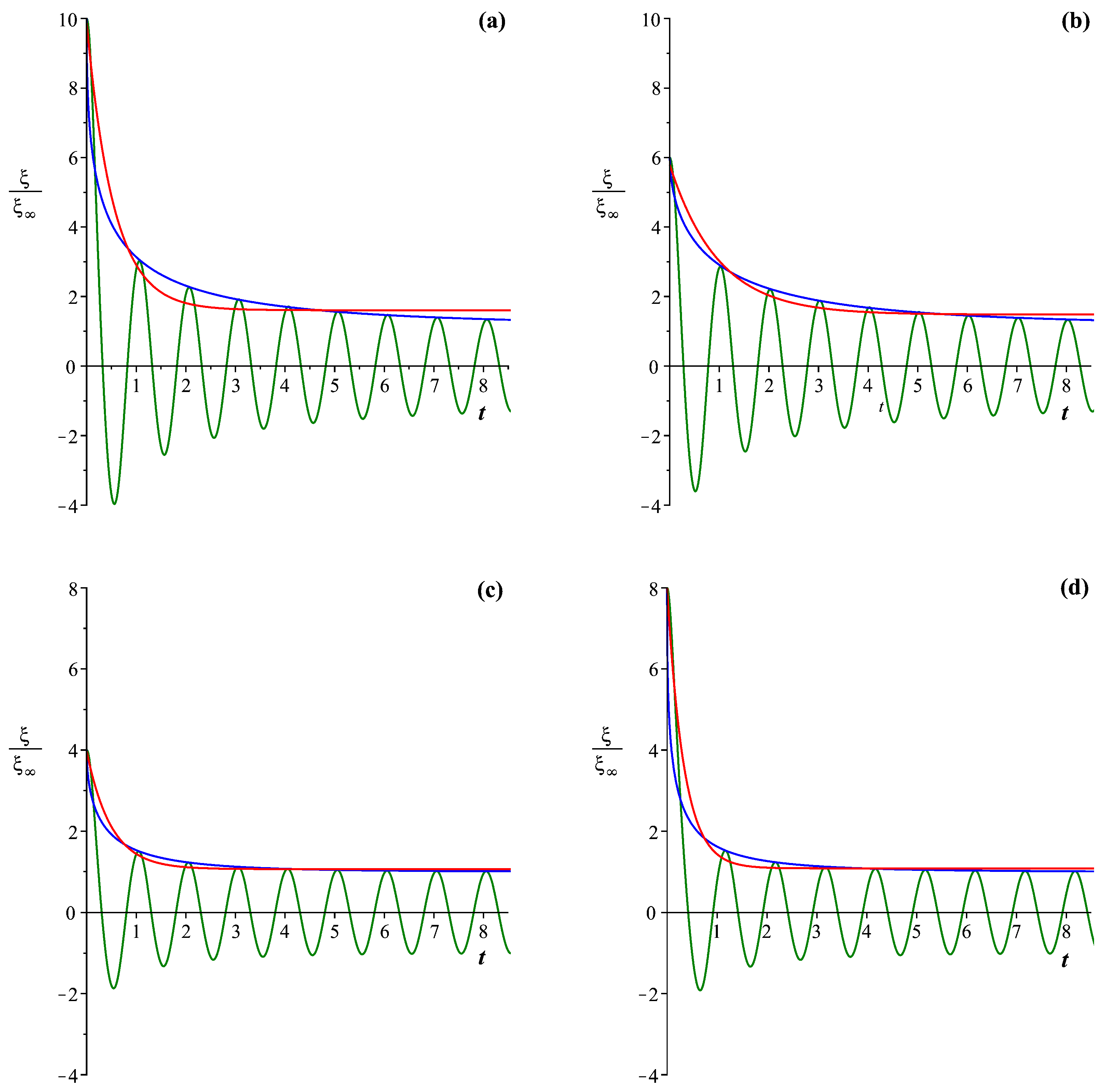
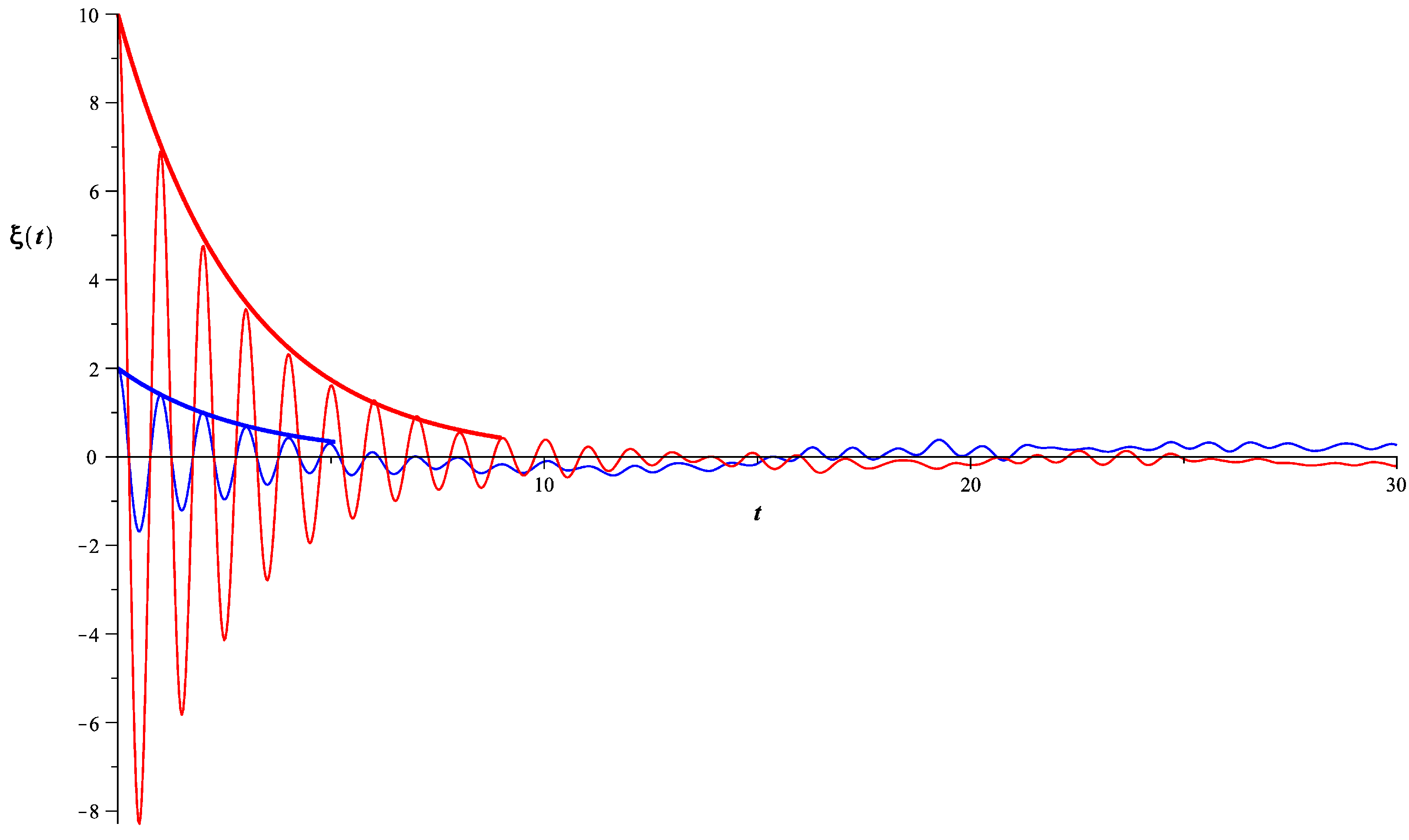
3. Results
3.1. Case of Self-Oscillations
3.2. Case of Randomly Driven Oscillations
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nakariakov, V.M.; Kolotkov, D.Y. Magnetohydrodynamic Waves in the Solar Corona. Annu. Rev. Astron. Astrophys. 2020, 58, 441–481. [Google Scholar] [CrossRef]
- Van Doorsselaere, T.; Srivastava, A.K.; Antolin, P.; Magyar, N.; Vasheghani Farahani, S.; Tian, H.; Kolotkov, D.; Ofman, L.; Guo, M.; Arregui, I.; et al. Coronal Heating by MHD Waves. Space Sci. Rev. 2020, 216, 140. [Google Scholar] [CrossRef]
- Banerjee, D.; Krishna Prasad, S.; Pant, V.; McLaughlin, J.A.; Antolin, P.; Magyar, N.; Ofman, L.; Tian, H.; Van Doorsselaere, T.; De Moortel, I.; et al. Magnetohydrodynamic Waves in Open Coronal Structures. Space Sci. Rev. 2021, 217, 76. [Google Scholar] [CrossRef]
- Li, B.; Antolin, P.; Guo, M.Z.; Kuznetsov, A.A.; Pascoe, D.J.; Van Doorsselaere, T.; Vasheghani Farahani, S. Magnetohydrodynamic Fast Sausage Waves in the Solar Corona. Space Sci. Rev. 2020, 216, 136. [Google Scholar] [CrossRef]
- Nakariakov, V.M.; Anfinogentov, S.A.; Antolin, P.; Jain, R.; Kolotkov, D.Y.; Kupriyanova, E.G.; Li, D.; Magyar, N.; Nisticò, G.; Pascoe, D.J.; et al. Kink Oscillations of Coronal Loops. Space Sci. Rev. 2021, 217, 73. [Google Scholar] [CrossRef]
- Wang, T.; Ofman, L.; Yuan, D.; Reale, F.; Kolotkov, D.Y.; Srivastava, A.K. Slow-Mode Magnetoacoustic Waves in Coronal Loops. Space Sci. Rev. 2021, 217, 34. [Google Scholar] [CrossRef]
- Roberts, B.; Edwin, P.M.; Benz, A.O. On coronal oscillations. Astrophys. J. 1984, 279, 857–865. [Google Scholar] [CrossRef]
- Anfinogentov, S.A.; Nakariakov, V.M.; Nisticò, G. Decayless low-amplitude kink oscillations: A common phenomenon in the solar corona? Astron. Astrophys. 2015, 583, A136. [Google Scholar] [CrossRef]
- Goddard, C.R.; Nisticò, G.; Nakariakov, V.M.; Zimovets, I.V. A statistical study of decaying kink oscillations detected using SDO/AIA. Astron. Astrophys. 2016, 585, A137. [Google Scholar] [CrossRef]
- Nechaeva, A.; Zimovets, I.V.; Nakariakov, V.M.; Goddard, C.R. Catalog of Decaying Kink Oscillations of Coronal Loops in the 24th Solar Cycle. Astrophys. J. Suppl. Ser. 2019, 241, 31. [Google Scholar] [CrossRef]
- Zimovets, I.V.; Nakariakov, V.M. Excitation of kink oscillations of coronal loops: Statistical study. Astron. Astrophys. 2015, 577, A4. [Google Scholar] [CrossRef]
- Goossens, M.; Hollweg, J.V.; Sakurai, T. Resonant Behaviour of Magnetohydrodynamic Waves on Magnetic Flux Tubes—Part Three. Sol. Phys. 1992, 138, 233–255. [Google Scholar] [CrossRef]
- Ruderman, M.S.; Roberts, B. The Damping of Coronal Loop Oscillations. Astrophys. J. 2002, 577, 475–486. [Google Scholar] [CrossRef]
- Goossens, M.; Andries, J.; Arregui, I. Damping of magnetohydrodynamic waves by resonant absorption in the solar atmosphere. Philos. Trans. R. Soc. Lond. Ser. 2006, 364, 433–446. [Google Scholar] [CrossRef]
- Pascoe, D.J.; Hood, A.W.; de Moortel, I.; Wright, A.N. Spatial damping of propagating kink waves due to mode coupling. Astron. Astrophys. 2012, 539, A37. [Google Scholar] [CrossRef]
- Hood, A.W.; Ruderman, M.; Pascoe, D.J.; De Moortel, I.; Terradas, J.; Wright, A.N. Damping of kink waves by mode coupling. I. Analytical treatment. Astron. Astrophys. 2013, 551, A39. [Google Scholar] [CrossRef]
- Soler, R.; Terradas, J. Magnetohydrodynamic Kink Waves in Nonuniform Solar Flux Tubes: Phase Mixing and Energy Cascade to Small Scales. Astrophys. J. 2015, 803, 43. [Google Scholar] [CrossRef]
- Terradas, J.; Andries, J.; Goossens, M.; Arregui, I.; Oliver, R.; Ballester, J.L. Nonlinear Instability of Kink Oscillations due to Shear Motions. Astrophys. J. Lett. 2008, 687, L115. [Google Scholar] [CrossRef]
- Magyar, N.; Van Doorsselaere, T. Damping of nonlinear standing kink oscillations: A numerical study. Astron. Astrophys. 2016, 595, A81. [Google Scholar] [CrossRef]
- Antolin, P.; Van Doorsselaere, T. Influence of resonant absorption on the generation of the Kelvin-Helmholtz Instability. Front. Phys. 2019, 7, 85. [Google Scholar] [CrossRef]
- Goddard, C.R.; Nakariakov, V.M. Dependence of kink oscillation damping on the amplitude. Astron. Astrophys. 2016, 590, L5. [Google Scholar] [CrossRef]
- Van Doorsselaere, T.; Goossens, M.; Magyar, N.; Ruderman, M.S.; Ismayilli, R. Nonlinear Damping of Standing Kink Waves Computed With Elsässer Variables. Astrophys. J. 2021, 910, 58. [Google Scholar] [CrossRef]
- Arregui, I.; Andries, J.; Van Doorsselaere, T.; Goossens, M.; Poedts, S. MHD seismology of coronal loops using the period and damping of quasi-mode kink oscillations. Astron. Astrophys. 2007, 463, 333–338. [Google Scholar] [CrossRef]
- Pascoe, D.J. Numerical simulations for MHD coronal seismology. Res. Astron. Astrophys. 2014, 14, 805–830. [Google Scholar] [CrossRef]
- Arregui, I. Bayesian coronal seismology. Adv. Space Res. 2018, 61, 655–672. [Google Scholar] [CrossRef]
- Pascoe, D.J.; Anfinogentov, S.; Nisticò, G.; Goddard, C.R.; Nakariakov, V.M. Coronal loop seismology using damping of standing kink oscillations by mode coupling. II. additional physical effects and Bayesian analysis. Astron. Astrophys. 2017, 600, A78. [Google Scholar] [CrossRef]
- Pascoe, D.J.; Hood, A.W.; Van Doorsselaere, T. Coronal loop seismology using standing kink oscillations with a lookup table. Front. Astron. Space Sci. 2019, 6, 22. [Google Scholar] [CrossRef]
- Mandal, S.; Tian, H.; Peter, H. Flare-induced decay-less transverse oscillations in solar coronal loops. Astron. Astrophys. 2021, 652, L3. [Google Scholar] [CrossRef]
- Gao, Y.; Tian, H.; Van Doorsselaere, T.; Chen, Y. Decayless Oscillations in Solar Coronal Bright Points. Astrophys. J. 2022, 930, 55. [Google Scholar] [CrossRef]
- Wang, T.; Ofman, L.; Davila, J.M.; Su, Y. Growing Transverse Oscillations of a Multistranded Loop Observed by SDO/AIA. Astrophys. J. Lett. 2012, 751, L27. [Google Scholar] [CrossRef]
- Tian, H.; McIntosh, S.W.; Wang, T.; Ofman, L.; De Pontieu, B.; Innes, D.E.; Peter, H. Persistent Doppler Shift Oscillations Observed with Hinode/EIS in the Solar Corona: Spectroscopic Signatures of Alfvénic Waves and Recurring Upflows. Astrophys. J. 2012, 759, 144. [Google Scholar] [CrossRef]
- Li, D.; Yuan, D.; Su, Y.N.; Zhang, Q.M.; Su, W.; Ning, Z.J. Non-damping oscillations at flaring loops. Astron. Astrophys. 2018, 617, A86. [Google Scholar] [CrossRef]
- Zhong, S.; Nakariakov, V.M.; Kolotkov, D.Y.; Anfinogentov, S.A. Long-term evolution of decayless kink oscillations of solar coronal loops. Mon. Not. R. Astron. Soc. 2022, 513, 1834–1841. [Google Scholar] [CrossRef]
- Mandal, S.; Chitta, L.P.; Antolin, P.; Peter, H.; Solanki, S.K.; Auchère, F.; Berghmans, D.; Zhukov, A.N.; Teriaca, L.; Cuadrado, R.A.; et al. What drives decayless kink oscillations in active-region coronal loops on the Sun? Astron. Astrophys. 2022, 666, L2. [Google Scholar] [CrossRef]
- Zhang, Q.M.; Dai, J.; Xu, Z.; Li, D.; Lu, L.; Tam, K.V.; Xu, A.A. Transverse coronal loop oscillations excited by homologous circular-ribbon flares. Astron. Astrophys. 2020, 638, A32. [Google Scholar] [CrossRef]
- Nisticò, G.; Nakariakov, V.M.; Verwichte, E. Decaying and decayless transverse oscillations of a coronal loop. Astron. Astrophys. 2013, 552, A57. [Google Scholar] [CrossRef]
- Afanasyev, A.N.; Van Doorsselaere, T.; Nakariakov, V.M. Excitation of decay-less transverse oscillations of coronal loops by random motions. Astron. Astrophys. 2020, 633, L8. [Google Scholar] [CrossRef]
- Ruderman, M.S.; Petrukhin, N.S. Excitation of decayless kink oscillations by random motion. Mon. Not. R. Astron. Soc. 2021, 501, 3017–3029. [Google Scholar] [CrossRef]
- Nakariakov, V.M.; Anfinogentov, S.A.; Nisticò, G.; Lee, D.H. Undamped transverse oscillations of coronal loops as a self-oscillatory process. Astron. Astrophys. 2016, 591, L5. [Google Scholar] [CrossRef]
- Karampelas, K.; Van Doorsselaere, T. Generating Transverse Loop Oscillations through a Steady-flow Driver. Astrophys. J. Lett. 2020, 897, L35. [Google Scholar] [CrossRef]
- Karampelas, K.; Van Doorsselaere, T. Transverse Loop Oscillations via Vortex Shedding: A Self-oscillating Process. Astrophys. J. Lett. 2021, 908, L7. [Google Scholar] [CrossRef]
- Nakariakov, V.M.; Kolotkov, D.Y.; Zhong, S. Do periods of decayless kink oscillations of solar coronal loops depend on noise? Mon. Not. R. Astron. Soc. 2022, 516, 5227–5231. [Google Scholar] [CrossRef]
- Anfinogentov, S.A.; Nakariakov, V.M. Magnetohydrodynamic Seismology of Quiet Solar Active Regions. Astrophys. J. Lett. 2019, 884, L40. [Google Scholar] [CrossRef]
- Hindman, B.W.; Jain, R. An Interpretation of Flare-induced and Decayless Coronal-loop Oscillations as Interference Patterns. Astrophys. J. 2014, 784, 103. [Google Scholar] [CrossRef]
- Antolin, P.; De Moortel, I.; Van Doorsselaere, T.; Yokoyama, T. Modeling Observed Decay-less Oscillations as Resonantly Enhanced Kelvin-Helmholtz Vortices from Transverse MHD Waves and Their Seismological Application. Astrophys. J. Lett. 2016, 830, L22. [Google Scholar] [CrossRef]
- Jenkins, A. Self-oscillation. Phys. Rep. 2013, 525, 167–222. [Google Scholar] [CrossRef]
- Rayleigh, J.W.S. The Theory of Sound; Dover: New York, NY, USA, 1945; Volume 2. [Google Scholar]
- Kaplan, B.Z.; Yaffe, I. The Rayleigh-van der Pol harmonic oscillator—Further comments. Int. J. Electron. 1977, 43, 615–619. [Google Scholar] [CrossRef]
- De Moortel, I.; Hood, A.W.; Ireland, J. Coronal seismology through wavelet analysis. Astron. Astrophys. 2002, 381, 311–323. [Google Scholar] [CrossRef]
- Ireland, J.; McAteer, R.T.J.; Inglis, A.R. Coronal Fourier Power Spectra: Implications for Coronal Seismology and Coronal Heating. Astrophys. J. 2015, 798, 1. [Google Scholar] [CrossRef]
- Yuan, D.; Feng, S.; Li, D.; Ning, Z.; Tan, B. A Compact Source for Quasi-periodic Pulsation in an M-class Solar Flare. Astrophys. J. Lett. 2019, 886, L25. [Google Scholar] [CrossRef]
- Liang, B.; Meng, Y.; Feng, S.; Yang, Y. Estimating red noise in quasi-periodic signals with MCMC-based Bayesian. Astrophys. Space Sci. 2020, 365, 40. [Google Scholar] [CrossRef]
- Ofman, L.; Aschwanden, M.J. Damping Time Scaling of Coronal Loop Oscillations Deduced from Transition Region and Coronal Explorer Observations. Astrophys. J. Lett. 2002, 576, L153–L156. [Google Scholar] [CrossRef]
- Ruderman, M.S.; Petrukhin, N.S.; Pelinovsky, E. Decayless Kink Oscillations Excited by Random Driving: Motion in Transitional Layer. Sol. Phys. 2021, 296, 124. [Google Scholar] [CrossRef]
- Arregui, I.; Montes-Solís, M.; Asensio Ramos, A. Inference of magnetic field strength and density from damped transverse coronal waves. Astron. Astrophys. 2019, 625, A35. [Google Scholar] [CrossRef]
- Karampelas, K.; Van Doorsselaere, T.; Antolin, P. Heating by transverse waves in simulated coronal loops. Astron. Astrophys. 2017, 604, A130. [Google Scholar] [CrossRef]
- Sprott, J.C.; Hoover, W.G. Harmonic Oscillators with Nonlinear Damping. Int. J. Bifurc. Chaos 2017, 27, 1730037. [Google Scholar] [CrossRef]
- Khaikin, V.B.; Storozhenko, A.A.; Bogod, V.M. Radioheliographs and Radio Reflectors in Solar Plasma Studies. Astrophys. Bull. 2019, 74, 221–233. [Google Scholar] [CrossRef]
- Kupriyanova, E.G.; Melnikov, V.F.; Shibasaki, K. Spatially Resolved Microwave Observations of Multiple Periodicities in a Flaring Loop. Sol. Phys. 2013, 284, 559–578. [Google Scholar] [CrossRef]
| Exponential Fitting | Super-Exponential Fitting | ||||
|---|---|---|---|---|---|
| Fitting Error in Percentage | Fitting Error in Percentage | ||||
| 2 | 3.47 | 1.39 | 3.94 | 0.873 | 0.42 |
| 4 | 1.58 | 11.47 | 1.69 | 0.69 | 2.50 |
| 6 | 0.97 | 25.03 | 0.96 | 0.57 | 5.10 |
| 8 | 0.68 | 36.17 | 0.60 | 0.49 | 8.48 |
| 10 | 0.54 | 43.16 | 0.40 | 0.44 | 12.27 |
| Exponential Fitting | Super-Exponential Fitting | ||||
|---|---|---|---|---|---|
| Fitting Error in Percentage | Fitting Error in Percentage | ||||
| 2 | 1.01 | 4.75 | 0.96 | 0.76 | 1.18 |
| 4 | 0.49 | 16.76 | 0.37 | 0.55 | 7.85 |
| 6 | 0.37 | 21.01 | 0.19 | 0.47 | 15.85 |
| 8 | 0.34 | 22.25 | 0.13 | 0.43 | 22.60 |
| 10 | 0.32 | 22.91 | 0.10 | 0.41 | 28.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakariakov, V.M.; Yelagandula, N.V. Damping Scenarios of Kink Oscillations of Solar Coronal Loops. Universe 2023, 9, 95. https://doi.org/10.3390/universe9020095
Nakariakov VM, Yelagandula NV. Damping Scenarios of Kink Oscillations of Solar Coronal Loops. Universe. 2023; 9(2):95. https://doi.org/10.3390/universe9020095
Chicago/Turabian StyleNakariakov, Valery M., and Naga V. Yelagandula. 2023. "Damping Scenarios of Kink Oscillations of Solar Coronal Loops" Universe 9, no. 2: 95. https://doi.org/10.3390/universe9020095
APA StyleNakariakov, V. M., & Yelagandula, N. V. (2023). Damping Scenarios of Kink Oscillations of Solar Coronal Loops. Universe, 9(2), 95. https://doi.org/10.3390/universe9020095







