Abstract
Within the framework of Einstein’s General Relativity we study strange quark stars assuming an interacting equation-of-state. Taking into account the presence of anisotropies in a sphere made of ultra dense matter, we employ the formalism based on the complexity factor. We integrate the structure equations numerically imposing the appropriate conditions both at the center and at the surface of the stars, thus obtaining interior solutions describing hydrostatic equilibrium. Making use of well-established criteria, we demonstrate that the solutions obtained here are well behaved and realistic. A comparison with another, more conventional approach, is made as well. Our numerical results are summarized in a number of figures.
1. Introduction
Unlike many other forms of matter, relativistic compact stars [1,2,3,4], which are formed during the final stages of stellar evolution, are excellent cosmic probes to study the properties of matter under exceptionally extreme conditions. Supernova explosions, either Type Ia or Type II, are the best known mechanisms to produce compact stars. Type Ia Supernovas occur when white dwarfs accrete matter from a companion in a binary (e.g., [5]). Type II corresponds to the core collapse of massive stars; although the mass range is not well defined, the current estimates predict a range from 8 to 30 solar masses (e.g., [6]). Although the most likely stellar remnants of these events are neutron stars, they could also form many other kinds of compact stars. Matter inside such objects is characterized by ultra-high mass/energy densities, for which the usual description of astrophysical plasmas in terms of non-relativistic Newtonian fluids is inadequate. Therefore, those very dense compact objects are relativistic in nature, and as such they are only properly described within the framework of Einstein’s General Relativity (GR) [7].
Neutron stars (NSs) are exciting astronomical objects, since understanding and explaining their properties, as well as their observed complex phenomena, require bringing together several scientific disciplines and lines of research, such as nuclear particle physics, astrophysics and gravitational physics. As NSs are the densest objects in the Universe after black holes, they can be used to probe, test and study properties of matter in an extreme gravitational regime, conditions that cannot be reproduced in earth-based experiments. For instance, supermassive star core collapses are known to trigger a complex network of physical processes that amplify magnetic fields up to tens of tera-tesla. This dramatic event involves neutrino emissions, convection [8] and magnetorotational instabilities [9], accompanied by a turbulent dynamo affecting the synthesis of heavy nuclides by r- and other atomic process nuclei (e.g., [10]). The result is the formation of a compact star with a strong magnetic field in its interior, possibly with a high degree of anisotropy in the local equation of state.
Therefore, those objects constitute an excellent cosmic laboratory to explore and possibly constrain non-conventional physics, as well as alternative theories of gravity.
Strange quark stars (QSs) [11,12,13,14,15,16], although at the moment theorized and less standard astronomical objects than NSs, may be viewed as ultra-compact neutron stars. Since quark matter is by assumption absolutely stable, it may be the true ground state of hadronic matter [17,18]. Therefore, this new class of relativistic compact objects has been proposed as an alternative to typical NSs. Though as of today they remain hypothetical objects, quarks stars cannot conclusively be ruled out yet. In fact investigating their properties is well motivated, both from the theoretical and observational point of view. For example, there are some claims in the literature that there are currently some observed compact objects exhibiting peculiar features, such as small radii for instance, that cannot be explained by the usual hadronic equations-of-state used in NS studies, see e.g., [19,20,21], and also Table 5 of [14] and the references therein. The present study is also relevant for the possible implications to understand the nature of compact stars. Recently, a few authors suggested that strange matter could exist in the core of NS-hybrid stars [22,23,24], while others claim such stars are almost indistinguishable from NS [25]. In addition to that, strange quark stars may explain some puzzling super-luminous supernovae [26,27], which occur in about one out of every 1000 supernovae explosions, and which are more than 100 times more luminous than regular supernovae. One plausible explanation is that since quark stars are much more stable than NSs, they could explain the origin of the huge amount of energy released in super-luminous supernovae. Many works have been recently proposed to validate their existence in different astrophysical scenarios [28,29].
In studies of compact objects, the authors usually focus their attention on relativistic stars made of isotropic matter, such that , where is the radial pressure, and is the tangential pressure. However, celestial bodies are not necessarily made of isotropic matter alone. As a matter of fact, it is now known that under certain conditions the fluid representing matter content may become anisotropic. The review article of Ruderman [30] mentioned for the first time such a possibility: the author observed that interactions among relativistic particles in a very dense nuclear matter medium could generate a non-vanishing anisotropic factor. Studies on anisotropies in relativistic stars received a boost thanks to the subsequent work of [31]. Indeed, anisotropies may arise in many different physical situations of a dense matter medium, such as in the presence of strong magnetic fields [32,33], in phase transitions [34], in pion condensation [35], slow rotation [36], viscosity-induced anisotropy [37], a mixture of two fluids [38] or in the presence of type 3A super-fluid [39] (see also [40,41,42] and the references therein for more recent works on the topic). In those works, relativistic models of anisotropic quark stars were studied, and the energy conditions were shown to be fulfilled. In particular, in [40] an exact analytic solution was obtained, in [41] an attempt was made to find a singularity-free solution to Einstein’s field equations and in [42] the Homotopy Perturbation Method was employed, which is a tool that facilitates the ability to tackle Einstein’s field equations. Furthermore, alternative approaches have been considered to incorporate new anisotropic solutions to already known isotropic ones [43,44,45].
In this work we propose to obtain interior solutions of relativistic stars, and in particular, of quark stars made of anisotropic matter, within the approach based on the complexity factor formalism. Originally, the new definition of the complexity factor was only investigated from a mathematical point of view, see [46,47,48,49] and the references therein. However, the real usefulness of such a definition becomes evident when we make use of it as a supplementary condition to close the set of structure equations describing the hydrostatic equilibrium of a self-gravitating spherical configuration. Moreover, the complexity factor may be used as a self-consistent way to incorporate anisotropies, which are generated in the presence of ultra dense matter in relativistic objects, as already mentioned before.
The plan of our work in the present article is the following: after this introductory section, we review the description of relativistic stars in the framework of Einstein’s theory in Section 2, while in the third section we present the vanishing complexity formalism. Next, in Section 4 we show and discuss our numerical results, and finally we finish our work with some concluding remarks in the last section. We work in geometrical units where , and we adopt the mostly negative metric signature in four space-time dimensions, namely .
2. Relativistic Stars in General Relativity
Let us start considering a static and spherically symmetric object in an anisotropic background bounded by a spherical surface . Assuming a line element that is written in Schwarzschild-like coordinates, i.e.,
The functions and are the metric potentials and depend on the radial coordinate only, whereas corresponds to the element of solid angle. We will take: . In the absence of a cosmological constant term, the classical Einstein field equations acquire the simple form:
with G being Newton’s constant (taken to be unity in the following for simplicity). Now, in the co-moving frame, the physical matter content is an anisotropic fluid of energy density , radial pressure , and tangential pressure , i.e., the covariant energy–momentum tensor in (local) Minkowski coordinates is then written as and the field equations can be written as:
where the symbol prime (′) denotes the derivative in relation to r.
Combining Equations (3)–(5), we obtain the hydrostatic equilibrium equation, best known as the generalized Tolman–Opphenheimer–Volkoff equation, which takes the simplest form
Such an equation can be understood as the balance between the following three forces: (i) gravitational, , (ii) hydrostatic, and (iii) anisotropic, , defined according to the following expressions
At this point it should be mentioned that the anisotropic factor, (sometimes also referred to as ), is defined as usual, i.e., . Accordingly, Equation (6), now reads
To clarify the situation, the last equation implies that this compact star results from the equilibrium between these three different forces, as is mentioned in Ref. [50]. In particular, if , we obtain the standard TOV equation. Moreover, in cases where (or equivalently ), causes a repulsive force in Equation (8) that counteracts the attractive force given by the combination . On the contrary, if we consider the case of (or ), is also an attractive force that adds to the other ones.
To remove the -dependence in Equation (6), we will take advantage of the following relation
and we then rewrite the generalized TOV equation as
In addition, m is the mass function, obtained by:
or,
The energy-momentum tensor can be rewritten as follows
From the expression of , we have to point out that the four-velocity is taken to be , and the four-acceleration is , whose any non-vanishing component is . Subsequently, the set is defined as
with the properties and . For the exterior solution, we match the problem with Schwarzschild space-time, i.e.,
We have to complete the problem with the appropriate matching conditions on the surface , with R being the radius of the star. Thus, by demanding continuity of the first and the second fundamental forms across that surface, we have
where M is the mass of the star, while the subscript indicates that the quantity is evaluated on the boundary surface . To finish, let us mention that the last three equations are the necessary and sufficient conditions for a smooth matching of the interior and exterior solutions, (1) and (19) respectively, on the surface .
3. Vanishing Complexity Factor Formalism
The present section summarizes the main ingredient behind the complexity factor formalism and its importance in astrophysical scenarios. To start, we should mention the original paper of Luis Herrera (L.H.) [51], in which the study of static anisotropic self-gravitating objects was performed. In that paper, the author introduced a modern definition of complexity and was motivated mainly by two concrete problems present in old descriptions: (i) the probability distribution is replaced by the energy density of the fluid distribution [52], and (ii) a complete inclusion of the components of the energy density fluid is missing, and the unique inclusion is the energy density of the fluid (ignoring possible additional contributions such as pressure). These two critical points are, in principle, the primary motivation used by L.H. to modify the more traditional complexity definition.
Albeit the standard definition of complexity was first introduced as a mathematical treatment only (see [46,47,48,49] and the references therein), its importance becomes evident when we recognize that such a condition can be used as an alternative route to bypass a standard ingredient in stellar interiors: the election of certain profiles of the system. Thus, the complexity factor formalism, or, more precisely, its simplified version, namely, when the complexity factor is zero, allows us to close the system and obtain novel and non-trivial spherically symmetric solutions unknown up to now. Thus, the vanishing complexity formalism offers a parallel way to deal with anisotropies in relativistic stars (see for instance [53,54]).
Now, let us move to the basic details behind the method. The essence of the complexity factor formalism emerges when we check the orthogonal splitting of the Riemann tensor for static self-gravitating fluids with spherical symmetry (please, for a detailed explanation, see [51] and also [55]). The (orthogonal) decomposition of the Riemann tensor is usually tedious labor and was well-studied in the original paper, thus we will avoid repetitions. We will take advantage of some helpful definitions:
where the symbol * is the dual tensor, i.e.,
and is the well-known Levi–Civita tensor. Utilizing the decomposition of the Riemann tensor, the set of tensors can be written in a convenient way, in terms of the physical variables, namely,
Also, the tensor (defined as ) can be written as
where E is precisely
satisfying the following properties:
At this point it is essential to mention that the tensors can be expressed in terms of alternative scalar functions, as was previously discussed in [56]. Now, consider the following tensors: and in the static case. Based on that, it is possible to define the so-called structure scalars , in terms of the physical variables, as follows:
From Equations (34)–(36), the local anisotropy of pressure is obtained utilizing and with help of the following relation:
The vanishing complexity condition, , implies the following relation between the energy density and the anisotropic factor
Thus, for a given density profile , we can compute the anisotropic factor for a self-gravitating system. Notice that the classical formalism, i.e., selecting a suitable form of the anisotropic factor by hand (among other alternatives), has also been significantly investigated over the years (see, for instance, [29,43,57,58,59,60,61,62,63,64,65,66,67] and the references therein). As the complexity factor formalism in the context of relativistic stars is so helpful, we will follow this idea and contrast the results obtained following such an approach with solutions coming from the canonical method, i.e., taking by hand the anisotropic factor, for instance.
4. Results and Discussion
In the present paper we have investigated within GR anisotropic stars made of quark matter in light of the vanishing complexity formalism. In particular, we compute numerically interior solutions of realistic spherical configurations of anisotropic matter, and we compare our solution against a more conventional approach, i.e., assuming an ansatz for the anisotropic factor by hand. For quark matter we adopt the interacting equation-of-state, , given by [68,69]
where is the radial pressure, and is the energy density of homogeneously distributed quark matter (also to in the Bag model). For the purpose of the present analysis, following Beringer et al. [70], we take the strange quark mass () to be , while the accepted values of the bag constant, B, lie within the range MeV/fm [71,72]. Also, the parameter comes from QCD corrections on the pressure of the quark-free Fermi sea, and it is directly related with the mass-radius relations of quark stars. Note that as far as the EoS is concerned, only the radial pressure is relevant. The tangential pressure has already been defined in the Introduction as well as after Equation (2).
After the numerical computations, we display in a number of figures, several quantities of interest. In Figure 1, Figure 2, Figure 3 and Figure 4, on the x-axis we put the normalized radial coordinate , while on the y-axis we put the quantities of interest, such as the mass of the star in solar masses, dimensionless quantities (for instance, the relativistic adiabatic index), and normalized quantities (e.g., the pressures and the energy density as well as the anisotropic factor in units of the bag constant, B). The curves exhibit the usual behaviour observed in interior solutions describing hydrostatic equilibrium. In particular, the mass function increases starting from 0 at the centre, while its mass at corresponds to the star’s mass. The energy density and the pressures start from their central value and monotonically decrease until the radial pressure vanishes at the star’s surface. In contrast, the energy density acquires a surface value. The energy density and the pressures remain positive throughout the star, while the energy density always remains larger than the pressures, such that the energy conditions are fulfilled. Moreover, both sound speeds vary slowly with the radial coordinate, taking values within the range 0–1 throughout the star, so causality is not violated. The anisotropic factor turns out to be negative, which is always the case within the vanishing complexity formalism. Finally, the relativistic adiabatic index increases monotonically and rapidly acquires large values as we approach the surface of the star. At the same time, it always remains larger than the Newtonian value . In particular, we notice that: (i) the mass function increase, the anisotropic factor decrease and the energy density and pressures decrease throughout the star, (ii) the speed of sound, radial and tangential, increase and decrease, respectively, and both are lower than , the relativistic adiabatic index, , increase and it is always higher than , (iii) the corresponding energy conditions are also satisfied. Thus, in light of the these numerical results, we can confirm that the complexity factor formalism is a solid approach to obtain well-defined solutions in the context of compact stars.
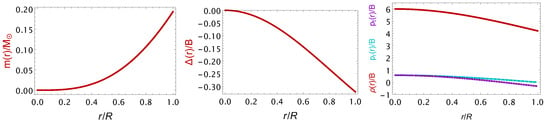
Figure 1.
Anisotropic SQ stars within the complexity factor: mass function in solar masses (left panel), anisotropic factor (middle panel), and energy density and pressures (right panel) versus the radial coordinate throughout the star.
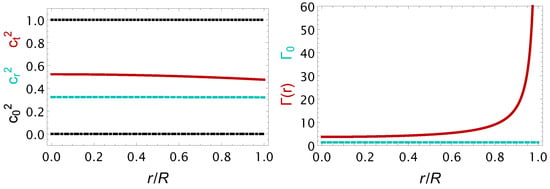
Figure 2.
Anisotropic SQ stars within the complexity factor: speed of sounds (left panel) and relativistic adiabatic index (right panel) versus the radial coordinate throughout the star. The horizontal straight line corresponds to the value .
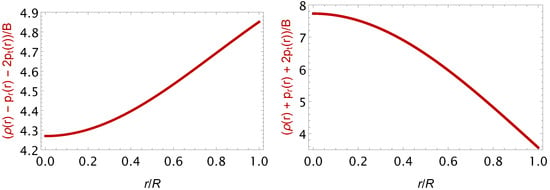
Figure 3.
Anisotropic QS stars within the complexity factor: energy conditions versus the radial coordinate throughout the star.
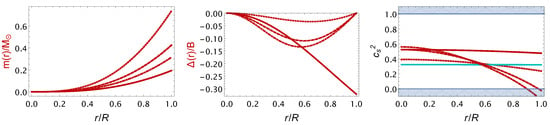
Figure 4.
Anisotropic QS stars considering a more standard approach and assuming (i) (dotted red line), (ii) (dashed red line), (iii) (dot-dashed red line), for: mass function in solar masses (left panel), anisotropic factor (middle panel), and sound speeds (right panel) versus the radial coordinate throughout the star. In particular, for the right-hand panel, we have plotted tangential (red color) and radial (cyan color) , respectively. For comparison, we added our solution utilizing the complexity formalism (solid red line).
As a supplementary independent check, we have obtained, numerically again, interior solutions using a more standard approach, i.e., adding external constraints to close the system of differential equations. As a toy model, we have considered an anisotropic factor, , as follows [73,74,75,76,77]
characterized by a dimensionless parameter, , which encodes the strength of the anisotropy. Also, we consider several values from to .
Our main results may be summarized as follows: the conventional method predicts more massive objects in comparison to the stars within the vanishing complexity formalism. The mass of the object decreases with the anisotropic factor, approaching the mass corresponding to the method based on vanishing complexity. Eventually, causality is violated as the tangential speed of sound becomes negative, and therefore the solution is no longer realistic.
Finally, in Figure 5, we show the mass-to-radius relationship for anisotropic stars for both approaches. First we study anisotropies within the vanishing complexity formalism, and we obtain the curve in red. Next, when we consider the conventional method, since now the ansatz for the anisotropic factor is characterized by a continuous parameter, we can observe the impact of that parameter on the profiles, corresponding to the other 3 curves in the figure. Increasing the anisotropy, the profile is gradually shifted towards the one corresponding to complexity. But at some point causality is violated, and therefore the solution is not realistic/viable any more. That is precisely the point where we must stop. The last allowed profile remains quite far away from the one obtained within complexity.
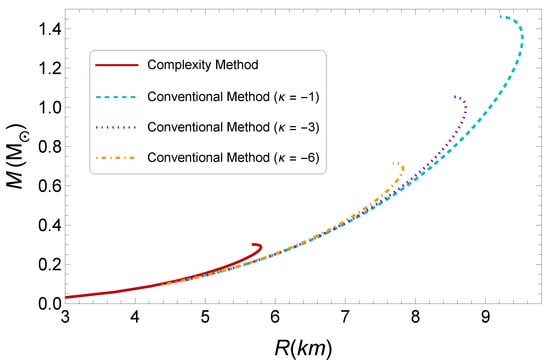
Figure 5.
Mass-radius profiles obtained by two alternative methods: (i) the vanishing complexity method (solid red line), and (ii) the conventional method for: (cyan dashed line), (dashed purple line), and (dot-dashed orange line).
Before we conclude our work, a final comment is in order. In the present article our main goal was to study the implications of the formalism based on vanishing complexity factor, and compare to a more standard approach. It would be interesting, however, to study the stability of anisotropic stars as well, analyzing radial oscillation modes and computing the corresponding frequencies. As this investigation lies beyond the scope of the present work, we propose to postpone it for the time being, and we hope to be able to do so in the future.
5. Conclusions
To summarize our work, in the present article we have obtained interior solutions of strange quark stars made of anisotropic matter. Assuming an interacting equation-of-state, we have taken into account the presence of anisotropies generated by ultra dense quark matter. The anisotropic factor has been introduced employing the formalism based on the complexity factor, and the structure equations have been integrated numerically. The solutions have been shown to be well-behaved and realistic. Moreover, we have made a comparison with another more conventional approach, where the form of the anisotropic factor is introduced by hand. Finally, we have obtained the mass-to-radius relationships within both methods, namely (i) employing the complexity formalism (where there are no free parameters), and (ii) adopting a certain form for the anisotropic factor (used in previous works, characterized by a free parameter). Our results show that as the anisotropy inceases, thus varying the free parameter, the profile is shifted towards the one corresponding to the complexity factor formalism.
Author Contributions
Conceptualization, Á.R., G.P. and I.L.; methodology, Á.R., G.P. and I.L.; formal analysis, Á.R., G.P. and I.L.; investigation, Á.R., G.P. and I.L.; writing—original draft preparation, Á.R., G.P. and I.L.; visualization, Á.R., G.P. and I.L. All authors have read and agreed to the published version of the manuscript.
Funding
A.R. is funded by the María Zambrano contract ZAMBRANO 21-25 (Spain). I.L. thanks the Fundação para a Ciência e Tecnologia (FCT), Portugal, for the financial support to the Center for Astrophysics and Gravitation (CENTRA/IST/ULisboa) through the Grant Project No. UIDB/00099/2020 and Grant No. PTDC/FIS-AST/28920/2017.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; John Wiley & Sons: Hoboken, NJ, USA, 1983. [Google Scholar]
- Psaltis, D. Probes and Tests of Strong-Field Gravity with Observations in the Electromagnetic Spectrum. Living Rev. Rel. 2008, 11, 9. [Google Scholar] [CrossRef]
- Lorimer, D.R. Binary and Millisecond Pulsars. Living Rev. Rel. 2008, 11, 8. [Google Scholar] [CrossRef] [PubMed]
- Zorotovic, M.; Schreiber, M.R. Cataclysmic variable evolution and the white dwarf mass problem: A Review. Adv. Space Res. 2020, 66, 1080–1089. [Google Scholar] [CrossRef]
- Ruiter, A.J. Type Ia supernova sub-classes and progenitor origin. IAU Symp. 2020, 357, 1–15. [Google Scholar] [CrossRef]
- Burrows, A.; Vartanyan, D. Core-collapse supernova explosion theory. Nature 2021, 589, 29–39. [Google Scholar] [CrossRef]
- Einstein, A. The Field Equations of Gravitation. Sitzungsber. Preuss. Akad. Wiss. Berl. (Math. Phys.) 1915, 1915, 844–847. [Google Scholar]
- Mösta, P.; Ott, C.D.; Radice, D.; Roberts, L.F.; Schnetter, E.; Haas, R. A large-scale dynamo and magnetoturbulence in rapidly rotating core-collapse supernovae. Nature 2015, 528, 376–379. [Google Scholar] [CrossRef]
- Guilet, J.; Müller, E. Numerical simulations of the magnetorotational instability in protoneutron stars—I. Influence of buoyancy. Mon. Not. R. Astron. Soc. 2015, 450, 2153–2171. [Google Scholar] [CrossRef]
- Kondratyev, V.N. R-Process with Magnetized Nuclei at Dynamo-Explosive Supernovae and Neutron Star Mergers. Universe 2021, 7, 487. [Google Scholar] [CrossRef]
- Alcock, C.; Farhi, E.; Olinto, A. Strange stars. Astrophys. J. 1986, 310, 261–272. [Google Scholar] [CrossRef]
- Alcock, C.; Olinto, A. Exotic Phases of Hadronic Matter and their Astrophysical Application. Ann. Rev. Nucl. Part. Sci. 1988, 38, 161–184. [Google Scholar] [CrossRef]
- Madsen, J. Physics and astrophysics of strange quark matter. Lect. Notes Phys. 1999, 516, 162–203. [Google Scholar] [CrossRef]
- Weber, F. Strange quark matter and compact stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Yue, Y.L.; Cui, X.H.; Xu, R.X. Is psr b0943+10 a low-mass quark star? Astrophys. J. Lett. 2006, 649, L95–L98. [Google Scholar] [CrossRef]
- Leahy, D.; Ouyed, R. Supernova SN2006gy as a first ever Quark Nova? Mon. Not. R. Astron. Soc. 2008, 387, 1193. [Google Scholar] [CrossRef]
- Witten, E. Cosmic Separation of Phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Farhi, E.; Jaffe, R.L. Strange Matter. Phys. Rev. D 1984, 30, 2379. [Google Scholar] [CrossRef]
- Henderson, J.A.; Page, D. RX J1856.5-3754 as a possible Strange Star candidate. Astrophys. Space Sci. 2007, 308, 513–517. [Google Scholar] [CrossRef]
- Li, A.; Peng, G.X.; Lu, J.F. Strange star candidates revised within a quark model with chiral mass scaling. Res. Astron. Astrophys. 2011, 11, 482–490. [Google Scholar] [CrossRef]
- Aziz, A.; Ray, S.; Rahaman, F.; Khlopov, M.; Guha, B.K. Constraining values of bag constant for strange star candidates. Int. J. Mod. Phys. D 2019, 28, 1941006. [Google Scholar] [CrossRef]
- Benic, S.; Blaschke, D.; Alvarez-Castillo, D.E.; Fischer, T.; Typel, S. A new quark-hadron hybrid equation of state for astrophysics—I. High-mass twin compact stars. Astron. Astrophys. 2015, 577, A40. [Google Scholar] [CrossRef]
- Yazdizadeh, T.; Bordbar, G.; Panah, B.E. The structure of hybrid neutron star in Einstein-λ gravity. Phys. Dark Universe 2022, 35, 100982. [Google Scholar] [CrossRef]
- Eslam Panah, B.; Yazdizadeh, T.; Bordbar, G.H. Contraction of cold neutron star due to in the presence a quark core. Eur. Phys. J. C 2019, 79, 815. [Google Scholar] [CrossRef]
- Jaikumar, P.; Reddy, S.; Steiner, A.W. The Strange star surface: A Crust with nuggets. Phys. Rev. Lett. 2006, 96, 041101. [Google Scholar] [CrossRef] [PubMed]
- Ofek, E.O.; Cameron, P.; Kasliwal, M.; Gal-Yam, A.; Rau, A.; Kulkarni, S.; Frail, D.; Chandra, P.; Cenko, S.; Soderberg, A.; et al. SN 2006gy: An extremely luminous supernova in the early-type galaxy NGC 1260. Astrophys. J. Lett. 2007, 659, L13–L16. [Google Scholar] [CrossRef]
- Ouyed, R.; Leahy, D.; Jaikumar, P. Predictions for signatures of the quark-nova in superluminous supernovae. arXiv 2009, arXiv:0911.5424. [Google Scholar]
- Mukhopadhyay, P.; Schaffner-Bielich, J. Quark stars admixed with dark matter. Phys. Rev. D 2016, 93, 083009. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Radial oscillations of strange quark stars admixed with fermionic dark matter. Phys. Rev. D 2018, 98, 083001. [Google Scholar] [CrossRef]
- Ruderman, M. Pulsars: Structure and dynamics. Ann. Rev. Astron. Astrophys. 1972, 10, 427–476. [Google Scholar] [CrossRef]
- Bowers, R.L.; Liang, E.P.T. Anisotropic Spheres in General Relativity. Astrophys. J. 1974, 188, 657–665. [Google Scholar] [CrossRef]
- Weber, F. Pulsars as Astrophysical Laboratories for Nuclear and Particle Physics; Routledge: New York, NY, USA, 2017. [Google Scholar]
- Bordbar, G.H.; Karami, M. Anisotropic magnetized neutron star. Eur. Phys. J. C 2022, 82, 74. [Google Scholar] [CrossRef]
- Sokolov, A.I. Universal effective coupling constants for the generalized Heisenberg model. Fiz. Tverd. Tela 1998, 40, 1284. [Google Scholar] [CrossRef]
- Sawyer, R.F. Condensed pi- phase in neutron star matter. Phys. Rev. Lett. 1972, 29, 382–385. [Google Scholar] [CrossRef]
- Herrera, L.; Santos, N.O. Local anisotropy in self-gravitating systems. Phys. Rep. 1997, 286, 53–130. [Google Scholar] [CrossRef]
- Barreto, W.; Rojas, S. An Equation of State for Radiating Dissipative Spheres in General Relativity. Astrophys. Space Sci. 1992, 193, 201–215. [Google Scholar] [CrossRef]
- Letelier, P.S. Anisotropic fluids with two-perfect-fluid components. Phys. Rev. D 1980, 22, 807–813. [Google Scholar] [CrossRef]
- Kippenhahn, R.; Weigert, A.; Weiss, A. Stellar Structure and Evolution; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 9783642303043. [Google Scholar] [CrossRef]
- Mak, M.K.; Harko, T. An exact anisotropic quark star model. Chin. J. Astron. Astrophys. 2002, 2, 248–259. [Google Scholar] [CrossRef]
- Deb, D.; Chowdhury, S.R.; Ray, S.; Rahaman, F.; Guha, B.K. Relativistic model for anisotropic strange stars. Ann. Phys. 2017, 387, 239–252. [Google Scholar] [CrossRef]
- Deb, D.; Roy Chowdhury, S.; Ray, S.; Rahaman, F. A New Model for Strange Stars. Gen. Rel. Grav. 2018, 50, 112. [Google Scholar] [CrossRef]
- Gabbanelli, L.; Rincón, A.; Rubio, C. Gravitational decoupled anisotropies in compact stars. Eur. Phys. J. C 2018, 78, 370. [Google Scholar] [CrossRef]
- Ovalle, J. Decoupling gravitational sources in general relativity: From perfect to anisotropic fluids. Phys. Rev. D 2017, 95, 104019. [Google Scholar] [CrossRef]
- Ovalle, J.; Casadio, R.; da Rocha, R.; Sotomayor, A. Anisotropic solutions by gravitational decoupling. Eur. Phys. J. C 2018, 78, 122. [Google Scholar] [CrossRef]
- Sharif, M.; Butt, I.I. Complexity Factor for Charged Spherical System. Eur. Phys. J. C 2018, 78, 688. [Google Scholar] [CrossRef]
- Sharif, M.; Butt, I.I. Complexity factor for static cylindrical system. Eur. Phys. J. C 2018, 78, 850. [Google Scholar] [CrossRef]
- Abbas, G.; Nazar, H. Complexity Factor For Anisotropic Source in Non-minimal Coupling Metric f(R) Gravity. Eur. Phys. J. C 2018, 78, 957. [Google Scholar] [CrossRef]
- Herrera, L.; Di Prisco, A.; Ospino, J. Complexity factors for axially symmetric static sources. Phys. Rev. D 2019, 99, 044049. [Google Scholar] [CrossRef]
- Prasad, A.K.; Kumar, J. Anisotropic relativistic fluid spheres with a linear equation of state. New Astron. 2022, 95, 101815. [Google Scholar] [CrossRef]
- Herrera, L. New definition of complexity for self-gravitating fluid distributions: The spherically symmetric, static case. Phys. Rev. D 2018, 97, 044010. [Google Scholar] [CrossRef]
- Sanudo, J.; Pacheco, A.F. Complexity and white-dwarf structure. Phys. Lett. A 2009, 373, 807–810. [Google Scholar] [CrossRef]
- Arias, C.; Contreras, E.; Fuenmayor, E.; Ramos, A. Anisotropic star models in the context of vanishing complexity. Ann. Phys. 2022, 436, 168671. [Google Scholar] [CrossRef]
- Andrade, J.; Contreras, E. Stellar models with like-Tolman IV complexity factor. Eur. Phys. J. C 2021, 81, 889. [Google Scholar] [CrossRef]
- Gomez-Lobo, A.G.P. Dynamical laws of superenergy in General Relativity. Class. Quant. Grav. 2008, 25, 015006. [Google Scholar] [CrossRef]
- Herrera, L.; Ospino, J.; Di Prisco, A.; Fuenmayor, E.; Troconis, O. Structure and evolution of self-gravitating objects and the orthogonal splitting of the Riemann tensor. Phys. Rev. D 2009, 79, 064025. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Millisecond pulsars modeled as strange quark stars admixed with condensed dark matter. Int. J. Mod. Phys. D 2018, 27, 1850093. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Panotopoulos, G.; Lopes, I. Anisotropic Dark Matter Stars. Phys. Rev. D 2021, 103, 084023. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, A. Electrically charged strange quark stars with a non-linear equation-of-state. Eur. Phys. J. C 2019, 79, 524. [Google Scholar] [CrossRef]
- Lopes, I.; Panotopoulos, G.; Rincón, A. Anisotropic strange quark stars with a non-linear equation-of-state. Eur. Phys. J. Plus 2019, 134, 454. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, A. Relativistic strange quark stars in Lovelock gravity. Eur. Phys. J. Plus 2019, 134, 472. [Google Scholar] [CrossRef]
- Abellán, G.; Rincon, A.; Fuenmayor, E.; Contreras, E. Beyond classical anisotropy and a new look to relativistic stars: A gravitational decoupling approach. arXiv 2020, arXiv:2001.07961. [Google Scholar]
- Panotopoulos, G.; Rincón, A.; Lopes, I. Interior solutions of relativistic stars in the scale-dependent scenario. Eur. Phys. J. C 2020, 80, 318. [Google Scholar] [CrossRef]
- Bhar, P.; Tello-Ortiz, F.; Rincón, A.; Gomez-Leyton, Y. Study on anisotropic stars in the framework of Rastall gravity. Astrophys. Space Sci. 2020, 365, 145. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, A.; Lopes, I. Radial oscillations and tidal Love numbers of dark energy stars. Eur. Phys. J. Plus 2020, 135, 856. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, A.; Lopes, I. Interior solutions of relativistic stars with anisotropic matter in scale-dependent gravity. Eur. Phys. J. C 2021, 81, 63. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, A.; Lopes, I. Slowly rotating dark energy stars. Phys. Dark Univ. 2021, 34, 100885. [Google Scholar] [CrossRef]
- Becerra-Vergara, E.A.; Mojica, S.; Lora-Clavijo, F.D.; Cruz-Osorio, A. Anisotropic Quark Stars with an Interacting Quark Equation of State. Phys. Rev. D 2019, 100, 103006. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Tangphati, T.; Banerjee, A. Electrically charged compact stars with an interacting quark equation of state. Chin. J. Phys. 2022, 77, 1682–1690. [Google Scholar] [CrossRef]
- Beringer, J.; Arguin, J.F.; Barnett, R.M.; Copic, K.; Dahl, O.; Groom, D.E.; Lin, C.J.; Lys, J.; Murayama, H.; Wohl, C.G.; et al. Review of Particle Physics (RPP). Phys. Rev. D 2012, 86, 010001. [Google Scholar] [CrossRef]
- Fiorella Burgio, G.; Fantina, A.F. Nuclear Equation of state for Compact Stars and Supernovae. Astrophys. Space Sci. Libr. 2018, 457, 255–335. [Google Scholar] [CrossRef]
- Blaschke, D.; Chamel, N. Phases of dense matter in compact stars. Astrophys. Space Sci. Libr. 2018, 457, 337–400. [Google Scholar] [CrossRef]
- Silva, H.O.; Macedo, C.F.B.; Berti, E.; Crispino, L.C.B. Slowly rotating anisotropic neutron stars in general relativity and scalar–tensor theory. Class. Quant. Grav. 2015, 32, 145008. [Google Scholar] [CrossRef]
- Folomeev, V.; Dzhunushaliev, V. Magnetic fields in anisotropic relativistic stars. Phys. Rev. D 2015, 91, 044040. [Google Scholar] [CrossRef]
- Cattoen, C.; Faber, T.; Visser, M. Gravastars must have anisotropic pressures. Class. Quant. Grav. 2005, 22, 4189–4202. [Google Scholar] [CrossRef]
- Horvat, D.; Ilijic, S.; Marunovic, A. Radial pulsations and stability of anisotropic stars with quasi-local equation of state. Class. Quant. Grav. 2011, 28, 025009. [Google Scholar] [CrossRef]
- Arbañil, J.D.V.; Panotopoulos, G. Tidal deformability and radial oscillations of anisotropic polytropic spheres. Phys. Rev. D 2022, 105, 024008. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).