Abstract
Stark broadening parameters, line widths and shifts, for 15 N VI multiplets are calculated using semiclassical perturbation theory for temperatures from 50,000 K to 2,000,000 K, and perturber density of 10 cm. As perturbers have been taken electrons, protons and He III ions (alpha particles), which are of interest particularly for white dwarfs. Moreover, B III, B IV, B V and B VI ions have been taken as well, due to their significance for proton-boron fusion investigations. An example of the importance of Stark broadening in comparison with thermal Doppler broadening in atmospheres of spectral class DO white dwarfs is also presented. The obtained results are of interest particularly for white dwarf atmospheres modelling and analysis and synthesis of their spectra as well as for laser driven plasma in proton-boron fusion investigations.
1. Introduction
Profiles of spectral lines emitted or absorbed in plasma environment enable the acquisition of valuable information for interactions there. In astrophysics, methods of passive spectroscopy diagnostics are powerful tools to reveal the nature of phenomena and processes in stellar plasma. Particle interactions in plasma provoke broadening and shift of spectral line profiles depending on the temperature and density conditions. Using line profiles broadened by interactions with surrounding charged particles (Stark broadening) one may deduce many pieces of informations useful for astrophysics (e.g., [1]), laboratory plasma (e.g., [2]) inertial fusion experiments ([3,4]), lasers and laser produced plasma ([5,6,7]) as well as for various plasmas in technology ([8]). Stark broadening data are particularly useful and needed in astrophysics, for example for stellar abundance determination, spectral line analysis and synthesis, radiative transfer calculation, modelling of stellar atmospheres, etc.
Nitrogen lines are widely present in stellar spectra (see e.g., [9,10,11,12,13,14,15,16,17]). For example, they are applied for the investigation of abundances, effective temperature, dynamics, etc.
A comprehensive spectral analysis of LSV + 4621 (DAO-type central star of the planetary nebula Sh 2-216) is performed in [9], where the photospheric properties are compared to predictions from stellar evolution theory and also from diffusion calculations, also. High-resolution, high-S/N ultraviolet observations obtained with the help of the Far Ultraviolet Spectroscopic Explorer () mission and Space Telescope Imaging Spectrograph (STIS) aboard on the Hubble Space Telescope (HST) and the optical spectrum are used. The effective temperature of (95 ± 2)·10 K is determined with high precision from a set of spectral lines of N IV–N V and other elements. The main limitation that authors have encountered is the lack of reliable atomic and line-broadening data.
Spectral lines of N VI, N VII, and N VIII ions from photospheric absorption lines in XMM-Newton (XMM—X-ray Multi-Mirror Mission [18]) spectra of the X-ray bursting neutron star in EXO0748-676 are used in [10] for an LTE and a non-local thermodynamic equilibrium (NLTE) model of atmospheres, and to constrain the neutron star mass-radius ratio.
According to [11], in the observation of LB3459 several photospheric absorption lines are prominent and isolated from interstellar medium (ISM) absorption lines where N II–N VI lines take a part. LB3459 (AA Doradus) is an eclipsing, close, post common-envelope binary (PCEB) consisting of an sdOB primary star and an unseen secondary with an extraordinarily low mass brown dwarf. A detailed spectral analysis of the far-UV spectrum by means of state-of the-art NLTE model-atmosphere techniques is performed.
Spectral lines of nitrogen atoms in different stages of ionization (N I–N VI) are included in the study of Nagel et al. [12], where AM CVn systems are object of interest. They are very compact interacting binary systems with unclear nature of the donor star. The accretion disc represents the chemical composition of the donor’s atmosphere, and the disc analyses contribute to the understanding of the donor star and of the formation of these systems. A new grid of NLTE accretion disc models is presented to study the influence of parameters such as primary mass, mass accretion rate, or chemical abundances on the disc spectrum.
Prominent resonance absorption lines of N VI are observed in the Chandra and XMM-Newton grating X-ray spectra of V4743 Sgr of outstanding quality [13], where comparison with calculated grids of synthetic energy distributions based on non-local thermal equilibrium model atmospheres for the analysis of the hottest white dwarfs (WDs) is performed. As a result, the effective temperature, chemical abundances, and gravity are adjusted.
N VI emission lines from 1.5 Seyfert galaxy NGC 3227, observed during several X-ray missions of two satellites (XMM-Newton and Suzaku), are reported in Newman et al. ([14] and references therein). A constructed unified model, consistent with the observations is proposed where the primary hard X-ray emission comes from a corona above an accretion disk. There, hot electrons from the hot corona, Comptonize softer photons from the colder disk. In the warm atmosphere of the inner part of the accretion disk, an additional soft excess may occur due to magnetically driven processes or additional warm Comptonization.
Recently, N I, N VI, and N VII spectral lines in the wavelength region between 20 and 30 Å are observed in the high-resolution X-ray spectra of nova RS Ophiuchi [15]. Swift, XMM-Newton, and Chandra observations from the two last outbursts are used. Direct comparison between the last outbursts enables researches to explore the reasons for the differences. The aim of that study is to obtain a better general understanding of the emission and absorption mechanisms. According to the authors, the emission mechanisms hold the key to the physics of novae and nuclear burning, while absorption processes could dominate. To explore the cause of the gross initial variability in the observed super-soft source (SSS) emission is another goal of the investigation.
Another work that deals with prominent absorption of N VI spectral lines in the X-ray spectra taken with the Chandra satellite is proposed in [16]. These lines are observed during the super-soft sources (SSS) phase of nova V 4743 Sgr. Applications of NLTE model atmospheres to (pre) white dwarfs during the hottest stages of their stellar evolution are given.
In 2022, a report on the first eruption of Galactic nova YZ Ret was published [17]. Fermi/LAT and NuSTAR observations complemented by XMM–Newton X-ray grating spectroscopy were simultaneously used. These observations revealed supersoft X-ray emission dominated by emission lines including those of N VI and N VII ions. The purpose of the long-term project is to identify the physical mechanisms responsible for high-energy emission in classical novae.
Another field of research that has been massively growing in the last decades is dedicated to energy production by fusion reactions which are aneutronic and without radioactive species. Such advantages are demonstrated by the proton-boron fusion reaction [19], where the products are three alpha particles and 8.7 MeV energy is released. As fuel, it serves a mixture of H and B. Both elements are abundant in nature, stable (no radioactivity as tritium in DT fusion) and cheap. Only charged particles are fusion products that enable direct energy conversion into electricity. From another side, the neutron generation luck means no induced activation of the surrounding environment. Also, the boron target does not need to be cryogenic. Nitrogen appears as a product in a fusion chain via intermediate nuclear reactions. In some experiments [20] two boron nitride (BN) targets are used. A laser beam focused on the first BN target generates protons which then collide with the second BN target to trigger nuclear reactions. In terms of optimizing the fusion yield, a plasma diagnostic is performed in these experiments [21]. When laser intensities I ≥ 10 W/cm the proton beam can provide energies up to ∼50 MeV which allows additional reactions to be grouped as “primary” or “secondary”. Primary reactions are initiated by the protons scattering on boron or boron-nitride solid targets. Nitrogen takes part in the primary nuclear reactions N(p, )C and N(p, n)O in the range of proton energies. Rescattering of the particles on the boron and nitrogen nuclei in the environment are secondary reactions. Such a reaction in the range of alpha particles is N(p, )F which is mentioned as a good candidate for yield. Another important result that could play a significant role in the Stark broadening of spectral lines in this environment is the presence of the multiply charged boron ions B IV, B V and B VI that are clearly identified in [22].
In this work, we present Stark broadening parameters (full width at half intensity maximum (FWHM) and shift), for 15 multiplets containing 33 spectral lines of N VI broadened by collisions with the most important charged constituents of stellar plasma: electrons, protons, and He III ions (alpha particles). Moreover, collisions with B III, B IV, B V and B VI ions are also included for the purposes of proton-boron fusion research. Calculations have been performed using the semiclassical perturbation theory (see for example [23] and references therein), and cover a wide range of temperatures and perturber densities.
2. The Semiclassical Perturbation Method
Within the semiclassical perturbation theory [23,24,25], full width at half intensity maximum (FWHM-W) and shift (d) of an isolated spectral line of a non-hydrogenic ion, broadened with collisions with charged particles, are expressed as:
where i and f are the inital and final level of the corresponding transition, and are their perturbing levels, is the perturber density, velocity of the perturber, the Maxwellian velocty distribution, and is the impact parameter of the perturbing particle.
The inelastic cross sections , , are expressed as an integral of the transition probability , over the impact parameter as:
The corresponding contributions of elastic collisions and resonances are expressed as:
Here, is the elastic cross section, () and (), are phase shifts due to the polarization and quadrupolar potential. More informations about them can be found in Section 3 of Chapter 2 in [24]. The symmetrization procedure and cut-offs , , , and are described in Section 1 of Chapter 3 in [25]. The term representing the contribution of Feshbach resonances, is described in [26].
In the case of positive ions as perturbers, the Coulomb force is repulsive as a difference from electrons where it is attractive and the consequence is that trajectories are different. Also, there is no contribution of Feshbach resonances.
Knowing the width and shift of a spectral line, the line profile may be obtained as:
Here
where , are the energies of initial and final atomic energy level, respectively.
3. Stark Broadening Parameter Calculations
Employing the semiclassical perturbation method [23,24,25], the calculations to obtain the Stark broadening parametters of spectral lines within 15 multiplets of N VI have been performed. Broadening due to collisions with electrons, protons, He III (alpha particles) and boron ions in different degrees of ionization (B III, B IV, B V and B VI), which are charged perturbers of particular significance for white dwarfs and proton-boron fusion, have been taken into consideration and the corresponding full width at half maximum of intensity (FWHM–W) and shift (d) have been calculated. The calculations have been performed for temperature values in a wide interval from 50,000 K to 2,000,000 K and perturber density of 10 cm.
The atomic energy levels for NVI, which are needed for the present calculations, are from [27] and have been taken from the NIST database [28]. The required oscillator strengths which are needed have been calculated with the help of the Bates and Damgaard [29] method and the corresponding tables in [30]. If the tables in [30] are not convenient for transitions involving higher energy levels, calculations are performed according to Ref. [31].
The obtained results for Stark widths (FWHM) and shifts, for 15 N VI multiplets containing 33 spectral lines broadened by collisions with electrons, protons, He III ions (alpha particles), B III, B IV, B V and B VI ions, namely with perturbers which are of interest first of all for white dwarfs and proton-boron fusion, are given in Table 1, Table 2, Table 3 and Table 4. Calculations have been performed for temperatures from 50,000 K to 2,000,000 K and a perturber density of 10 cm. The wavelengths in Table 1, Table 2, Table 3 and Table 4 are calculated with the help of atomic energy levels used in the calculations and may be different from atomic energy levels given in the NIST database. If we want to obtain a more accurate value for a line within a multiplet or change a wavelength with the experimental one in order to correct W or d for the difference we can do this for the width and in the same way for the shift as:
Here, W is the corrected width, is the NIST, or experimental, or observed value, or the value for a line within a multiplet, is the calculated wavelength, or the value for a multiplet as a whole and W is the width from Table 1, Table 2, Table 3 and Table 4.

Table 1.
In this table are presented FWHM—Full Widths at Half Intensity Maximum (W) and shift (d) for N VI spectral lines broadened by impacts with electrons and protons for a perturber density of 10 cm and temperatures from 50,000 K to 2,000,000 K.

Table 2.
In this table are presented FWHM—Full Widths at Half Intensity Maximum (W) and shift (d) for N VI spectral lines broadened by impacts with He III and B III ions for a perturber density of 10 cm and temperatures from 50,000 K to 2,000,000 K.

Table 3.
In this table are presented FWHM—Full Widths at Half Intensity Maximum (W) and shift (d) for N VI spectral lines broadened by impacts with B IV and B V ions for a perturber density of 10 cm and temperatures from 50,000 K to 2,000,000 K.

Table 4.
In this table are presented FWHM—Full Widths at Half Intensity Maximum (W) and shift (d) for N VI spectral lines broadened by impacts with B VI ions for a perturber density of 10 cm and temperatures from 50,000 K to 2,000,000 K.
The quantity C [32], which is provided in Table 1, Table 2, Table 3 and Table 4, when it is divided by the corresponding FWHM (W) gives the maximal perturber density for which we could assume that the line is isolated.
Stark broadening calculations of Stark widths for four N VI spectral lines exist in Ref. [33], where a modified semiempirical method [34] has been used and for the same four lines in Ref. [35] where calculations have been performed using Griem’s simplified semiclassical method ([36] Equation (526)). The values in these two references are too small in comparison with the present calculations. Both methods [34,36] used in [33,35] are based on data for singly, doubly and triply charged ions and give correct results for spectral lines of such emitters. However, it seems that for the case of highly charged ions they need the corresponding adaptations. For example in the formulation of the empirical part of the modified semiempirical theory [34], empirical data for cross sections of highly charged ions should be taken into account due to the increasing influence of relativistic effects.
4. Application to DO White Dwarf Atmospheres
The results for Stark broadening parameters obtained here, are also used to show the influence of collisions of N VI with various perturbers, considered in this work, in the spectrum of a DO white dwarf. To demonstrate the importance of Stark broadening, we took one line in the red part of the visible part of the spectrum (3sS–3pPo, = 6993.0 Å) and one in the UV part (2sS–2pPo, = 2897.2 Å) and compared Stark and Doppler widths for different Rosseland optical depths ().
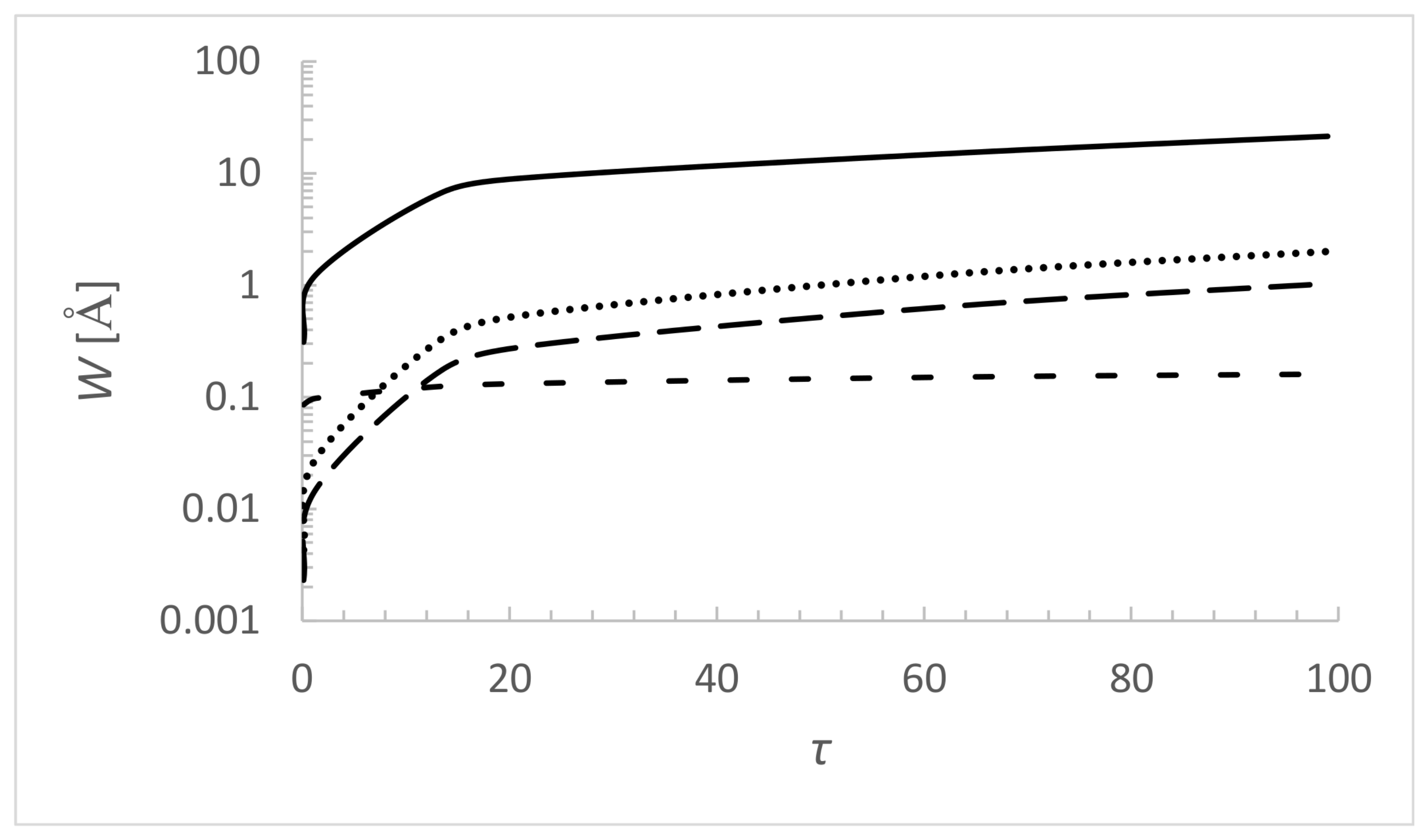
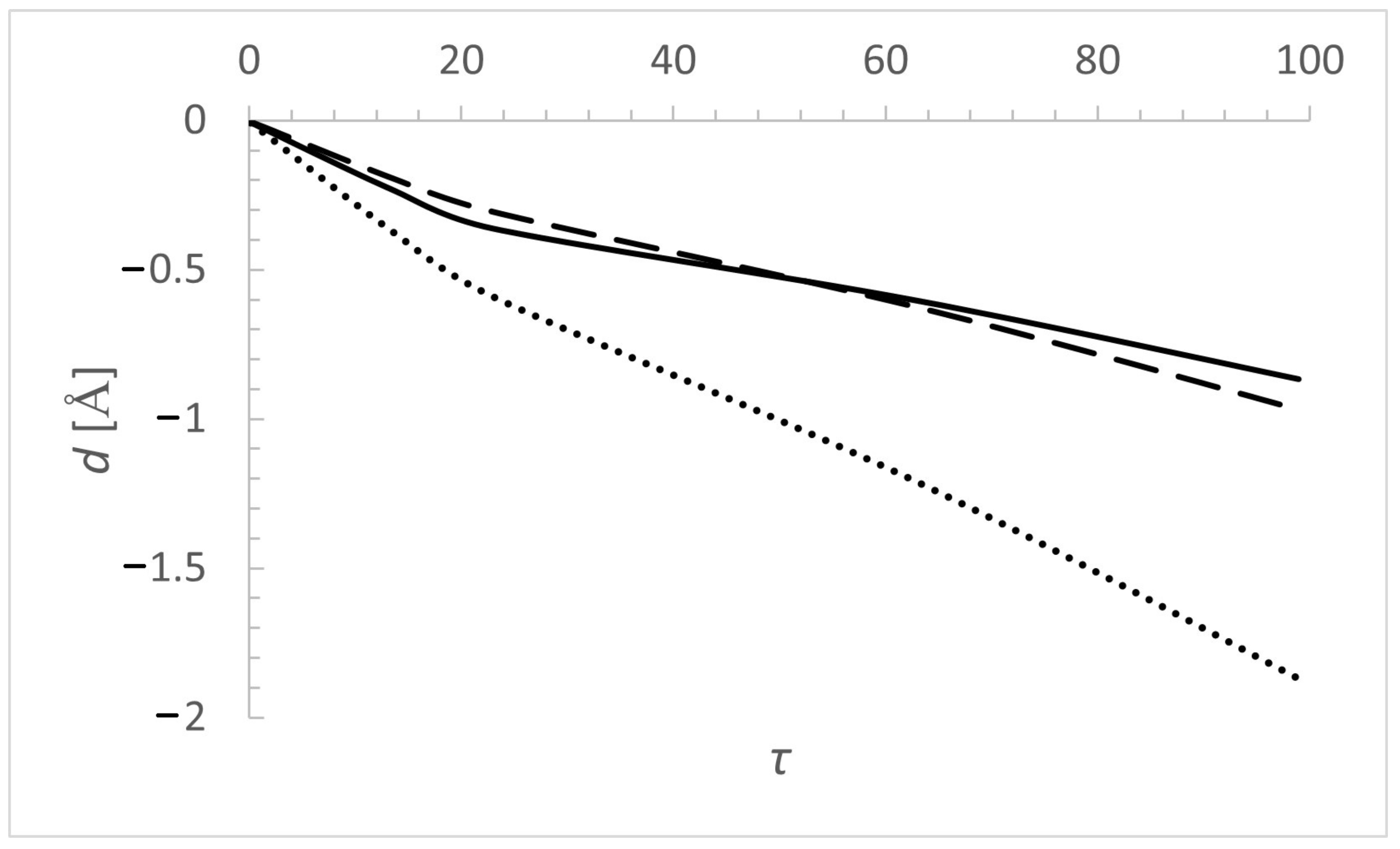
Figure 1 and Figure 2 illustrate the Stark width and shift of N VI 3sS–3pPo 6993.0 Å spectral line Rosseland optical depth, for effective temperature 60,000 K and log g = 8. The model of the stellar atmosphere of a DO white dwarf is taken from Ref. [37]. In Figure 1, the thermal Doppler width is added for comparison. The electron width is up to two orders of magnitude larger than the Doppler one. The widths due to collisions with protons and He III ions are close to each other and bigger than Doppler width except for the lowest values. This line is a very good candidate for spectral analysis in the atmosphere of a DO white dwarfs. Stark shift values (Figure 2) are negative. The shift of line broadened by He III ions dominates the whole Rosseland optical depth range. The electron and proton shifts are closer to each other. The absolute values of all of them increase with .
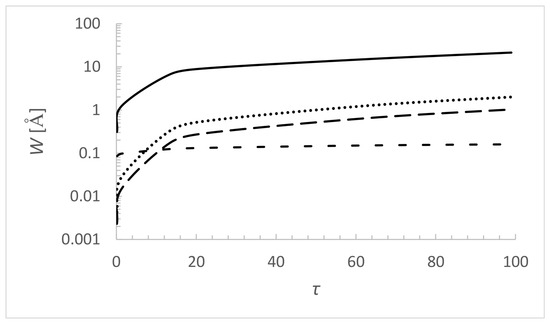
Figure 1.
Dependence of Stark and Doppler full widths at half intensity maximum of N VI 3sS–3pPo, = 6993.0 Å spectral line (perturbers: electrons—solid line, protons—long dashes, He III—dots, Doppler—dashes), on the Rosseland optical depth in the atmosphere of a DO white dwarf. Model of white dwarf atmosphere [37] is with parameters = 60,000 K and log g = 8.
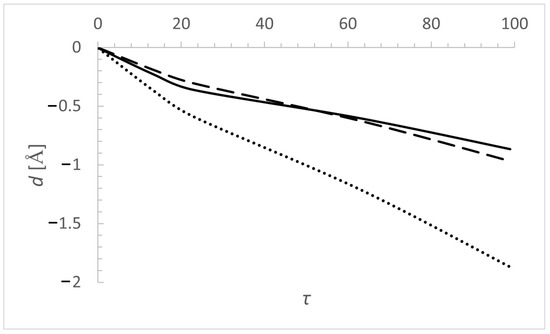
Figure 2.
Dependence of Stark shift of N VI 3sS–3pPo, = 6993.0 spectral line Å (perturbers: electrons—solid line, protons—long dashes, He III—dots), on the Rosseland optical depth in the atmosphere of a DO white dwarf. Model of white dwarf atmosphere [37] is with parameters = 60,000 K and log g = 8.
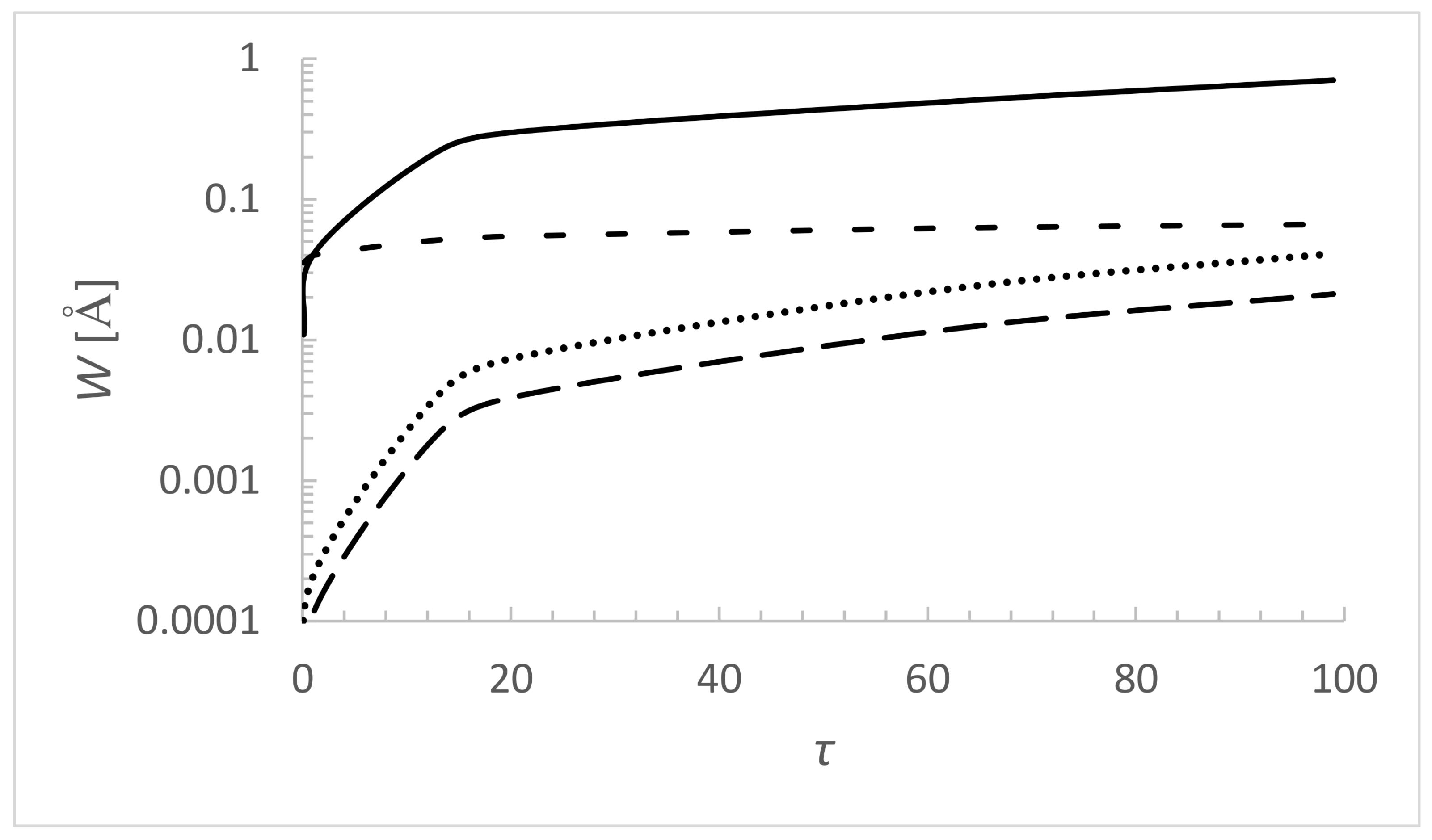
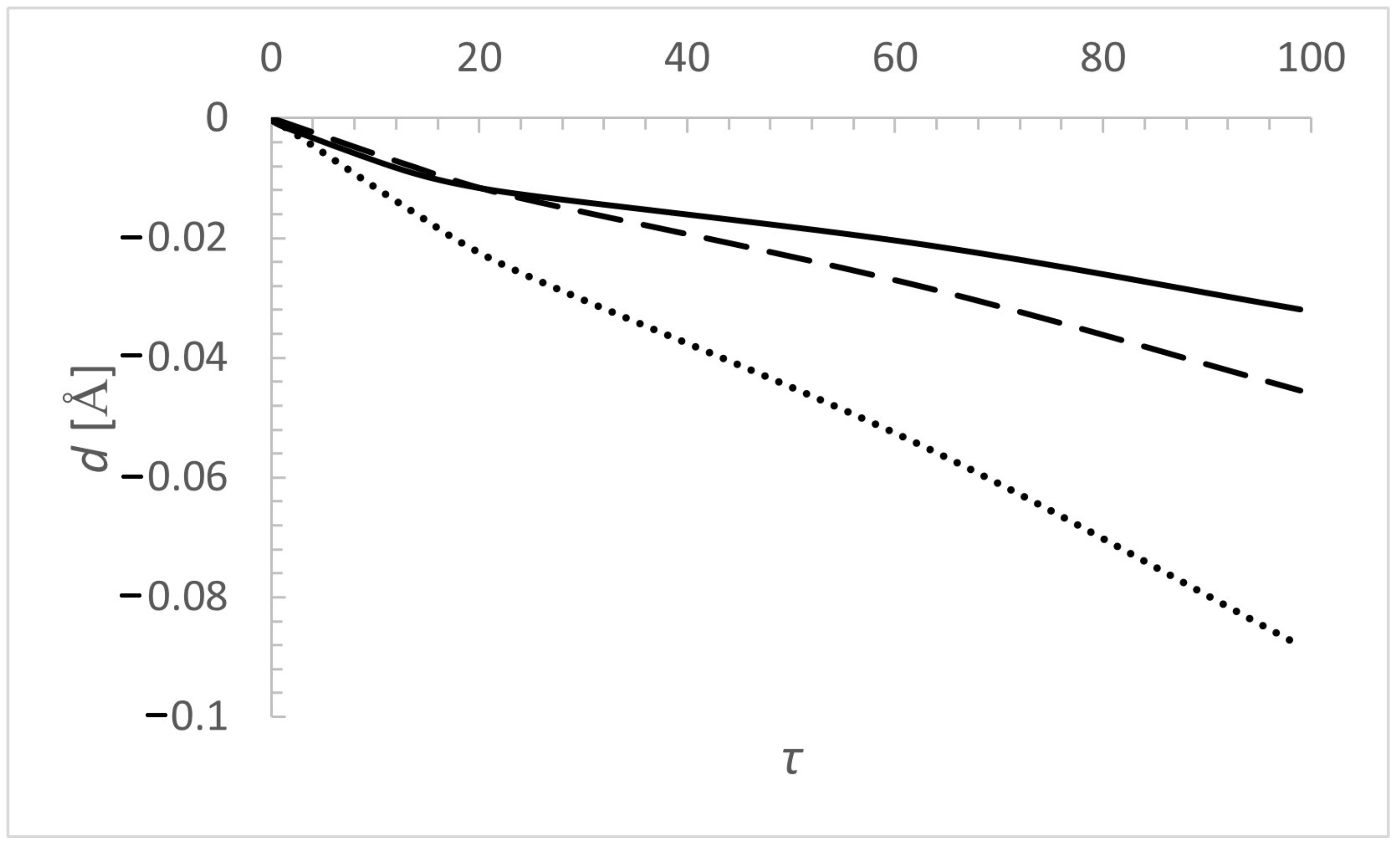
How Stark broadening parameters vary with for N VI 2sS–2pPo 2897.2 Å spectral line is shown in Figure 3 and Figure 4. In this case, Stark width values are notably smaller than for the previous line. In the whole temperature interval the broadening by electrons overcomes these by protons and He III, and also by Doppler width. It increases notably for lower values and varies slowly for 15. Stark widths due to collisions with protons and He III ions are lower than Doppler one for the whole interval. All Stark shift values for this line are negative, the line is blue shifted. Absolute values of the three shifts due to electrons, protons and He III ions increase with . The larger shift is due to He III ions where the difference is notable in comparison with the two others.

Figure 3.
Same as in Figure 1 but for N VI 2sS–2pPo, = 2897.2 Å spectral line.

Figure 4.
Same as in Figure 2 but for N VI 2sS–2pPo, = 2897.2 Å spectral line.
One can see that the Stark width values for the 6993.0 Å line in the red part of the spectrum (with larger wavelength) are larger than for the 2897.2 Å line in the UV (with smaller wavelength). This demonstrates the influence of values. In fact, in the calculations of Stark widths enters as a square while the Doppler width is linear with . Consequently, when increases, the Doppler width increases more slowly than the Stark one.
5. Conclusions
New calculated results for Stark broadening parameters, widths and shifts for 15 N VI multiplets, obtained employing semiclassical perturbation theory [23,24,25] are reported for a number of temperatures from 50,000 K to 2,000,000 K. Stark broadening parameters for N VI spectral lines broadened by collisions with electrons, protons, He III ions, and boron ions B III, B IV, B V and B VI are obtained. With the obtained data, the significance of Stark broadening for a model of DO white dwarf atmosphere with = 60,000 K and log g = 8.0 has been tested. The obtained results confirm that Stark broadening is very important broadening mechanism in the lower parts of DO white dwarf atmospheres, usually dominant, especially for larger vawelengths, towards the red part of the spectrum.
The results for Stark broadening parameters of N VI, published in this article, will also be entered in the STARK-B database (http://stark-b.obspm.fr/, accessed on 1 November 2023) [38,39], which is also a part of the European Virtual Atomic and Molecular Data Center VAMDC (http://www.vamdc.org/, accessed on 1 November 2023) [40,41,42]. The obtained results will be also prepared in VO (Virtual Observatory) and XSAMS (XML Schema for Atomic, Molecular and Solid Data) format for the implementation of results in the international, on-line database STARK-B (Sahal-Bréchot et al., 2015—https://stark-b.obspm.fr/) a part of VAMDC (Virtual Atomic and Molecular Data Center, Dubernet et al., 2010—https://portal.vamdc.org/vamdc_portal/home.seam), after the publication of the main article.
The obtained results are first of all of interest for astrophysical applications such as abundance determination, analysis and synthesis of stellar spectra, stellar atmosphere modelling and radiative transfer calculations, particularly for white dwarfs. They are also significant for proton-boron fusion investigations because the boron nitride BN, as a target for laser radiation, is important in such experiments, so that N VI spectral lines may be used for the diagnostic of created plasma.
Author Contributions
Conceptualization, M.S.D.; methodology, S.S.-B. and M.S.D.; software, S.S.-B. and M.S.D.; validation, M.S.D., M.D.C. and S.S.-B.; formal analysis, M.D.C. and M.S.D.; investigation, M.S.D. and M.D.C.; data curation, M.S.D. and M.D.C.; writing—original draft preparation, M.S.D. and M.D.C.; writing—review and editing, M.S.D. and M.D.C.; visualization, M.D.C.; supervision, S.S.-B. and M.S.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
All obtained data are in the paper.
Acknowledgments
This article/publication is based upon work from COST Action CA21128-PROBONO “PROton BOron Nuclear fusion: from energy production to medical applicatiOns”, supported by COST (European Cooperation in Science and Technology—www.cost.eu, accessed on 1 November 2023). Thanks also to Technical University of Sofia for the provided help. Sylvie Sahal-Bréchot acknowledges the French Research Laboratory LERMA (Paris Observatory and the CNRS UMR 8112) and the “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU, CEA and CNES, France for their support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Beauchamp, A.; Wesemael, F.; Bergeron, P. Spectroscopic Studies of DB White Dwarfs: Improved Stark Profiles for Optical Transitions of Neutral Helium. Astrophys. J. Suppl. Ser. 1997, 108, 559–573. [Google Scholar] [CrossRef]
- Konjević, N. Plasma broadening and shifting of non-hydrogenic spectral lines: Present status and applications. Phys. Rep. 1999, 316, 339–401. [Google Scholar] [CrossRef]
- Griem, H.R. Plasma spectroscopy in inertial confinement fusion and soft X-ray laser research. Phys. Fluids 1992, 4, 2346–2361. [Google Scholar] [CrossRef]
- Iglesias, E.; Griem, H.R.; Welch, B.; Weaver, J. UV Line Profiles of B V from a 10-Ps KrF-Laser-Produced Plasma. Astrophys. Space Sci. 1997, 256, 327–331. [Google Scholar] [CrossRef]
- Wang, J.S.; Griem, H.R.; Huang, Y.W.; Böttcher, F. Measurements of line broadening of B V Hα and Lδ in a laser-produced plasma. Phys. Rev. A 1992, 45, 4010–4014. [Google Scholar] [CrossRef] [PubMed]
- Gornushkin, I.B.; King, L.A.; Smith, B.W.; Omenetto, N.; Winefordner, J.D. Line broadening mechanisms in the low pressure laser-induced plasma. Spectrochim. Acta 1999, 54, 1207–1217. [Google Scholar] [CrossRef]
- Sorge, S.; Wierling, A.; Röpke, G.; Theobald, W.; Suerbrey, R.; Wilhein, T. Diagnostics of a laser-induced dense plasma by hydrogen-like carbon spectra. J. Phys. B 2000, 33, 2983–3000. [Google Scholar] [CrossRef]
- Yilbas, B.S.; Patel, F.; Karatas, C. Laser controlled melting of H12 hot-work tool steel with B4C particles at the surface. Opt. Laser Technol. 2015, 74, 36–42. [Google Scholar] [CrossRef]
- Rauch, T.; Ziegler, M.; Werner, K.; Kruk, J.W.; Oliveira, C.M.; Vande Putte, D.; Mignani, R.P.; Kerber, F. High-resolution FUSE and HST ultraviolet spectroscopy of the white dwarf central star of Sh 2-216. Astron. Astrophys. 2007, 470, 317–329. [Google Scholar] [CrossRef]
- Rauch, T.; Suleimanov, V.; Werner, K. Absorption features in the spectra of X-ray bursting neutron stars. Astron. Astrophys. 2008, 490, 1127–1134. [Google Scholar] [CrossRef][Green Version]
- Fleig, J.; Rauch, T.; Werner, K.; Kruk, J.W. FUSE spectroscopy of the sdOB primary of the post common-envelope binary LB3459 (AADoradus). Astron. Astrophys. 2008, 492, 565–573. [Google Scholar] [CrossRef]
- Nagel, T.; Rauch, T.; Werner, K. A new grid of NLTE accretion-disc models for AMCVn systems: Application to CE 315. Astron. Astrophys. 2009, 499, 773–781. [Google Scholar] [CrossRef]
- Rauch, T.; Orio, M.; Gonzales-Riestra, R.; Nelson, T.; Still, M.; Werner, K.; Wilms, J. Non-local thermal equilibrium model atmospheres for the hottest white dwarfs: Spectral analysis of the compact component in nova V4743 Sgr. Astrophys. J. 2010, 717, 363–371. [Google Scholar] [CrossRef]
- Newman, J.; Tsuruta, S.; Liebmann, A.C.; Kunieda, H.; Haba, Y. Combined Analysis of X-ray Spectra of NGC 3227. Astrophys. J. 2021, 907, 45. [Google Scholar] [CrossRef]
- Ness, J.-U.; Beardmore, A.P.; Bode, M.F.; Darnley, M.J.; Dobrotka, A.; Drake, J.J.; Magdolen, J.; Munari, U.; Osborne, J.P.; Orio, M.; et al. High-resolution X-ray spectra of RS Ophiuchi (2006 and 2021): Revealing the cause of SSS variability. Astron. Astrophys. 2023, 670, A131. [Google Scholar] [CrossRef]
- Rauch, T. White Dwarf Model Atmospheres: Synthetic Spectra for Supersoft Sources. In Proceedings of the IAU Symposium No. 281, Padova, Italy, 4–8 July 2011; Di Stefano, R., Orio, M., Moe, M., Eds.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Sokolovsky, K.V.; Li, K.L.; Lopes de Oliveira, R.; Ness, J.U.; Mukai, K.; Chomiuk, L.; Aydi, E.; Steinberg, E.; Vurm, I.; Metzger, B.D.; et al. The first nova eruption in a novalike variable: YZ Ret as seen in X-rays and γ-rays. Mon. Not. R. Astron. Soc. 2022, 514, 2239–2258. [Google Scholar] [CrossRef]
- Jansen, F.; Lumb, D.; Altieri, B.; Clavel, J.; Ehle, M.; Erd, C.; Gabriel, C.; Guainazzi, M.; Gondoin, P.; Much, R.; et al. XMM-Newton observatory. I. The spacecraft and operations. Astron. Astrophys. 2001, 365, L1–L6. [Google Scholar] [CrossRef]
- Batani, K. Perspectives on research on laser driven proton-boron fusion and applications. J. Instrum. 2023, 18, C09012. [Google Scholar] [CrossRef]
- Schollmeier, M.S. Investigation of Proton Beam-Driven Fusion Reactions Generated by an Ultra-Short Petawatt-Scale Laser Pulse. Laser Part. Beams 2022, 2404263. [Google Scholar] [CrossRef]
- Hegelich, B.M.; Labun, L.O.; Labun, Z.; Mehlhorn, T.A. Photon and Neutron Production as In Situ Diagnostics of Proton-Boron Fusion. Laser Part. Beams 2023, 6924841. [Google Scholar] [CrossRef]
- Kong, D.; Xu, S.; Shou, Y.; Gao, Y.; Mei, Z.; Pan, Z.; Liu, Z.; Cao, Z.; Liang, Y.; Peng, Z.; et al. Alpha-Particle Generation from H-11B Fusion Initiated by Laser-Accelerated Boron Ions. Laser Part. Beams 2022, 2022, 5733475. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S.; Dimitrijević, M.S.; Ben Nessib, N. Widths and Shifts of Isolated Lines of Neutral and Ionized Atoms Perturbed by Collisions with Electrons and Ions: An Outline of the Semiclassical Perturbation (SCP) Method and of the Approximations Used for the Calculations. Atoms 2014, 2, 225–252. [Google Scholar] [CrossRef]
- Sahal–Bréchot, S. Impact Theory of the Broadening and Shift of Spectral Lines due to Electrons and Ions in a Plasma. Astron. Astrophys. 1969, 1, 91–123. [Google Scholar]
- Sahal–Bréchot, S. Impact Theory of the Broadening and Shift of Spectral Lines due to Electrons and Ions in a Plasma (Continued). Astron. Astrophys. 1969, 2, 322–354. [Google Scholar]
- Sahal–Bréchot, S. The Semiclassical Limit of the Gailitis Formula Applied to Electron Impact Broadening of Spectral Lines of Ionized Atoms. Atoms 2021, 9, 29. [Google Scholar] [CrossRef]
- Kelly, R.L. Atomic and Ionic Spectrum Lines Below 2000 Angstroms: Hydrogen through Krypton. J. Phys. Chem. Ref. Data 1987, 16 (Suppl. S1), 1–1698, Erratum: J. Phys. Chem. Ref. Data 1998, 17, 953. [Google Scholar]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Ver. 5.10); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022. Available online: https://physics.nist.gov/asd (accessed on 30 October 2023).
- Bates, D.R.; Damgaard, A. The Calculation of the Absolute Strengths of Spectral Lines. Philos. Trans. R. Soc. Lond. Ser. A 1949, 242, 101–122. [Google Scholar]
- Oertel, G.K.; Shomo, L.P. Tables for the Calculation of Radial Multipole Matrix Elements by the Coulomb Approximation. Astrophys. J. Suppl. Ser. 1968, 16, 175–218. [Google Scholar] [CrossRef]
- Van Regemorter, H.; Dy Hoang, B.; Prud’homme, M. Radial transition integrals involving low or high effective quantum numbers in the Coulomb approximation. J. Phys. B 1979, 12, 1053–1061. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Sahal-Bréchot, S. Stark broadening of neutral helium lines. J. Quant. Spectrosc. Radiat. Transf. 1984, 31, 301–313. [Google Scholar] [CrossRef]
- Dimitrijević, M.S. Electron-impact widths of four- and five-times charged ion lines of astrophysical importance. Astron. Astrophys. Suppl. Ser. 1993, 100, 237–241. [Google Scholar]
- Dimitrijević, M.S.; Konjević, N. Stark widths of doubly- and triply-ionized atom lines. J. Quant. Spectrosc. Radiat. Transf. 1980, 24, 451–459. [Google Scholar] [CrossRef]
- Dimitrijević, M.S. Stark widths of fourtly and fifthly charged ion lines. Astrophys. Lett. Commun. 1993, 28, 385–388. [Google Scholar]
- Griem, H.R. Spectral line Broadening by Plasmas; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
- Wesemael, F. Atmospheres for hot, high-gravity stars. II. Pure helium models. Astrophys. J. Suppl. Ser. 1981, 45, 177–257. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S.; Dimitrijević, M.S.; Moreau, N.; Ben Nessib, N. The STARK-B database VAMDC node: A repository for spectral line broadening and shifts due to collisions with charged particles. Phys. Scr. 2015, 90, 054008. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S.; Dimitrijević, M.S.; Moreau, N. STARK-B Database. Available online: http://stark-B.obspm.fr (accessed on 30 October 2023).
- Dubernet, M.L.; Boudon, V.; Culhane, J.L.; Dimitrijevic, M.S.; Fazliev, A.Z.; Joblin, C.; Kupka, F.; Leto, G.; Le Sidaner, P.; Loboda, P.A.; et al. Virtual atomic and molecular data centre. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 2151–2159. [Google Scholar] [CrossRef]
- Dubernet, M.L.; Antony, B.K.; Ba, Y.A.; Babikov, Y.L.; Bartschat, K.; Boudon, V.; Braams, B.J.; Chung, H.K.; Daniel, F.; Delahaye, F.; et al. The virtual atomic and molecular data centre (VAMDC) consortium. J. Phys. B 2016, 49, 074003. [Google Scholar] [CrossRef]
- Albert, D.; Antony, B.K.; Ba, Y.A.; Babikov, Y.L.; Bollard, P.; Boudon, V.; Delahaye, F.; Del Zanna, G.; Dimitrijević, M.S.; Drouin, B.J.; et al. A Decade with VAMDC: Results and Ambitions. Atoms 2020, 8, 76. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).