Geodesic Structure of Generalized Vaidya Spacetime through the K-Essence
Abstract
:1. Introduction
2. Summary of the Relation between K-Essence and Generalized Vaidya Spacetime
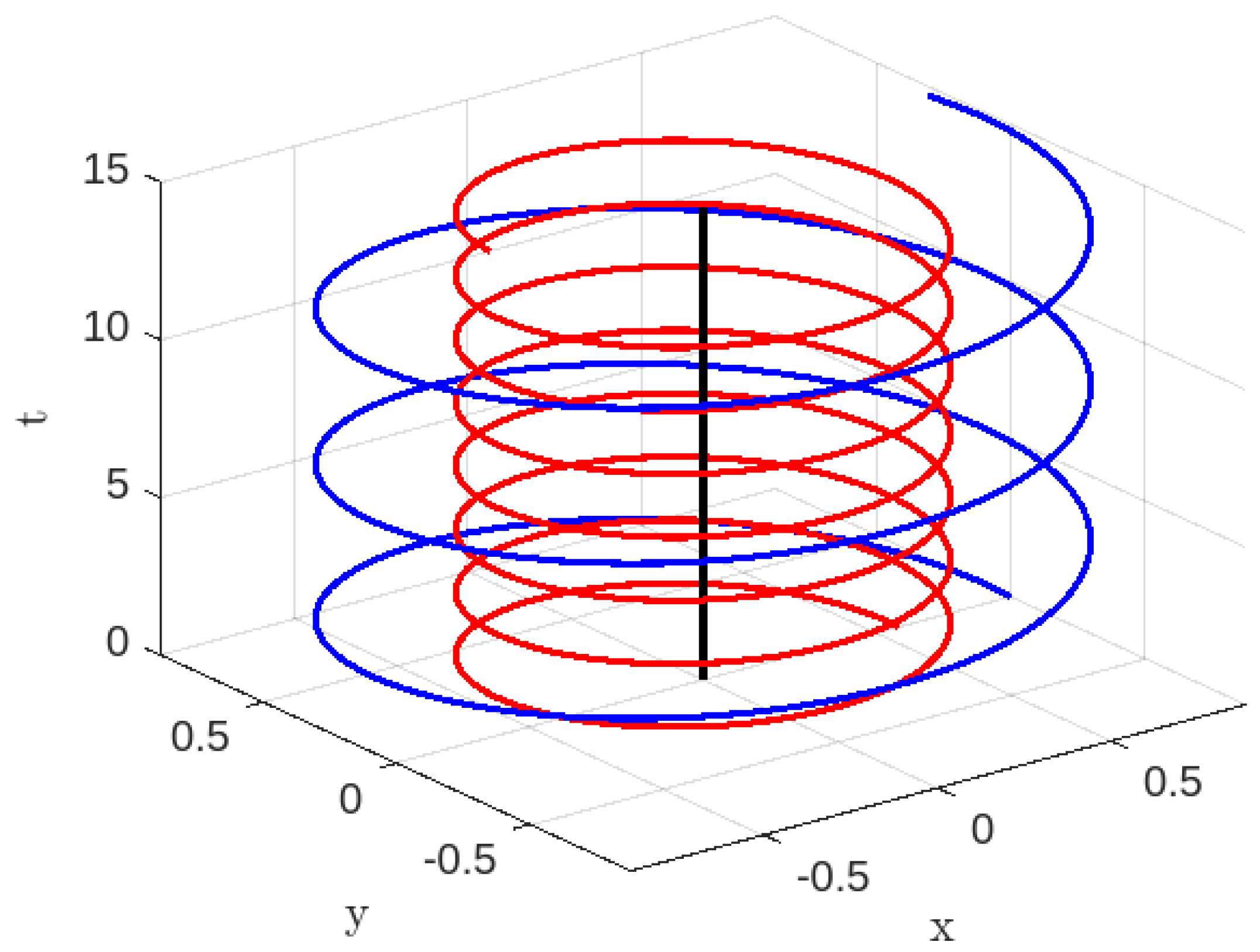
3. Geodesics for the Generalized K-Essence Vaidya Spacetime
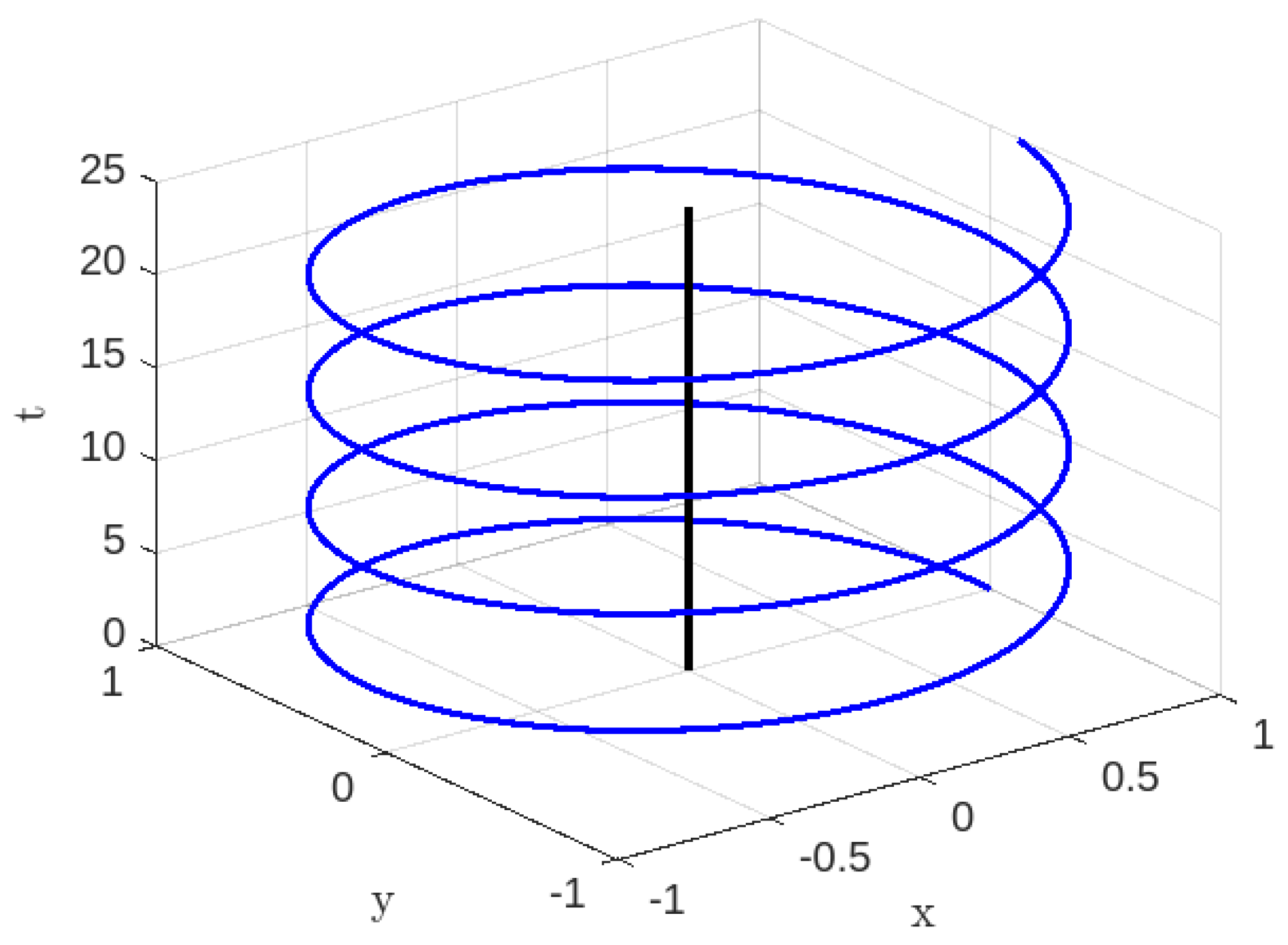
3.1. Case-I:
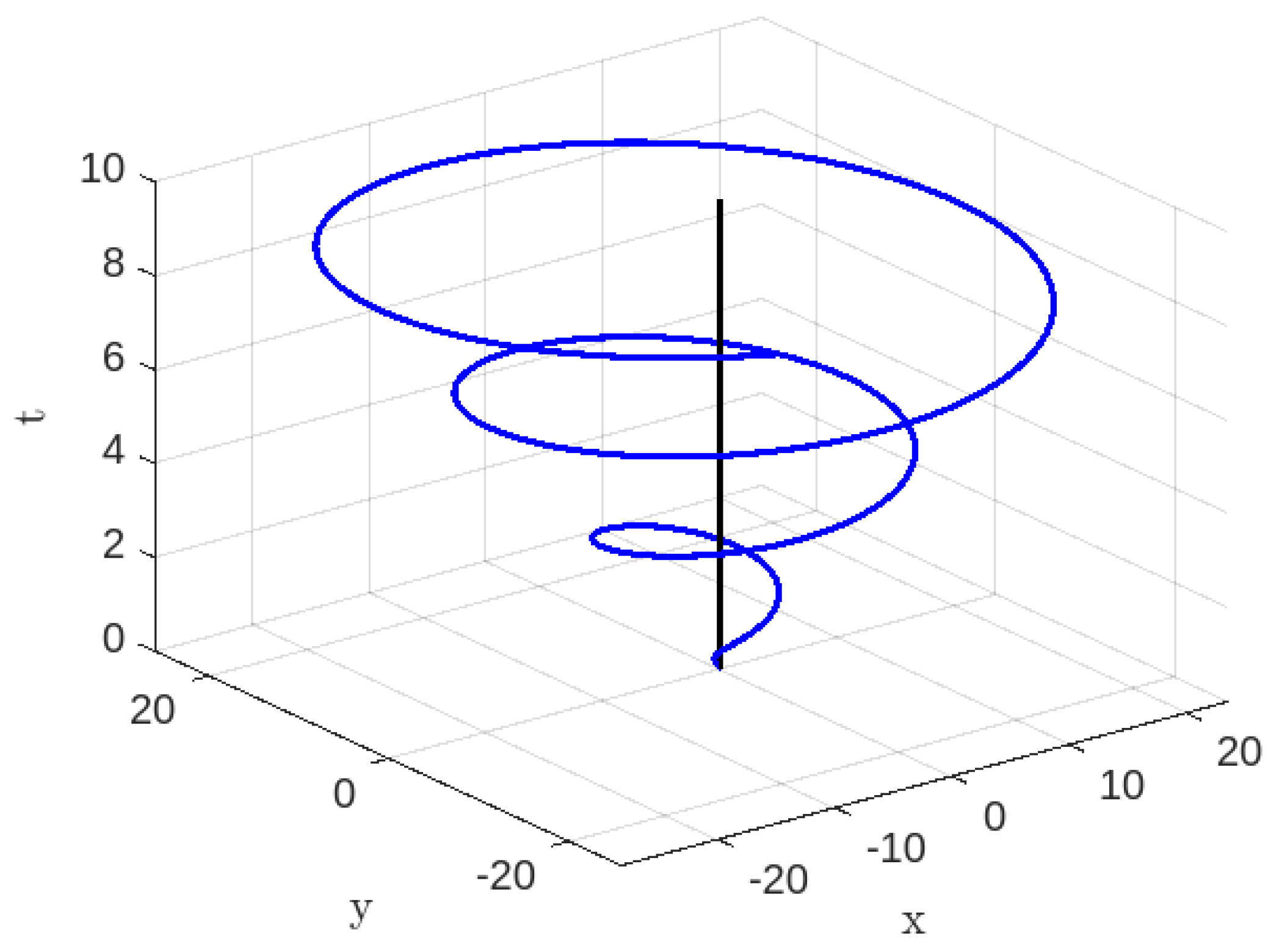
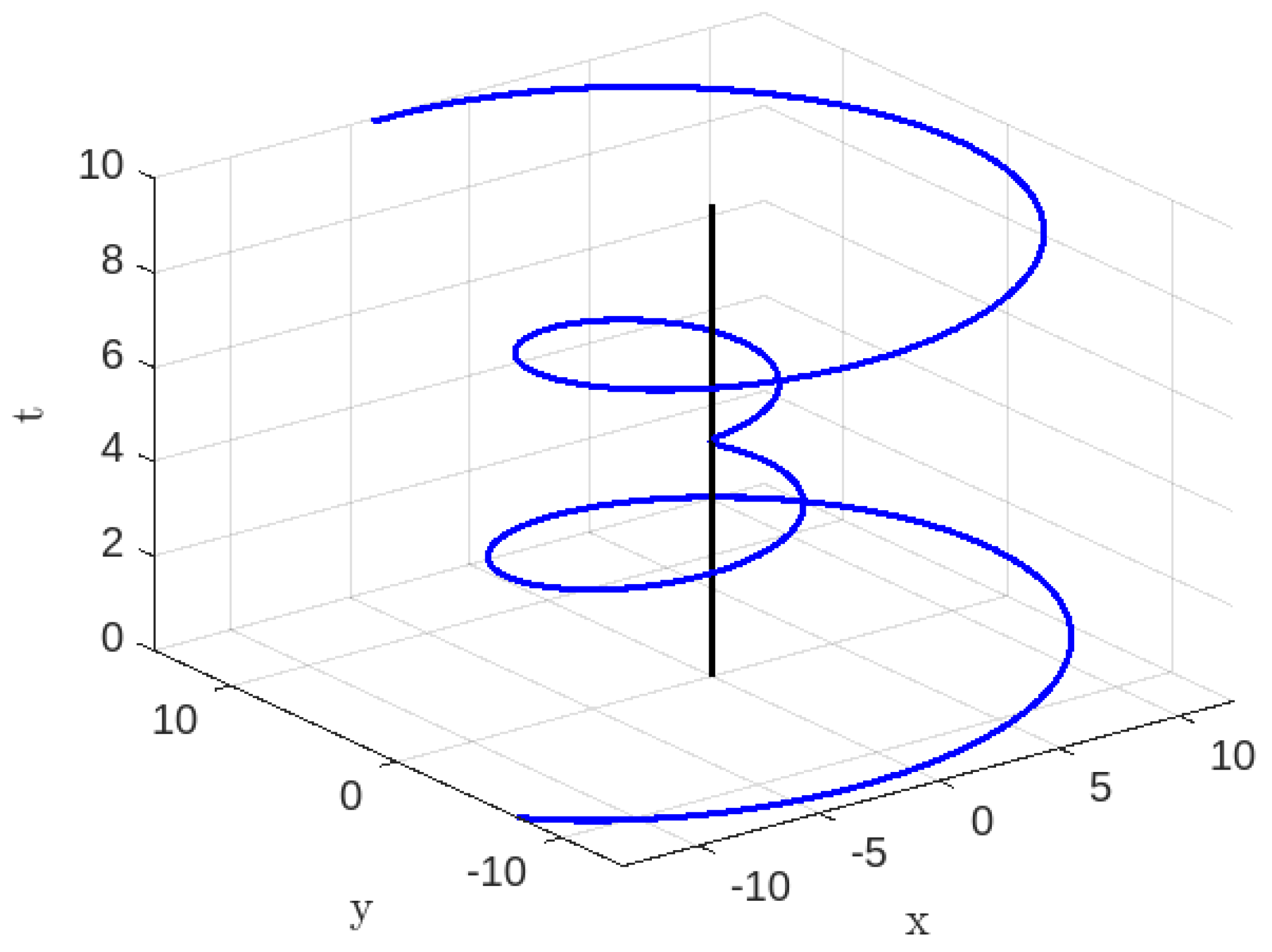
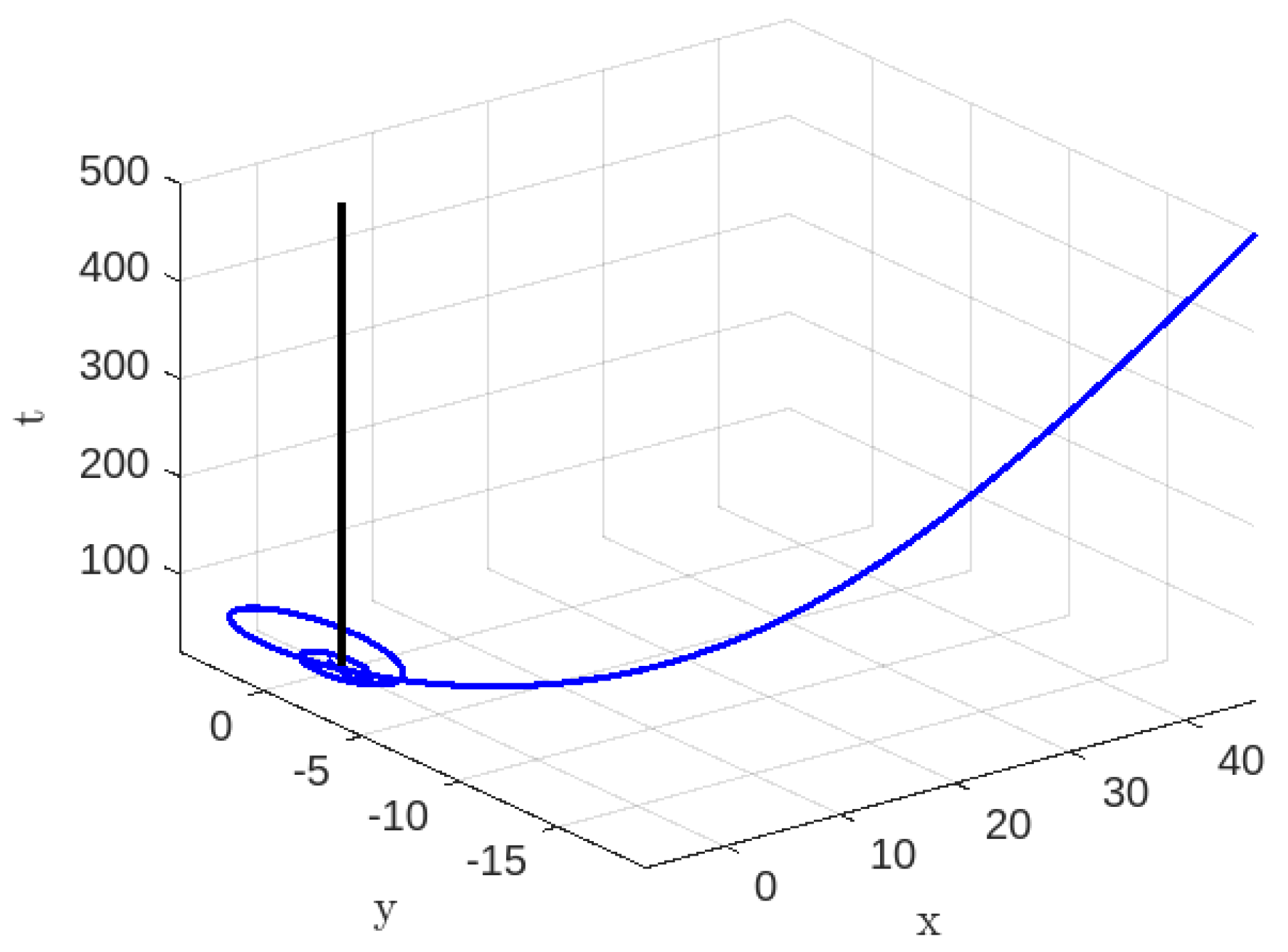
3.1.1. Time-like Geodesics for Case-I
3.1.2. Null Geodesics for Case-I
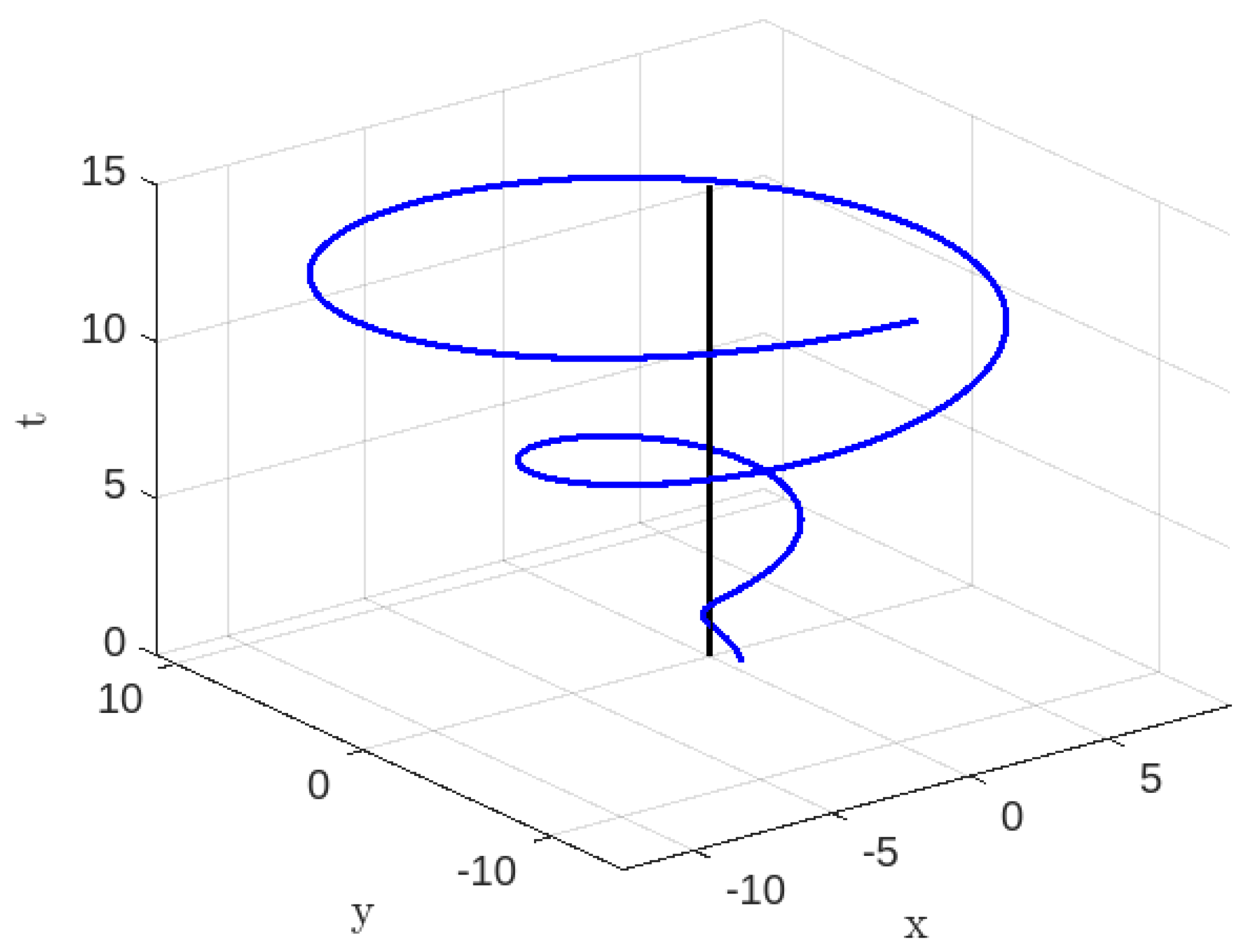
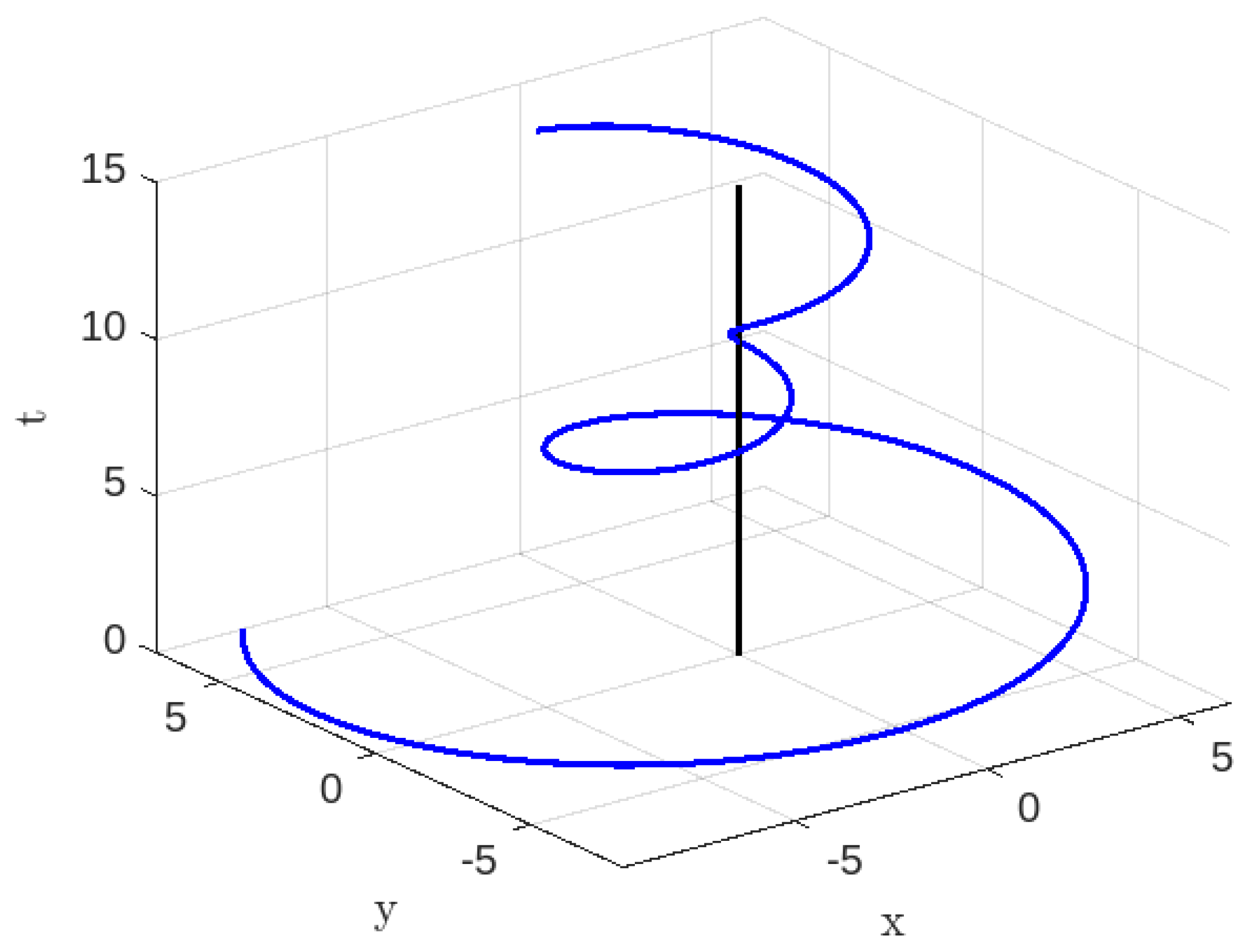
3.2. Case-II:
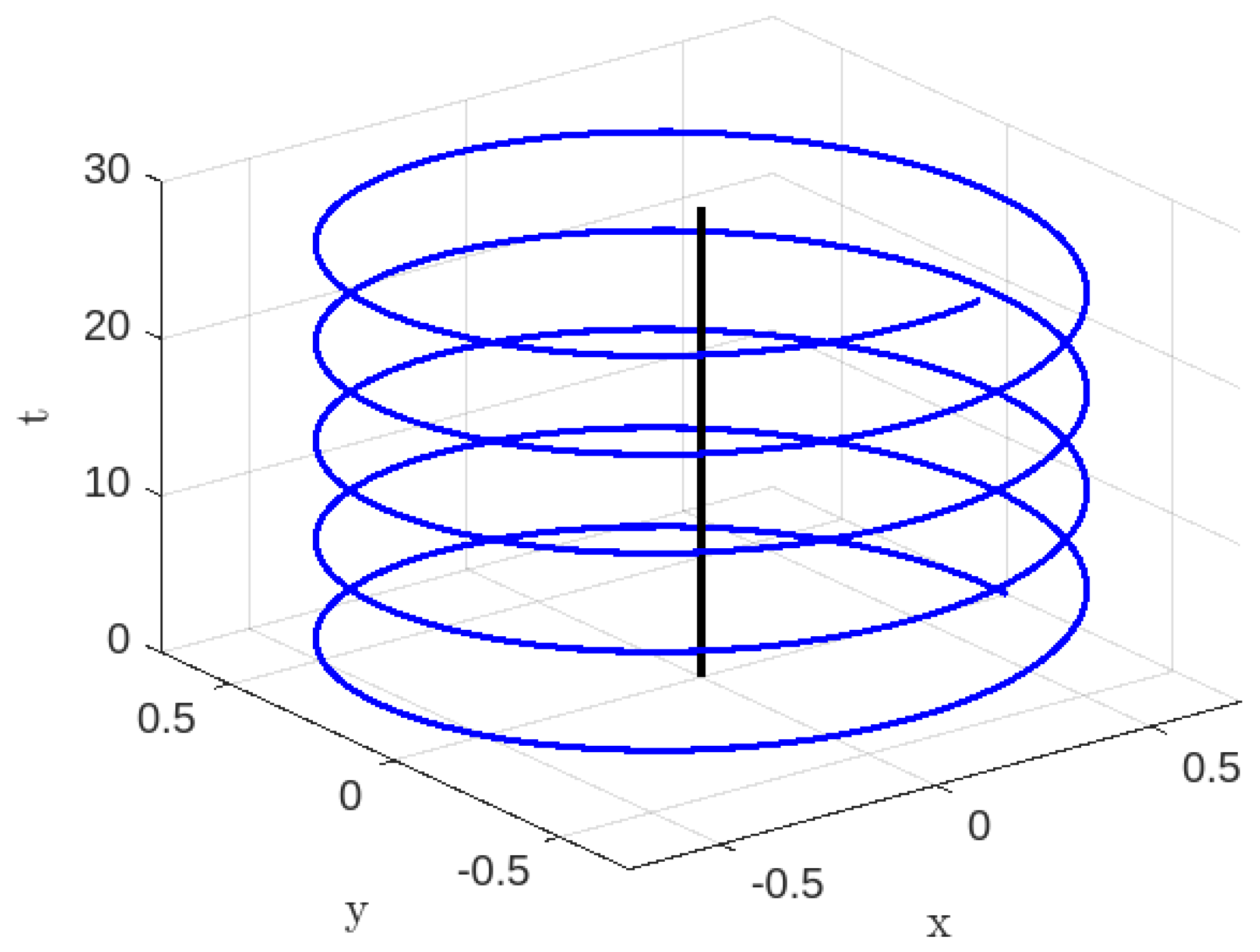
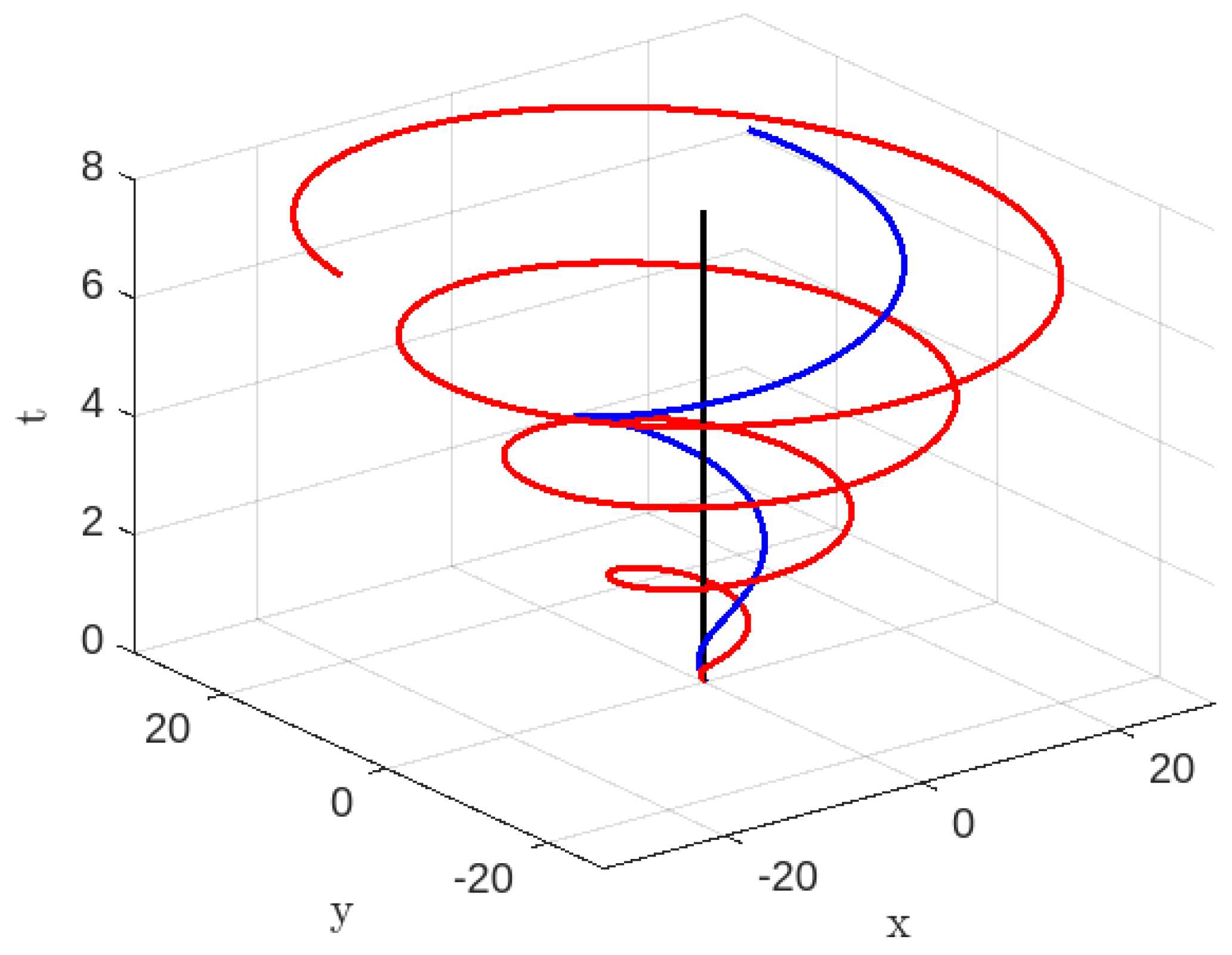
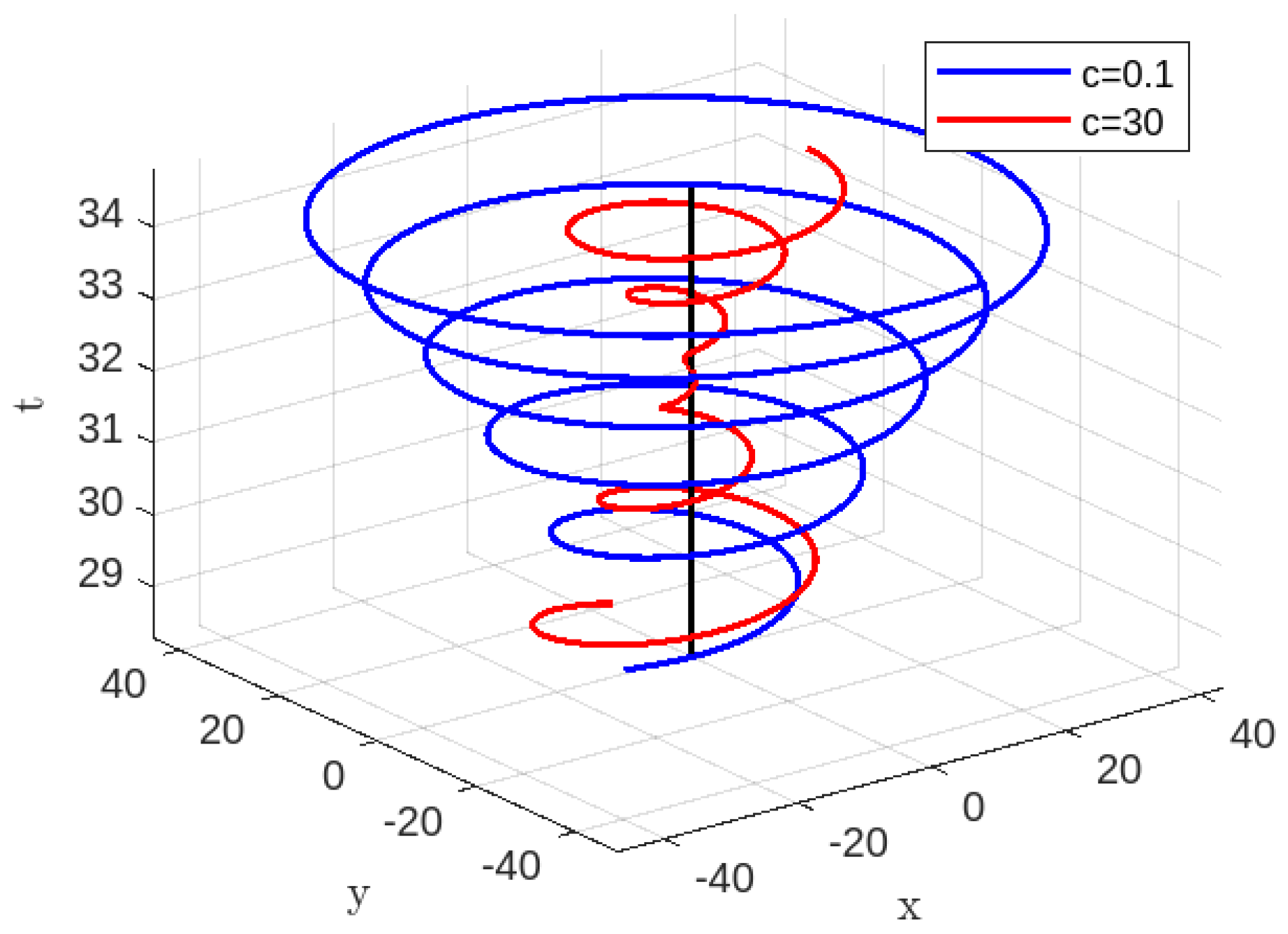
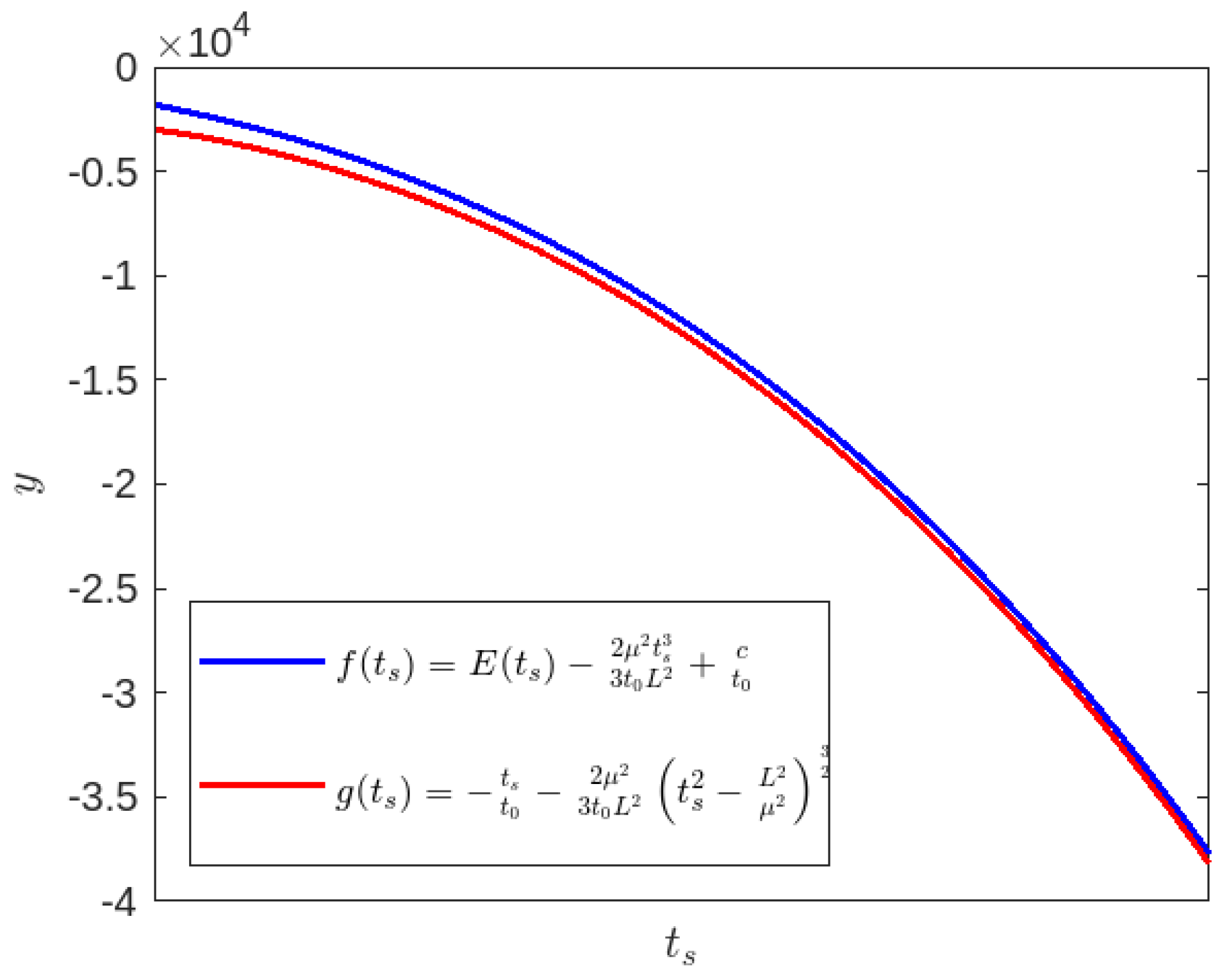
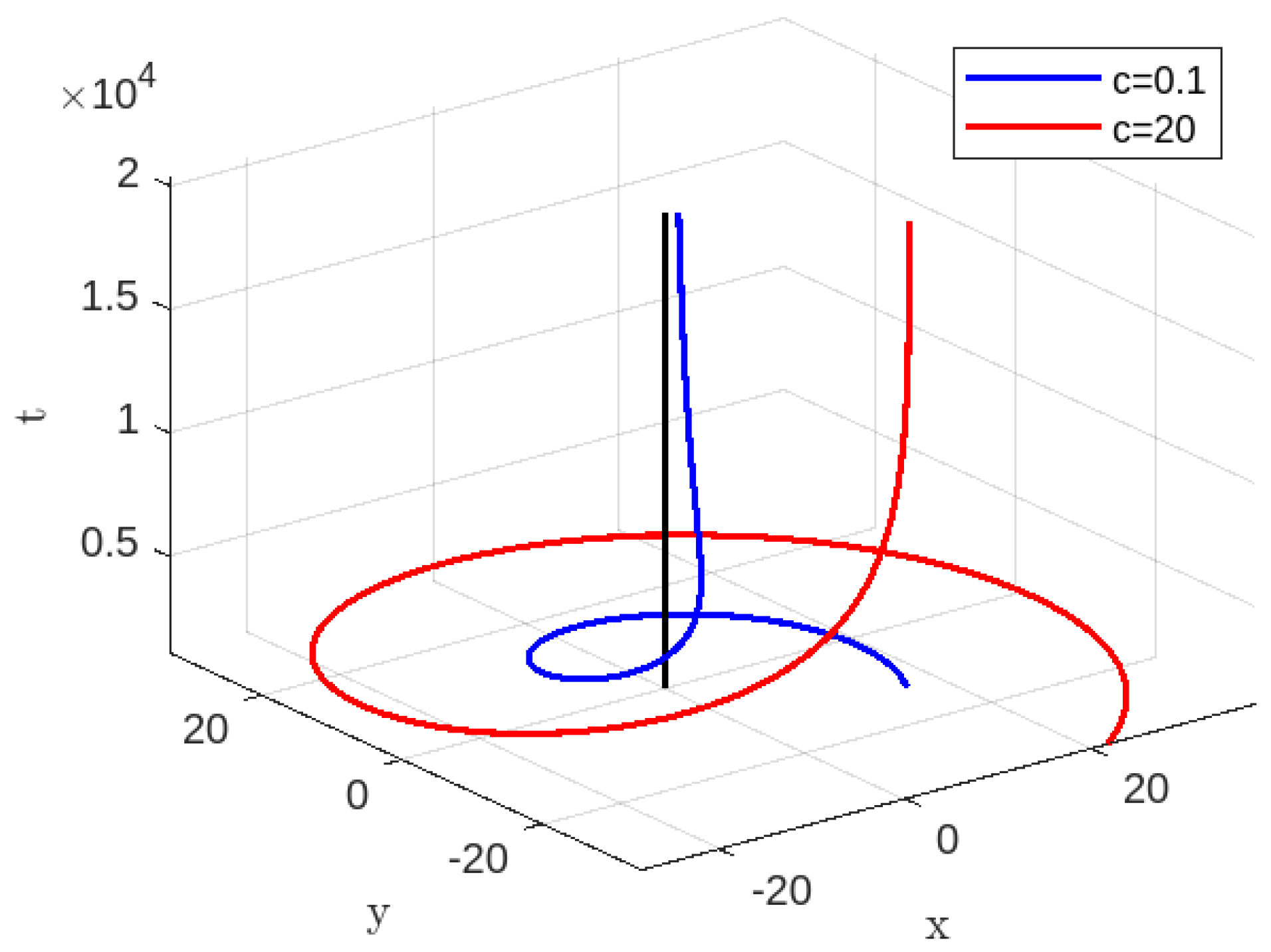
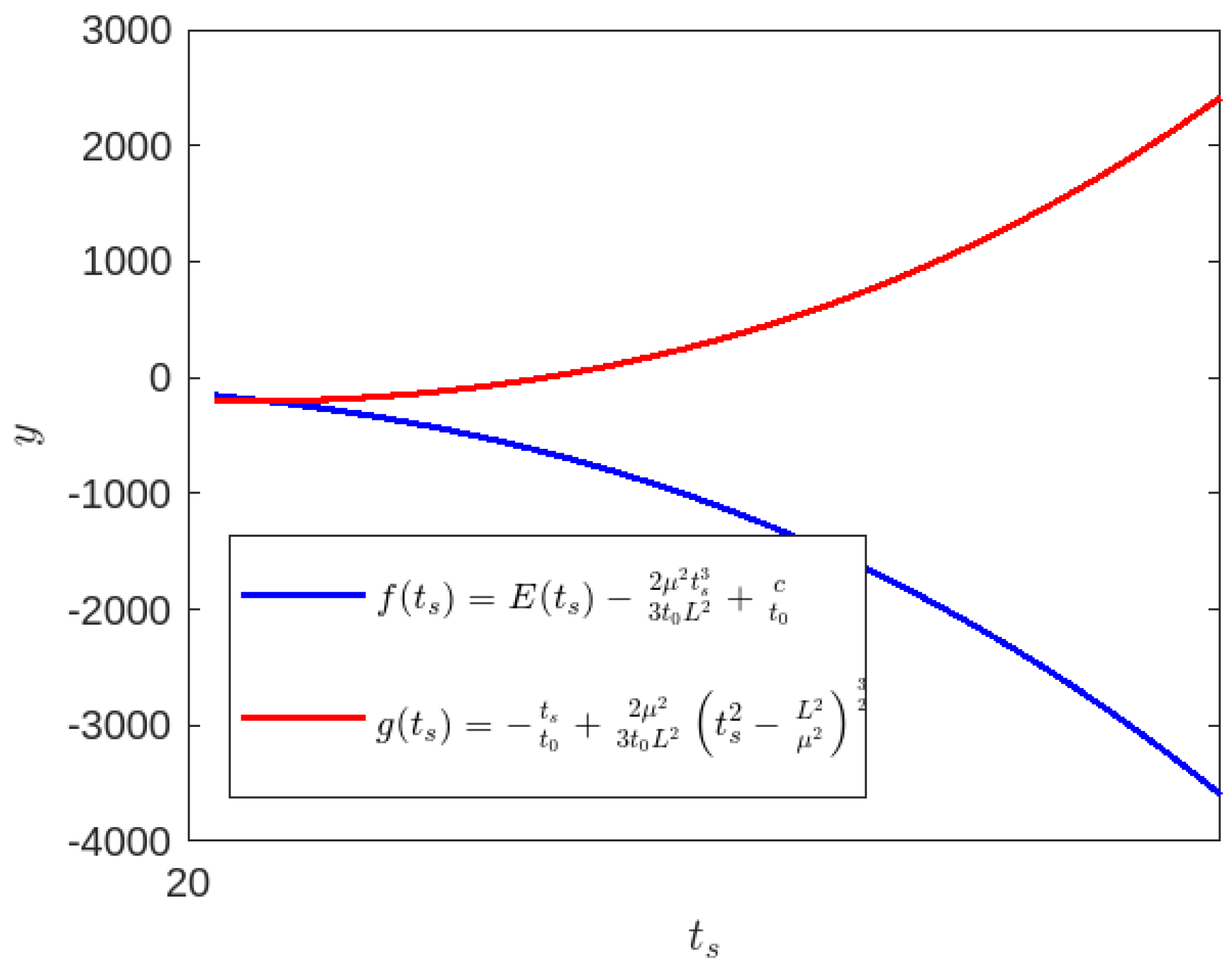
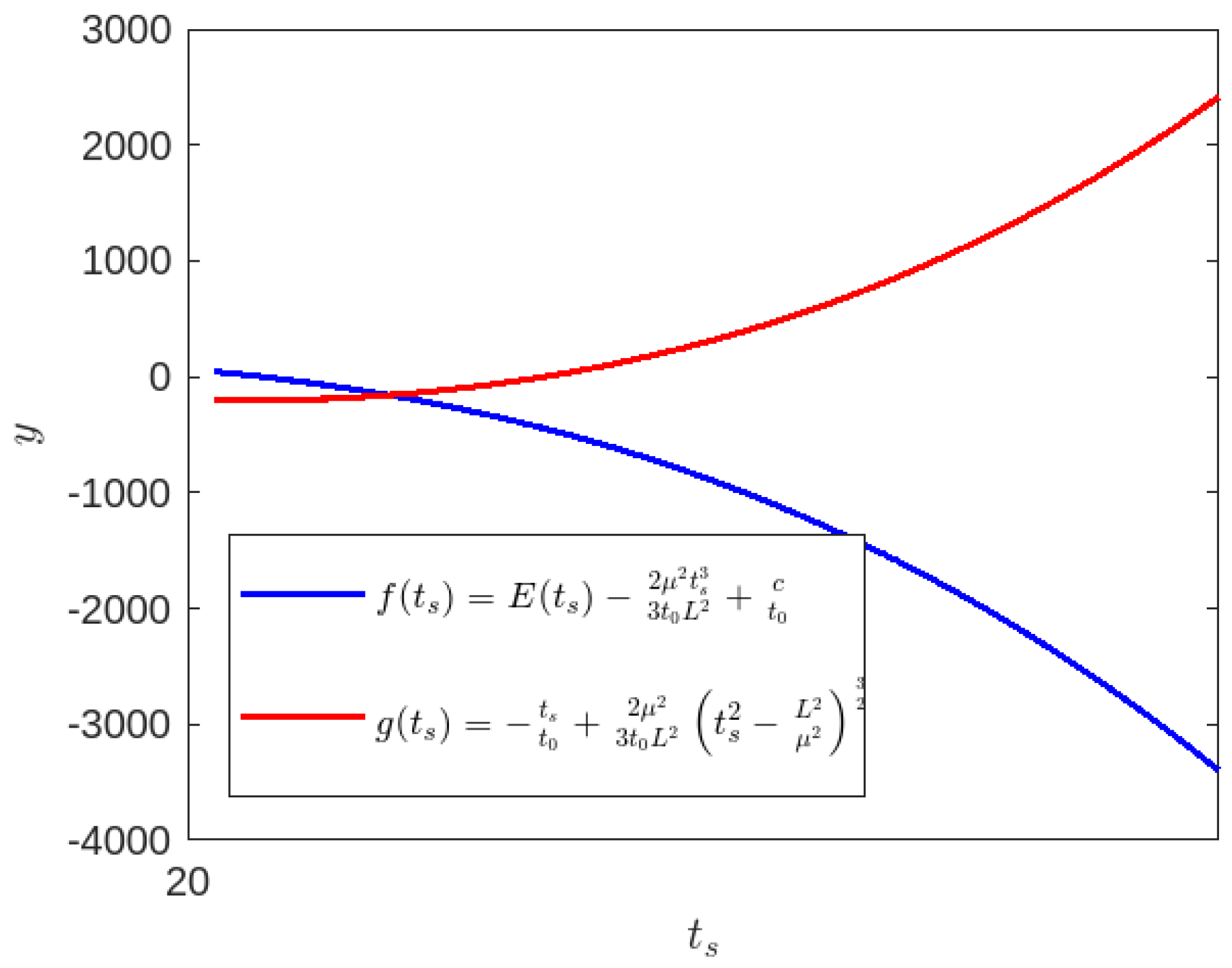
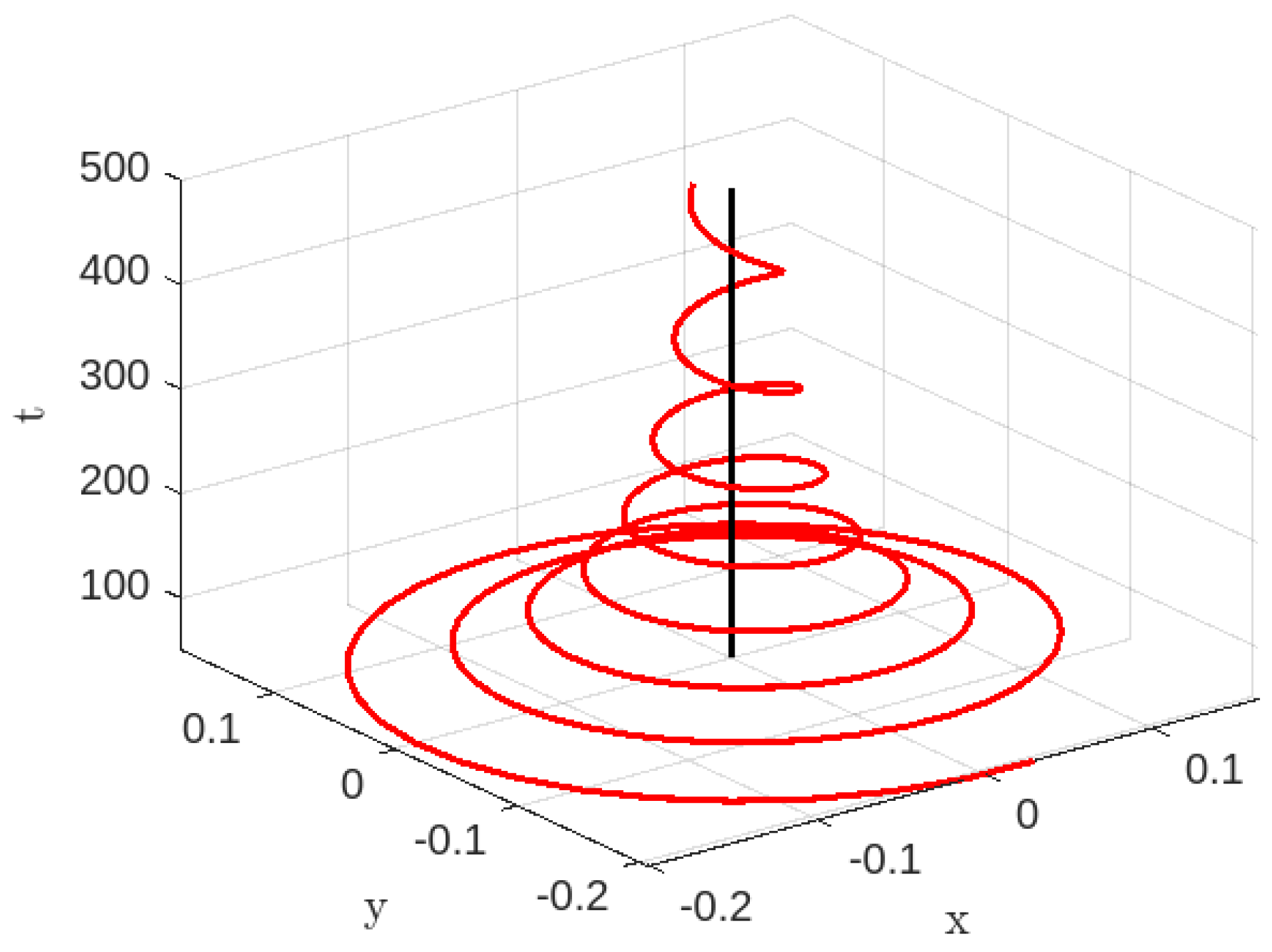
3.2.1. Time-like Geodesics for Case-II
3.2.2. Null Geodesics for Case-II
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
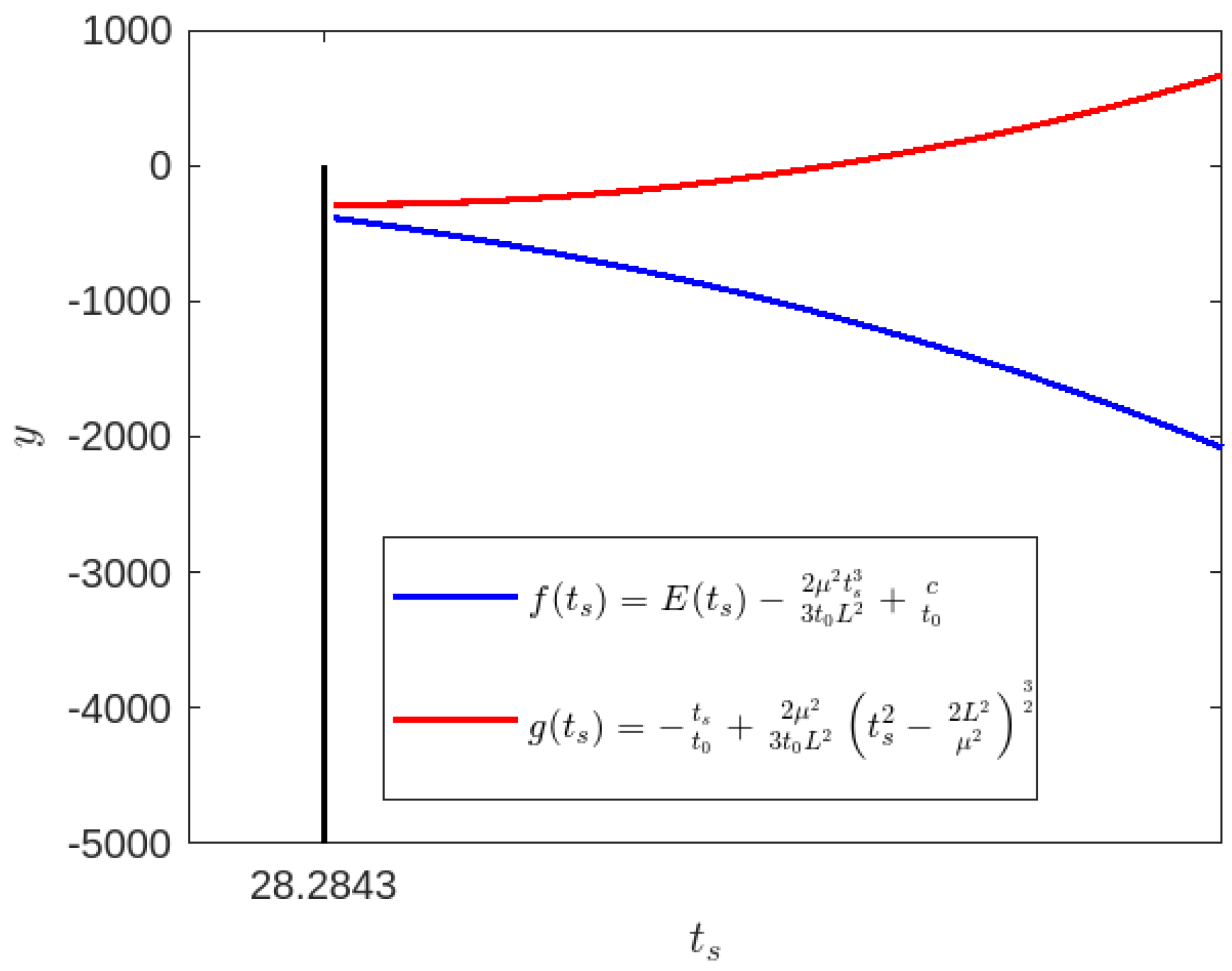
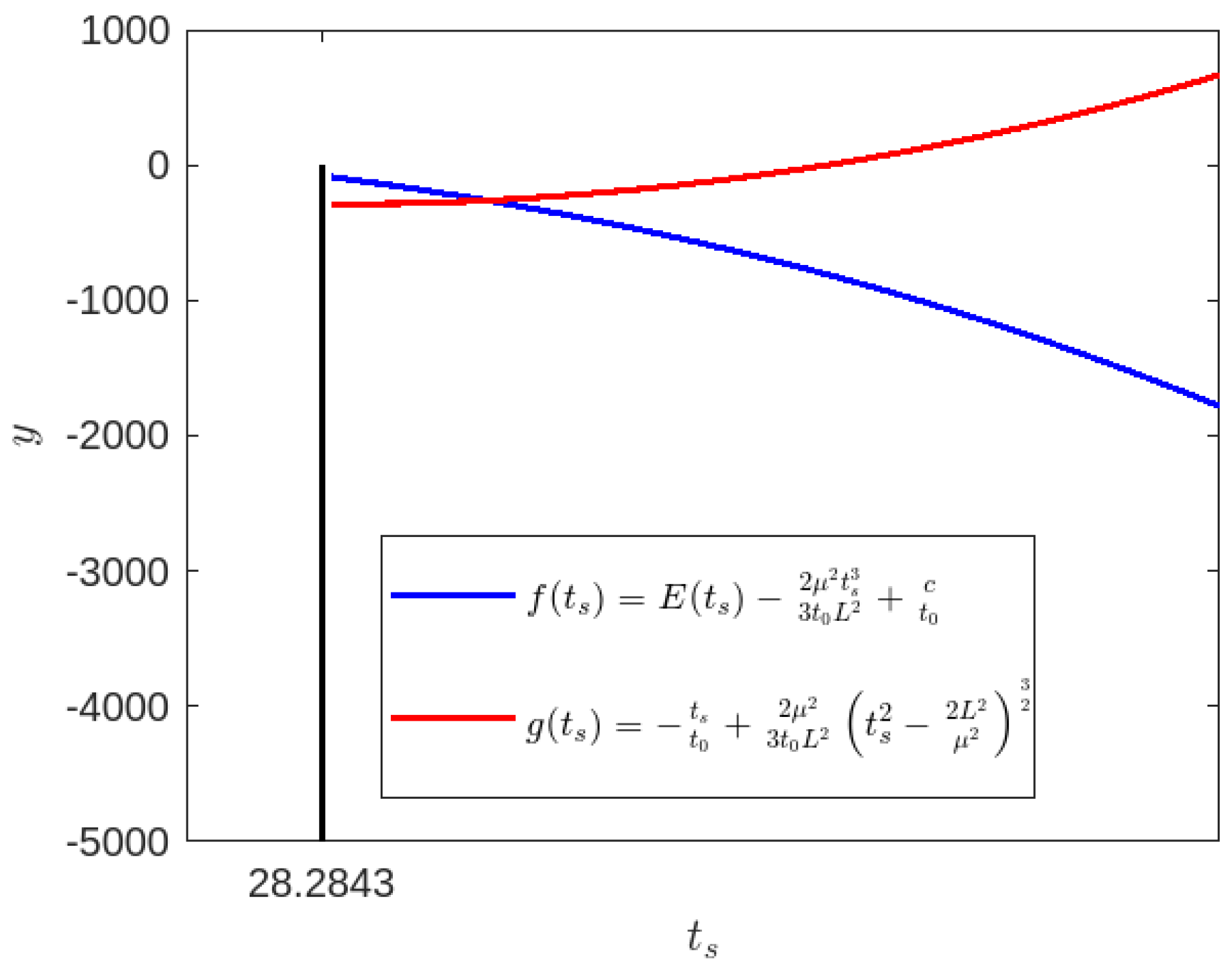
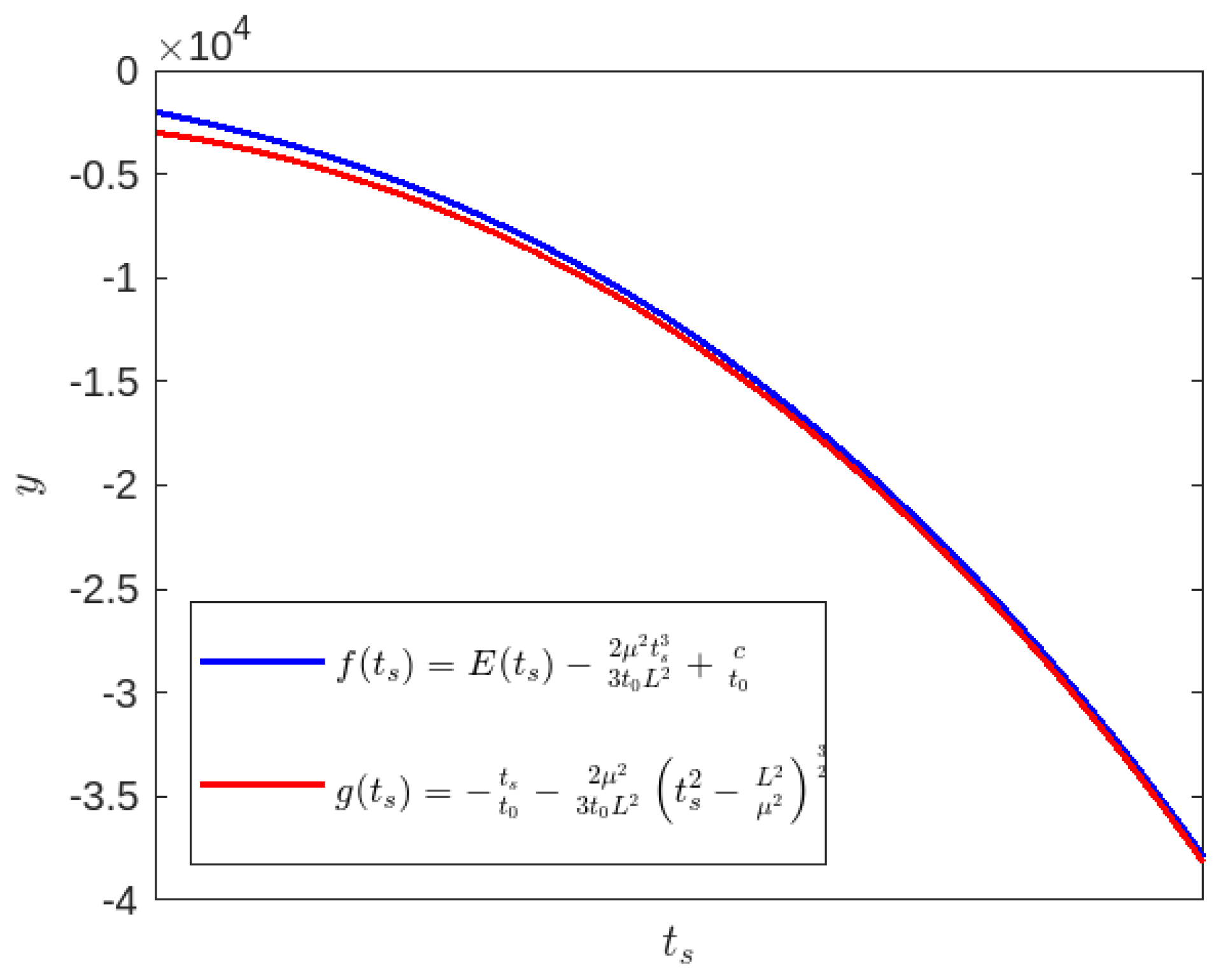
Appendix A. Radius of the Dynamical Horizon
Detail Derivation
References
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Indian Edition 2010; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Cruz, N.; Olivares, M.; Saavedra, J.; Villanueva, J.R. The geodesic structure of the Schwarzschild anti-de Sitter black hole. Class. Quantum Grav. 2005, 22, 1167–1190. [Google Scholar] [CrossRef]
- Berti, E. A Black-Hole Primer: Particles, Waves, Critical Phenomena and Superradiant Instabilities. arXiv 2014, arXiv:1410.4481. [Google Scholar]
- Gibbons, G.W. The Jacobi metric for timelike geodesics in static spacetimes. Class. Quantum Grav. 2016, 33, 025004. [Google Scholar] [CrossRef]
- Chanda, S.; Gibbons, G.W.; Guha, P. Jacobi-Maupertuis-Eisenhart metric and geodesic flows. J. Math. Phys. 2017, 58, 032503. [Google Scholar] [CrossRef]
- Eisenhart, L.P. Dynamical Trajectories and Geodesics. Ann. Math. Second Ser. 1928, 30, 591–606. [Google Scholar] [CrossRef]
- Duval, C.; Burdet, G.; Künzle, H.P.; Perrin, M. Bargmann structures and Newton-Cartan theory. Phy. Rev. D 1985, 31, 1841. [Google Scholar] [CrossRef]
- Majumder, B.; Manna, G.; Das, A. Time-like geodesic structure for the emergent Barriola–Vilenkin type spacetime. Class. Quantum Grav. 2020, 37, 115002. [Google Scholar] [CrossRef]
- Barriola, M.; Vilenkin, A. Gravitational field of a global monopole. Phys. Rev. Lett. 1989, 63, 341. [Google Scholar] [CrossRef]
- Gangopadhyay, D.; Manna, G. The Hawking temperature in the context of dark energy. Europhys. Lett. 2012, 100, 49001. [Google Scholar] [CrossRef]
- Vaidya, P.C. The gravitational field of a radiating star. Proc. Indian Acad. Sci. Sect. A 1951, 33, 264. [Google Scholar] [CrossRef]
- Joshi, P.S. Gravitational collapse: The story so far. Pramana J. Phys. 2000, 55, 529. [Google Scholar] [CrossRef]
- Joshi, P.S. Global Aspects in Gravitation and Cosmology; Clarendon: Oxford, UK, 1993. [Google Scholar]
- Joshi, P.S.; Dwivedi, I.H. Naked singularities in spherically symmetric inhomogeneous Tolman-Bondi dust cloud collapse. Phys. Rev. D 1993, 47, 5357. [Google Scholar] [CrossRef] [PubMed]
- Joshi, P.S.; Dwivedi, I.H. The structure of naked singularity in self-similar gravitational collapse: II. Commun. Math. Phys. 1992, 146, 333. [Google Scholar] [CrossRef]
- Joshi, P.S.; Singh, T.P. Role of initial data in the gravitational collapse of inhomogeneous dust. Phys. Rev. D 1995, 51, 6778. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Snyder, H. On Continued Gravitational Contraction. Phys. Rev. 1939, 56, 455. [Google Scholar] [CrossRef]
- Malafarina, D. Classical Collapse to Black Holes and Quantum Bounces: A Review. Universe 2017, 3, 48. [Google Scholar] [CrossRef]
- Dwivedi, I.H.; Joshi, P.S. On the nature of naked singularities in Vaidya spacetimes: II. Class. Quantum Gravit. 1989, 6, 1599. [Google Scholar] [CrossRef]
- Papapetrou, A. A Random Walk in Relativity and Cosmology; Dadhich, N., Rao, J.K., Narlikar, J.V., Vishveshwara, C.V., Eds.; John Wiley and Sons: New York, NY, USA, 1985; p. 184. [Google Scholar]
- Penrose, R. Gravitational Collapse: The Role of General Relativity. Riv. Nuovo Cim. 1969, 1, 252. Available online: https://ui.adsabs.harvard.edu/abs/1969NCimR...1..252P/abstract (accessed on 3 April 2023).
- Penrose, R. “Golden Oldie”: Gravitational Collapse: The Role of General Relativity. Gen. Rel. Grav. 2002, 34, 1141. [Google Scholar] [CrossRef]
- Vertogradov, V. Gravitational collapse of Vaidya spacetime. Int. J. Mod. Phys. Conf. Ser. 2016, 41, 1660124. [Google Scholar] [CrossRef]
- Vaidya, P.C. Nonstatic Solutions of Einstein’s Field Equations for Spheres of Fluids Radiating Energy. Phys. Rev. 1951, 83, 1. [Google Scholar] [CrossRef]
- Vaidya, P.C.; Pandya, I.M. Gravitational Field of a Radiating Spheroid. Prog. Theor. Phys. 1966, 35, 1. [Google Scholar] [CrossRef]
- Vaidya, P.C. Nonstatic Analogs of Schwarzschild’s Interior Solution in General Relativity. Phys. Rev. 1968, 174, 5. [Google Scholar] [CrossRef]
- Vaidya, P.C. An Analytical Solution for Gravitational Collapse with Radiation. APJ 1966, 144, 943. [Google Scholar] [CrossRef]
- Vaidya, P.C. The External Field of a Radiating Star in General Relativity. Gen. Rel. Grav. 1999, 31, 119. [Google Scholar] [CrossRef]
- Griffiths, J.B.; Podolsky, J. Exact Space-Times in Einstein’s General Relativity; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Husain, V. Exact solutions for null fluid collapse. Phys. Rev. D 1996, 53, 4. [Google Scholar] [CrossRef]
- Wang, A.; Wu, Y. LETTER: Generalized Vaidya Solutions. Gen. Rel. Grav. 1999, 31, 107. Available online: https://www.springer.com/journal/10714 (accessed on 3 April 2023). [CrossRef]
- Mkenyeleye, M.D.; Goswami, R.; Maharaj, S.D. Collapsing spherical stars in f(R) gravity. Phys. Rev. D 2014, 90, 064034. [Google Scholar] [CrossRef]
- Patil, K.D. Gravitational collapse in higher-dimensional charged-Vaidya space-time. Pramana—J. Phys. 2003, 60, 423. [Google Scholar] [CrossRef]
- Coudray, A.; Nicolas, J.P. Geometry of Vaidya spacetimes. Gen. Rel. Gravit. 2021, 53, 73. [Google Scholar] [CrossRef]
- Vertogradov, V. The structure of the generalized Vaidya space–time containing the eternal naked singularity. Int. J. Mod. Phys. A 2022, 37, 2250185. [Google Scholar] [CrossRef]
- Solanki, J.; Perlick, V. Photon sphere and shadow of a time-dependent black hole described by a Vaidya metric. Phys. Rev. D 2022, 105, 064056. [Google Scholar] [CrossRef]
- Manna, G.; Majumdar, P.; Majumder, B. k-essence emergent spacetime as a generalized Vaidya geometry. Phys. Rev. D 2020, 101, 124034. [Google Scholar] [CrossRef]
- Manna, G. Gravitational collapse for the K-essence emergent Vaidya spacetime. Eur. Phys. J. C 2020, 80, 813. [Google Scholar] [CrossRef]
- Majumder, B.; Ray, S.; Manna, G. Evaporation of Dynamical Horizon with the Hawking Temperature in the K-essence Emergent Vaidya Spacetime. Fortschr. Phys. 2023, 71, 2300133. [Google Scholar] [CrossRef]
- Sawayama, S. Evaporating dynamical horizon with the Hawking effect in Vaidya spacetime. Phys. Rev. D 2006, 73, 064024. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V. k-Inflation. Phys. Lett. B 1999, 458, 209–218. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. Dynamical Solution to the Problem of a Small Cosmological Constant and Late-Time Cosmic Acceleration. Phys. Rev. Lett. 2000, 85, 4438. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. Essentials of k-essence. Phys. Rev. D 2001, 63, 103510. [Google Scholar] [CrossRef]
- Visser, M.; Barcelo, C.; Liberati, S. Analogue Models of and for Gravity. Gen. Rel. Grav. 2002, 34, 1719. [Google Scholar] [CrossRef]
- Scherrer, R.J. Purely Kinetic k Essence as Unified Dark Matter. Phys. Rev. Lett. 2004, 93, 011301. [Google Scholar] [CrossRef]
- Chimento, L.P. Extended tachyon field, Chaplygin gas, and solvable k-essence cosmologies. Phys. Rev. D 2004, 69, 123517. [Google Scholar] [CrossRef]
- Vikman, A. K-Essence: Cosmology, Causality and Emergent Geometry. Doctoral Dissertation, der Ludwig-Maximilians-Universitat Munchen, Munchen, Germany, 2007. [Google Scholar]
- Babichev, E.; Mukhanov, V.; Vikman, A. k-Essence, superluminal propagation, causality and emergent geometry. J. High Energy Phys. 2008, 2, 101. [Google Scholar] [CrossRef]
- Babichev, E.; Mukhanov, V.; Vikman, A. Looking beyond the horizon. Looking beyond the Horizon. arXiv 2007, arXiv:0704.3301. [Google Scholar]
- Chimento, L.P. Internal space structure generalization of the quintom cosmological scenario. Phys. Rev. D 2009, 79, 043502. [Google Scholar] [CrossRef]
- Singh, T.; Chaubey, R.; Singh, A. k-essence cosmologies in Kantowski–Sachs and Bianchi space–times. Can. J. Phys. 2015, 93, 1319. [Google Scholar] [CrossRef]
- Singh, A.; Raushan, R.; Chaubey, R.; Mandal, S.; Mishra, K.C. Lagrangian formulation and implications of barotropic fluid cosmologies. Int. J. Geom. Meth. Mod. Phys. 2022, 19, 2250107. [Google Scholar] [CrossRef]
- Tian, S.X.; Zhu, Z.H. Early dark energy in k-essence. Phys. Rev. D 2021, 103, 043518. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Sebastiani, L. k-Essence Non-Minimally Coupled with Gauss–Bonnet Invariant for Inflation. Symmetry 2016, 8, 57. [Google Scholar] [CrossRef]
- Sen, A.A.; Devi, N.C. Cosmology with non-minimally coupled k-field. Gen. Relativ. Gravit. 2010, 42, 821. [Google Scholar] [CrossRef]
- Chatterjee, A.; Hussain, S.; Bhattacharya, K. Dynamical stability of the k-essence field interacting nonminimally with a perfect fluid. Phys. Rev. D 2021, 104, 103505. [Google Scholar] [CrossRef]
- Velten, H.E.S.; Vom Marttens, R.F.; Zimdahl, W. Aspects of the cosmological “coincidence problem”. Eur. Phys. J. C 2014, 74, 3160. [Google Scholar] [CrossRef]
- Erickson, J.K.; Caldwell, R.R.; Steinhardt, P.J.; Armendariz-Picon, C.; Mukhanov, V. Measuring the Speed of Sound of Quintessence. Phys. Rev. Lett. 2002, 88, 121301. [Google Scholar] [CrossRef] [PubMed]
- DeDeo, S.; Caldwell, R.R.; Steinhardt, P.J. Effects of the Sound Speed of Quintessence on the Microwave Background and Large Scale Structure. Phys. Rev. D 2003, 67, 103509. [Google Scholar] [CrossRef]
- Bean, R.; Dore, O. Probing dark energy perturbations: The dark energy equation of state and speed of sound as measured by WMAP. Phys. Rev. D 2004, 69, 083503. [Google Scholar] [CrossRef]
- Manna, G.; Gangopadhyay, D. The Hawking temperature in the context of dark energy for Reissner–Nordstrom and Kerr background. Eur. Phys. J. C 2014, 74, 2811. [Google Scholar] [CrossRef]
- Manna, G.; Majumder, B. The Hawking temperature in the context of dark energy for Kerr–Newman and Kerr–Newman–AdS backgrounds. Eur. Phys. J. C 2019, 79, 553. [Google Scholar] [CrossRef]
- Manna, G.; Majumder, B.; Das, A. Quantum corrections to the accretion onto a Schwarzschild black hole in the background of quintessence. Eur. Phys. J. Plus 2020, 135, 107. [Google Scholar] [CrossRef]
- Manna, G.; Panda, A.; Karmakar, A.; Ray, S. -gravity in the context of dark energy with power law expansion and energy conditions*. Chin. Phys. C 2023, 47, 025101. [Google Scholar] [CrossRef]
- Ray, S.; Panda, A.; Majumder, B.; Islam, M.R.; Manna, G. Collapsing scenario for the k-essence emergent generalized Vaidya spacetime in the context of massive gravity’s rainbow. Chin. Phys. C 2022, 46, 125103. [Google Scholar] [CrossRef]
- Das, S.; Panda, A.; Manna, G.; Ray, S. Raychaudhuri Equation in K-essence Geometry: Conditional Singular and Non-Singular Cosmological Models. Fortschr. Phys. 2023, 2023, 2200193. [Google Scholar] [CrossRef]
- Mukohyama, S.; Namba, R.; Watanabe, Y. Is the DBI scalar field as fragile as other k-essence fields? Phys. Rev. D 2016, 94, 023514. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. Foundations of the new field theory. Proc. R. Soc. Lond. A 1934, 144, 425. [Google Scholar] [CrossRef]
- Heisenberg, W. Production of Meson Showers. Zeit. Phys. 1939, 113, 61. [Google Scholar] [CrossRef]
- Dirac, P.A.M. An extensible model of the electron. Proc. R. Soc. Lond. A 1962, 268, 57. [Google Scholar] [CrossRef]
- Panda, A.; Manna, G.; Ray, S.; Khlopov, M.; Islam, M.R. Gravitational collapse in generalized K-essence emergent Vaidya spacetime via gravity. arXiv 2023, arXiv:2308.13574. [Google Scholar]
- Panda, A.; Das, S.; Manna, G.; Ray, S.; Islam, M.R.; Ranjit, C. gravity in a Non-canonical theory. arXiv 2022, arXiv:2206.14808. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Battaner, E.; et al. [Planck Collaboration]. XIV. Dark energy and modified gravity. Astron. Astrophys. 2016, 594, A14. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdow, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. [Planck Collaboration]. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Arroja, F.; Ashdow, M.; Aumon, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreir, R.B.; Bartolo, N.; et al. [Planck Collaboration]. I. Overview and the cosmological legacy of Planck. Astron. Astrophys. 2020, 641, A1. [Google Scholar] [CrossRef]
- Ishihara, H.; Kimura, M.; Matsuno, K. Charged black strings in a five-dimensional Kasner universe. Phys. Rev. D 2016, 93, 024037. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the LambertW function. Adv. Comp. Math. 1996, 5, 329. [Google Scholar] [CrossRef]
- Blau, M. Lecture Notes on General Relativity. 8 October 2022. Available online: http://www.blau.itp.unibe.ch/GRLecturenotes.html (accessed on 3 April 2023).
- Einstein, A.; Rosen, N. The Particle Problem in the General Theory of Relativity. Phys. Rev. 1935, 48, 73. [Google Scholar] [CrossRef]
- Fuller, R.W.; Wheeler, J.A. Causality and Multiply Connected Space-Time. Phys. Rev. 1962, 128, 919. [Google Scholar] [CrossRef]
- Ellis, H.G. Ether flow through a drainhole: A particle model in general relativity. J. Math. Phys. 1973, 14, 104. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395. [Google Scholar] [CrossRef]
- Visser, M. Traversable wormholes: Some simple examples. Phys. Rev. D 1989, 39, 3182. [Google Scholar] [CrossRef] [PubMed]
- Hayward, S.A. Wormhole dynamics in spherical symmetry. Phys. Rev. D 2009, 79, 124001. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Lipatova, L.N.; Novikov, I.D.; Shatskiy, A.A. Example of a stable wormhole in general relativity. Gravit. Cosmol. 2013, 19, 269. [Google Scholar] [CrossRef]
- Garattini, R. Casimir wormholes. Eur. Phys. J. C 2019, 79, 951. [Google Scholar] [CrossRef]
- Mishra, B.; Agrawal, A.S.; Tripathy, S.K.; Ray, S. Wormhole solutions in f(R) gravity. Int. J. Mod. Phys. D 2021, 30, 2150061. [Google Scholar] [CrossRef]
- Mishra, B.; Agrawal, A.S.; Tripathy, S.K.; Ray, S. Traversable wormhole models in f(R) gravity. Int. J. Mod. Phys. A 2022, 37, 2250010. [Google Scholar] [CrossRef]
- Mustafa, G.; Maurya, S.K.; Ray, S. On the Possibility of Generalized Wormhole Formation in the Galactic Halo Due to Dark Matter Using the Observational Data within the Matter Coupling Gravity Formalism. Astrophys. J. 2022, 941, 170. [Google Scholar] [CrossRef]
- Ashtekar, A.; Krishnan, B. Dynamical horizons and their properties. Phys. Rev. D 2003, 68, 104030. [Google Scholar] [CrossRef]
- Ashtekar, A.; Krishnan, B. Dynamical Horizons: Energy, Angular Momentum, Fluxes, and Balance Laws. Phys. Rev. Lett. 2002, 89, 261101. [Google Scholar] [CrossRef]
- Ashtekar, A.; Krishnan, B. Isolated and Dynamical Horizons and Their Applications. Living Rev. Relativ. 2004, 7, 10. [Google Scholar] [CrossRef]
- Hayward, S.A. General laws of black-hole dynamics. Phys. Rev. D 1994, 49, 6467. [Google Scholar] [CrossRef]
- Firouzjaee, J.T.; Ellis, G.F.R. Particle creation rate for dynamical black holes. Eur. Phys. J. C 2016, 76, 620. [Google Scholar] [CrossRef]
- Hawking, S.W.; Perry, M.J.; Strominger, A. Soft Hair on Black Holes. Phys. Rev. Lett. 2016, 116, 231301. [Google Scholar] [CrossRef]
- Kerr, R. Do Black Holes have Singularities? arXiv 2023, arXiv:2312.00841. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational Collapse and Space-Time Singularities. Phys. Rev. Lett. 1965, 14, 57. [Google Scholar] [CrossRef]
- Hawking, S.W. Black holes in general relativity. Commun. Math. Phys. 1972, 25, 152–166. [Google Scholar] [CrossRef]
- Hochberg, D.; Visser, M. Geometric structure of the generic static traversable wormhole throat. Phys. Rev. D 1997, 56, 4745. [Google Scholar] [CrossRef]
- Krasnikov, S. Traversable wormhole. Phys. Rev. D 2000, 62, 084028. [Google Scholar] [CrossRef]
- Matos, T.; Nunez, D. Rotating scalar field wormhole. Class. Quantum Gravit. 2006, 23, 4485. [Google Scholar] [CrossRef]
- Rahaman, F.; Islam, S.; Kuhfittig, P.K.F.; Ray, S. Searching for higher-dimensional wormholes with noncommutative geometry. Phys. Rev. D 2012, 86, 106010. [Google Scholar] [CrossRef]
- Rahaman, F.; Karmakar, S.; Karar, I.; Ray, S. Wormhole inspired by non-commutative geometry. Phys. Lett. B 2015, 746, 73. [Google Scholar] [CrossRef]
- Chew, X.Y.; Kleihaus, B.; Kunz, J. Geometry of spinning Ellis wormholes. Phys. Rev. D 2016, 94, 104031. [Google Scholar] [CrossRef]
- Mustafa, G.; Maurya, S.K.; Ray, S.; Javed, F. Construction of thin-shell around new wormhole solutions via solitonic quantum wave dark matter. Ann. Phys. 2014, 460, 169551. [Google Scholar] [CrossRef]
- Hawking, S. Black Holes and Baby Universes and Other Essays; Bantam Dell Publishing Group: New York, NY, USA, 1993. [Google Scholar]

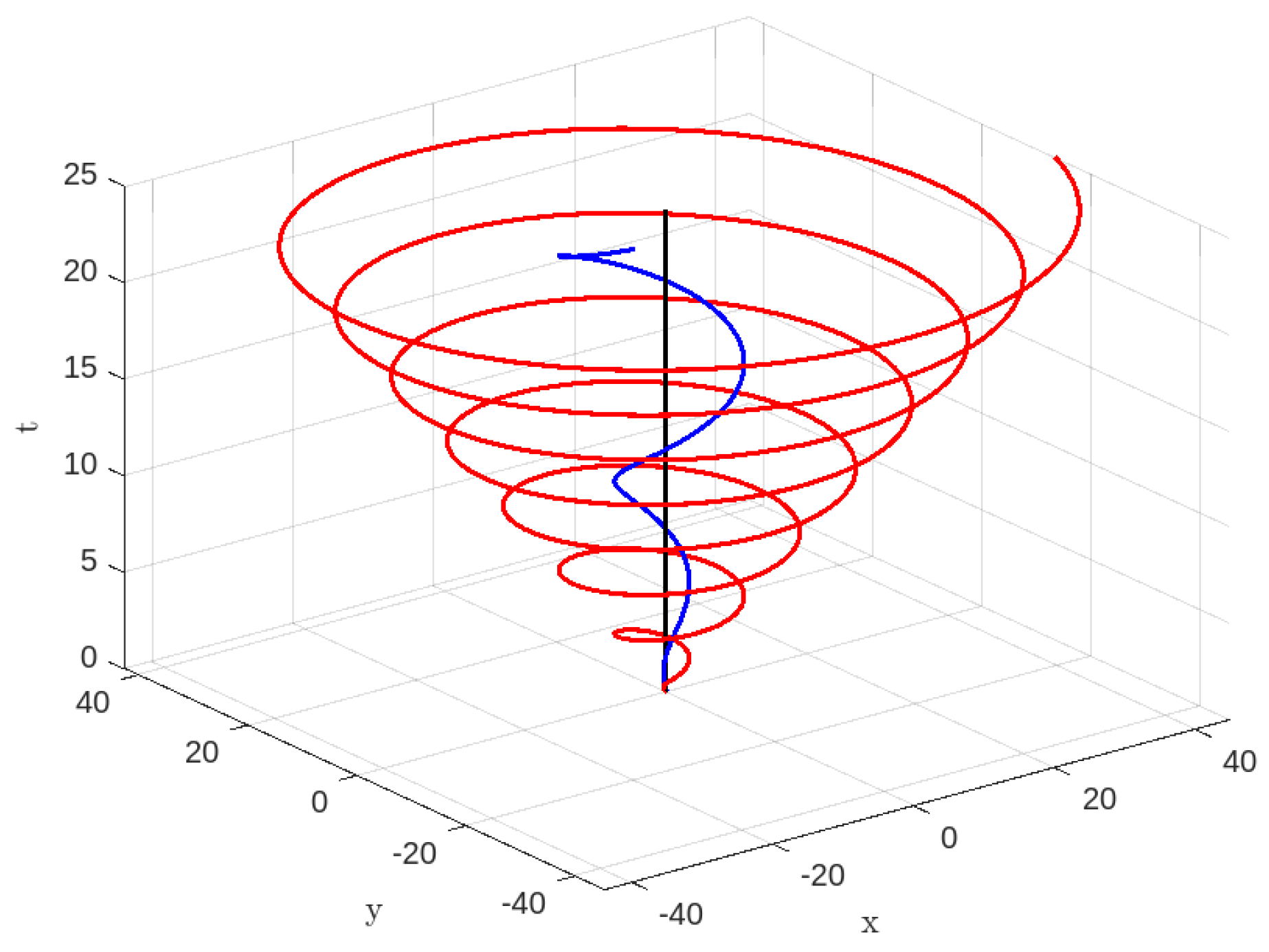
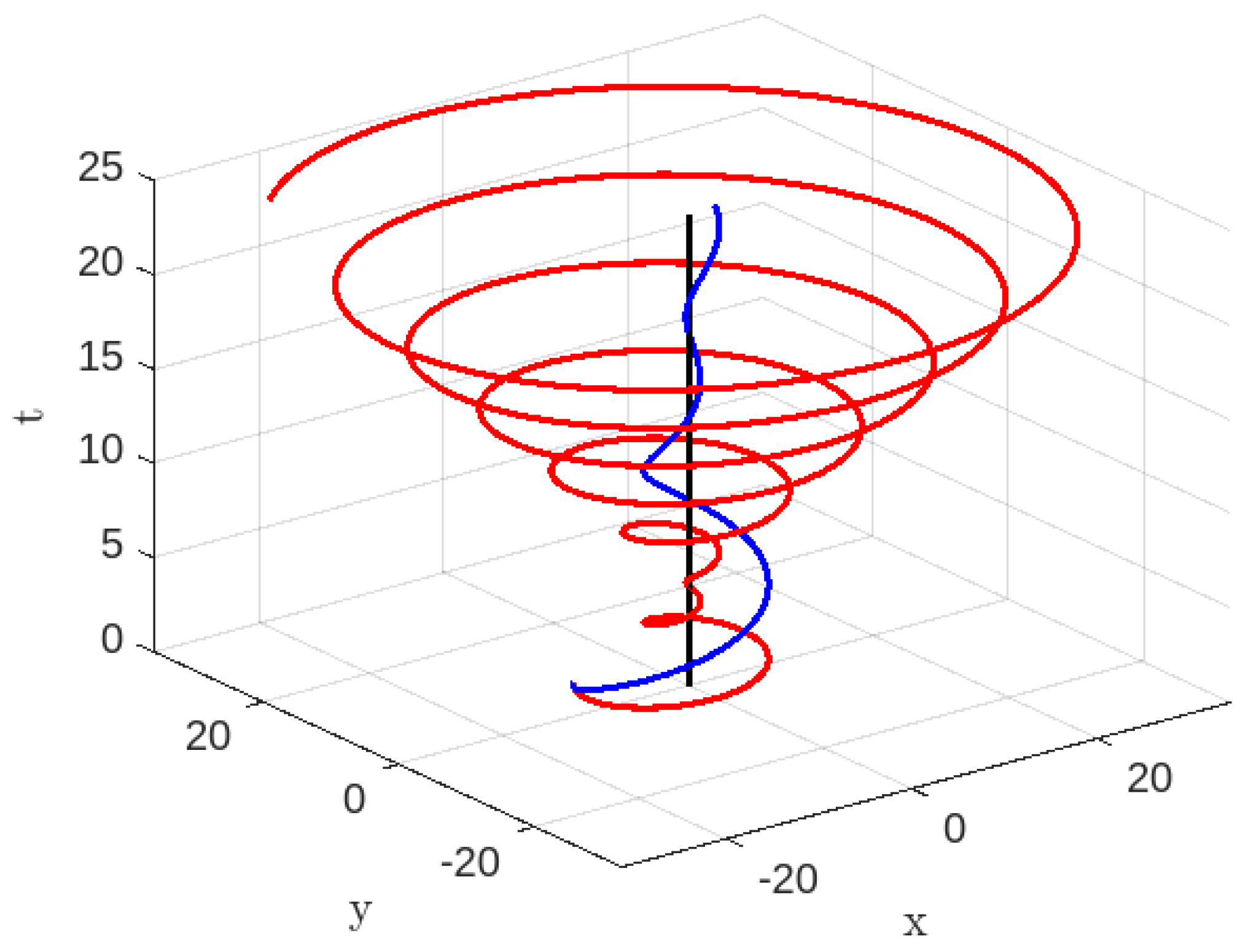
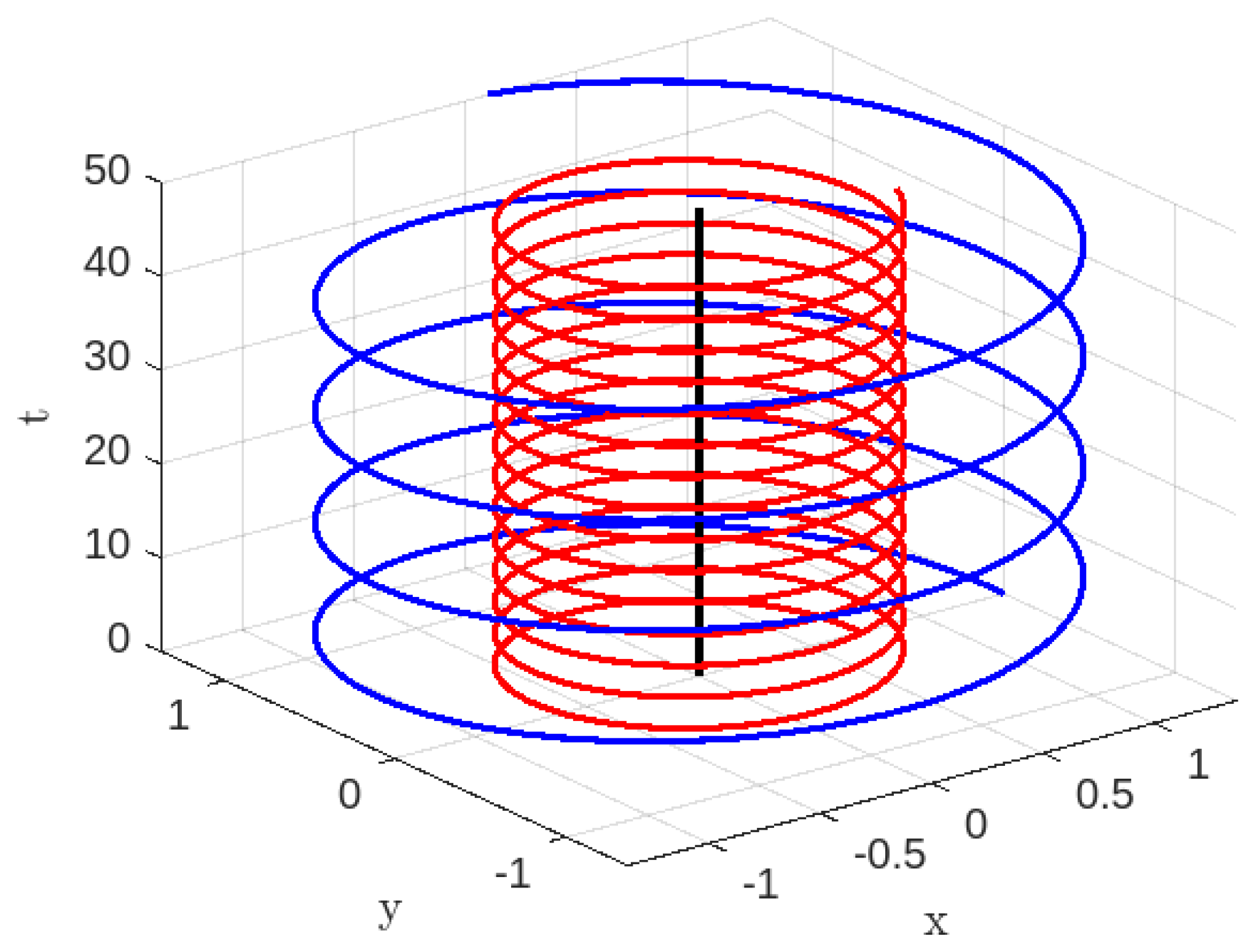


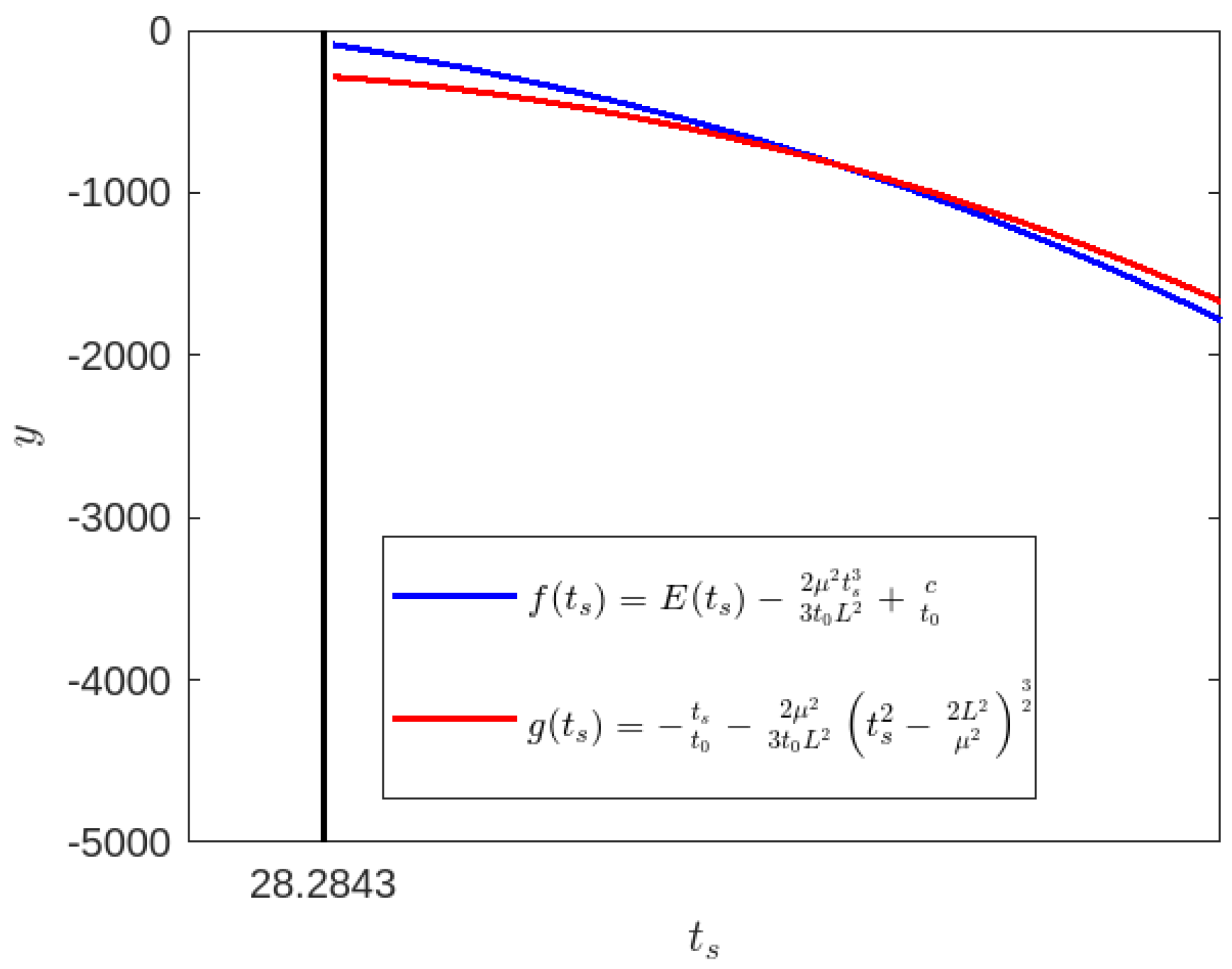




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majumder, B.; Khlopov, M.; Ray, S.; Manna, G. Geodesic Structure of Generalized Vaidya Spacetime through the K-Essence. Universe 2023, 9, 510. https://doi.org/10.3390/universe9120510
Majumder B, Khlopov M, Ray S, Manna G. Geodesic Structure of Generalized Vaidya Spacetime through the K-Essence. Universe. 2023; 9(12):510. https://doi.org/10.3390/universe9120510
Chicago/Turabian StyleMajumder, Bivash, Maxim Khlopov, Saibal Ray, and Goutam Manna. 2023. "Geodesic Structure of Generalized Vaidya Spacetime through the K-Essence" Universe 9, no. 12: 510. https://doi.org/10.3390/universe9120510
APA StyleMajumder, B., Khlopov, M., Ray, S., & Manna, G. (2023). Geodesic Structure of Generalized Vaidya Spacetime through the K-Essence. Universe, 9(12), 510. https://doi.org/10.3390/universe9120510






