Gauge-Invariant Lagrangian Formulations for Mixed-Symmetry Higher-Spin Bosonic Fields in AdS Spaces
Abstract
1. Introduction
2. HS Fields of Integer Spin in AdS Spaces
2.1. HS Symmetry Algebra for Mixed-Symmetry Tensor Fields with
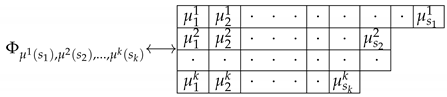
2.2. On Additive Conversion for Polynomial Algebras
3. Auxiliary HS Symmetry Algebra
3.1. On Representations of
3.2. Verma Module for Quadratic Algebra with Rows
3.3. Fock Space Realization of
4. Construction of Lagrangian Actions
4.1. Explicit Form of
4.2. BRST Operator for Converted Algebra
4.3. Lagrangian Formulation
5. BRST Approach to Cubic Interaction Vertices
6. Examples
6.1. Spin- Totally Symmetric Tensor Field
6.2. Spin- Antisymmetric Tensor Field
6.2.1. Action
6.2.2. Zero-Level Gauge Transformations
6.2.3. First-Level Gauge Transformations
6.2.4. Gauge-Fixing and Partial Use of Equations of Motion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proposition Proof
Appendix B. Polynomial Deformations of su(1,1) Algebra
Appendix C. Verma Module Construction for
Appendix C.1. Auxiliary Calculation for
Appendix D. Oscillator Realization of Additional Parts: New Fock Space
Appendix E. Reduction to Initial Irreducible Relations
Appendix E.1. Gauge Fixing
Appendix E.2. Removal of Auxiliary Fields by Resolving Equations of Motion
| 1 | For recent developments in the ambient flat space-time techniques of the incomplete BRST approach to totally symmetric tensor fields in AdS spaces, see [43]. |
| 2 | For the AKSZ model used in higher-spin gravity, see, for example, [51]. |
| 3 | This choice of oscillators corresponds to the case of a symmetric basis, whereas there also exists another realization of an auxiliary Fock space, generated by fermionic oscillators (antisymmetric basis) , , with the anticommutation relations , for . The treatment below proceeds along the lines of [62] for totally antisymmetric tensors with . |
| 4 | The operators , satisfy the usual (in the space ) commutation relations for . |
| 5 | The term higher-spin symmetry algebra, applied here to a free HS formulation, is not to be confused with the algebraic structure known as a higher-spin algebra which arises in describing HS interactions; see, for example, [15]. |
| 6 | There is no summation with respect to the indices in (16), and the figure brackets for the indices , in the quantity imply symmetrization: =. These indices are raised and lowered using the Euclidean metric tensors , , . |
| 7 | This superalgebra can be equally used for both bosonic HS fields in an antisymmetric basis and fermionic HS fields in an AdS space. |
| 8 | One can choose in a Cartan–Weyl basis for a unified description; however, without loss of generality, the basis elements and structure constants of the algebra under consideration are chosen as in Table 1. |
| 9 | Here, the symbols , , denote the universal enveloping algebras, respectively, for g, for the Borel subalgebra, and for the lower-triangular subalgebra , such as in (41). |
| 10 | For the first time [63], the treatment of quadratic “primed” quantities has been presented in the case of so that the following properties hold true: , . |
| 11 | |
| 12 | The momenta satisfy the independent non-vanishing anticommutation relations , as well as possessing the standard ghost number distribution = = 1, providing the property = 1, and have the Hermitian conjugation properties of zero-mode pairs, . |
| 13 | |
| 14 | |
| 15 | The algebraic relations (31) for the algebra are different from those for the polynomial algebra in view of a non-homogeneous character of the structure functions in , due to the presence of the elements . |
| 16 | In the case , the corresponding algebra must be of zero order because of the relation (A6), which has the form ; however, in this case, we can add the unity 1 to the set of , as was done with the Heisenberg algebra , and then remove the element from , due to the possibility of the representation . |
| 17 | Explicitly, , which follows from by Hermitian conjugation. |
| 18 | |
| 19 | In (A92) for , there are no double sums. The products are equal to 1, and the terms inside the internal brackets, , are the only ones to survive. |
| 20 |
References
- Baumgart, M.; Bishara, F.; Brauner, T.; Brod, J.; Cabass, G.; Cohen, T.; Craig, N.; de Rham, C.; Draper, P.; Fitzpatrick, A.L.; et al. Snowmass theory frontier: Effective field theory topical group summary. arXiv 2022, arXiv:2210.03199. [Google Scholar]
- Buschmann, M.; Kopp, J.; Liu, J.; Machado, P.A.N. Lepton jets from radiating dark matter. J. High Energy Phys. 2015, 7, 45. [Google Scholar] [CrossRef]
- Kelly, K.J.; Sen, M.; Tangarife, W.; Zhang, Y. Origin of sterile neutrino dark matter via secret neutrino interactions with vector bosons. Phys. Rev. D 2020, 101, 115031. [Google Scholar] [CrossRef]
- Adshead, P.; Lozanov, K.D. Self-gravitating vector dark matter. Phys. Rev. D 2021, 103, 103501. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Finkbeiner, D.P.; Slatyer, T.R.; Weiner, N. A theory of dark matter. Phys. Rev. D 2009, 79, 015014. [Google Scholar] [CrossRef]
- de Swart, J.; Bertone, G.; van Dongen, J. How dark matter came to matter. Nat. Astron. 2017, 1, 59. [Google Scholar] [CrossRef]
- Sharapov, A.; Skvortsov, E.; Sukhanov, A. Minimal model of Chiral Higher Spin Gravity. J. High Energy Phys. 2022, 9, 134. [Google Scholar] [CrossRef]
- de Haro, J.; Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K.; Pan, S. Finite-time cosmological singularities and the possible fate of the Universe. Phys. Rep. 2023, 1034, 1–114. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rept. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59. [Google Scholar] [CrossRef]
- Calderon, R.; L’Huillier, B.; Polarski, D.; Starobinsky, A.A. Joint reconstructions of growth and expansion histories from stage-IV surveys with minimal assumptions. II. Modified gravity and massive neutrinos. Phys. Rev. D 2023, 108, 023504. [Google Scholar] [CrossRef]
- Vasiliev, M. Higher Spin Gauge Theories in Various Dimensions. Fortsch. Phys. 2004, 52, 702–717. [Google Scholar] [CrossRef]
- Sorokin, D. Introduction to the Classical Theory of Higher Spins. AIP Conf. Proc. 2005, 767, 172–202. [Google Scholar]
- Francia, D.; Sagnotti, A. Higher-Spin Geometry and String Theory. J. Phys. Conf. Ser. 2006, 33, 57. [Google Scholar] [CrossRef]
- Vasiliev, M.A. Higher spin theory and space-time metamorphoses. Lect. Notes Phys. 2015, 892, 227–264. [Google Scholar]
- Bekaert, X.; Boulanger, N.; Campaneoni, A.; Chodaroli, M.; Francia, D.; Grigoriev, M.; Sezgin, E.; Skvortsov, E. Snowmass white paper: Higher spin gravity and higher spin symmetry. arXiv 2022, arXiv:2205.01567. [Google Scholar]
- Ponomarev, D. Basic introduction to higher spin theories. arXiv 2022, arXiv:2206.15385. [Google Scholar] [CrossRef]
- Fotopoulos, A.; Tsulaia, M. Gauge invariant Lagrangians for free and interacting higher spin fields. A review of the BRST formulation. Int. J. Mod. Phys. A 2008, 24, 1–59. [Google Scholar]
- Dixmier, J. Algebres Enveloppantes; Gauthier-Villars: Paris, France, 1974; [In English: Dixmier, J. Enveloping Algebras; North Holland: New York, NY, USA, 1977]. [Google Scholar]
- Burdik, C.; Navratil, O.; Pashnev, A. On the Fock space realizations of nonlinear algebras describing the high spin fields in AdS spaces. arXiv 2002, arXiv:hep-th/0206027. [Google Scholar]
- Buchbinder, I.L.; Krykhtin, V.A.; Lavrov, P.M. Gauge invariant Lagrangian formulation of higher massive bosonic field theory in AdS space. Nucl. Phys. B 2007, 762, 344–376. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Krykhtin, V.; Reshetnyak, A. BRST approach to Lagrangian construction for fermionic higher spin fields in (A)dS space. Nucl. Phys. B 2007, 787, 211. [Google Scholar] [CrossRef]
- Kuleshov, A.; Reshetnyak, A. Programming realization of symbolic computations for non-linear commutator superalgebras over the Heisenberg–Weyl superalgebra: Data structures and processing method. arXiv 2009, arXiv:0905.2705. [Google Scholar]
- Wigner, E.P. On unitary representations of the inhomogeneous Lorentz group. Ann. Math. 1939, 40, 149–204. [Google Scholar] [CrossRef]
- Labastida, J.M.F.; Morris, T.R. Massless mixed symmetry bosonic free fields. Phys. Lett. B 1986, 180, 101–106. [Google Scholar] [CrossRef]
- Labastida, J.M.F. Massless bosonic free fields. Phys. Rev. Lett. 1987, 58, 531. [Google Scholar] [CrossRef] [PubMed]
- Metsaev, R.R. Massless mixed symmetry bosonic free fields in d-dimensional anti-de Sitter space-time. Phys. Lett. B 1995, 354, 78–84. [Google Scholar] [CrossRef]
- Metsaev, R.R. Massive totally symmetric fields in AdS(d). Phys. Lett. B 2004, 590, 95. [Google Scholar] [CrossRef]
- Metsaev, R.R. Mixed-symmetry massive fields in AdS(5). Class. Quant. Grav. 2005, 22, 2777. [Google Scholar] [CrossRef][Green Version]
- Becchi, C.; Rouet, A.; Stora, R. Renormalization of the Abelian Higgs-Kibble Model. Comm. Math. Phys. 1975, 42, 127–162. [Google Scholar] [CrossRef]
- Becchi, C.; Rouet, A.; Stora, R. Renormalization of Gauge Theories. Ann. Phys. 1976, 98, 287–321. [Google Scholar] [CrossRef]
- Tyutin, I.V. Gauge Invariance in Field Theory and Statistical Physics in Operator Formalism. Lebedev Inst. 1975, N39, 62. [Google Scholar]
- Fradkin, E.S.; Vilkovisky, G.A. Quantization of Relativistic Systems with Constraints. Phys. Lett. B 1975, 55, 224–226. [Google Scholar] [CrossRef]
- Batalin, I.A.; Vilkovisky, G.A. Relativistic S Matrix of Dynamical Systems with Boson and Fermion Constraints. Phys. Lett. B 1977, 69, 309–312. [Google Scholar] [CrossRef]
- Henneaux, M. Hamiltonian Form of the Path Integral for Theories with a Gauge Freedom. Phys. Rep. 1985, 126, 1–66. [Google Scholar] [CrossRef]
- Pashnev, A.; Tsulaia, M. Description of the higher massless irreducible integer spins in the BRST approach. Mod. Phys. Lett. A 1998, 13, 1853–1864. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Pashnev, A.; Tsulaia, M. Lagrangian formulation of the massless higher integer spin fields in the AdS background. Phys. Lett. B 2001, 523, 338–346. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Reshetnyak, A.A. General cubic interacting vertex for massless integer higher spin fields. Phys. Lett. B 2021, 820, 136470. [Google Scholar] [CrossRef]
- Alkalaev, K.B.; Grigoriev, M.; Tipunin, I.Y. Massless Poincaré modules and gauge invariant equations. Nucl. Phys. B 2009, 823, 509–545. [Google Scholar] [CrossRef]
- Witten, E. Noncommutative Geometry and String Field Theory. Nucl. Phys. B 1986, 268, 253–294. [Google Scholar] [CrossRef]
- Siegel, W.; Zwiebach, B. Gauge String Fields from the Light Cone. Nucl. Phys. B 1987, 282, 125–141. [Google Scholar] [CrossRef]
- Reshetnyak, A.A. Constrained BRST–BFV Lagrangian formulations for higher spin fields in Minkowski spaces. J. High Energy Phys. 2018, 1809, 104. [Google Scholar] [CrossRef]
- Bekaert, X.; Boulanger, N.; Grigoriev, M.; Goncharov, Y. Ambient-space variational calculus for gauge fields on constant-curvature spacetimes. arXiv 2023, arXiv:2305.02892. [Google Scholar]
- Burdik, C.; Reshetnyak, A. On representations of higher spin symmetry algebras for mixed-symmetry HS fields on AdS-spaces. Lagrangian formulation. J. Phys. Conf. Ser. 2012, 343, 012102. [Google Scholar] [CrossRef]
- Fronsdal, C. Massless Fields with Integer Spin. Phys. Rev. D 1978, 18, 3624–3629. [Google Scholar] [CrossRef]
- Fang, J.; Fronsdal, C. Massless Fields with Half Integral Spin. Phys. Rev. D 1978, 18, 3630–3636. [Google Scholar] [CrossRef]
- Fronsdal, C. Singletons and massless, integral-spin fields on de Sitter space. Phys. Rev. D 1979, 20, 848–856. [Google Scholar] [CrossRef]
- Grigoriev, M.; Damgaard, P.H. Superfield BRST charge and the master action. Phys. Lett. B 2000, 474, 323–330. [Google Scholar] [CrossRef]
- Gitman, D.M.; Moshin, P.Y.; Reshetnyak, A.A. Local superfield Lagrangian BRST quantization. J. Math. Phys. 2005, 46, 072302. [Google Scholar] [CrossRef]
- Gitman, D.M.; Moshin, P.Y.; Reshetnyak, A.A. An embedding of the BV quantization into an N = 1 local superfield formalism. Phys. Lett. B 2005, 621, 295–308. [Google Scholar] [CrossRef]
- Sharapov, A.; Skvortsov, E. Higher spin gravities and presymplectic AKSZ models. Nucl. Phys. B 2021, 972, 115551. [Google Scholar] [CrossRef]
- Alexandrov, M.; Kontsevich, M.; Schwarz, A.; Zaboronsky, O. The geometry of the master equation and topological quantum field theory. Int. J. Mod. Phys. A 1997, 12, 1405–1429. [Google Scholar] [CrossRef]
- Faddeev, L.D.; Shatashvili, S.L. Realization of the Schwinger Term in the Gauss Law and the Possibility of Correct Quantization of a Theory with Anomalies. Phys. Lett. B 1986, 167, 225–228. [Google Scholar] [CrossRef]
- Batalin, I.A.; Tyutin, I.V. Existence theorem for the effective gauge algebra in the generalized canonical formalism with Abelian conversion of second class constraints. Int. J. Mod. Phys. A 1991, 6, 3255–3282. [Google Scholar] [CrossRef]
- Burdik, C.; Pashnev, A.; Tsulaia, M. On the mixed symmetry irreducible representations of the Poincaré group in the BRST approach. Mod. Phys. Lett. A 2001, 16, 731–746. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Krykhtin, V.; Takata, H. Gauge invariant Lagrangian construction for massive bosonic mixed symmetry higher spin fields. Phys. Lett. B 2007, 656, 253–264. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Krykhtin, V.A.; Pashnev, A. BRST approach to Lagrangian construction for fermionic massless higher spin fields. Nucl. Phys. B 2005, 711, 367–391. [Google Scholar] [CrossRef]
- Moshin, P.Y.; Reshetnyak, A.A. BRST approach to Lagrangian formulation for mixed-symmpetry fermionic higher-spin fields. J. High Energy Phys. 2007, 10, 40. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Reshetnyak, A.A. General Lagrangian Formulation for Higher Spin Fields with Arbitrary Index Symmetry. I. Bosonic fields. Nucl. Phys. B 2012, 862, 270–326. [Google Scholar] [CrossRef]
- Howe, R. Transcending classical invariant theory. J. Am. Math. Soc. 1989, 2, 535–552. [Google Scholar] [CrossRef]
- Reshetnyak, A.A. General Lagrangian formulation for higher spin fields with arbitrary index symmetry. 2. Fermionic fields. Nucl. Phys. B 2013, 869, 523–597. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Krykhtin, V.A.; Ryskina, L.L. BRST approach to Lagrangian formulation of bosonic totally antisymmeric tensor fields in curved space. Mod. Phys. Lett. A 2009, 24, 401–415. [Google Scholar] [CrossRef]
- Reshetnyak, A.A. Nonlinear operator superalgebras and BFV–BRST operators for Lagrangian description of mixed-symmetry HS fields in AdS spaces. arXiv 2008, arXiv:0812.2329. [Google Scholar]
- Buchbinder, I.L.; Lavrov, P.M. Classical BRST charge for nonlinear algebras. J. Math. Phys. 2007, 48, 082306. [Google Scholar] [CrossRef]
- Alkalaev, K.B.; Vasiliev, M.A. N=1 supersymmetric theory of higher spin gauge fields in AdS(5) at the cubic level. Nucl. Phys. B 2003, 655, 57–92. [Google Scholar] [CrossRef]
- Alkalaev, K.B. Two column higher spin massless fields in AdS(d). Theor. Math. Phys. 2004, 140, 1253–1263. [Google Scholar] [CrossRef]
- Alkalaev, K.B.; Shaynkman, O.V.; Vasiliev, M.A. Lagrangian formulation for free mixed-symmetry bosonic gauge fields in (A)dS(d). J. High Energy Phys. 2005, 508, 69. [Google Scholar] [CrossRef]
- Alkalaev, K.B.; Shaynkman, O.V.; Vasiliev, M.A. Frame-like formulation for free mixed-symmetry bosonic massless higher-spin fields in AdS(d). arXiv 2006, arXiv:hep-th/0601225. [Google Scholar]
- Alkalaev, K.B. Mixed-symmetry massless gauge fields in AdS(5). Theor. Math. Phys. 2006, 149, 1338–1348. [Google Scholar] [CrossRef]
- Zinoviev, Y. Toward frame-like gauge invariant formulation for massive mixed symmetry bosonic fields. Nucl. Phys. B 2009, 812, 46–63. [Google Scholar] [CrossRef]
- Zinoviev, Y. Frame-like gauge invariant formulation for massive high spin particles. Nucl. Phys. B 2009, 808, 185–204. [Google Scholar] [CrossRef]
- Zinoviev, Y. Towards frame-like gauge invariant formulation for massive mixed symmetry bosonic fields. II. General Young tableau with two rows. Nucl. Phys. B 2010, 826, 490–510. [Google Scholar] [CrossRef]
- Alkalaev, K.B.; Grigoriev, M. Unified BRST description of AdS gauge fields. Nucl. Phys. B 2010, 835, 197–220. [Google Scholar] [CrossRef]
- Alkalaev, K.; Grigoriev, M. Unified BRST approach to (partially) massless and massive AdS fields of arbitrary symmetry type. Nucl. Phys. B 2011, 853, 663–687. [Google Scholar] [CrossRef]
- Metsaev, R.R. Mixed-symmetry fields in AdS(5), conformal fields, and AdS/CFT. J. High Energy Phys. 2015, 1, 77. [Google Scholar] [CrossRef]
- Metsaev, R.R. BRST–BV approach to massless fields adapted to AdS/CFT correspondence. Theor. Math. Phys. 2016, 187, 730–742. [Google Scholar] [CrossRef]
- Metsaev, R.R. Mixed-symmetry continuous-spin fields in flat and AdS spaces. Phys. Lett. B 2021, 820, 136497. [Google Scholar] [CrossRef]
- Metsaev, R.R. Light-cone gauge massive and partially-massless fields in AdS(4). Phys. Lett. B 2023, 839, 137790. [Google Scholar] [CrossRef]
- Campoleoni, A.; Francia, D.; Mourad, J.; Sagnotti, A. Unconstrained Higher Spins of Mixed Symmetry. I. Bose Fields. Nucl. Phys. B 2009, 815, 289–367. [Google Scholar] [CrossRef]
- Zinoviev, Y.M. Spin 3 cubic vertices in a frame-like formalism. J. High Energy Phys. 2010, 1008, 84. [Google Scholar] [CrossRef]
- Boulanger, N.; Skvortsov, E.D. Higher-spin algebras and cubic interactions for simple mixed-symmetry fields in AdS spacetime. J. High Energy Phys. 2011, 1109, 63. [Google Scholar] [CrossRef]
- Manvelyan, R.; Mkrtchyan, K.; Ruhl, W. General trilinear interaction for arbitrary even higher spin gauge fields. Nucl. Phys. B 2010, 836, 204–221. [Google Scholar] [CrossRef]
- Manvelyan, R.; Mkrtchyan, K.; Ruhl, W. A generating function for the cubic interactions of higher spin fields. Phys. Lett. B 2011, 696, 410–415. [Google Scholar] [CrossRef][Green Version]
- Joung, E.; Taronna, M. Cubic interactions of massless higher spins in (A)dS: Metric-like approach. Nucl. Phys. B 2012, 861, 145–174. [Google Scholar] [CrossRef]
- Vasiliev, M. Cubic vertices for symmetric higher spin gauge fields in (A)dSd. Nucl. Phys. B 2012, 862, 341–408. [Google Scholar] [CrossRef]
- Metsaev, R.R. Cubic interaction vertices for fermionic and bosonic arbitrary spin fields. Nucl. Phys. B 2012, 859, 13–69. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Fotopoulos, A.; Petkou, A.C.; Tsulaia, M. Constructing the cubic interaction vertex of higher spin gauge fields. Phys. Rev. D 2006, 74, 105018. [Google Scholar] [CrossRef]
- Fotopoulos, A.; Tsulaia, M. Current exchanges for reducible higher spin multiplets and gauge fixing. J. High Energy Phys. 2009, 10, 50. [Google Scholar] [CrossRef]
- Metsaev, R.R. BRST–BV approach to cubic interaction vertices for massive and massless higher spin fields. Phys. Lett. B 2013, 720, 237–243. [Google Scholar] [CrossRef]
- Khabarov, M.V.; Zinoviev, Y.M. Cubic interaction vertices for massless higher spin supermultiplets in d=4. J. High Energy Phys. 2021, 2, 167. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Krykhtin, V.A.; Tsulaia, M.; Weissman, D. Cubic vertices for N=1 supersymmetric massless higher spin fields in various dimensions. Nucl. Phys. B 2021, 967, 115427. [Google Scholar] [CrossRef]
- Metsaev, R.R. Interacting massive and massless arbitrary spin fields in 4d flat space. arXiv 2022, arXiv:2206.13268. [Google Scholar] [CrossRef]
- Metsaev, R.R. Cubic interaction vertices for massive and massless higher spin fields. Nucl. Phys. B 2006, 759, 147–201. [Google Scholar]
- Reshetnyak, A.A. Towards the structure of a cubic interaction vertex for massless integer higher spin fields. Phys. Part. Nucl. Lett. 2022, 19, 631–637. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Krykhtin, V.A.; Snegirev, T.V. Cubic interactions of d4 irreducible massless higher spin fields within BRST approach. Eur. Phys. J. C 2022, 82, 1007. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Reshetnyak, A.A. Covariant cubic interacting vertices for massless and massive integer higher spin fields. arXiv 2022, arXiv:2212.07097. [Google Scholar]
- Burdik, C. Realizations of the real simple Lie algebras: The method of construction. J. Phys. A Math. Gen. 1985, 18, 3101–3112. [Google Scholar] [CrossRef]
- Burdik, C.; Pashnev, A.; Tsulaia, M. Auxiliary representations of Lie algebras and the BRST constructions. Mod. Phys. Lett. A 2000, 15, 281–292. [Google Scholar] [CrossRef]
- Burdlk, C.; Grozman, P.; Leites, D.; Sergeev, A. Realization of Lie algebras and superalgebras in terms of creation and annihilation operators: I. Theor. Math. Phys. 2000, 124, 1048–1058. [Google Scholar] [CrossRef]
- Fotopoulos, A.; Panigrahi, K.L.; Tsulaia, M. Lagrangian formulation of higher spin theories on AdS space. Phys. Rev. D 2006, 74, 085029. [Google Scholar] [CrossRef]
- Joung, E.; Lopez, L.; Taronna, M. On the cubic interactions of massive and partially-massless higher spins in (A)dS. J. High Energy Phys. 2012, 07, 41. [Google Scholar] [CrossRef]
- Francia, D.; Monaco, G.L.; Mkrtchyan, K. Cubic interactions of Maxwell-like higher spins. J. High Energy Phys. 2017, 4, 68. [Google Scholar] [CrossRef]
- Prokushkin, S.F.; Vasiliev, M.A. Higher spin gauge interactions for massive matter fields in 3-D AdS space-time. Nucl. Phys. B 1999, 545, 385–433. [Google Scholar] [CrossRef]
- Joung, E.; Mkrtchyan, K.; Poghosyan, G. Looking for partially-massless gravity. J. High Energy Phys. 2019, 7, 116. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Vasiliev, M.A. On the gravitational interaction of massless higher spin fields. Phys. Lett. B 1987, 189, 89–95. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Vasiliev, M.A. Cubic interaction in extended theories of massless higher spin fields. Nucl. Phys. B 1987, 291, 141–171. [Google Scholar] [CrossRef]
- Boulanger, N.; Leclercq, S.; Sundell, P. On the uniqueness of minimal coupling in higher-spin gauge theory. J. High Energy Phys. 2008, 8, 56. [Google Scholar] [CrossRef]
- Joung, E.; Taronna, M. Cubic-interaction-induced deformations of higher-spin symmetries. J. High Energy Phys. 2014, 3, 103. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Reshetnyak, A.A. Consistent Lagrangians for irreducible interacting higher-spin fields with holonomic constraints. arXiv 2023, arXiv:2304.10358. [Google Scholar]
- Burdik, C.; Reshetnyak, A. BRST–BV quantum actions for constrained totally-symmetric integer HS fields. Nucl. Phys. B 2021, 965, 115357. [Google Scholar] [CrossRef]
- Reshetnyak, A.A. BRST–BV approach for interacting higher-spin fields. Theor. Math. Phys. 2023, 217, 1505–1527. [Google Scholar] [CrossRef]
- Taronna, M. Higher-spin interactions: Four-point functions and beyond. J. High Energy Phys. 2021, 4, 29. [Google Scholar] [CrossRef]
- Dempster, P.; Tsulaia, M. On the structure of quartic vertices for massless higher spin fields on minkowski background. Phys. Rev. D 2012, 86, 025007. [Google Scholar] [CrossRef]
- Taronna, M. On the non-local obstruciton to interacting higher-spins in flat space. J. High Energy Phys. 2017, 5, 26. [Google Scholar] [CrossRef]
- Didenko, V.E.; Gelfand, O.A.; Korybut, A.V.; Vasiliev, V.A. Limiting shifted homotopy in higher-spin theory. J. High Energy Phys. 2019, 12, 86. [Google Scholar] [CrossRef]
- Vasiliev, M.A. Projectively-compact spinor veritices and space-time spin locality in higher spin theory. Phys. Lett. B 2022, 834, 137401. [Google Scholar] [CrossRef]
- Didenko, V.E. On holomorphic sector of higher-spin theory. arXiv 2022, arXiv:2209.01966. [Google Scholar] [CrossRef]
- Didenko, V.E.; Korybut, A.V. On z-dominance, shift symmetry and spin locality in higher-spin theory. arXiv 2022, arXiv:2212.05006. [Google Scholar] [CrossRef]
- Moshin, P.Y.; Reshetnyak, A.A. Composite and background fields in non-abelian gauge models. Symmetry 2020, 12, 1985. [Google Scholar] [CrossRef]
- Moshin, P.Y.; Reshetnyak, A.A.; Castro, R.A. Non-abelian gauge theories with composite fields in the background field method. Universe 2023, 9, 18. [Google Scholar] [CrossRef]
- Lee, Y.H.; Yang, W.L.; Zhang, Y.Z. Polynomial algebras and exact solutions of general quantum non-linear optical models I: Two-mode boson systems. J. Phys. A Math. Theor. 2010, 43, 185204. [Google Scholar] [CrossRef]
| 0 | |||||||
| 0 | |||||||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | |||||||
| 0 | |||||||
| 0 | 0 | 0 | |||||
| 0 | 0 | 0 | |||||
| 0 |
| 0 | |||
| 0 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reshetnyak, A.A.; Moshin, P.Y. Gauge-Invariant Lagrangian Formulations for Mixed-Symmetry Higher-Spin Bosonic Fields in AdS Spaces. Universe 2023, 9, 495. https://doi.org/10.3390/universe9120495
Reshetnyak AA, Moshin PY. Gauge-Invariant Lagrangian Formulations for Mixed-Symmetry Higher-Spin Bosonic Fields in AdS Spaces. Universe. 2023; 9(12):495. https://doi.org/10.3390/universe9120495
Chicago/Turabian StyleReshetnyak, Alexander Alexandrovich, and Pavel Yurievich Moshin. 2023. "Gauge-Invariant Lagrangian Formulations for Mixed-Symmetry Higher-Spin Bosonic Fields in AdS Spaces" Universe 9, no. 12: 495. https://doi.org/10.3390/universe9120495
APA StyleReshetnyak, A. A., & Moshin, P. Y. (2023). Gauge-Invariant Lagrangian Formulations for Mixed-Symmetry Higher-Spin Bosonic Fields in AdS Spaces. Universe, 9(12), 495. https://doi.org/10.3390/universe9120495






