Sparsity and M-Estimators in RFI Mitigation for Typical Radio Astrophysical Signals
Abstract
1. Introduction
2. A Review of the M-Estimators
3. Sparse Representation and Features of Radio Signals
3.1. Sparse Representation
3.2. Examples of Astrophysical Features
- Dispersion relationship. Search processes for radio astrophysical sources in multichannel signals consist of looking for dispersed pulses. In observed signal profiles, different observing frequency channels correspond to different amounts of dispersions. The dispersion frequency relationship [51,52] at (which is the central frequency of channel a) is calculated aswhere () is the dispersion constant, and is the reference frequency, which is chosen to be the center frequency of the broad band (with and as the central frequencies of the lowest and highest channels). The dispersion measure is defined as , where is the electron number density, l is the path length along the line-of-sight, and d is the distance to a radio source. This dispersion relationship is a widely presented feature in multichannel radio signals. The dispersion effect generates curve-like signals with typical C singularities. In this paper, the shearlet will be first applied in RFI mitigation of pulsar signals, and it is expected to guarantee accurate sparse representation and approximation for this feature.
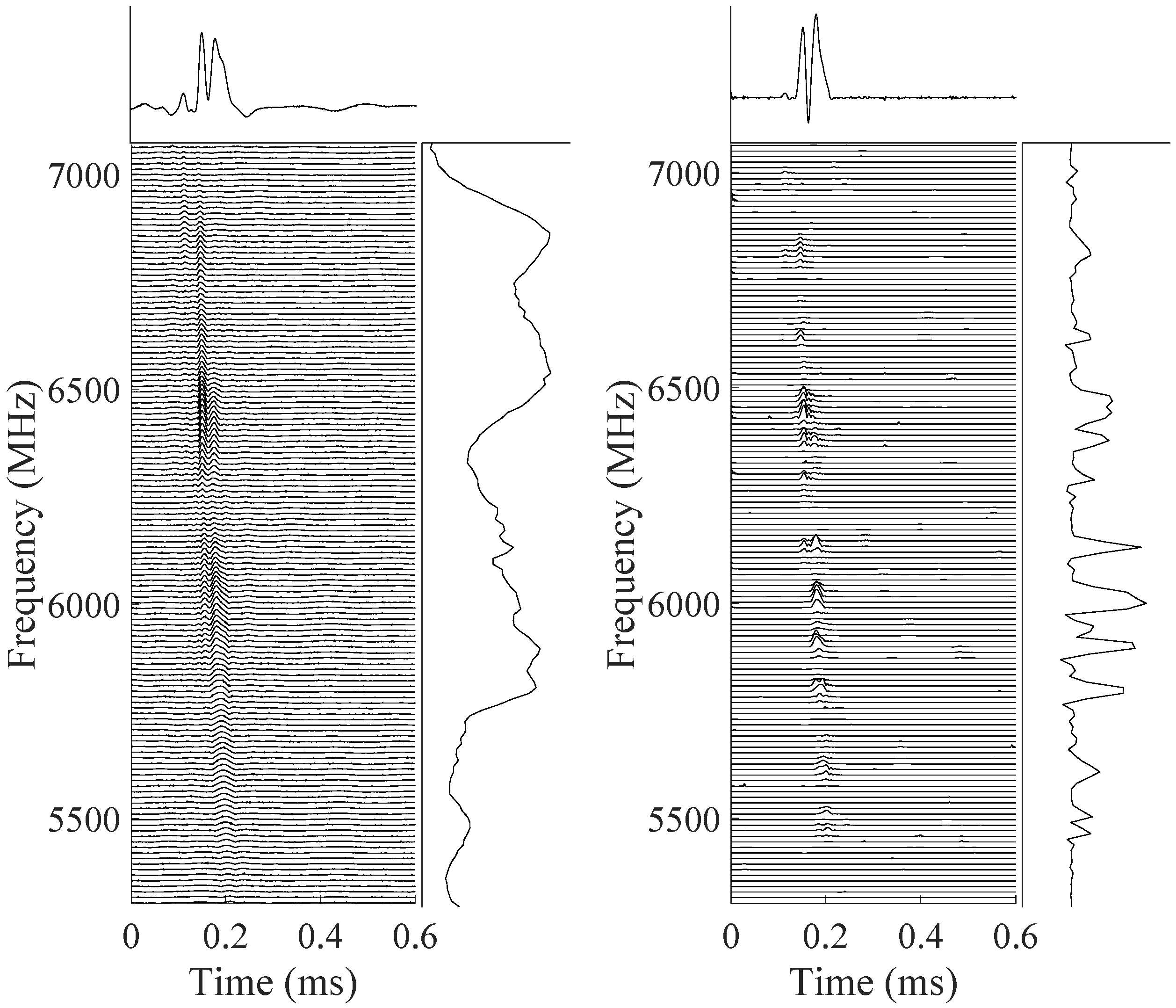
- In FRB signals, the isotropic narrow-band superradiance, and directional time–frequency extensions (including extensions around the downward frequency drifting; distortions by the scattering effect). The dispersion effect will not be considered for the dedispersed FRB signals applied in this paper. Around the isotropic flux areas of superradiance, there are curve-like and local elliptical time–frequency extensions. Accurate approximation for these extensions helps to explore the changing trend of energy envelope and energy distribution morphologies.Subbursts in FRB signals have characteristic frequencies that drift lower at later times in the total burst envelope. FRB spectra with downward frequency drifting differ from those smooth and wide-band spectra of typical pulsars and radio-emitting magnetars. The dynamical and relativistic model proposed by Rajabi et al. (2020) [53] can explain the downward frequency drifting in multicomponent bursts according to Dicke’s superradiance. According to [53], superradiance occurs in a medium moving at relativistic speeds. This will cause narrow-band processes to be emitted at multiple descending frequencies in FRBs. In this paper, the narrow-band flux regions are regarded as isotropic (or quasi-isotropic) features and will be characterized by wavelets. The anisotropic drifting extensions with diffusing energy will be represented by curvelet.The scattering effect can temporally broaden the FRB signals and induce multi-path propagation, resulting in later arrival times for the signal portions traveling longer path [52]. Scattering tails can be seen in a large proportion of FRB signal profiles. Aggarwal et al. (2021) [54] modeled the components of the FRB spectra as the convolution of a Gaussian function (with a median width of 230 MHz) with a one-sided exponential function. The scattering measure (SM) defines the distribution of free electrons along the line-of-sight, where indicates the strength of the fluctuations along the line-of-sight. The scattering effect reflected in the profiles complicates the signal shapes, but it can be fitted along with the signal portions by the highly directionally sensitive needle-shaped base functions of curvelet on different scales.
4. Mitigation Model for Multichannel Radio Signals
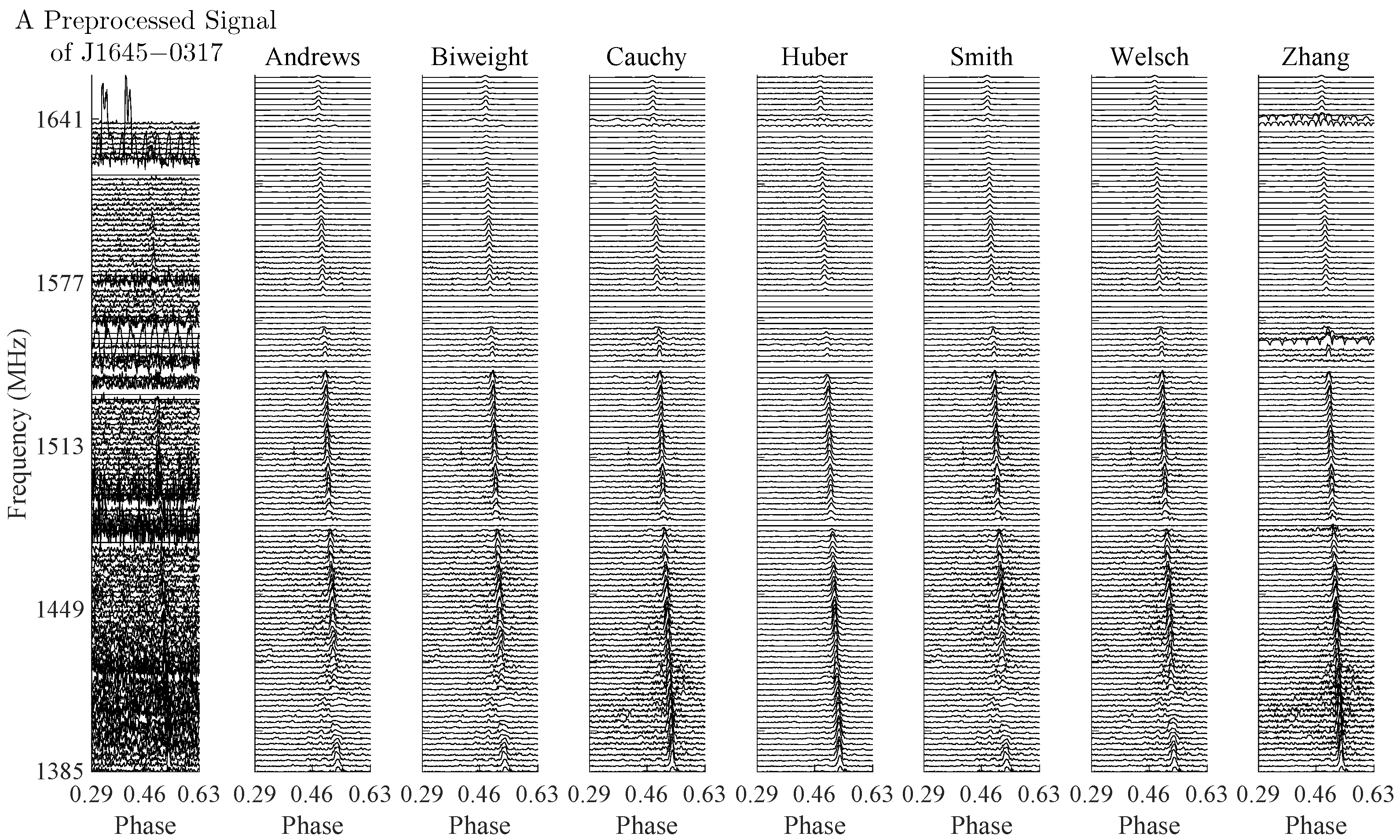
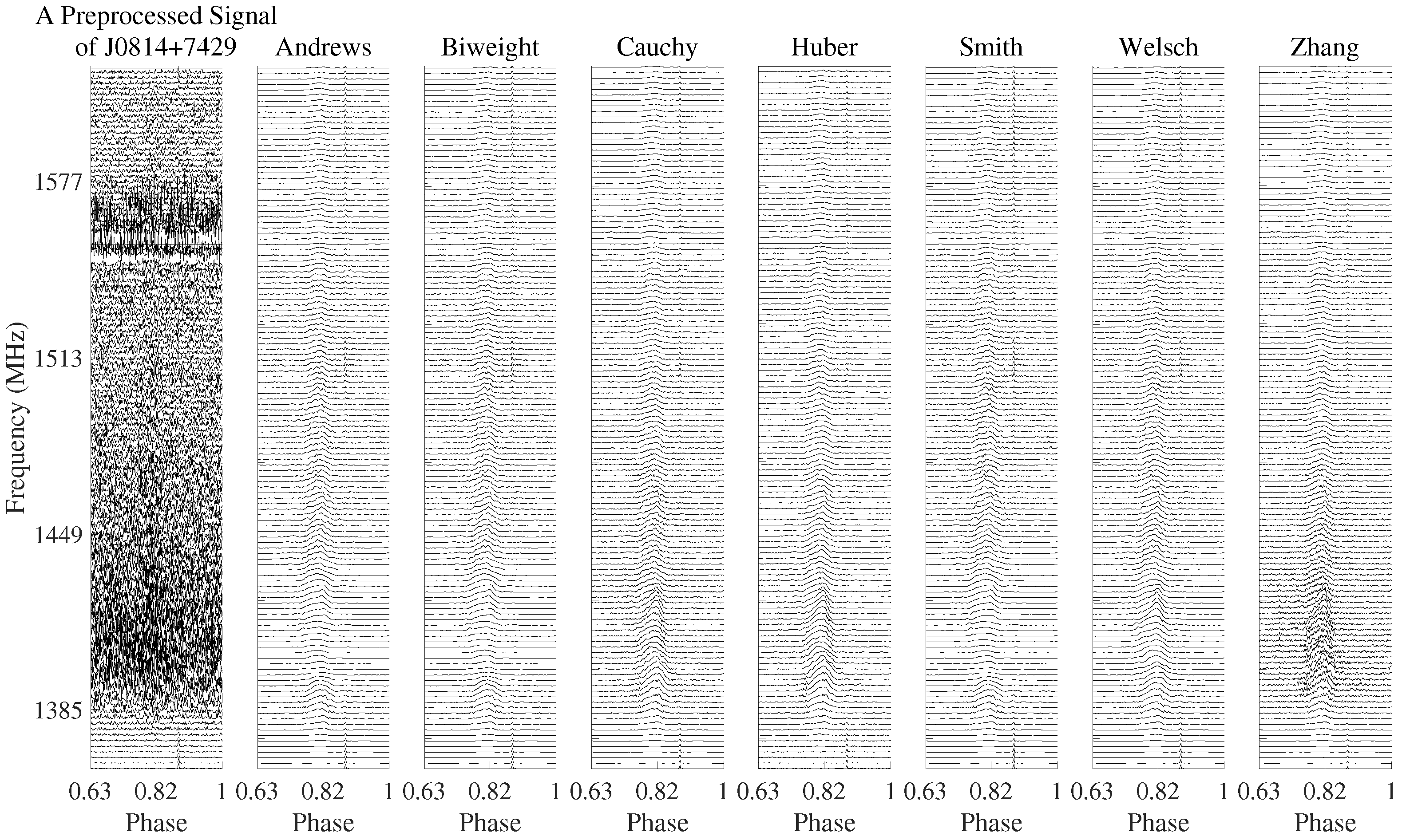
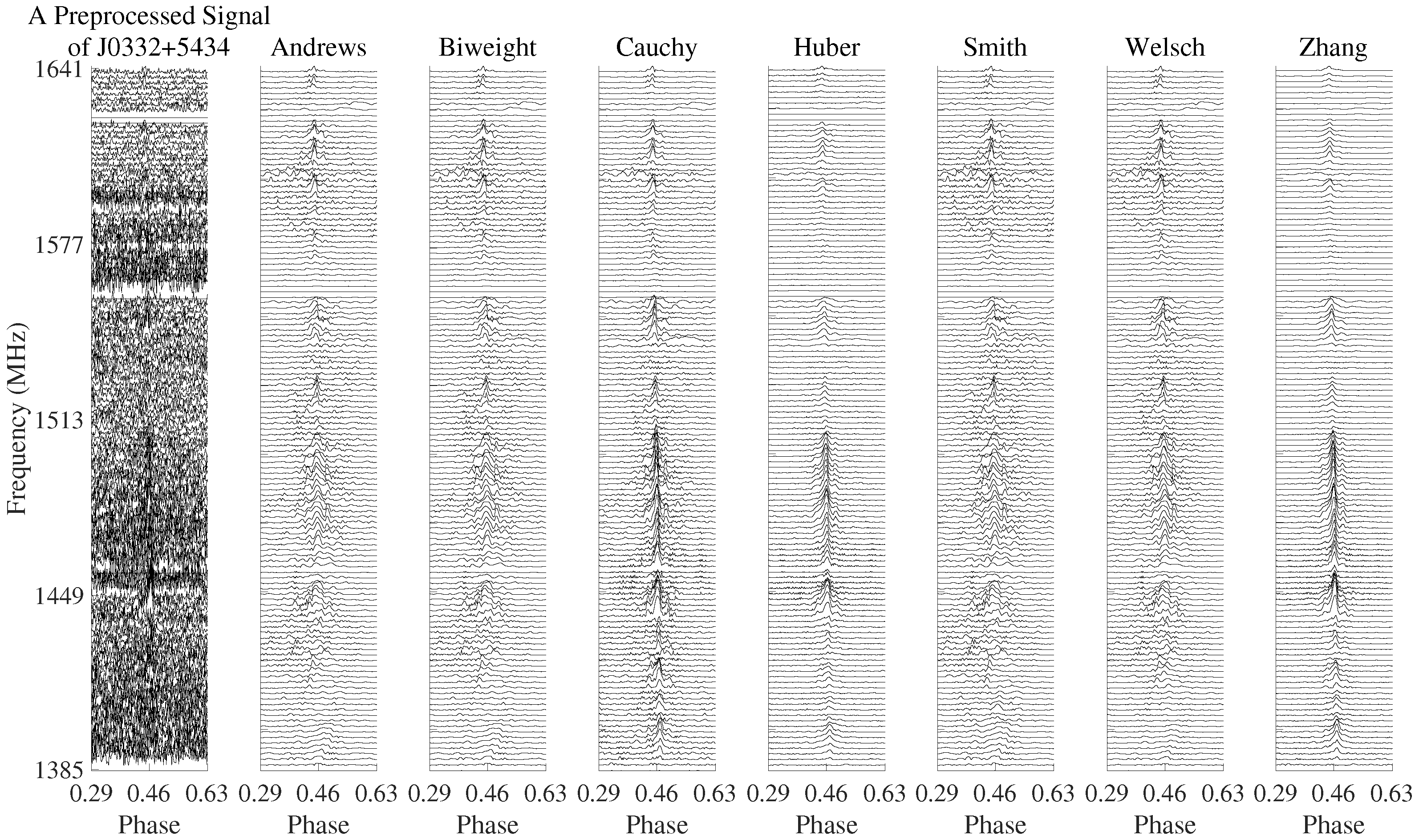
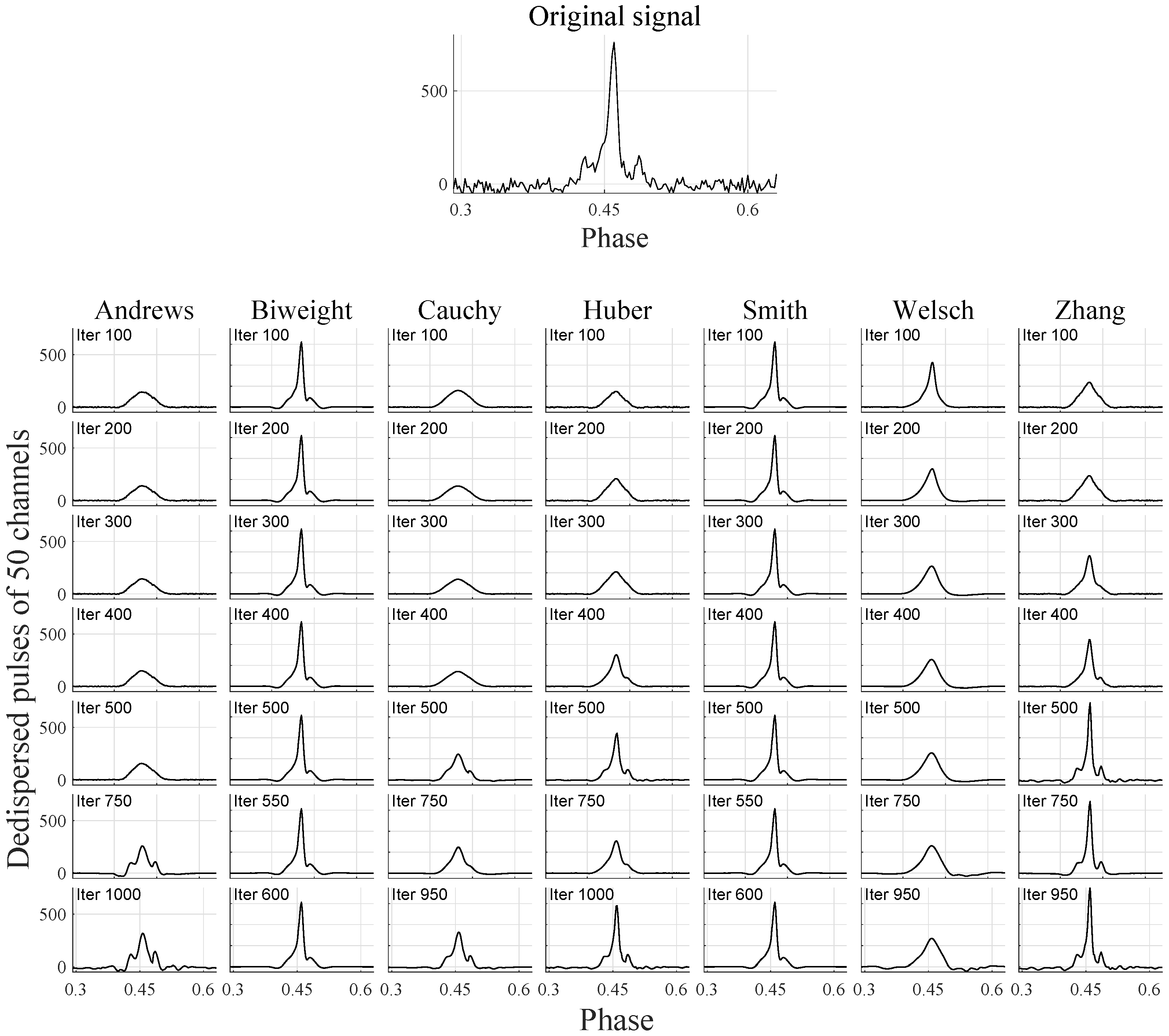
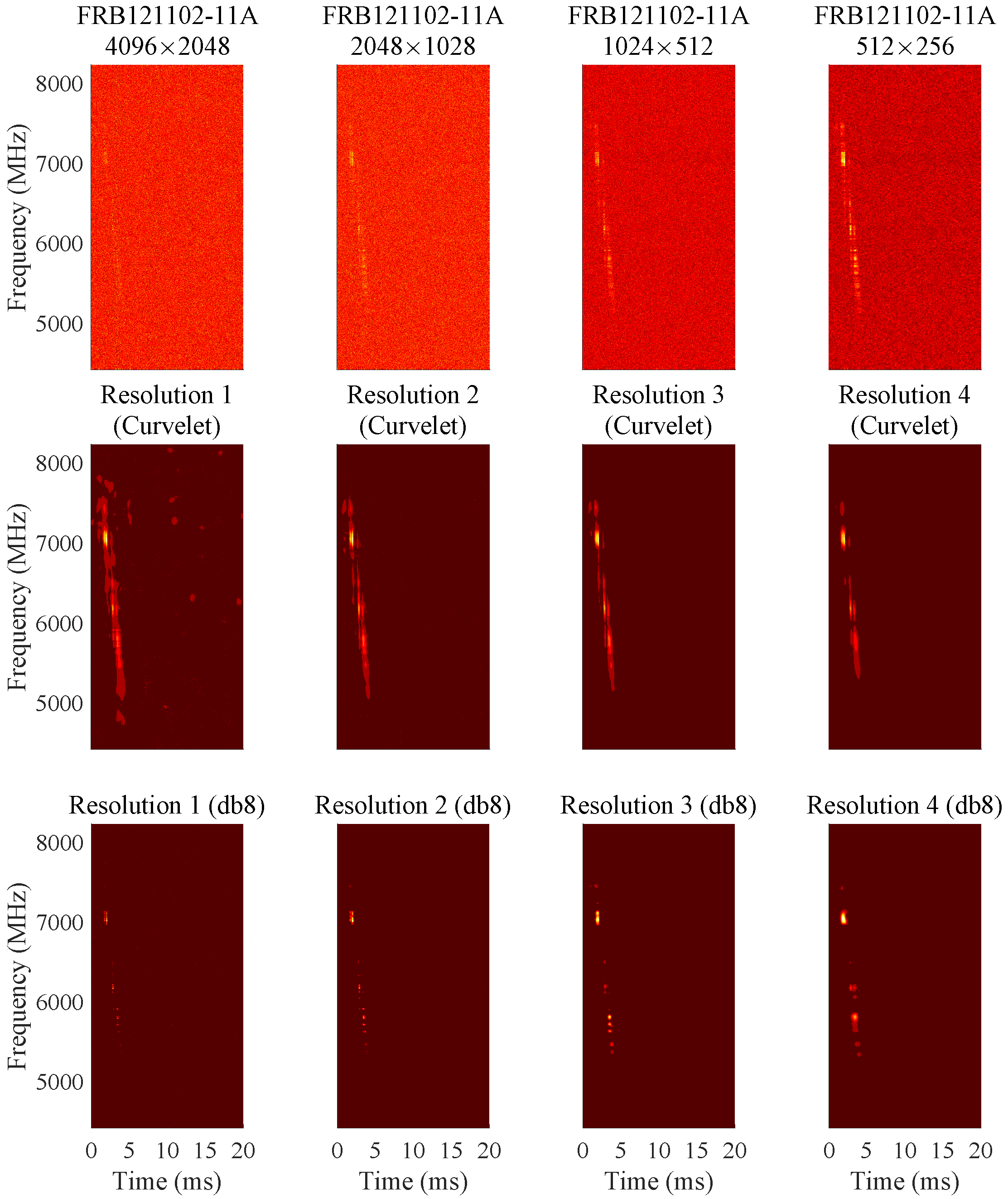
5. Experimental Results
5.1. Pulsar Signals
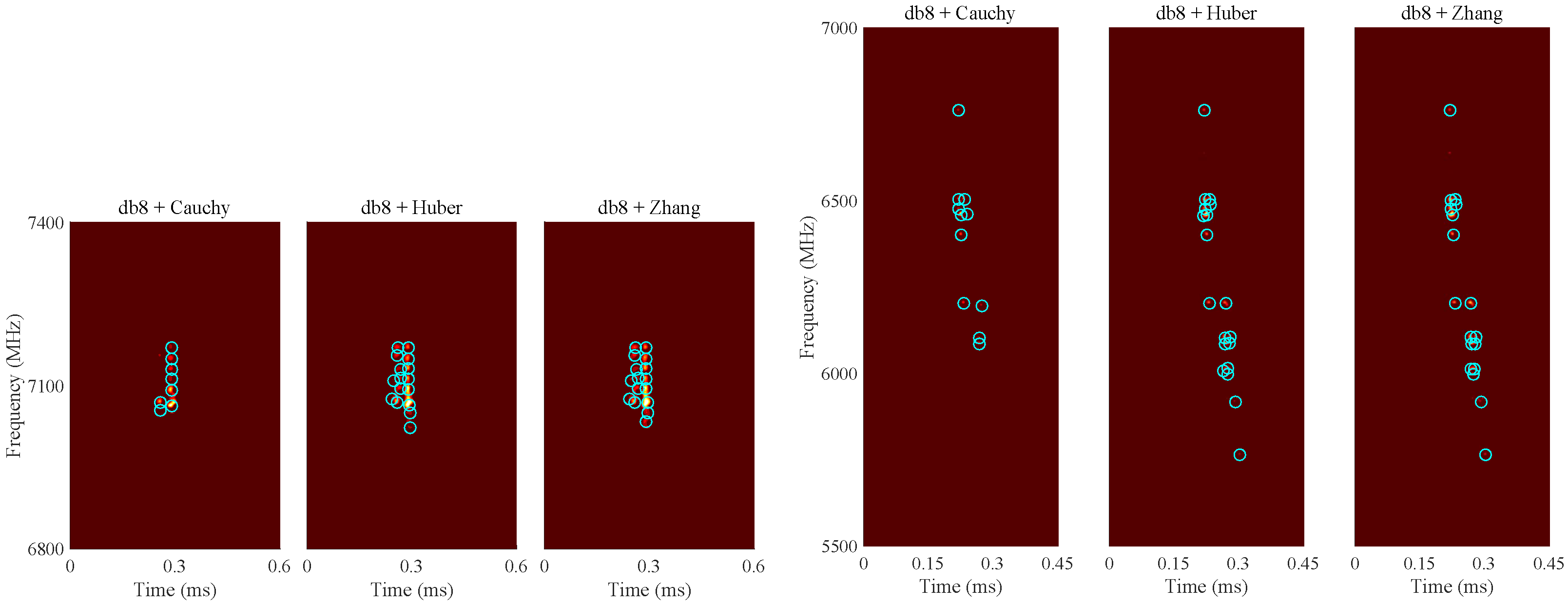
5.2. FRBs
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| 1 | http://seti.berkeley.edu/frb121102/technical.html (accessed 8 April 2022). |
References
- Offringa, A.; de Bruyn, A.; Biehl, M.; Zaroubi, S.; Bernardi, G.; Pandey, V. Postcorrelation radio frequency interference classification methods. Mon. Not. R. Astron. Soc. 2010, 405, 155–167. [Google Scholar]
- Fridman, P.; Baan, W. RFI mitigation methods in radio astronomy. Astron. Astrophys. 2001, 378, 327–344. [Google Scholar] [CrossRef]
- Li, L.; Gaiser, P.W.; Bettenhausen, M.H.; Johnston, W. WindSat Radio-Frequency Interference Signature and Its Identification Over Land and Ocean. IEEE Trans. Geosci. Remote Sens. 2006, 44, 530–539. [Google Scholar] [CrossRef]
- Pen, U.-L.; Chang, T.-C.; Hirata, C.M.; Peterson, J.B.; Roy, J.; Gupta, Y.; Odegova, J.; Sigurdson, K. The GMRT EoR experiment: Limits on polarized sky brightness at 150 MHz. Mon. Not. R. Astron. Soc. 2009, 399, 181–194. [Google Scholar] [CrossRef]
- Kocz, J.; Bailes, M.; Barnes, D.; Burke-Spolaor, S.; Levin, L. Enhanced pulsar and single pulse detection via automated radio frequency interference detection in multipixel feeds. Mon. Not. R. Astron. Soc. 2012, 420, 271–278. [Google Scholar] [CrossRef][Green Version]
- Baan, W.A.; Fridman, P.A.; Millenaar, R.P. Radio Frequency Interference Mitigation at the Westerbork Synthesis Radio Telescope: Algorithms, Test Observations, and System Implementation. Astron. J. 2004, 128, 933–949. [Google Scholar] [CrossRef]
- Nita, G.M.; Gary, D.E.; Liu, Z. Radio Frequency Interference Excision Using Spectral-Domain Statistics. Publ. Astron. Soc. Pac. 2007, 119, 805–827. [Google Scholar] [CrossRef]
- Gary, D.E.; Liu, Z.; Nita, G.M. A Wideband Spectrometer with RFI Detection. Publ. Astron. Soc. Pac. 2010, 122, 560–572. [Google Scholar] [CrossRef]
- Eatough, R.P.; Keane, E.F.; Lyne, A.G. An interference removal technique for radio pulsar searches. Mon. Not. R. Astron. Soc. 2009, 395, 410–415. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Wang, N.; Li, J.; Yuen, R. An interference removal technique for radio pulsar searches. Astrophys. J. 2021, 922, 94. [Google Scholar] [CrossRef]
- Maslakovic, S.; Linscott, I.R.; Oslick, M.; Twicken, J.D. Excising radio frequency interference using the discrete wavelet transform. In Proceedings of the Third International Symposium on Time-Frequency and Time-Scale Analysis (TFTS-96), Paris, France, 18–21 June 1996; pp. 349–352. [Google Scholar]
- Demorest, P.B.; Ferdman, R.D.; Gonzalez, M.E.; Nice, D.; Ransom, S.; Stairs, I.H.; Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.J.; et al. Limits on the Stochastic Gravitational Wave Background from the North American Nanohertz Observatory for Gravitational Waves. Astrophys. J. 2013, 762, 94. [Google Scholar] [CrossRef]
- Shan, H.; Yuan, J.; Wang, N.; Wang, Z. Compressed Sensing Based RFI Mitigation and Restoration for Pulsar Signals. Astrophys. J. 2022, 935, 117. [Google Scholar] [CrossRef]
- Shan, H. Robust RFI Excision for Pulsar Signals by a Novel Nonlinear M-type Estimator with an Application to Pulsar Timing. Astrophys. J. 2023, 952, 70. [Google Scholar] [CrossRef]
- Vos, E.E.; Luus, P.S.F.; Finlay, C.J.; Bassett, B.A. A Generative Machine Learning Approach to RFI Mitigation for Radio Astronomy. In Proceedings of the 2019 IEEE 29th International Workshop on Machine Learning for Signal Processing (MLSP-2019), Pittsburgh, PA, USA, 13–16 October 2019; pp. 1–6. [Google Scholar]
- Collobert, R.; Weston, J. A unified architecture for natural language processing: Deep neural networks with multitask learning. In Proceedings of the 25th International Conference on Machine Learning (ICML-08), Helsinki, Finland, 5–9 July 2008; pp. 160–167. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems (NIPS-12), Lake Tahoe, NV, USA, 3–6 December 2012; Volume 1, pp. 1097–1105. [Google Scholar]
- Akeret, J.; Chang, C.; Lucchi, A.; Refregier, A. Radio frequency interference mitigation using deep convolutional neural networks. Astron. Comput. 2017, 18, 35–39. [Google Scholar] [CrossRef]
- Sun, H.; Deng, H.; Wang, F.; Mei, Y.; Xu, T.; Smirnov, O.; Deng, L.; Wei, S. A Robust RFI Identification For Radio Interferometry based on a Convolutional Neural Network. Mon. Not. R. Astron. Soc. 2022, 512, 2025–2033. [Google Scholar] [CrossRef]
- Hogden, J.; Vander Wiel, S.; Bower, G.C.; Michalak, S.; Siemion, A.; Werthimer, D. Comparison of RFI Mitigation Strategies for Dispersed Pulse Detection. Astrophys. J. 2012, 747, 141. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Estimation of a Location Parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Starck, J.-L.; Fadili, J.; Murtagh, F. The Undecimated Wavelet Decomposition and its Reconstruction. IEEE Trans. Signal Process. 2007, 16, 297–309. [Google Scholar] [CrossRef]
- Starck, J.-L.; Murtagh, F.; Bertero, M. The Starlet Transform in Astronomical Data Processing: Application to Source Detection and Image Deconvolution. In Handbook of Mathematical Methods in Imaging, 1st ed.; Scherzer, O., Ed.; Springer: New York, NY, USA, 2011; pp. 1489–1531. [Google Scholar]
- Starck, J.-L.; Murtagh, F. Astronomical Image and Data Analysis, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006; 360p. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets, 1st ed.; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1992; p. 357. [Google Scholar]
- Vetterli, M.; Kovacevic, J. Wavelets and Subband Coding, 1st ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995; p. 519. [Google Scholar]
- Strang, G.; Nguyen, T.Q. Wavelets and Filter Banks, 2nd ed.; Wellesley-Cambridge Press: Boston, MA, USA, 1996; p. 500. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing, 1st ed.; Academic Press: San Diego, CA, USA, 1997; p. 123. [Google Scholar]
- Mertins, A. Signal Analysis: Wavelet, Filter Banks, Time-Freuency Transforms and Applications, 1st ed.; John Wiley & Sons Inc.: New York, NY, USA, 1999; p. 317. [Google Scholar]
- Vichare, N.S. Robust Mahalanobis Distances in Power System State Estimation. Ph.D. Thesis, Faculty of the Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, January 1993. [Google Scholar]
- de Menezes, D.Q.F.; Prata, D.M.; Secchi, A.R.; Pinto, J.C. A review on robust M-estimators for regression analysis. Comput. Chem. Eng. 2021, 147, 107254. [Google Scholar] [CrossRef]
- Koul, H.; Ossiander, M. Weak convergence of randomly weighted dependent residual empiricals with applications to autoregression. Ann. Stat. 1994, 22, 540–562. [Google Scholar] [CrossRef]
- Mukherjee, K. Generalized R-estimators under conditional heteroscedasticity. J. Econom. 2007, 141, 383–415. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Regression: Asymptotics, Conjectures and Monte Carlo. Ann. Stat. 1973, 1, 799–821. [Google Scholar] [CrossRef]
- Rey, W. Introduction to Robust and Quasi-Robust Statistical Methods, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1983; p. 236. [Google Scholar]
- Zoubir, A.M.; Koivunen, V.; Ollila, E.; Muma, M. Robust Statistics for Signal Processing, 1st ed.; Cambridge University Press: Cambridge, UK, 2018; p. 315. [Google Scholar]
- Hampel, F.R. Contribution to the Theory of Robust Estimation. Ph.D. Thesis, University of California, Berkeley, CA, USA, January 1968. [Google Scholar]
- Hampel, F.R. A general qualitative definition of robustness. Ann. Math. Stat. 1971, 42, 1887–1896. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics, 1st ed.; John Wiley & Sons: New York, NY, USA, 1981; p. 312. [Google Scholar]
- Zhang, Z.; Shao, Z.; Chen, X.; Wang, K.; Qian, J. Quasi-weighted least squares estimator for data reconciliation. Comput. Chem. Eng. 2010, 34, 154–162. [Google Scholar] [CrossRef]
- Holl, P.W.; Welsch, R.E. Robust regression using iteratively reweighted least-squares. Commun. Stat.-Theory Methods 1977, 6, 813–827. [Google Scholar]
- Andrews, D.F.; Bickel, P.J.; Hampel, F.R.; Huber, P.J.; Rogers, W.H.; Tukey, J.W. Robust Estimates of Location: Survey and Advances, 1st ed.; Princeton University Press: Princeton, NJ, USA, 1972; p. 373. [Google Scholar]
- Smith, R.H. True average of observations? Nature 1888, 37, 464. [Google Scholar] [CrossRef][Green Version]
- Mallat, S.; Hwang, W.L. Singularity detection and processing with wavelets. IEEE Trans. Inf. Theory 1992, 38, 617–643. [Google Scholar] [CrossRef]
- Mallat, S.; Zhong, S. Characterization of signals from multiscale edges. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 710–732. [Google Scholar] [CrossRef]
- Labate, D.; Lim, W.-Q.; Kutyniok, G.; Weiss, G. Sparse multidimensional representation using shearlets. In Wavelet Applications in Signal and Image Processing XI; SPIE: San Diego, CA, USA, 2005; Volume 5914, pp. 254–262. [Google Scholar]
- Easley, G.R.; Labate, D.; Lim, W.-Q. Sparse directional image representations using the discrete shearlet transform. Appl. Comput. Harmon. Anal. 2008, 25, 25–46. [Google Scholar] [CrossRef]
- Candès, E.J.; Donoho, D.L. Curvelets—A surprisingly effective nonadaptive representation for objects with edges. In Curves and Surface Fitting: Saint-Malo 1999; Cohen, A., Rabut, C., Schumaker, L., Eds.; Vanderbilt University Press: Nashville, TN, USA, 2000; pp. 105–120. [Google Scholar]
- Starck, J.-L.; Candès, E.J.; Donoho, D.L. The curvelet transform for image denoising. IEEE Trans. Image Process. 2002, 11, 670–684. [Google Scholar] [CrossRef]
- Easley, G.R.; Labate, D.; Colonna, F. Shearlet-Based Total Variation Diffusion for Denoising. IEEE Trans. Image Process. 2009, 18, 260–268. [Google Scholar] [CrossRef]
- Lorimer, D.R.; Kramer, M. Handbook of Pulsar Astronomy; Cambridge University Press: Cambridge, UK, 2005; p. 312. [Google Scholar]
- Petroff, E.; Hessels, J.W.T.; Lorimer, D.R. Fast radio bursts. Astron. Astrophys. Rev. 2019, 27, 75. [Google Scholar] [CrossRef]
- Rajabi, F.; Chamma, M.A.; Wyenberg, C.M.; Mathews, A.; Houde, M. A Simple Relationship for the Spectro-Temporal Structure of Bursts From FRB 121102. Mon. Not. R. Astron. Soc. 2020, 498, 4936–4942. [Google Scholar] [CrossRef]
- Aggarwal, K.; Agarwal, D.; Lewis, E.F.; Anna-Thomas, R.; Tremblay, J.C.; Burke-Spolaor, S.; McLaughlin, M.A.; Lorimer, D.R. Comprehensive Analysis of a Dense Sample of FRB 121102 Bursts. Astrophys. J. 2021, 922, 20. [Google Scholar] [CrossRef]
- Simonoff, J.S. Smoothing Methods in Statistics, 1st ed.; Springer: New York, NY, USA, 1996; p. 340. [Google Scholar]
- Oh, H.-S.; Nychka, D.W.; Lee, T.C.M. The Role of Pseudo Data for Robust Smoothing with Application to Wavelet Regression. Biometrika 2007, 94, 893–904. [Google Scholar] [CrossRef]
- Figueiredo, A.T.M.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- van den Berg, E.; Friedlander, M.P. In Pursuit of a Root; Tech. Rep. TR2007-19; Department of Computer Science, University of British Columbia: Vancouver, BC, Canada, 2007. [Google Scholar]
- Bertsekas, D.P. Projected Newton Methods for Optimization Problems with Simple Constraints. SIAM J. Control Optim. 1982, 20, 221–246. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Spitler, L.G.; Cordes, J.M.; Hessels, J.W.T.; Lorimer, D.R.; McLaughlin, M.A.; Chatterjee, S.; Crawford, F.; Deneva, J.S.; Kaspi, V.M.; Wharton, R.S.; et al. Fast Radio Burst Discovered in the Arecibo Pulsar ALFA Survey. Astrophys. J. 2014, 790, 101. [Google Scholar] [CrossRef]
- Spitler, L.G.; Scholz, P.; Hessels, J.W.T.; Bogdanov, S.; Brazier, A.; Camilo, F.; Chatterjee, S.; Cordes, J.M.; Crawford, F.; Deneva, J.; et al. A Repeating Fast Radio Burst. Nature 2016, 531, 202–205. [Google Scholar] [CrossRef]
- Hessels, J.W.T.; Spitler, L.G.; Seymour, A.D.; Cordes, J.M.; Michilli, D. FRB 121102 Bursts Show Complex Time–Frequency Structure. Astrophys. J. Lett. 2019, 876, L23. [Google Scholar] [CrossRef]
- Shan, H.; Cui, L.; Hong, X.Y.; Liu, X.; Chang, N. Wavelet based tone mapping (TM) enhancement to a detection system for faint and compact sources in HDR and large FOV radio scenes. Astron. Comput. 2023, 42, 100684. [Google Scholar] [CrossRef]




| M-Estimators | Functions | Tuning Parameters |
|---|---|---|
| Huber (monotone) | (x) = | |
| Zhang (monotone) | (x) = | |
| Cauchy (soft-redescending) | ||
| Welsch (soft-redescending) | (x) = | |
| Biweight (hard-redescending) | (x) = | |
| Andrews (hard-redescending) | (x) = | |
| Smith (hard-redescending) | (x) = |
| J1645−0317 | J1136+1551 | J0814+7429 | J0332+5434 | |
|---|---|---|---|---|
| Andrews | 1.73 | 1.63 | 4.40 | 2.11 |
| Biweight | 1.76 | 1.69 | 4.52 | 2.15 |
| Cauchy | 2.60 | 5.41 | 9.15 | 0.94 |
| Huber | 5.40 | 5.17 | 7.83 | 5.75 |
| Smith | 1.33 | 1.27 | 4.07 | 1.75 |
| Welsch | 2.37 | 2.42 | 7.60 | 2.79 |
| Zhang | 0.81 | 2.63 | 7.18 | 4.55 |
| Resolutions (MHz, s) | (0.86875, 10.1) | (1.7375, 20.2) | (3.475, 40.4) | (6.95, 80.8) |
|---|---|---|---|---|
| Signals | −26.5026 | −17.6826 | −6.6232 | −1.9036 |
| Results of curvelet | −8.5827 | 2.2026 | 8.4972 | 11.4321 |
| Results of db8 wavelet | −2.0663 | −0.6488 | −0.1546 | −0.0494 |
| Original | Andrews | Biweight | Cauchy | Huber | Smith | Welsch | Zhang | |
|---|---|---|---|---|---|---|---|---|
| 4096 × 2048 | −29.57 | −14.37 | −14.42 | −2.57 | −8.43 | −14.49 | −14.02 | −5.97 |
| 2048 × 1024 | −23.03 | −6.37 | −7.37 | −2.47 | 2.20 | −8.30 | −5.08 | 2.22 |
| 1024 × 512 | −16.77 | 5.63 | 5.73 | −2.46 | 8.50 | 5.63 | 2.84 | 7.76 |
| 512 × 256 | −11.52 | 8.03 | 8.04 | −2.41 | 11.43 | 8.04 | 8.15 | 11.12 |
| 256 × 128 | −6.93 | 8.25 | 8.22 | −2.48 | 10.03 | 8.19 | 8.21 | 10.02 |
| 128 × 64 | −1.63 | 9.64 | 9.50 | −2.60 | 10.26 | 9.52 | 9.66 | 10.18 |
| Wavelets | bior4.4 | coif5 | db8 | dmey | fk8 | rbio2.8 | sym8 |
|---|---|---|---|---|---|---|---|
| Cauchy | 10, 6 | 10, 10 | 8, 11 | 11, 11 | 8, 12 | 2, 1 | 9, 10 |
| Huber | 14, 12 | 15, 18 | 16, 19 | 15, 18 | 15, 19 | 9, 6 | 14, 17 |
| Zhang | 16, 6 | 16, 18 | 16, 18 | 15, 19 | 15, 20 | 11, 8 | 14, 19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, H.; Jiang, M.; Yuan, J.; Yang, X.; Yan, W.; Wang, Z.; Wang, N. Sparsity and M-Estimators in RFI Mitigation for Typical Radio Astrophysical Signals. Universe 2023, 9, 488. https://doi.org/10.3390/universe9120488
Shan H, Jiang M, Yuan J, Yang X, Yan W, Wang Z, Wang N. Sparsity and M-Estimators in RFI Mitigation for Typical Radio Astrophysical Signals. Universe. 2023; 9(12):488. https://doi.org/10.3390/universe9120488
Chicago/Turabian StyleShan, Hao, Ming Jiang, Jianping Yuan, Xiaofeng Yang, Wenming Yan, Zhen Wang, and Na Wang. 2023. "Sparsity and M-Estimators in RFI Mitigation for Typical Radio Astrophysical Signals" Universe 9, no. 12: 488. https://doi.org/10.3390/universe9120488
APA StyleShan, H., Jiang, M., Yuan, J., Yang, X., Yan, W., Wang, Z., & Wang, N. (2023). Sparsity and M-Estimators in RFI Mitigation for Typical Radio Astrophysical Signals. Universe, 9(12), 488. https://doi.org/10.3390/universe9120488







